22直线的投影(97-03)
第三章直线的投影(完整版)

垂直于一个投影面 ——投影面垂直线
§3-2 特殊位置的直线
V
Z b' a" W b"
一、投影面平行线 水平线的投影
X
a' A a H a'
B
O
b Z b' a" O a β γ b
特性:
1、 a' b' ∥OX
a" a" ∥OY;
Y b"
2、ab=AB;
3、反映β、γ实角。
X
Y1
Y
正平线的投影
b' V Z b" O W a" X a'
a' b' X a b
Z a" b" O Y1 X
a' b' a (b)
Z a" b" O Y 1 Y a' a
Z
X
b' O Y1 b a" ") (b Y 属于OX轴的直线
Y 属于V面的直线
属于V面的铅垂线
属于投影面或投影轴的直线
§3-3一般位置线段的实长及其与投影面的夹角
对于特殊位置直线,其投影可以反映出直线的实长及其与 各投影面的夹角,而一般位置直线的投影不能反映出其实长和 夹角。 工程上常用直角三角形法求一般位置直线的实长和对投影 面的夹角。 β 在直观图中作AC∥ab b' V —Rt Δ 则:ΔABC为 B a' ∠BCA为 —直角 C
a' X O b
c
a
AC :CB=2 :3
b' k' k" a" b"
a'
《机械制图习题集》(第四版)答案

一、点、直线、平面的投影1.1 点的投影∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙第24~24页习题1.2 直线的投影∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙第25~27页习题1.3 平面的投影∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙第28~29页习题1.4 直线与平面、平面与平面相对关系∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙第30~32页习题1234题号:题号:56789101112131415题号:161718192021题号:2223242526272829303132333435363738391.5 换面法∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙第33~35页习题1.6 旋转法∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙第36~36页习题1.7 投影变换综合题∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙第37~37页习题点、直线、平面的投影题号:404142434445464748495051题号:525354555657题号:58596061621. 已知A、B、C三点的直观图,画出它们的投影图,并将各点的坐标值填入表中。
2. 已知A、B、C各点对投影面的距离,画出它们的三面投影图和直观图。
3. 已知点A的坐标(40,15,0),画出其三面投影并作出点B和点C的三面投影。
(a)点B ——在点A右面20mm,前面15mm,上面20mm;(b)点C ——在点A左面10mm,后面15mm,上面15mm。
第二章正投影的基本原理
V a′ α a
b′ B A α
△ Z ZA
29
C O b
H
2016/4/26
机械设计教研室
ZB
2.4.4.2直角三角形法的作图方 法和步骤 用一般位置直线在某一投 影面上的投影作为直角三 角形的底边,用直线的两 端点到该投影面的距离差 为另一直角边,作出一直 角三角形。此直角三角形 的斜边就是空间线段的真 实长度,而斜边与底边的 夹角就是空间线段对该投 影面的倾角。
Z V W V
Z
a′ Z
X
aZ
a′ (x,z)
a″ O X Y
aZ
W (y,z) a″
A
aX
X
O aX aYW YW
X
a
aY Y H
Z
a(x,y)
a YH
YH
8
2016/4/26
机械设计教研室
2.3.2 点的三面投影规律 2.3.2.1点的投影与点的空间位置的关系 A a = a′a x = a″a y (即a″aYW),反映空间点A到H面的距离; A a′ =a a x = a″a z ,反映空间点A到V面的距离; A a″ = a′a z = a a y (即aYH),反映空间点A到W面的距离;
Z b′B a′ X A a b O b″ b′ Z b″ O b a YH
2016/4/26 机械设计教研室
Z b′ a″ YW X a YH
22
b″ a″ YW
V
W
a″ Y a′ X a′ b O
H
2.4.2 直线对于一个投影面的投影特性 空间直线相对于一个投影面的位置有平行、垂直、倾斜三种,三 种位 置有不同的投影特性。 1、真实性:当直线与投影面平行时,则直线的投影为实长。 2、积聚性:当直线与投影面垂直时,则直线的投影积聚为一点。 3、收缩性:当直线与投影面倾斜时,则直线的投影小于直线的实长。
完整版直线的投影
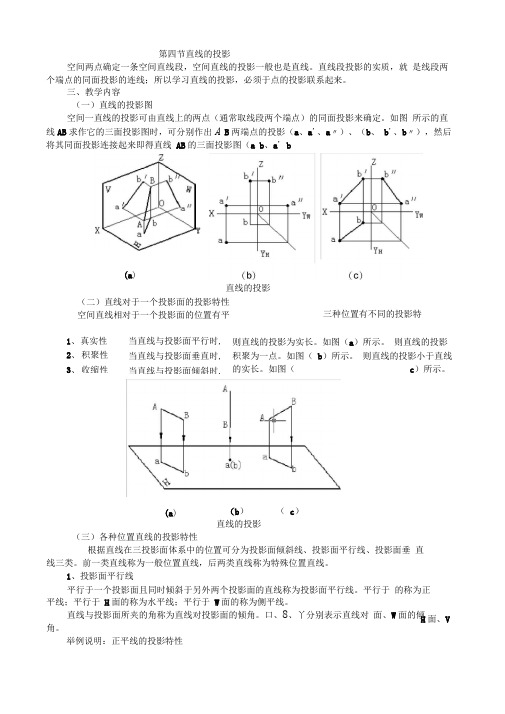
第四节直线的投影空间两点确定一条空间直线段,空间直线的投影一般也是直线。
直线段投影的实质,就 是线段两个端点的同面投影的连线;所以学习直线的投影,必须于点的投影联系起来。
三、教学内容(一)直线的投影图空间一直线的投影可由直线上的两点(通常取线段两个端点)的同面投影来确定。
如图 所示的直线AB 求作它的三面投影图时,可分别作出A B 两端点的投影(a 、a '、a 〃)、(b 、 b '、b 〃),然后将其同面投影连接起来即得直线 AB 的三面投影图(a b 、a ' b(a )直线的投影(二)直线对于一个投影面的投影特性 空间直线相对于一个投影面的位置有平三种位置有不同的投影特1、 真实性2、 积聚性3、 收缩性当直线与投影面平行时, 当直线与投影面垂直时, 当直线与投影面倾斜时, 则直线的投影为实长。
如图(a )所示。
则直线的投影积聚为一点。
如图( b )所示。
则直线的投影小于直线的实长。
如图(c )所示。
(b )( c )直线的投影(三)各种位置直线的投影特性根据直线在三投影面体系中的位置可分为投影面倾斜线、投影面平行线、投影面垂 直线三类。
前一类直线称为一般位置直线,后两类直线称为特殊位置直线。
1、投影面平行线 平行于一个投影面且同时倾斜于另外两个投影面的直线称为投影面平行线。
平行于 的称为正平线;平行于 H 面的称为水平线;平行于 W 面的称为侧平线。
直线与投影面所夹的角称为直线对投影面的倾角。
口、8、丫分别表示直线对 面、W 面的倾角。
举例说明:正平线的投影特性H 面、V Y(a )V作正垂线AB强调:(1)斜线反映实长;(2)直线的倾角a 、Y 。
总结投影面平行线的投影特性:两平一斜。
要求学生必须掌握表中的图例。
对于投影面平行线的辨认:当直线的投影有两个平行于投影轴, 第三投影与投影轴倾斜时,则该直线一定是投影面平行线,且一定平 行于其投影为倾斜线的那个投影面。
《建筑识图与构造》教学课件 第2章 投影的基本知识

平面的投影-平面内的点和直线
根据平面内点和直线的判 定,可以解决下面三类问题。
① 判别已知点、直线是否 属于已知平面。 ② 完成已知平面上的 点和直线的投影。 ③ 完成多边形的投影。
点在平面内的几何 条件:若点属于一直线, 直线属于一平面,则该 点必属于该平面
直线在平面内的几何条 件:若一直线通过平面 上的两点,或通过平面 内的一点,并且平行于 平面上的另一直线,则 此直线必在该平面内。
直线上的点-点在线上
点在直线上,则点的各个投影必在该直线的同面投影上,且点分直线 的两线段长度之比等于其投影长度之比;反之亦然,此即为定比关系。
两直线的相对位置-平行
空间两直线的相对位置有平行、相交和交叉三种。
(a)立体图
(b)投影图
两直线的相对位置-相交
其同面投影必相交,且交点的投影符合点的投影规律,如图所示。
点的投影-两点相对位置的识读
➢ 通过方位的判断,可以确定出两点在空间的相对位置。此外,由于 X轴、Y轴、Z轴的正方向表示空间点左、前、上方,因此也可直接 根据空间点的坐标来确定两点的相对位置。
空间点的六个方位
直线的投影
➢ 作直线投影图时,只需作出直线上任意两点的投影,并连接 该两点在同一投影面上的投影即可,如图所示
三面投影体系
三面投影图-三面投影图的形成与展开
➢ 将物体置于三面投影体系中,并使其主要表面与投影面 平行或垂直,然后按正投影法分别向V面、H面和W面进 行投影,即可得到该物体的三面投影,如图所示。
三面投影图-三面投影图的对应关系
三面投影图的投影对应关系
➢ 如图所示,三面投影图不仅反映了物体的长、宽、高,同时也 反映了物体的上、下、左、右、前、后六个方向的位置关系。
点与直线的投影

工程制图
投影基础:点和直线的投影
两点的相对位置
两点的相对位置指两点 在空间的上下、前后、左右 位置关系。
判断方法:两点间的相对位置可通 过它们的坐标差来确定。
◆x坐标大的在左
◆y坐标大的在前
◆z坐标大的在上 B点在A点之左、之前、之下。
工程制图
投影基础:点和直线的投影
无轴投影图
不画投影轴的投影图,称为无 轴投影图。 无轴投影图 是根据相对坐标 来绘制的,其投 影图仍符合点的 投影规律。
工程制图
投影基础:点和直线的投影
本节内容:
一、点的投影 点的投影规律 两点的相对位置和重影点 二、直线的投影 各种位置直线的投影特性 直线上点的投影 两直线的相对位置
工程制图
投影基础:点和直线的投影
一、点的投影 直角坐标系下的点 :点A(x,y,z)
Z A X O X
●
Z a (x,z)
两点的相对位置
两点的相对位置是根据两点相对于 投影面的距离远近(或坐标大小)来确 定的。X坐标值大的点在左;Y坐标值大 的点在前;Z坐标值大的点在上。 根据一个点相对于另一点上下、左 右、前后坐标差,可以确定该点的空间 位置并作出其三面投影。
工程制图
投影基础:点和直线的投影
例5:已知点B的投影和点A 的两个投影,
工程制图
投影基础:点和直线的投影
a ●
● ●
二、直线的投影
两点确定一条直线,将两 点的同面投影用直线连接,就 得到直线在该投影面上的投影 一、直线的投影特性
直线对一个投影面的投影特性
A
●
a
●
b
b
a● b
●
●
四川省建筑面积计算规则97-03
第四章建筑面积计算规则4.1 计算建筑面积的条件能够计算建筑面积的房屋一般应具备以下普遍性的条件:1)应具有永久性上盖。
2)应有围护结构。
3)结构牢固,属永久性的建筑物。
4)层高在2.20米以上(含2.20米,以下同)。
5)可作为人们生产或生活的场所。
4.2 计算全部建筑面积的范围4.2.1永久性结构的单层房屋,按一层计算建筑面积;多层房屋按各层建筑面积的总和计算建筑面积。
4.2.2房屋内的夹层、插层、技术层、结构转换层及其梯间、电梯间等高度在2.20米以上部位计算建筑面积。
4.2.3穿过房屋的通道,房屋内的门厅、大厅,均按一层计算建筑面积。
门厅、大厅内的回廊部分,层高在2.20米以上的,按其水平投影计算建筑面积。
4.2.4室内楼梯、楼梯间、电梯(含观光梯)井、提物井、垃圾道、管道井、通风井、排气井等均按房屋自然层计算建筑面积。
4.2.5房屋天面上,属永久性建筑,层高在2.20米以上的楼梯间、水箱间、电梯机房、设备用房及其附属用房、斜面结构屋顶高度在2.20米以上的部位以及经主管部门批准的有明确使用功能的非装饰性建筑空间,按其外围水平投影计算建筑面积。
4.2.6挑楼、封闭的挑廊、封闭的阳台按其外围水平投影计算建筑面积。
4.2.7属永久性结构有上盖的室外楼梯,按各层水平投影计算建筑面积。
4.2.8与房屋相连的有柱走廊(剪力墙视为有柱),两房屋间有上盖和非单排柱的走廊,均按其柱的外围水平投影计算建筑面积。
4.2.9房屋间永久性的封闭的架空通廊,按外围水平投影计算建筑面积。
4.2.10地下室、半地下室及其相应出入口,层高在2.20米以上的,按其外墙(不包括采光井、防潮层及保护墙)外围水平投影计算建筑面积。
4.2.11与房屋相连属永久性的且有非独立柱或有围护结构的门廊、门斗按其柱或围护结构的外围水平投影计算建筑面积。
有柱又有围护结构的门斗按围护结构的外围水平投影计算建筑面积。
4.2.12玻璃幕墙、金属幕墙以及其它材料幕墙等作为房屋外墙的,按其外围水平投影计算建筑面积。
第2章 投影理论2(直角投影定律、平面、平面的倾角)
一 线 两 面
正垂面
(V)
侧垂面 (W)
2、平面上的直线和点
P54~55
点在平面上的条件: 如果点在平面上的某一直线上,则 此点必在该平面上 。
直线在平面上的条件: 1、通过平面上的两个点。
2、通过平面上的一个点, 且平行于平面上的一条直线 。
[例1]已知三棱锥SAB面上一点K的V投影k′, 试求其H投影k 。
b
H
AB
ab
ΔZ
作图步骤:
V
AB
ΔZ
b
AB
ΔZ
b
B
ΔZ
ab a
X
ΔZ
ab
a X
A a
O C b H a
b
AB
ΔZ
求直线的实长及对正面投影面的夹角 角。
方法一
ห้องสมุดไป่ตู้AB
ΔY
AB
ab ΔY
b
a b
X
ab ΔY a
AB
方法二
已知直线AB的β=30º ,试求其另一投影。
2)连接b、d,bd交ac于e;
X
a e b
c′
d
3)由e在a′c′上求出e′;
4)连接b′e′, 在b′e′上求出d′; 5)分别连接a′d′及
c′d′,即为所求。 c
3、平面上的特殊位置直线
平面上的投影面平行线
P55
平面上的投影面平行线,有平面上的水平 线、正平线和侧平线三种
平面上的投影面平行线: 正平线AE, 水平线CD。
2) 当直线的两个 投影都相交,且其 中一直线平行于第 三个投影面时,一 般应观察投影面平 行线所平行的那个 投影面上的投影, 或按线上点的等比 关系,来判断两直 线是否相交。
直线的投影
AE︰EB=ae︰eb=a′e′︰e′b′
➢ 当直线为一般位置直线或投影面垂直线时,判断点是否在直 线上,通过两面投影即可
➢ 当直线为投影面平行线时,应根据投影情况通过两面或三面 投影或定比性才能判断
1.ab ⊥OX a″b″⊥OZ
2.ab =a″b″=AB 3.a ′b′积聚成一点
1.a′b′⊥OZ ab ⊥OYH
2.ab =a′b′=AB 3.a″b″积聚成一点
课堂练习
1.当直线与投影面平行时,该投影面上的投影具有( ) A.积聚性 B.真实性 C.类似性 D.收缩性
2.当直线与投影面垂直时,该投影面上的投影具有( ) A.积聚性 B.真实性 C.类似性 D.收缩性
在《房屋建筑制图统一标准》中 规定,图线的宽度b宜从下列线宽 中选取:1.4,1.0,0.7,0.5, 0.35,0.25,0.18,0.13 mm。 每个图样应根据图样复杂程度与 比例大小先确定基本线宽b,再选 用表1-6中的相应线宽组。对于图 纸的图框线、标题栏外框线和标 题栏分格线,可采用表1-7所示的 线宽。
项目四
直线的投影
目录 CONTENTS
01 任务一 一般位置直线 02 任务二 特殊位置直线 03 任务三 直线上的点 04 任务四 两直线的相对位置
项目四
直线的投影
技术目标
能够根据直线的三面投影判 断直线的类型
能够判断两直线的相对位置
04
01
知识目标
了解直线的类型
第3页
教学 目标
02
知识目标
掌握一般位置直线、投影 面平行线、投影面垂直线 的投影特性
土木工程制图习题答案
β
β
Δy
Δy
Δz
Δz
α
α
班级
姓名
学号
β Δy
Δz α
已知直线AB=50,求其正面投影a'b'和倾角 γ 。 γ
已知直线AB与V面的倾角 β =50°,求其水平投影a b 。
β =30° Δy
Δx
6
2-16 判定点K是否在直线AB上。
班级
姓名
学号
2-17 在直线AB上找一点K,使AK:KB=3:2。
n'
(m')
m n
(m') n'
(m) n
(3). (n')
m'
n (m)
k'
c'
a' b
QV
a
PH
c
2-37 已知正方形ABCD为正垂面,其对角线为AC,完成该正方形的投影图。
c'
屣
b'(d')
層
屢
a' 屡
d
k
a
c
a
c
b
2-38 已知直线AB为△ABC的最大坡度线,完成该三角形的投影图。 a'
班级
姓名
学号
2-39 求由两条平行线AB、CD所确定的平面与H面的倾角。
b'
2-23 已知矩形ABCD的顶点D在EF上,完成该矩形的两面投影。
8
试求两条直线AB、CD之间的距离。
已知正方形ABCD的对角线位于侧平线EF上,试完成该正 方形的正面、侧面投影。
判断下列平面与投影面的相对位置及其与投影面的倾角。
水平面 0° 90° 90°
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
29
一、各种位置直线的投影特性
⒈ 一般位置直线
三个投影与各投影轴都倾斜。
⒉ 投影面平行线
在其平行的投影面上的投影反映线段实长 及与相应投影面的夹角。另两个投影平行于相 应的投影轴。
⒊ 投影面垂直线
在其垂直的投影面上的投影积聚为一点。 另两个投影反映实长且垂直于相应的投影轴。
30
二、直线上的点 ⒈ 点的投影在直线的同名投影上。 ⒉ 点分线段成定比,点的投影必分线段的投影 成定比——定比定理。 三、两直线的相对位置 ⒈ 平行 同名投影互相平行。 ⒉ 相交 同名投影相交,交点是两直线的共有点, 且符合空间一个点的投影规பைடு நூலகம்。 ⒊ 交叉(异面) 同名投影可能相交,但“交点”不符合空 间一个点的投影规律。“交点”是两直线上一 对重影点的投影。 31
直角边BC//H面 BC⊥AB, 同时BC⊥Bb BC⊥ABba平面 BC∥bc bc ⊥ABba平面 bc⊥ab ∠abc为直角
直线在H面上的 投影互相垂直
25
b c
a
例1、过C点作直线与AB垂直相交。
a
.
d
AB为正平线, 正 面投影反映直角。
b
c
c
●
●
a
d
b
26
例2、已知直线AB的两面投影和C点的水平投影,试 过C点作一条直线CE垂直于AB,求直线CE的两面 a' e' 投影。
13
例3、已知点C 在线段AB上,求点C 的正面投影。
V b b c X O a b c b a
14
cb ac
c
a X B C
A
a
c
H
二、两直线的相对位置
平行
相交
交叉
垂直相交
15
空间两直线的相对位置分为: 平行、相交、交叉。 投影特性: ⒈ 两直线平行
b
a A a b B c C c d H D d V
① 在其垂直的投影面上,投影有积聚性。 ② 另外两个投影,反映线段实长。且垂直 于相应的投影轴。
6
3、 一般位置直线
7
b a a b a
b
投影特性:
三个投影都缩短。 即: 都不反映空间线段 的实长及与三个投影面 夹角的实大,且与三根 投影轴都倾斜。
8
2.4 直线与点及两直线的相对位置
一、直线与点的相对位置
21
例1、判断两直线的相对位置
c 1 b
a
X a
d d 1
c
1d 1c
b
22
判断两直线重影点的可见性
c
b 1 (3)4 2 d C B 判断重影点的可 见性时,需要看重影 点在另一投影面上的 投影,坐标值大的点 投影可见,反之不可 见,不可见点的投影 加括号表示。 O A c a 1(2) 3 4 d
投 影 特 性: ① 在其平行的那个投影面上的投影反映实长, 并反映直线与另两投影面倾角的实大。 ② 另两个投影面上的投影平行于相应的投影 轴。
4
2、 投影面垂直线
正垂线
铅垂线
侧垂线
5
铅垂线
a b
●
正垂线
c(d)
●
侧垂线
e f e(f)
●
a
d c
b
d c e f
a(b)
投影特性:
A a c b c
O
11
例1、判断点C是否在线段AB上。
① a b
c b ②
a
c
●
b c a c b
a
点C在直 线AB上
点C不在 直线AB上
12
例2、判断点K是否在线段AB上。
a k● b
a k● b a
●
k
b
因k不在a b上, 故点K不在AB上。
另一判断法?
应用定比定理
a≡b≡m
●
●
b
b
a●
a●
直线垂直于投影面 投影重合为一点 积 聚 性
直线平行于投影面 投影反映线段实长 ab=AB
直线倾斜于投影面 投影比空间线段短 ab=ABcosα
1
二、 直线在三个投影面中的投影特性
正平线(平行于V面)
投影面平行线 侧平线(平行于W面) 平行于某一投影面而
水平线(平行于H面) 统称特殊位置直线 与其余两投影面倾斜
2.3 直线的投影
两点确定一条直线,将两点 b 的同名投影用直线连接,就得 到直线的同名投影。 直线投影的基本特性 a 一、直线的投影特性
●
●
a ●
●
a
●
b
一般情况下, 直线对一个投影面的投影特性
A
●
b 直线的投影
●
仍然为直线,特殊情况为一 α M A A B个点。
B ●
● ● ● ●
●
B
●
1 从属性 若点在直线上,则点的各个投影必在直线的各同面 投影上。利用这一特性可以在直线上找点,或判断已知点是否在 直线上。 2 定比性 属于线段上的点分割线段之比等于其投影之比。即 A C: C B = a c : c b= ac : cb = ac : c b
b
c B
C
X
a
投影面垂直线
正垂线(垂直于V面) 侧垂线(垂直于W面) 铅垂线(垂直于H面)
垂直于某一投影面
一般位置直线
与三个投影面都倾斜的直线
2
1、投影面平行线
正平线
水平线
侧平线
3
水平线
a a b
a b
实长 a
b
α γ
正平线
a b
a b a
侧平线
β
a 实长
α
b
β
γ
b
b
a
b
实长
与H面的夹角:α 与V面的角:β 与W面的夹角: γ
c'
e'
X c'
b'
O
a
e e
b
27
c
两直线交叉
例3、过点E 作线段AB、CD 的公垂线EF。
b e f
c X e
b
a
d O
a d
f
c
28
小 结
重点掌握:
★点与直线的投影特性,尤其是特殊位置 直线的投影特性。 ★点与直线及两直线的相对位置的判断方 法及投影特性。 ★定比定理。 ★直角定理,即两直线垂直时的投影特性。
四、相互垂直的两直线的投影特性 ⒈ 两直线同时平行于某一投影面时,在该 投影面上的投影反映直角。
⒉ 两直线中有一条平行于某一投影面时, 在该投影面上的投影反映直角。
⒊ 两直线均为一般位置直线时, 在三个投影面上的投影都不 反映直角。
直角定理
32
19
例:过C点作水平线CD与AB相交。
b
c● a k d
a c k
●
d b
先作正面投影
20
⒊ 两直线交叉
d
a
c’
1(2) 3 4
●
为什么? 投影特性: 两直线相交吗?
b
●
●
c
●
2
●
b d
a
1 3(4 )
●
Ⅰ、Ⅱ是V面的重影点, Ⅲ、Ⅳ是H面的重影点。
★ 同名投影可能相交, 但 “交点”不符合空间 一个点的投影规律。 ★ “交点”是两直线上 的一 对重影点的投影, 用其可帮助判断两直线 的空间位置。
9
点在直线上的判别方法:
◆ 若点在直线上, 则 点的投影必在直线的同 名投影上。并将线段的 同名投影分割成与空间 相同的比例。即: ◆若点的投影有一个不 在直线的同名投影上, 则 该点必不在此直线上。
V c a
C A
b
B
b
AC/CB=ac/cb= ac / cb
a
c
H
定比定理
10
直线上的点具有两个特性:
对于特殊位置直线, 只有两个同名投影互相 平行,空间直线不一定 平行。 求出侧面投影后可知: AB与CD不平行。
求出侧面投影
18
⒉ 两直线相交
V a A a c
c k
C
b d K D d k
交点是两直 线的共有点
b B a c
k
d
b
H
a
c k
d b
判别方法:
若空间两直线相交,则其同名投影必 相交,且交点的投影必符合空间一点的投 影规律。
空间两直线平 行,则其各同名投 影必相互平行,反 之亦然。
16
例1:判断图中两条直线是否平行。
①
a
b d c c b d
a
对于一般位置直 线,只要有两个同名 投影互相平行,空间 两直线就平行。
AB//CD
17
例2:判断图中两条直线是否平行。
②
c c
a
d
a b d
b c
b d a 如何判断?
23
a
1 3
2 4 D
X
b
例2、判断两直线重影点的可见性
c b 1 3(4)
2
a X
d
b 4 c a 1(2)
3
d
24
4、两直线垂直相交(或垂直交叉)
直角的投影特性:
若直角有一边平行于投影面,则它在该投影面 上的投影仍为直角。 证明:
B C A b a
c H b
c
a
.
设 因 所以 又因 故 因此 即
