二向应力状态下的应力分析(应力圆)
合集下载
应力圆
•
• •
• •
点面对应--应力圆上某一点的坐标值对应着微元某一方 向面上的正应力和切应力； 转向对应--半径旋转方向与方向面法线旋转方向一致； 二倍角对应--半径转过的角度是方向面法线旋转角度的 两倍。 有这三个对应关系，画应力圆和从应力圆得到一些重要 关系就比较方便。 首先是点面对应。如图是一个平面应力状态，建立图示 坐标系，图中的应力圆圆周上a点对应于微元的一个方向 面A，A面上的正应力和切应力就对应着应力圆上a点的坐 标。
应力圆
• 数字转换是很麻烦的，但若是把数学公式 加以简单的变换，可以发现任意方向面上 的应力所满足的方程可以转换为一个圆的 方程，这个圆就叫做应力圆。
பைடு நூலகம்
• • • •
应力圆方程 几种对应关系 应力圆的画法 应力圆的应用
•
利用三角恒等式，可以将前面所得的关于和的方程写成：
•
利用三角恒等式进行转换，于是写成如图上面的两个方程，再经过简单的 数学转换，就得到图中最下的方程。 • 应力圆的圆心坐标是（σx +σy）/2，半径为R，因此应力圆就是如图所示 的圆。
•
通过求圆心坐标和半径 的画法比较复杂，所以利 用上面的三种对应关系来 画。首先建立坐标系， 在 坐标系中，标定与微元垂 直的A、D面上应力对应的 点a和d，连d交轴于c点， c即为圆心，cd或ca为应 力圆半径。
例题
应力状态概述二向和三向应力状态的实例二向
2．作应力圆 主应力为 1 , 3 ，并可 确定主平面的法线。
材料力学
第七章
应力和应变分析
3．分析 纯剪切应力状态的两个主应力绝对值相等， 但一为拉应力，另一为压应力。由于铸铁抗拉强度较 低，圆截面铸铁构件扭转时构件将沿倾角为 45º 的螺旋面因拉伸而发生断裂破坏。
材料力学
第七章
2 2
x y
xy
n
材料力学
y a xy
y On D( x , ) a a
a
第七章
n
应力和应变分析
二、应力圆的画法
建立应力坐标系，如下图所 示，（注意选好比例尺） 在坐标系内画出点A( x， xy)和B(y，yx)
x
C O
2a
AB与a 轴的交点C便是圆 A( x , xy) 心。
150°
第七章
应力和应变分析
x y 2 2 1 x y （ ） xy 2 2 2
解法2—解析法：分析——建立坐标系如图
95
60°
y 45MP a yx 25 3MP a xy
25 3
x ?
y O x
60 95MPa 60 25 3MPa
材料力学
第七章
应力和应变分析
应力表示——单元体：
①dx、dy、dz（微小的正六面体） ②单元体某斜截面上的应力就代表了构件内 对应点同方位截面上的应力。
B P
dz
dx
dy
A
C
பைடு நூலகம்
B
D
C
B、C——单向受力，τ ＝0 A——纯剪切， σ ＝0
D
D——既有 σ ，又有τ
应力圆概念
σ1
例题7-1 从水坝体内某点处取出的单元体如图所示, sx= - 1MPa , sy= - 0.4MPa , tx= - 0.2MPa , ty= 0.2MPa , （1）绘出相应的应力圆 （2）确定此单元体在 a =30°和a = - 40°两斜面上的应力。
σy τy
σ x = -1
σx τx
C
D1 (-1,-0.2)
B2
s
(2) 确定 a = 30°斜截面上的应力 将 半径 CD1 逆时针转动 2a = 60°到半径 CE, E 点的坐标就
代表 a = 30°斜截面上的应力。
(-0.4,0.2) t D2 B1 C o
B2
D1 (-1,0.2)
s
σ 30 = -0.68 MPa
0
60
C
D1 (-1,0.2)
B2
σ -40 = -0.95 MPa
0
τ -40 = 0.26 MPa
0
σ 30 = -0.68 MPa
0
τ 30 = -0.36 MPa
0
σ -40 = -0.95 MPa
0
τ -40 = 0.26 MPa
0
y
α =30
0
x
α = 400
例题 7-2 两端简支的焊接工字钢梁及其荷载如图 a , b 所示,
0
τ 30
E
τ 30 = -0.36 MPa
0
0
σ 30
0
(3) 确定 a = - 40°斜截面上的应力 将 半径 CD1 顺时针转 2a = 80°到半径 CF, F 点的坐标就 代表a = - 40°斜截面上的应力。 F
σ -40
-80
二向应力状态分析—图解法
§7–4 二向应力状态分析—图解法
x
2
y
x
2
y
cos 2
x
sin
2
x
2
y
sin
2
x
cos 2
1、 莫尔圆的概念
(
x
y 2
)2
2
(x
y )2 2
2 x
(
x
y 2
)2
2
(x
y 2
)2
2x
当斜截面随方位角 变化时, 其上的应力 ， 在 - 直角坐标系内的轨迹是一个圆 。
圆心的坐标为(the coordinates of MOHR circle’s center)
y
xm
900
t
450
k
D
y
xm
900
t
450
k
D
y
3
τ max
x
τ max
k
450
1
解: 从圆筒表面 k 点处取出单元体, 其各面上的应力分量如图 所示
可求得
y 1 max 80MPa
x 3 max 80MPa
z 0
k点处的线应变 x , y 为
y
x
1 E
(x
y )
1 E
(max
z
x
二、纯剪的本构关系
xy
xy
G
i 0 ( i x,y,z ) yz zx 0
y
xy
z
x
三、复杂状态下的本构关系
y
依叠加原理,得
y
z
z
x
xy
x
x
x
E
y
E
x
2
y
x
2
y
cos 2
x
sin
2
x
2
y
sin
2
x
cos 2
1、 莫尔圆的概念
(
x
y 2
)2
2
(x
y )2 2
2 x
(
x
y 2
)2
2
(x
y 2
)2
2x
当斜截面随方位角 变化时, 其上的应力 ， 在 - 直角坐标系内的轨迹是一个圆 。
圆心的坐标为(the coordinates of MOHR circle’s center)
y
xm
900
t
450
k
D
y
xm
900
t
450
k
D
y
3
τ max
x
τ max
k
450
1
解: 从圆筒表面 k 点处取出单元体, 其各面上的应力分量如图 所示
可求得
y 1 max 80MPa
x 3 max 80MPa
z 0
k点处的线应变 x , y 为
y
x
1 E
(x
y )
1 E
(max
z
x
二、纯剪的本构关系
xy
xy
G
i 0 ( i x,y,z ) yz zx 0
y
xy
z
x
三、复杂状态下的本构关系
y
依叠加原理,得
y
z
z
x
xy
x
x
x
E
y
E
应力圆的画法课件
实例三：多向应力圆
多向应力圆，考虑多种受力方向和大小
输入 标题
详细描述
当物体受到多个方向的力和力矩作用时，应力圆呈现 多向性，圆心位于所有力和力矩的合力矩中心，半径 表示各方向应力的合力大小。
总结词
公式
F表示合力，F_i表示各方向力，M表示合力矩，M_i表 示各方向力矩。
解释
F=ΣF_i, M=ΣM_i
应力圆的应用
应力圆被广泛应用于工程和科学领域，特别是在材料力学、结构分析和机械设计中。通过 应力圆，工程师可以直观地了解应力的分布和变化，从而优化设计、提高结构的稳定性和 安全性。
对未来研究的展望
01
应力圆理论的发展
随着科学技术的发展，对应力圆理论的深入研究有望进一步揭示其内在
规律和性质，为解决更复杂的应力问题提供更有效的工具。
02
应力圆与其他领域的交叉研究
可以探索应力圆与其他领域（如物理学、生物学等）的交叉研究，以发
现新的应用和研究方向。
03
应力圆的计算机辅助分析
随着计算机技术的发展，利用计算机辅助分析工具进行应力圆的分析和
模拟将成为一个重要的研究方向，有助于提高分析的效率和准确性。
THANK YOU
应力圆的画法课件
目 录
• 应力圆的基本概念 • 应力圆的画法 • 应力圆的应用 • 应力圆的实例分析 • 总结与展望
01
应力圆的基本概念
定义与特性
定义
应力圆是一种表示平面应力状态 的工具，通过将平面内的应力分 量表示为圆周上的角度，以直观 地展示应力分布。
特性
应力圆具有直观性、易理解性、 易绘制性等特点，是工程中常用 的应力分析工具。
公式ቤተ መጻሕፍቲ ባይዱ
应力状态的概念
t xy 10MPa
600
600
n
s
40 (20) 2
40 (20) cos(1200 ) (10) sin(1200 ) 2
13.67MPa
t
40 (20) sin(1200 ) (10) cos(1200 ) 21MPa 2
20MPa
10MPa
300
40MPa
300
xn
解： s x 20MPa
P
A
P sx
sx
A
y
B
C z
P
sx B sx
Mx
tzx
txz
课堂练习
t yx
t C
xy
用单元体表达圆轴受扭时，轴表面任一点旳应力状态。
用单元体表达矩形截面梁横力弯曲时，梁顶、梁底及其他各
点旳应力状态。
七、主平面、主应力：
sy
y
主平面(Principal Plane)： 剪应力为零旳截面。
sx
sz
z
1 2 3
体积应变与应力分量间旳关系:
1 2
E
(s 1
s2
s3)
例5 已知一受力构件自由表面上某一点处于表面内旳主应变分别
为：1=24010-6， 3=–16010-6，弹性模量E=210GPa，泊松比 为 =0.3， 试求该点处旳主应力及另一主应变。
1 E
s
z
s
x s
y
xy
t
xy
G
yz
t
yz
G
zx
t zx
G
上式称为广义胡克定律
主应力 --- 主应变关系
s1 s3
1
1 E
应力与应力状态分析
应力与应力状态分析拉伸模量拉伸模量是指材料在拉伸时的弹性，其计算公式如下：拉伸模量（㎏/c ㎡)=△f/△h(㎏/c ㎡)其中，△f 表示单位面积两点之间的力变化，△h 表示以上两点之间的应变化。
更具体地说，△h ＝（L-L0）/L0，其中L0表示拉伸长前的长度，L 表示拉伸长后的长度。
§4-1 几组基本术语与概念一、变形固体的基本假设1、均匀连续性假设：假设在变形固体的整个体积内均匀地、毫无空隙地充满着物质，并且各点处的力学性质完全相同。
根据这一假设，可从变形固体内任意一点取出微小单元体进行研究，且各点处的力学性质完全相同，因而固体内部各质点的位移、各点处的内力都将是连续分布的，可以表示为各点坐标的连续函数。
2、各向同性假设：假设变形固体在所有方向上均具有相同的力学性质。
3、小变形假设：认为构件的变形与构件的原始尺寸相比及其微小。
根据小变形假设，在研究构件上力系的简化、研究构件及其局部的平衡时，均可忽略构件的变形而按构件的原始形状、尺寸进行计算。
二、应力的概念1、正应力的概念分布内力的大小（或称分布集度），用单位面积上的内力大小来度量，称为应力。
由于内力是矢量，因而应力也是矢量，其方向就是分布内力的方向。
沿截面法线方向的应力称为正应力，用希腊字母σ表示。
应力的常用单位有牛/米2 （2/m N ，12/m N 称为1帕，代号a P ）、千米/米2（2/m KN ，12/m KN 称为1千帕，代号Ka P ），此外还有更大的单位兆帕（M a P ）、吉帕（G a P ）。
几种单位的换算关系为：1 K a P =310a P 1 M a P =310K a P 1 G a P =310M a P =610K a P =910a P2、切应力与全应力的概念与截面相切的应力分量称为切应力，用希腊字母τ表示。
K 点处某截面上的全应力K p 等于该点处同一截面上的正应力K σ与切应力K τ的矢量和。
材料力学08应力状态分析_2图解法
x
2
y
2
2 xy
OC
1
一、应力圆的画法
1. 在 - 坐标系中确定两点： D (x , xy )、D′(y , yx )
2. 连接 D、D′，交 轴于
C点 3. 以 C 点为圆心、CD 为半
径作圆即得
2
二、由图解法（应力圆）确定斜截面上的应力
将 CD 沿同样的转向旋转 2 至 CE ，则 E 点的横坐标、纵坐标即 为 斜截面上的正应力、切应力，即有
在主平面。
11
[例3] 在过 A 点的两个截面上的应力如图所示，试用图解法确定其 主应力以及主平面位置。
D
20 MPa 60 MPa
20 MPa
C B1 O
D
20 20
A1
60
解： 1）画应力圆
按选定比例尺，由 y = 20 MPa、yx = -60 MPa 确定 D′点，由 = -20 MPa、 = 0 确定 B1 点。由于B1、 D′均在应力圆的圆周上，故 作 B1D′的垂直平分线，交 轴于点 C ；以点 C 为圆心、CD′为半径
故在单元体上，从 x 轴以顺时针转向量取 0 = 33.5°，即得 1
所在主平面。
主应力单元体如图所示
14
作出应力圆。
12
D
20 MPa 60 MPa
20 MPa
C B1 O
2）确定主应力和主平面
D
20 20 70 110
根据应力圆，按选定比例尺，量得主应力
60
A1
20 MPa
1 OA1 110 MPa 2 0 3 OB1 20 MPa
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
(
x
-s y )2
2
+
t
2 x
当斜截面随方位角 a 变化时, 其上的应力 σα , τ α 在
s - t 直角坐标系内的轨迹是一个圆 ,圆心位于横坐标轴
(
s
轴
)上,离原点的距离为
sx
+sy
2
半径为
此圆习惯上称为应力圆 , 或称为莫尔圆。
s
(
x
2
s
y
)2
+
t
2 x
(sa
-sx
+s
2
y )2
+ ta2
A1 s
α o 确定后， s1 对应的主平面方位即确定。
tg(-2a 0 )
=
B1D1 CB1
=
2t x (s x -s
y)
再根据应力圆判断α0的
合理范围
由此可定出主应力s1 所 o 在平面的位置。由于A1A2 为 应力圆的直径, 则s2 所在的另 一主平面与s1 所在的主平面 垂直 。
t
σ2
A2 B2
σy
t
o
B2
sy
D2
sx
量取 OB2=sy , B2D2= ty ,
得D2 点
(b)
D1
B1 s
连接D1D2两点的直线与 s 轴相交于C 点, 以C为 圆心, CD1或CD2为半径 作圆
σy τy
σx
σx
τx
τx
τy
σy
t
(b)
D1
o
B2
B1
C
s
sy
D2
sx
t
该圆的圆心 C 点到 坐标
(b)
D1
250KN
A
B
C
1.6m
2m
200KN
+
50KN
+
I
Z
=
1203003
12
-
1112703
12
=
88106
mm4
(s
M
=
y
)
S Q *
(t = Z )
IZ
IZd
ya = 135mm 120
S* za
=
120
15
(150
-
7.5)
=
256000mm3
270
横截面C上a 点的应力为
t
B1 2 A1
A
s
B
o
c
t 四、利用应力圆求主应力
σ2
数值和主平面位置
主应力数值
O
A2 B2
C
A1和 A2两点为与主平面 对应的点，其横坐标 为主 应
sy
D2
σx
σ1
力OAs11 ,=s2OC + CA1 OA2 = OC - CA1
OC = σ x +σ y 2
CA
=
1
(s
x-s
y
2
)
+t
2 x
B1 C
o
B2
s
600
D1 (-1,0.2)
τ 300
σ E
300
σ 300 = -0.68MPa τ 300 = -0.36MPa
(3) 确定 a = - 40°斜截面上的应力
将 半径 CD1 顺时针转 2a = 80°到半径 CF, F 点的坐标就 代表a = - 40°斜截面上的应力。
F
σ -400
2
D1
B1
s
A1
t
σ2
D1
o
A2 B2
C B1
sy
D2
σx
σ1
s
A1
s1 s2
=
sx
+sy
2
s
x
2
s
y
2
+t
2 xy
t
主平面方位
σ2
D1
由 CD1 顺时针转 2α o
o
到 CA1
所以从 x 轴顺时针转α o
（负值）即到s1对应的主平 面的外法线
A2 B2
B1 C
sy
D2 2 α o
σx
σ1
以 D1 D2 为直径绘出的圆即为应力圆。 t
(-0.4,0.2) D2
B1
O
C B2
s
D1 (-1,-0.2)
(2) 确定 a = 30°斜截面上的应力
将 半径 CD1 逆时针转动 2a = 60°到半径 CE, E 点的坐标就 代表 a = 30°斜截面上的应力。
(-0.4,0.2) t D2
§7-3 二向应力状态下的应力分析(应力圆)
一、 应力圆的概念
由
sa
=sx
+sy
2
+sx
-s y
2
cos2a
-tx
sin 2a
ta
=sx
-s y
2
sin 2a
+tx
cos2a
削去α得到
(sa
-sx
+s y )2
2
+ ta2
=
s
(
x
-s y )2
2
+
t
2 x
(sa
-sx
+s y )2
2
+ ta2
=
s
σy
sy
D2
sx
三、利用应力圆求单元体上任一 a 截面上的应力 从应力圆的半径 CD 1 按方位角 a 的转向转动 2a , 得到半径 CE ,
圆周上 E 点的 s ¸t 坐标 就依次为 sa ¸ta 。（ 证明略 ）
说明
点面之间的对应关系：单元体某一面上的应力，必对 应于应力圆上某一点的坐标。
夹角关系：圆周上任意两点所引半径的夹角等于单 元体上对应两截面夹角的两倍。两者的转向一致。
=
s
(
x
-s y )2
2
+
t
2 x
t
O
C
(σ
x
-σ
y
2
)
2
+τ
2 x
s
σ x +σ y
2
二、应力圆作法 在 s - t 坐标系内 , 选定比例尺
量取 OB1 = s x , B1D1 = t x , 得 D1点
t D1
σy τy
σx
σx
o
B1 s sx
τx
τx
τy
σy
σy τy
σx
σx
τx
τx
τy
σy τy
σx τ x
σx
τx
x
τy σy
σ x = -1 τ x = -0.2 σ y = -0.4 τ y = 0.2
解: (1) 画应力圆
OB1 = sx= - 1MPa , B1 D1 = tx= - 0.2MPa,定出 D1点;
OB2 =sy= - 0.4MPa 和 B2D2 = ty = 0.2MPa , 定出 D2 点 .
x
α = 400
例题 7-2 两端简支的焊接工字钢梁及其荷载如图 a , b 所示, 梁的横截面尺寸示于图 c 中。试绘出截面 c 上 a , b 两点处 的应力圆，并用应力圆求出这两点处的主应力。
120
270
250KN
9ABiblioteka BCz1.6m
a
b 2m
(a)
(c)
单位：mm
解: 首先计算支反力, 并作出 梁的剪力图和弯矩图 QC左 = 200 kN MC = 80 kN•m
原点的 距离为 s x + s y
2
o
B2
B1
半径为
s
(
x
2
s
y
)2
+
t
2 x
C
sy
D2
s
该圆就是相应于该单元体
sx
应力状态的应力圆
D1 点的坐标为 ( sx , tx ) 因而 D1 点代表单元体 x 平面上的应力 。
t
σα
σy τy
e
σx
a
σx
E
o τα
B2
2a
D1
B1 C
s
x
τx
f τx
τy
t
τ -400
-800
B1
C
(-0.4,0.2) D2
o
B2
s
σ -400 = -0.95MPa τ -400 = 0.26MPa
D1 (-1,0.2)
σ 300 = -0.68MPa σ -400 = -0.95MPa
τ 300 = -0.36MPa τ -400 = 0.26MPa
y
α =300
C
sy
D2 2 α o
σx
σ1
D1 B1 A1 s
例题7-1 从水坝体内某点处取出的单元体如图所示, sx= - 1MPa , sy= - 0.4MPa , tx= - 0.2MPa , ty= 0.2MPa ,
（1）绘出相应的应力圆 （2）确定此单元体在 a =30°和a = - 40°两斜面上的应力。
x
-s y )2
2
+
t
2 x
当斜截面随方位角 a 变化时, 其上的应力 σα , τ α 在
s - t 直角坐标系内的轨迹是一个圆 ,圆心位于横坐标轴
(
s
轴
)上,离原点的距离为
sx
+sy
2
半径为
此圆习惯上称为应力圆 , 或称为莫尔圆。
s
(
x
2
s
y
)2
+
t
2 x
(sa
-sx
+s
2
y )2
+ ta2
A1 s
α o 确定后， s1 对应的主平面方位即确定。
tg(-2a 0 )
=
B1D1 CB1
=
2t x (s x -s
y)
再根据应力圆判断α0的
合理范围
由此可定出主应力s1 所 o 在平面的位置。由于A1A2 为 应力圆的直径, 则s2 所在的另 一主平面与s1 所在的主平面 垂直 。
t
σ2
A2 B2
σy
t
o
B2
sy
D2
sx
量取 OB2=sy , B2D2= ty ,
得D2 点
(b)
D1
B1 s
连接D1D2两点的直线与 s 轴相交于C 点, 以C为 圆心, CD1或CD2为半径 作圆
σy τy
σx
σx
τx
τx
τy
σy
t
(b)
D1
o
B2
B1
C
s
sy
D2
sx
t
该圆的圆心 C 点到 坐标
(b)
D1
250KN
A
B
C
1.6m
2m
200KN
+
50KN
+
I
Z
=
1203003
12
-
1112703
12
=
88106
mm4
(s
M
=
y
)
S Q *
(t = Z )
IZ
IZd
ya = 135mm 120
S* za
=
120
15
(150
-
7.5)
=
256000mm3
270
横截面C上a 点的应力为
t
B1 2 A1
A
s
B
o
c
t 四、利用应力圆求主应力
σ2
数值和主平面位置
主应力数值
O
A2 B2
C
A1和 A2两点为与主平面 对应的点，其横坐标 为主 应
sy
D2
σx
σ1
力OAs11 ,=s2OC + CA1 OA2 = OC - CA1
OC = σ x +σ y 2
CA
=
1
(s
x-s
y
2
)
+t
2 x
B1 C
o
B2
s
600
D1 (-1,0.2)
τ 300
σ E
300
σ 300 = -0.68MPa τ 300 = -0.36MPa
(3) 确定 a = - 40°斜截面上的应力
将 半径 CD1 顺时针转 2a = 80°到半径 CF, F 点的坐标就 代表a = - 40°斜截面上的应力。
F
σ -400
2
D1
B1
s
A1
t
σ2
D1
o
A2 B2
C B1
sy
D2
σx
σ1
s
A1
s1 s2
=
sx
+sy
2
s
x
2
s
y
2
+t
2 xy
t
主平面方位
σ2
D1
由 CD1 顺时针转 2α o
o
到 CA1
所以从 x 轴顺时针转α o
（负值）即到s1对应的主平 面的外法线
A2 B2
B1 C
sy
D2 2 α o
σx
σ1
以 D1 D2 为直径绘出的圆即为应力圆。 t
(-0.4,0.2) D2
B1
O
C B2
s
D1 (-1,-0.2)
(2) 确定 a = 30°斜截面上的应力
将 半径 CD1 逆时针转动 2a = 60°到半径 CE, E 点的坐标就 代表 a = 30°斜截面上的应力。
(-0.4,0.2) t D2
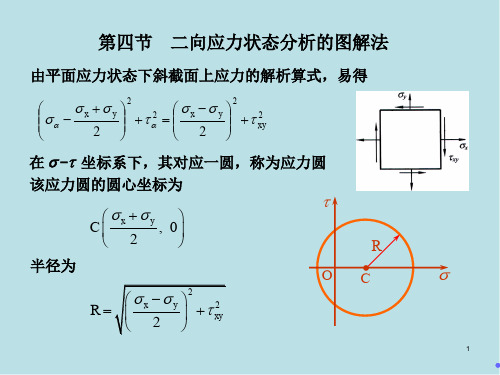
§7-3 二向应力状态下的应力分析(应力圆)
一、 应力圆的概念
由
sa
=sx
+sy
2
+sx
-s y
2
cos2a
-tx
sin 2a
ta
=sx
-s y
2
sin 2a
+tx
cos2a
削去α得到
(sa
-sx
+s y )2
2
+ ta2
=
s
(
x
-s y )2
2
+
t
2 x
(sa
-sx
+s y )2
2
+ ta2
=
s
σy
sy
D2
sx
三、利用应力圆求单元体上任一 a 截面上的应力 从应力圆的半径 CD 1 按方位角 a 的转向转动 2a , 得到半径 CE ,
圆周上 E 点的 s ¸t 坐标 就依次为 sa ¸ta 。（ 证明略 ）
说明
点面之间的对应关系：单元体某一面上的应力，必对 应于应力圆上某一点的坐标。
夹角关系：圆周上任意两点所引半径的夹角等于单 元体上对应两截面夹角的两倍。两者的转向一致。
=
s
(
x
-s y )2
2
+
t
2 x
t
O
C
(σ
x
-σ
y
2
)
2
+τ
2 x
s
σ x +σ y
2
二、应力圆作法 在 s - t 坐标系内 , 选定比例尺
量取 OB1 = s x , B1D1 = t x , 得 D1点
t D1
σy τy
σx
σx
o
B1 s sx
τx
τx
τy
σy
σy τy
σx
σx
τx
τx
τy
σy τy
σx τ x
σx
τx
x
τy σy
σ x = -1 τ x = -0.2 σ y = -0.4 τ y = 0.2
解: (1) 画应力圆
OB1 = sx= - 1MPa , B1 D1 = tx= - 0.2MPa,定出 D1点;
OB2 =sy= - 0.4MPa 和 B2D2 = ty = 0.2MPa , 定出 D2 点 .
x
α = 400
例题 7-2 两端简支的焊接工字钢梁及其荷载如图 a , b 所示, 梁的横截面尺寸示于图 c 中。试绘出截面 c 上 a , b 两点处 的应力圆，并用应力圆求出这两点处的主应力。
120
270
250KN
9ABiblioteka BCz1.6m
a
b 2m
(a)
(c)
单位：mm
解: 首先计算支反力, 并作出 梁的剪力图和弯矩图 QC左 = 200 kN MC = 80 kN•m
原点的 距离为 s x + s y
2
o
B2
B1
半径为
s
(
x
2
s
y
)2
+
t
2 x
C
sy
D2
s
该圆就是相应于该单元体
sx
应力状态的应力圆
D1 点的坐标为 ( sx , tx ) 因而 D1 点代表单元体 x 平面上的应力 。
t
σα
σy τy
e
σx
a
σx
E
o τα
B2
2a
D1
B1 C
s
x
τx
f τx
τy
t
τ -400
-800
B1
C
(-0.4,0.2) D2
o
B2
s
σ -400 = -0.95MPa τ -400 = 0.26MPa
D1 (-1,0.2)
σ 300 = -0.68MPa σ -400 = -0.95MPa
τ 300 = -0.36MPa τ -400 = 0.26MPa
y
α =300
C
sy
D2 2 α o
σx
σ1
D1 B1 A1 s
例题7-1 从水坝体内某点处取出的单元体如图所示, sx= - 1MPa , sy= - 0.4MPa , tx= - 0.2MPa , ty= 0.2MPa ,
（1）绘出相应的应力圆 （2）确定此单元体在 a =30°和a = - 40°两斜面上的应力。