二向应力状态分析--解析法和图解法
合集下载
应力状态概述二向和三向应力状态的实例二向
2．作应力圆 主应力为 1 , 3 ，并可 确定主平面的法线。
材料力学
第七章
应力和应变分析
3．分析 纯剪切应力状态的两个主应力绝对值相等， 但一为拉应力，另一为压应力。由于铸铁抗拉强度较 低，圆截面铸铁构件扭转时构件将沿倾角为 45º 的螺旋面因拉伸而发生断裂破坏。
材料力学
第七章
2 2
x y
xy
n
材料力学
y a xy
y On D( x , ) a a
a
第七章
n
应力和应变分析
二、应力圆的画法
建立应力坐标系，如下图所 示，（注意选好比例尺） 在坐标系内画出点A( x， xy)和B(y，yx)
x
C O
2a
AB与a 轴的交点C便是圆 A( x , xy) 心。
150°
第七章
应力和应变分析
x y 2 2 1 x y （ ） xy 2 2 2
解法2—解析法：分析——建立坐标系如图
95
60°
y 45MP a yx 25 3MP a xy
25 3
x ?
y O x
60 95MPa 60 25 3MPa
材料力学
第七章
应力和应变分析
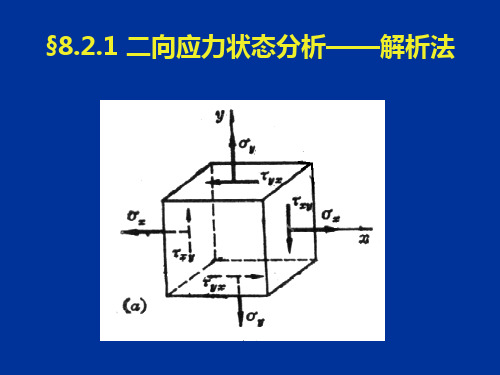
应力表示——单元体：
①dx、dy、dz（微小的正六面体） ②单元体某斜截面上的应力就代表了构件内 对应点同方位截面上的应力。
B P
dz
dx
dy
A
C
பைடு நூலகம்
B
D
C
B、C——单向受力，τ ＝0 A——纯剪切， σ ＝0
D
D——既有 σ ，又有τ
工程力学 材料力学M7-复杂应力状态
σ3
σ2
σ1
《材料力学》
第7章(1) 复杂应力状态
20
四、应力状态的分类
4. 简单应力状态
σ
单向应力状态
( One Dimensional State of Stresses )
τ
纯切应力状态
( ShearingState of Stresses )
《材料力学》
第7章(1) 复杂应力状态
21
例题 1
《材料力学》 第7章(1) 复杂应力状态 37
三、主平面、主应力与主方向
考查一下正应力的极值
x y
2
x y
2
cos 2 xy sin 2
将上式对α求一次导数，并令其等于零，有
x y d 2[ sin 2 xy cos 2 ] 0 d 2
二、应力的三个重要概念
应力的点的概念; 应力的面的概念; 应力状态的概念。
《材料力学》
第7章(1) 复杂应力状态
9
二、应力的三个重要概念
FQ
不同点的应力各不相同（大小、方向） ------------应力的点的概念
cos 2
F
K
2
sin 2
同一点在不同方向面上的应力也各不相同----------应力 的面的概念。
《材料力学》
第7章(1) 复杂应力状态
10
二、应力的三个重要概念
应 力
指明
哪一个面上？ 哪一点？ 哪一点？ 哪个方向面？
过一点不同方向面上应力的集合，称为这一点 的应力状态（State of the Stresses of a Given Point）。
材料力学第七章应力状态和强度理论
2
x y 2 a 0 2
x y x y 2
x y
2
) x
2
2
例题1: 已知:单元体各侧面应力 x=60MPa,
求: (1) = - 450斜截面上的应力,(2)主应力和主平面
dA
y
x y
2
sin 2 xy cos2
y
yx
应力圆
y
1 R 2
x
y
2
4 2 xy
x
yx xy x
y
R c
x y
2
2
x
xy
x´
dA
yx
y´
y
x y 1 2 2 2
40
x y
2 0.431MPa
sin( 80 ) xy cos(80 )
C
C
C
例题3：已知梁上的M、Q，试用单元体表示截面上1、2、
3、4点的应力状态。
1
2 0
2
1点 2点
1 2 0 3
3Q ＝ 2A
M x Wz
2 xy
x y
2 20.6 0.69 60 0
17.2
x y
2 (
6.4MPa
2 34.4
max(min)
x
17.20
x y
2
) xy
2
2
x
66.4MPa
60 0 60 0 2 ( ) 20.6 2 2 2 66.4(6.4) MPa
x y 2 a 0 2
x y x y 2
x y
2
) x
2
2
例题1: 已知:单元体各侧面应力 x=60MPa,
求: (1) = - 450斜截面上的应力,(2)主应力和主平面
dA
y
x y
2
sin 2 xy cos2
y
yx
应力圆
y
1 R 2
x
y
2
4 2 xy
x
yx xy x
y
R c
x y
2
2
x
xy
x´
dA
yx
y´
y
x y 1 2 2 2
40
x y
2 0.431MPa
sin( 80 ) xy cos(80 )
C
C
C
例题3：已知梁上的M、Q，试用单元体表示截面上1、2、
3、4点的应力状态。
1
2 0
2
1点 2点
1 2 0 3
3Q ＝ 2A
M x Wz
2 xy
x y
2 20.6 0.69 60 0
17.2
x y
2 (
6.4MPa
2 34.4
max(min)
x
17.20
x y
2
) xy
2
2
x
66.4MPa
60 0 60 0 2 ( ) 20.6 2 2 2 66.4(6.4) MPa
材料力学应力分析(共143张PPT)
Mz Wz
17
y
1
4
z
2
x
3
S平面
18
y
1
FQy
1
4
4 Mz
x
z
2
Mx
3
3
19
应力状态的概念
主平面：单元体中剪应力等于零的平面。
主单元体：在单元体各侧面只有正应力而
无剪应力
3
2
主应力：主平面上的正应力。
主方向：主平面的法线方向。
约定：
1
12 320
应力状态的分类
3
2
1
1
2
3
单向应力状态：三个主应力中，只有一个主应力不等于零的情况。
3
一、什么是应力状态？
〔一〕、应力的点的概念:
最大正应力所在的面上切应力一定是零； 它与塑性较好材料的试验结果比第三强度理论符合得更好； 7-2 二向应力状态分析--解析法 面将单元体截为两局部， 并注意到 化简得 三、如何描述一点的应力状态 应力圆上一点( ， ) 7-8 广义胡克定律 该单元体的三个主应力按其代数值的大小顺序排列为 解: 该单元体有一个主应力 例2：纯剪切状态的主应力 它与塑性较好材料的试验结果比第三强度理论符合得更好；
5
F
F
A
F
co2s
2
sin2
过同一点不同方向面上的应力各不相同， 即应力的面的概念
6
应力的点的概念与面的概念
应力
指明
哪一个面上？ 哪一点？
哪一点？ 哪个方向面？
应力状态: ——过同一点不同方向面上应力的集合，称为
这一点的应力状态；
7
二、为什么要研究应力状态？
第三强度理论.
第七章 应力和应变分析 强度理论§7.1应力状态概述过构件上一点有无数的截面，这一点的各个截面上应力情况的集合，称为这点的应力状态§7.2二向和三向应力状态的实例§7.3二向应力状态分析—解析法1．任意斜截面上的应力在基本单元体上取任一截面位置，截面的法线n 。
在外法线n 和切线t 上列平衡方程αασαατσc o s )c o s (s i n )c o s (dA dA dA x xy a -+0s i n )s i n (c o s )s i n (=-+αασαατdA dA y yxαασααττsin )cos (cos )cos (dA dA dA x xya --0sin )sin (cos )sin (=++ααταασdA dA yx y根据剪应力互等定理，yx xy ττ=，并考虑到下列三角关系 22sin 1sin ,22cos 1cos 22αααα-=+=，ααα2sin cos sin 2=简化两个平衡方程，得ατασσσσσα2sin 2cos 22xy yx yx --++=xyτyxτnαtατασστα2cos 2sin 2xy yx +-=2．极值应力将正应力公式对α取导数，得⎥⎦⎤⎢⎣⎡+--=ατασσασα2cos 2sin 22xy y x d d 若0αα=时，能使导数0=ασαd d ，则 02cos 2sin 200=+-ατασσxy yxyx xytg σστα--=220上式有两个解：即0α和 900±α。
在它们所确定的两个互相垂直的平面上，正应力取得极值。
且绝对值小的角度所对应平面为最大正应力所在的平面，另一个是最小正应力所在的平面。
求得最大或最小正应力为22min max )2(2xy y x yx τσσσσσσ+-±+=⎭⎬⎫ 0α代入剪力公式，0ατ为零。
这就是说，正应力为最大或最小所在的平面，就是主平面。
二向应力状态分析--解析法和图解法-PPT
d d
( x y )cos2 2 xysin2
0
由此得出另一特征角，用α1表示
tan
21＝
x
2τ xy
y
tan
21＝
x
2τ xy
y
得到α 的极值
x
y
2
sin21
xycos21
max
min
(x
y
2
)2
2 xy
特别指出：
上述切应力极值仅对垂直于xy坐标面的方向面而言， 因而称为面内最大切应力与面内最小切应力
x
y
)2
2
xy
2
排序??
48.3MPa
1 68.3MPa, 2 0, 3 48.3MPa
2 面内最大切应力
y xy
x
x 60MPa， xy 30MPa,
y 40MPa,
max
(
x
y
)2
2
xy
2
3400
3 主平面的位置
y xy
x
代入 表达式可知
x 60MPa， y 40MPa,
状态下的应力圆
的应力圆
o
结论：二向等值拉伸下,
习题7-5 P253-254 所有的面 都是主平面
要求 一、 应力圆方程
二、 应力圆的画法 三、 应力圆的应用 四、 几种特殊应力状态的应力圆
y
y yx
x
xy x
x
求任意斜截面上的应力 （斜截面的位y 置？？）
解决问题的方法 平衡 的思想
2、单元体的局部平衡
y
y yx
n+
x
xy
x
x
x
材料力学第9章 应力状态分析
B
方位角α, 对应于应力圆上为2 α
a τy σy τx e σα σx a ταf
n
c
τ
a
B 2a
τσx x x o C
角, 自起始半径旋转, 且与α转向 一致；
A 单元体上A、B面夹角α, σ 应力圆上弧长AB的圆心角
b
σyτy d
为2 α角, 且转向一致。
3、主应力、主平面与主单元体
t
图解法
tadA (t xdAcosa ) cosa (s xdAcosa )sina (t ydAsina )sina (s ydAsina) cosa 0
关系式
t x =t
(负号已包含在指向中）；
y
sin
2a
2 sin a
cosa；
cos2 a 1 cos 2a ； sin2 a 1 cos 2a
t
图解法
注意A1、A2点
σx
σ( 2,0)
A2 B2
σ τ E(
2a
Dα1，σ( xα,)τ x )
2a
数值 方位
τy τx
o
σ a C B1 A1 σ
( 1,0) 主点法
s1 = sx s y
s2
2
s
(
x
s
2
y
)2
t
2 x
tan
2a0
2t x sx s
y
(σy ,Dτ2y) σy
K
s1的方位
作D1K⊥σ轴, 交圆与K点, 则A2K方向
2
2
sa、ta
计算公式
sa
ta
sx sx
sy
2
s y
二向应力状态分析PPT课件
2
+
4
2 x
z
25mm
1
2
3
2
4
h
1
3
3
Fs 4 2、计算各点主应力
1点
Iz
bh3 12
500cm4
1
My Iz
11000M10P3a 50 500 104
2点 (处于纯剪状态)
1 2 0 3 -100MPa
max
3 2
Fs A
330M12P0a103 2 60100
3点 (一般平面状态)
2
300 + -600 x + y 40MPa
在二向应力状态下，任意两个垂直面上，其σ的和为一常数。
分析轴向拉伸杆件的最大切应力的作用面，说明 低碳钢拉伸时发生屈服的主要原因。
低碳钢拉伸时，其上任意一点都是单向应力状态。
x
x + y
2
+ x - y cos 2
2
- x sin 2
x
平面应力状态的几种特殊情况
x + y
2
+ x - y cos 2
2
- x sin 2
x - y sin 2
2
+ x cos 2
扭转
- x sin 2 x cos 2
1 ＝ x 2 ＝0 3 ＝- x max x
min
弯
x
2
+x
2
cos 2
- x sin 2
曲
x
2
sin 2
D(x, xy)
2
2
A1
C L A 1
yx y
D’ (y, yx) G2 "
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
σ
TSINGHUA UNIVERSITY
σ 0
σ
2 求正应力的极值面
x y
x - y
2 2 上式对α 求一次导数，并令其等于零
cos2 - xysin2
TSINGHUA UNIVERSITY
d -( x - y )sin2 - 2 xy cos2 0 d
xy
x
tg 2 0 -
2 xy
- 60 0. 6 60 40
0 15.5 ,
x - y
代入 表达式可知
0 15.5 90 105.5
主应力 1 方向： 0 15.5
主应力方向
3 方向：0 105.5 ---主平面的法线方向 主应力
x 60MPa， -40MPa, xy -30MPa, y
xy
x
max
x - y 2 2 ( ) xy 2 3400
3 主平面的位置
x 60MPa，
xy -30MPa,
y -40MPa,
y
TSINGHUA UNIVERSITY
2 2
TSINGHUA UNIVERSITY
x - y
2
sin2 xy cos2
y yx
y
x
y
xy x x
例题1求斜面ab上的正应力和切应力
y
TSINGHUA UNIVERSITY
解：x 10MPa, y -30MPa
20MPa
a
300
要求 掌握主应力计算！！牢记公式，并进行 排序！
二
主平面、主应力与主应力方向 x y x - y cos2 - xysin2 2 2
1
x - y
2
TSINGHUA UNIVERSITY
sin2 xy cos2
sin2 0 xy cos2 0 0
(
O
TSINGHUA UNIVERSITY
x y
2
x - y
2
2 )2 xy
''' 0
max min
(
x - y
2
2 )2 xy
例题2：一点处的应力状态如图。 已知
TSINGHUA UNIVERSITY
x 60MPa， xy -30MPa,
切应力为零的面为主平面
0
x - y
2
2 τ xy
tan 2 0＝－
x - y
0 0 90
O
该式确定了两个相互垂直的主平面的位置
对于平面应力状态， 平行于xy坐标面的平 面，其上既没有正应 力，也没有切应力作 用，前后面是一个主 平面。 这一主平面上的主应力等于零
30
xy 20MPa, yx -20MPa, 30
x y
2
10MPa
x - y
2
cos 2 - xy sin 2
b
30
20MPa
x
0
30
10 - 30 10 30 cos 60 - 20sin 60 2 2
yx
x
y
左 右 面 上 的 切 应力
xy
x
各量的含义 1) 左右面上的正应力 上下面上的正应力 2 )
1 方向角与应力分量的正负号规定 正应力正负规定 拉应力为正压应力为负 切应力正负号规定
TSINGHUA UNIVERSITY
x y
' '
xy
yx
y
外法线
使微元或其局部顺时针方向转动为正； 反之为负
1
?????
1 68.3MP a, 2 0, 3 -48.3MP a 二向应力状态 若 y 0, 二向应力状态
特别说明
y 0,
TSINGHUA UNIVERSITY
二向应力状态
xy
x
横力弯曲 中性轴
除了梁顶(底)
其它点
xy
中性轴
圆轴扭转
二向应力状态
2
TSINGHUA UNIVERSITY
yx
xy
y
x y x - y cos 2 xy sin 2 2 2
-
x - y
sin 2 - xy cos 2
90 x y
0
即单元体两个相互垂直面上 的正应力之和是一个常数
68.3MPa
TSINGHUA UNIVERSITY
x x y - ( x - y ) 2 2 min xy 2 2
-48.3MPa
排序??
1 68.3MP a, 2 0, 3 -48.3MP a
2 面内最大切应力
y
TSINGHUA UNIVERSITY
简单方法 主（应力）单元体
1 习惯直角坐标系按公式确定 绝对值小于45度角的
0
TSINGHUA UNIVERSITY
2 判断
给出原始单元体中代数值大的那个正应力 面的法线方向(的区间)
3 判断 最大主应力(的区间) (两个切应力箭头指向决定) 4
第一主应力方向
大(求出的主应力)
之间夹角
(小)
大(原始单元体中代数值)
y -40MPa,
y
xy
x
1 主应力大小 2 （面内）最大切应力 3 主平面位置 4 绘出主（应力)单元体
1 主应力计算
正应力的两个极值就是 两个主应力
x 60MPa， -40MPa, xy -30MPa, y
y
xy
x y x - y 2 2 公式 max ( ) xy 2 2
例题3
P
70
TSINGHUA UNIVERSITY
50
解：
x -70MPa
1 主应力大小 2 主平面位置 3 绘出(主应力)单元体。
y 0
xy 50MPa
1 求主应力
max x y - y 2 x xy min 2 2
由此得出另一特征角，用α1表示
tan 21＝
x - y
2 τ xy
tan 21＝
x - y
2 τ xy
max min
x - y
2
sin21 xy cos21
2 )2 xy
得到α 的极值
(
x - y
2
TSINGHUA UNIVERSITY
y
dA - (dA cos ) sin - xy (dA cos ) cos x yx (dA sin ) sin y (dA sin ) cos 0
3、平面应力状态任意方向面上的正应力 与切应力 x y x - y cos2 - xysin2
2
大 27.5 大
1
- 70 0 - 70 - 0 2 ( ) (50) 2 2 2
26MPa -96MPa
3
TSINGHUA UNIVERSITY
70
二向应力状态
50
1 26MPa 2 0MPa 3 -96MPa
大
3 主单元体
大
2 求主平面位置
x - y
2
30MPa
-17.32MPa
sin 2 xy cos 2
30
10 30 sin 60 20 cos 60 2
27.32MPa
思考 900 ？
90 ？？
0
x
用 斜截面截取，此截面上的应力为
2
x - y
2
x - y
cos2 0 - xysin2 0
2 )2 xy
max min
x y
2
(
x - y
2
''' 0
将三个主应力代数值由大到小顺序排列;
1 2 3 就是所谓的应力状态的不变性
主应力是一点应力状态的最终度量
自学提纲 一、 写出应力圆方程 并判断应力圆的圆心在那个轴上？
TSINGHUA UNIVERSITY
自学§7-4
二向应力状态分析-图解法
二、 应力圆的画法 1 定圆心 2 定半径 3 画圆 三、 应力圆的应用 1 求主应力 2 面内最大切应力
(1)
四、 几种特殊应力状态的应力圆
1：单向拉伸应力状态的应力圆 2 ：纯剪切应力状态的应力圆
解决问题的方法
平衡
的思想
2、单元体的局部平衡
y yx
y
n+
TSINGHUA UNIVERSITY
x
xy x x x
y
xy
yx
y
2、单元体的局部平衡
Fn 0
????
+ 0
x
xy
t
n
TSINGHUA UNIVERSITY
yx
dA
解出的角度
tan 2＝－
2 τ xy
x - y
角度α与α 0 完全重合。