高三高考数学复习之凹凸函数之切线放缩

合集下载

高中数学专题微专题11 切线放缩

由题意，f′(x)＝1x－(x＋1)ex＋a≤0 在[1，＋∞)上恒成立，从而 a≤(x＋1)ex－1x，设 g(x)＝(x＋1)ex－1x(x≥1)，则 g′(x)＝(x＋2)ex＋x12>0，所以g(x)在[1，＋∞)上单调递增，故g(x)min＝g(1)＝2e－1，
因为a≤g(x)恒成立，所以a≤2e－1，
方法一 (切线放缩，利用ex≥x＋1)
对任意的x>0，f(x)≤xe2x 恒成立，
xe2x－ln x＋1
等价于 a≤
x
在(0，＋∞)上恒成立.
因为xe2x－(ln x＋1)＝e2x＋ln x－(ln x＋1)≥(2x＋ln x＋1)－(ln x＋1)＝2x，
xe2x－ln
所以
x
x＋1≥2xx＝2.
所以h′(x)>0⇔－2<x<－1，h′(x)<0⇔x>－1，从而h(x)在(－2，－1)上单调递增，在(－1，＋∞)上单调递减，故h(x)max＝h(－1)＝0，所以h(x)≤0，故ln(x＋2)≤x＋1，当且仅当x＝－1时等号成立，综上所述，有ln(x＋2)≤x＋1≤ex，且两个等号不能同时成立，所以ln(x＋2)<ex，故ex－ln(x＋2)>0，因为当m≤2时，f(x)＝ex－ln(x＋m)≥ex－ln(x＋2)，所以f(x)>0.
即e2x0 ＝x10，2＝－lnx0x0，所以 m(x)≥m(x0)＝e2x0－ln xx00＋1＝x10－lnx0x0－x10＝2，则有 a≤2，
所以实数a的取值范围为(－∞，2].
考点二利用切线放缩证明不等式
典例2 已知函数f(x)＝ex－ln(x＋m). (1)设x＝0是f(x)的极值点，求m的值，并讨论f(x)的单调性；

第12讲切线放缩

第12讲切线放缩本讲义由作业帮周永亮老师（白哥）独家编撰，侵权必究知识导航1．两个常见的切线放缩公式（1） ;（2）2．切线放缩在求导过程中的应用在求导的过程中，我们很多时候需要求二次导，乃至三次或多次，其实，对于几乎所有的问题，如果我们能够很好的利用放缩的技巧的话，我们最多只需要求二次导就可以了.3．切线放缩在数列不等式中的应用数列不等式有很多种，其中有一种最常见的叫做“拆和之函数放缩”，而这个函数，一般都是由我们这两个最常见的切线放缩公式演变而来的．知识札记例2（★★★☆☆）（2018·河北石家庄市一模）已知函数（）在处的切线方程为．（1）求，．（2）若，证明：．例1（★★★☆☆）（2018·河北保定市模拟【文】）已知函数，函数，证明：当且时，．考点1 切线放缩的基础应用注：本讲对于切线放缩公式的应用，都写了易证，但在正常考试中，需要同学们证明.经典例题例5（★★★★☆）（2017·黑龙江大庆市期中【文】）已知，求证：当时，恒成立．例4（★★★★☆）已知函数，在点处的切线方程为．（1）求，；（2）证明：．例3（★★★★☆）证明：．考点2 切线放缩拓展应用例8（★★★★☆）证明：当，时，．考点3 切线放缩在数列不等式中的应用例7（★★★★★）证明：．例6（★★★★★）（2018·江苏泰州市期末【文】）已知函数，（，），当，时，求证：．例11（★★★★☆）（2013·安徽合肥市月考【理】）设函数（），数列满足：，（）．（1）求数列的通项公式；（2）求证：．例10（★★★★☆）（2018·辽宁月考【文】）求证：（）．例9（★★★★☆）（2016·湖南模拟【理】）证明不等式：（）．课后练习练1（★★★☆☆）（2017·贵州一模【文】）已知函数，证明：对任意，成立．练2（★★★★★）（2017·重庆渝中区模拟【理】）已知函数（为实数，为自然对数的底数），曲线在处的切线与直线平行．（1）求实数的值；（2）证明：当时，．练3（★★★★☆）（2016·全国卷）求证：当且时，．。

导数中证明不等式技巧——构造、切线放缩、二元变量、凹凸反转,唯手熟尔!

导数中证明不等式技巧——构造、切线放缩、二元变量、凹凸反转,唯手熟尔!导数中的不等式证明导数中的不等式证明是高考中的一个经典考点。

由于不等式证明的灵活性和多样性，该考点备受命题者的青睐。

本文将从五个方面系统地介绍一些常规的不等式证明手段。

命题角度1：构造函数典例1】（赣州市2018届高三摸底考试）已知函数$f(x)=1-\ln x+\frac{e}{x}$，$g(x)=x-\frac{e}{x}$，若曲线$y=f(x)$与曲线$y=g(x)$的一个公共点是$A(1,1)$，且在点$A$处的切线互相垂直。

求$a,b$的值，并证明当$x\geq1$时，$f(x)+g(x)\geq\frac{2}{x}$。

解析】（1）$a=b=-1$；2）$g(x)=-\frac{e}{2\ln x}+\frac{x}{2}-\frac{e}{2x}$，$f(x)+g(x)\geq\frac{2}{x}$ $\Leftrightarrow 1-\frac{1}{x}+\frac{e}{x}-\frac{e}{2\ln x}+\frac{x}{2}-\frac{e}{2x}\geq\frac{2}{x}$ $\Leftrightarrow\frac{1}{x}+\frac{ e}{2\ln x}-\frac{x}{2}+\frac{e}{2x}\leq1$。

令$h(x)=f(x)+g(x)-\frac{2}{x}$，则$h(x)=1-\frac{1}{x}+\frac{e}{x}-\ln x-\frac{e}{2\ln x}+\frac{x}{2}-\frac{e}{2x}$，$h'(x)=-\frac{1}{x^2}+\frac{e}{x^2}-\frac{1}{x}-\frac{e}{2x^2}+\frac{1}{2}-\frac{e}{2x^2}$，$h''(x)=\frac{2}{x^3}-\frac{3e}{x^3}+\frac{2e}{x^3}$。

导数的应用-切线放缩证明不等式

点P处的切线。
单切线放缩
例1.求证:当x>0时，1+2x<e2x
例1：
单切线放缩
例2：
注：（1）该方法适用于凹函数与凸函数且它们的凹凸性相反
的问题（拆成两个函数）； ----数形结合
（2）两函数有斜率相同的切线，这是切线放缩的基础。引入
一个中间量，分别证明两个不等式成立，然后利用不等式的传
递性即可；
明.
小结
1.切线放缩法实质是以直（切线）代曲（原函数）；
2.切线放缩法中常用的两个定理必须先证明后使用；
3.证明流程为：求切线—构造差函数—证明差函数恒正
（负）--原不等式成立．
4.对于较为简单的导数试题，往往只涉及到一次切线放缩，
但是有些压轴试题涉及到两次不同的切线放缩．
----以直代曲
（3）难点在合理拆分函数，寻找它们斜率相等的切线隔板.
单切线放缩
例3：
略，
注：含参函数有时需要根据函数特征将原函数进行适当放缩.
单切线放缩
例4：
注：复杂形式的函数需要将函数适当转化后再进行放缩.
双切线放缩
例5：
a>1
注：含有两个零点的f(x)的解析式(可能含有参数, )，
告知方程f(x)=b有两个实根，要证明两个实根之差小于
(或大于)某个表达式．求解策略是画出f(x)的图象，并
求出f(x)在两个零点处(有时候不一定是零点处)的切线
方程(有时候不是找切线，而是找过曲线上某两点的直
线)，然后严格证明曲线f(x)在切线(或所找直线)的上
方或下方，进而对, 作出放大或者缩小，从而实现证
导数的应用
--切线放缩法证明不等式
复习引入：曲线在某一点处的切线的定义

【导数经典技巧与方法】第30讲-双参数最值问题与切线放缩-解析版

第30讲双参数最值问题知识与方法含参问题一直是高考中的重点与难点. 高考真题及模拟题中常出现“恒成立”为背景的双参数的范围或最值问题. 处理此类问题, 常用有以下方法:1消元法2零点比大小法零点比大小是指将函数y=ax+b与函数y=f(x)的零点比较大小, 进而解决问题. 图象上看, 是观察直线y=ax+b与曲线y=f(x)的横截距的大小关系. 此方法要求y=f(x)函数具有凹凸性, 可以解决形如“已知ax+b⩾f(x) (或⩽f(x))恒成立, 求b的最值”的问题,一般有如下两种形式:k(1) 若ax+b⩾f(x)恒成立, f(x)为上凸函数, 如下左图, 则x1⩽x2;(2) 若y=ax+b⩽f(x)恒成立, f(x)为下凸函数, 如下右图, 则x1⩾x2.的最值.由(1)或(2)得出x1,x2的大小,进而可以求得bk3. 赋值法对比不等式与目标式的结构, 发现当自变量取某个值时恰好构造出目标式.赋值法是零点比大小法方法的优化和改进,能快速解决线性表达式型、比值型的客观题 . 点睛意领会“等比例赋值法”进行恰到好处的赋值.典型例题【例1】若(x2+x)ln⁡1x −ax⩽23x3+(1−a)x2−2ax+b恒成立, 求b−2a的最小值 .【答案】−53【解析】解法 1: 消元法设F(x)=23x3+(1−a)x2−2ax+b−(x2+x)ln⁡1x+ax,则F′(x)=(2x+1)(ln⁡x+x+1−a),令ℎ(x)=ln⁡x+x+1−a得ℎ(x)单调递增, 故存在唯一x0使得ℎ(x0)=0, 即a= x0+ln⁡x0+1当x∈(0,x0)时, F(x)单调递减当x∈(x0,+∞)时, F(x)单调递增,故F(x)min=F(x0)=−13x03−x02−x0+b.所以F(x)min=F(x0)⩾0, 即b⩾13x03+x02+x0,b−2a⩾13x03+x02−x0−2ln⁡x0−2,t(x)=13x3+x2−x−2ln⁡x−2,t′(x)=(x−1)(x2+3x+2)x,当x∈(0,1),t(x)单调递减; 当x∈(1,+∞),t(x)单调递增,故 t(x)min =t(1)=−53. 所以 b −2a 的最小值为 −53.解法 2: :赋值法f(x)⩽g(x)⇔b −(x 2+x )a ⩾−(x 2+x )ln⁡x −23x 3−x 2令 x 2+x =2 (等比例赋值法), 解得 x =1 (舍 x =−2 ), 则 b −2a ⩾−53.当 b −2a =−53 时, 由 f(x)−g(x)⩽0=f(1)−g(1) 知 x =1 是 f(x)−g(x) 的极值点,所以 f ′(1)−g ′(1)=0, 解得 a =2,b =73.下面证明: 当 a =2,b =73时, f(x)⩽g(x).证明:令 ℎ(x)=g(x)−f(x)=23x 3−x 2−2x +73+(x 2+x )ln⁡x .则 ℎ′(x)=(2x +1)(x −1+ln⁡x),当 x >1 时, ℎ′(x)>0,ℎ(x) 递增; 当 0<x <1 时, ℎ′(x)<0,ℎ(x) 递减.所以 ℎ(x)⩾ℎ(1)=0, 即 f(x)⩽g(x) 恒成立.综上可知, b −2a 的最小值为 −53.【点睛】求线性表达式型 ma +nb(m,n 为常数) 的最值时, 赋值的要点在于把原不等式变成关于 a,b 的二元一次不等式, 然后根据 a,b 的系数比与 m:n 相等求出 x 0 (简称等比例赋值法 ).【例2】若函数 f(x)=aln⁡x +12x 2+2bx 在区间 [1,3] 上单调递增, 则 a +4b 的最小值为 .【答案】−4【点睛】这里用了等比【例】赋值法, 要点睛意等号成立的条件. 由已知得ax+2b+x⩾0对x∈[1,3]恒成立, 与目标式a+4b比较, 令1x:2=1:4, 得x=2, 因此令x= 2. 当a+4b=−4时, 由g(x)⩾0=g(2)知x=2是g(x)的极值点, 所以g′(2)=0⇒a=4,b=−2.比值型【例3】已知函数f(x)=ln⁡x+(e−a)x−2b, 若不等式f(x)⩽0对x∈(0,+∞)恒成立, 则ba的最小值为 .【答案】- 12e.【解析】解法 1 : 消元法显然a>e,f′(x)=1x +(e−a), 易知x=1a−e为f(x)的极大值点,所以只需f(1a−e )⩽0, 即2b⩾−ln⁡(a−e)−1, 所以2ba⩾−ln⁡(a−e)−1a.今ेℎ(a)=−12⋅[ln⁡(a−e)+1]a,则ℎ′(a)=−12⋅ea−e−ln⁡(a−e)a2, 点睛意到ℎ′(2e)=0,易知a=2e为ℎ(a)的极小值点, ℎ(2e)=−12e .所以ba⩾−12e, 故ba的最小值为−12e.解法 2:零点比大小f(x)⩽0⇔ln⁡x+(e−a)x−2b⩽0⇔ln⁡x+ex⩽ax+2b, 即ln⁡x+ex⩽a(x+2ba)函数y=ln⁡x+ex与y=a(x+2ba )的零点分别为1e,−2ba由图可知: −2ba ⩾1e⇒ba⩽−12e, 故ba的最小值为−12e.解法 3 : 赋值法f(x)⩽0⇔ln⁡x +ex ⩽ax +2b , 令 x =1e , 则 a ⋅1e +2b ⩾0⇒ba ⩾−12e .故 ba的最小值为 −12e.【点睛 1】求比值型的最值时, 赋值的要点在于把原不等式改写成一边只含有目标式分子、分母的线性结构, 再令另一边为 0 , 找到 x 0.【点睛 2】观察不等式 ln⁡x +ex ⩽ax +2b 与目标式 ba 的结构, 进行恰到好处的赋值. 只需让 ln⁡x +ex =0, 便得 a ⋅1e+2b ⩾0, 进而可求得 ba的最值. 解方程 ln⁡x +ex =0, 可得 x =1e , 从而有上面的解法.【点睛 3】本题我们用了消元法、零点比大小和赋值法, 显然赋值法最为简捷.【例4】已知不等式 (e −a)e x +x +b +1⩽0 恒成立, 其中 e 为自然常数, 则 b+1a的最大值为 .【答案】 1e【解析】赋值法(e −a)e x +x +b +1⩽0⇔ae x −(b +1)⩾e x+1+x , 令 e x+1+x =0, 得 x =−1, 则 a ⋅1e −(b +1)⩾0⇒b+1a⩽1e , 故b+1a的最大值为 1e .乘积型【例5】若e x−x+12x2⩾12x2+ax+b恒成立, 求(a+1)b的最大值.【答案】e2【解析】解法 1 : 消元法e x−x+12x2⩾12x2+ax+b⇔e x−(a+1)x−b⩾0,令g(x)=e x−(a+1)x−b, 则g′(x)=e x−(a+1),(1)若a+1<0, 则g′(x)>0, 则g(x)=e x−(a+1)x−b在R上单增,当x→−∞时, f(x)→−∞,与g(x)⩾0矛盾, 舍去.(2)若a+1>0, 由g′(x)=0得x=ln⁡(a+1),所以g(x)在(−∞,ln⁡(a+1))单减, 在(ln⁡(a+1),+∞)单增, 则g(x)min=g(ln⁡(a+ 1))=(a+1)−(a+1)ln⁡(a+1)−b⩾0,即b⩽(a+1)−(a+1)ln⁡(a+1)，则b(a+1)⩽(a+1)2−(a+1)2ln⁡(a+1)令ℎ(t)=t2−t2ln⁡t,t>0, 则ℎ′(t)=t−2tln⁡t=t(1−2ln⁡t)所以ℎ(t)在(0,√e)单增, (√e,+∞)单减, 所以ℎ(t)max=ℎ(√e)=e2,(3) 当a+1=0时, (a+1)b=0,综上: (a+1)b最大值为e2.解法 2: 消元法e x −x +12x 2⩾12x 2+ax +b ⇔e x −(a +1)x −b ⩾0,即 b ⩽e x −(a +1)x(1) 若 a +1<0, 则 (a +1)b ⩾(a +1)e x −(a +1)2x ,令ℎ(x)=(a +1)e x −(a +1)2x,ℎ′(x)=(a +1)e x −(a +1)2=(a +1)[e x −(a +1)]<0所以当 x →−∞ 时, f(x)→+∞, 则 (a +1)b ⩾(a +1)e x −(a +1)2x 不成立(2) 若 a +1>0, 则 (a +1)b ⩽(a +1)e x −(a +1)2x ；令 ℎ(x)=(a +1)e x −(a +1)2x ,由 ℎ′(x)=0 得 x =ln⁡(a +1), 则 ℎ(x) 在 (0,ln⁡(a +1)) 单减, (ln⁡(a +1),+∞) 单增,所以 ℎ(x)=(a +1)2−(a +1)2ln⁡(a +1),令 g(t)=t 2−t 2ln⁡t,t >0, 则 g ′(t)=t −2tln⁡t =t(1−2ln⁡t),所以 g(t) 在 (0,√e) 单增, (√e,+∞) 单减, 所以 g(t)max =g(√e)=e2(3) 当 a +1=0 时, (a +1)b =0,综上: (a +1)b 最大值为 e2.【点睛】根据所求目标, 在 a,b 都在变的情况下, 求 (a +1)b 的最大值, 把 b 移到一边, 同乘以 (a +1), 构造出 (a +1)b , 在等式的右边成功地消灭了变量 b .【例6】已知函数 f(x)=e x −xa −b , 当实数 a >0 时, 对于 x ∈R 都有 f(x)⩾0 恒成立, 则 a 2b 的最大值为（）A. −1e2B. 1e2C. −2e2D. 2e2【答案】A【解析】f′(x)=e x−1a , 易知x=ln⁡1a为极小值点, 则f(x)min=f(1a)=1a+ln⁡aa−b⩾ 0 , 所以1a +ln⁡aa⩾b, 则a2b⩽a+aln⁡a, 令g(a)=a+aln⁡a, 易得g(a)min=g(1e2)=−1e2. 故a2b的最大值为−1e2.强化训练1.已知不等式ln⁡(x+1)−1⩽a(x+ba )对一切正数x恒成立, 则ba的最小值为 .【答案】1-e【解析】解法1:零点比大小ln⁡(x+1)−1⩽a(x+ba)恒成立,直线y=a(x+ba)在函数y=ln⁡(x+1)−1图象的上方,直线y=a(x+ba )在x轴上的截距为−ba,函数y=ln⁡(x+1)−1在(e−1,0)处的切线为y=1e[x−(e−1)],则 −ba⩽e −1⇒b a ⩾1−e , 故 (ba)min=1−e解法 2 : 赋值法取 x =e −1,便有 ba ⩾1−e2.已知函数 f(x)=2ax 2+bx −3a +1,x ∈[−4,4], 若 f(x)⩾0 恒成立, 则 5a +b 的取值范围是当 5a +b 取得最小值时, a = .【答案】 a =121【解析】赋值法2ax 2+bx −3a +1⩾0,x ∈[−4,4], 即 (2x 2−3)a +xb +1⩾0,x ∈[−4,4]. 令，解得或则由 f(3)⩾0, 得 5a +b ⩾−13; 由 f (−12)⩾0, 得5a +b ⩽2.所以 5a +b 的取值范围是 [−13,2].当 5a +b =−13时, f(x)⩾0=f(3),可知 x =3 是函数 f(x) 的极值点 (或对称轴), 所以 −b 4a =3, 易得 a =121.3.已知不等式 x −3ln⁡x +1⩾mln⁡x +n(m ≠−3) 对 x >0 恒成立, 则 n−3m+3 的最大值为 .【答案】 −ln⁡2 【解析】赋值法，令，可得4.若对于任意正实数 x , 都有 ln⁡x −aex −b +1⩽0 (e 为自然对数的底数) 成立, 则 a +b 的最小值是 .【答案】0【解析】令x=1e, 代入得: a+b⩾0,以下说明a+b=0时满足条件,当a=1,b=−1时, 令f(x)=ln⁡x−ex+1+1=ln⁡x−ex+2,则f′(x)=1x −e=1−exx, 令f′(x)=0, 解得: x=1e,可知当x∈(0,1e )时, f′(x)>0, 当x∈(1e,+∞)时, f′(x)<0,故对任意正实数x, 都有f(x)⩽f(1e)=0,故a=1,b=−1时, a+b=0, 满足题意, 故a+b的最小值是 0 ,故答案为: 0 .5.已知不等式e x⩾ax+b(a,b∈R, 且a≠0)对任意实数x恒成立, 则b−2a的最大值为A. 2−ln⁡2B. 1−ln⁡2C. −2ln⁡2D. −ln⁡2【答案】D【解析】解法 1:零点比大小由e x⩾ax+b得e x−2⩾ax+(b−2)=a(x+b−2a),考虑y=e x−2与y=a(x+b−2a)在x轴上的截距,只需−b−2a ⩾ln⁡2⇒b−2a⩽−ln⁡2.解法 2 : 赋值法令e x−2=0即x=ln⁡2, 结合a>0, 立得b−2a⩽−ln⁡2.6.已知函数f(x)=e x−12x2+x3, 若x∈R时, 恒有f′(x)⩾3x2+ax+b, 则ab+ b的最大值为（）A. √eB. √e2C. e2D. e【答案】C【解析】因为函数f(x)=e x−12x2+x3, 则f′(x)=e x−x+3x2, 由题可知, 对x∈R, 恒有e x−x+3x2⩾3x2+ax+b⇒e x−x−ax−b⩾0成立, 令g(x)=e x−x−ax, 则g′(x)=e x−1−a当a<−1时, 函数g(x)在R上单调递增, 且x→−∞时, g(x)→−∞, 不符合题意;当a=−1时, ab+b=0, 当a>−1时, 令g′(x)=e x−1−a>0⇒x>ln⁡(1+ a),所以函数 g(x) 在 (ln⁡(1+a),+∞) 上单调递增, 且在 (−∞,ln⁡(1+a)) 上单调递减;所以 g(x)min =g[ln⁡(1+a)]=e ln⁡(1+a)−ln⁡(1+a)−aln⁡(1+a)=(1+a)− (1+a)ln⁡(1+a),故 (1+a)−(1+a)ln⁡(1+a)−b ⩾0⇒b(1+a)⩽(1+a)2−(1+a)2ln⁡(1+a),令 t =1+a >0, 则 ℎ(t)=t 2−t 2ln⁡t , 且 ℎ′(t)=2t −(2tln⁡t +t)=t(1−2ln⁡t),当 t ∈(0,√e) 时, ℎ′(t)>0, 函数 ℎ(t) 单调递增; 当 t ∈(√e,+∞) 时, ℎ′(t)<0, 函数ℎ(t) 单调递减,所以 ℎ(t)max =ℎ(√e)=(√e)2−(√e)2ln⁡√e =e2, 故 b(1+a)⩽e2, 综上所述, ab +b 的最大值为 e2.7.设函数 f(x)=ln⁡(ax +b)−x(a,b ∈R), 若 f(x)⩽0 恒成立, 则 ab 的最大值为 . 【答案】 e2【解析】 ln⁡(ax +b)⩽x 恒成立, 即 e x ⩾ax +b >0 恒成立, a,x,b >0e x ⩾ax +b ⩾2√ax ⋅b , 所以 ab ⩽e 2x 4x(x >0), 于是 ab ⩽(e 2x4x)min=e2.8.已知 a ≠0, 函数 y =f(x)=ae x ,y =g(x)=ealn⁡x +b ( e 为自然对数的底数), 若存在一条直线与曲线 y =f(x) 和 y =g(x) 均相切, 则 ba 最大值是【答案】e切线放缩知识与方法1. 切线放缩对于含有指数、对数或三角函数等超越式的函数或不等式问题, 有时我们可以利用导数的几何意义进行以直代曲, 即考虑函数f(x)图象上某点x=x0处的切线y=kx+b, 结合函数的凹凸性进行切线放缩, 使问题便于解决.特别地, 当f(x)⩾kx+b为下凸函数时, 则f(x)⩾kx+b; 当f(x)为上凸函数时, 则f(x)⩽kx+b. 两个不等式中等号成立的条件刚好是x=x0.将f(x)放大或缩小为kx+b, 得到f(x)⩾kx+b或f(x)⩽kx+b, (其中k=f′(x0),y=kx+b为f(x)在x=x0处的切线y=f′(x0)(x−x0)+f(x0))叫做切线放缩.对某些求函数的最小值或证明不等式的问题, 巧用切线放缩, 会有意想不到的效果.2. 常用的切线不等式x;(5)sin⁡x⩽x(x⩾0).(1) e x⩾x+1;(2)ln⁡x⩽x−1;(3)e x⩾ex;(4)ln⁡x⩽1e【点睛】在e x⩾x+1中, 将x换成ln⁡x, 即得x⩾ln⁡x+1⇒ln⁡x⩽x−1;在e x⩾x+1中, 将x换成x−1, 即得e x−1⩾x⇒e x⩾ex;x;在e x⩾ex中, 将x换成ln⁡x, 即得x⩾elnx⇔ln⁡x⩽1e在ln⁡x⩽x−1中, 将x换成x+1, 即得ln⁡(x+1)⩽x.典型例题逆用求导法则型【例1】若x,y是实数, e是自然对数的底数, e x+y+2−3⩽ln⁡(y−2x+1)+3x, 则2x+y= .【答案】- 83【解析】结合不等式e x⩾x+1 (当且仅当x=0时等号成立),可得: e x+y+2⩾(x+y+2)+1=x+y+3 (1),结合不等式ln⁡x⩽x−1 (当且仅当x=1时等号成立),则ln⁡(y−2x+1)⩽(y−2x+1)−1, 所以−ln⁡(y−2x+1)⩾2x−y(1) (2) 两式相加, 即得: e x+y+2−ln⁡(y −2x +1)⩾(x +y +3)+(2x −y)=3x +3 又已知 e x+y+2−3⩽ln⁡(y −2x +1)+3x ,所以 e x+y+2−3=ln⁡(y −2x +1)+3x , 于是(1)与 (2) 中的等号同时成立,所以 {x +y +2=0,y −2x +1=1, 解得 {x =−23,y =−43,所以 2x +y =−83. 故答案为: −83.【点睛】本题利用了夹逼法. 根据切线不等式 e x ⩾x +1 与 ln⁡x ⩽x −1, 并结合已知条件, 通过夹逼由不等式得到了方程, 最后点睛意到两个不等式中等号成立的条件, 解方程组即可得到答案.【例2】已知函数 f(x)=ax +ln⁡x +1, 若对任意的 x >0,f(x)⩽xe 2x 恒成立, 则求实数 a 的取值范围是 .【答案】 (−∞,2]【解析】解法 1: :切线放缩, 利用 e x ⩾x +1 对任意的 x >0,f(x)⩽xe 2x 恒成立,等价于 a ⩽xe 2x −(ln⁡x+1)x在 (0,+∞) 上恒成立.因为 xe 2x −(ln⁡x +1)=e 2x+ln⁡x −(ln⁡x +1)⩾(2x +ln⁡x +1)−(ln⁡x +1)=2x ,所以 xe 2x −(ln⁡x+1)x⩾2x x=2. 当且仅当 2x +ln⁡x =0 时等号成立 (方程显然有解),即 (xe 2x −(ln⁡x+1)x)min=2, 所以 a ⩽2.故答案为: (−∞,2].解法 2: 隐零点因为 f(x)=ax +ln⁡x +1, 所以对任意的 x >0,f(x)⩽xe 2x 恒成立, 等价于 a ⩽e 2x −ln⁡x+1x在 (0,+∞) 上恒成立.令 m(x)=e 2x −ln⁡x+1x(x >0), 则只需 a ⩽m(x)min 即可, 则 m ′(x)=2x 2e 2x +ln⁡xx 2,再令 g(x)=2x 2e 2x +ln⁡x(x >0), 则 g ′(x)=4(x 2+x )e 2x +1x>0, 所以 g(x) 在(0,+∞)上单调递增, 因为 g (14)=√e 8−2ln⁡2<0,g(1)=2e 2>0,所以 g(x) 有唯一的零点 x 0, 且 14<x 0<1,所以当 0<x <x 0 时, m ′(x)<0, 当 x >x 0 时, m ′(x)>0, 所以 m(x) 在 (0,x 0) 上单调递减, 在 (x 0,+∞) 上单调递增,因为 2x 02e 2x 0+ln⁡x 0=0, 所以 ln⁡2+2ln⁡x 0+2x 0=ln⁡(−ln⁡x 0), 即 ln⁡(2x 0)+2x 0=ln⁡(−ln⁡x 0)+(−ln⁡x 0) ，设 s(x)=ln⁡x +x(x >0), 则 s ′(x)=1x +1>0, 所以函数 s(x) 在 (0,+∞) 上单调递增,因为 s (2x 0)=s (−ln⁡x 0), 所以 2x 0=−ln⁡x 0, 即 e 2x 0=1x 0,2=−ln⁡x 0x 0,所以 m(x)⩾m (x 0)=e 2x 0−ln⁡x 0+1x 0=1x 0−ln⁡x 0x 0−1x 0=2, 则有 a ⩽2,所以实数a的取值范围为(−∞,2]. 故答案为: (−∞,2].【例3】已知a1,a2,a3,a4成等比数列, 且a1+a2+a3+a4=ln⁡(a1+a2+a3), 若a1>1, 则（）A. a1<a3,a2<a4B. a1>a3,a2<a4C. a1<a3,a2>a4D. a1>a3,a2>a4【答案】B【解析】(利用ln⁡x⩽x−1)由a1+a2+a3+a4=ln⁡(a1+a2+a3), 可得a1+a2+a3+a4=ln⁡(a1+a2+a3)⩽a1+a2+a3−1, 所以a4⩽−1, 故公比q<0. 若q⩽−1, 则a1+a2+a3+a4=a1(1+q)(1+q2)⩽0, 而a1+a2+a3=a1(1+q+q2)⩾a1>1, 即ln⁡(a1+a2+a3)>0, 矛盾; 所以−1<q<0, 所以a1−a3=a1(1−q2)> 0,a2−a4=a1q(1−q2)<0, 所以a1>a3,a2<a4, 故选B.多变量轮换式的切线放缩,x∈[0,3], 已知数列{a n}满足0<a n⩽3,n∈N∗, 且满足a1+【例4】f(x)=3+x1+x2a2+⋯+a2010=670, 则f(a1)+f(a2)+⋯+f(a2010)=A. 有最大值 6030B. 有最大值 6027C. 有最小值 6027D. 有最小值 6030【答案】A【解析】由 f(x)=3+x 1+x2(0⩽x ⩽3), 得 f ′(x)=−x 2−6x+1(1+x 2)2, 所以 f ′(13)=−910,f(x) 在x =13 处的切线方程为 y =−910x +3310, 下证 f(x)=3+x1+x 2⩽310(11−3x). 而 f(x)=3+x 1+x 2⩽310(11−3x)⇔(x −3)(x −13)2⩽0.因为 x ∈[0,3], 所以 (x −3)(x −13)2⩽0 成立, 故 f(x)=3+x 1+x 2⩽310(11−3x). 所以当 0<a n ⩽3,n ∈N ∗ 时, 有 f (a n )⩽310(11−3a n ),f (a 1)+f (a 2)+⋯+f (a 2010)⩽310[11×2010−3(a 1+a 2+⋯+a 2010)]=6030. 故 f (a 1)+f (a 2)+⋯+f (a 2010) 最大值 6030 .【点睛】本题利用函数 f(x)=3+x1+x 2 在 x =13 处的切线进行放缩, 思路如下: 点睛意到 a 1+ a 2+⋯+a 2010=670, 当 a 1=a 2=⋯=a 2010 时, 有 a 1=a 2=⋯=a 2010=13,即 13是各元相等时候的平衡点, 于是求出函数在平衡点的切线方程 y =−910x +3310, 可得 f(x)⩽310(11−3x).双参数最值的切线放缩【例5】已知不等式 ln⁡(x +1)−1⩽a (x +ba ) 对一切正数 x 恒成立, 则 ba 的最小值为【解析】 ln⁡(x +1)−1⩽a (x +ba ) 恒成立,直线 y =a (x +ba ) 在函数 y =ln⁡(x +1)−1 图象的上方,直线y=a(x+ba )在x轴上的截距为−ba,函数y=ln⁡(x+1)−1在(e−1,0)处的切线为y=1e[x−(e−1)],则−ba ⩽e−1⇒ba⩾1−e, 故(ba)min=1−e【点睛】本题利用两函数的零点比较大小, 其实就是切线放缩.强化训练1.已知函数f(x)=e x−1,g(x)=ln⁡(x+1), 直线l与y=f(x)的图象相切, 与y= g(x)的图象也相切, 则直线的l方程是 .【答案】y=x【解析】f(x)=e x−1与g(x)=ln⁡(x+1)互为反函数, 其图象如图,其公共点为O(0,0),由f(x)=e x−1, 得f′(x)=e x, 所以f′(0)=1,曲线f(x)=e x−1在O(0,0)处的切线方程为y=x,由g(x)=ln⁡(x+1), 得g′(x)=1, 所以g′(0)=1,x+1曲线g(x)=ln⁡(x+1)在O(0,0)处的切线方程为y=x,所以曲线f(x)=e x−1与曲线g(x)=ln⁡(x+1)的公切线为y=x.故答案为: y=x.2.已知实数a,b,c满足e a+c+e2b−c−1⩽a+2b+1 (e 为自然对数的底数), 则a2+b2的最小值是 .【答案】15【解析】设u(x)=e x−(x+1), 则u′(x)=e x−1, 可知u(x)⩾u(0)=0, 即e x⩾x+1;由不等式性质可知e a+c+e2b−c−1⩾a+c+1+2b−c=a+2b+1, 当且仅当a+c= 2b30第 21 页共 21页 −c −1=0 时取等号;又因为 e a+c +e 2b−c−1⩽a +2b +1,即有: e a+c +e 2b−c−1=a +c +1,所以 a +c =2b −c −1=0; 即 a =−c,b =c+12;所以 a 2+b 2=c 2+(c+1)24=54c 2+c 2+14=54(c +15)2+15⩾15当且仅当 c =−15 时取等号, 故 a 2+b 2 的最小值是 15, 答案为 :15.3.函数 f(x)=e x−a +x,g(x)=ln⁡(x +2)−4e a−x , 若 ∃x 0 使得 f (x 0)−g (x 0)=3, 则 a = .【答案】-1- ln⁡2 【解析】令 f(x)−g(x)=x +e x−a −1n(x +2)+4e a−x ,令 y =x −ln⁡(x +2),y ′=1−1x+2=x+1x+2,故 y =x −ln⁡(x +2) 在 (−2,−1) 上是减函数 (−1,+∞) 上是增函数,故当 x =−1 时, y 有最小值 −1−0=−1,而 e x−a +4e a−x ⩾4. ( 当且仅当 e x−a =4e a−x , 即 x =ln⁡2+a 时, 等号成立)。

2023届高考数学二轮复习大题专讲专练：双参数最值问题与切线放缩

第30讲双参数最值问题知识与方法含参问题一直是高考中的重点与难点. 高考真题及模拟题中常出现“恒成立”为背景的双参数的范围或最值问题. 处理此类问题, 常用有以下方法:1消元法2零点比大小法零点比大小是指将函数y=ax+b 与函数y=f(x) 的零点比较大小, 进而解决问题. 图象上看, 是观察直线y=ax+b 与曲线y=f(x) 的横截距的大小关系. 此方法要求y=f(x) 函数具有凹凸性, 可以解决形如“已知ax+b⩾f(x) (或⩽f(x)) 恒成立, 求bk 的最值”的问题,一般有如下两种形式:(1) 若ax+b⩾f(x) 恒成立, f(x) 为上凸函数, 如下左图, 则x1⩽x2;(2) 若y=ax+b⩽f(x) 恒成立, f(x) 为下凸函数, 如下右图, 则x1⩾x2.由(1)或(2)得出x1,x2的大小,进而可以求得bk的最值.3. 赋值法对比不等式与目标式的结构, 发现当自变量取某个值时恰好构造出目标式.赋值法是零点比大小法方法的优化和改进,能快速解决线性表达式型、比值型的客观题. 点睛意领会“等比例赋值法”进行恰到好处的赋值.典型例题【例1】若(x2+x)ln 1x −ax⩽23x3+(1−a)x2−2ax+b 恒成立, 求b−2a 的最小值.【答案】−53【解析】解法1: 消元法设F(x)=23x3+(1−a)x2−2ax+b−(x2+x)ln 1x+ax ,则F′(x)=(2x+1)(ln x+x+令 ℎ(x)=ln x +x +1−a 得 ℎ(x) 单调递增, 故存在唯一 x 0 使得 ℎ(x 0)=0 , 即 a =x 0+ln x 0+1当 x ∈(0,x 0) 时, F(x) 单调递减当 x ∈(x 0,+∞) 时, F(x) 单调递增,故 F(x)min =F (x 0)=−13x 03−x 02−x 0+b.所以 F(x)min =F (x 0)⩾0, 即 b ⩾13x 03+x 02+x 0,b −2a ⩾13x 03+x 02−x 0−2ln x 0−2,t(x)=13x 3+x 2−x −2ln x −2,t ′(x)=(x−1)(x 2+3x+2)x,当 x ∈(0,1),t(x) 单调递减; 当 x ∈(1,+∞),t(x) 单调递增, 故 t(x)min =t(1)=−53. 所以 b −2a 的最小值为 −53.解法 2: :赋值法f(x)⩽g(x)⇔b −(x 2+x )a ⩾−(x 2+x )ln x −23x 3−x 2令 x 2+x =2 (等比例赋值法), 解得 x =1 (舍 x =−2 ), 则 b −2a ⩾−53.当 b −2a =−53 时, 由 f(x)−g(x)⩽0=f(1)−g(1) 知 x =1 是 f(x)−g(x) 的极值点,所以 f ′(1)−g ′(1)=0, 解得 a =2,b =73.下面证明: 当 a =2,b =73时, f(x)⩽g(x).证明:令 ℎ(x)=g(x)−f(x)=23x 3−x 2−2x +73+(x 2+x )ln x. 则 ℎ′(x)=(2x +1)(x −1+ln x),当 x >1 时, ℎ′(x)>0,ℎ(x) 递增; 当 0<x <1 时, ℎ′(x)<0,ℎ(x) 递减. 所以 ℎ(x)⩾ℎ(1)=0, 即 f(x)⩽g(x) 恒成立. 综上可知, b −2a 的最小值为 −53.【点睛】求线性表达式型 ma +nb(m,n 为常数) 的最值时, 赋值的要点在于把原不等式变成关于 a,b 的二元一次不等式, 然后根据 a,b 的系数比与 m:n 相等求出 x 0 (简称等比例赋值法 ).【例2】若函数 f(x)=aln x +12x 2+2bx 在区间 [1,3] 上单调递增, 则 a +4b 的最小值为 . 【答案】 −4【解析】 g(x)=f ′(x)=ax +x +2b ⩾0 对 x ∈[1,3] 恒成立, 即 ax +2b +x ⩾0 对 x ∈[1,3] 恒成立, 与目标式 a +4b 比较, 令 1x :2=1:4, 得 x =2,因此令 x =2 (等比例赋值则 g(2)=a2+2+2b ⩾0⇒a +4b ⩾−4. ( a =1,b =−54时等号成立)所以 a +4b 的最小值为 −4.【点睛】这里用了等比【例】赋值法, 要点睛意等号成立的条件. 由已知得 ax +2b +x ⩾0 对 x ∈ [1,3] 恒成立, 与目标式 a +4b 比较, 令 1x :2=1:4 , 得 x =2 , 因此令 x =2 . 当 a +4b = −4 时, 由 g(x)⩾0=g(2) 知 x =2 是 g(x) 的极值点, 所以 g ′(2)=0⇒a =4,b =−2.比值型【例3】已知函数 f(x)=ln x +(e −a)x −2b, 若不等式 f(x)⩽0 对 x ∈(0,+∞) 恒成立, 则 ba 的最小值为 . 【答案】-12e.【解析】解法 1 : 消元法显然 a >e,f ′(x)=1x +(e −a), 易知 x =1a−e为 f(x) 的极大值点,所以只需 f (1a−e)⩽0, 即 2b ⩾−ln (a −e)−1, 所以 2b a⩾−ln (a−e)−1a.今े ℎ(a)=−12⋅[ln (a−e)+1]a,则 ℎ′(a)=−12⋅ea−e−ln (a−e)a 2, 点睛意到 ℎ′(2e)=0,易知 a =2e 为 ℎ(a) 的极小值点, ℎ(2e)=−12e .所以 ba ⩾−12e , 故 ba 的最小值为 −12e . 解法 2:零点比大小f(x)⩽0⇔ln x +(e −a)x −2b ⩽0⇔ln x +ex ⩽ax +2b, 即 ln x +ex ⩽a (x +2b a)函数 y =ln x +ex 与 y =a (x +2ba) 的零点分别为 1e ,−2b a由图可知: −2b a⩾1e⇒b a⩽−12e, 故 ba的最小值为 −12e.解法 3 : 赋值法f(x)⩽0⇔ln x +ex ⩽ax +2b, 令 x =1e, 则 a ⋅1e+2b ⩾0⇒b a⩾−12e.故 b a的最小值为 −12e.【点睛 1】求比值型的最值时, 赋值的要点在于把原不等式改写成一边只含有目标式分子、分母的线性结构, 再令另一边为 0 , 找到 x 0.【点睛 2】观察不等式 ln x +ex ⩽ax +2b 与目标式 ba 的结构, 进行恰到好处的赋值. 只需让 ln x +ex =0 , 便得 a ⋅1e +2b ⩾0 , 进而可求得 b a 的最值. 解方程 ln x +ex =0 , 可得 x =1e , 从而有上面的解法.【点睛 3】本题我们用了消元法、零点比大小和赋值法, 显然赋值法最为简捷. 【例4】已知不等式 (e −a)e x +x +b +1⩽0 恒成立, 其中 e 为自然常数, 则 b+1a的最大值为 . 【答案】 1e【解析】赋值法(e −a)e x +x +b +1⩽0⇔ae x −(b +1)⩾e x+1+x , 令 e x+1+x =0 , 得 x =−1 , 则 a ⋅1e−(b +1)⩾0⇒b+1a⩽1e, 故 b+1a的最大值为 1e.乘积型【例5】若 e x −x +12x 2⩾12x 2+ax +b 恒成立, 求 (a +1)b 的最大值. 【答案】 e2【解析】解法 1 : 消元法e x −x +12x 2⩾12x 2+ax +b ⇔e x −(a +1)x −b ⩾0,令 g(x)=e x −(a +1)x −b, 则 g ′(x)=e x −(a +1),(1)若 a +1<0, 则 g ′(x)>0, 则 g(x)=e x −(a +1)x −b 在 R 上单增, 当 x →−∞ 时, f(x)→−∞,与 g(x)⩾0 矛盾, 舍去. (2)若 a +1>0, 由 g ′(x)=0 得 x =ln (a +1),所以 g(x) 在 (−∞,ln (a +1)) 单减, 在 (ln (a +1),+∞) 单增, 则 g(x)min =g(ln (a +1))=(a +1)−(a +1)ln (a +1)−b ⩾0,即 b ⩽(a +1)−(a +1)ln (a +1) ，则 b(a +1)⩽(a +1)2−(a +1)2ln (a +1)令 ℎ(t)=t 2−t 2ln t,t >0, 则 ℎ′(t)=t −2tln t =t(1−2ln t)所以ℎ(t) 在(0,√e) 单增, (√e,+∞) 单减, 所以ℎ(t)max=ℎ(√e)=e2, (3) 当a+1=0 时, (a+1)b=0,综上: (a+1)b 最大值为e2.解法2: 消元法e x−x+12x2⩾12x2+ax+b⇔e x−(a+1)x−b⩾0,即b⩽e x−(a+1)x(1)若a+1<0, 则(a+1)b⩾(a+1)e x−(a+1)2x,令ℎ(x)=(a+1)e x−(a+1)2x,ℎ′(x)=(a+1)e x−(a+1)2=(a+1)[e x−(a+1)]<0所以当x→−∞ 时, f(x)→+∞, 则(a+1)b⩾(a+1)e x−(a+1)2x 不成立(2) 若a+1>0, 则(a+1)b⩽(a+1)e x−(a+1)2x；令ℎ(x)=(a+1)e x−(a+1)2x,由ℎ′(x)=0 得x=ln (a+1), 则ℎ(x) 在(0,ln (a+1)) 单减, (ln (a+1),+∞) 单增,所以ℎ(x)=(a+1)2−(a+1)2ln (a+1),令g(t)=t2−t2ln t,t>0, 则g′(t)=t−2tln t=t(1−2ln t),所以g(t) 在(0,√e) 单增, (√e,+∞) 单减, 所以g(t)max=g(√e)=e2(3) 当a+1=0 时, (a+1)b=0,综上: (a+1)b 最大值为e2.【点睛】根据所求目标, 在a,b 都在变的情况下, 求(a+1)b 的最大值, 把b 移到一边, 同乘以(a+1), 构造出(a+1)b, 在等式的右边成功地消灭了变量b.【例6】已知函数f(x)=e x−xa −b ,当实数a>0 时, 对于x∈R 都有f(x)⩾0 恒成立, 则a2b 的最大值为（）A. −1e2B. 1e2C. −2e2D. 2e2【答案】A【解析】f′(x)=e x−1a , 易知x=ln 1a为极小值点, 则f(x)min=f(1a)=1a+ln aa−b⩾ 0 ,所以1a +ln aa⩾b ,则a2b⩽a+aln a ,令g(a)=a+aln a ,易得g(a)min=g(1e2)= −1e2.故a2b 的最大值为−1e2.强化训练1.已知不等式ln (x+1)−1⩽a(x+ba ) 对一切正数x 恒成立, 则ba的最小值为.【答案】1-e【解析】解法 1: 零点比大小ln (x +1)−1⩽a (x +ba) 恒成立,直线 y =a (x +ba ) 在函数 y =ln (x +1)−1 图象的上方, 直线 y =a (x +ba ) 在 x 轴上的截距为 −ba ,函数 y =ln (x +1)−1 在 (e −1,0) 处的切线为 y =1e [x −(e −1)],则 −b a ⩽e −1⇒b a ⩾1−e, 故 (ba )min=1−e解法 2 : 赋值法取 x =e −1,便有 ba ⩾1−e2.已知函数 f(x)=2ax 2+bx −3a +1,x ∈[−4,4] , 若 f(x)⩾0 恒成立, 则 5a +b 的取值范围是当 5a +b 取得最小值时, a = . 【答案】 a =121【解析】赋值法2ax 2+bx −3a +1⩾0,x ∈[−4,4], 即 (2x 2−3)a +xb +1⩾0,x ∈[−4,4]. 令，解得或则由 f(3)⩾0, 得 5a +b ⩾−13; 由 f (−12)⩾0, 得 5a +b ⩽2.所以 5a +b 的取值范围是 [−13,2].当 5a +b =−13 时, f(x)⩾0=f(3), 可知 x =3 是函数 f(x) 的极值点 (或对称轴), 所以 −b4a =3, 易得 a =121. 3.已知不等式 x −3ln x +1⩾mln x +n(m ≠−3) 对 x >0 恒成立, 则 n−3m+3 的最大值为 .【答案】 −ln 2 【解析】赋值法，令，可得4.若对于任意正实数x, 都有ln x−aex−b+1⩽0 (e 为自然对数的底数) 成立, 则a+b 的最小值是.【答案】0【解析】令x=1e, 代入得: a+b⩾0,以下说明a+b=0 时满足条件,当a=1,b=−1 时, 令f(x)=ln x−ex+1+1=ln x−ex+2,则f′(x)=1x −e=1−exx, 令f′(x)=0, 解得: x=1e,可知当x∈(0,1e ) 时, f′(x)>0, 当x∈(1e,+∞) 时, f′(x)<0,故对任意正实数x, 都有f(x)⩽f(1e)=0,故a=1,b=−1 时, a+b=0, 满足题意, 故a+b 的最小值是0 ,故答案为: 0 .5.已知不等式e x⩾ax+b(a,b∈R, 且a≠0) 对任意实数x 恒成立, 则b−2a 的最大值为A. 2−ln 2B. 1−ln 2C. −2ln 2D. −ln 2【答案】D【解析】解法1:零点比大小由e x⩾ax+b 得e x−2⩾ax+(b−2)=a(x+b−2a),考虑y=e x−2 与y=a(x+b−2a) 在x 轴上的截距,只需−b−2a ⩾ln 2⇒b−2a⩽−ln 2.解法2 : 赋值法令e x−2=0 即x=ln 2, 结合a>0, 立得b−2a⩽−ln 2.6.已知函数f(x)=e x−12x2+x3, 若x∈R 时, 恒有f′(x)⩾3x2+ax+b, 则ab+b的最大值为（） A. √e B.√e 2C. e2D. e【答案】C【解析】因为函数 f(x)=e x −12x 2+x 3 , 则 f ′(x)=e x −x +3x 2 , 由题可知, 对 x ∈R ,恒有 e x −x +3x 2⩾3x 2+ax +b ⇒e x −x −ax −b ⩾0 成立, 令 g(x)=e x −x −ax , 则 g ′(x)=e x −1−a 当 a <−1 时, 函数 g(x) 在 R 上单调递增, 且 x →−∞ 时, g(x)→−∞, 不符合题意;当 a =−1 时, ab +b =0, 当 a >−1 时, 令 g ′(x)=e x −1−a >0⇒x >ln (1+a), 所以函数 g(x) 在 (ln (1+a),+∞) 上单调递增, 且在 (−∞,ln (1+a)) 上单调递减; 所以 g(x)min =g[ln (1+a)]=e ln (1+a)−ln (1+a)−aln (1+a)=(1+a)− (1+a)ln (1+a),故 (1+a)−(1+a)ln (1+a)−b ⩾0⇒b(1+a)⩽(1+a)2−(1+a)2ln (1+a), 令 t =1+a >0, 则 ℎ(t)=t 2−t 2ln t, 且 ℎ′(t)=2t −(2tln t +t)=t(1−2ln t), 当 t ∈(0,√e) 时, ℎ′(t)>0, 函数 ℎ(t) 单调递增; 当 t ∈(√e,+∞) 时, ℎ′(t)<0, 函数 ℎ(t) 单调递减,所以 ℎ(t)max =ℎ(√e)=(√e)2−(√e)2ln √e =e2, 故 b(1+a)⩽e2, 综上所述, ab +b 的最大值为 e2.7.设函数 f(x)=ln (ax +b)−x(a,b ∈R), 若 f(x)⩽0 恒成立, 则 ab 的最大值为 .【答案】 e2【解析】 ln (ax +b)⩽x 恒成立, 即 e x ⩾ax +b >0 恒成立, a,x,b >0 e x ⩾ax +b ⩾2√ax ⋅b, 所以 ab ⩽e 2x 4x(x >0), 于是 ab ⩽(e 2x4x)min=e2.8.已知 a ≠0, 函数 y =f(x)=ae x ,y =g(x)=ealn x +b ( e 为自然对数的底数), 若存在一条直线与曲线 y =f(x) 和 y =g(x) 均相切, 则 ba 最大值是【答案】e【解析】 f ′(x)=ae x ,g ′(x)=ae x, 设切点分别为 (t,ae t ),(m,aelnm +b) , 则切线方程分别为 y −ae t =ae t (x −t);y −aelnm −b =ae m(x −m),由题意存在一条直线与曲线 y =f(x) 和 y =g(x) 均相切, 所以可得 ae m=ae t ,且 b =ae t (1−t)+ae −aelnm; 因为ae m=ae t , 且 a ≠0,=(1−t)e t+e−elnm=(1−t)e t−e(1−t)+e=e t+et−te t;所以ba令ℎ(t)=e t+et−te t, 则ℎ′(t)=−te t+e.当t=1 时, ℎ′(1)=0 ;当t<1 时, ℎ′(t)>0,ℎ(t) 单调递增; 当t>1 时, ℎ′(t)< 0,ℎ(t)单调递减;故当t=1 时取得最大值ℎ(1)=e.故答案为: e.切线放缩知识与方法1. 切线放缩对于含有指数、对数或三角函数等超越式的函数或不等式问题, 有时我们可以利用导数的几何意义进行以直代曲, 即考虑函数f(x) 图象上某点x=x0处的切线y=kx+b, 结合函数的凹凸性进行切线放缩, 使问题便于解决.特别地, 当f(x)⩾kx+b 为下凸函数时, 则f(x)⩾kx+b ;当f(x) 为上凸函数时, 则f(x)⩽kx+b. 两个不等式中等号成立的条件刚好是x=x0.将f(x) 放大或缩小为kx+b , 得到f(x)⩾kx+b 或f(x)⩽kx+b , (其中k= f′(x0),y =kx+b 为f(x) 在x=x0处的切线y=f′(x0)(x−x0)+f(x0)) 叫做切线放缩.对某些求函数的最小值或证明不等式的问题, 巧用切线放缩, 会有意想不到的效果.2. 常用的切线不等式(1) e x⩾x+1;(2)ln x⩽x−1;(3)e x⩾ex;(4)ln x⩽1x;(5)sin x⩽x(x⩾0).e【点睛】在 e x⩾x +1 中, 将 x 换成 ln x, 即得 x ⩾ln x +1⇒ln x ⩽x −1;在 e x ⩾x +1 中, 将 x 换成 x −1, 即得 e x−1⩾x ⇒e x ⩾ex; 在 e x ⩾ex 中, 将 x 换成 ln x, 即得 x ⩾elnx ⇔ln x ⩽1e x; 在 ln x ⩽x −1 中, 将 x 换成 x +1, 即得 ln (x +1)⩽x.典型例题逆用求导法则型【例1】若 x,y 是实数, e 是自然对数的底数, e x+y+2−3⩽ln (y −2x +1)+3x , 则2x +y = .【答案】- 83【解析】结合不等式 e x ⩾x +1 (当且仅当 x =0 时等号成立), 可得: e x+y+2⩾(x +y +2)+1=x +y +3 (1), 结合不等式 ln x ⩽x −1 (当且仅当 x =1 时等号成立),则 ln (y −2x +1)⩽(y −2x +1)−1, 所以 −ln (y −2x +1)⩾2x −y(1) (2) 两式相加, 即得: e x+y+2−ln (y −2x +1)⩾(x +y +3)+(2x −y)=3x +3 又已知 e x+y+2−3⩽ln (y −2x +1)+3x,所以 e x+y+2−3=ln (y −2x +1)+3x, 于是(1)与 (2) 中的等号同时成立, 所以 {x +y +2=0,y −2x +1=1, 解得 {x =−23,y =−43,所以 2x +y =−83. 故答案为: −83.【点睛】本题利用了夹逼法. 根据切线不等式 e x ⩾x +1 与 ln x ⩽x −1, 并结合已知条件,通过夹逼由不等式得到了方程, 最后点睛意到两个不等式中等号成立的条件, 解方程组即可得到答案.【例2】已知函数 f(x)=ax +ln x +1, 若对任意的 x >0,f(x)⩽xe 2x 恒成立, 则求实数 a 的取值范围是 . 【答案】 (−∞,2]【解析】解法 1: :切线放缩, 利用 e x ⩾x +1 对任意的 x >0,f(x)⩽xe 2x 恒成立, 等价于 a ⩽xe 2x −(ln x+1)x在 (0,+∞) 上恒成立.因为 xe 2x −(ln x +1)=e 2x+ln x −(ln x +1)⩾(2x +ln x +1)−(ln x +1)=2x, 所以 xe 2x −(ln x+1)x⩾2x x=2. 当且仅当 2x +ln x =0 时等号成立 (方程显然有解),即 (xe 2x −(ln x+1)x)min=2, 所以 a ⩽2.故答案为: (−∞,2]. 解法 2: 隐零点因为 f(x)=ax +ln x +1, 所以对任意的 x >0,f(x)⩽xe 2x 恒成立, 等价于 a ⩽e 2x −ln x+1x在 (0,+∞) 上恒成立.令 m(x)=e 2x −ln x+1x(x >0), 则只需 a ⩽m(x)min 即可, 则 m ′(x)=2x 2e 2x +ln xx 2,再令 g(x)=2x 2e 2x +ln x(x >0) , 则 g ′(x)=4(x 2+x )e 2x +1x>0 , 所以 g(x) 在(0,+∞)上单调递增, 因为 g (14)=√e 8−2ln 2<0,g(1)=2e 2>0,所以 g(x) 有唯一的零点 x 0, 且 14<x 0<1,所以当 0<x <x 0 时, m ′(x)<0, 当 x >x 0 时, m ′(x)>0, 所以 m(x) 在 (0,x 0) 上单调递减, 在 (x 0,+∞) 上单调递增,因为 2x 02e 2x 0+ln x 0=0, 所以 ln 2+2ln x 0+2x 0=ln(−ln x 0), 即 ln(2x 0)+2x 0=ln (−ln x 0)+(−ln x 0) ，设 s(x)=ln x +x(x >0), 则 s ′(x)=1x +1>0, 所以函数 s(x) 在 (0,+∞) 上单调递增,因为 s (2x 0)=s (−ln x 0), 所以 2x 0=−ln x 0, 即 e 2x 0=1x 0,2=−ln x 0x 0,所以 m(x)⩾m (x 0)=e 2x 0−ln x 0+1x 0=1x 0−ln x 0x 0−1x 0=2, 则有 a ⩽2,所以实数 a 的取值范围为 (−∞,2]. 故答案为: (−∞,2].【例3】已知 a 1,a 2,a 3,a 4 成等比数列, 且 a 1+a 2+a 3+a 4=ln(a 1+a 2+a 3), 若 a 1>1, 则（）A. a 1<a 3,a 2<a 4B. a 1>a 3,a 2<a 4C. a 1<a 3,a 2>a 4D. a 1>a 3,a 2>a 4 【答案】 B【解析】(利用 ln x ⩽x −1) 由 a 1+a 2+a 3+a 4=ln(a 1+a 2+a 3), 可得 a 1+a 2+a 3+a 4= ln(a 1+a 2+a 3)⩽a 1+a 2+a 3−1 , 所以 a 4⩽−1 , 故公比 q <0 . 若 q ⩽−1 , 则 a 1+a 2+a 3 +a 4=a 1(1+q)(1+q 2)⩽0 , 而 a 1+a 2+a 3=a 1(1+q +q 2)⩾a 1>1 ,即 ln(a 1+a 2+a 3)>0 , 矛盾; 所以 −1<q <0 , 所以 a 1−a 3=a 1(1−q 2)>0,a 2−a 4= a 1q (1−q 2)<0, 所以 a 1>a 3,a 2<a 4, 故选 B.多变量轮换式的切线放缩【例4】f(x)=3+x1+x 2,x ∈[0,3], 已知数列 {a n } 满足 0<a n ⩽3,n ∈N ∗, 且满足 a 1+a 2+⋯ +a 2010=670, 则 f (a 1)+f (a 2)+⋯+f (a 2010)= A. 有最大值 6030 B. 有最大值 6027 C. 有最小值 6027 D. 有最小值 6030 【答案】A【解析】由 f(x)=3+x1+x 2(0⩽x ⩽3) , 得 f ′(x)=−x 2−6x+1(1+x 2)2, 所以 f ′(13)=−910,f(x) 在x =13 处的切线方程为 y =−910x +3310 , 下证 f(x)=3+x 1+x 2⩽310(11−3x) . 而 f(x)=3+x 1+x 2⩽310(11−3x)⇔(x −3)(x −13)2⩽0.因为 x ∈[0,3], 所以 (x −3)(x −13)2⩽0 成立, 故 f(x)=3+x1+x 2⩽310(11−3x).所以当 0<a n ⩽3,n ∈N ∗ 时, 有 f (a n )⩽310(11−3a n ),f (a 1)+f (a 2)+⋯+f (a 2010)⩽310[11×2010−3(a 1+a 2+⋯+a 2010)]=6030.故 f (a 1)+f (a 2)+⋯+f (a 2010) 最大值 6030 . 【点睛】本题利用函数 f(x)=3+x 1+x 2在 x =13处的切线进行放缩, 思路如下: 点睛意到a 1+ a 2+⋯+a 2010=670 , 当 a 1=a 2=⋯=a 2010 时, 有 a 1=a 2=⋯=a 2010=13 , 即 13是各元相等时候的平衡点, 于是求出函数在平衡点的切线方程 y =−910x +3310, 可得 f(x)⩽310(11−3x).双参数最值的切线放缩【例5】已知不等式ln (x+1)−1⩽a(x+ba ) 对一切正数x 恒成立, 则ba的最小值为【解析】ln (x+1)−1⩽a(x+ba ) 恒成立,直线y=a(x+ba) 在函数y=ln (x+1)−1图象的上方,直线y=a(x+ba ) 在x 轴上的截距为−ba,函数y=ln (x+1)−1 在(e−1,0) 处的切线为y=1e[x−(e−1)],则−ba ⩽e−1⇒ba⩾1−e, 故(ba)min=1−e【点睛】本题利用两函数的零点比较大小, 其实就是切线放缩.强化训练1.已知函数f(x)=e x−1,g(x)=ln (x+1), 直线l 与y=f(x) 的图象相切, 与y= g(x) 的图象也相切, 则直线的l 方程是.【答案】y=x【解析】f(x)=e x−1 与g(x)=ln (x+1) 互为反函数, 其图象如图,其公共点为O(0,0),由f(x)=e x−1, 得f′(x)=e x, 所以f′(0)=1,曲线f(x)=e x−1 在O(0,0) 处的切线方程为y=x,由g(x)=ln (x+1), 得g′(x)=1x+1, 所以g′(0)=1,曲线g(x)=ln (x+1) 在O(0,0) 处的切线方程为y=x,所以曲线f(x)=e x−1 与曲线g(x)=ln (x+1) 的公切线为y=x.故答案为: y=x.2.已知实数a,b,c 满足e a+c+e2b−c−1⩽a+2b+1 (e 为自然对数的底数), 则a2+b2的最小值是.【答案】15【解析】设u(x)=e x−(x+1), 则u′(x)=e x−1, 可知u(x)⩾u(0)=0, 即e x⩾x+1;由不等式性质可知e a+c+e2b−c−1⩾a+c+1+2b−c=a+2b+1 ,当且仅当a+c= 2b−c−1=0 时取等号;又因为e a+c+e2b−c−1⩽a+2b+1,即有: e a+c+e2b−c−1=a+c+1,所以a+c=2b−c−1=0; 即a=−c,b=c+12;所以a2+b2=c2+(c+1)24=54c2+c2+14=54(c+15)2+15⩾15当且仅当c=−15时取等号, 故a2+b2的最小值是15, 答案为:15.3.函数f(x)=e x−a+x,g(x)=ln (x+2)−4e a−x, 若∃x0使得f(x0)−g(x0)=3, 则a= .【答案】-1- ln 2【解析】令f(x)−g(x)=x+e x−a−1n(x+2)+4e a−x,令y=x−ln (x+2),y′=1−1x+2=x+1x+2,故y=x−ln (x+2) 在(−2,−1) 上是减函数(−1,+∞) 上是增函数,故当x=−1 时, y 有最小值−1−0=−1,而e x−a+4e a−x⩾4. ( 当且仅当e x−a=4e a−x, 即x=ln 2+a 时, 等号成立);。

导数中放缩法(切线放缩、对数均值不等式)

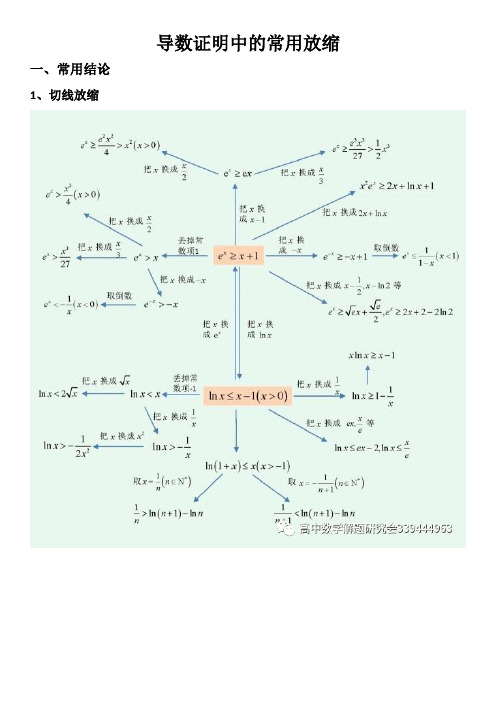
导数证明中的常用放缩一、常用结论1、切线放缩2、其它对数放缩（对数均值不等式）3、常用放缩公式：（考试时需给出证明过程）第一组：对数放缩（放缩成一次函数）ln 1x x ≤-，ln x x <，()ln 1x x +≤ （放缩成双撇函数）()11ln 12x x x x ⎛⎫<-> ⎪⎝⎭，()11ln 012x x x x ⎛⎫>-<< ⎪⎝⎭， )ln 1x x<>，)ln 01x x ><<，（放缩成二次函数）2ln x x x ≤-，()()21ln 1102x x x x +≤--<<，()()21ln 102x x x x +≥-> （放缩成类反比例函数）1ln 1x x≥-，()()21ln 11x x x x ->>+，()()21ln 011x x x x -<<<+，()ln 11x x x +≥+，()()2ln 101x x x x +>>+，()()2ln 101x x x x+<<+ 第二组：指数放缩（放缩成一次函数）1x e x ≥+，x e x >，x e ex ≥，（放缩成类反比例函数）()101x e x x ≤≤-，()10x e x x<-<，（放缩成二次函数）()21102x e x x x ≥++>，2311126x e x x x ≥+++，第三组：指对放缩()()ln 112x e x x x -≥+--=第四组：三角函数放缩()sin tan 0x x x x <<>，21sin 2x x x ≥-，22111cos 1sin 22x x x -≤≤-. 第五组：以直线1y x =-为切线的函数ln y x =，11x y e -=-，2y x x =-，11y x=-，ln y x x =.二、基础练习：练习题组一练习题组二：二、经典例题：母题 (2017·全国Ⅲ)已知函数f (x )＝ln x ＋ax 2＋(2a ＋1)x .(1)讨论f (x )的单调性；(2)当a <0时，证明f (x )≤－34a－2.(1)解 f (x )的定义域为(0，＋∞)，f ′(x )＝1x ＋2ax ＋2a ＋1＝(x ＋1)(2ax ＋1)x. 若a ≥0，则当x ∈(0，＋∞)时，f ′(x )>0，故f (x )在(0，＋∞)上单调递增．若a <0，则当x ∈⎝⎛⎭⎫0，－12a 时，f ′(x )>0；当x ∈⎝⎛⎭⎫－12a ，＋∞时，f ′(x )<0. 故f (x )在⎝⎛⎭⎫0，－12a 上单调递增，在⎝⎛⎭⎫－12a ，＋∞上单调递减． (2)证明由(1)知，当a <0时，f (x )在x ＝－12a 处取得最大值，最大值为f ⎝⎛⎭⎫－12a ＝ln ⎝⎛⎭⎫－12a －1－14a，所以f (x )≤－34a －2等价于ln ⎝⎛⎭⎫－12a －1－14a ≤－34a－2，即ln ⎝⎛⎭⎫－12a ＋12a＋1≤0. 设g (x )＝ln x －x ＋1，则g ′(x )＝1x－1. 当x ∈(0,1)时，g ′(x )>0；当x ∈(1，＋∞)时，g ′(x )<0.所以g (x )在(0,1)上单调递增，在(1，＋∞)上单调递减．故当x ＝1时，g (x )取得最大值，最大值为g (1)＝0.所以当x >0时，g (x )≤0.从而当a <0时，ln ⎝⎛⎭⎫－12a ＋12a ＋1≤0，即f (x )≤－34a－2. [子题1] 设函数f (x )＝ln x －x ＋1.证明：当x ∈(1，＋∞)时，1<x －1ln x<x . 证明 f ′(x )＝1x －1＝1－x x，x >0，当x >1时，f ′(x )<0，f (x )单调递减，当0<x <1时，f ′(x )>0，f (x )单调递增，∴f (x )＝ln x －x ＋1≤f (1)＝0，∴ln x ≤x －1，∴当x >1时，ln x <x －1，①且ln 1x <1x－1，② 由①得，1<x －1ln x ，由②得，－ln x <1－x x， ∴ln x >x －1x ，∴x >x －1ln x，综上所述，当x >1时，1<x －1ln x<x . [子题2] 已知函数f (x )＝e x －x 2.求证：当x >0时，e x ＋(2－e )x －1x≥ln x ＋1. 证明设g (x )＝f (x )－(e －2)x －1＝e x －x 2－(e －2)x －1(x >0)，则g ′(x )＝e x －2x －(e －2)，设m (x )＝e x －2x －(e －2)(x >0)，则m ′(x )＝e x －2，易得g ′(x )在(0，ln 2)上单调递减，在(ln 2，＋∞)上单调递增，又g ′(0)＝3－e>0，g ′(1)＝0，由0<ln 2<1，则g ′(ln 2)<0，所以存在x 0∈(0，ln 2)，使得g ′(x 0)＝0，所以当x ∈(0，x 0)∪(1，＋∞)时，g ′(x )>0；当x ∈(x 0,1)时，g ′(x )<0.故g (x )在(0，x 0)上单调递增，在(x 0,1)上单调递减，在(1，＋∞)上单调递增，又g (0)＝g (1)＝0，所以g (x )＝e x －x 2－(e －2)x －1≥0，故当x >0时，e x ＋(2－e )x －1x≥x . 又由母题可得ln x ≤x －1，即x ≥ln x ＋1，故e x ＋(2－e )x －1x≥ln x ＋1. 规律方法利用导数证明不等式f (x )>g (x )的基本方法(1)若f (x )与g (x )的最值易求出，可直接转化为证明f (x )min >g (x )max .(2)若f (x )与g (x )的最值不易求出，可构造函数h (x )＝f (x )－g (x )，然后根据函数h (x )的单调性或最值，证明h (x )>0.(3)通过题目中已有的或常用的不等式进行证明．(4)利用赋值法证明与正整数有关的不等式.跟踪演练1．(2018·全国Ⅰ)已知函数f (x )＝a e x －ln x －1.(1)设x ＝2是f (x )的极值点，求a ，并求f (x )的单调区间；(2)证明：当a ≥1e时，f (x )≥0. (1)解 f (x )的定义域为(0，＋∞)，f ′(x )＝a e x －1x. 由题设知，f ′(2)＝0，所以a ＝12e 2. 从而f (x )＝12e 2e x －ln x －1，f ′(x )＝12e 2e x －1x. 当0<x <2时，f ′(x )<0；当x >2时，f ′(x )>0.所以f (x )的单调递增区间为(2，＋∞)，单调递减区间为(0,2)．(2)证明当a ≥1e 时，f (x )≥e x e－ln x －1. 设g (x )＝e x e－ln x －1(x ∈(0，＋∞))，则g ′(x )＝e x e －1x. 当0<x <1时，g ′(x )<0；当x >1时，g ′(x )>0.所以x ＝1是g (x )的最小值点．故当x >0时，g (x )≥g (1)＝0.因此，当a ≥1e时，f (x )≥0. 2．(2020·北京市陈经纶中学模拟)已知函数f (x )＝ln x －1x－ax .若1<a <2，求证：f (x )<－1. 证明 f (x )的定义域为(0，＋∞)，为了证明f (x )<－1，即ln x －1x－ax <－1，只需证明ln x －1－ax 2<－x ，即ln x <ax 2－x ＋1，令m (x )＝ln x －x ＋1(x >0)，则m ′(x )＝1x－1，令m ′(x )>0，得0<x <1；令m ′(x )<0，得x >1，所以m (x )在(0,1)上单调递增，在(1，＋∞)上单调递减，所以m (x )max ＝m (1)＝0，即ln x －x ＋1≤0，则ln x ≤x －1.令n (x )＝ax 2－2x ＋2，因为1<a <2，所以Δ＝4－8a <0，所以n (x )>0恒成立，即ax 2－2x ＋2>0，所以ax 2－x ＋1>x －1.综上所述，ln x <ax 2－x ＋1，即当1<a <2时，f (x )<－1.（2017年全国新课标1·理·21）已知()()22x x f x ae a e x =+--.（1）讨论()f x 的单调性；（2）若()f x 有两个零点，求a 的取值范围.解析：（1）()()()()2'221211x x x x f x ae a e e ae =+--=+-若0a ≤，则()'0f x <恒成立，所以()f x 在R 上递减；若0a >，令()'0f x =，得11,ln x e x a a ==. 当1ln x a <时，()'0f x <，所以()f x 在1,ln a ⎛⎫-∞ ⎪⎝⎭上递减；当1lnx a >时，()'0f x >，所以()f x 在1ln ,a ⎛⎫+∞ ⎪⎝⎭上递增. 综上，当0a ≤时，()f x 在R 上递减；当0a >时，()f x 在1,ln a ⎛⎫-∞ ⎪⎝⎭上递减，在1ln ,a ⎛⎫+∞ ⎪⎝⎭上递增. （2）()f x 有两个零点，必须满足()min 0f x <，即0a >，且()min 111ln1ln 0f x f a a a ⎛⎫==--< ⎪⎝⎭. 构造函数()1ln g x x x =--，0x >. 易得()1'10g x x =--<，所以()1ln g x x x =--单调递减. 又因为()10g =，所以()11111ln 01101g g a a a a a ⎛⎫--<⇔<⇔>⇔<< ⎪⎝⎭. 下面只要证明当01a <<时，()f x 有两个零点即可，为此我们先证明当0x >时，ln x x >. 事实上，构造函数()ln h x x x =-，易得()1'1h x x=-，∴()()min 11h x h ==，所以()0h x >，即ln x x >. 当01a <<时，()()22222110a ea e a a f e e e++---=++=>， ()2333333ln 121ln 11ln 10a f a a a a a a a a -⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+----=---> ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭，其中11ln a -<，31ln ln a a a ->，所以()f x 在11,ln a ⎛⎫- ⎪⎝⎭和13ln ,ln a a a -⎛⎫ ⎪⎝⎭上各有一个零点. 故a 的取值范围是()0,1.注意：取点过程用到了常用放缩技巧。

专题一培优点1 切线放缩

所以 G(x) 在 ( － ∞ ， 0) 上单调递减，在 (0 ，＋ ∞) 上单调递增，所以 G(x)≥G(0)＝0，所以f(x)≥t(x)恒成立，所以f(x2)≥t(x2)，设t(x)＝m的根为x4，则x4＝m，又函数t(x)单调递增，且m＝t(x4)＝f(x2)≥t(x2)，所以x4≥x2，所以 x2－x1≤x4－x3＝m－－1＋1e－me
则 F′(x)＝(x＋2)ex－1e，令 m(x)＝F′(x)＝(x＋2)ex－1e，则m′(x)＝(x＋3)ex，所以当x<－3时，m′(x)<0；当x>－3时，m′(x)>0，所以F′(x)在(－∞，－3)上单调递减，在(－3，＋∞)上单调递增，
当 x→－∞时，F′(x)→－1e，又 F′(－1)＝0，所以当x<－1时，F′(x)<0，F(x)单调递减；当x>－1时，F′(x)>0，F(x)单调递增，所以F(x)≥F(－1)＝0，所以f(x)≥h(x)恒成立，则f(x1)≥h(x1)，设 h(x)＝m 的根为 x3，则 x3＝－1＋1e－me，又h(x)单调递减，且m＝h(x3)＝f(x1)≥h(x1)，
培优点1 专题一函数与导数切线放缩
专题一函数与导数
在高考压轴题中，经常考查与导数有关的不等式问题，这些问题可以用常规方法求解，也可以用切线不等式进行放缩.导数切线放缩法是一种非常实用的数学方法，它可以帮助我们更好地理解函数的性质和变化规律，更能使问题简单化，利用切线不等式进行求解，能起到事半功倍的效果.
规该方法适用于凹函数与凸函数且它们的凹凸性相反的问题(拆成两
律
方个函数)，两函数有斜率相同的切线，这是切线放缩的基础，引入法一个中间量，分别证明两个不等式成立，然后利用不等式的传递

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

凹凸函数之切线放缩
很多不等式的证明都涉及放缩法、构造法、拆分、引入增量，记得前不久看到泰勒展开，谈到超越函数（不等式）可以近似成多项式函数（不等式），其中就有一个特例，将超越函数利用导数的几何意义（切线）进行放缩，即变成b kx x g +≥)(，或b kx x g +≤)(（等号成立的条件恰好是切点时满足）。

这里特例举几个题目来谈谈它的应用吧。

例1、()[]2
3,0,31x f x x x
+=
∈+，已知数列{}n a 满足03,n a n N *
<≤∈，且满足122010670a a a ++
+=，则122010()()()f a f a f a +++( )
A . 最大值6030
B . 最大值6027
C 有最小值6027.
D . 有最小值6030
解析：A ．
1()33f =，当1220101
3a a a ====时，122010()()()f a f a f a +++=6030 对于函数2
3()(03)1x f x x x +=≤≤+,19()316k f '==-,在13x =处的切线方程为即3
(11)10y x =-，则()2
2331(11)(3)()01103
x f x x x x x +=≤-⇔--≤+成立，
所以当03,n a n N *
<≤∈时，有()3(113)10
n n f a a ≤-
122010()()()f a f a f a +++[]1220103
1120103()603010
a a a ≤⨯-+++=
例2、已知函数2
901x
f x a ax =
>+()() ．（1）求f x ()在1
2
2[,]上的最大值；
（2）若直线2y x a =-+为曲线y f x =()的切线，求实数a 的值；
（3）当2a =时，设1214122x x x ,⎡⎤
∈⎢⎥⎣⎦
…,,, ，且121414x x x =…+++ ，若不等式
1214f x f x +f x λ≤…()+()+()恒成立，求实数λ的最小值．
解析：（1）222222
9[1(1)2]9(1)
()(1)(1)ax x ax ax f x ax ax ⋅+-⋅-'==++，
令()0f x '=，解得x a =±
（负值舍去），由122a <
<，解得1
44a <<．（ⅰ）当104a <≤时，由1[,2]2x ∈，得()0f x '≥，∴()f x 在1
[,2]2上的最大值为18(2)41f a =+．
（ⅱ）当4a ≥时，由1[,2]2x ∈，得()0f x '≤，∴()f x 在1
[,2]2上的最大值为118()24f a =+．
（ⅲ）当1
44
a <<时，在12x <<时，()0f x '>2x <<时，()0f x '<，
∴()f x 在1
[,2]2
上的最大值为=2f a a ）．
（2）设切点为(,())t f t ，则()1,
()2.f t f t t a '=-⎧⎨=-+⎩ 由()1f t '=-，有2
22
9[1]1(1)at at -=-+，化简得2427100a t at -+=，即22at =或25at =， …① 由()2f t t a =-+，有
2
921t
a t at
=-+，…② 由①、②解得2a =
或4a =．
（3）当2a =时，2
9()12x
f x x
=+，由（2）的结论直线4y x =-为曲线()y f x =的切线， (2)2f =，
∴点(2,(2))f 在直线4y x =-上，根据图像分析，曲线()y f x =在线4y x =-下方．下面给出证明：当1
[,2]2
x ∈时，()4f x x ≤-．
3222928104()(4)41212x x x x f x x x x x -+---=-+=++2
2
21(2)
12x x x
--=+（），当1
[,2]2
x ∈时，()(4)0f x x --≤，即()4f x x ≤-．
∴12141214()()()414()f x f x f x x x x +++≤⨯-+++，
121414x x x +++=，
1214()()()561442f x f x f x ∴++
+≤-=．
∴要使不等式1214()()()f x f x f x λ++
+≤恒成立，必须42λ≥．
又
当12141x x x ==
==时，满足条件121414x x x ++
+=，
且1214()()()42f x f x f x ++
+=，因此，λ的最小值为42．
例3、若)3,2,1(,0=>i x i ，且3
1
1i i x ==∑，则
2111x ++2211x ++2311x +≤27
10
证明：设g(x)= 2
1
1x +,则g ´(x)= 222(1)x x -+，g ´´(x)= 2232(31)(1)x x -+，
由g ´´(x)＜0得
＜x
g ´´(x)＞0得x
x ＜
∵g(x)在R 上连续，故g(x)= 2
1
1x +在［
］上是上凸的，在区间(-∞，
)，
(+∞)上是下凸的。

由3
1
1i i x ==∑，则平衡值x 0= 13，由导数知识易求得g(x) = 2
11x +在 x=
13处的切线为y=2750（2-x ）,因x 0= 13∈［
- 3
，3］，g(x) = 2
11x
+在［
- 3
，3］上是上凸的，故g(x) = 211x +≤2750（2-x ）恒成立。

即2111x +≤2750（2-x 1）
，2211x +≤27
50
（2-x 2），2311x +≤2750（2-x 3），三式相加并结合3
11i i x ==∑即得2111x ++2211x ++2
3
11x +≤27
10。

若将该题条件改为：若)3,2,1(,0=>i x i ，且3
1
3i
i x
==∑时，解法同理。

此时平衡值x 0=1，而g(x) =
211x +在x= 1处的切线为y=-1
2
x+1, 因x 0= 1∈
+∞)，g(x) = 211x +在
，+∞)上是下凸的，故g(x) = 211x +≥- 12x+1恒成立。

即2111x +≥- 12
x 1+1，
2211x +≥- 12x 2+1，2311x +≥- 12x 3+1三式相加并结合3
13i i x ==∑即得2111x ++2211x ++2
311x +≥3
2。

即得一个新的不等式：若x i
，且3
13i i x ==∑，则2111x ++2211x ++2
3
11x +≥3
2。

所以，在证明一类多元不等式时，我们经常用到的一个办法就是假设这些变元的和为1。

例4、若实数c b a ,,，证明：2
3
≥+++++b a c c a b c b a 。

提示：不妨设1=++c b a ，则平衡点是31=
x 。

x x x f -=1)(在31=x 的切线4
19-=x y ，有 4
1
9)(-≥
x x f 。

5、若z y x ,,非负，且12
2
2
=++z y x ，证明：43
1112
22≤+++++z
z y y x x 提示：平衡点是33=x 。

2
1)(x
x
x f +=在33=x 的切线12321+=x y ，有12321)(+≤x x f
练习1：已知函数)2()
20()
2(11)(2>≤≤⎪⎩⎪
⎨⎧++=x x f x x x f ，
⑴求函数)(x f 在定义域上的单调区间。

⑵若关于x 的方程0)(=-a x f 恰有两个不等的实根，求实数a 的范围；
⑶已知实数]1,0[,21∈x x ，121=+x x ，若不等式)ln()()(21p x x x f x f --≤在),(+∞∈p x 上恒成立，求实数p 的最小值。

（可以利用切线求)()(21x f x f 的最大值）
练习2：若z y x ,,非负，且12
22=++z y x ，证明：4
3111222≤+++++z z y y x x
提示：平衡点是33=
x 。

2
1)(x x
x f +=在33=x 的切线12321+=x y ，有12321)(+≤x x f。