黑龙江省高考数学二轮复习专题10:解析几何
高三数学二轮复习专题突破课件:解析几何

A.[1,+∞) B.[-1,- )
3
C.( ,1]
4
4
D.(-∞,-1]
答案:B
解析:∵y=kx+4+2k=k(x+2)+4,所以直线过定点(-2,4),曲线y=
4 − x 2 变形为x2+y2=4(y≥0),表示圆的上半部分,当直线与半圆相切时直线斜
3
率为k=- ,当直线过点(2,0)时斜率为-1,结合图象可知实数k的取值范围是
a=2
所以 ሺ2 − 3 − ሻ2 + 2 = 2 ,解得 b = 1 .
r=2
2 + ሺ1 − ሻ2 = 2
所以圆的方程为(x-2)2+(y-1)2=4.
4.[2023·广东深圳二模]过点(1,1)且被圆x2 +y2 -4x-4y+4=0所
x+y-2=0
截得的弦长为2 2的直线的方程为___________.
-2)的距离为 2 − 0 2 + 0 + 2 2 =2 2,由于圆心
α
2
5
=
2 2 2 2
α
αபைடு நூலகம்
α = 2sin cos =
2
2
与点(0,-2)的连线平分角α,所以sin =
10
α
6
, 所 以 cos = , 所 以 sin
4
2
4
10
6
15
2×
× = .故选B.
4
4
4
r
=
(2)[2023·河南郑州二模]若圆C1:x2+y2=1与圆C2:(x-a)2+(y-b)2
解析:圆x2+y2-4x-4y+4=0,即(x-2)2+(y-2)2=4,
圆心为(2,2),半径r=2,
高三数学总复习专题10 解析几何(答案及解析)

高三数学总复习专题10 解析几何方法点拨1.圆锥曲线中的最值 (1)椭圆中的最值12,F F 为椭圆()222210+=>>x y a b a b的左、右焦点,P 为椭圆上的任意一点,B 为短轴的一个端点,O 为坐标原点,则有: ①[],∈OP b a ; ②[]1,∈-+PF a c a c ;③2212,⎡⎤⋅∈⎣⎦PF PF b a ;④1212∠≤∠F PF F BF . (2)双曲线中的最值12,F F 为双曲线()222210,0-=>>x y a b a b的左、右焦点,P 为双曲线上的任一点,O 为坐标原点,则有:①≥OP a ;②1≥-PF c a . (3)抛物线中的最值点P 为抛物线()220=>y px p 上的任一点,F 为焦点,则有: ①2≥pPF ;②(),A m n 为一定点,则+PA PF 有最小值. 2.定点、定值问题(1)由直线方程确定定点,若得到了直线方程的点斜式:()00-=-y y k x x ,则直线必过定点()00,x y ;若得到了直线方程的斜截式:=+y kx m ,则直线必过定点()0,m . (2)解析几何中的定值问题是指某些几何量(线段的长度、图形的面积、角的度数、直线的斜率等)的大小或某些代数表达式的值等和题目中的参数无关,不依参数的变化而变化,而始终是一个确定的值. 3.圆锥曲线中范围、最值的求解策略(1)数形结合法:利用待求量的几何意义,确定出临界位置后数形结合求解. (2)构建不等式法:利用已知或隐含的不等关系,构建以待求量为元的不等式求解.(3)构建函数法:先引入变量构建以待求量为因变量的函数,再求其值域. 4.定点问题的l 过定点问题的解法:设动直线方程(斜率存在)为=+y kx t 由题设条件将t 用k 表示为=t mk ,得()=+y k x m ,故动直线过定点(),0-m .(2)动曲线C 过定点问题的解法:引入参变量建立曲线C 的方程,再根据其对参变量恒成立,令其系数等于零,得出定点.(3)从特殊位置入手,找出定点,再证明该点符合题意. 5.求解定值问题的两大途径(1)首先由特例得出一个值(此值一般就是定值)然后证明定值:即将问题转化为证明待证式与参数(某些变量)无关.(2)先将式子用动点坐标或动线中的参数表示,再利用其满足的约束条件使其绝对值相等的正负项抵消或分子、分母约分得定值. 6.解决探索创新问题的策略存在性问题,先假设存在,推证满足条件的结论,若结论正确则存在,若结论不正确则不存在.(1)当条件和结论不唯一时,要分类讨论.(2)当给出结论而要推导出存在的条件时,先假设成立,再推出条件. (3)当条件和结论都不知,按常规方法解题很难时,要思维开放,采取另外的途径.经典试题汇编一、选择题.1.(陕西省渭南市临渭区2021届高三一模)若直线:3=-l y kx 与直线2360+-=x y 的交点位于第一象限,则直线l 的倾斜角的取值范围是( )A .ππ,43⎡⎫⎪⎢⎣⎭B .ππ,32⎡⎫⎪⎢⎣⎭C .ππ,42⎛⎫⎪⎝⎭ D .ππ,32⎛⎫⎪⎝⎭2.(安徽省淮北市2020-2021学年高三一模)过圆2216+=x y 上的动点作圆22:4+=C x y 的两条切线,两个切点之间的线段称为切点弦,则圆C 内不在任何切点弦上的点形成的区域的面积为( ) A .πB .32πC .2πD .3π3.(山西省大同市天镇县实验中学2021-2022学年高三一模)圆222440+-+-=x y x y 与直线2140()---=∈R tx y t t 的位置关系为( ) A .相离B .相切C .相交D .以上都有可能4.(吉林省长春市2022届高三一模)已知圆22:(2)(3)2-+-=C x y ,直线l 过点(3,4)A 且与圆C 相切,若直线l 与两坐标轴交点分别为,M N ,则MN =( )A .B .6C .D .85.(河南省联考2021-2022学年高三一模)若点()2,1--P 为圆229+=x y 的弦AB 的中点,则弦AB 所在直线的方程为( )A .250++=x yB .250+-=x yC .250-+=x yD .250--=x y6.(四川省南充市2021-2022学年高三一模)若A ,B 是O :224+=x y 上两个动点,且2⋅=-OA OB ,A ,B 到直线l 40+-=y 的距离分别为1d ,2d ,则12+d d 的最大值是( ) A .3B .4C .5D .67.(湖南省长沙市雅礼中学2021届高三一模)过双曲线2214-=y x 的左焦点1F 作一条直线l 交双曲线左支于P ,Q 两点,若4=PQ ,2F 是双曲线的右焦点,则2△PF Q 的周长是( ) A .6B .8C .10D .128.(四川省成都市2020-2021学年高三一模)已知抛物线24=x y 的焦点为F ,过F的直线l 与抛物线相交于A ,B 两点,70,2⎛⎫⎪⎝-⎭P .若⊥PB AB ,则=AF ( )A .32B .2C .52D .39.(湖南省湘潭市2021-2022学年高三上学期一模)已知抛物2:2C y px =(0>p )的焦点为F ,点T 在C 上,且52=FT ,若点M 的坐标为()0,1,且⊥MF MT ,则C 的方程为( ) A .22=y x 或28=y x B .2=y x 或28=y x C .22=y x 或24=y xD .2=y x 或24=y x10.(河南省联考2021-2022学年高三一模)点F 为抛物线22=y px ()0>p 的焦点,l 为其准线,过F 的一条直线与抛物线交于A ,B 两点,与l 交于点C .已知点B 在线段CF 上,若BF ,AF ,BC 按照某种排序可以组成一个等差数列,则AFBF的值为( ) A .32或3B .2或4C .32或4D .2或311.(贵州省遵义市2021届高三一模)双曲线221927-=x y 上一点P 到右焦点2F 距离为6,1F 为左焦点,则12∠F PF 的角平分线与x 轴交点坐标为( )A .()1,0-B .()0,0C .()1,0D .()2,012.(吉林省长春市2022届高三一模)已知P 是抛物线24=y x 上的一动点,F 是抛物线的焦点,点(3,1)A ,则||||+PA PF 的最小值为( )A .3B .C .4D .13.(多选)(湖南省湘潭市2021-2022学年高三一模)已知双曲线2222:1-=x y C a b(0>a ,0>b )的左,右焦点为1F ,2F ,右顶点为A ,则下列结论中,正确的有( )A .若=a b ,则CB .若以1F 为圆心,b 为半径作圆1F ,则圆1F 与C 的渐近线相切C .若P 为C 上不与顶点重合的一点,则12△PF F 的内切圆圆心的横坐标=x aD .若M 为直线2=a x c(=c 0的一点,则当M 的纵坐标为时,2MAF 外接圆的面积最小 14.(江西省赣州市2021届高三3月一模)已知M 、N 是双曲线()2222:10,0-=>>x y C a b a b上关于原点对称的两点,P 是C 上异于M 、N 的动点,设直线PM 、PN 的斜率分别为1k 、2k .若直线12=y x 与曲线C 没有公共点,当双曲线C 的离心率取得最大值时,且123≤≤k ,则2k 的取值范围是( ) A .11,128⎡⎤⎢⎥⎣⎦B .11,812⎡⎤--⎢⎥⎣⎦ C .11,32⎡⎤⎢⎥⎣⎦D .11,23⎡⎤--⎢⎥⎣⎦15.(四川省成都市2021-2022学年高三一模)已知双曲线()222210,0-=>>x y a b a b的一条渐近线方程为=y ,则该双曲线的离心率为( )A B C .2D .316.(四川省成都市2020-2021学年高三一模)已知平行于x 轴的一条直线与双曲线()222210,0-=>>x y a b a b 相交于P ,Q 两点,4=PQ a ,π3∠=PQO (O 为坐标原点),则该双曲线的离心率为( )A B C D17.(甘肃省嘉谷关市第一中学2020-2021学年高三一模)已知双曲线22221(0,0)-=>>y x a b a b与抛物线2=x 共焦点F ,过点F 作一条渐近线的垂线,垂足为M ,若三角形OMF 的面积为2,则双曲线的离心率为( )AB .16C D .4或4318.(四川省乐山市高中2022届一模)已知双曲线()222210,0-=>>x y a b a b,过原点的直线与双曲线交于A ,B 两点,以线段AB 为直径的圆恰好过双曲线的右焦点F ,若ABF 的面积为22a ,则双曲线的离心率为( )AB C D .219.(四川省达州市2021-2022学年高三一模)双曲线()222210,0-=>>x y a b a b的左顶点为A ,右焦点(),0F c ,若直线=x c 与该双曲线交于B 、C 两点,ABC 为等腰直角三角形,则该双曲线离心率为( )A .2BCD .320.(陕西省汉中市2022届高三一模)已知F 是椭圆2222:1(0)+=>>x y C a b a b 的右焦点,点P 在椭圆C 上,线段PF 与圆22239⎛⎫-+= ⎪⎝⎭c b x y 相切于点Q ,且2=PQ QF ,则椭圆C 的离心率等于( )A B .23C .2D .1221.(广西柳州市2022届高三一模)已知1F ,2F 分别为双曲线C :22221-=x y a b()0,0>>a b 的左,右焦点,以12F F 为直径的圆与双曲线C 的右支在第一象限交于A 点,直线2AF 与双曲线C 的右支交于B 点,点2F 恰好为线段AB 的三等分点(靠近点A ),则双曲线C 的离心率等于( )A B C .3D .12+ 二、填空题.22.(贵州省遵义市2021届高三一模)直线1=-+y kx k 与圆224+=x y 交于,A B 两点,则AB 最小值为________.23.(湖南省长沙市雅礼中学2021届高三一模)若抛物线22=y px 上一点()02,P y 到其准线的距离为4,则抛物线的标准方程为___________.24.(四川省成都市第七中学2021-2022学年高三一模)已知12,F F 为双曲线22:1169-=x y C 的两个焦点,,P Q 为C 上关于坐标原点对称的两点,且12=PQ F F ,则四边形12PF QF 的面积为________.25.(四川省达州市2021-2022学年高三一模)设直线()y kx k =∈R 交椭圆221164+=x y 于A ,B 两点,将x 轴下方半平面沿着x 轴翻折与x 轴上方半平面成直二面角,则AB 的取值范围是___________.26.(四川省成都市2021-2022学年高三一模)已知斜率为13-且不经过坐标原点O的直线与椭圆22+197x y =相交于A ,B 两点,M 为线段AB 的中点,则直线OM 的斜率为________. 三、解答题.27.(四川省成都市第七中学2021-2022学年高三一模)已知两圆221:(2)54C x y -+=,222:(2)6C x y ++=,动圆M 在圆1C 内部且和圆1C 内切,和圆2C 外切.(1)求动圆圆心M 的轨迹C 的方程;(2)过点()3,0A 的直线与曲线C 交于,P Q 两点,P 关于x 轴的对称点为R ,求ARQ 面积的最大值.28.(四川省成都市2020-2021学年高三一模)已知椭圆()2222:10+=>>x y C a b a b的离心率为2,且直线1+=x ya b与圆222+=x y 相切. (1)求椭圆C 的方程;(2)设直线l 与椭圆C 相交于不同的两点A ﹐B ,M 为线段AB 的中点,O 为坐标原点,射线OM 与椭圆C 相交于点P ,且O 点在以AB 为直径的圆上.记AOM ,△BOP的面积分别为1S ,2S ,求12S S 的取值范围. 29.(陕西省汉中市2022届高三一模)已知椭圆2222:1(0)+=>>x y C a b a b 的离心率为12,左、右焦点分别为12,F F ,O 为坐标原点,点P 在椭圆C 上,且满足2122,3π=∠=PF F PF .(1)求椭圆C 的方程;(2)已知过点(1,0)且不与坐标轴垂直的直线l 与椭圆C 交于M ,N 两点,在x 轴上是否存在定点Q ,使得∠=∠MQO NQO ,若存在,求出点Q 的坐标;若不存在,说明理由.30.(四川省南充市2021-2022学年高三一模)已知椭圆()2222:10+=>>x y C a b a b的离心率为2,椭圆C 的下顶点和上顶点分别为1B ,2B ,且122=B B ,过点()0,2P 且斜率为k 的直线l 与椭圆C 交于M ,N 两点.(1)求椭圆C 的标准方程; (2)当1=k 时,求OMN 的面积;(3)求证:直线1B M 与直线2B N 的交点T 的纵坐标为定值.31.(江西省赣州市2021届高三3月一模)设离心率为12的椭圆2222:1(0)+=>>x y E a b a b 的左,右焦点分别为1F ,2F ,点P 在E 上,且满足1260∠=︒F PF ,12△PF F(1)求a ,b 的值;(2)设直线:2(0)=+>l y kx k 与E 交于M ,N 两点,点A 在x轴上,且满足0⋅+⋅=AM MN AN MN ,求点A 横坐标的取值范围.32.(广西柳州市2022届高三一模)已知椭圆C :22221+=x y a b()0>>a b 的左右焦点分别为1F ,2F ,过2F 且与x 轴垂直的直线与椭圆C 交于A ,B 两点,AOB 的面积为﹐点P 为椭圆C 的下顶点,2=PF . (1)求椭圆C 的标准方程;(2)椭圆C 上有两点M ,N (异于椭圆顶点且MN 与x 轴不垂直).当OMN 的面积最大时,直线OM 与ON 的斜率之积是否为定值,若是,求出该定值;若不是,请说明理由. 33.(湖南省湘潭市2021-2022学年高三一模)已知圆锥曲线E 上的点M 的坐标(),x y=.(1)说明E 是什么图形,并写出其标准方程;(2)若斜率为1的直线l 与E 交于y 轴右侧不同的两点A ,B ,点P 为()2,1. ①求直线l 在y 轴上的截距的取值范围; ②求证:∠APB 的平分线总垂直于x 轴.34.(四川省乐山市高中2022届一模)如图,从椭圆22221(0)+=>>x y a b a b上一点P 向x轴作垂线,垂足恰为左焦点1F .又点A 是椭圆与x 轴正半轴的交点,点B 是椭圆与y轴正半轴的交点,且=OP AB k ,13=F A . (1)求椭圆的方程;(2)直线l 交椭圆于M 、Q 两点,判断是否存在直线l ,使点2F 恰为MQB △的重心?若存在,求出直线l 的方程;若不存在,请说明理由.35.(安徽省淮北市2020-2021学年高三一模)已知椭圆2222:1(0)+=>>x y C a b a b的离心率为12,左顶点为A ,右焦点F ,3=AF .过F 且斜率存在的直线交椭圆于P ,N 两点,P 关于原点的对称点为M . (1)求椭圆C 的方程;(2)设直线AM ,AN 的斜率分别为1k ,2k ,是否存在常数λ,使得12λ=k k 恒成立?若存在,请求出λ的值;若不存在,请说明理由.36.(湖南省长沙市雅礼中学2021届高三一模)已知椭圆()222210:x y a b a bC +=>>,连接椭圆上任意两点的线段叫作椭圆的弦,过椭圆中心的弦叫做椭圆的直径.若椭圆的两直径的斜率之积为22-b a,则称这两直径为椭圆的共轭直径.特别地,若一条直径所在的斜率为0,另一条直径的斜率不存在时,也称这两直径为共轭直径.现已知椭圆22:143x y E +=.(1)已知点31,2⎛⎫ ⎪⎝⎭A ,31,2⎛⎫-- ⎪⎝⎭B 为椭圆E 上两定点,求AB 的共轭直径的端点坐标;(2)过点()作直线l 与椭圆E 交于1A 、1B 两点,直线1A O 与椭圆E 的另一个交点为2A ,直线1B O 与椭圆E 的另一个交点为2B .当11A OB 的面积最大时,直径12A A 与直径12B B 是否共轭,请说明理由;(3)设CD 和MN 为椭圆E 的一对共轭直径,且线段CM 的中点为T .已知点P 满足:λ=OP OT ,若点P 在椭圆E 的外部,求λ的取值范围.参考答案一、选择题. 1CACCADDDADDC 13.【答案】ABD【解析】对于A 中,因为=a b ,所以222=a c ,故C的离心率==ce a所以A 正确; 对于B 中,因为()1,0-F c 到渐近线0-=bx ay的距离为==d b ,所以B 正确;对于C 中,设内切圆与12△PF F 的边1221,,F F F P F P 分别切于点1,,A B C , 设切点1A (,0)x ,当点P 在双曲线的右支上时,可得121212-=+--=-PF PF PC CF PB BF CF BF1112=-A F A F ()()22=+--==c x c x x a ,解得=x a ,当点P 在双曲线的左支上时,可得=-x a ,所以12△PF F 的内切圆圆心的横坐标=±x a ,所以C 不正确; 对于D 中,由正弦定理,可知2MAF 外接圆的半径为222sin =∠AF R AMF ,所以当2sin ∠AMF 最大时,R 最小,因为2<a a c,所以2∠AMF 为锐角,故2sin ∠AMF 最大,只需2tan ∠AMF 最大,由对称性,不妨设2,⎛⎫ ⎪⎝⎭a M t c (0>t ),设直线2=a x c 与x 轴的交点为N ,在直角2△NMF 中,可得222tan ==∠-a c NF NM NMF ct , 在直角△NMA 中,可得2tan =-=∠a a NA A NM NM c t,又由2222tan tan tan tan()1tan tan NMF NMAAMF NMF NMA NMF NMA∠-∠∠=∠-∠=∠⋅+∠222222()1c c a ab c a a a a c ct t a a c t a c c t tc t -==≤+-----⨯-+, 当且仅当()22-=ab c a t c t ,即=t 2tan ∠AMF 取最大值, 由双曲线的对称性可知,当=t 2tan ∠AMF 也取得最大值,所以D 正确,故选ABD . 14.【答案】A【解析】因为直线12=y x 与双曲线()2222:10,0-=>>x y C a b a b 没有公共点,所以双曲线C 的渐近线的斜率12=≤bk a ,而双曲线C的离心率====c e a 当双曲线C 的离心率取最大值时,b a 取得最大值12,即12=b a ,即2=a b ,则双曲线C 的方程为222214-=x y b b,设()11,M x y 、()11,--N x y 、()00,P x y ,则2211222200221414⎧-=⎪⎪⎨⎪-=⎪⎩x y b b x y b b , 两式相减得()()()()10101010224+-+-=x x x x y y y y b b ,即1010101014-+⋅=-+y y y y x x x x , 即1214⋅=k k , 又123≤≤k ,211,128⎡⎤∈⎢⎥⎣⎦k ,故选A . 15.【答案】B【解析】双曲线22221-=x y a b 的渐近线方程为=±by x a,因为渐近线方程为=y ,所以=ba故可得====e B . 16.【答案】D【解析】如图,由题可知,△POQ 是等边三角形,4=PQ a ,()2,∴P a ,将点P 代入双曲线可得22224121-=a a a b ,可得224=b a,∴离心率===c e a D .17.【答案】C【解析】抛物线2=x 的交点坐标为(F ,又双曲线22221(0,0)-=>>y x a b a b与抛物线2=x 共焦点,∴双曲线的半焦距=c ,三角形OMF 的面积为2,且=OM a ,=MF b ,∴122=⋅ab ,即4=ab , 有22217+==a b c ,∴1=a 或4=a ,∴双曲线的离心率为=e ,故选C .18.【答案】B【解析】设双曲线的左焦点为'F ,连接'AF ,'BF , 因为以AB 为直径的圆恰好经过双曲线的右焦点(),0F c , 所以⊥AF BF ,圆心为()0,0O ,半径为c , 根据双曲线的对称性可得四边形'AFBF 是矩形,设=AF m ,=BF n ,则222224122⎧⎪-=⎪+=⎨⎪⎪=⎩n m a n m c mn a ,由()2222-=+-n m m n mn ,可得222484-=c a a ,所以223=c a ,所以2223==c e a,所以=e ,故选B .19.【答案】A【解析】联立22222221=⎧⎪⎪-=⎨⎪=+⎪⎩x cxy a b c a b,可得2=±b y a ,则22=b BC a ,易知点B 、C 关于x 轴对称,且F 为线段BC 的中点,则=AB AC ,又因为ABC 为等腰直角三角形,所以2=BC AF ,即()222=+b c a a, 即()222+==-a c a b c a ,所以=-a c a ,可得2=c a , 因此,该双曲线的离心率为2==ce a,故选A . 20.【答案】A【解析】圆22239⎛⎫-+= ⎪⎝⎭c b x y 的圆心为,03⎛⎫ ⎪⎝⎭c A ,半径为3=b r . 设左焦点为1F ,连接1PF ,由于124,33==AF c AF c , 所以12==AF PQAF QF,所以1//AQ PF ,所以12,2==-PF b PF a b , 由于⊥AQ PF ,所以1⊥PF PF , 所以()()()22222224+-==-b a b c a b ,2320,3-==b b a a ,===c e a ,故选A .21.【答案】C【解析】设2=AF x ,则22=BF x ,由双曲线的定义可得1222=+=+AF AF a a x ,12222=+=+BF BF a a x , 因为点A 在以12F F 为直径的圆上,所以190∠=F AB ,所以22211+=AF AB BF ,即()()()2222322++=+a x x a x ,解得23=x a , 在12△AF F 中,1823=+=AF a x a ,223=AF a ,122=F F c , 由2221212+=AF AF F F 可得()22282233⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭a a c ,即22179=a c ,所以双曲线离心率为3===e ,故选C .二、填空题. 22.【答案】【解析】直线1=-+y kx k 过定点过()1,1M , 因为点()1,1M在圆的内部,且OM == 由圆中弦的性质知当直线与OM 垂直时,弦长最短, 此时结合垂径定理可得AB ==故答案为 23.【答案】28=y x【解析】抛物线的准线方程为2=-p x ,点()02,P y 到其准线的距离为22+p , 由题意可得242+=p,解得4=p , 故抛物线的标准方程为28=y x ,故答案为28=y x . 24.【答案】18【解析】由双曲线的对称性以及12=PQ F F 可知,四边形12PF QF 为矩形,所以1222212284100⎧-==⎪⎨+==⎪⎩PF PF a PF PF c ,解得1218=PF PF , 所以四边形12PF QF 的面积为1218=PFPF , 故答案为18.25.【答案】(⎤⎦【解析】设1122(,),(,)A x y B x y ,联立方程组221164=⎧⎪⎨+=⎪⎩y kx x y ,可得22(14)160+-=k x , 可得1212216,014=-+=+x x x x k ,所以221221614==+x x k , 将椭圆x 轴下方半平面沿着x 轴翻折与x 轴上方半平面成直二面角, 分别作,⊥⊥BC x AD x 于点,C D ,如图所示, 则2222=++AB BC CD AD ,又由222222222211,====BC y k x AD y k x ,2222212*********64()2()414=-=+-=+-=+CD x x x x x x x x x x k, 所以222222221226414=++=+++AB BC CD AD k x k x k 2222232648(417)78(1)141414+⋅++===⋅++++k k k k k , 因为∈R k ,所以20≥k ,所以2411+≥k ,所以270741<≤+k ,所以2788(1)6414<⋅+≤+k ,即2864<≤AB,所以8<≤AB ,所以AB的取值范围是(⎤⎦,故答案为(⎤⎦.26.【答案】73【解析】设直线AB 的方程为13=-+y x b ,联立2213197⎧=-+⎪⎪⎨⎪+=⎪⎩y x b x y ,得221()3197-++=x b x ,即22869630-+-=x bx b ,由223632(963)0b b ∆=-->,得-<<b 设11(,)A x y ,22(,)B x y ,00(,)M x y ,则120328+==x x b x ,0011373388=-+=-⨯+=b by x b b , 即37(,)88b bM ,则直线OM 的斜率为0073==y k x ,故答案为73.三、解答题.27.【答案】(1)2212420+=x y ;(2.【解析】(1)依题意,圆1C 的圆心()12,0C,半径1=r 圆2C 的圆心()22,0-C,半径2=r设圆M 的半径为r ,则有11=-MC r r ,22=+MC r r ,因此,1212124+=+=>=MC MC r r C C ,于是得点M 的轨迹是以12,C C为焦点,长轴长2=a 此时,焦距24=c ,短半轴长b 有22220=-=b a c ,所以动圆圆心M 的轨迹C 的方程为2212420+=x y .(2)显然直线PQ 不垂直于坐标轴,设直线PQ 的方程为3(0)=+≠x my m ,1122(,),(,)P x y Q x y ,由22356120=+⎧⎨+=⎩x my x y ,消去x 得22(56)30750++-=m x my , 则1226350+=-+m y y m ,1227556=-+y y m , 点P 关于x 轴的对称点11(,)-R x y ,1211|2|||2=⋅⋅-PQRSy x x ,111232=⋅⋅-APRS y x ,如图,显然1x 与2x 在3的两侧,即21-x x 与13-x 同号, 于是得()()()1211121133=-=---=⋅---AQRPQRAPRSSSy x x x y x x x121212275|||75|||3|||||||6565|||==⋅-==⋅==++≤m y x y my my y m m m , 当且仅当65||||=m m ,即=m 时取“=”,因此,当=m 时,max ()=AQR S,所以ARQ 面积的最大值4. 28.【答案】(1)22163+=x y;(2)⎣⎦.【解析】(1)∵椭圆的离心率为2,∴2=c a (c 为半焦距), ∵直线1+=xy ab与圆222+=x y=,又∵222+=c b a ,∴26=a ,23=b ,∴椭圆C 的方程为22163+=x y .(2)∵M 为线段AB 的中点,∴12==AOM BOP OMS S S S OP△△. (ⅰ)当直线l 的斜率不存在时,由⊥OA OB 及椭圆的对称性,不妨设OA 所在直线的方程为=y x ,得22=Ax .则22=Mx ,26=P x,∴123==OM S S OP ; (ⅱ)当直线l 的斜率存在时,设直线():0=+≠l y kx m m ,()11,A x y ,()22,B x y ,由22163=+⎧⎪⎨+=⎪⎩y kx mx y ,消去y ,得()222214260++-=+k x kmx m , ∴()()()2222221682138630k m k m k m ∆=-+-=-+>,即22630-+>k m .∴122421+=-+kmx x k ,21222621-=+m x x k .∵点O 在以AB 为直径的圆上,∴0⋅=OA OB ,即12120+=x x y y , ∴()()221212121210+=++++=x x y y k x x km x x m ,∴()22222264102121-⎛⎫++-+= ⎪++⎝⎭m km k km m k k . 化简,得2222=+m k ,经检验满足0∆>成立, ∴线段AB 的中点222,2121⎛⎫-⎪++⎝⎭km m M k k , 当0=k 时,22=m,此时123==S S ; 当0≠k 时,射线OM 所在的直线方程为12=-y x k, 由2212163⎧=-⎪⎪⎨⎪+=⎪⎩y x k x y ,消去y ,得2221221=+P k x k ,22321=+P y k , ∴==M P OM y OP y ∴12==S S12,33⎛∈ ⎝⎭S S , 综上,12S S的取值范围为⎣⎦.29.【答案】(1)22143+=x y ;(2)存在,()4,0.【解析】(1)在12△PF F 中,1122,2=-=cPF a a ,所以,由余弦定理()224(22)4222=-+--c a a,解得2,==a b ,所以,椭圆方程为22143+=x y .(2)假设存在点(),0Q m 满足条件,设直线l 的方程为()10=+≠x ty t ,设()()1122,,,M x y N x y ,联立()22221,34690143=+⎧⎪++-=⎨+=⎪⎩x ty t y ty x y , 121212221269,,3434--+==+=+++--MQ NQy y t y y y y k K t t x m x m, 又因为∠=∠MQO NQO ,所以0+=MQ NQ K K ,即1212=--y y x m m x , 即()()1211-=-y m x y m x ,将11221,1=+=+x ty x ty 代入化简得()()121212-+=m y y ty y , 即()2261183434---=++t m tt t ,计算得4=m ,所以存在()4,0点使得∠=∠MQO NQO .30.【答案】(1)2212+=x y ;(2)面积不存在;(3)证明见解析.【解析】(1)因为122=B B ,所以22=b ,即1=b ,因为离心率为2,所以2=c a ,设=c m,则=a ,0>m , 又222=-c a b ,即2222=-m m b ,解得1=m 或1-(舍去),所以=a 1=b ,1=c ,所以椭圆的标准方程为2212+=x y .(2)由22122⎧+=⎪⎨⎪=+⎩x y y x ,得()222220++-=x x ,23860++=x x ,284360∆=-⨯⨯<,所以直线与椭圆无交点,故OMN 的面积不存在.(3)由题意知,直线l 的方程为2=+y kx ,设()11,M x y ,()22,N x y ,则22212=+⎧⎪⎨+=⎪⎩y kx x y ,整理得()2221860+++=k x kx ,则()()22122122846120821621Δk k k x x k x x k ⎧=-⨯+>⎪⎪⎪+=-⎨+⎪⎪=⎪+⎩,因为直线和椭圆有两个交点,所以()()22824210k k ∆=-+>,则232>k ,设(),T m n ,因为1B ,T ,M 在同一条直线上,则111111313+++===+y kx n k m x x x , 因为2B ,T ,N 在同一条直线上,则222221111-+-===+y kx n k m x x x , 由于()21212283311213440621⎛⎫⋅- ⎪++-+⎝⎭+⋅=+=+=+k x x n n k k k m m x x k ,所以12=n , 则交点T 恒在一条直线12=y 上,故交点T 的纵坐标为定值12.31.【答案】(1)2=a,=b (2)6⎡⎫-⎪⎢⎪⎣⎭. 【解析】(1)设椭圆短轴的端点为B ,则21sin 2∠=OBF ,所以26π∠=OBF ,123π∠=F BF ,所以点P 即为点B,所以12122=⋅⋅==△PF F S c b bc ,又12=c a ,222=-a b c ,所以2=a,=b(2)设(,0)A m ,()11,M x y ,()22,N x y ,MN 的中点()00,H x y ,由2223412=+⎧⎨+=⎩y kx x y ,得()22431640+++=k x kx , 所以()()222(16)164348410k k k ∆=-+=->, 又0>k ,所以12>k ,所以1221643+=-+kx x k , 所以12028243+==-+x x k x k ,0026243=+=+y kx k ,即2286,4343⎛⎫- ⎪++⎝⎭k H k k , 因为()20⋅+⋅=+⋅=⋅=AM MN AN MN AM AN MN AH MN , 所以⊥AH MN ,所以226143843+=---+k k k mk ,得2223434=-=-++k m k k k , 因为12>k,所以34+≥k k,当且仅当=k =”号,所以⎡⎫∈⎪⎢⎪⎣⎭m , 故点A的横坐标的取值范围是6⎡⎫-⎪⎢⎪⎣⎭. 32.【答案】(1)22184+=x y ;(2)12-,理由见解析.【解析】(1)由题意可得:在2OPF Rt 中,22222+=OP OF PF ,即)222+=b c ,所以=b c ,椭圆C :22221+=x y a b 中,令=x c 可得2422221⎛⎫=-= ⎪⎝⎭c b y b a a,所以2=±b y a ,可得22=b AB a,所以22122=⋅⋅==AOBb bc Sc a a所以2=b c ,因为=b c ,222=+a b c,所以34====b b , 可得24=b ,所以2==c b ,2228=+=a b c ,所以椭圆C 的标准方程为22184+=x y .(2)设直线MN 的方程为=+y kx t ,()11,M x y ,()22,N x y ,由22184=+⎧⎪⎨+=⎪⎩y kx tx y ,可得()222214280+++-=k x ktx t , ()()222216421280k t k t ∆=-+->,即2284<+t k ,122412-+=+ktx x k,21222812-=+t x x k , 所以()()()2212121212=++=+++y y kx t kx t k x x kt x x t()()22222222222228124812121212-+-=-+=++++k t k t k t t k k k k k,12=-=MN x==, 点()0,0O 到直线=+y kx t的距离=d所以OMN的面积为1122⋅==MN d222284212+-+≤=+t k t k, 当且仅当22284=-+t k t 即2224-=t k 时等号成立,2222222122222128128241122828282-+--+⋅==⨯===-+---OM ONy y t k k t k t t k k x x k t t t , 所以当OMN 的面积最大时,直线OM 与ON 的斜率之积是12-.33.【答案】(1)E是以(),)为焦点,长轴长为22163+=x y ;(2)①(3,-;②证明见解析. 【解析】(1)圆锥曲线E是以(),)为焦点,长轴长为的椭圆,其标准方程为22163+=x y .(2)①设直线l :=+y x m ,()11,A x y ,()22,B x y ,由22163⎧+=⎪⎨⎪=+⎩x y y x m ,消去y ,得2234260++-=x mx m , 由题意,有()()22122124432604032603m m mx x m x x ∆⎧=-⨯->⎪⎪⎪+=->⎨⎪⎪-=>⎪⎩,解得3-<<m , 所以直线l 在y轴上的截距的取值范围为(3,-.②因为点P 在椭圆上,若直线l 过点P ,即点A (或点B )与P 重合,则l 与E 的另一个交点为25,33⎛⎫--⎪⎝⎭,不合题意,所以点A (或点B )与P 不重合; 若AP 或BP 的斜率不存在,则直线l 过点()2,1-,此时,l 与E 只有一个交点, 所以AP 与BP 的斜率都存在,设直线AP 的斜率为1k ,直线BP 的斜率为2k , 因为A ,B 在轴的右侧,结合图象,可知,要证∠APB 的平分线总垂直于x 轴,只要证120=+k k , 因为11112-=-y k x ,22212-=-y k x ,也即证()()()()122112120--+--=y x y x ,而()()()()()()()()1221122112121212--+--=+--++--y x y x x m x x m x()()()2121241242344344033-⎛⎫=+-+-+=+---+= ⎪⎝⎭m m x x m x x m m m 成立, 故∠APB 的平分线总垂直于x 轴.34.【答案】(1)22143+=x y ;(2)存在,:80--=l y .【解析】(1)由题可知,(,0)A a ,(0,)B b ,2,⎛⎫- ⎪⎝⎭b P c a ,因为=OP AB k,则200--=---b b a c a,解得=b ,故有2223+=⎧⎪=⎨⎪+=⎩a cb bc a ,解得2=a,=b椭圆方程为22143+=x y .(2)法一:假设存在,易知直线l 的斜率存在, 设直线l 的方程为=+y kx m ,()11,M x y ,()22,Q x y ,联立22143=+⎧⎪⎨+=⎪⎩y kx mx y ,得()2223484120+++-=k x kmx m , 则122212283441234⎧+=-⎪⎪+⎨-⎪=⎪+⎩km x x k m x x k , 因为2F 为MQB △的重心,则121201303++⎧=⎪⎪⎨++⎪=⎪⎩x x y y,解得12123+=⎧⎪⎨+=⎪⎩x x y y则122128334⎧+=-=⎪+⎨⎪+++=⎩km x x k kx m kx m,化简得228334634⎧=-⎪⎪+⎨⎪=⎪+⎩km k m k,解得⎧=⎪⎪⎨⎪=⎪⎩k m ,所以直线:80--=l y .法二:设()11,M x y ,()22,Q x y ,因为2F 为MQB △的重心,则120130++⎧=⎪⎪=x x,解得12123+=⎧⎪⎨+=⎪⎩x x y y设MQ 的中点R,则3,2⎛ ⎝⎭R , 因为M ,Q 在椭圆22143+=x y 上,则22112222143143⎧+=⎪⎪⎨⎪+=⎪⎩x y x y ,两式相减得34⋅=-MQ OR k k,即=MQ k所以直线:80--=l y .35.【答案】(1)22143+=x y ,(2)3λ=.【解析】(1)因为离心率为12,所以12==c e a , 又3=AF ,所以3+=a c ,解得2=a ,1=c , 又222=-c a b ,所以23=b ,所以椭圆方程为22143+=x y .(2)由(1)知()1,0F ,()2,0-A ,设直线PN 的方程为1=+x my ,()11,P x y ,()22,N x y , 因为M 与P 关于原点对称,所以()11,--M x y , 所以1112=-y x k ,2222=+yk x , 若存在λ,使得12λ=k k 恒成立,所以121222λ=-+y yx x , 所以()()122122λ+=-y x y x ,两边同乘1y 得()()21221122λ+=-y x y y x ,又因为()11,P x y 在椭圆上,所以2211143+=x y ,所以()()2112113223144-+⎛⎫=-= ⎪⎝⎭x x x y ,所以()()()()112211322224λ-++=-x x x y y x ,当12≠x 时,则()()12213224λ-++=x x y y , 所以()21212136124λ--+-=x x x x y y ①; 当12=x 时,M 与A 重合,联立方程221143=+⎧⎪⎨+=⎪⎩x my x y ,消元得()2234690++-=m y my ,所以212212934634-⎧=⎪⎪+⎨-⎪+=⎪+⎩y y m m y y m ,所以()212128234+=++=+x x m y y m ,()222121212412134-=+++=+m x x m y y m y y m ,代入①得22221236489124343434λ-+--+-=+++m m m m , 整理得10836λ-=-,解得3λ=. 36.【答案】(1)2-⎭和2⎛ ⎝⎭;(2)直径12A A 与直径12B B 共轭,理由见解析;(3)λ>λ< 【解析】(1)由题设知32=AB k ,设所求直线方程为=y kx ,则34⋅=-AB k k ,则12=-k , 故共轭直径所在直线方程为12=-y x .联立椭圆与12=-y x ,即2212143⎧=-⎪⎪⎨⎪+=⎪⎩y x x y 可得23=x,=x故端点坐标为⎭和⎛ ⎝⎭.(2)由题设知,l 不与x 轴重合,故设l:=x my ()111,A x y 、()122,B x y ,联立方程()22223430143⎧=⎪⇒+--=⎨+=⎪⎩x my m y x y ,则12234+=+y y m ,122334-=+y y m ,2122121234-=+m x x m ,122223434=-=⋅=++S y mm 63=≤=,当且仅当2313+=m ,即223=m 时取等号, 此时121221222123312124-⋅===-=--A A B By y b k k x x m a,故直径12A A 与直径12B B 共轭. (3)设点()11,C x y ,()22,M x y ,当CD 不与坐标轴重合时,设CD l :=y kx ,则MN l :34=-y x k, 联立2222211221212,3434143=⎧⎪⇒==⎨+++=⎪⎩y kx k x y x y k k , 同理可得22221634=+k x k ,222934=+y k. 由椭圆的对称性,不妨设C 在第一象限,则M 必在第二象限或第四象限,则1=x1=y若M在第二象限,则2=x2=y ,从而 ⎪⎝⎭T ,则⎫⎪⎪⎪ ⎪⎝⎭P .又P在椭圆外,则223412⎫⎪⎪+>⎪ ⎪ ⎪⎝⎭⎝⎭, 化简可得22λ>,即λ>λ<若M 在第四象限,同理可得22λ>,即λ>λ<当CD 与x 轴垂直或重合时,由椭圆的对称性,不妨取()2,0C,(M ,则λ⎛⎫⎪ ⎪⎝⎭P . 又P 在椭圆外,则2223341224λλλ+⋅>⇒>,即λ>λ<综上:λ>λ<。
高三高三数学第二轮复习专题练习题解析几何高考题型精品

高三高三数学第二轮复习专题练习题解析几何高考题型精品IMB standardization office【IMB 5AB- IMBK 08- IMB 2C】复习六解析几何高考题型 解析几何中的基本量如直线方程、点到直线的距离、圆及圆锥曲线的各种基本量。
[例1]对于每个自然数n ,抛物线22()(21)1y n n x n x =+-++与x 轴交于n A 、n B 两点,以n n A B 表示该两点间的距离,则112219991999A B A B A B +++的值是() (A )19981999(B )20001999(C )19991998(D )19992000[例2](97年高考题〈文〉)已知圆满足:①截y 轴所得弦长为2;②被x 轴分成两段圆弧,其弧长之比为3∶1;③圆心到直线:20l x y -=1.过点(2,4)M -作圆22:(2)(1)25C x y -+-=的切线1,l 已知直线2:320l ax y a ++=与1l 平行,则1l 与2l 之间的距离为()(A )85(B )25(C )285(D )125 2.已知两直线1:sin 10l x y θ+-=和2:2sin 10,l x y θ++=当12∥l l 时,θ=__________________;当12l l ⊥时,θ=____________________.3.已知双曲线的一条准线与渐近线的交点为A 、B ,这条准线的相应焦ABF ∆是等边三角形,那么此双曲线的离心率为________.椭圆的第一定义12122(2)MF MF a a F F +=>; 双曲线的第一定义12122(02)MF MF a a F F -=±<<;统一定义MF e d=(d 为动点M 到相应准线的距离)01e <<时为椭圆:1e >时为双曲线:1e =时为抛物线。
[例3]P 是椭圆2212516x y +=上一点,1F 、2F 是焦点,若1230F PF ∠=则12PF F ∆的面积是_______________.[例4]过双曲线22145x y -=的右焦点F 作一条长为AB (A 、B 均在双曲线的的右支上),将双曲线绕右准线旋转90,则弦AB 扫过的面积为()(A )32π(B )16π(C )8π(D )4π[例5]已知点(2,6),A P 为抛物线216y x =上任一点,P 到y 轴上的距离为d ,则_____________.4.P 是长轴在x 轴上的椭圆22221x y a b+=上的点,1F 、2F 分别为椭圆的两个焦点,椭圆的半焦距为c ,则12PF PF ⋅的最大值与最小值之差一定是()(A )1(B )2a (C )2b (D )2c5.抛物线21:4C y x =与椭圆222(5):11680x y C -+=在x 轴上方的交点为A 、B ,设2C 的左顶点为F ,则________.AF BF +=6.设1F 、2F 是双曲线22221(0,0)x y a b a b-=>>的两个焦点,P 是双曲线上一点,且1290F PF ∠=,已知双曲线的离心率为54,12Rt F PF ∆的面积是9,则a b +=()5(C )6(D )7直线与圆锥曲线联立直线与圆锥曲线的方程,再结合函数与方程的思想来解决问题。
2021-2022年高三数学第二轮专题复习解析几何问题的题型与方法人教版

2021年高三数学第二轮专题复习解析几何问题的题型与方法人教版一.复习目标:1. 能正确导出由一点和斜率确定的直线的点斜式方程;从直线的点斜式方程出发推导出直线方程的其他形式,斜截式、两点式、截距式;能根据已知条件,熟练地选择恰当的方程形式写出直线的方程,熟练地进行直线方程的不同形式之间的转化,能利用直线的方程来研究与直线有关的问题了.2.能正确画出二元一次不等式(组)表示的平面区域,知道线性规划的意义,知道线性约束条件、线性目标函数、可行解、可行域、最优解等基本概念,能正确地利用图解法解决线性规划问题,并用之解决简单的实际问题,了解线性规划方法在数学方面的应用;会用线性规划方法解决一些实际问题.3. 理解“曲线的方程”、“方程的曲线”的意义,了解解析几何的基本思想,掌握求曲线的方程的方法.4.掌握圆的标准方程:(r >0),明确方程中各字母的几何意义,能根据圆心坐标、半径熟练地写出圆的标准方程,能从圆的标准方程中熟练地求出圆心坐标和半径,掌握圆的一般方程:022=++++F Ey Dx y x ,知道该方程表示圆的充要条件并正确地进行一般方程和标准方程的互化,能根据条件,用待定系数法求出圆的方程,理解圆的参数方程(θ为参数),明确各字母的意义,掌握直线与圆的位置关系的判定方法.5.正确理解椭圆、双曲线和抛物线的定义,明确焦点、焦距的概念;能根据椭圆、双曲线和抛物线的定义推导它们的标准方程;记住椭圆、双曲线和抛物线的各种标准方程;能根据条件,求出椭圆、双曲线和抛物线的标准方程;掌握椭圆、双曲线和抛物线的几何性质:范围、对称性、顶点、离心率、准线(双曲线的渐近线)等,从而能迅速、正确地画出椭圆、双曲线和抛物线;掌握a 、b 、c 、p 、e 之间的关系及相应的几何意义;利用椭圆、双曲线和抛物线的几何性质,确定椭圆、双曲线和抛物线的标准方程,并解决简单问题;理解椭圆、双曲线和抛物线的参数方程,并掌握它的应用;掌握直线与椭圆、双曲线和抛物线位置关系的判定方法.二.考试要求:(一)直线和圆的方程1.理解直线的斜率的概念,掌握过两点的直线的斜率公式,掌握直线方程的点斜式、两点式、一般式,并能根据条件熟练地求出直线方程。
高考数学二轮复习指导系列-解析几何.doc
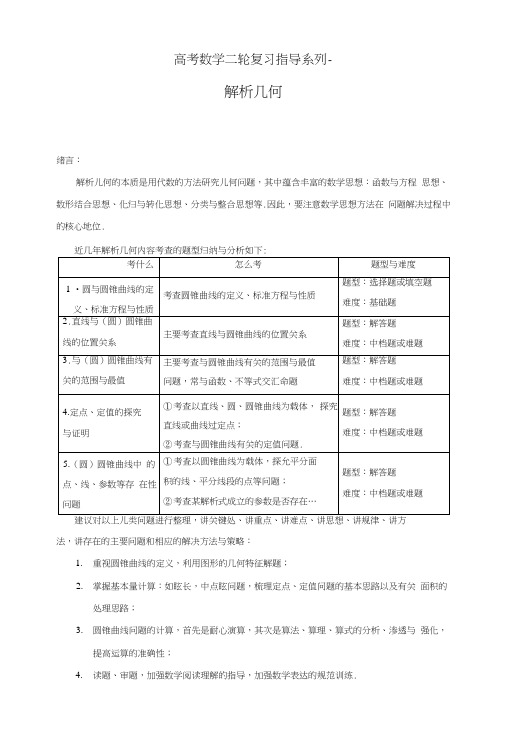
高考数学二轮复习指导系列-解析几何绪言:解析儿何的本质是用代数的方法研究儿何问题,其中蕴含丰富的数学思想:函数与方程思想、数形结合思想、化归与转化思想、分类与整合思想等.因此,要注意数学思想方法在问题解决过程中的核心地位.近几年解析几何内容考查的题型归纳与分析如下:建议对以上儿类问题进行整理,讲关键处、讲重点、讲难点、讲思想、讲规律、讲方法,讲存在的主要问题和相应的解决方法与策略:1.重视圆锥曲线的定义,利用图形的几何特征解题;2.掌握基本量计算:如眩长,中点眩问题,梳理定点、定值问题的基本思路以及有关面积的处理思路;3.圆锥曲线问题的计算,首先是耐心演算,其次是算法、算理、算式的分析、渗透与强化,提高运算的准确性;4.读题、审题,加强数学阅读理解的指导,加强数学表达的规范训练.一、存在的问题及原因分析:(一)缺乏科学规范的作图意识,识图、用图能力待提高科学规范地画出图形是研究几何问题的基础,作图的过程也是问题条件的理解与解题思路的探究过程.【例1】(2016全国I卷理20)设圆x2+ y2+2x-\5 = 0的圆心为A,直线/过点B (1, 0)且与x轴不重合,/交圆人于两点,过B作AC的平行线交AD于点E.⑴证明|创+ |皿为定值,并写出点E的轨迹方程.评析:由于作图潦草、没有使用尺规作图、不够精确,导致难以发现关键的几何特征信息.识图、用图能力差,没有从图形中发现AC = AD t以及BE = DE・究其原因在于课堂教学作图环节缺失,教师多用手工绘制草图、缺乏刈•图形中几何特征与数量关系的细致量化分析.建议教师注意使用尺规规范作图,示范指导,并要求学生当堂作图练习.所给的练习,不给图形,要求学生通过审题自己作图,结合图形从整体角度理解题意寻找解题思路.(二)缺乏利用圆锥曲线的定义研究相关问题的意识与模式习惯定义是数学问题研究的起点.圆锥曲线的定义蕴含了丰富的内涵,对我们的问题的理解与思考有深刻的意义.【例2】(2016全国I卷理20)设圆x2 + y2+2x-\5 =0的圆心为A,直线/过点B (1, 0)且与x轴不重合,/交圆A于C,D两点,过B作4C的平行线交AD于点E.⑴证明|创+ |比为定值,并写出点E的轨迹方程.解答:圆的方程可化为(^ + 1)2 + /=16的圆心为4(70),半径为4;动点C, D落在圆上,满足|AC| = |AD| = 4;(点在圆上,根据圆的定义有\AC\ = \AD\ = 4)等腰三角形AACD 中,BE//AC=>\BE\ = \DE\;・•. AE| + |ED|=|AE| + |BE| = 4;由题设得A(-l,0) , B(l,0), | AB |=2,由椭圆定义可得点E的轨迹方程为:手+斗"(〉'工°)・(|個+岡二4根据定义知点E的轨迹是椭圆)评析:未能从动点与定点的位置关系角度理解问题,去探究目标“证明\AE\ + \EB\为定值” 的证明思路,未能结合定义预判可能的轨迹类型,从而没能联系已有的几何条件寻找突破口.究其原因在于研究求轨迹方程这类问题时,没有养成优先站在“观察发现动点运动变化 过程中不变的儿何关系”的角度探究问题的意识;没有养成“定义”的应用意识,未能从圆 锥曲线的定义审视动点满足的不变的几何关系,选择简便的方法实现几何条件代数化.建议复习教学中凡涉及轨迹问题,均需先回顾梳理各种方法,结合问题背景比较、优化 方法;强调要在大问题(圆锥曲线的定义与几何图形中的位置关系与数量关系)下研究几何 性质;加强逻辑严密的课堂推演与条理清晰试题剖析.(三)缺乏对几何条件代数化(坐标化)方法策略的深入研究解析几何就是用代数的方法研究几何问题.那么,对题目所给的几何条件如何代数化(坐 标化)很值得研究,我们追求的是既要准确转化,又要简便、减少运算量的转化.点,分别为「的左、右顶点,P 为「上一点,且PF 丄x 轴,过点A 的直线/与线段"交 于点M ,与轴交于点E ,直线与『轴交于点N ,若\OE\ = 2\ON\ ,则「的离心率为()3 4A. 3B. 2C. -D.- 2 3解答:从试题中的关键条件\OE\ = 2\ON\出发,因为三点均在y 轴上,从坐标关系角度加以理解,从而引入关联参数实现几何条件代数化:设点2V (O,r )E (O,-2r ),则直线/疔+士 = 1,直线B 陀+沪,联立即可得:M (-3d,4f ), ・・・_c=-3a,答案:A【例3](唐山2017)已知O 为坐标原点, F 是双曲线r:罕-* = 1(。
二轮专题复习——解析几何
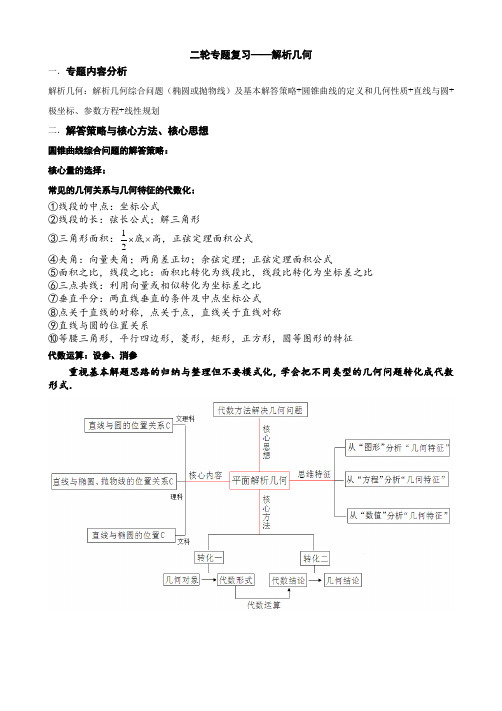
二轮专题复习——解析几何一.专题内容分析解析几何:解析几何综合问题(椭圆或抛物线)及基本解答策略+圆锥曲线的定义和几何性质+直线与圆+极坐标、参数方程+线性规划二.解答策略与核心方法、核心思想 圆锥曲线综合问题的解答策略:核心量的选择:常见的几何关系与几何特征的代数化:①线段的中点:坐标公式②线段的长:弦长公式;解三角形③三角形面积: 21底×高,正弦定理面积公式④夹角:向量夹角;两角差正切;余弦定理;正弦定理面积公式⑤面积之比,线段之比:面积比转化为线段比,线段比转化为坐标差之比 ⑥三点共线:利用向量或相似转化为坐标差之比 ⑦垂直平分:两直线垂直的条件及中点坐标公式 ⑧点关于直线的对称,点关于点,直线关于直线对称 ⑨直线与圆的位置关系⑩等腰三角形,平行四边形,菱形,矩形,正方形,圆等图形的特征代数运算:设参、消参重视基本解题思路的归纳与整理但不要模式化,学会把不同类型的几何问题转化成代数形式.三.典型例题分析1.(海淀区2017.4)已知椭圆C :22221(0)x y a b a b+=>>的左、右顶点分别为A ,B ,且||4AB =,离心率为12. (Ⅰ)求椭圆C 的方程;(Ⅱ)设点(4,0)Q , 若点P 在直线4x =上,直线BP 边形APQM 为梯形?若存在,求出点P解法1:(Ⅰ)椭圆C 的方程为22143x y +=.(Ⅱ)假设存在点,P 使得四边形APQM 为梯形.由题可知,显然,AM PQ 不平行,所以AP 与MQ AP MQ k k =.设点0(4,)P y ,11(,)M x y ,06AP y k =,114MQ y k x =-,∴01164y y x =-① ∴直线PB 方程为0(2)2yy x =-, 由点M 在直线PB 上,则011(2)2y y x =-② ①②联立,0101(2)264y x y x -=-,显然00y ≠,可解得1x =又由点M 在椭圆上,211143y +=,所以132y =±,即3(1,)2M ±, 将其代入①,解得03y =±,∴(4,3)P ±.解法2:(Ⅰ)椭圆C 的方程为22143x y +=.(Ⅱ)假设存在点,P 使得四边形APQM 为梯形.由题可知,显然,AM PQ 不平行,所以AP 与MQ 平行, AP MQ k k =, 显然直线AP 斜率存在,设直线AP 方程为(2)y k x =+.由(2)4y k x x =+⎧⎨=⎩,所以6y k =,所以(4,6)P k ,又(2,0)B ,所以632PB k k k ==.∴直线PB 方程为3(2)y k x =-,由223(2)34120y k x x y =-⎧⎨+-=⎩,消y ,得2222(121)484840k x k x k +-+-=.又(2,0)B , 所以212482121k x k +=+,即212242121k x k -=+,∴112123(2)121ky k x k -=-=+.∴22224212(,)121121k k M k k --++.由APMQ k k =可得22212612124264121kk k k k -+=--+, 解得12k =±, ∴3(1,)2M ±,(4,3)P ±,解法3:(Ⅰ)椭圆C 的方程为22143x y +=.(Ⅱ)假设存在点,P 使得四边形APQM 为梯形.由题可知,显然,AM PQ 不平行,所以AP 与MQ 平行, AP MQ k k = . 显然直线MB 存在斜率且斜率不为0,∴设直线MB 方程为2x ty =+(0)t ≠.24x ty x =+⎧⎨=⎩由,得2(4,)P t .∴2163APt k t ==,由22234120x ty x y =+⎧⎨+-=⎩得22(34)120t y ty ++=, 设11(,)M x y ,又因为(2,0)B ,∴121234ty t -=+, ∴211268234t x ty t -+=+=+,即2226812(,)3434t tM t t -+-++.由APMQ k k =,所以22212134683434tt t t t -+=-+-+,解得23t =±解法4:假设存在点,P 使得四边形APQM 为梯形. 由题可知,显然,AM PQ 不平行,所以AP 与MQ 平行, 所以||1||2BM BP =. 过点M 作M H AB ⊥于H ,则有||||BH BQ =∴||1BH =,∴(1,0)H ,即11x =,代入椭圆方程,求得∴(4,3)P ±.2.(东城区2016.4理科)已知抛物线2:2(C y px p =>x 轴)过点F 且与抛物线C 交于,A B 两点,直线OA 与OB 的斜率之积为p -.(Ⅰ)求抛物线C 的方程;(Ⅱ)若M 为线段AB 的中点,射线OM 交抛物线C 于点D ,求证:2OD OM>.备注:以抛物线为背景,核心变量的选择(直线方程的不同形式);几何特征翻译代数关系(先转化再翻译)解:(Ⅰ)因为直线AB 过点F 且与抛物线C 交于,A B 两点,(,0)2PF , 设11(,)A x y ,22(,)B x y ,直线AB (不垂直x 轴)的方程可设为()(0)2py k x k =-≠. 所以2112(0)y px p =>,2222y px =. 因为直线OA 与OB 的斜率之积为p -, 所以1212y y p x x =-. 所以221212()y y p x x =,得 124x x =. ……4分 由2(),22,p y k x y px ⎧=-⎪⎨⎪=⎩ 消y 得22222(2)04k p k x k p p x -++= 其中 22222(2)0k p p k p k =+->V所以2124p x x =, 21222k P P x x k ++=. 所以4p =,抛物线2:8C y x =. ……8分 (Ⅱ)设0033(,),(,)M x y P x y ,因为M 为线段AB 的中点,所以2201222122(2)()22k P P k x x x k k ++=+==,004(2)y k x k =-=. 所以直线OD 的斜率为02022op y kk x k ==+. 直线OD 的方程为222op ky k x x k ==+代入抛物线2:8C y x =的方程, 得22322(2)k x k +=.所以23(2)x k x =+.因为 20k >, 所以23(2)2OD x k OMx ==+>. ……13分 3.(东城区2018.5文科)已知椭圆2222:1(0)x y C a b a b+=>>的右焦点为(1,0)F ,离心率为12.(Ⅰ)求椭圆C 的方程;(Ⅱ),A B 是椭圆C 在y 轴右侧部分上的两个动点,若原点O 到直线ABABF的周长为定值.解:(Ⅰ)椭圆C 的方程为22143x y +=.(Ⅱ)①当AB 垂直于x 轴时,可得 4AF BF AB ++=. ②当AB 不垂直于x 轴时,设AB 的方程为m kx y +=. 因为原点O 到直线AB=223(1)m k =+.由22,1,43y kx m x y =+⎧⎪⎨+=⎪⎩得222(34)84120k x kmx m +++-=,即222(34)8120k x kmx k +++=.设11(,)A x y ,22(,)B x y ,则122834km x x k -+=+,21221234k x x k=+.所以12|||AB x x =-====24||||34m k k =+. 因为A ,B 在y 轴右侧,所以0mk <,所以24||34mkAB k=-+. 22222111122111(1)(1)3(1)41124(2)42.x AF x y x x x x =-+=-+-=-+=-又所以11||22AF x =-,同理21||22BF x =-. 所以121||||4()2AF BF x x +=-+221844()423434km kmk k -=-=+++. 所以2244||||||443434km kmAF BF AB k k ++=+-=++.综上,△ABF 的周长等于椭圆C 的长轴长4.解法2:作OH AB ⊥于H ,所以||OH =所以2222222211111||||||33(1)344x x AH OA OH x y x =-=+-=+--=,即1||2x AH =, 同理2|B |2x H =, 所以121||||||()2AB AH BH x x =+=+, 又11||22AF x =-,同理21||22BF x =-. 所以.1212111||||||22()4222AF BF AB x x x x ++=-+-++= 综上,△ABF 的周长等于椭圆C 的长轴长4.解析几何选择填空题练习:1.(2018年全国3卷)设12,F F 是双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点,O 是原点.过2F作C 一条渐近线的垂线,垂足为P.若1|||PF OP = ,则C 的离心率为( )2分析:由题可知22||,||PF b OF c == ,所以||PO a =, 在2Rt POF ∆中,222||cos ||PF bPF O OF c∠== , 又在12PF F ∆中,2222121212|PF ||FF |||cos 22|PF ||FF |PF PF O +-∠=⋅,=,所以b c = 所以223c a =,所以离心率ce a==.故选C. 解法二:过左焦点作渐近线的垂线,垂足为Q ,利用直角三角形勾股定理建立关系,可求。
高考数学解析几何知识点归纳

高考数学解析几何知识点归纳解析几何是高考数学中的一个重要板块,它将代数与几何巧妙地结合在一起,具有较强的综合性和逻辑性。
以下是对高考数学中解析几何知识点的详细归纳。
一、直线1、直线的倾斜角与斜率倾斜角:直线与 x 轴正方向所成的角,范围是0, π)。
斜率:当倾斜角不是 90°时,斜率 k =tanα(α 为倾斜角)。
过两点 P(x₁, y₁),Q(x₂, y₂)的直线斜率 k =(y₂ y₁) /(x₂ x₁)(x₁≠ x₂)。
2、直线的方程点斜式:y y₁= k(x x₁),适用于已知斜率和一点的情况。
斜截式:y = kx + b,其中 k 为斜率,b 为截距。
两点式:(y y₁) /(y₂ y₁) =(x x₁) /(x₂ x₁),适用于已知两点的情况。
截距式:x / a + y / b = 1,其中 a、b 分别为 x 轴和 y 轴上的截距(a ≠ 0,b ≠ 0)。
一般式:Ax + By + C = 0(A、B 不同时为 0)。
3、两直线的位置关系平行:斜率相等且截距不相等,即 k₁= k₂且 b₁ ≠ b₂(斜截式);A₁B₂ A₂B₁= 0 且 A₁C₂ A₂C₁ ≠ 0 (一般式)。
垂直:斜率之积为-1,即 k₁k₂=-1 (斜率都存在);A₁A₂+ B₁B₂= 0 (一般式)。
4、点到直线的距离公式点 P(x₀, y₀)到直线 Ax + By + C = 0 的距离 d =|Ax₀+ By₀+ C| /√(A²+ B²)二、圆1、圆的方程标准方程:(x a)²+(y b)²= r²,圆心为(a, b),半径为 r。
一般方程:x²+ y²+ Dx + Ey + F = 0(D²+ E² 4F > 0),圆心为(D/2, E/2),半径为 r =√(D²+ E² 4F) / 2 。
高三数学二轮复习冲刺:例谈解析几何中的齐次化技巧

例谈解析几何中齐次化技巧一.基本原理在解析几何计算与二次曲线“半径”(曲线上一点到坐标原点的连线)斜率有关的问题时,我们可以进行“1”代换的齐次化计算,即一般计算步骤为:22222)(1b kx y ny mx ny mx b kx y -=+⇒⎩⎨⎧=++=,整理可得:0(2=+⋅+C xy B x y A 0(2=+⋅+C x y B x y A 中的几何意义为:直线与曲线的交点与原点的连线的斜率,即,OA OB 的斜率,设为12,k k ,由韦达定理知12B k k A +=-,12C k k A=,从而能通过最初的二次曲线和直线相交,得出,OA OB 的性质,倒过来,我们也可以通过,OA OB 的性质与二次曲线得出AB 的性质.下面通过例题予以分析.二.典例分析例1.已知双曲线22:154x y Γ-=的左右焦点分别为1F ,2F ,P 是直线8:9l y x =-上不同于原点O 的一个动点,斜率为1k 的直线1PF 与双曲线Γ交于A ,B 两点,斜率为2k 的直线2PF 与双曲线Γ交于C ,D 两点.(1)求1211k k +的值;(2)若直线OA ,OB ,OC ,OD 的斜率分别为OA k ,OB k ,,OC k ,OD k ,问是否存在点P ,满足0OA OB OC OD k k k k +++=,若存在,求出P 点坐标;若不存在,说明理由.解析:(1)由已知1(3,0)F -,2(3,0)F ,设(9,8)P λλ-,(0)λ≠,∴1839k λλ=--,2893k λλ-=-,121139939884k k λλλλ---+=+=--.(2)由题意知直线113k x k y AB =-:,与双曲线方程联立得2121229)(45k x k y y x -=-,同除以2x ,令x y k =得0454929141(1221=--+k k k k ,因此498914192211211+=+=+k k k k k k OB OA .同理将直线223:k x k y CD -=-与双曲线方程联立可得498222+=+k k k k OD OC ,所以0498498222211=+++=+++k k k k k k k k OD OC OB OA ,即0)49)((2121=++k k k k .由(1)知21k k -≠,令点)98,(00x x P -,所以94398398000021-=--⋅+-=x x x x k k ,所以解得590±=x ,∴存在98(,55P -或98(,)55P -满足题意.例2.如图,已知椭圆12222=+b y a x (a b 0)>>过点(1,22),离心率为22,左右焦点分别为12F F .点P 为直线l :2x y +=上且不在x 轴上的任意一点,直线1PF 和2PF 与椭圆的交点分别为A B 、和,C D O 、为坐标原点.(1)求椭圆的标准方程;(2)设直线1PF 、2PF 斜率分别为1k 2k 、.()i 证明:12132k k -=(ⅱ)问直线l 上是否存在一点P ,使直线OA OB OC OD 、、、的斜率OA OB OC OD k k k k 、、、满足0OA OB OC OD k k k k +++=?若存在,求出所有满足条件的点P 的坐标;若不存在,说明理由.解析:(1)椭圆方程为2212x y +=.(2)设B A ,的坐标为),(),,(2211y x y x ,AB 方程为)1(1+=x k y ,022)11(12)1(21221221=-+-⇒⎪⎩⎪⎨⎧=++=x xy k y k y x x k y 即021(2)(11(1221=-+-x y k x y k 故12211--=+k k k k OB OA .同理,设D C ,坐标为),)(,(4433y x y x ,CD 方程:)1(2-=x k y ,则12222--=+k k k k OD OC ,故:0))(1(012122121222211=+-⇒=--+--k k k k k k k k .则⎪⎩⎪⎨⎧=-=23112121k k k k ,解得:P 的坐标为)43,45(或⎪⎩⎪⎨⎧=-=+23102121k k k k ,解得:P 的坐标为)2,0(三.习题演练已知椭圆C :()222210x y a b a b+=>>24y x =的焦点F .(1)求椭圆C 的标准方程;(2)O 为坐标原点,过O 作两条射线,分别交椭圆于M ,N 两点,若OM ,ON 斜率之积为45-,求证:MON △的面积为定值.答案:(1)椭圆方程为22154x y +=;(2)MON S =△为定值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
黑龙江省高考数学二轮复习专题 10:解析几何
姓名:________
班级:________
成绩:________
一、 单选题 (共 12 题;共 24 分)
1. (2 分) 已知方程 A . k<1 B . k>2 C . k<1或 k>2 D . 1<k<2
的图象是双曲线,那么 k 的取值范围是( )
2.(2 分)(2019 高三上·清远期末) 已知抛物线
与双曲线
为抛物线的焦点,若
=3,则该双曲线的离心率为( )
的一条渐近线的交点为 ,
A.
B.
C.
D.
3. (2 分) (2020 高二上·上海期中) 两内切圆的半径长是方程
为 1,其中一圆的半径为 3,则
()
A . 2或4
B.4
C . 1或5
D.5
的两根,已知两圆的圆心距
4. (2 分) (2017 高二上·黑龙江月考) 已知焦点在 轴上的椭圆的长轴长是 8,离心率是
第 1 页 共 24 页
,则此椭圆
的标准方程是( )
A. B. C. D. 5. (2 分) (2016 高二上·鹤岗期中) 已知△ABC 的周长为 20,且顶点 B (0,﹣4),C (0,4),则顶点 A 的轨迹方程是( )
A.
(x≠0)
B.
(x≠0)
C.
(x≠0)
D.
(x≠0)
6.(2 分)(2017 高二上·牡丹江月考) 抛物线
A.
上到直线
距离最近的点的坐标是( )
B. C. D . (2,4) 7. (2 分) 已知圆 x2+y2﹣4ax+2by+b2=0(a>0,b>0)关于直线 x﹣y﹣1=0 对称,则 ab 的最大值为( ) A. B.
第 2 页 共 24 页
C.
D.
8. (2 分) (2020·丽江模拟) 设 、 分别是椭圆
的焦点,过 的直线交椭
圆于 、 两点,且
,
,则椭圆的离心率为( )
A.
B.
C.
D.
9. (2 分) (2018 高二上·湛江月考) 已知
分别是椭圆的左,右焦点,现以 为圆心作一个圆恰好
经过椭圆中心并且交椭圆于点
,若过 的直线
是圆 的切线,则椭圆的离心率为( )
A. B.
C. D. 10. (2 分) 若直线 y=0 的倾斜角为 α,则 α 的值是( ) A.0 B. C.
第 3 页 共 24 页
D . 不存在
11. (2 分) 已知圆 O:x2+y2=4 上有三个不同的点 P、A、B,且满足 =x ﹣ 的取值范围是( )
(其中 x>0),则实数 x
A . (0,1)
B . [1,3]
C.( , )
D.[ , ]
12. (2 分) (2019 高二上·滁州月考) 在椭圆 线方程为( )
内,过点 M(1,1)且被该点平分的弦所在的直
A . 9x-16y+7=0
B . 16x+9y-25=0
C . 9x+16y-25=0
D . 16x-9y-7=0
二、 填空题 (共 6 题;共 7 分)
13. (1 分) (2020 高二上·丽水期末) 已知直线
和
则实数
________,两直线 与 间的距离是________.
.若
,
14.(1 分)(2018 高二上·扶余月考) 抛物线
的焦点为 F,其准线 l 与双曲线
相
交于 A、B 两点,若
为等边三角形,则 P 等于________.
15.(2 分)(2019 高二上·辽宁月考) 过点
的直线 与圆
相交于 , 两
点,且
,则直线 的方程为________.
16. (1 分) (2016 高二下·深圳期中) 已知点 A(﹣2,0),B(0,4)到直线 l:x+my﹣1=0 的距离相等,则 m 的值为________.
第 4 页 共 24 页
17. (1 分) (2019·天河模拟) 已知点 A 是抛物线
的对称轴与准线的交点,点 B 为抛物线的焦点,P
在抛物线上且满足 ________.
,当 m 取最大值时,点 P 恰好在以 A,B 为焦点的双曲线上,则双曲线的离心率为
18. (1 分) (2019 高二上·太原月考) 椭圆上点到其焦点的距离最大为 5,最小为 3,则该椭圆的离心率为 ________.
三、 解答题 (共 9 题;共 90 分)
19. (5 分) 已知圆 C 与 y 轴相切,圆心 C 在直线 l1:x-3y=0 上,且在直线 l2:x-y=0 上截得的弦长为 ,求圆 C 的方程.
20.(10 分)(2019 高二上·吉安月考) 在平面直角坐标系
中,已知
的顶点坐标分别是
,
,
,记
外接圆为圆 M.
(1) 求圆 M 的方程;
(2) 在圆 M 上是否存在点 ,使得
?若存在,求点 P 的个数;若不存在,说明理由.
21. (10 分) (2020 高二上·临澧期中) 已知 P 为圆 :
,线段
的垂直平分线交直线
于点 Q.
上一动点,点 坐标为
(1) 求点 Q 的轨迹 方程;
(2) 已知
,过点
作与 轴不重合的直线 交轨迹 于
两点,直线
分
别与 轴交于
两点.试探究
的横坐标的乘积是否为定值,并说明理由.
22. (15 分) (2019·鞍山模拟) 已知椭圆 :
的左、右焦点分别为
,离心率
为
,直线 :
与椭圆交于
(Ⅰ)求 的方程;
,四边形
的面积为
.
(Ⅱ)作与 平行的直线与椭圆交于
,求
的取值范围.
两点,且线段 的中点为 ,若
的斜率分别为
23. (10 分) (2018 高二上·海口期中) 如图,已知抛物线
第 5 页 共 24 页
的焦点为 F,A 是抛物线上横坐
标为 4,且位于 x 轴上方的点,点 A 到抛物线准线的距离等于 5,过点 A 作 AB 垂直于 y 轴,垂足为点 B,OB 的中点 为 M.
(1) 求抛物线的方程; (2) 过点 M 作 MN⊥ FA,垂足为 N,求点 N 的坐标.
24. (10 分) (2017 高二上·阜宁月考) 已知椭圆 圆心,椭圆 C 的长半轴长为半径的圆与直线
相切.
(1) 求椭圆 C 的标准方程;
的离心率为 ,以原点 O 为
(2)已知点 A、B 为动直线
与椭圆 C 的两个交点,问:在 x 轴上是否存在定点 E,使得
为定值?若存在,试求出点 E 的坐标和定值;若不存在,请说明理由.
25. (10 分) (2017·上饶模拟) 已知椭圆 x2+y2﹣2x+4y﹣3=0 的直径.
(1) 求椭圆 C 的方程;
,离心率
,它的长轴长等于圆
(2) 若过点
的直线 l 交椭圆 C 于 A,B 两点,是否存在定点 Q,使得以 AB 为直径的圆经过这个定点,
若存在,求出定点 Q 的坐标;若不存在,请说明理由?
26. (10 分) 已知某圆拱桥的水面跨度为 20m,拱高为 4m,现有一船,船宽为 10m,水面以上高为 3m,问这 条船能否从桥下通过?
27. (10 分) (2019·镇江模拟) 在平面直角坐标系
中,已知椭圆 C:
( > >0)的右
焦点为 F(1,0),且过点(1, ),过点 F 且不与 轴重合的直线 与椭圆 C 交于 A , B 两点,点 P 在椭圆上,
第 6 页 共 24 页
且满足
.
(1) 求椭圆 C 的标准方程;
(2) 若
,求直线 AB 的方程.
第 7 页 共 24 页
一、 单选题 (共 12 题;共 24 分)
答案:1-1、 考点: 解析:
参考答案
答案:2-1、 考点: 解析:
答案:3-1、 考点:
第 8 页 共 24 页
解析: 答案:4-1、 考点:
解析: 答案:5-1、 考点: 解析:
第 9 页 共 24 页
答案:6-1、 考点: 解析:
答案:7-1、 考点: 解析:
第 10 页 共 24 页
答案:8-1、考点:
解析:
答案:9-1、考点:
解析:
答案:10-1、考点:
解析:
答案:11-1、考点:
解析:
答案:12-1、
考点:
解析:
二、填空题 (共6题;共7分)答案:13-1、
考点:
解析:
答案:14-1、考点:
解析:
答案:15-1、考点:
解析:
答案:16-1、考点:
解析:
答案:17-1、考点:
解析:
答案:18-1、
考点:
解析:
三、解答题 (共9题;共90分)
答案:19-1、考点:
解析:
答案:20-1、
答案:20-2、考点:
解析:
答案:21-1、
答案:21-2、考点:
解析:
答案:22-1、考点:
解析:
答案:23-1、
答案:23-2、考点:
解析:
答案:24-1、。
