半导体物理与器件公式以及全参数
半导体物理与器件

k 并不是晶格中电子的动量,但却有着类似于自由电子
动量的表达(
p k
第三章
),因而被称作准动量。
固体量子理论初步 13
半导体物理与器件
有效质量和加速度
实际的半导体器件在一定的电压下工作,半导体内部产 生外加电场。
电场强度为E时
f eE
外力对电子做功等于能量的改变:
dE fds fvdt
第三章
固体量子理论初步
4
半导体物理与器件
在不满带中,部分电子状态被占据。在没有外力作用 的情况下,半满带内的电子可以在热的影响下改变自 己的能量而跑到别的k状态中。但由于E~k是偶函数 (晶体的对称性),处于k状态和-k状态的几率相等, 即有向一个方向运动的电子,平均地就有一个相应的 向相反方向运动的电子。即电子杂乱无章的热运动在 各个方向是等价而对称的,因而没有宏观电流。(k和 电子的运动速度即方向有关)
半制的物理作用“Fext”作用 于晶体中的电子时,有效质量可以描绘出该作用对该 电子的影响。 教材p53页给出了一个对有效质量的直观解释
第三章
固体量子理论初步
8
半导体物理与器件
有效质量与E-k图的关系
能量的改变对应于状态的改变。在无外力作用的情况下, 晶体中电子的能量是恒定的(平均)。当外力作用于晶体 电子时,其能量就要改变(平均),因而我们用能量E和 状态k之间的变化关系来描绘有效质量。 对应于经典理论:
第三章 固体量子理论初步 21
半导体物理与器件
用能带理论解释导体、半导体、绝缘体的导电性:
0<Eg<6eV
Eg>6eV
金属
半导体
绝缘体
第三章
固体量子理论初步
半导体物理与器件基础知识

一、肖特基势垒二极管欧姆接触:通过金属-半导体的接触实现的连接。
接触电阻很低。
金属与半导体接触时,在未接触时,半导体的费米能级高于金属的费米能级,接触后,半导体的电子流向金属,使得金属的费米能级上升。
之间形成势垒为肖特基势垒。
在金属与半导体接触处,场强达到最大值,由于金属中场强为零,所以在金属——半导体结的金属区中存在表面负电荷。
影响肖特基势垒高度的非理想因素:肖特基效应的影响,即势垒的镜像力降低效应。
金属中的电子镜像到半导体中的空穴使得半导体的费米能级程下降曲线。
附图:电流——电压关系:金属半导体结中的电流运输机制不同于pn结的少数载流子的扩散运动决定电流,而是取决于多数载流子通过热电子发射跃迁过内建电势差形成。
附肖特基势垒二极管加反偏电压时的I-V曲线:反向电流随反偏电压增大而增大是由于势垒降低的影响。
肖特基势垒二极管与Pn结二极管的比较:1.反向饱和电流密度(同上),有效开启电压低于Pn结二极管的有效开启电压。
2.开关特性肖特基二极管更好。
应为肖特基二极管是一个多子导电器件,加正向偏压时不会产生扩散电容。
从正偏到反偏时也不存在像Pn结器件的少数载流子存储效应。
二、金属-半导体的欧姆接触附金属分别与N型p型半导体接触的能带示意图三、异质结:两种不同的半导体形成一个结小结:1.当在金属与半导体之间加一个正向电压时,半导体与金属之间的势垒高度降低,电子很容易从半导体流向金属,称为热电子发射。
2.肖特基二极管的反向饱和电流比pn结的大,因此达到相同电流时,肖特基二极管所需的反偏电压要低。
10双极型晶体管双极型晶体管有三个掺杂不同的扩散区和两个Pn结,两个结很近所以之间可以互相作用。
之所以成为双极型晶体管,是应为这种器件中包含电子和空穴两种极性不同的载流子运动。
一、工作原理附npn型和pnp型的结构图发射区掺杂浓度最高,集电区掺杂浓度最低附常规npn截面图造成实际结构复杂的原因是:1.各端点引线要做在表面上,为了降低半导体的电阻,必须要有重掺杂的N+型掩埋层。
精简版-半导体物理与器件复习资料

精简版-半导体物理与器件复习资料(1).状态密度函数:有效量子态的密度。
它是能量的函数,表示为单位体积单位能量中的量子态数量。
(2).电子的有效质量:该参数将晶体导带中电子的加速度与外加的作用力联系起来,该参数包含了晶体中的内力。
(3).费米-狄拉克概率函数:该函数描述了电子在有效能级中的分布,代表了一个允许能量状态被电子占据的概率。
(4).费米能级:用最简单的话说,该能量在T=0K时高于所有被电子填充的状态的能量,而低于所有空状态能量。
(5).空穴的有效质量:该参数同样将晶体价带中空穴的加速度与外加作用力联系起来,而且包含了晶体中的内力。
(6).k空间能带图:以k为坐标的晶体能连曲线,其中k为与运动常量有关的动量,该运动常量结合了晶体内部的相互作用。
(7).克龙尼克-潘纳模型:由一系列周期性阶跃函数组成,是代表一维单晶晶格周期性势函数的数学模型。
(8).杂质补偿半导体:同一半导体区域内既含有施主杂质又含有受主杂质的半导体。
(9).完全电离:所有施主杂质原子因失去电子而带正电,所有受主杂质原子因获得电子而带负电的情况。
(10).简并半导体:电子或空穴的浓度大于有效状态密度,费米能级位于导带中(n型)或价带中(p型)的半导体。
(11).有效状态密度:即在导带能量范围内对量子态密度函数gc(E)与费米函数fF(E)的乘积进行积分得到的参数Nc;在价带能量范围内对量子态密度函数gv(E)与【1-fF(E)】的乘积进行积分得到的参数N。
(12).非本征半导体:进行了定量施主或受主掺杂,从而使电子浓度或空穴浓度偏离本征载流子浓度产生多数载流子电子(n型)或多数载流子空穴(p型)的半导体。
(13).束缚态:低温下半导体内的施主与受主呈现中性的状态。
此时,半导体内的电子浓度与空穴浓度非常小。
n:本征半导体内导带电子的浓度和价带空穴的浓度(数值相等)。
(14).本征载流子浓度iE:本征半导体内的费米能级位置。
(15).本征费米能级Fi(16).本征半导体:没有杂质原子且晶体中无晶格缺陷的纯净半导体材料。
半导体物理与器件
电阻率和温度的变化关系:
ρ
杂质全部电离,载流子浓度不变;晶格振动散 射起主要作用,随温度升高迁移率下降 本征区,载 流子浓度随 温度升高而 迅速升高,
低温 饱和 本征
T
低温下晶格振动不明显,本征载流子浓度低。 电离中心散射随温度升高而减弱,迁移率增加
载流子的漂移速度饱和效应 前边关于迁移率的讨论一直建立在一个基础之上:弱场 条件。即电场造成的漂移速度和热运动速度相比较小,从而不 显著改变载流子的平均自由时间。但在强场下,载流子从电场 获得的能量较多,从而其速度(动量)有较大的改变,这时, 会造成平均自由时间减小,散射增强,最终导致迁移率下降, 速度饱和。对于热运动的电子:
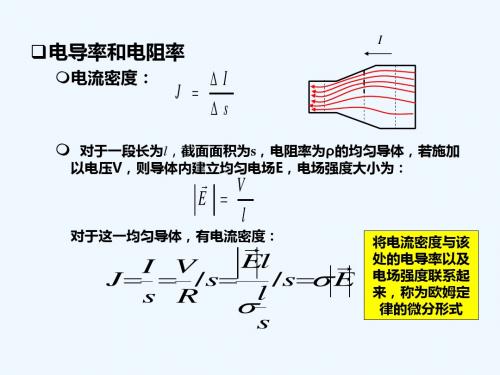
电导和电阻率
电流密度:
I
I J s
对于一段长为l,截面面积为s,电阻率为ρ 的均匀导体,若施加
以电压V,则导体内建立均匀电场E,电场强度大小为:
对于这一均匀导体,有电流密度:
V E l
El I V J /s /s E l s R s
将电流密度与该 处的电导率以及 电场强度联系起 来,称为欧姆定 律的微分形式
上述随机热运动能量对应于硅材料中电子的平均热运动速度为 107cm/s;如果我们假设在低掺杂浓度下硅材料中电子的迁移 率为μ n=1350cm2/V· s,则当外加电场为75V/cm时,对应的 载流子定向漂移运动速度仅为105cm/s,只有平均热运动速度 的百分之一。
在弱场条件下,载流子的平均自由运动时间基本上由载流子的 热运动速度决定,不随电场的改变而发生变化,因此弱场下载 流子的迁移率可以看成是一个常数。 当外加电场增强为7.5kV/cm之后,对应的载流子定向漂移 运动速度将达到107cm/s,这与载流子的平均热运动速度持平。 此时,载流子的平均自由运动时间将由热运动速度和定向漂移 运动速度共同决定,因此载流子的平均自由运动时间将随着外 加电场的增强而不断下降,由此导致载流子的迁移率随着外加 电场的不断增大而出现逐渐下降的趋势,最终使得载流子的漂 移运动速度出现饱和现象,即载流子的漂移运动速度不再随着 外加电场的增加而继续增大。
半导体物理1-5章公式总结

电子有效质量:*==⎪⎪⎭⎫ ⎝⎛nk m dk E d 11022能带极值附近电子速度:*=nm kv 浅能级杂质电离能的简单计算:()20*2204*42r n r n D E m m qm E εεπε==∆()20*2204*42r p r p A E m m qm E εεπε==∆硅、锗的相对介电常数r ε分别为16和12;锗0*12.0m m n =,硅0*26.0m m n =导带底的状态密度:2/132/3*2)()2(2)(c nc E E m V E g -= π 硅0*062.1m m n =,锗0*56.0m m n =价带顶的状态密度:2/132/3*2)()2(2)(E E m V E g v p v -=π 硅0*59.0m m p =,锗0*29.0m m n =费米分布函数(对于能量为E 的一个量子态被电子占据的概率):()⎪⎪⎭⎫ ⎝⎛-+=Tk E E E f Fexp 11玻耳兹曼分布函数(适用范围,T k E E F 0>>-):()⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛--=T k E T k E Tk E E E f F FB 000exp exp exp 导带中的电子浓度:⎪⎪⎭⎫⎝⎛--=Tk E E N n Fc c 00exp()32/30*22hT k m N n cπ=价带中的空穴浓度:⎪⎪⎭⎫⎝⎛--=T k E E N p v F v 00exp()32/30*22hT k m N p vπ=本征半导体, 费米能级:**0ln 432npv c F i m m T k E E E E ++==载流子浓度:()⎪⎪⎭⎫ ⎝⎛-===T k E N N p n n g v c i 02/1002exp“单”杂质半导体,电子(空穴)占据施主(受主)能级的概率:()⎪⎪⎭⎫⎝⎛-+=T k E E g E f F D D D 0exp 111()⎪⎪⎭⎫ ⎝⎛-+=T k E E g E f A F A A 0exp 111施主(受主)能级上电子(空穴)浓度:()⎪⎪⎭⎫⎝⎛-+==T k E E g N E f N n F D D DD D D 0exp 11()⎪⎪⎭⎫ ⎝⎛-+==T k E E g N E f N p AF A AA A A 0exp 11电离施主(受主)浓度:()[]⎪⎪⎭⎫⎝⎛--+=-=+Tk E E g N E f N n FD D DD D D 0exp 11()[]⎪⎪⎭⎫⎝⎛--+=-=-T k E E g N E f N p A F A AA A A 0exp 11n 型p 型电中性方程:00p n n D +=+00n p p A +=-弱电离区cD D c F N NT k E E E 2ln 220++=cD v A F N NT k E E E 4ln 220-+=⎪⎪⎭⎫ ⎝⎛--⎪⎭⎫⎝⎛=T k E E N N n D c D c 02/102exp 2⎪⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛=T k E E N N n v A v A 02/102exp 4强电离区cDc F N N T k E E ln0+=vAv F N N T k E E ln0-= D N n =0,D D N D n -=A N p =0,A A N D p +=过渡区⎪⎪⎭⎫⎝⎛+=i D i F n N T k E E 2arcsh 0⎪⎪⎭⎫⎝⎛-=i A i F n N T k E E 2sh 1-0()242/1220i D D n N N n ++=()242/1220i A A n N N p ++=在有杂质补偿情况下,n 型 p 型极低温情况下⎪⎪⎭⎫⎝⎛-+=A A D D F N N N T k E E 2ln 0⎪⎪⎭⎫⎝⎛--=D D A A F N N N T k E E 4ln 0()⎪⎪⎭⎫⎝⎛∆--=T k E N N N N n D Ac A D 00exp 2()⎪⎪⎭⎫⎝⎛∆--=T k E N N N N n A Dv D A 00exp 4低温下,与“单”杂质半导体低温下弱电离相同 强电离,以A D D N N N -=D A A N N N -=当A D N N -(或D A N N -)与i n 相近时,D A N p N n +=+00(或A D N p N n +=+00)()()[]⎪⎪⎭⎫⎝⎛+-+-+=i i A D A Di F n n N N N N T k E E 24ln 2/1220()()[]⎪⎪⎭⎫⎝⎛+-+--=i i D A D Ai F n n N N N N T k E E 24ln 2/1220 ()[]2422/1220iA D A D n N N N N n +-+-=()[]2422/1220iD A D A nN N N N p +-+-=载流子的漂移运动d v nq J -=,E J σ=,E v d μ=迁移率:Edv =μ 电导率:E nq J μ=,μσnq =半导体电导率:p n pq nq μμσ+=半导体的主要散射机构:1.电离杂质散射 (散射概率)2/3-∝T N P i i 2.晶格震动散射(声学波散射)2/3T P s ∝(光学波散射)1011ex p -⎥⎦⎤⎢⎣⎡-⎪⎪⎭⎫ ⎝⎛∝T k P o ω平均自由时间: P1=τ电子、空穴迁移率:*nnn m q τμ=,*p p p m q τμ=存在多种散射机构时:⋅⋅⋅+++=IIIII I1111ττττ,⋅⋅⋅+++=III II I 1111P P P P 随非平衡载流子注入产生的附加电导率:()n p pq μμσ+∆=∆单位时间单位体积内净复合消失的电子—空穴对数称为非平衡载流子的复合率。
半导体物理与器件

n0 Na p0 Nd
n0 Na pa p0 Nd nd
其中,n0:导带电子浓度;p0:价带空穴浓度。nd是施 主中电子密度;Nd+代表离化的施主杂质浓度;pa:受 主中的空穴密度;Na-:离化的受主杂质浓度。
掺杂时为本征载流子浓度
偿,类本征半导体
掺杂浓度大于ni时,杂质 电子浓度才起主要作用
半导体物理与器件
同理利用
p0
ni 2 n0
可推导出空穴浓度为:
p0
Na
2
Nd
Na
2
Nd
2
ni 2
例4.9的结果显示,在非 简并条件下,多数载流 子浓度近似等于掺杂浓
度(非补偿)
例4.10结果显示,在掺 杂浓度和本征载流子浓 度相差不大时,须考虑 本征载流子浓度的影响
Nc 2Nd
1
exp
Ec kT
Ed
1
绝对零度时,所有施主杂质 能级都被电子所占据,导带 无电子。
半导体物理与器件
§4.5 掺杂半导体的载流子浓度
前边讨论了本征半导体的载流子浓度;讨论了施主杂质和 受主杂质在半导体中的表现。定性的给出了杂质在不同温 度下的电离情况,并且定性的知道了载流子浓度和掺杂水 平的相关性。这节我们要具体推导掺杂半导体的载流子浓 度和掺杂的关系。
E Ec dE
Ec
1
exp
E
EF kT
仍然做变量代换
并且定义:
E Ec
kT
F
EF Ec kT
半导体物理与器件
载流子浓度公式变为:
(完整版)半导体公式
φm为金属功函数φs为半导体功函数X为半导体的电子亲和势
费米势φf=(Es-EFs)/qP型φf>0;N型φf<0 .
电荷面密度Qs=εε0Es
耗尽区宽度达到最大值 氧化层压降Vox= - Qs/CoxCox=εox/toxεox=εrε0Cox为氧化层单位面积电容εox为栅氧化层介电常量tox为氧化层厚度
强反型时的表ቤተ መጻሕፍቲ ባይዱ势力φsi2=2φfp
1.理想MOSFET的阈值电压:
n沟道阈值电压Qd= - qNAXdmax
2. 金属半导体功函数差对VT的影响
3. 氧化层及界面电荷对VT的影响
为基区少数载流子浓度
缓变:
基区自建电场 为梯度因子
第4章:
结型场效应晶体管:
夹断电压: ,夹断时所需要加的栅源电压Vp=Vbi-VP0。Vbi为 结的接触电势差。Vbi= 沟道电导:G0=2qμn(a-x0)Z/L即: VDS=VDsat称为饱和漏源电压VDsat=VP0-(Vbi-VGS)
绝缘栅场效应晶体管 MOS结构:
第1章:
第二章:
第3章:
共基极直流电流放大系数 为集电极电流与发射极电流之比
基极运输系数 发射结注入效率
发射结复合系数 , ,
均匀:
为共发射极直流电流放大系数
为基区渡越时间, 为基区少数载流子的寿命, 为中性基区宽度
, 分别为发射区和基区杂质浓度。 和 分别为发射区和基区的电阻率, 和 分别为发射区和基区的方块电阻
半导体物理与器件公式以及全参数
半导体物理与器件公式以及参数KT=0.0259ev N c=2.8∗1019N v=1.04∗1019 SI材料的禁带宽度为:1.12ev. 硅材料的n i=1.5∗1010Ge材料的n i=2.4∗1013 GaAs材料的n i=1.8∗106介电弛豫时间函数:瞬间给半导体某一表面增加某种载流子,最终达到电中性的时间,ρ(t)=ρ(0)e−(t/τd),其中τd =ϵσ,最终通过证明这个时间与普通载流子的寿命时间相比十分的短暂,由此就可以证明准电中性的条件。
E F热平衡状态下半导体的费米能级,E Fi本征半导体的费米能级,重新定义的E Fn是存在过剩载流子时的准费米能级。
准费米能级:半导体中存在过剩载流子,则半导体就不会处于热平衡状态,费米能级就会发生变化,定义准费米能级。
n0+∆n=n i exp(E Fn−E FikT) p0+∆p=n i exp[−(E Fp−E Fi)kT]用这两组公式求解问题。
通过计算可知,电子的准费米能级高于E Fi,空穴的准费米能级低于E Fi,对于多子来讲,由于载流子浓度变化不大,所以准费米能级基本靠近热平衡态下的费米能级,但是对于少子来讲,少子浓度发生了很大的变化,所以费米能级有相对比较大的变化,由于注入过剩载流子,所以导致各自的准费米能级都靠近各自的价带。
过剩载流子的寿命:半导体材料:半导体材料多是单晶材料,单晶材料的电学特性不仅和化学组成相关而且还与原子排列有关系。
半导体基本分为两类,元素半导体材料和化合物半导体材料。
GaAs主要用于光学器件或者是高速器件。
固体的类型:无定型(个别原子或分子尺度内有序)、单晶(许多原子或分子的尺度上有序)、多晶(整个范围内都有很好的周期性),单晶的区域成为晶粒,晶界将各个晶粒分开,并且晶界会导致半导体材料的电学特性衰退。
空间晶格:晶格是指晶体中这种原子的周期性排列,晶胞就是可以复制出整个晶体的一小部分晶体,晶胞的结构可能会有很多种。
半导体物理与器件公式以及全参数
半导体物理与器件公式以及参数KT=0.0259ev N c=2.8∗1019N v=1.04∗1019 SI材料的禁带宽度为:1.12ev. 硅材料的n i=1.5∗1010Ge材料的n i=2.4∗1013 GaAs材料的n i=1.8∗106介电弛豫时间函数:瞬间给半导体某一表面增加某种载流子,最终达到电中性的时间,ρ(t)=ρ(0)e−(t/τd),其中τd =ϵσ,最终通过证明这个时间与普通载流子的寿命时间相比十分的短暂,由此就可以证明准电中性的条件。
E F热平衡状态下半导体的费米能级,E Fi本征半导体的费米能级,重新定义的E Fn是存在过剩载流子时的准费米能级。
准费米能级:半导体中存在过剩载流子,则半导体就不会处于热平衡状态,费米能级就会发生变化,定义准费米能级。
n0+∆n=n i exp(E Fn−E FikT) p0+∆p=n i exp[−(E Fp−E Fi)kT]用这两组公式求解问题。
通过计算可知,电子的准费米能级高于E Fi,空穴的准费米能级低于E Fi,对于多子来讲,由于载流子浓度变化不大,所以准费米能级基本靠近热平衡态下的费米能级,但是对于少子来讲,少子浓度发生了很大的变化,所以费米能级有相对比较大的变化,由于注入过剩载流子,所以导致各自的准费米能级都靠近各自的价带。
过剩载流子的寿命:半导体材料:半导体材料多是单晶材料,单晶材料的电学特性不仅和化学组成相关而且还与原子排列有关系。
半导体基本分为两类,元素半导体材料和化合物半导体材料。
GaAs主要用于光学器件或者是高速器件。
固体的类型:无定型(个别原子或分子尺度内有序)、单晶(许多原子或分子的尺度上有序)、多晶(整个范围内都有很好的周期性),单晶的区域成为晶粒,晶界将各个晶粒分开,并且晶界会导致半导体材料的电学特性衰退。
空间晶格:晶格是指晶体中这种原子的周期性排列,晶胞就是可以复制出整个晶体的一小部分晶体,晶胞的结构可能会有很多种。
半导体物理公式总结
半导体物理公式总结半导体物理这门学科里的公式那可真是不少,今天咱们就来好好总结总结。
咱先从最基础的开始,比如说电导公式。
电导,简单来说就是衡量材料导电能力的一个指标。
电导公式G = σA/L ,这里面的σ 是电导率,A 是导体的横截面积,L 则是导体的长度。
这就好比咱们生活中的水管,水管越粗(A 大),管子越短(L 小),水流通过就越顺畅,就相当于电导越大。
再来说说电流密度公式 J = nqv 。
这里的 n 是载流子浓度,q 是电荷量,v 是载流子的平均漂移速度。
想象一下,在一个繁忙的马路上,车的数量(n)越多,每辆车开得速度(v)越快,整体的交通流量(J)也就越大。
还有一个重要的公式是漂移电流密度公式。
这就像是在一条拥挤的道路上,交警(电场 E )指挥着车辆(载流子)快速且有方向地移动。
有一次我在给学生们讲这些公式的时候,有个特别调皮的学生就问我:“老师,这些公式跟我们生活有啥关系啊?”我笑着回答他:“那关系可大啦!比如说你手机里的芯片,它能工作可就靠这些公式背后的原理呢。
没有半导体物理,你的手机可能就没法这么智能,不能让你随时随地玩游戏、刷视频啦。
”这孩子一听,眼睛瞪得大大的,好像突然明白了这些公式的重要性。
接着说,爱因斯坦关系,这个公式反映了扩散系数和迁移率之间的内在联系。
然后是能态密度公式。
这个公式能帮助我们了解半导体中能量状态的分布情况。
再看看费米分布函数,它描述了电子在不同能量状态下的分布概率。
半导体物理中的公式虽然看起来复杂,但只要我们把它们和实际生活中的现象联系起来,理解起来就会容易很多。
就像我们通过观察交通流量来理解电流密度,通过了解芯片的工作原理来感受这些公式的应用。
总之,半导体物理的公式是这门学科的重要基石,掌握好它们,我们才能更好地理解半导体的特性和行为,为未来的科技发展打下坚实的基础。
希望大家在学习的过程中,多思考,多联系实际,相信你们一定能学好这门有趣又有用的学科!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
半导体物理与器件公式以及参数KT =0.0259ev N c =2.8∗1019N v =1.04∗1019SI 材料的禁带宽度为:1.12ev. 硅材料的n i =1.5∗1010Ge 材料的n i =2.4∗1013 GaAs 材料的n i =1.8∗106介电弛豫时间函数:瞬间给半导体某一表面增加某种载流子,最终达到电中性的时间,ρ(t )=ρ(0)e −(t /τd ),其中τd =ϵσ,最终通过证明这个时间与普通载流子的寿命时间相比十分的短暂,由此就可以证明准电中性的条件。
E F 热平衡状态下半导体的费米能级,E Fi 本征半导体的费米能级,重新定义的E Fn 是存在过剩载流子时的准费米能级。
准费米能级:半导体中存在过剩载流子,则半导体就不会处于热平衡状态,费米能级就会发生变化,定义准费米能级。
n 0+∆n =n i exp (E Fn −E Fi kT )p 0+∆p =n i exp [−(E Fp −E Fi )kT] 用这两组公式求解问题。
通过计算可知,电子的准费米能级高于E Fi ,空穴的准费米能级低于E Fi ,对于多子来讲,由于载流子浓度变化不大,所以准费米能级基本靠近热平衡态下的费米能级,但是对于少子来讲,少子浓度发生了很大的变化,所以费米能级有相对比较大的变化,由于注入过剩载流子,所以导致各自的准费米能级都靠近各自的价带。
过剩载流子的寿命:半导体材料:半导体材料多是单晶材料,单晶材料的电学特性不仅和化学组成相关而且还与原子排列有关系。
半导体基本分为两类,元素半导体材料和化合物半导体材料。
GaAs主要用于光学器件或者是高速器件。
固体的类型:无定型(个别原子或分子尺度内有序)、单晶(许多原子或分子的尺度上有序)、多晶(整个范围内都有很好的周期性),单晶的区域成为晶粒,晶界将各个晶粒分开,并且晶界会导致半导体材料的电学特性衰退。
空间晶格:晶格是指晶体中这种原子的周期性排列,晶胞就是可以复制出整个晶体的一小部分晶体,晶胞的结构可能会有很多种。
原胞就是可以通过重复排列形成晶体的最小晶胞。
三维晶体中每一个等效的格点都可以采用矢量表示为r=pa̅+qb̅+sc̅,其中矢量a̅,b̅,c̅称为晶格常数。
晶体中三种结构,简立方、体心立方、面心立方。
原子体密度=每晶胞的原子数每晶胞的体积米勒指数,对所在平面的截距取倒数在进行通分,所有平行平面的米勒指数相等,平面集的计算方式。
原子面密度=每个晶面的原子数每个晶面的面积晶向表示的是某条射线的方向,在简立方体重相同数值的米勒指数的晶向和晶面是相互垂直的。
金刚石结构:Ge和硅具有金刚石结构,一个原子周围通过共价键和其余的四个原子相连接。
金刚石结构指的是由同种原子组成的结构,金刚石总共有8个原子,6个面心原子,四个晶体内部的原子。
金刚石的体积是a3.原子共价键:热平衡系统的总能量趋于达到某个最小值,原子间的相互作用力以及所能达到的最小能量取决与原子团或原子类型。
四种原子间离子键、共价键、金属键、范德华键(HF正负电荷的有效中心不再统一点,最终形成电偶极子,相邻的电偶极子之间相互作用)。
量子力学的基本原理:能量量子化原理(实验结果是发射出来的光子的能量随着入射频率变化进行线性变化,光强改变没办法改变射出光子的最大动能而只会改变粒子射出的概率E=hμ=hcλ=1mv2)、波粒二象性原理(光子的动量p=hλ,所以我们就可以假设物质波的存在并且其波长λ=hp)、不确定性原理(ΔpΔx≥ℏ,ΔEΔt≥ℏ,并且要会利用E=p22m,如果先知道Δp,就可以通过两边求导的方式求出ΔE)薛定谔波动方程:−ℏ22m ∂2Ψ∂x 2+V (x )Ψ(x ,t )=j ℏ∂Ψ(x ,t )∂t 最终将这个表达式分解为与时间相关的部分和与时间无关的部分,与时间相关的表达式为ϕ(t )=e −jwt =e−j E ℏt 所以就可以推导出角频率w =E ℏ与时间无关的表达式∂2ψ(x )∂x 2+2m ℏ2[E −V (x )]ψ(x )=0 将|Ψ(x ,t )|2成为概率密度函数,|Ψ(x ,t )|2=|ψ(x )|2,其与时间无关。
对应的边界条件:∫|ψ(x )|2dx =1+∞−∞ψ(x )必须单值、连续、有界(如果其无界,相当改点发现粒子的概率确定了) E 与V (x )均有限,相当于∂2ψ(x )∂x 2必须有限,对应的一阶导数必须单值连续有界个别情况是例外的。
薛定谔方程的应用:自由空间中的电子(粒子表现为行波特性其中+x表示沿着x轴正方向运动的波,反之沿着x轴负方向运动的波,λ=2πk,其中)、无限深势肼(束缚态粒子的运动状态,波函数表现为行波特性k=nπa=√2mEℏ2,ψ(x)=√2asin(kx)上面的表达式就可以求解能量,看到束缚态粒子的能量是量子化分布的)、阶跃势函数(粒子能量小于势能,粒子被完全返回去,但是区域II中存在粒子的分布函数,但最后还是返回到区域I中,这个与经典的力学不一样)、矩形势垒隧道效应(粒子撞击势垒的时候,会有一部分粒子穿过势垒,T=16(EV0)(1−EV0)exp(−2k2a)T表示的是透射。
原子波动理论的延伸:n,l,m称为量子数,每一组n,l,m称为量子态n=1,2,3……l=n−1,n−2,n−3 0|m|=l,l−1,l−2 0随着能级的增加,对核外电子的束缚力减少,电子存在自旋状态,注意周期表每一层的电子数目。
半导体中的载流子:导带电子的分布为导带中允许量子态密度与某个量子态被占据的概率n(E)=gc(E)f F(E)对其在整个导带范围内进行积分就可以得到电子浓度。
价带中空穴的分布为价带中允许的量子态与某个量子态被占据的概率成绩p(E)=gv(E)[1−f F(E)]对其在整个价带范围内积分就可以求出空穴的浓度。
理想的本征半导体指的是不含杂质和缺陷的纯净的半导体,在T=0是,本征半导体的价带被完全占满,导带中为空,本征半导体的电子浓度与空穴浓度相等。
如果电子的有效质量等于空穴的有效质量,那么gc (E)和gv(E)关于禁带中心对称,当E>E F时的f F(E)与E<E F时的1−f F(E)相等。
如果有效质量不相等,那么这两条曲线不会对称。
当E C−E F≫KT费米概率分布函数简化为波尔兹曼分布,求解出n0=N C exp[−(E C−E F)KT]N C=2(2πm n∗KTh2)32=2.5×1019cm−3相当于一旦有效质量发生变化,那么对应的N C就会变同理可以求出空穴的浓度为p 0=N v exp[(E v−E F)KT]N V=2(2πm p∗KTh2)32=1.04×1019cm−3本证载流子的浓度n i,并且其电子浓度等于空穴浓度,具体的表达式n i =N C exp [−(E C −E Fi )KT ]=p i =N v exp [(E v −E Fi )KT] n i 2=N C N v exp (−E g KT) 其实求出的n i 可能与公认的存在差别原因有二,有效质量实际上是测试结果,并且与温度有关,所以可能会产生差别,状态密度函数可能与实际模型不相符合。
本征费米能级的位置E FI −E midgap =34KTln (m p ∗m n ∗) 有效质量越大,状态密度越大,所以本征费米能级的位置必将发生变化,确保电子和空穴的浓度相等。
参杂原子与能级:n 型半导体形成了一个施主能级,P 型半导体形成了一个受主能级,参入杂质的半导体称为非本征半导体,电离能为激发施主电子进入导带所需要的能量,非本征半导体:非本征半导体中电子或者是空穴的一种成为主导作用。
费米能级与分布函数相关,所以参入杂质后费米能级位置发生变化,E F >E Fi 电子浓度大于空穴浓度,成为n 型半导体,E F <E Fi 电子浓度小于空穴浓度,成为p 型半导体,通过计算可以即使费米能级改变很小,但是电子和空穴的浓度相对于本征半导体变化几个数量级。
n 0=n i exp (E F −E FI KT) p 0=n i exp (−E F −E FI KT)E F>E Fi导带中的电子的概率分布函数增加同时价带中的空穴概率分布减少。
在热平衡状态下始终满足n0p=n i2非简并半导体杂质浓度相比于晶体浓度要小很多,在半导体中引入分离的施主能级,各杂质之间没有相互作用。
简并半导体随着杂质浓度增加,杂质之间存在相互作用力,施主能级分裂成为能带,n半导体为例,当杂质浓度超多状态密度时,费米能级进入导带位置,在导带底部和费米能级之间电子被填充满,所以电子浓度很大。
简并半导体的判断标准:E C−E F>2KK,非简并半导体0<K C−E F<2KK,弱简并半导体E C−E F<0,简并半导体简并效应:施主和受主的统计分布:电子占据施主能级的分布函数n d=N d1+12exp(E d FKT)≅2N d exp(−E d−E FKT)施主能级的电子占据总电子数的比例p a =N a1+12exp(E F aKT)≅2N a exp(E a−E FKT)完全电离施主能级的电子全部跃迁到导带中,在T=0时,费米能级高于施主能级,所以就是没有电子跃迁到导带上,这个状态也成为束缚态。
电中性状态:补偿半导体的定义,相当于同时给半导体中加入施主和受主杂质,此时计算n 0,p 0就需要采用响应的公式计算。
随着施主杂质的加入,响应的电子的有效能量状态需要重新分布,导致抵消了一部分空穴。
费米能级的位置:随着施主浓度的增加,费米能级的位置会向导带底或者是价带顶部移动,完全补偿半导体的费米能级就是本征半导体的费米能级,因为n i 是温度的函数所以费米能级也是温度的函数,高温情况下半导体的非本征特性开始消失,在低温情况下,其完全处于束缚态。
载流子的产生和复合:热平衡状态下,经载流子的浓度保持不变,相当于是载流子的产生和复合的速率相等。
过剩载流子的复合速率是相等的,对于p 型半导体R n ′=R p ′=∆n (t )τn0其中∆n (t )=∆n (0)e (−t τn0)对于n 型半导体R n ′=R p ′=∆n (t )τp0其中∆n (t )=∆n (0)e (−t τp0)过剩载流子的性质:过剩载流子的时间和空间状态D P ∂2p∂x 2−μp (E ∂p ∂x +p ∂E ∂x )+g p −p τpt =∂p ∂t D n ∂2n∂x 2−μn (E ∂n +n ∂E )+g n −p τnt=∂n因为p=p0+∆p,又因为p为常数,所以上面表达式可以化简为D P∂2∆p∂x2−μp(E∂∆p∂x+p∂E∂x)+gp−pτpt=∂∆p∂tD n∂2∆n∂x2−μn(E∂∆n∂x+n∂E∂x)+gn−pτnt=∂∆n∂t双极运输:外加电场的半导体的某个位置产生过剩载流子,那么过剩载流子就可以再起内部产生一个新的内建电场,阻碍过剩载流子的扩散,求出双极运输方程为。
