平均自由程和概率分布
气体分子平均自由程

子间的引力,但考虑了分子斥力起作用时两个分子质心间的距离,即考虑了 分子的体积,而不象理想气体,忽略了分子本身的大小。
4
自由程 : 分子两次相邻碰撞之间自由通过 的路程 .
5
气体分子平均自由程(mean free path) 平均自由程λ 为分子在连续两次碰撞之间所自 由走过的路程的平均值。
dN K exp( Kx)dx N0
18
由分子自由程的概率分布可求平均自由程 dN K exp( Kx)dx N0
1 K exp( Kx) xdx K 0
dN Kdx N
N Kdx Ln N
0 0
x
N N 0 exp( Kx )
17
N N 0 exp( Kx )
表示从 x =0 处射出了刚被碰撞过的N0个分子,它们 行进到 x 处所残存的分子数 N 按指数衰减。 对上式之右式两边微分,得到
既然(-dN )表示 N0 个分子中自由程为 x 到x + dx 的平均分子数,则(-dN /N0 )是分子的自由程在 x 到 x + dx范围内的概率。这就是分子自由程的概率分布。 即分子按自由程分布的规律。
Z 2 π d vn
2
v 1 2 z 2π d n
当气体较稀薄时
p nkT
1 T 一定时 p
kT 2π d 2 p
p 一定时
T
11
例 计算空气分子在标准状态下的平均自由程 10 和碰撞频率。取分子的有效直径 d 3.5 10 m 已知空气的平均相对分子量为29。 解: 标准状态下
《气体分子运动的统计规律》 讲义

《气体分子运动的统计规律》讲义一、气体分子的热运动在我们的日常生活中,气体无处不在,比如我们呼吸的空气、充满气球的氢气等。
那么,这些气体分子是如何运动的呢?气体分子处于永不停息的无规则运动之中,这种运动被称为热运动。
想象一下,在一个封闭的容器中,充满了气体分子,它们就像一群顽皮的孩子,四处乱跑,相互碰撞,没有固定的方向和轨迹。
气体分子的热运动具有以下几个特点:速度的多样性:不同的气体分子具有不同的速度。
有的分子运动速度快,有的则慢。
无规则性:它们的运动方向是随机的,无法预测下一刻某个分子会往哪个方向跑。
频繁的碰撞:分子之间会不断地发生碰撞,这使得它们的运动状态不断改变。
二、气体分子运动的统计规律既然气体分子的运动如此复杂和无规则,那我们要如何去描述和理解它们的整体行为呢?这就需要依靠统计规律。
什么是统计规律呢?简单来说,就是通过对大量个体行为的观察和分析,总结出的总体的、平均的规律。
对于气体分子,我们无法确切知道每个分子在每一时刻的具体运动状态,但我们可以通过统计方法来了解它们的一些总体特征。
比如,我们可以统计在一定温度和压强下,气体分子的速度分布情况。
麦克斯韦速度分布律就是描述气体分子速度分布的重要规律。
它告诉我们,在一定条件下,气体分子的速度分布呈现出一定的规律性,速度较小和较大的分子较少,而具有中等速度的分子较多。
再比如,气体分子对容器壁的压强,也是通过对大量分子撞击容器壁的行为进行统计得出的。
三、麦克斯韦速度分布律麦克斯韦速度分布律是描述气体分子运动速度分布的关键规律。
假设在一个容器中充满了理想气体,处于平衡态。
麦克斯韦速度分布律表明,分子速度在三个方向上(x、y、z)的分量的分布都是独立的,且满足一定的概率分布。
具体来说,速度分量 vx 的分布函数为 f(vx) , vy 和 vz 的分布函数类似。
通过对这些分布函数的积分,可以得到分子速度的大小 v 的分布函数 f(v) 。
麦克斯韦速度分布律在许多方面都有重要的应用。
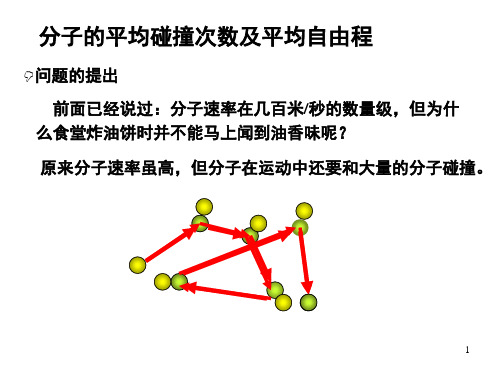
分子的平均碰撞次数及平均自由程
较大的分子数较少,能量较小的分子数较多。 (3)在大小相等的各区间(坐标区间和速度区间)中比较,
分子总是处于低能态的概率大些。 (4)分布在某一坐标区间具有各种速度的分子总数只与坐标
区间的间隔成正比,与粒子的能量无关。 (A)只有(1),(2)是正确的; (B)只有(2),(3)是正确的; (C)只有(1),(2),(3)是正确的;(D)全部是正确的;
(`1) 10-10m (2) 102~103m/s (3) 108~109s-1
v 1.6 RT M mol
T=300K
v kT z 2d 2 P
把 P 1.01105 Pa
z 2d 2vP
kT T 273K 代入即可得到。
8
例6-12 气缸内有一定量的氢气(可视作理想气体),当
温度不变而压强增大一倍时,氢气分子的平均碰撞次数 z
分子的平均碰撞次数及平均自由程
问题的提出 前面已经说过:分子速率在几百米/秒的数量级,但为什
么食堂炸油饼时并不能马上闻到油香味呢? 原来分子速率虽高,但分子在运动中还要和大量的分子碰撞。
1
一、分子的有效直径d
分子的一种最简单的模型:将分子看成是具有一定体积 的弹性小球。
则分子的有效直径d定义为:两个分子质心之间所能允许的 最小距离。
距离小于或等于分子有效直径d的分子都会与A分子发生碰撞。
为此我们以A分子中心的运动轨迹为曲线,以分子直径d
为半径,做一曲折圆柱体,那么,凡分子中心在圆柱体内的
分子,都会与A分子发生碰撞,
z n d 2 u
4
理论证明:气体分子的平均相对速率 u与平均速率 v间有
分子蒸馏技术的原理和应用

分子蒸馏技术的原理和应用分子蒸馏技术的基本原理(一)分子运动平均自由程:任一分子在运动过程中都在不断变化自由程。
在某时间间隔内自由程的平均值为平均自由程。
设Vm=某一分子的平均速度f =碰撞频率λm =平均自由程则λm =Vm/f∴f=Vm/λmπd²P由热力学原理可知,f=(2)½Vm•────KT其中:d-分子有效直径P-分子所处空间的压强T-分子所处环境的温度K-波尔兹曼常数K T则:λm =────•────(2)½πd²P(二)分子运动平均自由程的分布规律:分子运动自由程的分布规律为正态分布,其概率公式为:F = 1 - e-λ/λm 其中:F-自由程度≤λm的概率λm-分子运动的平均自由程λ-分子运动自由程由公式可以得出,对于一群相同状态下的运动分子,其自由程等于或大于平均自由程λm的概率为:1 - F = e-λ/λm = e-1 = 36.8%(三)分子蒸馏的基本原理:由分子平均自由程的公式可以看出,不同种类的分子,由于其分子有效直径不同,其平均自由程也不同,换句话说,不同种类的分子溢出液面后不与其它分子碰撞的飞行距离是不同的。
分子蒸馏技术正是利用不同种类分子溢出液面后平均自由程不同的性质实现的。
轻分子的平均自由程大,重分子的平均自由程小,若在离液面小于轻分子的平均自由程而大于重分子平均自由程处设置一冷凝面,使得轻分子落在冷凝面上被冷凝,而重分子因达不到冷凝面而返回原来液面,这样混合物就分离了。
(三)分子蒸馏技术中的相关模型:对于许多物料而言,至今还没有可供实际应用的数学模型来准确地描述分子蒸馏中的变量参数,实际的应用仍靠经验的总结。
但由经验从各种规格蒸发器中获得的蒸发条件,可以安全地推广到生产装置的设计中。
相关的模型有:1、膜形成对于降膜、无机械运动的垂直壁上的膜厚,Nasselt公式为:σm=(3v2Re/g)1/3其中:σm-名义膜厚[米]v-物料动力粘度[米2•秒-1]g-重力加速度[米•秒-2]Re-雷诺数,无因次Re>400时,该方程成立。
热学气体分子平均自由程

气体分子的碰撞截面
碰撞截面
截面对平均自由程的影响
气体分子间的碰撞截面决定了分子间 的相互作用和碰撞概率。
碰撞截面越大,分子间的碰撞概率越 高,平均自由程越短。
截面大小
不同气体分子间的碰撞截面大小不同, 与分子间的距离和相互作用力有关。
气体分子的能量损失
能量损失
01
气体分子在碰撞过程中会损失能量,导致平均自由程的变化。
特性
与气体分子的速度、气体分子的分布、气体分子的碰撞频率等因素有关。
平均自由程与气体分子碰撞频率的关系
碰撞频率
气体分子在单位时间内所发生的碰撞 次数。
关系
平均自由程与气体分子碰撞频率成反 比,碰撞频率越高,平均自由程越小。
平均自由程在热学中的重要性
热传导
平均自由程是影响气体热传导的重要因素之一,通过 改变平均自由程可以调节气体的热传导性能。
总结词
在高温高压条件下,气体分子间的相互 作用力减弱,分子间的碰撞频率降低, 因此平均自由程较大。
VS
详细描述
在高温高压条件下,气体分子间的平均距 离增大,分子间的碰撞频率减少,导致气 体分子的平均自由程增大。这种情况下, 气体分子的运动受到的相互碰撞的限制较 小,运动路径较长。
04 气体分子平均自由程的影 响因素
探索气体分子平均自由程在极端条件下的行为
研究高温、高压、高密度等极端 条件下气体分子平均自由程的变 化规律,揭示其与温度、压力、
密度的关系。
探讨极端条件下气体分子与障碍 物的相互作用,以及气体分子间 的相互作用,以理解其行为特性。
研究极端条件下气体分子输运性 质的变化,为相关领域的应用提
供理论支持。
感谢您的观看
概率分布名词解释

概率分布名词解释概率分布名词解释:【解析】:。
事件A(n)可能的状态的集合,记为{x|Y|Z|w}。
如果{x|Y|Z|w}包含于{X|Y|Z|k|l},则称{X|Y|Z|k|l}是事件A(n)出现的概率空间。
【详细说明】: 1、多样性:①随机变量的取值集合中,包含数据点数目越大,该随机变量的多样性就越小;②任一随机变量集合中各元素对于该随机变量来说具有相同的统计特征,该随机变量就称为独立。
2、平均数:定义:平均数( average)是描述一组数据集中位置的统计指标,即对每个数据点所属类型的数据按照数据点的个数计算得到的平均值。
计算公式: a=(某个数据点的总数/所有数据点的总数)/n。
3、均值:定义:均值( mean)是描述一组数据集中位置的统计指标,即对每个数据点所属类型的数据按照数据点的个数计算得到的平均值。
计算公式: a=(数据点的总数/数据点的个数) /n。
4、方差:定义:方差( variance)是描述一组数据集中位置的统计指标,即对每个数据点所属类型的数据按照数据点的个数计算得到的平均值的离散程度。
计算公式:var=n/n×100,其中var=5、期望:定义:是在参数取值服从正态分布时,预期值与真实值之间的差距。
计算公式:,其中, v=6、方差:定义:方差( variance)是描述一组数据集中位置的统计指标,即对每个数据点所属类型的数据按照数据点的个数计算得到的平均值的离散程度。
计算公式:var=n/n×100,其中, var=7、协方差:定义:协方差( covar)是描述两个随机变量间相关程度的统计指标。
定义为:Cov=(EsρEsw)/Esρ,其中Esw=8、方差:定义:方差( variance)是描述一组数据集中位置的统计指标,即对每个数据点所属类型的数据按照数据点的个数计算得到的平均值的离散程度。
计算公式:var=n/n×100,其中, var=9、期望:定义:是在参数取值服从正态分布时,预期值与真实值之间的差距。
3.5气体分子平均自由程详解
3. 在一容积不变的封闭容器内理想气体分子的平均速率若提高为原来 的2倍,则 (A) 温度和压强都提高为原来的2倍.
(B) 温度为原来的2倍,压强为原来的4倍.
(C) 温度为原来的4倍,压强为原来的2倍. (D)温度和压强都为原来的4倍. 4.
v 446 m 6.9 108 m 9 Z 6.5 10
与分子直径3.5×10-10m相比,标况下是其d的200倍。
第二章复习小结
一、概率的基本性质及求平均值的方法 1等概率性
2运算法则
3平均值公式 4概率分布函数
二、麦克斯韦速率、速度分布
1两种分布曲线 2三种统计速率 3速度空间、代表点 三、重力场中自由粒子分布、等温大气压强公式
经上述分析,存在一个以分子A的质心 为圆心、d为半径垂直于射线束的圆: 所有射向圆区的分子都有不同程度的散 射,而圆外区域分子轨迹不发生偏折。
定义:分子散射截面: d 2
对两个分子有效直径分别为d1和d2的分子,其碰撞截面:
d1 d 2 1 2 d d 1 2 2 4
2
(A) 图中a表示氧气分子的速率分布曲线; v p O
v (B) 图中a表示氧气分子的速率分布曲线; v v (C) 图中b表示氧气分子的速率分布曲线; v v (D) 图中b表示氧气分子的速率分布曲线; v v
2
2
p H 2 p H 2 p H 2
2
2、分子间平均碰撞频率
分子间平均碰撞频率▬▬单位时间内一个分子的平均碰撞次数。 转换研究对象,现在假设B分子束相对静止,A分子以相对速度v12 运动,其运动发生碰撞的轨迹如图: A分子每碰到一个视为质点的B分子就 改变一次运动方向。
6-3 气体分子速率分布率和平均自由程

100~200
200~300 300~400
0.081
0.165 0.214
400~500
500~600 600~700
0.206
0.151 0.092
700~800
800~900 900以上
0.048
0.021 0.009
第三节
气体分子速率分布律和能量分布律
N 1 由此数据为依据,以v N v 为横轴,以单位速率间隔 21.4% 内的分子数在总分子数内 所占的百分比为纵轴,作 16.5% 如图所示的锯齿形图。注 8.0% 意在速率间隔∆ν内实际包 200 400 括由v到v+∆ν内的所有速率 的分子。
f (v)
平 均 速 率
O
v
v
第三节
气体分子速率分布律和能量分布律
方均根速率:
气体分子速率平方的平均值的平方根。
v
2
N
0
v dN N
2
0
m e v f (v) 4p 2pkT
3 dN 2 2 mv 2 f (v )dv 2 2 kT RT 3kT 3 RT v N m 1.73
dN f (v )dv N
或
dN f (v ) Ndv
分子速率分布函数
第三节
气体分子速率分布律和能量分布律
速率分布函数
dN f (v ) Ndv
a、物理意义: 速率在v 附近的单位速率区间的 分子数占总分子的百分比。 b、应用: 确定分布在任一有限速率分布范围v1~v2 内的分子数占总分子数的百分比。
mv2 2 kT v 2 e
第三节
气体分子速率分布律和能量分布律
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一.平均碰撞频率和平均自由程的概念
1. 平均碰撞频率(
z
)
单位时间内一个分子与其它分子碰撞的平均次数。
2. 平均自由程( )
一个分子在两次连续碰撞间自由运动的平均路程。
在分子的平均速率一定的情况下,分子间的碰撞越频繁, Z 就越大,而 就越小。
二.平均碰撞频率和平均自由程的计算
u
1、平均碰撞频率 z
对于化学纯气体,分子A与其他分子发生碰撞时,可假 定其他分子不动,而分子A以平均相对速率 u 运动。
假定分子的有效直径为d,即两分子的中心距小于或等于 d时发生碰撞。
z
d u t n
2
t
2
d nu
2
可以证明:
u 2v
z 2d nv 2nv
其中 d 2 称为分子碰撞截面。
y
x N,
x dx N dN
残存数
x z 0 0 N0 x t N x+dx t+dt N+dN
dN Ndx
dN Kdx N
dN KNdx
dN Kdx N
N N0e
Kx
N为气体分子行进到x处未被碰撞的分子数(残存数)。
对
N N0e
Kx
求微分
dN Ke Kx dx N0
分子按自由程分布规律
dN Kx Ke p( x) N 0 dx
分子自由程分布概率密度
平均自由程
f ( x) xdx
0
0
1 Kx Ke dx K
P(x) 1/λ
N N0e
1
x
0 x x+dx x
N e N0
x
分子按自程分布规律
x dN 1 e dx N0
气体分子行进到x处未被碰撞的分子数占总 分子数的比率——概率
例:求自由程大于和小于平均自由程的分子概率 解:
N (x ) N0
0
1 e
x
1 dx 0.37 e
N (x ) N0
x 1 e dx 1
u
p nkT ,
v
气体,设气体由两种成分的气体组成。显然:
1 d d ( d1 d 2 ) 2
碰撞截面为
2
1 ( d1 d 2 ) 2 4
z
2d nv12
由上面的证明可知:
v12 v1 v2
2
2
2、平均自由程
v z
1 2 2d n
v z
由
1 2 2d n
得
p nkT
kT 2 2d p
2
z
2d nv
4p mkT
平均自由程 和碰撞频率 Z 态决定的。
的大小是由气体的性质和状
例 : 计算标态下 O2 系统分子的平均碰撞次数和平均自由程。
1 1 0.37 0.63 e
气体分子碰撞的概率分布
一、气体分子的自由程分布
分子间碰撞的平均频率及平均自由程,虽然它们均能表示 分子间碰撞的主要特征,但不能反映分子间碰撞的随机性质。 分子在两次碰撞之间所走过的路程有长有短。为了描述 这种随机性质,必须找到它x到x+dx范围内受到碰撞的概率, 即分子的自由程处于x到x+dx范围内的概率。
10 d 3 . 6 10 (m ) ) (
p 25 3 2.69 10 ( m ) 解: n kT
8 RT v 4.25 10 2 ( m / s ) M z 2d 2 v n 6.85 109 (次/秒) v / z 6.46 10 8 ( m )
