变量与函数1
一次函数-变量与函数

变量与函数(知识讲解)【学习目标】1.知道现实生活中存在变量和常量,变量在变化的过程中有其固有的范围(即变量的取值范围);2.能初步理解函数的概念;能初步掌握确定常见简单函数的自变量取值范围的基本方法;给出自变量的一个值,会求出相应的函数值.【要点梳理】要点一、变量、常量的概念在一个变化过程中,我们称数值发生变化的量为变量.数值保持不变的量叫做常量.要点诠释:一般地,常量是不发生变化的量,变量是发生变化的量,这些都是针对某个变化过程而言的.例如,60s t =,速度60千米/时是常量,时间t 和里程s 为变量.要点二、函数的定义一般地,在一个变化过程中. 如果有两个变量x 与y ,并且对于x 的每一个确定的值,y 都有唯一确定的值与其对应,那么我们就说 x 是自变量,y 是x 的函数.要点诠释:对于函数的定义,应从以下几个方面去理解:(1)函数的实质,揭示了两个变量之间的对应关系;(2)对于自变量x 的取值,必须要使代数式有实际意义;(3)判断两个变量之间是否有函数关系,要看对于x 允许取的每一个值,y 是否都有唯一确定的值与它相对应.(4)两个函数是同一函数至少具备两个条件:①函数关系式相同(或变形后相同);②自变量x 的取值范围相同.否则,就不是相同的函数.而其中函数关系式相同与否比较容易注意到,自变量x 的取值范围有时容易忽视,这点应注意.要点三、函数值y 是x 的函数,如果当x =a 时y =b ,那么b 叫做当自变量为a 时的函数值.要点诠释:对于每个确定的自变量值,函数值是唯一的,但反过来,可以不唯一,即一个函数值对应的自变量可以是多个.比如:2y x =中,当函数值为4时,自变量x 的值为±2.要点四、自变量取值范围的确定使函数有意义的自变量的取值的全体实数叫自变量的取值范围.要点诠释:自变量的取值范围的确定方法:首先,要考虑自变量的取值必须使解析式有意义:(1)当解析式是整式时,自变量的取值范围是全体实数;(2)当解析式是分式时,自变量的取值范围是使分母不为零的实数;(3)当解析式是二次根式时,自变量的取值范围是使被开方数不小于零的实数;(4)当解析式中含有零指数幂或负整数指数幂时,自变量的取值应使相应的底数不为零;(5)当解析式表示实际问题时,自变量的取值必须使实际问题有意义.【典型例题】类型一、变量与函数例1、下列是关于变量x 与y 的八个关系式:① y = x ;② y 2 = x ;③ 2x 2 − y = 0;④ 2x − y 2 = 0;⑤ y = x 3 ;⑥ y =∣x ∣;⑦ x = ∣y ∣;⑧ x =2y .其中y 不是x 的函数的有_____.(填序号)【变式】下列:①2y x ;②21y x =+;③22(0)y x x =≥;④0)y x =≥,具有函数关系(自变量为x )的是______.类型二、函数解析式的取值范围 例2、求出下列函数中自变量x 的取值范围(1)2321y x x =--; (2)2131x y x -=+;(3)y =(4)y =.举一反三:【变式】等腰三角形的周长为10,底边长y 与腰x 的函数关系式是102y x =-,则自变量x 的取值范围是________.类型三、函数解析式例3.如图,一农户要建一个矩形猪舍,猪舍的一边利用住房墙(住房墙的长度大于BC ),另外三边用25m 长的建筑材料围成,为方便进出,在CD 边上留一个1m 宽的门.若设AB 为()y m ,BC 为()x m ,则y 与x 之间的函数关系式为______.【变式】如图,ABC 中,90BAC ∠=,4BC =,BD 是ABC 的角平分线,过点C 作BD 的垂线,交BD 的延长线于点E .若设AB x =,CE y =,则y 关于x 的函数解析式为___________.类型四、函数值例4、 若y 与x 的关系式为306y x =-,当x =时,y 的值为( )A .5B .10C .4D .-413课后练习1.下列式子:①y=3x ﹣5;②y=1x ;③y 2=x ;⑤y=|x|,其中y 是x 的函数的个数是( ) A .2个 B .3个 C .4个 D .5个2.下列说法中,正确的是( )A .对于两个变量x ,y ,若y x =,则y 是x 的函数B .对于两个变量x ,y ,若22016x y +=,则y 是x 的函数C .对于两个变量x ,y ,若2y x =,则y 是x 的函数D .对于两个变量x ,y ,若22y x =,则y 是x 的函数3.函数y =的自变量的取值范围是( ) A .0x B .0x > C .0x ≠ D .0x =4.下列曲线中不能表示y 与x 的函数的是( )A .B .C .D .5.下列图象中,表示y 不是x 的函数的是( )A .B .C .D .6.“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了 一觉. 当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终 点……. 用 s 1 、s2 分别表示乌龟和兔子所行的路程, t 为时间,则下列图像中与故事情节相吻合的是( )A .B .C .D .。
2.1.1(一)变量与函数的概念教案

第二章函数§2.1函数2.1.1 函数第1课时变量与函数的概念【学习要求】1.通过丰富实例,加深对函数概念的理解,学会用集合与对应的语言来刻画函数,体会对应关系在刻画函数概念中的作用.2.了解构成函数的三要素.3.能够正确使用“区间”的符号表示某些集合.【学法指导】通过实例体会函数是描述变量之间的依赖关系的重要数学模型,在此基础上学习用集合与对应的语言来刻画函数,体会用集合与对应刻画函数的必要性的重要性.填一填:知识要点、记下疑难点1.函数的概念:设集合A是一个非空的数集,对A中的任意数x,按照确定的法则f,都有唯一确定的数y与它对应,则这种对应关系叫做集合A上的一个函数.记作y=f(x),x∈A.其中x叫做自变量,自变量的取值范围(数集A)叫做这个函数的定义域.2.区间概念:设a,b∈R,且a<b.(1)满足a≤x≤b的全体实数x的集合,叫做闭区间,记作 [a,b].(2)满足 a<x<b 的全体实数x的集合,叫做开区间,记作(a,b).(3)满足a≤x<b或a<x≤b的全体实数x的集合,叫做半开半闭区间,分别记作 [a,b)或(a,b].(4)满足x≥a,x>a,x≤a,x<a的全体实数x的集合分别表示为[a,+∞) ,(a,+∞) ,(-∞,a] ,(-∞,a) .研一研:问题探究、课堂更高效[问题情境] 初中是用运动变化的观点对函数进行定义,虽然这种定义较为直观,但并未完全揭示出函数概念的本质.对于y=1(x∈R)是不是函数,如果用运动变化的观点去看它,就不好解释,显得牵强.但如果用集合与对应的观点来解释,就十分自然.因此,用集合与对应的思想来理解函数,对函数概念的再认识,就很有必要.探究点一变量与函数的概念问题1 阅读教材29-30页中的(1),(2),(3),(4)四个函数关系的例子,指出这四个例子的共同特点是什么?变量之间的对应关系采用什么形式表达的?答:在上面的每个例子中,都指出了自变量的变化范围、由自变量确定因变量的对应法则,以及由此确定的因变量的取值范围.例子(1)和(2)中的两变量关系通过图象的形式表达的,例子(3)中的变量间的关系通过列表的形式表达的,例子(4)中的变量间的关系通过关系式表达的.问题2 从上述的四个例子中,你能感悟到一个函数关系涉及到哪些量?答:一个函数关系必须涉及到两个数集和一个对应法则.问题3如何用集合与对应的观点来阐述上面四个例子有什么共同特点?答:共同特点是:对于集合A中的任意一个数x,按照确定的对应法则f,都有唯一确定的数y和它对应.问题4确定一个函数最少需要几个要素?为什么?答:最少需要两个要素:定义域和对应法则.因为函数的值域被函数的定义域和对应法则完全确定.问题5 若检查给定两个变量之间是否具有函数关系,只须检查什么?答:(1)定义域和对应法则是否给出;(2)根据给出的对应法则,自变量x在其定义域中的每一个值,是否都能确定唯一的函数值y.例1 对于函数y=f(x),以下说法正确的有 ( )①y是x的函数;②对于不同的x,y的值也不同;③f(a)表示当x =a 时函数f(x)的值,是一个常量; ④f(x)一定可以用一个具体的式子表示出来.A .1个B .2个C .3个D .4个解析: ①③正确,②是错误的,对于不同的x ,y 的值可以相同,这符合函数的定义,④是错误的,f(x)表示的是函数,而函数并不是都能用具体的式子表示出来.小结: (1)在y =f(x)中f 表示对应法则,不同的函数其含义不一样;(2)f(x)不一定是解析式,有时可能是“列表”、“图象”;(3)f(x)与f(a)是不同的,前者为变数,后者为常数.跟踪训练1 下列函数中哪个与函数y =x 相等?(1)y =(x)2;(2)y =3x 3;(3)y =x 2;(4)y =x 2x . 解:(1)y =(x)2=x(x≥0),y≥0,定义域不同且值域不同,所以两函数不相等;(2)y =3x 3=x(x∈R ),y∈R ,对应法则相同,定义域和值域都相同,所以相等;(3)y =x 2=|x|=⎩⎨⎧x ,x≥0-x ,x<0,y≥0;值域不同,且当x<0时,它的对应法则与函数y =x 不相同,所以不相等;(4)y =x 2x的定义域为{x|x≠0},与函数y =x 定义域不相同,所以不相等. 探究点二 区间的概念问题1 阅读教材31页下半段,然后回答区间的概念是如何定义的?答:设a ,b∈R,且a<b,(1)满足a≤x≤b 的全体实数x 的集合,叫做闭区间,记作[a ,b].(2)满足a<x<b 的全体实数x 的集合,叫做开区间,记作(a ,b).(3)满足a≤x<b 或a<x≤b 的全体实数x 的集合,叫做半开半闭区间,分别记作[a ,b)或(a ,b]. 问题2 实数集R 及x≥a,x>a ,x≤b,x<b 如何用区间表示?答:实数集R 可以用区间(-∞,+∞)表示;x≥a,x>a ,x≤b,x<b 分别用区间表示为:[a ,+∞),(a ,+∞),(-∞,b],(-∞,b).问题3 在数轴上如何表示区间[a ,b]、(a ,b)、[a ,b)、(a ,b]、[a ,+∞)、(a ,+∞)? 答: 如图所示:a ,b 叫做区间的端点,在数轴上表示区间时,属于这个区间端点的实数,用实心点表示,不属于这个区间端点的实数,用空心点表示.探究点三 求函数的定义域导引 在函数关系式的表述中,函数的定义域有时可以省略,这时就约定这个函数的定义域就是使得这个函数关系式有意义的实数的全体构成的集合.问题1 对于一个确定的函数关系式,我们通常从哪些方面考虑求函数的定义域?答: (1)分母不为零;(2)偶次根式的被开方数非负;(3)若函数由几部分构成,则定义域是使各部分式子都有意义的实数集合;(4)如果是实际问题,除应考虑解析式本身有意义外,还应考虑实际问题有意义.问题2 在初中已学函数的定义域和值域是怎样的?答: 一次函数f(x)=ax +b(a≠0):定义域为R, 值域为R ;反比例函数f(x)=k x(k ≠0):定义域为{x|x ≠0}, 值域为{y|y ≠0};二次函数f(x)=ax 2+bx +c(a ≠0):定义域为R ,值域为当a>0时,⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫y|y ≥4ac -b 24a ;当a<0时,⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫y|y ≤4ac -b 24a . 例2 求下列函数的定义域:(1)f(x)=1x -2;(2)f(x)=3x +2;(3)f(x)=x +1+12-x. 解: (1)∵x≠2时,分式1x -2有意义, ∴这个函数的定义域是{x|x≠2}.(2)∵3x+2≥0,即x≥-23时,根式3x +2才有意义, ∴这个函数的定义域是{x|x≥-23}.(3)∵要使函数有意义,必须⎩⎨⎧ x +1≥02-x≠0⇒⎩⎨⎧x≥-1x≠2. ∴这个函数的定义域是{x|x≥-1且x≠2}.小结: 求函数定义域的原理:使函数表达式有意义的自变量的取值范围.跟踪训练2 求函数f(x)=1x +1的定义域. 解: 要使已知函数有意义,当且仅当x +1>0.所以,这个函数的定义域是{x|x>-1},即(-1,+∞).探究点四 求函数值和值域例3 求函数f(x)=1x 2+1(x∈R),在x =0,1,2处的函数值和值域. 解: f(0)=102+1=1, 容易看出,这个函数当x =0时,函数取得最大值1,当自变量x 的绝对值逐渐变大时,函数值逐渐变小至趋向于0,但永远不会等于0. 于是可知这个函数的值域为(0,1].小结: (1)f(a)表示x =a 时函数f(x)的值,而f(x)是一个函数.(2)由于函数的定义域和值域都是一个集合,在求函数定义域和值域的时候,要把定义域和值域写成集合的形式,所以常用两种方法表示:集合、区间.跟踪训练3 求下列函数的值域.(1)y =2x +1,x∈{1,2,3,4};(2)y =x +1.解: (1)值域为{3,5,7,9}; (2)∵x ≥0,∴x +1≥1,∴值域为[1,+∞).例4 (1)已知函数f(x)=x 2,求f(x -1);(2)已知函数f(x -1)=x 2,求f(x).解: (1)f(x -1)=(x -1)2=x 2-2x +1;(2)因为f(x -1)=x 2=[(x -1)+1]2=(x -1)2+2(x -1)+1.所以f(t)=t 2+2t +1,即f(x)=x 2+2x +1.小结: 函数f(x)=x 2,即x→x 2,表示自变量通过“平方运算”得到它的函数值,所以x→x 2与y→y 2,t→t 2,u→u 2,…都表示同一个函数关系.f(x -1)表示自变量x 用代数式x -1代替后得到的新函数. 跟踪训练4 (1)已知函数f(x)的定义域为(0,1),求f(x 2)的定义域.(2)已知函数f(2x +1)的定义域为(0,1),求f(x)的定义域.解: (1)∵f(x)的定义域为(0,1),∴要使f(x 2)有意义,须使0<x 2<1,即-1<x<0或0<x<1,∴函数f(x 2)的定义域为{x|-1<x<0或0<x<1}.(2)∵f(2x+1)的定义域为(0,1),即其中的函数自变量x 的取值范围是0<x<1,令t =2x +1, ∴1<t<3,∴f(t)的定义域为1<t<3,∴函数f(x)的定义域为{x|1<x<3}.练一练:当堂检测、目标达成落实处1.下列说法中,不正确的是 ( )A .函数值域中的每一个数都有定义域中的一个数与之对应B .函数的定义域和值域一定是无限集合C .定义域和对应法则确定后,函数值域也就确定D .若函数的定义域只有一个元素,则值域也只有一个元素解析: 由于函数的关系可以用列表的方法表示,有些用列表法表示的函数其定义域和值域都不是无限集合,故选项B 错.2.下列关于函数与区间的说法正确的是 ( )A .函数定义域必不是空集,但值域可以是空集B .函数定义域和值域确定后,其对应法则也就确定了C .数集都能用区间表示D .函数中一个函数值可以有多个自变量值与之对应解析: 函数的值域不可能为空集,故A 错;当两函数的定义域和值域分别相同时,但两函数的对应法则可以不同,故B 错;由于整数集没法用区间表示,故C 错.所以选D.3.已知函数f(1-x 1+x)=x ,求f(2)的值. 解: 由1-x 1+x =2,解得x =-13, 所以f(2)=-13. 课堂小结:1.函数的本质:两个非空数集间的一种确定的对应关系.由于函数的定义域和对应法则一经确定,值域随之确定,所以判断两个函数是否相等只须两个函数的定义域和对应法则一样即可.2. f(x)是函数符号,f 表示对应法则,f(x)表示x 对应的函数值,绝对不能理解为f 与x 的乘积.在不同的函数中f 的具体含义不同,由课本的四个实例可看出对应法则可以是解析式、图象、表格等.函数除了可用符号f(x)表示外,还可用g(x),F(x)等表示.。
变量与函数大一高数知识点

变量与函数大一高数知识点高等数学是大一大二学生必修的一门基础课程,其中包括了许多重要的知识点。
其中,变量与函数是高等数学中最为基础和重要的概念之一。
一、变量变量是数学中使用的一种概念,它可以表示不同数值的符号或字母。
在数学中,我们常常用字母来表示变量,如x、y、z等等。
变量可以代表任意数的集合,也可以代表某一个具体的数值。
在数学中,我们通常用变量来表示未知数,通过解方程等方法来求解变量的数值。
变量在实际问题中也很常见,我们可以通过设定变量来描述实际问题的各种情况,从而得到数学模型并解决问题。
二、函数函数是数学中另一个重要的概念。
函数是一个特殊的关系,它将一个集合的元素(自变量)映射到另一个集合(因变量)。
函数常用符号表示为y = f(x),其中x为自变量,y为因变量,f为函数关系。
函数包含了定义域、值域和对应关系三个重要的概念。
定义域是自变量的取值范围,值域是因变量的取值范围,对应关系是自变量和因变量之间的映射关系。
函数在数学中有着广泛的应用。
它们可以用来描述各种数学模型,如直线方程、曲线方程等等。
通过函数的性质和图像,我们可以研究函数的增减性、极值、导数等,从而了解函数的行为和特点。
函数可以用来解决各种实际问题,如经济学中的生产函数、物理学中的运动方程等等。
因此,对于函数的理解和掌握是我们学习高等数学的基础。
三、变量与函数的关系变量与函数之间有着密切的关系。
在函数中,自变量常常是一个或多个变量,而函数则是对自变量的一种规定或设定。
变量作为函数中的自变量,它的取值范围和变化规律会影响到函数的性质和行为。
因此,变量的取值是函数研究中一个非常重要的问题。
在实际问题中,我们可以通过设定变量来描述问题的各种情况,从而建立函数模型。
通过分析自变量的取值范围和变化规律,我们可以研究函数的图像、性质和规律。
例如,我们可以用变量来表示一个物体的位置,然后建立位置和时间的函数关系,通过分析函数曲线的形状和变化趋势,我们可以了解物体的运动规律和特点。
一次函数讲义变量与函数
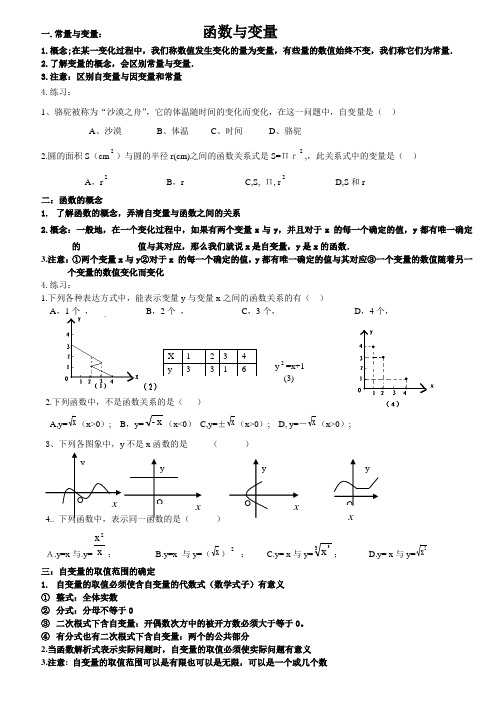
一.常量与变量:函数与变量1.概念;在某一变化过程中,我们称数值发生变化的量为变量,有些量的数值始终不变,我们称它们为常量.2.了解变量的概念,会区别常量与变量.3.注意:区别自变量与因变量和常量4.练习:1、骆驼被称为“沙漠之舟”,它的体温随时间的变化而变化,在这一问题中,自变量是( )A 、沙漠B 、体温C 、时间D 、骆驼2.圆的面积S (cm 2)与圆的半径r(cm)之间的函数关系式是S=Πr2,,此关系式中的变量是( )A ,r 2B ,r C,S, Π, r 2D,S 和r二:函数的概念1. 了解函数的概念,弄清自变量与函数之间的关系2.概念:一般地,在一个变化过程中,如果有两个变量x 与y ,并且对于x•的每一个确定的值,y 都有唯一确定的 值与其对应,那么我们就说x 是自变量,y 是x 的函数.3.注意:①两个变量x 与y ②对于x•的每一个确定的值,y 都有唯一确定的值与其对应③一个变量的数值随着另一个变量的数值变化而变化 4.练习:1.下列各种表达方式中,能表示变量y 与变量x 之间的函数关系的有( )A ,1个 ,B ,2个 ,C ,3个,D ,4个,2.下列函数中,不是函数关系的是( )A,y=x (x>0); B ,y=x -(x<0) C,y=±x (x>0); D, y=-x (x>0); 3、下列各图象中,y 不是x 函数的是 ( )4.. 下列函数中,表示同一函数的是( )A.y=x 与.y=x x 2; B.y=x 与y=(x )2; C.y= x 与y=33x ; D.y= x 与y=2x三:自变量的取值范围的确定1. 自变量的取值必须使含自变量的代数式(数学式子)有意义 ① 整式:全体实数 ② 分式:分母不等于0③ 二次根式下含自变量:开偶数次方中的被开方数必须大于等于0。
④ 有分式也有二次根式下含自变量:两个的公共部分2.当函数解析式表示实际问题时,自变量的取值必须使实际问题有意义3.注意: 自变量的取值范围可以是有限也可以是无限,可以是一个或几个数X 1 2 3 4 y33 16O yxOxyOxyxyOy 2=x+1 (3)4.有的要列不等式或不等式组来求5.练习: 1、在函数y=xx 32+中,自变量的取值范围是( )A 、x ≥-2且x ≠0; B 、x ≤2且x ≠0; C 、x ≠0; D 、x ≤-2; 2.、函数212-++=x x y 的自变量x 的取值范围是( ) A 、x ≥-2; B 、x >-2且x ≠2; C 、x ≥0且x ≠2; D 、x ≥-2且x ≠2。
变量与函数第1课时教学设计

14.1变量与函数(第1课时)(八年级上册)吉林省扶余县蔡家沟镇职业中学聂洪利教学任务分析教学过程设计问题1:汽车以60千米/时的速度匀速行驶,行驶里程为s千米,行驶时间为t小时,请填写下面的表格.t/时 1 2 3 4 5s/千米问题2:在一根弹簧的下端挂重物,弹簧原长为10cm,每1kg重物使弹簧伸长0.5cm,设重物质量为m kg,受力后的弹簧长度为l cm,怎样用含m的式子表示l?问题3:某地在24小时内的气温变化图如下,图中有哪些量?教师:提出问题1.学生:思考并回答.教师:问题1中有哪些量?学生:回答问题.教师:提出问题2.学生:思考并回答.教师:问题1中有哪些量?学生:回答问题.教师:提出问题3.问题3的师生行为同上.这里所举的例子是为了引出变量与常量的概念而设计的,分别用表格、式子、图象表示变量之间的关系,为后续学习函数的三种表示方法埋下伏笔.【活动3】归纳定义在一个变化过程中,数值发生变化的量,我们称之为变量.数值始终不变的量,我们称之为常量.教师:让学生对上述问题中的量进行分类,并指出分类的标准.学生:分类,并指出分类的标准.教师:给出变量与常量的定义.通过上面几个问题的探索,可以自然地归纳出变量与常量的定义.【活动4】知识应用举出生活中变量与常量的例子,并指出变量与常量.(以组为单位,选出汇报)教师提出问题,学生回答.学生联系生活实际,体会数学的应用价值,感受成功的喜悦.【活动5】探索新知在前面的每个问题中,同一个问题中的两个变量之间有什么联系?教师提出问题,学生思考后进行小组讨论.在此过程中,教师要参与学生的活动中,了解各小组讨论的情况.让学生经历分析具体问题中变量之间联系的过程,在间接经验积累到。
14.1变量与函数 (第1课时)变量

第十四章一次函数
14.1变量与函数( 课时) 14.1变量与函数(第1课时) 变量与函数
问题一: 问题一
汽车以60千米 时的速度匀速行驶 千米, 汽车以 千米/时的速度匀速行驶,行驶里程为 s 千米, 千米 时的速度匀速行驶, 小时,先填下面的表,再试用含t的式子表示 的式子表示s. 行驶时间为 t 小时,先填下面的表,再试用含 的式子表示
1 s = x(10 − 2x) = x(5 − x) 2
(1)S = 60t (2) y = 10x ) ) (3)l =10+0.5x
(4)r =
1 (5)ms = x(10 − 2x) = x(5 − x) 2
s π
发生变化的量为变量 1、变量:在一个变化过程中,数值发生变化的量为变量。 变量:在一个变化过程中,数值发生变化的量为变量。 始终不变的量为常量 常量:在一个变化过程中,数值始终不变的量为常量。 2、常量:在一个变化过程中,数值始终不变的量为常量。
y = 10x
问题三: 问题三
在一根弹簧的下端挂重物,改变并记录重物的质量, 在一根弹簧的下端挂重物,改变并记录重物的质量,观 并记录弹簧长度的变化,探索它们的变化规律。 察并记录弹簧长度的变化,探索它们的变化规律。如果 弹簧长原长为10cm,每1千克重物使弹簧伸长 千克重物使弹簧伸长0.5cm,怎 弹簧长原长为 , 千克重物使弹簧伸长 怎 样用含重物质量m(单位: ) 样用含重物质量 (单位:kg)的式子表示受力后的弹 单位: 簧长度 l (单位:cm)? 单位
6a2 , 2、如图 正方体的棱长为 表面积 正方体的棱长为a,表面积 、如图2正方体的棱长为 表面积S=
体积V= 体积
2.1.1函数(一)变量与函数的概念
f(a)=f((a+1)-1) =(a+1)2-2(a+1)+7=a2+6.
(2)方法一
(配凑法)
f(x)=f((x+1)-1)=(x+1)2-2(x+1)+7=x2+6, (或 f(x-1)=(x-1)2+6), ∴f(x)=x2+6. ∴f(x+1)=(x+1)2+6=x2+2x+7. 方法二 (换元法)设 t=x-1,即 x=t+1, ∴f(t)=(t+1)2-2(t+1)+7=t2+6, 故 f(x)=x2+6. f(x+1)=(x+1)2+6=x2+2x+7.
( B )
解析
1 2-1 2 2 -1 3 1 2 3 ∵f(2)= 2 =5,f2=1 =-5 2 +1 2+1 2
f(2) ∴ 1 =-1 f2
(x-1)0 4.函数 y= 的定义域是 |x|+x A.(0,+∞) B.(-∞,0) C.(0,1)∪(1,+∞) D.(-∞,-1)∪(-1,0)∪(0,+∞)
1 010.
1 2 2 2 x 2 4 1 1 2 解 (1)∵f(x)= 2,∴f(2)= 2= ,f = 1 =5, 5 2 1+x 1+2 1+22 1 2 2 3 9 1 1 3 f(3)= ,f3= 2= 1 =10. 1+3 10 1+32
(5)把满足 x≥a,x>a,x≤b,x<b 的全体实数 x 的集合分 别表示为 [a,+∞),(a,+∞),(-∞,b],(-∞,b) .
对点讲练
知识点一 例1 已知解析式求函数的定义域 求下列函数的定义域: 1 3 (1)y=3- x;(2)y= ; 2 1- 1-x -x 1 1 (3)y= 2 ;(4)y= 2x+3- + . 2x -3x-2 2-x x 点拨
11.1 变量与函数1
11.1 变量与函数第一教时 11.1.1 变 量教学要求:通过课本上的五个问题,引入并理解常量、变量的概念,会求函数自变量的取值范围教学重点:针对具体问题,分清常量与变量教学难点:在不同的变化过程中,常量与变量并不是固定不变的教学过程:一、导入新课:1.有关图形的体积、面积、周长公式:图形的周长:C 圆=2лR ;C 正方形=4a ;图形的面积:S △ABC =21×ah ; S 圆=лR 2;S 梯形=21×(a+b)h ; 图形的体积:V 圆柱=лR 2h , V 圆锥=31лR 2h ;V 正方体=a 3. 2.从实际问题出发,出于从具体到抽象在认识事物的考虑,列举课本上的物理问题、销售问题、几何问题等,要求学生会用填表、求值、写解析式等二、新授:1.常量、变量:在一个变化过程中,数值发生变化的量叫变量;数值不发生变化的量叫常量两个变量之间相互依赖、互相制约、互相转化.如在匀速直线运动中,当速度是常量,时间和路程都是变量,即s=vt ;当路程一定时,速度、时间是变量.例如,v=t s , t=v s.2.共同解答例子:[例1]下表是某市2000年统计的该市男学生各年龄组(岁)的平均身高(cm).(1)从表中你能看出该市14岁的男学生的平均身高是多少吗?(2)该市男学生的平均身高从哪一岁开始迅速增加?(3)上表反映了哪些变量之间的关系?其中哪个是自变量?哪个是函数?[思维点拨] 借助表格,可以直接找到自变量与函数的具体对应值.从中挖掘有用的信息.[解] (1)从表中能看出该市14岁的男学生的平均身高为146.1㎝;(2)该市男学生的平均身高是从14岁开始迅速增加(在14~17岁之间,后一年比上一年的身高分别增加了8.7cm,8.1cm,5.3cm);(3)表中反映了2000年某市男生的平均身高与学生年龄的关系.三、小结:由学生举一实际问题,说明哪些量是变量?哪些量是常量?四、课堂练习:课本18页第1、2、8、9题.五、教学后记:第二教时 11.1.2 函 数教学要求:通过经历从具体到抽象的认识过程,理解函数的概念、函数的单值对应. 教学重点:针对具体问题,利用表格、解析式和图象,体会相关变量之间的对应关系 教学难点:变量之间的单值对应关系教学过程:一、导入新课:从上节课的五个实际问题出发,直接导入新课二、新授:1.理解单值对应:变量之间的单值对应关系,当一个变量取定一个值时,单值对应有两重含义:(一)另一变量有对应值;(二)对应值只有一个2.理解函数的概念一般地,在一个变化过程中,如果有两个变量x 与y ,并且对于x 的每一个确定的值,y 都有唯一确定的值与其对应,那么我们就说x 是自变量,y 是x 的函数.函数的定义中包括了对应值的存在性和唯一性,函数是对变量而言的;函数值是对具体数值而言的。
初中数学人教版《变量与函数》优质公开课1
(1)请写出弹簧的总长y(cm)与所挂物体的质量x(kg)之间的函数关系式; (2)当所挂物体的质量是10 kg时,弹簧的总长是多少? 解:(1)y=x+12 (2)当x=10时,y=17,故弹簧的总长是17 cm
17.某学校组织学生到离校6 km的光明科技馆去参观,学生小明因事没能
乘上学校的包车,于是准备在学校门口改乘出租车去光明科技馆,出租车的
17.某学校组织学生到离校6 km的光明科技馆去参观,学生小明因事没能乘上学校的包车,于是准备在学校门口改乘出租车去光明科技馆,出租车的收费标准如下表:
A.s=120-30t(0≤t≤4)
13.小亮利用计算机设计了计算程序,输入和输出的数据如下:
那么当输入的数据是 8 时,输出的数据是( C )
A.681
18.木材加工厂堆放木料的方式按如图所示堆放,随着层数的增加,物体
总数也会变化. (1)根据变化规律填写下表: (2)求出y与n的函数关系式;
层数n 物体总数y
1234… …
(3)当物体堆放的层数为10时,物体总数为多少?
解:(1)1,3,6,10 (2)y=n(n2+1) (3)55
合作探究
新知 函数的概念
1.函数 一般地,在一个变化过程中,如果有两个变量 x 与 y,并且对于 x 的每一个确定的值,y 都有唯一确定的值 与其对应,那么我们就说x是自变量,y是x的函数.
2.判断一个关系是否是函数关系的方法
①看是否在一个变化过程中;
②看是否存在两个变量;
③看每当变量确定一个值时,另外一个变量是否都有唯一
B.683
C.685
D.687
输入 1
2
3
4
5
…
输出
湘教版数学八年级下册4.1.1《变量与函数》说课稿
湘教版数学八年级下册4.1.1《变量与函数》说课稿一. 教材分析《变量与函数》是湘教版数学八年级下册4.1.1的内容,本节内容是在学生已经掌握了代数式的知识基础上进行讲述的,旨在让学生了解变量的概念,并引入函数的概念。
教材通过生活中的实例,引导学生理解变量和函数的关系,从而为后续的函数学习打下基础。
二. 学情分析八年级的学生已经具备了一定的代数基础,对于代数式、方程等概念有一定的了解。
但是,对于变量和函数的概念,学生可能还比较陌生。
因此,在教学过程中,需要通过生动的实例和生活情境,帮助学生理解变量和函数的概念,并建立它们之间的关系。
三. 说教学目标1.知识与技能:让学生理解变量和函数的概念,并掌握它们之间的关系。
2.过程与方法:通过实例分析,让学生学会如何用变量和函数来描述实际问题。
3.情感态度与价值观:培养学生对数学的兴趣,提高学生运用数学知识解决实际问题的能力。
四. 说教学重难点1.重点:变量和函数的概念及其关系。
2.难点:如何用变量和函数来描述实际问题。
五. 说教学方法与手段1.教学方法:采用问题驱动法、案例分析法、小组合作学习法等。
2.教学手段:多媒体课件、实例分析、小组讨论等。
六. 说教学过程1.导入:通过生活中的实例,如气温变化、物体运动等,引导学生思考变量和函数的关系。
2.新课导入:介绍变量的概念,让学生理解变量是如何表示事物的变化。
3.案例分析:分析生活中的实例,引导学生理解函数的概念。
4.知识讲解:讲解变量和函数之间的关系,让学生掌握它们的基本概念。
5.练习巩固:让学生通过练习题,巩固所学知识。
6.课堂小结:对本节课的内容进行总结,帮助学生形成知识体系。
7.课后作业:布置相关作业,让学生进一步巩固所学知识。
七. 说板书设计板书设计如下:1.变量与函数2.变量的概念3.函数的概念4.变量与函数的关系八. 说教学评价教学评价主要从学生的学习效果、课堂表现、作业完成情况等方面进行。
教师应及时关注学生的学习进度,针对不同学生进行差异化指导,提高教学效果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
;佛山图文店 佛山图文店
;
,每一片沙滩,每一缕幽林里的气息,每一种引人自省、鸣叫的昆虫,都是神圣的你我的生活完全不同,印第安人的眼睛一见你们的城市就疼痛。你们没有安静,听不见春天里树叶绽开的声音、昆虫振翅的声音,听不到池塘边青蛙在争论你们的噪音羞辱我的双耳,这种生活,算活着? 我是印第 安人,我不懂。” 我是印第安人,我不懂。 后来,华盛顿州首府取了这位酋长的名字:西雅图。 有个当代故事:一个长年住山里的印第安人,受纽约人邀请,到城里做客。出机场穿越马路时,他突然喊:“你听到蟋蟀声了吗?”纽约人笑:“您大概坐飞机久了,是幻听吧。”走了两步,印第 安人又停下:“真的有蟋蟀,我听到了。”纽约人乐不可支:“瞧,那儿正在施工打洞呢,您说的不会是它吧?”印第安人默默走到斑马线外的草地上,翻开了一段枯树干,果真,趴着两只蟋蟀。 城市人的失聪,因为其器官只向某类事物敞开,比如金钱、欲望、键盘、电话、券、计算器从而关 闭了灵性。印第安人的听力不是“好”,而是正常和清澈,未被污染和干扰的正常,没有积垢和淤塞的清澈。一个印第安人耳朵里常年居住的,都是纯净而纤细的东西,所以只要对方一闪现,他就会收听到。 作为忠告,作为签约的条件,西雅图酋长继续对白人们说 “记得并教育你们的孩子, 河川是我们的兄弟,也是你们的,今后,你们须以手足之情对待它你们须把地上的野兽当兄弟,我听说,成千上万的野牛横尸草原,是白人从火车中射杀了它们。我们只为求活才去捕猎,若没了野兽,人又算是什么呢?若兽类尽失,人类亦将寂寞而死。发生在野兽身上的,必将回到人类身上若 继续弄脏你的床铺,你必会在自己的污秽中窒息。” 可惜,这些以火车和枪弹自负的工业主义者,并未被插着羽毛的话给吓住。他们不怕,什么都不怕。 清晨之人的声音,傍晚之人怎能听得进呢? 犹太作家以萨·辛格说:“就人类对其他生物的行为而言,人人都是纳粹。” 北美大陆的野牛, 盛时有4亿至5 亿只,19世纪中叶有4000万只,随着白人的火车行驶,50年后,仅剩数百只。 果真,野兽的命运来到了人身上。1874年,印第安人的领地发现了金矿,白人断然撕毁和平协议,带上炸药、地图和酒瓶出发了。很快,野牛的血泊变成了人的血泊。 印第安人的清晨陨落了,剩下的, 是星条旗的黄昏和庆祝焰火。 李奥帕德说过:“许多供我们打造出美国的各种野地已经消 失了。” 美利坚,基于北美的童年基因而诞生,乃流落欧洲几世纪的自由精神遇到辽阔大陆和清新野地的结果。而它功成之日,却蹂躏了赋予它容貌、体征、气质和恩泽的母腹。从此,它再也无法复制古 希腊的童话,只能以现代名义去铸造一个以理性、逻辑和法律见长而非以美丽著称的国家。 我常想,印第安人的挽歌,是否人类童年的丧钟? 若世间没有了孩子,还有诗意的未来吗? 叶芝在《偷走的孩子》中唱道 “走吧,人间的孩子! 与一个精灵手拉着手,走向荒野和河流。 这世界哭声 太多,你不懂。” 如果能选择,我也想做一个印第安人。 那些很少很少的人。 哪怕清晨开始,清晨死去。 谁偷走了夜里的“黑” ? 1 你见过真正的黑夜吗?深沉的、浓烈的、黑魆魆的夜? 儿时是有的,小学作文里,我还用过“漆黑”,还说它“伸手不见五指”。 从何时起?昼夜的边界模 糊了,夜变得浅薄,没了厚度和深意,犹如墨被稀释渐渐,口语中也剥掉了“黑”字,只剩下“夜”。 夜和黑夜,是两样事物。 夜是个时段,乃光阴的运行区间;黑夜不然,是一种境,一种栖息和生态美学。一个是场次,一个是场。 在大自然的原始配置中,夜天经地义是黑的,黑了亿万年。 即使有了人类的火把,夜还是黑的,底蕴和本质还是黑的。 “夜如何其?夜未央。庭燎之光。” 这是《诗经·庭燎》开头的话,给我的印象就是:夜真深啊。 那会儿的夜,很纯。 一位苗寨兄弟进京参加“原生态民歌大赛”,翻来覆去睡不着,为什么?城里的夜太亮了。没法子,只好以厚毛 巾蒙面,诈一回眼睛。在他看来,黑的浓度不够,即算不上夜,俨然掺水的酒,不配叫酒。 习惯了夜的黑,犹如习惯了酒之烈,否则难下咽。 宋时,人们管睡眠叫“黑甜”,入梦即“赴黑甜”。意思是说,又黑又甜才算好觉,睡之酣,须仰赖夜之黑:夜色浅淡,则世气不宁;浮光乱渡,则心 神难束。所以古代养生,力主亥时(约晚10点)前就寝,唯此,睡眠才能占有夜的深沉部分。 现代人的“黑甜”,只好求助于厚厚的窗帘了,人工围出一角来。 伪造黑夜,虚拟黑夜 难怪窗帘生意如此火爆。 2 昼夜轮值,黑白往复;日出而作,日落而息 乃自然之道、人生正解。 夜,是上天 之手撒下的一块布,一座氤氲的罩体,其功能即覆护万物、取缔喧哗、纳藏浮尘,犹若海绵吸水、收杂入屉。无夜,谁来叫停芸众的熙攘纷扰和劳顿之苦?何以平息白昼的手舞足蹈与嘈沸之亢?夜,还和精神的营养素 “寂”“定”“谧”相通,“夜深人静”意思是夜深,心方静远而这一切,须 靠结结实实的“黑”来完成:无黑,则万物败露,星月萎怠;无黑则无隐,无隐则无宁。 所以我一直觉得,黑,不仅是夜之色相,更是夜的价值核心。 黑,是夜的光华,是夜的能量,是夜的灵魂,也是夜的尊严。 “不夜城”,绝对是个贬义词。等于把夜的独立性给废黜了,把星空给挤兑和欺 负了。它侵略了夜,丑化了夜,羞辱了夜,仿佛闯到人家床前掀被子。 将白昼肆意加长,将黑夜胡乱点燃,是一场美学暴乱、一场自然事故。无阴润,则阳萎;无夜育,则昼疲。黑白失调,糟蹋了两样好东西。 往实了说,这既伤耗能源,又损害生理。我一直纳闷为何现代鸡发育那么快。真相 是:笼舍全天照明,鸡无法睡觉,于是拼命吃。见光吃食,乃鸡的秉性,人识破了这点,故取缔了黑,令其不舍昼夜地膨胀身子。 现代鸡是在疯狂的植物神经紊乱中被速成的。它们没有童年,没有青春,只有起点和终点。人享用的,即这些可怜的被篡改了生命密码的鸡,这些一声不吭、无一日 之宁的鸡。毕其一生,它们连一次黑夜都没体会,连鸣都没打过。 我想,应给其重新起个名:昼鸡,或胃鸡。 无黑,对人体的折磨更大,可谓痛不欲生。据说逼供多用此法,不打不骂,只用大灯泡照你,一两日挺过去,第三天,你会哭喊着哀求睡一会儿,哪怕随后拉出去枪毙。 3 黑夜,不仅 消隐物象,它还让生命睁开另一双眼,去感受和识别更多无形而贴心的东西。 成年后,我只遇上一回真正的夜。 那年,随福建的朋友游武夷山,在山里一家宾舍落脚。夜半,饥饿来了,大伙驱车去一条僻静的江边寻夜宵。 吃到一半,突然一片漆黑,断电了。 等骚动过去,我猛然意识到:它 来了,真正的夜来了。 亿万年前的夜,秦汉的夜,魏晋的夜,唐宋的夜 来了。 此时此刻,我和一个古人面对的一模一样? 山河依旧?草木依旧?虫鸣依旧? 是,应该是。那种弥漫天地、不含杂质、水墨淋漓的黑,乃我前所未遇。 星月也恢 复了古意,又亮又大,神采奕奕。还有脚下那条江, 初来时并未听到哗哗的流淌,此刻,它让我顿悟了什么叫“川流不息”,什么叫“逝者如斯”,它让我意识到它已在这儿住了几千年 我被带入了一幅古画,成了其中一员,成了高山流水的一部分。 其实,这不过是夜的一次显形,恢复其本来面目罢了。 而我们每天乃至一生的面对,皆为被改造 过的不实之夜。 几小时后,灯火大作,酒消梦散。 21世纪又回来了。 这是一次靠“事故”收获的夜。 对都市人来说,这样的机会寥寥无几。第一,你须熄掉现代光源,遭遇或制造一次停电。第二,你须走出足够远,甩掉市声人沸的跟踪,最好荒山野岭、人烟稀少,否则一束过路车灯、一架 红眼航班,即会将梦惊飞。 所以,这是运气。 4 夜的美德还在于,其遮蔽性给人生营造了一种社会文化:个体感和隐私性。 如果说,白昼之人,不得不在光天化日、众目睽睽下演绎集体生活模式,那么,黑则让人生从“广场状态”移入角落状态,夜成了除住宅空间外更辽阔的私生活舞台。所 以,“夜生活”即同义于“私生活”。 我向来觉得,生活的本质即私生活,私生活才是真正的生活。白天,人属于人群,不属于自我,正是夜,让世界还原成一个个私人领地和精神单元,正是黑的降临,才预示着生活帷幕的拉开。 但棘手的是:现代之夜的“黑”,明显减量了,不足值了。 现 代生活和城市发展的一个趋向是:愈发地白昼化,愈发地广场性。风靡各地的“灯光工程”“不夜工程”、无孔不入的摄像头,即为例。 凡诱惑之物,必成为一种资源,进而孕育一份产业。 终于,有人瞄上了“黑”,并把它变成巧克力一样的东西 2005年,商务区开了一家名为“巨鲸肚”的黑 暗餐厅,顾名思义,这是个伸手不见五指的人造空间。该餐厅分亮光区和黑暗区,客人先在亮区点餐,将手机、打火机、表链等发光品存储,再由佩夜视镜的侍者引入暗区。 一时间,该餐厅生意火爆,预订期长达一周。说是进餐,不如说猎奇,因为没人把吃当回事,据说饭菜并不可口,大家消 费的是黑绝对的、久违的、正宗的、业已消逝的“黑”。 我想,谁要打造一个名叫“夜未央”的诗意空间,肯定更卖座。 我也会去消费。夜如何其?夜未央,夜未央 说了这么多,其实我一点不厌光,相反,我深爱星月之华、烛火之灿。 夜里,微光最迷人,最让人心荡漾。 我厌倦的是“白夜 城市”“不夜工程”,它恶意篡改了大自然的逻辑和黑白之比,将悦目变成了刺眼。 对“黑”的偏见和驱逐,让这个时代有点蠢。 我觉得,人类应干好两件事 一是点亮黑夜,一是修复黑夜。 同属文明,一样伟大。 生活在险境中 ? 打开电视,一警官大学教授在教人同短信诈骗作斗争。另一 频道,专家正详解新版百元假钞的破绽,其仿真度已让验钞机歇了菜;紧接着,主持人纳闷为何黄瓜顶花戴刺、娇若新娘,谜底是避孕药的滋润。再换个频道,说了两件事:一是银行卡里的钱为何不翼而飞,专家提醒,操作ATM机时一定要警惕可疑摄像头,以防密码被钓;二是购房纠纷,律师告 诫,一定要反复推敲合同的每一句、每一字、每一标点 好了,我都铭记在心、烂熟于心了。感谢,感恩涕零。 站起来,朝电视机深鞠一躬。 我们生活在险境中,我们居住在楚歌里。 我们警惕地、愤怒地,如履薄冰、担惊受怕地过日子。 是不是有点悲壮? 我想,我若是个傻瓜,可怎么活啊! 这么多陷阱,这么多圈套和天罗地网
1、都有两个变量
共同特征:2、其中的一个变量取定一个值,另
一个变量的值也唯一确定
在心电图中,时间、心脏电流都是变量
§11.1.2函数(一)
在一个变化过程中,如果有两个变量x与y,并 且对于x的每一个确定的值,y都有唯 一确定的 值与其对应,那么我们就说是x自变量 ,y是x 的函数。如果当x=a时y=b,那么b叫做当自变 量x的值为a时y的函数值
