劳斯判据例题
劳斯判据练习题
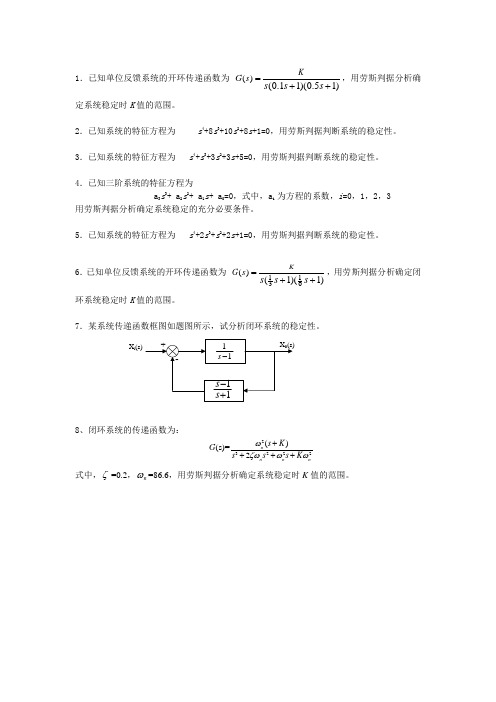
1.已知单位反馈系统的开环传递函数为 ()(0.11)(0.51)K
G s s s s =++,用劳斯判据分析确
定系统稳定时K 值的范围。
2.已知系统的特征方程为 s 4+8s 3+10s 2+8s +1=0,用劳斯判据判断系统的稳定性。
3.已知系统的特征方程为 s 4+s 3+3s 2+3s +5=0,用劳斯判据判断系统的稳定性。
4.已知三阶系统的特征方程为
a 3s 3+ a 2s 2+ a 1s + a 0=0,式中,a i 为方程的系数,i =0,1,2,3
用劳斯判据分析确定系统稳定的充分必要条件。
5.已知系统的特征方程为 s 4+2s 3+s 2+2s +1=0,用劳斯判据判断系统的稳定性。
6.已知单位反馈系统的开环传递函数为 1136()(1)(1)K
G s s s s =++,用劳斯判据分析确定闭
环系统稳定时K 值的范围。
7.某系统传递函数框图如题图所示,试分析闭环系统的稳定性。
X i (s)
8、闭环系统的传递函数为:
G (s)=23222()2n n n n
s K s s s K ωζωωω++++ 式中,ζ=0.2,n ω=86.6,用劳斯判据分析确定系统稳定时K 值的范围。
系统稳定性分析—劳斯稳定判据

© BIP
例题4:s6 s5 6s4 5s3 9s2 4s 4 0
S6 1
6
S5 1
5
9
4
辅助方程
4
0
S4 1
5
4
S3
0 4
0 10
0 0
S2 2.5
4
0
0 s4 5s2 4 0
0 0 4s3 10s 0 0
S1 3.6
0
0
0
S0 4
0
0
0
某一行全为零,说明存在对称于原点的根,系统不稳定
No.15
© BIP
图7 K=15时系统的单位阶跃响应曲线
No.16
© BIP
图8 K=20时系统的单位阶跃响应曲线
No.17
© BIP
例题2:液位控制系统的稳定性分析。
进水
阀门
进水阀门的 传递函数K3
减速器
+ 电位器
-
连杆
执行电机和 减速器的传
递函数
K2/S(TS+1)
电动机
放大器
控制对象水箱的
系统稳定性分析之 ——劳斯判据
一、系统稳定的重要性
图1“舞动的格蒂”—首座塔科马大桥
No.2
© BIP
二、系统稳定性的基本概念和条件
1、定义:如果线性控制系统在初始扰动的作 用下,使被控量产生偏差,当扰动消失后,该 偏差随着时间的推移逐渐减小并趋于零,即系 统趋于原来的工作状态,则称该系统为渐进稳 定。反之,如果在初始扰动的作用下,系统的 偏差随着时间的推移而发散,系统无法趋于原 来的工作状态,则称系统不稳定。
传递函数K4/S
1习题集第五章系统稳定性

【解】 由特征方程列劳斯表如下:
S4
1
T 100
S3
2
10
S 2 T 5 100
S1 10(T 5) 200
S0
100
T 50 由劳斯判据,系统稳定,则
10(T 5) 200 0 解得: T 25
5-8 已知系统特征方程如下,试求系统在 s 右平面的根数及虚根值. (1) s5 3s4 12s3 24s2 32s 48 0
1.5K 0
解得: 0 K 5 3 5
5-12 试确定如下图所示系统的稳定性.
【解】 由系统方框图可得系统的闭环传递函数为:
10(10s 1)
(s)
特征方程为: s(s 1) 10(10s 1) 0
s(s 1) 10(10s 1)
即: s2 101s 10 0
5-3 设单位反馈系统的开环传递函数分别为
K (s 1) G(s)
s (s 1) (s 5)
1 K * (s 1) 【解】 G(s) 5
1 s(s 1)( s 1)
5
所以开环增益 K 1 K * 5
由开环传递函数可得系统的闭环传递函数为:
K (s 1) (s)
1 s(s 1)( s 1) K (s 1)
,试用对数频率特性判别系统的稳定性。
【解】画出开环频率特性,并依系统中有两个积分环节做出辅助线如图所示:
在 L() 0范围内,N N 0 ,故 P 2N ,则系统闭环稳定。
10
0.1K A 0
0.1K A (0.09 0.2K A ) 0.1K A 0
劳斯判据的证明

1、劳斯判据证明思路:(1)将给定的描述系统运动的高阶齐次微分方程变换为齐次状态方程.(2)给定对称正定(或非负定)矩阵Q,根据式Ax x= ,Q PA P A T -=+求出相应的矩阵P(3)由要求矩阵P为正定的条件证明赫尔维茨稳定判据2、赫尔维茨稳定性判据证明.Ax x= (1) Q PA P A T -=+ (2)设在输入信号为零的情况下,系统的齐次微分方程为01111=++⋅⋅⋅++---x a dtdx a dt x d a dt x d n n n n n n (3) 式(3)的系数行列式为:n n n a a a a a a a a a a a 0000000000000000010000011123451231-⋅⋅⋅⋅⋅⋅⋅⋅⋅=∆ 赫尔维茨判据为:系数行列式n ∆的各阶顺序主子式大于0.证明:首先将系统的高阶微分方程写成状态方程的形式.选择系统的状态变量为 []T n x x x x 21=令x x =1,则式(2)等价于下列状态方程:Ax x= ,其中 1210000010000000001000000100000010b b b b A n n----=-(4)该矩阵特点是:主对角线上除最后一个元素外,其余元素均为0;主对角线以上各元素为1;主对角线以下各元素从第二行开始依次为-bn 到-b1。
其次,应给定矩阵Q,并根据式(2)去求矩阵P设⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=21200000000b Q (5) 这是一个对称非负定矩阵,由此可知李雅普诺夫函数的导数为 2212nT x b Qx x V -=-= 。
只要x1,x2,…,xn 不全都为零,则0≠n x ,于是()x V 不可能恒为零.所以按式(4)选定的矩阵Q是合理的.再假设矩阵P是对角线矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=-121000000000000p p p p P n n (6) 将式(4)、式(5)、式(6)代人式(2),即可得 ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=-11212112000000000000b b b b b b b b b P n n 最后检验矩阵P的正定性.如欲系统的半衡点是大范围渐近稳定的,则矩阵P应是正定的,亦即矩阵P主对角线上各元素均应大于零,即有 0,0,012121>>>b b b b b b n 。
劳斯判据的证明及应用

劳斯判据的证明及应用劳斯判据(Rayleigh's criterion)是描述两个正交振动的符合条件的充分必要条件。
它由英国物理学家勒克·埃尔斯利·劳斯(Lord Rayleigh)于1879年提出,并被广泛应用于光学、声学、信号处理等领域。
首先,我们来推导劳斯判据的证明。
假设有两列正交的振动,分别用x(t)和y(t)表示,其中t表示时间。
为了方便计算,我们可以将振动表示为复指数形式:x(t) = Re [ Xexp(iωt) ]和y(t) = Re [ Y exp(iωt) ],其中X和Y是复振幅,ω是角频率。
我们定义振动的互强度(cross-intensity)为Ix,y(t) =x(t)y*(t),其中y*表示y的复共轭。
根据定义,我们有:Ix,y(t) = Re [ X exp(iωt) Y* exp(-iωt) ] = Re [ XY* ]为了计算Ix,y(t)的平均值,我们需要对振动周期T进行时间平均:<Ix,y> = (1/T) ∫[0,T] Ix,y(t) dt将Ix,y(t)代入上式,并利用Euler公式(exp(iθ) = cosθ + isinθ)展开,可以得到:<Ix,y> = (1/T) ∫[0,T] Re [ XY* ] dt= (1/T) Re [ X∫[0,T] Y* dt ]= (1/T) Re [ X∫[0,T] Re [ Y* ] dt ]根据劳斯判据的定义,<Ix,y>=0,因此我们有:Re [ X∫[0,T] Re [ Y* ] dt ] = 0由于X是任意复振幅,我们可以独立地选取它的实部和虚部分别为1和0。
这样,上式可以简化为:Re [ ∫[0,T] Re [ Y* ] dt ] = 0我们知道,对于任意实函数f(t),其实部的积分与f(t)的本征函数cos(ωt)正交。
∫[0,T] Re [ Y* ] dt = 0这就是劳斯判据的证明,根据这个证明,我们可以得到劳斯判据的应用。
自动控制原理第3章 习题及解析

自动控制原理(上)习 题3-1 设系统的结构如图3-51所示,试分析参数b 对单位阶跃响应过渡过程的影响。
考察一阶系统未知参数对系统动态响应的影响。
解 由系统的方框图可得系统闭环响应传递函数为/(1)()()111K Ts Ks Kbs T Kb s Ts +Φ==++++ 根据输入信号写出输出函数表达式:111()()()()()11/()K Y s s R s K s T Kb s s s T bK =Φ⋅=⋅=-++++对上式进行拉式反变换有1()(1)t T bKy t K e-+=-当0b >时,系统响应速度变慢;当/0T K b -<<时,系统响应速度变快。
3-2 设用11Ts +描述温度计特性。
现用温度计测量盛在容器内的水温,发现1min 可指示96%的实际水温值。
如果容器水温以0.1/min C ︒的速度呈线性变化,试计算温度计的稳态指示误差。
考察一阶系统的稳态性能分析(I 型系统的,斜坡响应稳态误差)解 由开环传递函数推导出闭环传递函数,进一步得到时间响应函数为:()1t T r y t T e -⎛⎫=- ⎪⎝⎭其中r T 为假设的实际水温,由题意得到:600.961Te-=-推出18.64T =,此时求输入为()0.1r t t =⋅时的稳态误差。
由一阶系统时间响应分析可知,单位斜坡响应的稳态误差为T ,所以稳态指示误差为:lim ()0.1 1.864t e t T →∞==3-3 已知一阶系统的传递函数()10/(0.21)G s s =+今欲采用图3-52所示负反馈的办法将过渡过程时间s t 减小为原来的1/10,并保证总的放大倍数不变,试选择H K 和0K 的值。
解 一阶系统的调节时间s t 与时间常数成正比,则根据要求可知总的传递函数为10()(0.2/101)s s Φ=+由图可知系统的闭环传递函数为000(10()()1()0.211010110()0.21110H HHHK G s K Y s R s K G s s K K K s s K ==++++==Φ++)比较系数有101011011010HHK K K ⎧=⎪+⎨⎪+=⎩ 解得00.9,10H K K ==3-4 已知二阶系统的单位阶跃响应为1.5()1012sin(1.6+53.1t y t e t -=-)试求系统的超调量%σ,峰值时间p t ,上升时间r t 和调节时间s t 。
课件:第4讲 3.6 劳斯稳定判据

解: 列劳斯表 s3 1 517
0
s2 41.5 2.3104 s1 - 38.5 s0 2.3104
由于该表第一列系数的符号变化了两次,所以该方程中有2 个根在s的右半平面,因而系统是不稳定的。
例2 设系统特征方程为: 劳斯表介绍
s6+2s5+3s4+4s3+5s2+6s+z1 1
2
有一个根在垂直线s=-1的右方。 z0 1
应用之二: 用劳斯判据确定系统参数
例7: 已知系统的特征方程为 s3 41.5s2 517s 16701 K 0
求系统稳定的K值范围.
解: 列劳斯表
s3
s2
1
517
41.5 16701 K
1<K<11.9
一调速系统的特征方程为 s3 41.5s2 517s 2.3104 0
3.6 劳斯稳定判据
令系统特征方程为
a0 s n
a sn1 1
an1s
an
0,a0> 0
排劳斯表: sn
a0
a2
a4
a6
s n1
a1
a3
a5
a7
s n2
b1
s n3
c1
b2 c2
b3
b4
c3
表中
s2
d1
d2
d3
s1
e1
e2
s0
f1
b1
a1a 2 a 0a 3 a1
,b2
a1a 4 a 0a 5 a1
, b3
a1a 6 a 0a 7 a1
,
c1
b1a 3 a1b2 b1
6-劳斯判据

注意: 由于模型的近似化,且系统的参数又处在不断 的微小变化中,所以,临界稳定实际上也应视为不稳定。
3-2 劳思稳定性判据
[判据] (1) 系统稳定的必要条件:特征方程中所有项的系数均大 于 0 (同号);只要有1项等于或小于 0 ,则为不稳定系 统。
(2)系统稳定的充分条件:劳思表第一列元素均大于0 (同号) 。
s0 7
5 分母总是上一行第一个元素
8 再令正无穷小量ε趋近于6 一行可同乘或同除某正数
0,得到真正的劳斯表如下。7 第一列出现零元素时,
用正无穷小量ε代替。
系统稳定的必要条件: 特征方程各项系数 均大于零! 同号! 有正有负一定不稳定! 缺项一定不稳定!
-s2-5s-6=0稳定吗?
系统稳定的充分条件:
系统在虚轴上有重根, 响应中含有tsin(t)成分, 是发散的。
3-3 劳思判据的应用举例
例3.8 试分析如下系统的稳定性,其中K>0
s 1
s 1
R(s)
_
k
ss 1
Y(s)
系统的特征方程为:
1
Gs
1
Ks 1 ss 1s 1
0
系统稳定否? 不稳定!
例3.9 焊接控制(p256例6.5)
Ks a
劳斯表情况一 例3.3、含参变量的例子:设系统特征方程为:
s3+s2+s+K=0; K不等于1或0
劳 s3 1 1
s2 1 K
斯 s1 1-K 0 表 s0 K
参数取值影响稳定性!
于是: K小于0,系统不稳定;
K大于1,系统不稳定;
K大于0且小于1时,系 统稳定。
例3.4 设系统特征方程为: 劳斯表情况二 s6+2s5+3s4+4s3+5s2+6s+7=0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3-17 已知单位负反馈系统的开环传递函数为:)
2)(1()(++=
s s s K s G ,试应用劳斯判据确定欲使闭环系统稳定时开环放大倍数K 的取值范围 解:由开环传递函数可得到系统特征方程:0232
3=+++K s s s ,写出劳斯表 K s K s K s s 0
1
2
3
32321- 则有03-
20>>K K 且 所以60<<K
补充题:设系统特征方程为05025482422
345=--+++s s s s s ;试用劳斯稳定判据判别系统稳定性,并确定在右半平面根的个数及纯虚根
解:列出劳斯表: 50
07.11250
24096
8000
504822524101
234
5
----s s s s s s 由此可看出系统不稳定,在右半平面根的个数为1,同时存在共轭虚根
求解辅助方程可得到共轭虚根05048224=-+s s ,令y s =2
则有0504822=-+y y 解得y=1,-25
j s s 5,14,32,1±=±=
其它题型:给出开环传递函数,求解系统稳定性,并判断在右半平面根的个数
1、由开环传递函数写出闭环传递函数,进而得到系统特征方程
2、根据特征方程写出劳斯阵列,并判断系统稳定性
3、第一列符号改变的次数为s右半平面根的个数
4、若存在全0行,则有共轭虚根,可根据辅助方程求得共轭虚根。
