物理专业英语洛伦兹力原文和翻译
物理洛伦兹力知识点

物理洛伦兹力知识点嘿,朋友们!今天咱来聊聊物理里超有意思的洛伦兹力呀!你说这洛伦兹力,就像是一个神秘又调皮的小精灵。
它呀,只在磁场里才会现身呢!当电荷在磁场中穿梭时,这个小精灵就会跑出来和电荷“玩耍”,给它施加一个力。
咱可以把磁场想象成一个巨大的游乐场,电荷就是在里面玩耍的小朋友。
而洛伦兹力呢,就是游乐场里的各种设施,会让小朋友的运动轨迹发生变化。
你想想看呀,要是没有这个洛伦兹力,电荷就会直直地跑过去,多没意思呀!但有了它,一切就变得有趣多啦。
电荷可能会被它带着转圈,或者改变方向。
那洛伦兹力到底有多大呢?这可就跟电荷的大小、速度以及磁场的强度有关系啦。
就好像小朋友在游乐场里玩不同的设施,受到的“乐趣”程度也不一样呢。
而且哦,洛伦兹力还有个很特别的地方,它永远和电荷的运动方向垂直。
这就好像有个小伙伴总是在你侧面推你,让你改变方向,但又不会让你停下来。
咱生活中也有很多类似洛伦兹力的现象呢!比如说,你有没有见过那种会拐弯的水流?水在流动的时候,要是遇到了磁场之类的影响,是不是就像电荷在磁场中一样会改变方向呀?学习洛伦兹力可不能马虎哦!这可是物理世界里的一个重要角色呢。
要是能把它搞清楚,那对我们理解很多物理现象都有很大的帮助。
你说,要是没有洛伦兹力,那这个世界会变成什么样呢?很多电器设备可能都没法正常工作啦,那多不方便呀!所以呀,我们得好好感谢这个神奇的洛伦兹力,是它让我们的世界变得更加丰富多彩。
洛伦兹力虽然有点复杂,但只要我们用心去学,就一定能掌握它。
就像攻克一个难关,只要我们有决心,有毅力,就一定能成功。
咱可不能被它吓倒,要勇敢地去探索,去发现它的奥秘呀!总之呢,洛伦兹力是个非常有趣又非常重要的物理概念,我们可得好好对待它,让它为我们打开更多物理世界的大门!。
大学物理洛伦兹力、B-S定律分解
B
的方向。
(2)B线的密度给出 B 的大小。
各种典型的磁感应线的分布:
直线电流的磁感线
圆形电流的磁感线
直螺线管电流的磁感线
环形螺线管电流的磁感线
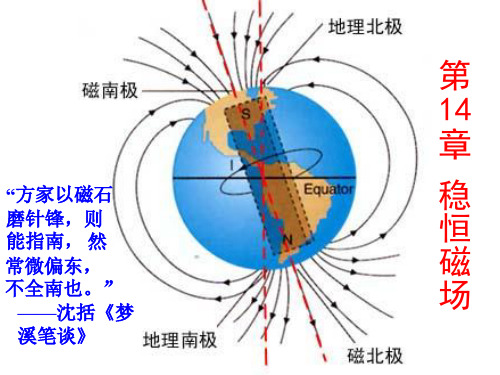
绚丽多彩的极光
在地磁两极附近,由于磁感线与地面垂直,外层空 间入射的带电粒子可直接射入高空大气层内,它们 和空气分子的碰撞产生的辐射就形成了极光。
星 空 极 光
B线的特点:
(1)任何两条 B 线不相交。 (2)每一条B 线都闭合
磁场是涡旋场、无源场。
(3)B线和闭合电流回路互相套连,B 线
方向与 I 方向服从右手螺旋法则。
§14-2 毕奥-萨伐尔定律(Biot—Savart law)
一、B-S定律
d B
电流元 Idl在P点产生的磁
生产和科研中经常 要把样品放在均匀 磁场中作测试, 利用 亥姆霍兹线圈获得 均匀磁场比较方便。
3、密绕载流直螺线管轴线上的磁场
密绕→将每匝看作一个圆形
R
线圈。
N匝
(推导见书p72-73,自学)
结论:轴线上磁场方向与电流绕向满足右螺关系。
(1)对无限长(l>>R)密绕载流直螺线管轴
线上一点:
B 0nI
dl ad / sin2
B
0 I 4a
2
1
s
ind
I
2
Idl
r
l
Oa
1
B
0 I 4a
(cos1
cos2 )
1 、 2分别是直导线两端的电流
P B
元 与它们到P点的径矢之夹角。 B的方向,与I 流向成右螺关系。
应用物理专业英语English Vocabulary

Chapter 8adjacent 邻近的barrier 障碍物compensation 补偿板double slit 双缝electromagnetic 电磁的grating diffraction 光栅衍射illumination 照明,照亮,阐明intensity 强度missing order 缺级monochromatic 单色的,单频的opaque 不透明的prediction 预言prevail 优胜,主导scatter 散射speck 斑点spherical 球的,球形的substitute 替代subtend 对应于(张角)transparency 透明,透明度Chapter 9analyzer 检偏器antenna 天线arbitrary 任意的,专断的circular polarized light 圆偏振光crossed polaroids 正交偏振片eliminate 排除,消除,除去elliptical 椭圆的,省略的incident 入射的molecule 分子oscillatory 摆动的orientation 取向partially polarized 部分偏振光polaroid sheet 偏振片polarizer 起偏器preferential 优先的propagation 声波symmetry 对称性transverse 横向的,横断的unpolarized light 自然光Chapter 10 anode 阳极cathode ray 阴极射线conversion factor 变换量current-varying solenoid 载流线圈curvature 曲度cyclotron 螺旋加速器cylindrical 圆柱体differential 微分的discharge tube 放电管electric field intensity 电场强度electromotive force 电动势electric motor 电动机electromagnetic 电磁铁electrostatic 静电的field lines 场力线flux 通量ferromagnetic 铁磁性galvanometer 电流计impurity 杂质integration 积分loop 环Lorentz Force 洛伦兹力magnetic monopole 磁单极magnetron 磁控管magnetic induction磁感应强度oscillator 震荡器permanent magnet 永磁铁polarity 极性repel 排斥resistivity 电阻率spiral 螺旋的test charge 试验电荷trace 轨迹uniform electric field 匀强电场Chapter 11accidentally 偶然地antiparallel 反平行bubble chamber 气泡室compass needle 罗盘针current-varying solenoid 载流线圈deflect 偏转eddy current 涡电流electromagnetic induction 电磁感应electric current 电流episode 插曲gyroscope 回转仪induced EMF 感应电动势induced current 感应电流insulation 绝缘intuitive 直观的laminate 分成薄片monopole 单极neutron star 中子星permanent magnet 永磁铁prestige 威信positron正电子rate of change 时间变化率repel 排斥rudimentary 基础的,初步的seismograph 地震仪sinusoidal 正弦的summarize 总结symmetric 对称的tenacity 韧性transformer 变压器vicinity 临近,周围voltmeter 伏特计vortex 漩涡Chapter 12annihilation 湮没angular momentum 角动量classical 经典的classical physics 经典物理学contraction 收缩,缩减deceive 欺骗delay-controlled exponential 缓发中子控制指数disappear 不见,失踪exponential 指数的General Theory of Relativity 广义相对论inertial reference frame 惯性参考系intrinsic 固有的,内在的,本质的meter stick 米尺microscopic 微观的Newtonian 牛顿的,牛顿学说的paradox 自相矛盾者platform 平台,站台postulate 假设relativistic physics 相对论性物理学satellite 卫星simultaneity 同时性spectrum 光谱special Relativity 狭义相对论subtle 稀薄的,精巧的time dilation时间膨胀transformation 转换vacuum 真空,真空状态Chapter 13amplitude 振幅barrier penetration 势垒穿透binding energy 结合能boundary 边界classical mechanics 经典力学confine 限制cosmic rays 宇宙射线de Broglie wavederivative 派生的,导出的decay 放射性衰变dimensional 空间的,维的discrete 不连续的distribution 分布double slit 双缝duality 双重性,二象性electron cloud 电子云energy level splitting 能及分裂entangle 纠缠,卷入excited energy level 激发能级exponentially 以指数级的形式地external force 外力fission 裂变ground state 基态half-life 半衰期harmonic 谐波insulator 绝缘体infinite potential well 无限深势阱integration 积分interference pattern 干涉图样judicious 明智的kinetic 动力学的,运动的leak through 漏过macroscopic 宏观的molecular 分子的muon 介子neutron 中子nucleus 原子核nuclear fission 核子分裂out of phase 反相peak 峰phase shift 相移photon 光子piezoelectric 压电的potential barrier 势垒potential well 势阱probability 概率,几率proportional 成比例的probability density 几率密度proton 质子quantum mechanics 量子力学quantization 量子化quantum 定量,量子quantum equivalence 量子当量quantum physics 量子物理学quantum state 量子态tabletop 桌面transition 跃进,迁移trapped electron 俘获电子tunneling effect 隧道效应wave function 波函数wave-particle duality波粒二象性Chapter 14absorption 吸收acronym 字首缩略词amplification 放大aperture 孔径bumper 缓冲器,减震器carve 雕刻coherent 相干的,一致的convergence 会聚性covalent bonds 共价键density gradient 密度梯度depletion 耗散层,耗尽donor 施主,给予体energy gap 禁带energy band 能带fluorescent 荧光的helium 氦hologram 全息inelastic 无弹性的kinematic 运动学的majority 多数metastable 亚稳态的metallic 金属(性)的minority 少数mono-chromatic 单色的optical pump 光泵pentavalency 五价population inversion 粒子数反转propagation 传播rectification 整流resistivity 抵抗力,电阻率semiconductor 半导体spiraling 螺旋式spontaneous 自发的stimulate 受刺激tetravalene 四价threshold 阈值triode 三极管valance electron 价电子Chapter 15antiquark 反夸克baryon 重子boson 波色子chain reaction 链式反应deuterium 氘flavor 味fusion 聚变hadron 强子ionization 电离lepton 轻子nuclear fission 原子核裂变neutron 中子penetrate 穿透proton 质子radioactive decay 放射性衰变radioisotope 放射性同位素。
物理学名词中英文索引-苏科版九年级物理上册教案

物理学名词中英文索引-苏科版九年级物理上册教案一、力和运动中文名词英文名词力force张力tension弹力elastic force摩擦力friction阻力resistance重力gravity合力resultant force分力component force动量定理momentum theorem牛顿第一定律Newton’s first law牛顿第二定律Newton’s second law牛顿第三定律Newton’s third law惯性inertia计算机模拟computer simulation二、力的作用中文名词英文名词工作work功率power机械效率mechanical efficiency能量energy势能potential energy动能kinetic energy机械能mechanical energy热能thermal energy等效能equivalent energy能量定理energy theorem三、电现象和电路中文名词英文名词电荷charge电场electric field静电场electrostatic field电势差potential difference电位potential电容capacitance并联电容parallel capacitance串联电容series capacitance电流current电阻resistance电阻率resistivity等效电阻equivalent resistance欧姆定律Ohm’s law布尔定理Kirchhoff’s law白炽灯泡incandescent bulb四、电磁现象中文名词英文名词电磁感应electromagnetic induction感应电流induced current感生电动势induced electromotive force 磁通量magnetic flux感应定律Faraday’s law楞次定律Lenz’s law感应电磁场induced electromagnetic field 交流电alternating current直流电direct current变压器transformer电源的交流和直流AC and DC power supply五、光学中文名词英文名词波长wavelength频率frequency光线light ray光束light beam反射reflection折射refraction透镜lens成像image formation高锟定理Gauss’s theorem光的折射refraction of light灯芯和LED filament and LED显微镜microscope以上是本文档所列举的物理学名词索引,可以为九年级物理上册学生和老师提供帮助,帮助他们更好的掌握物理学知识,完成物理学的学业。
《洛伦兹力》 讲义

《洛伦兹力》讲义一、什么是洛伦兹力在物理学中,当带电粒子在磁场中运动时,会受到一种力的作用,这种力被称为洛伦兹力。
洛伦兹力是由荷兰物理学家亨德里克·安东·洛伦兹首先提出的。
要理解洛伦兹力,我们先来看看带电粒子的运动。
带电粒子可以是电子、质子等,它们带有一定的电荷量。
当这些带电粒子在没有磁场的情况下做直线运动时,它们遵循牛顿运动定律。
然而,当存在磁场时,情况就变得复杂了。
磁场是一种特殊的物质,它具有能量和动量。
带电粒子在磁场中运动时,会与磁场发生相互作用,从而受到洛伦兹力的影响。
洛伦兹力的大小与带电粒子的电荷量、速度以及磁场的磁感应强度有关。
具体来说,洛伦兹力的大小可以用公式 F =qvBsinθ 来表示,其中 F 是洛伦兹力的大小,q 是带电粒子的电荷量,v 是带电粒子的速度,B 是磁场的磁感应强度,θ 是速度方向与磁感应强度方向的夹角。
从这个公式可以看出,如果带电粒子的运动方向与磁场方向平行(即θ = 0 或 180°),那么洛伦兹力为零;只有当带电粒子的运动方向与磁场方向不平行时,才会受到洛伦兹力的作用。
二、洛伦兹力的方向洛伦兹力的方向可以用左手定则来判断。
左手定则的具体方法是:伸出左手,让磁感线垂直穿过手心,四指指向正电荷运动的方向(或者负电荷运动的反方向),那么大拇指所指的方向就是洛伦兹力的方向。
需要注意的是,洛伦兹力的方向始终与带电粒子的运动方向垂直,所以洛伦兹力永远不做功。
这是因为做功的条件是力在力的方向上有位移,而洛伦兹力与运动方向垂直,在运动方向上没有分力,也就不会做功。
举个例子,如果一个带正电的粒子以速度 v 向右运动,磁场方向垂直纸面向里,那么根据左手定则,洛伦兹力的方向向上。
三、洛伦兹力与电场力的区别在研究带电粒子的运动时,我们经常会遇到洛伦兹力和电场力。
虽然它们都是对带电粒子的作用力,但它们有很多不同之处。
首先,产生的原因不同。
电场力是由电场对带电粒子的作用产生的,只要带电粒子处于电场中,就会受到电场力的作用。
洛伦兹力——精选推荐

洛伦兹⼒洛伦兹⼒在这篇⽂章内,⽮量与标量分别⽤粗体与斜体显⽰。
例如,位置⽮量通常⽤表⽰;⽽其⼤⼩则⽤来表⽰。
不同电荷量的带电粒⼦,由于磁场(磁场⽅向从银幕内指出来)的影响,感受到洛伦兹⼒的作⽤,所呈现的可能运动轨道。
由于磁场的影响,电⼦射束的移动路径呈圆形。
电⼦经过的路径会有紫⾊光发射出来。
这是因为电⼦与玻璃球内的⽓体分⼦碰撞⽽产⽣的现象。
在电动⼒学⾥,洛伦兹⼒ (Lorentz force) 是运动于电磁场的带电粒⼦所感受到的作⽤⼒。
洛伦兹⼒是因荷兰物理学者亨德⾥克·洛伦兹⽽命名。
根据洛伦兹⼒定律,洛伦兹⼒可以⽤⽅程,称为洛伦兹⼒⽅程,表达为;其中,是洛伦兹⼒,是带电粒⼦的电荷量,是电场,是带电粒⼦的速度,是磁场。
洛伦兹⼒定律是⼀个基本公理,不是从别的理论推导出来的定律,⽽是由多次重复完成的实验所得到的同样的结果。
感受到电场的作⽤,正电荷会朝着电场的⽅向加速;但是感受到磁场的作⽤,按照右⼿定则,正电荷会朝着垂直于速度和磁场的⽅向弯曲(详细地说,假设右⼿的⼤拇指与同向,⾷指与同向,则中指会指向的⽅向)。
洛伦兹⼒⽅程的项⽬是电场⼒项⽬,项⽬是磁场⼒项⽬。
处于磁场内的载电导线感受到的磁场⼒就是这洛伦兹⼒的磁场⼒分量。
洛伦兹⼒⽅程的积分形式为。
其中,是积分的体积,是电荷密度,是电流密度,是微⼩体元素。
洛伦兹⼒密度是单位体积的洛伦兹⼒,表达为:。
历史亨德⾥克·洛伦兹1892年,荷兰物理学家亨德⾥克·洛伦兹提出洛伦兹⼒的概念。
但是,在洛伦兹之前,就已经有发掘出洛伦兹⼒⽅程的形式,特别是在詹姆斯·麦克斯韦的1861 年论⽂《论物理⼒线》⾥的公式 (77):、、;其中,、、分别为电场的三个分量,是磁导率,、、分别为导电体的移动速度的三个分量,、、分别为磁场强度的三个分量,、、分别为磁⽮势的三个分量,是电势。
后来,在他的 1864 年论⽂《电磁场的动⼒学理论》⾥,麦克斯韦将这公式列为麦克斯韦⽅程组的⼋个原本⽅程中的⽅程(D) :;其中,是速度,是磁场强度,是磁导率,是磁⽮势,是电势。
3.5洛伦兹力(人教版)

θ为B和I 之间的夹角
B B1
B2
θ
1、磁场对通电导线的作用力 大小: F ILB sin 安培力: 方向: 左手定则 运用左手定则判断安培力的方向
B F B
I
I
30 °
I
F
为什么磁场对通电导线有作用力?
复习回顾
1、磁场对通电导线的作用力 大小: F ILB sin 安培力: 方向: 左手定则
B
D.带电粒子速度方向不变
课堂练习
电荷量为+q的粒子在匀强磁场中运动,下 列说法正确的是( )
B
A.只要速度大小相同,所受洛伦兹力就相同 B.如果把+q改为-q,且速度反向,大小不 变,则洛伦兹力的大小方向不变 C.洛伦兹力方向一定与电荷速度方向垂直,磁 场方向一定与电荷运动方向垂直 D.粒子的速度一定变化
显像管的工作原理:
课堂练习
来自宇宙的质子流,以与地球表面垂直 的方向射向赤道上空的某一点,则这些质子 在进入地球周围的空间时,将( B ) A.竖直向下沿直线射向地面 B.相对于预定地面向东偏转 C.相对于预定点稍向西偏转 D.相对于预定点稍向北偏转
V
课堂练习
当一带正电q的粒子以速度v沿螺线管中轴 线进入该通电螺线管,若不计重力,则( CD ) A.带电粒子速度大小改变 B.带电粒子速度方向改变 C.带电粒子速度大小不变
v
F安 ILB B(nqvS) L (3)这段导线内的自由电荷数 N nSL
(4)每个电荷所受的洛伦兹力
I v
F
v
v
F安 B(nqvS) L F洛 qvB N nSL
洛伦兹力大小
电荷量为q的粒子以速度v运动时,如 果速度方向与磁感应强度方向垂直,那么 粒子所受的洛伦兹B
物理洛伦兹力-概述说明以及解释

物理洛伦兹力-概述说明以及解释1.引言1.1 概述在物理学中,洛伦兹力是一种与带电粒子在电场和磁场中的相互作用有关的力。
这种力是由19世纪的荷兰物理学家洛伦茨提出的,他发现当带电粒子移动时,会受到电场和磁场的双重影响,从而产生一种受力。
洛伦茨力的存在和性质对于解释许多物理现象和现代科学的发展都至关重要。
本文将会对洛伦兹力的概念、公式以及其在物理学中的应用进行深入探讨,同时也将探讨洛伦兹力在现代科学中的作用以及展望其未来的发展。
通过本文的阐述,读者将能更全面地了解洛伦兹力对于物理学和科学发展的重要性。
1.2文章结构1.2 文章结构本文将分为以下几个部分来详细介绍物理洛伦兹力的相关概念、公式和应用。
首先,在引言部分将对物理洛伦兹力进行简要概述,介绍文章的结构和目的。
接下来,在正文部分将详细解释洛伦兹力的概念,介绍洛伦兹力的公式以及讨论洛伦兹力在实际应用中的重要性。
最后,在结论部分将总结洛伦兹力在物理学中的重要性,并探讨其在现代科学中的作用,展望未来洛伦兹力的发展方向。
通过以上分析和讨论,读者将能够更深入地了解物理洛伦兹力的相关知识,为其在科学研究和实践中的应用提供更多参考和启发。
1.3 目的本文的主要目的是探讨物理学中的洛伦兹力,并深入了解其在电磁学和磁场中的重要性。
通过对洛伦兹力的概念、公式和应用进行全面的分析和讨论,我们希望读者能够更加深入地理解洛伦兹力在物理学领域中的作用和意义。
此外,本文也将探讨洛伦兹力在现代科学研究中的应用以及未来的发展趋势,以便读者能够更好地认识和理解这一重要力学概念的前沿研究和应用领域。
通过阐述洛伦兹力的重要性和影响,本文旨在引发读者对物理学领域的兴趣和思考,促进科学研究和相关学科的发展。
2.正文2.1 洛伦兹力的概念洛伦兹力是指在电磁场中,带电粒子受到的力。
这个力是由荷电粒子在电场和磁场中相互作用而产生的。
洛伦兹力的大小和方向取决于带电粒子的电荷量、速度以及电场和磁场的强度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
物理专业英语组别:19组专业:物理学姓名:9.5 THE LORENTZ FORCEA charge moving in a magnetic field experiences a force which we shall call magnetic . The force is determined by the chang q,its velocity v ,and the magnetic inductionB at the point where the charge is at the moment of time being considered .The simplest assumption is that the magnitude of the force F is proportional to each of the three quantities q,v,and B .In addition ,F can be expected to depend on the mutual orientation of the vectors v and B .The direction of the vector F should be determined by those of vectors v and B.To”construct”che vector F form the scalar q and the vectors v and B ,let us find the vector of v and B and then multiply then multiply the result obtained by the scalar q.The result is the expressionq[vB (9.31)It has been established experimentally that the force F acting on a charge moving in a magnetic field is determined by the formulaFa=kq[vB] (9.32)Where k is a proportionality constant depending on the choice of the units for the quantities in the formula .It must be borne in mind that the reasoning which led us to expression(9.31)must by no means be considered as the derivation of Eq.(9.32)This reasoning does not have conclusive force .Its aim is to help us memorize Eq(9.32).The correctness of this equation can be established only experimentally .We must note that Eq.(9.32)can be considered as a definition of The magnetic induction B.The unit of magnetic induction B -the tesla-is determined so that the proportionality constant k in Eq.(9.32)equals unity .Hence,In SI units ,this equation becomesF=q[vB] (9.33)The magnitude of the magnetic force isF=qvBsin∂(9.34) Where ∂is the angle between the vectors v and B .It can be seen from Eq.(9.34) that a charge moving along the lines of a magnetic field does not experience the action of a magneticforce .The magnetic force is directed at right angles to the plane containing the vectors v and B.If the charge q is positive ,then direction of the force coincides with that of the vector [vB].Where q is negative ,the directions of the vectors F and [vB] are opposite (Fig.9.6).Since the magnetic force is always directed at right angles to the velocity of a charged particle ,it does no work on the particle .Hence ,we cannot change the energy of a charged particle by acting on it with a constant magnetic field .The force exerted on a charged particle that is simultaneously in an electric and a magnetic field isF=qE+q[vB] (9.35)This expression was obtained from the results of experiments by the Dutch physicist Hendrik Lorentz (1853~1928)and is called the Lorentz force.Assume that the charge q is moving with the velocity v parallel to a straight infinite wire along which the current I flows(Fig.9.7).According to Eqs .(9.30)and(9.34),the charge in this case experiences a magnetic force whose magnitude isF=qvB=qv b240I πμ (9.36) Where b is the distance from the charge to the wire .The force is directed toward the wire when charge is positive if the directions of the current and motion of the charge are the same ,and away from the wire if these directions are opposite (see Fig.9.7).When the charge is negative ,the direction of the force is reversed ,the other conditions being equal.Let us consider two like point charges q 1and q2 moving along parallel straight lines with the same velocity v that is much smaller than c (Fig.9.8).When v ∝c,the electric field does not virtually differ form the field of stationary charges (see Sec 。
9.3).Therefore the magnitude of the electric force F e exerted on the charges can be considered equal toF e ,1=F e ,2=F e =041πε221q rq (9.37) Equations (9.21)and (9.33)give us the following expression for the magnetic force m F exerted on the charges :222102,1,m 4r v q q F F F m m πμ=== (9.38) (the position vector r is perpendicular to v). Let us find the ratio between the magnetic and electric forces It follows from Eqs.(9.37)and(9.38)that22200m cv v Fe F ==με (9.39) [see Eq(9.15)].We have obtained Eq.(9.39) on the assumption that v<<c.This ratio holds ,however,with any v ,s.The forces F e and m F are directed oppositely .Figure 9.8 has been drawn for like and positive charges.For like negative charges, the directions of the forces will remain the same ,while the directions of the electric and magnetic forces will be the reverse of those shown in the figure .Inspection of Eq.(9.39)shows that the magnetic force is weaker than the Coulomb one by a factor equal to the square of ratio of the speed of the charge to that of light.The explanation is that the magnetic interaction between moving charges is a relativistic effect. Magnetism would disappear if the speed of light were infinitely great.9.5 洛伦兹力移动的电荷在磁场中收到磁场力的作用,这种力是由电荷的电量q,速度v和在磁场中所在的位置和该时刻所对应的磁感应强度B决定。
