SPSS回归模型分析答案及解题思路
SPSS—回归—多元线性回归结果分析
SPSS—回归—多元线性回归结果分析（二），最近一直很忙，公司的潮起潮落，就好比人生的跌岩起伏，眼看着一步步走向衰弱，却无能为力，也许要学习“步步惊心”里面“四阿哥”的座右铭：“行到水穷处”，”坐看云起时“。
接着上一期的“多元线性回归解析”里面的内容，上一次，没有写结果分析，这次补上，结果分析如下所示：结果分析1：由于开始选择的是“逐步”法，逐步法是“向前”和“向后”的结合体，从结果可以看出，最先进入“线性回归模型”的是“price in thousands"建立了模型1，紧随其后的是“Wheelbase"建立了模型2，所以，模型中有此方法有个概率值，当小于等于0.05时，进入“线性回归模型”（最先进入模型的，相关性最强，关系最为密切）当大于等0.1时，从“线性模型中”剔除结果分析：1：从“模型汇总”中可以看出，有两个模型，（模型1和模型2）从R2 拟合优度来看，模型2的拟合优度明显比模型1要好一些（0.422>0.300）2：从“Anova"表中，可以看出“模型2”中的“回归平方和”为115.311，“残差平方和”为153.072，由于总平方和=回归平方和+残差平方和，由于残差平方和(即指随即误差，不可解释的误差）由于“回归平方和”跟“残差平方和”几乎接近，所有，此线性回归模型只解释了总平方和的一半，3：根据后面的“F统计量”的概率值为0.00，由于0.00<0.01，随着“自变量”的引入，其显著性概率值均远小于0.01，所以可以显著地拒绝总体回归系数为0的原假设，通过ANOVA方差分析表可以看出“销售量”与“价格”和“轴距”之间存在着线性关系，至于线性关系的强弱，需要进一步进行分析。
结果分析：1：从“已排除的变量”表中，可以看出：“模型2”中各变量的T检的概率值都大于“0.05”所以，不能够引入“线性回归模型”必须剔除。
从“系数a” 表中可以看出：1：多元线性回归方程应该为：销售量=-1.822-0.055*价格+0.061*轴距但是，由于常数项的sig为（0.116>0.1) 所以常数项不具备显著性，所以，我们再看后面的“标准系数”，在标准系数一列中，可以看到“常数项”没有数值，已经被剔除所以：标准化的回归方程为：销售量=-0.59*价格+0.356*轴距2：再看最后一列“共线性统计量”，其中“价格”和“轴距”两个容差和“vif都一样，而且VIF 都为1.012，且都小于5，所以两个自变量之间没有出现共线性，容忍度和膨胀因子是互为倒数关系，容忍度越小，膨胀因子越大，发生共线性的可能性也越大从“共线性诊断”表中可以看出：1：共线性诊断采用的是“特征值”的方式，特征值主要用来刻画自变量的方差，诊断自变量间是否存在较强多重共线性的另一种方法是利用主成分分析法，基本思想是：如果自变量间确实存在较强的相关关系，那么它们之间必然存在信息重叠，于是就可以从这些自变量中提取出既能反应自变量信息（方差），而且有相互独立的因素（成分）来，该方法主要从自变量间的相关系数矩阵出发，计算相关系数矩阵的特征值，得到相应的若干成分。
《SPSS数据分析教程》中的回归分析解释
多元线性回归的模型
• 多元线性回归的模型为： Y = ¯0 +¯1 X1 + ¯2 X2 + +¯p Xp +²
• 回归系数的估计和简单线性回归据分析教程》中的回归分 析解释
回归方程的显著性检验
与一元的情形一样，上面的讨论是在响应变 量Y与预测变量X之间呈现线性相关的前提 下进行的，所求的经验方程是否有显著意 义，还需对X与Y间是否存在线性相关关系 作显著性假设检验，与一元类似，回归方 程是否有显著意义，需要对回归参数 ¯0,¯1,,¯p进行检验。
《SPSS数据分析教程》中的回归分 析解释
• F检验的H 0被拒绝，并不能说明所有的自变 量都对因变量Y有显著影响，我们希望从回 归方程中剔除那些统计上不显著的自变量， 重新建立更为简单的线性回归方程，这就 需要对每个回归系数做显著性检验。
• 即使所有的回归系数单独检验统计上都不 显著，而F检验有可能显著，这时我们不能 够说模型不显著。这时候，尤其需要仔细 对数据进行分析，可能分析的数据有问题， 譬如共线性等。
• 打开数据文件，选择【分析】→【回归】 →【线性】，如图8-3所示。把变量Y选入 到因变量框中，把变量X1到X6选入到自变 量框中，其他选项保留默认值。单击【确 定】。
《SPSS数据分析教程》中的回归分 析解释
《SPSS数据分析教程》中的回归分 析解释
结果及其解释
《SPSS数据分析教程》中的回归分 析解释
《SPSS数据分析教程》中的回归分 析解释
调整的R2
• 随着自变量个数的增多，不管增加的自变 量是否和因变量的关系密切与否，R方都会 增大；调整的R方是根据回归方程中的参数 的个数进行调整的R方，它对参数的增多进 行惩罚，调整R方它没有直观的解释意义， 它的定义为
SPSS实验6-回归分析
SPSS作业6：回归分析（一）回归分析多元线性回归模型的基本操作：（1）选择菜单Analyze－Regression－Linear；（2）选择被解释变量（能源消费标准煤总量）和解释变量（国内生产总值、工业增加值、建筑业增加值、交通运输邮电业增加值、人均电力消费、能源加工转换效率）到对应框中；（3）在Method框中，选择Enter方法；在Statistics框中，选择Estimates、Model fit、Covariancematrix、Collinearity diagnostics选项；在Plots框中，选择ZRESED到Y框，ZPRED到X框，再选择Histogram和Normal plot；（4）选择菜单Analyze－Non Test－1-Sanple K-S;选择菜单Analyze－Correlate－Brivariate;结果如下：Regression能源消费需求的多元线性回归分析结果（强制进入策略）（一）Model Summary bModel R R Square Adjusted R Square Std. Error of the Estimate1 .990a.980 .973 8480.38783a. Predictors: (Constant), 能源加工转换效率/%, 交通运输邮电业增加值/亿元, 工业增加值/亿元, 人均电力消费/千瓦时, 建筑业增加值/亿元, 国内生产总值/亿元b. Dependent Variable: 能源消费标准煤总量/万吨分析：被解释变量和解释变量的复相关系数为0.990，判定系数为0.980，调整的判定系数为0.973，回归方程的估计标准误差为8480.38783。
该方程有6个解释变量，调整的判定系数为0.973，，接近于1，所以拟合优度较高，被解释变量可以被模型解释的部分较多，未能解释的部分较少。
分析：由上可知，被解释变量的总离差平方和为5.882E10，回归平方和及均方分别为5.766E10和9.611E9，剩余平方和及均方分别为1.151E9和7.192E7，F检验统计量的观测值为133.636，对应的概率p值近似为0。
《SPSS数据分析教程》——回归分析
SPSS在回归输出结果的ANOVA表中给出SSR， SSE，SST和F统计量的取值，同时给出F值的显 著性值（即p值）。
用回归方程预测
在一定范围内，对任意给定的预测变量取值， 可以利用求得的拟合回归方程进行预测。其预 测值为：
回归模型的显著性的F检验
总平方和SST反映因变量Y的波动程度或者不确 定性，在建立了Y对X的回归方程后，总平方和 SST分解成回归平方和SSR与参差平方和SSE两 部分。其中SSR是由回归方程确定的，SSE是不 能由自变量X解释的波动，是由X之外的未加控 制的因素引起的。这样，SST中能够由自变量 解释的部分为SSR，不能由自变量解释的部分 为SSE。这样回归平方和越大，回归的效果越 好，据此构造F检验统计量
回归方程
回归关系一般用下列方程表示
Y=f(X1,X2,,Xp)+² (¤) Y被称作因变量，或者响应变量；而X1,X2,,Xp称 作自变量、控制变量、解释变量或者预测变量；而 f(.)则称为回归函数， ² 为随机误差或随机干扰，它 是一个分布与自变量无关的随机变量，我们常假定 它是均值为0的正态变量。
0
调整的R2
随着自变量个数的增多，不管增加的自变量是 否和因变量的关系密切与否，R方都会增大； 调整的R方是根据回归方程中的参数的个数进 行调整的R方，它对参数的增多进行惩罚，调 整R方它没有直观的解释意义，它的定义为
R调整
2
SSE /(n p 1) n 1 11 (1 R 2 ) SST /(n 1) n p 1
第九章 spss的回归分析
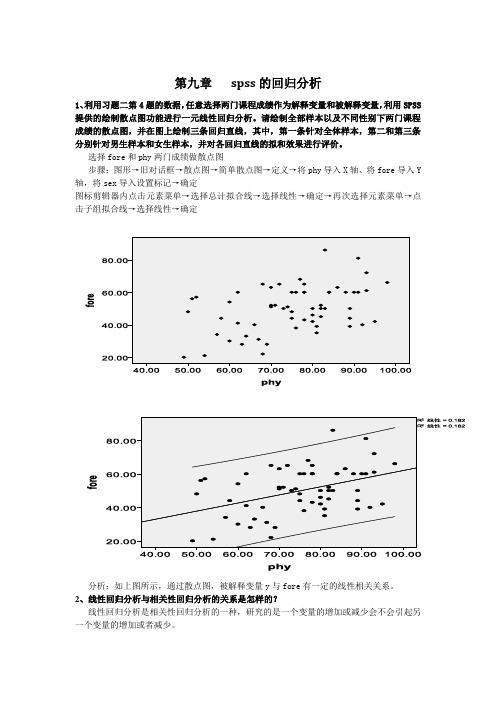
第九章spss的回归分析1、利用习题二第4题的数据，任意选择两门课程成绩作为解释变量和被解释变量，利用SPSS 提供的绘制散点图功能进行一元线性回归分析。
请绘制全部样本以及不同性别下两门课程成绩的散点图，并在图上绘制三条回归直线，其中，第一条针对全体样本，第二和第三条分别针对男生样本和女生样本，并对各回归直线的拟和效果进行评价。
选择fore和phy两门成绩做散点图步骤：图形→旧对话框→散点图→简单散点图→定义→将phy导入X轴、将fore导入Y 轴，将sex导入设置标记→确定图标剪辑器内点击元素菜单→选择总计拟合线→选择线性→确定→再次选择元素菜单→点击子组拟合线→选择线性→确定分析：如上图所示，通过散点图，被解释变量y与fore有一定的线性相关关系。
2、线性回归分析与相关性回归分析的关系是怎样的？线性回归分析是相关性回归分析的一种，研究的是一个变量的增加或减少会不会引起另一个变量的增加或者减少。
3、为什么需要对线性回归方程进行统计检验？一般需要对哪些方面进行检验？线性回归方程能够较好地反映被解释变量和解释变量之间的统计关系的前提是被解释变量和解释变量之间确实存在显著的线性关系。
回归方程的显著性检验正是要检验被解释变量和解释变量之间的线性关系是否显著，用线性模型来描述他们之间的关系是否恰当。
一般包括回归系数的检验，残差分析等。
4、SPSS多元线性回归分析中提供了哪几种解释变量筛选策略？包括向前筛选策略、向后筛选策略和逐步筛选策略。
5、先收集到若干年粮食总产量以及播种面积、使用化肥量、农业劳动人数等数据，请利用建立多元线性回归方程，分析影响粮食总产量的主要因素。
数据文件名为“粮食总产量.sav”。
步骤：分析→回归→线性→粮食总产量导入因变量、其余变量导入自变量→确定结果如图：Variables Entered/Removed bModel Variables Entered Variables Removed Method1 农业劳动者人数(百万人),总播种面积(万公顷), 风灾面积比例(%), 粮食播种面积(万公顷), 施用化肥量(kg/公顷), 年份a. Entera. All requested variables entered.b. Dependent Variable: 粮食总产量(y万吨)ANOVA bModel Sum of Squares df Mean Square F Sig.1 Regression 2.025E9 6 3.375E8 414.944 .000aResidual 2.278E7 28 813478.405Total 2.048E9 34a. Predictors: (Constant), 农业劳动者人数(百万人), 总播种面积(万公顷), 风灾面积比例(%),粮食播种面积(万公顷), 施用化肥量(kg/公顷), 年份b. Dependent Variable: 粮食总产量(y万吨)Coefficients aModel UnstandardizedCoefficients StandardizedCoefficientst Sig.B Std. Error Beta1 (Constant) -613605.817 230903.867 -2.657 .013年份304.688 119.427 .402 2.551 .016粮食播种面积(万公顷) .736 .782 .053 .942 .354总播种面积(万公顷) 1.939 .650 .111 2.984 .006施用化肥量(kg/公顷) 141.077 11.186 .755 12.612 .000风灾面积比例(%) -307.209 51.870 -.174 -5.923 .000-5.121 22.286 -.038 -.230 .820 农业劳动者人数(百万人)a. Dependent Variable: 粮食总产量(y万吨)分析：如以上4个表所示，影响程度来由大到小依次是风灾面积、使用化肥量、总播种面积和年份。
曲线回归估计的spss分析
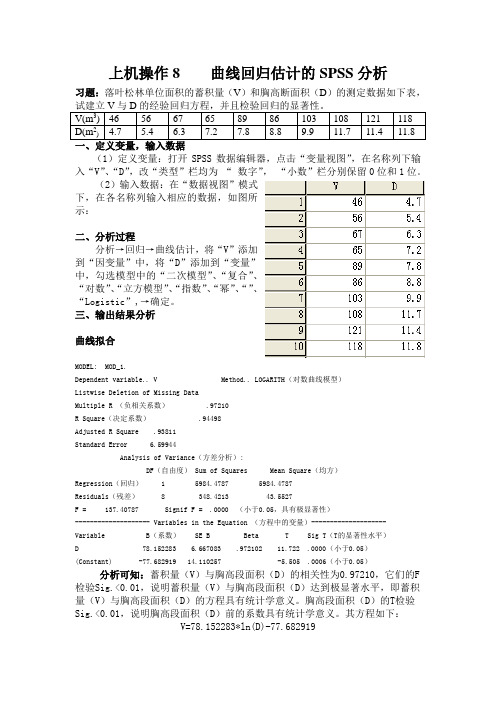
上机操作8 曲线回归估计的SPSS分析习题：落叶松林单位面积的蓄积量（V）和胸高断面积（D）的测定数据如下表，V(m3) 46 56 67 65 89 86 103 108 121 118D(m2) 4.7 5.4 6.3 7.2 7.8 8.8 9.9 11.7 11.4 11.8（1）定义变量：打开SPSS数据编辑器，点击“变量视图”，在名称列下输入“V”、“D”，改“类型”栏均为“数字”，“小数”栏分别保留0位和1位。
（2）输入数据：在“数据视图”模式下，在各名称列输入相应的数据，如图所示：二、分析过程分析→回归→曲线估计，将“V”添加到“因变量”中，将“D”添加到“变量”中，勾选模型中的“二次模型”、“复合”、“对数”、“立方模型”、“指数”、“幂”、“”、“Logistic”,→确定。
三、输出结果分析曲线拟合MODEL: MOD_1.Dependent variable.. V Method.. LOGARITH（对数曲线模型）Listwise Deletion of Missing DataMultiple R （负相关系数） .97210R Square（决定系数） .94498Adjusted R Square .93811Standard Error 6.59944Analysis of Variance（方差分析）:DF（自由度） Sum of Squares Mean Square（均方）Regression（回归） 1 5984.4787 5984.4787Residuals（残差） 8 348.4213 43.5527F = 137.40787 Signif F = .0000 （小于0.05，具有极显著性）-------------------- Variables in the Equation （方程中的变量）--------------------Variable B（系数） SE B Beta T Sig T（T的显著性水平）D 78.152283 6.667083 .972102 11.722 .0000（小于0.05）(Constant) -77.682919 14.110257 -5.505 .0006（小于0.05）分析可知：蓄积量（V）与胸高段面积（D）的相关性为0.97210，它们的F 检验Sig.<0.01，说明蓄积量（V）与胸高段面积（D）达到极显著水平，即蓄积量（V）与胸高段面积（D）的方程具有统计学意义。
SPSS专题2回归分析线性回归Logistic回归对数线性模型
(Constant)
410.150
18.817
21.797
.000
l i fe_expectancy_ femal e(year)
-4.896
.284
-.885
-17.252
.000
cl eanwateraccess_ rural (%)
-.237
a. Dependent Vari abl e: Di e before 5 per 1000
Kendall Spearman
Corre la ti ons
Kendal l's tau_b cl eanwateraccess_ rural (%)
cl eanwateracc
ess_rural (%)
Correl ati on Coeffi ci ent
1 . 00 0
Si g. (2-tai l ed)
Corre la ti ons
cl eanwateraccess_ rural (%)
Pearson Correl ati on Si g. (2-tai l ed)
cl eanwateracc e ss_ ru ra l(% )
l i fe_expectancy_ femal e(year)
N
Die before 5 per 1000
5
还有定性变量
下面是对三种收入对高一成绩和高一与初三成绩差的盒 形图
高一成绩与初三成绩之差 高一成绩
110
100
90
80
70
60
50
39 25
40
30
N=
11
27
12
1
2
spss思考与练习解析
1、 （1）操作：分析-回归-线性，因变量y,自变量x1，x2-确定。
得方程y=209.875+0.292x1-87.647x2。
（2）对回归方程的显著性检验：采用P 值法做检验，提出原假设H 0：β1=β2=0，构造统计量F=1)-p -SSE/(n SSR/p，p 是自变量个数此时是2，n 是样本个数14。
F 服从分布：F~F（2,11）。
从上图最后两列看出，在显著性水平α=0.05的条件下，p 值=sig<α，从而拒绝原假设，即在显著性水平α=0.05的条件下，认为y 与x1，x2有显著的线性关系。
对回归系数的显著性检验：采用P 值法做检验，提出原假设H 0：βi=0（i=1,2），构造统计量)1(t ~iii--=∧∧p n i c t σβ，其中1--=∧p n SSEσ。
从上图最后两列看出，在显著性水平α=0.05的条件下，ti （i=1,2）值（即看p 值=sig<α），从而拒绝原假设，即在显著性水平α=0.05的条件下，认为xi （i=1,2）对因变量y 的线性效果显著。
（3）操作：分析-回归-线性，因变量y,自变量x1，x2-统计量-回归系数-置信区间、估计。
得到βi 的1-α的置信区间为（）β1的置信水平为0.95的置信区间是（0.096,0.488）；β2的置信水平为0.95的置信区间是（-115.034，-60.261）；（4）回归方程的复相关系数SST SSRR2=0.885，比较接近1，说明回归方程拟合效果较好。
（5）操作：先把待预测的数据输入表格，分析-回归-线性，因变量y,自变量x1，x2，保存-预测值、残差项选择“未标准化”-预测区间（“均值”）。
得到E （y ）的点估计值是165.9985，置信水平为0.95的置信区间是（150.61813,181.37887）3、（1）操作：分析-回归-线性，因变量y,自变量x，确定。
得方程y=0.004x-0.831。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
电视广告费用和报纸广告费用对公司营业收入
的回归模型分析
SPSS录入数据：
本研究关注的是电视广告费用和报纸广告费用对公司收入的影响。
公司收入样本总数为8，M=93.75，SD=1.909；电视广告费用（X1）M=3.19，SD=0.961；报纸广告费用（x2）M=2.48，SD=0.911。
通过皮尔逊相关性分析得出因变量与自变量x1和x2的相关系数分别为（r=0.8，p=0.008）和（r=-0.02，p=0.48），说明公司收入与电视广告费用呈显著性正相关，而公司收入与报纸广告费用相关不显著。
以电视广告费用和报纸广告费用分别作为自变量，以公司收入作为因变量，进行线性回归。
具体结果见表1。
结果发现，电视广告费用对公司收入存在显著的正向影响（β=0.808，B=1.604，t=3.357，p<0.05,R2=0.653），即电视广告费用的增长会提升公司收入，且该模型能够解释结果的65.3%；报纸广告费用对公司收入不存在显著的正向影响（β=-0.021,t=-0.05,p=0.96）。
表1：广告费用对公司收入的回归结果表
注: 表格中呈现了预测变量的非标准化系数, 括号内是标准误。
以电视广告费用和报纸广告费用同时作为自变量，以公司收入作为因变量，则两个费用对公司收入存在显著的正向影响（β电视=1.153，B电视=2.29，t=7.532，p<0.05；β报纸=0.621，B报纸=1.301，t=4.057，p<0.052, R2=0.919），即电视广告和报纸广告费用的同时增长会提升公司收入，且该模型能够解释结果的91.9%。
共线性分析：VIF电视广告=1.448，VIF报纸广告=1.448，均小于5，说明电视广告和报纸广告之间共线性可能性较低。
思路及步骤：
1、公司收入样本总数为8，M=93.75，SD=1.909；电视广告费用M=3.19，SD=0.961；
报纸广告费用M=2.48，SD=0.911。
步骤：回归-线性，之后选择如下：【均值、标准差】
2、通过皮尔逊相关性分析得出因变量与自变量x1和x2的相关系数分别为
（r=0.808，p=0.008）和（r=-0.021，p=0.481），说明公司收入与电视广告费用呈显著性正相关，而公司收入与报纸广告费用相关不显著。
步骤，同上【皮尔逊相关性】：
3、以电视广告费用和报纸广告费用分别作为自变量，以公司收入作为因变量，
进行线性回归。
具体结果见表1。
结果发现，电视广告费用对公司收入存在显著的正向影响（β=1.064，t=3.357，p<0.05,R2=0.653），即电视广告费用的增长会提升公司收入，且该模型能够解释结果的65.3%；
步骤：回归-线性，之后如下【因变量分别采用“输入”方式进行回归】：
报纸广告费用对公司收入不存在显著的正向影响（β= -0.043 , t= -0.050, p=0.962）。
步骤：回归-线性，之后如下【因变量分别采用“输入”方式进行回归分析】：
4、
表1：广告费用对公司收入的回归结果表
注: 表格中呈现了预测变量的非标准化系数, 括号内是标准误。
步骤：回归-线性，之后选择如下【因变量共同采用“步进”方式进行回归分析】：
5、以电视广告费用和报纸广告费用同时作为自变量，以公司收入作为因变
=2.290，t=7.532，量，则两个费用对公司收入存在显著的正向影响（β
电视
p<0.05；β报纸=1.301，t=4.057，p<0.05, R2=0.919），即电视广告和报纸广告费用的同时增长会提升公司收入，且该模型能够解释结果的91.9%。
共线性分析：VIF电视广告=1.448，VIF报纸广告=1.448，均小于5，说明电视广告和报纸广告之间共线性可能性较低。
步骤，同上：。