整数规划解法-匈牙利 算法部分
运筹学04-整数规划-匈牙利解法
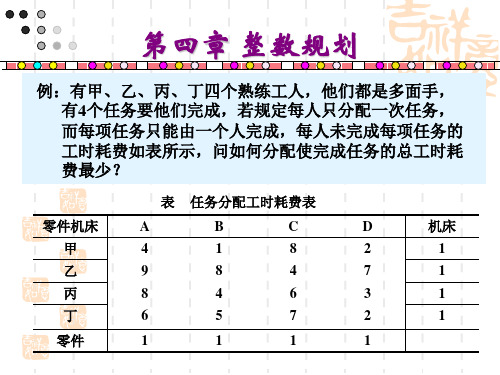
第四章 整数规划
B、任务分配问题的数学模型
设:xij为第i个工人分配去做第j项任务 aij为第i个工人为完成第 j 项任务时的工时消耗。则
1 当分配第j项任务给第i个工人时 x ij 0 当不分配第j项任务给第i个工人时
i,j=1,2,…,n
由于每人只允许分 配一项任务, 且每项任务只能由 一人来完成, 故其数学模型、目 标函数及约束条件 如下:
定理1
设一个任务分配问题的效率矩阵为{aij},若{aij}中每一行元素分别减去 一个常数ui,每一列元素分别减去一个常数vj,得到一个新的效率矩阵{bij}, 其中一个元素bij=aij-ui-vj,则{bij}的最优解等价于{aij}的最优解。
第四章 整数规划
定理2
若一个方阵中的一部分元素为零,一部分元素非零,则覆盖方阵中所 有元素的最少直线等于位于不同行、不同列的零元素最多个数。
m
m
a ij x ij
这样得到新效率矩阵的最优解,根据定理 1,他也是原问题的最优解。 (3)验证最优解的方法:设法用最少的直线数覆盖方阵中位于不同行、 不同列的零元素。 如果覆盖所有零元素的最少直线数等于m,则得到最优解,否则不是
第四章 整数规划
3、匈牙利解法的计算步骤: 第一步:效率矩阵的初始变换----零元素的获得 (1)行变换:找出每行的最小元素,该行各元素减去这个最小元素。 (2)列变换:找出每列的最小元素,该列各元素减去这个最小元素。
分配问题与匈牙利法
C (95 c ij )
解: M=95,令
10 0 C = 13 9
0 1 X= 0 0
3 8 12 5
22 17 16 15
5 0 5 7
指派问题的匈牙利法

第三步:作最少的直线覆盖所有0元素。 (1)对没有◎的行打√号; (2)对已打√号的行中所有含Ø元素的列打√号; (3)再对打有√号的列中含◎ 元素的行打√号;
(4)重复(2),(3)直到得不出新的打√号的行、列为止; (5)对没有打√号的行画横线,有打√号的列画纵线, 这就得到覆盖所有0元素的最少直线数 l 。l 应等于m, 若不相等,说明试指派过程有误,回到第二步(4),另 行试指派;若 l=m < n,须再变换当前的系数矩阵, 以找到n个独立的0元素,为此转第四步。
√
l =m=4 < n=5
2 ◎0 4 2 4 2 5 Ø0 3 ◎0 4 1 ◎0 1 3 4 Ø0 3 5 1 ◎0 2 3 0Ø 5
1 0 3 1 3 2 6 0 3 0 4 2 0 1 3 3 0 2 4 0 0 3 3 0 5
1 0 3 1 3 2 6 0 3 0 4 2 0 1 3 3 0 2 4 0 0 3 3 0 5
0Ø ◎0 3 0Ø 3 1 6 0◎ 2 Ø0 3 2 0Ø 0◎ 3 2 Ø0 2 3 ◎0 ◎0 4 4 0Ø 6
28
此问题有多个最优解
0◎ 0Ø 3 0Ø 3 1 6 0Ø 2 ◎0 3 2 0◎ 0Ø 3 2 ◎0 2 3 0Ø 0Ø 4 4 0◎ 6
Ø0 0Ø 3 ◎0 3 1 6 0Ø 2 ◎0 3 2 0◎ 0Ø 3 2 ◎0 2 3 0Ø 0◎ 4 4 0Ø 6
15 14 6 6 10
4 10 7 10 9
减去最小元素
5 0 2 0 2
2
3
0
0
指派问题的匈牙利算法

摘要在企业、公司的运营与管理中,管理者总是希望把人员最佳分派以发挥其最大工作效率,从而降低成本、提高效益。
然而,如果没有科学的方法是很难实现优化管理的,由此我们引入了指派问题。
指派问题多是求项目的工时最少,而很多情况下人们并不关心项目总工时的多少,而只关心项目能否在最短的时间内完成,即历时最少的指派问题。
这类问题研究的是n个人执行n项任务,执行每项任务的人数以及总的指派人项数均有限制,要求最优指派。
在运筹学中求解整数规划的指派问题通常是通过匈牙利算法来求解,但指派问题也可以归结为一个0-1整数规划问题,本文先对指派问题进行陈述,引出对实际问题的求解。
在指派问题的背景、描述中充分理解该问题,先运用匈牙利算法实现指派问题,然后再建立一个0-1整数规划模型,并运用matlab和lingo编译程序对问题进行编译,运用软件解决模型问题,最终实现指派问题在实际问题中的运用。
通过运用匈牙利算法和0-1整数规划同时对指派问题求解,我们发现用0-1整数规划的方法来求解可以更简单,也更方便程序的阅读和理解。
与此同时,我们还对0-1整数规划问题由整数数据深入研究到小数数据。
最后通过实例来说明运用matlab,lingo编译程序来解决整数规划问题的简便和有效性。
关键词:指派问题;匈牙利算法;0-1整数规划;matlab模型;lingo模型AbstractIn business, the company's operations and management, managers always want the best distribution of the staff to maximize their efficiency, reduce costs and improve efficiency. However, if there is no scientific method is difficult to achieve optimal management, which we introduced the assignment problem. Multi-assignment problem is to get the project working hours at least, and in many cases people do not care about how much the total project work, but only care about whether the project can be completed within the shortest possible time, that lasted for at least the assignment problem. Such problems is the n individual execution of tasks n, the number of people to perform each task and assign the total number of items are restricted to two people, requiring the optimal assignment. Integer programming in operations research for solving the assignment problem is usually solved by Hungarian algorithm, but the assignment problem can be reduced to a 0-1 integer programming problem, this paper first to make a statement on the assignment problem, leads to the solution of practical problems. Assignment problem in the background to fully understand the problem description, the first assignment problem using Hungarian algorithm, and then a 0-1 integer programming model and compiler using matlab and the lingo of the problem to be compiled using the software solution model problem Ultimately in the assignment of the application in practical problems. By using the Hungarian algorithm and the 0-1 integer programming to solve assignment problems simultaneously, we found that 0-1 integer programming method to solve a more simple and easier to read and understand the program. At the same time, we also 0-1 integer programming problem in-depth study by the integer data to a decimal data. Finally, an example to illustrate the use of matlab, lingo compiler to solve the integer programming problem is simple and effective.Keywords:assignment problem; Hungarian algorithm; 0-1 integer programming;matlab model; lingo model目录1. 问题陈述 (1)2. 指派问题的背景 (1)3. 指派问题的描述 (1)3.1 指派问题的一般形式 (1)3.2 问题的数学模型一般形式 (2)3.3 目标函数极大化的指派问题 (2)4.指派问题实现 (3)4.1 匈牙利算法 (3)4.1.1 匈牙利算法的理论基础 (3)4.1.2 匈牙利算法的实现步骤 (3)4.1.3 匈牙利算法实现指派问题 (4)4.2 0-1整数规划 (5)4.2.1 模型假设 (6)4.2.2 模型建立 (6)4.2.3 模型求解 (7)5. 问题的深入(0-1整数规划) (10)5.1 模型建立 (10)5.2 模型求解 (11)5.2.1 用matlab求解问题 (11)5.2.2 用lingo求解问题 (12)6. 结论 (14)6.1 总结概论 (14)6.2 具体分工.................................. 错误!未定义书签。
匈牙利算法和KM算法简介

KM算法
❖ 穷举旳效率-n!,我们需要愈加优异旳算法。 ❖ 定理: ❖ 设M是一种带权完全二分图G旳一种完备匹配,给
每个顶点一种可行顶标(第i个x顶点旳可行标用lx[i] 表达,第j个y顶点旳可行标用ly[j]表达),假如对全 部旳边(i,j) in G,都有lx[i]+ly[j]>=w[i,j]成立(w[i,j]表达 边旳权),且对全部旳边(i,j) in M,都有lx[i]+ly[j]=w[i,j] 成立,则M是图G旳一种最佳匹配。证明很轻易。
KM算法
❖ 对于任意旳G和M,可行顶标都是存在旳:
❖ l(x) = maxw(x,y)
❖ l(y) = 0 ❖ 欲求完全二分图旳最佳匹配,只要用匈牙利算法求
其相等子图旳完备匹配;问题是当标号之后旳Gl无 完备匹配时怎么办?1957年(居然比匈牙利算法 早???),Kuhn和Munkras给出了一种处理该问 题旳有效算法,用逐次修改可行顶标l(v)旳方法使相 应旳相等子图之最大匹配逐次增广,最终出现完备 匹配。
KM算法
❖ 修改措施如下:
❖ 先将一种未被匹配旳顶点u(u in {x})做一次增广路, 记下哪些结点被访问那些结点没有被访问。求出 d=min{lx[i]+ly[j]-w[i,j]}其中i结点被访问,j结点没有 被访问。然后调整lx和ly:对于访问过旳x顶点,将 它旳可行标减去d,对于全部访问过旳y顶点,将它 旳可行标增长d。修改后旳顶标仍是可行顶标,原 来旳匹配M依然存在,相等子图中至少出现了一条 不属于M旳边,所以造成M旳逐渐增广。
Empty Grass Wall
例题1 Place the Robots(ZOJ)
模型一
在问题旳原型中,草地,墙这些信 息不是我们所关心旳,我们关心旳 只是空地和空地之间旳联络。所以, 我们很自然想到了下面这种简朴旳 模型:
整数规划问题的求解

C o 3 4
x1
分支定界法
x2
A
Page 16
由 于Z 21 Z 1, 选 择 LP 21进 行 分 枝 , 增 加 约 束 x1 4及x1 5, 得 线 性 规 划 LP 211 及LP 212 :
10
A
x2 7不可行
max Z 4 x1 3 x 2 1.2 x1 0.8 x 2 10 2 x1 2.5 x 2 25 LP 22 : x1 4,x 2 7 x1 , x 2 0
B 6 LP1
LP21
LP21:X=(4.33,6),Z21=35.33
整数规划问题的求解
整数规划问题的求解方法: 分支定界法和割平面法
Page 1
匈牙利法(指派问题)
分支定界法
分支定界法的解题步骤:
Page 2
1)求整数规划的松弛问题最优解; 若松弛问题的最优解满足整数要求,得到整数规划的最优解,否则转下 一步; 2)分支与定界: 任意选一个非整数解的变量xi,在松弛问题中加上约束: xi≤[xi] 和 xi≥[xi]+1 组成两个新的松弛问题,称为分枝。新的松弛问题具有特征:当原问题 是求最大值时,目标值是分枝问题的上界;当原问题是求最小值时,目 标值是分枝问题的下界。 检查所有分枝的解及目标函数值,若某分枝的解是整数并且目标函数 值大于(max)等于其它分枝的目标值,则将其它分枝剪去不再计算,若 还存在非整数解并且目标值大于(max)整数解的目标值,需要继续分枝, 再检查,直到得到最优解。
4.2-分配问题和匈牙利法

0 0 0 1 0
0 0 1 0 0
0 0 0 0 1
0 1 0 0 0
0 1 3 2 0
0 3 0 3 6 0 2 0 2 0 0 3 0 2 3 0 4 4 0 6
此问题有多个最优解
匈牙利法
第三种情况
矩阵中所有零元素或被划去,或打上( )号,但打( )号的 零元素个数仍小于n.
整数规划
整数规划的数学模型 设置逻辑变量建立整数规划模型 分配问题与匈牙利法 分支定界法、割平面法 应用举例
§3 分配问题与匈牙利法
分配问题的标准形式及其数学模型
分配问题也称指派问题(assignment problem),在我们现实 生活中,常有各种性质的分配问题.例如:应如何分配若干 项工作给若干个人(或部门)来完成,以达到总体的最佳效果 等等.由于分配问题的多样性,我们有必要定义分配问题的 标准形式.
可用表上作 解:这是一个标准的分配问题.若设0-1变量 业法求解
1 表示学生i翻译语种j xij (i, j 1, 2,3, 4) 0 表示学生i不翻译语种j 则问题的数学模型为
min z 14 x11 9 x12 4 x13 15 x14 11x21 7 x22 9 x23 10 x24 13 x31 6 x32 10 x33 5 x34 17 x41 9 x42 15 x43 13 x44 4 xij 1 i 1, 2,3, 4 j 1 4 s.t. xij 1 j 1, 2,3, 4 i 1 xij 0或1 i, j 1, 2,3, 4
匈牙利法
0 8 11 0 上述例子完成一、二、三步之后如右: 2 3 转向第四步: 0 11
匈牙利算法——精选推荐

匈⽛利算法0 - 相关概念0.1 - 匈⽛利算法 匈⽛利算法是由匈⽛利数学家Edmonds于1965年提出,因⽽得名。
匈⽛利算法是基于Hall定理中充分性证明的思想,它是⼆部图匹配最常见的算法,该算法的核⼼就是寻找增⼴路径,它是⼀种⽤增⼴路径求⼆分图最⼤匹配的算法。
0.2 - ⼆分图 若图G的结点集合V(G)可以分成两个⾮空⼦集V1和V2,并且图G的任意边xy关联的两个结点x和y分别属于这两个⼦集,则G是⼆分图。
1 - 基本思想1. 找到当前结点a可以匹配的对象A,若该对象A已被匹配,则转⼊第3步,否则转⼊第2步2. 将该对象A的匹配对象记为当前对象a,转⼊第6步3. 寻找该对象A已经匹配的对象b,寻求其b是否可以匹配另外的对象B,如果可以,转⼊第4步,否则,转⼊第5步4. 将匹配对象b更新为另⼀个对象B,将对象A的匹配对象更新为a,转⼊第6步5. 结点a寻求下⼀个可以匹配的对象,如果存在,则转⼊第1步,否则说明当前结点a没有可以匹配的对象,转⼊第6步6. 转⼊下⼀结点再转⼊第1步2 - 样例解析 上⾯的基本思想看完肯定⼀头雾⽔(很⼤程度是受限于我的表达能⼒),下⾯通过来就匈⽛利算法做⼀个详细的样例解析。
2.1 - 题⽬⼤意 农场主John有N头奶⽜和M个畜栏,每⼀头奶⽜需要在特定的畜栏才能产奶。
第⼀⾏给出N和M,接下来N⾏每⾏代表对应编号的奶⽜,每⾏的第⼀个数值T表⽰该奶⽜可以在多少个畜栏产奶,⽽后的T个数值为对应畜栏的编号,最后输出⼀⾏,表⽰最多可以让多少头奶⽜产奶。
2.1 - 输⼊样例5522532342153125122.2 - 匈⽛利算法解题思路2.2.1 - 构造⼆分图 根据输⼊样例构造如下⼆分图,蓝⾊结点表⽰奶⽜,黄⾊结点表⽰畜栏,连线表⽰对应奶⽜能在对应畜栏产奶。
2.2.2 - 模拟算法流程为结点1(奶⽜)分配畜栏,分配畜栏2(如图(a)加粗红边所⽰)为结点2(奶⽜)分配畜栏,由于畜栏2已经被分配给结点1(奶⽜),所以寻求结点1(奶⽜)是否能够分配别的畜栏,以把畜栏2腾给结点2(奶⽜)。
整数规划---匈牙利法

x1 (1) 1 0 0 0 x2 0 (1) 1 0 0 x3 0 1 0 0 (1) x4 0 0 (1) 0 0 x5 0 0 1 (1) 1
y1
y2
y3
y4
y5
但礼让原则未必都能得到最大 匹配,其次礼让原则当规模大 时无法使用,且无法用计算机 实现
z' = ∑∑C'ij xij =∑∑Cij xij − a∑xij + b∑xij = ∑Cij xij − a + b = z − a + b
j =1 i =1 n n
利用这个性质,可使原效益矩阵变换为含有很多零 元素的新的矩阵(即每行减去该行的最小值,再每列 也类似),其余C’ij ≥0. 如果C=(C’ij)有n个不同行,不同列的零元素,以下 简称为独立的零元素,则令矩阵x=( xij )中,对这n个独 立的零元素位置取1,其余取0,代入目标函数得z’= 0,它一定是最小(因为C’ij ≥0 )
Step4:增加(转移)零元素 a.求出未被直线覆盖的元素中的最小值k(本例中 k=2). b.对打√行减去k,对打√列加上k go to step2
2 (0) 8 11 (0) 5 2 3 (0) 0 13 4
√
5 √ 4 0 √ 5
0 (0) 6 13 (0) 5 4 3 (0) 0 11 2
进一步考虑
指派问题用匈牙利法计算,模型需要满足的形式: (1)目标函数是求最小值 (2)效益矩阵必须是n阶方阵 (3)效益矩阵中每个元素Cij ≥0,且是常数
如人员分配问题:
x1 x2 x3 x4 x5 y1 y2 y3 y4 y5
x1 x2 A = (aij ) = x3 x4 x5 1 0 0 0 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
选X1分枝 问题(2) (1) X1 4 问题(3) (1) X1 5
7
将[4,5]之间的非整数部分舍去
问题2
解为 X1 =4 Z=349.0 解为
问题3 X1 =5 Z=341.39
X2 =2.1
X2 =1.571
选(2)继续分枝
(2) (2)
问题(4)
X2 2
问题(5)
X2 3
实际含义:从事情的角度来考虑,表示此事分配给此人效率最高。
24
min
步骤二:继续产生零元素 方法:再找出矩阵每列的最小元素,再分 别从各列中减去它。
0 8 7 5 0 8 11 0 10 4 11 0 2 3 5 0 2 3 0 11 9 5 0 11
max Z=CX
maxZ=CX (B) AX=b X 0
AX=b
(A) X 0
X为整数 (B)为(A)的松弛问题。
3
(2)替代问题的求解 max Z=CX
(B)
AX=b X 0
采用相应的方法(如图解法)求解出替代问题的 最优解,观察其是否满足整数解的要求。如其最 优解就为整数,则结束;如含有分数,则需要进 行分支定界操作。
28
例:从行开始的独立零元素的寻找与判断 (0 )
2 5 11 ( 0 5 4 ) 2 3 0 0 0 11 4 5 8
(0) 8 2 5 11 (0) 5 4 2 3 0 0 0 11 4 5
从行开始标定独立零元 素时,只能找到两个独 立的零元素。
29
非直观法-步骤2
(2) <从人的角度>在行寻找的基础上,从第一 列开始,若该列只有一个零元素就对这个 零元素打上( )号(同样不考虑已划去的零元 素), 对打( )号零元素所在行画一条直线(任务分
配完毕,不能再分配给其他人)。
若该列没有零元素或有两个以上零元素, 则转下一列,依次进行到最后一列;
1 0 1 2
2 0 0 2 0 3 2 4 0 0 3 0
1 0 0 2
2 0 0 2 0 3 2 4 0 2 3 1
19
若矩阵A的元素可分成“0”与非“0”两 部分,则覆盖“0”元素的最少直线数等 于位于不同行、不同列的“0”元素的最 大个数。 将确定一个效率矩阵中最大独立零元素的 个数,转化为寻找覆盖所有零元素所需的 最少直线数。
31
问
题
2 5 (0) 8 11 (0) 5 4 2 3 (0) 0 0 11 4 5
只能对三个零元素进行标定(代表独立的零 元素只有三个),后续如何操作?
32
非直观法-步骤3(第一种情形)
(3) 重复(1)、(2)两个步骤,可能出现三种 情况: ① 效率矩阵每行都有一个打( )号的零元 素,很显然,按上述步骤得到的打( )号 的零元素都位于不同行不同列,只要令 对应打( )号零元素对应的决策变量xij=1 就找到了问题的最优解;
人
从人的 角度看 从任务 角度看
工作 译成英文 译成日文 译成德文 译成俄文
甲 2 15 13 4
乙 10 4 14 15
丙 9 14 16 13
丁 7 8 11 9
12
指派问题的一般模型
假设: [aij]表示指派问题的效率矩阵 xij表示决策变量,决策变量的取值:
1, 分配第i个人去完成第j项任务 xij 0, 不分配第i个人去完成第j项任务 (i 1,..., m; j 1,...,m)
8
(1)
4.809 355.890 1.817
分支定界过程
X1 5
(3)
X1 4
(2)
4 2.1
X2 2 (4) 4 2 340
349.0 X2 3 (5) 340 (6) 5.444 1
5 341.39 1.571
X2 1 340 X2 2 (7) 无解
9
1.428 327.12 3
只能给两个零元素打括号, 还有四个零元素不能打上括 号。剩下的未被划去和未打 括号的零元素存在闭回路。
4
(3)分支与定界—增加约束
•如替代问题的解不符合整数条件,则需要对原问题进行分支。
•分支方法:假设替代问题的解为[i,i+1]之间的一个数,则分成两支:
一支增加约束xj≤i,另一支增加约束xj ≥ i+1; •对上述两个问题进行求解:不考虑整数问题时,求解对应的线性规划 问题,观察其最优解是否是整数,如不是,则继续分支定界,直到得到 全部整数解为止。 i+1
13
指派问题的一般模型
指派问题的一般数学模型
min z aij xij
i 1 j 1 m m
m xij 1 (i 1,...,m) j 1 m xij 1 (j 1,...,m) i 1 xij 0 或 1
14
2、指派问题的求解方法
如何让效率矩阵中产生零元素; 如何让产生的零元素位于不同行和不同列。
17
(2)零元素的产生方法: 匈牙利法的基本定理1
如果从分配问题效率矩阵[aij]的每一行元 素中分别减去(或加上)一个常数ui (被称 为该行的位势),从每一列分别减去(或 加上)一个常数vj (称为该列的位势),得 到一个新的效率矩阵[bij],若其中 bij aij ui v j
33
第一种情形
甲
任务一
任务二 任务三 任务四
乙
丙
丁 x11=1,x22=1, x33=1,x44=1。
2 3 (0) 1 1 (0) 3 4 1 2 (0) 5 8 2 (0) 3
任务一→甲;二 →乙;三→丙; 四→丁
34
非直观法-4(第二种情形)
② 打( )号的零元素个数小于m,但未被划去的 零元素之间存在闭回路(全以0为拐点),这 时可顺着闭回路的走向,对每个间隔的零元素打 一( )号,然后对所有打( )号的零元素,或所在 行,或所在列画一条直线(一般会出现多种方 案)。如:
10
4.5.3 整数规划的解法——匈牙利法
应用于分配问题或指派问题
分配问题也称指派问题,是一种特殊的 整数规划问题。 假定有m项任务分配给m个人去完成,并 指定每人完成其中一项,每项只交给其 中一个人去完成,应如何分配使总的效 率为最高。
11
1、指派问题一般模型的引出
例:有一份说明书,要分别译成英、日、德、俄四种文字, 交甲、乙、丙、丁四个人去完成。因各人专长不同,他们 完成翻译不同文字所需的时间(h)如表所示。问:如何分 配任务使效率最高(所需总时间最短)?
非直观法:m很大时,根据一定规则寻找。
26
直观法
0 8 11 0 2 3 0 11
2 5 0 4
5 4 0 5
只有3个0元素 位于不同行、 不同列
27
非直观法-步骤1(试指派过程)
(1) <从任务的角度来挑选>从第一行开始,若该行 只有一个零元素,就对这个零元素打上( )号。< 表示该0元素处在单独的一行> 同时,对打( )号零元素所在列画一条直线,表示 此列已经确定(人员确定),不能再从事其他行 的工作(任务) 。 若该行没有零元素或有两个以上零元素(已划去的 零元素不计在内),则转下一行,按照上述方法依 次进行到最后一行;
30
例:从列开始的独立零元素的寻找与判断
(0) 8 2 5 11 (0) 5 4 ) 2 3 ( 0 0 0 11 4 5
2 5 (0) 8 11 (0) 5 4 2 3 (0) 0 0 11 4 5
在行标定后的基础上, 从第一列开始标定独立 零元素时,只能找到一 独立的零元素。
4.5 整数规划的解法
分支定界法 割平面法 匈牙利法
1
4.5.1 整数规划解法 ——分枝定界法
步骤: 1、寻找替代问题并求解 2、分枝与定界 3、剪枝
2
1、基本思路:整数规划的最优解不会优于相应
的线性规划的最优解。对于极大值问题,相应线性 规划的最大值成为整数规划目标函数的上界。
(1)替代问题的确定
22
效率矩阵
2 10 15 4 A 13 14 4 15
7 14 8 16 11 13 9 9
23
步骤一:零元素的产生。 方法:找出效率矩阵每行的最小元素,并 分别从每行中减去它。
2 10 9 7 2 0 8 7 5 15 4 14 8 4 11 0 10 4 13 14 16 11 11 2 3 5 0 4 15 13 9 4 0 11 9 5
20
匈牙利法的计算步骤
基本步骤:在效率矩阵中产生零元素→ 判断独立的零元素个数是否等于任务数 或人数?→如是,则对效率矩阵中独立 零元素所处的位置进行指派(对应的决 策变量为1),完成→如否,则要继续产 生足够的独立零元素。 通过实例来说明匈牙利法求解指派问题 的过程。
21
例:
有一份说明书,要分别译成英、日、德、俄四种文 字,交甲、乙、丙、丁四个人去完成。因各人专长 不同,他们完成翻译不同文字所需的时间(h)如表所 示。问:如何分配任务使效率最高? 人 工作 译成英文 译成日文 译成德文 译成俄文 甲 2 15 13 4 乙 10 4 14 15 丙 9 14 16 13 丁 7 8 11 9
307.76
4.5.2 整数规划解法2——割平面法
