力法 (2)
合集下载
第九章吸收2
• ②.适用条件： • a 气液平衡线为直线 • b 操作线为直线
y=mx+b
2）解吸因数法 适用于气液平衡关系为 通过原点的直线。 Y＊＝mX
L Y Y2 V X X2
（9-108）
联立解得：Y＊＝m[（V/L）(Y-Y2)+X2]
Y＊＝m[（V/L）(Y-Y2)+X2]
N OG
9.4 9.4.1. 9.4.2. 9.4.3. 9.4.4.
吸收塔的计算
Hale Waihona Puke 物料衡算与操作线方程 吸收剂用量的确定 填料层高度的计算 吸收塔的操作型计算
吸收塔的计算内容 1、设计型计算： 塔高、塔径、吸收剂用量、 吸收剂浓度 等的计算 2、操作型计算： 核算塔设备是否合用，操作条件与吸收结 果的关系。 物料衡算 ， 3、计算依据： 气液相平衡关系， 吸收速率方程
④在吸收操作时，因Y > Y*或X* > X，操作线 在平衡线的上方，
• ⑤解吸操作时，Y<Y*或X*<X，故解吸操作 线在平衡线的下方， • ⑥平衡线与操作线共同决定吸收推动力， 操作线离平衡线愈远，吸收的推动力愈大；
9．4．2 最小液气比与吸收剂用量
1、最小液气比 对一定的分离任务，当操作条件和吸收物 系一定、塔内某截面的吸收推动力为零时，达 到分离要求所需要的塔高将为无穷大，此时的 液气比即为最小液气比 ：
吸收塔填料层高度的计算
1、填料层高度的计算方法： 传质单元数法
2、计算依据：
1）物料衡算 2）吸收速率方程 3）相平衡关系
• 3．塔高计算基本关系式 • 1)取微元体积的原因， • 2）对溶质A作物料衡算
• • • • • •
对微元填料层dZ作物料衡算： 在单位时间内： 气相溶质减少量 VdY =液相溶质增加的量 LdX =由气相转移到液相溶质A的量 dG， 即： dG ＝VdY= LdX dG=NAdS =NA(aAdZ) 微元填料层dZ所提供的气液传质面积
chap2 推移质运动
第二章 推移质运动
韩智明
本章知识要点：
泥沙运动的形式 泥沙的起动 沙波运动 动床阻力 推移质输沙率
ቤተ መጻሕፍቲ ባይዱ
2
§2－1 泥沙运动的形式
悬 移 区 动 床 区
u
跃移质 接触质 层移质 定床区（床沙，河床质）
悬移区 床面区
层移区
3
运动泥沙的分类
沙床
跃移质（跳跃，主要运动形式） 接触质（滑动、滚动，为数不多）
㈣止动流速Uc’-小于起动流速，避免推移质输沙率误算为0
⑴概念：泥沙由运动状态到静止状态(并不表示停止下沉)的临界垂线 平均流速 ⑵计算方法：通常采用Uc’＝KUc 计算，K<1??? 岗恰洛夫：K＝0.71, 窦国仁and沙莫夫：K＝0.83
㈡起动流速与起动拖曳力公式的比较
⑴受力确定性方面：采用起动拖曳力法好，但应用不便， 因需要U*2＝gRJ，而J (水面比降)通常难以测量。 ⑵应用性方面:起动流速法好，因流速容易量测，精度较高 ⑶目前我国多用起动流速
㈢砾石与卵石的起动
砾石、卵石的形状(扁平度)以及排列方式对起动影响较大，需深入 研究；可针对不同的具体河段进行研究，如现有寸滩公式等
（四）、起动垂线平均流速Uc的推导
1、以指数流速分布公式为例的推导
2、假定起动时起动底流速 位置在 yoc=aD
y0c
uo uoc
3、Uc 的确定
s 泥沙起动 u0c gD 力矩平衡
s s 1 h h Uc gD gD m 1 m a D D
1、采用滚动模式的力矩平衡推导 2、多家公式： • 窦国仁：
• 张瑞瑾：
• 唐存本： 公式括号内的第一项代表重力作用项，第二项代表粘结力作用： D>1mm时 ，重力作用为主；D≤0.01mm时，粘结力作用为主；D=0.1mm左右时，两 者影响相当
韩智明
本章知识要点：
泥沙运动的形式 泥沙的起动 沙波运动 动床阻力 推移质输沙率
ቤተ መጻሕፍቲ ባይዱ
2
§2－1 泥沙运动的形式
悬 移 区 动 床 区
u
跃移质 接触质 层移质 定床区（床沙，河床质）
悬移区 床面区
层移区
3
运动泥沙的分类
沙床
跃移质（跳跃，主要运动形式） 接触质（滑动、滚动，为数不多）
㈣止动流速Uc’-小于起动流速，避免推移质输沙率误算为0
⑴概念：泥沙由运动状态到静止状态(并不表示停止下沉)的临界垂线 平均流速 ⑵计算方法：通常采用Uc’＝KUc 计算，K<1??? 岗恰洛夫：K＝0.71, 窦国仁and沙莫夫：K＝0.83
㈡起动流速与起动拖曳力公式的比较
⑴受力确定性方面：采用起动拖曳力法好，但应用不便， 因需要U*2＝gRJ，而J (水面比降)通常难以测量。 ⑵应用性方面:起动流速法好，因流速容易量测，精度较高 ⑶目前我国多用起动流速
㈢砾石与卵石的起动
砾石、卵石的形状(扁平度)以及排列方式对起动影响较大，需深入 研究；可针对不同的具体河段进行研究，如现有寸滩公式等
（四）、起动垂线平均流速Uc的推导
1、以指数流速分布公式为例的推导
2、假定起动时起动底流速 位置在 yoc=aD
y0c
uo uoc
3、Uc 的确定
s 泥沙起动 u0c gD 力矩平衡
s s 1 h h Uc gD gD m 1 m a D D
1、采用滚动模式的力矩平衡推导 2、多家公式： • 窦国仁：
• 张瑞瑾：
• 唐存本： 公式括号内的第一项代表重力作用项，第二项代表粘结力作用： D>1mm时 ，重力作用为主；D≤0.01mm时，粘结力作用为主；D=0.1mm左右时，两 者影响相当
结构力学力法(2)
qC
EI
B
cv
一次超静定
1 ql2 8
l
B
2
q
X
cv
1
=RB
P 1
MP
M1
例1：求k点竖向位移
I k△
2 I
图
k
I
2 I
图
ky
M K d p
M K M P ds
EI
C yC
EI
3
pa 3
1408EI
()
例1：求k点竖向位移
如取基本结构求虚拟状态的内力， 可使 问题简化。
k
I
2I
200
100 60
2
2
40
150
1
对封闭框架结构：可利用封闭框架上任意截 面相对转角为零的条件来校核。
30
M 1 dx 0 EI
1
4m
1
1
20
15
2m 2m
4m
1
1
M kN m M
2.校核相对转角：
M 1 dx 1 40 20 4 1 30 60 4 1 30 15 4
图
图
二、位移条件的校核
200
A2
100 60
2
(圆圈中的数字表示截面E I 的相对值) 30
40
4m
15011源自2015图2m 2m
4m
M kN m
1.校核A点竖向位移：
1P
1 2EI
1 100 4 8
2
3
1 2EI
1 200 4 2
2
1 2EI
1 4 4 30 2
0
二、位移条件的校核
20 M kN m 15 125
化工原理 第五章 吸收课后习题及答案
第五章 吸收相组成的换算【5-1】 空气和CO 2的混合气体中，CO 2的体积分数为20%，求其摩尔分数y 和摩尔比Y 各为多少？解 因摩尔分数=体积分数，.02y =摩尔分数 摩尔比 ..020251102y Y y ===--． 【5-2】 20℃的l00g 水中溶解lgNH 3, NH 3在溶液中的组成用摩尔分数x 、浓度c 及摩尔比X 表示时，各为多少？解 摩尔分数//117=0．010*******／18x =+浓度c 的计算20℃，溶液的密度用水的密度./39982s kg m ρ=代替。
溶液中NH 3的量为 /311017n kmol -=⨯ 溶液的体积 /.33101109982 V m -=⨯溶液中NH 3的浓度//.33311017==0．581／101109982n c kmol m V --⨯=⨯ 或 . 3998200105058218s sc x kmol m M ρ==⨯=．．／ NH 3与水的摩尔比的计算 //1170010610018X ==．或 ..00105001061100105x X x ===--． 【5-3】进入吸收器的混合气体中，NH 3的体积分数为10%，吸收率为90%，求离开吸收器时NH 3的组成，以摩尔比Y 和摩尔分数y 表示。
吸收率的定义为122111Y Y Y Y Y η-===-被吸收的溶质量原料气中溶质量解 原料气中NH 3的摩尔分数0.1y = 摩尔比 (11101)01111101y Y y ===-- 吸收器出口混合气中NH 3的摩尔比为 ()...211109011100111Y Y η=-=-⨯=（）摩尔分数 (22200111)=0010981100111Y y Y ==++ 气液相平衡【5-4】 l00g 水中溶解lg 3 NH ，查得20℃时溶液上方3NH 的平衡分压为798Pa 。
此稀溶液的气液相平衡关系服从亨利定律，试求亨利系数E(单位为kPa )、溶解度系数H[单位为/()3kmol m kPa ⋅]和相平衡常数m 。
第十四次课——第05章 力法(2)
FP
FP
FP
FP
28 / 87
第五章 力 法
第五节 力法计算的简化
判断荷载的对称性
FP
M
正对称荷载
反对称荷载
29 / 87
第五章 力 法
对称荷载分析:
FP FP X2 FP X3 X3 X2 X1 X1 FP
Δ1P 0
X1 0
X1 1
X2 1
X3 1
M1
M2
FP FP
对称结构当 作用对称荷 载时，反对 称未知量为 零。其结构 的内力和变 形是对称的
13 / 87
第五章 力 法
第三节 力法示例(一次超静定结构)
弹性支座情况下的计算
FP EI
l
FP 基本体系1
当把弹簧考虑成支座时，铰 接端弹簧处竖向位移与弹簧 k 内力有关： X1 Δ1 k X1 11 X 1 Δ1P k X1 1 ( 11 ) X 1 Δ1P 0 k 14 / 87
M X i Mi
由于多余力的存在，当温度改变或支座移动时会引起弹性变 形，产生内力，这是超静定结构不同于静定结构的特征之一。
10 / 87
第五章 力 法
第三节 力法示例(一次超静定结构)
温度改变情况下的计算
t1 t2
h b
EI
l
11 X1 Δ1t 0
X1
l
3t EI 2h
22 / 87
第五章 力 法
第五节 力法计算的简化
判断方法:
结构化成铰接体系，荷载仍然作用在结点，若在当 前状态体系能平衡外荷载，则可断定原体系无弯矩。
FP FP FP FP
23 / 87
第六章-力法(二) ,同济大学结构力学课件,朱慈勉版教材,吕凤悟老师课件
根据对称结构的受力特征，在对称或反对称荷载作用下，可以取半结构 计算，另外半结构的内力可通过对称或反对称镜像得到。
半结构选取的关键在于正确判别另外半结构对选取半结构的约束作用。 判别方法有两种：
根据对称轴上的杆件和截面的变形（或位移）特征判别。(适用于所有结构)
根据对称轴上的杆件和截面的内力特征判别。 (一般只适用于奇数跨结构)
【例】试用力法求作图示刚架的弯矩图。 各杆 EI C 。
Strucural Analysis
School of Civil Engineering, Tongji Univ.
§6-5 对称性的利用—力法简化计算
【例】试用力法求作图示刚架的弯矩图。各杆 EI C 。
【解】利用对称性简化为一次超静定。
11X1 1p 0
11
144 EI
,
1 p
1800 EI
X1 12.5kN
M M1X1 M p
Strucural Analysis
School of Civil Engineering, Tongji Univ.
§6-5 对称性的利用—力法简化计算
取半结构计算
§6-5 对称性的利用—力法简化计算
对称性的概念
对称结构：几何形状、支承情况、刚度分布均对称的结构。
支承不对称
对称结构
几何对称 支承对称 刚度对称
非对称结构
刚度不对称
对称荷载：作用在对称结构对称轴两侧,大小相等,方向和作用点对称的荷载。 反对称荷载：作用在对称结构对称轴两侧,大小相等，作用点对称,方向
13X 3 23X 3
1 p 2p
0 0
31X1 32 X 2 33 X 3 3 p 0
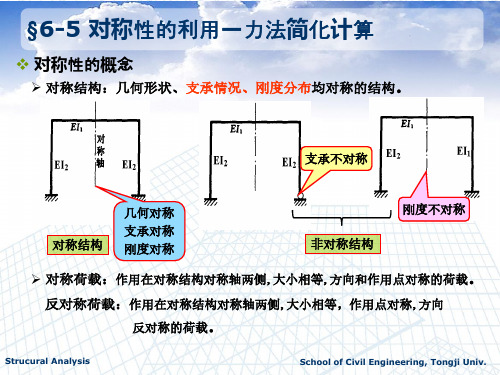
半结构选取的关键在于正确判别另外半结构对选取半结构的约束作用。 判别方法有两种：
根据对称轴上的杆件和截面的变形（或位移）特征判别。(适用于所有结构)
根据对称轴上的杆件和截面的内力特征判别。 (一般只适用于奇数跨结构)
【例】试用力法求作图示刚架的弯矩图。 各杆 EI C 。
Strucural Analysis
School of Civil Engineering, Tongji Univ.
§6-5 对称性的利用—力法简化计算
【例】试用力法求作图示刚架的弯矩图。各杆 EI C 。
【解】利用对称性简化为一次超静定。
11X1 1p 0
11
144 EI
,
1 p
1800 EI
X1 12.5kN
M M1X1 M p
Strucural Analysis
School of Civil Engineering, Tongji Univ.
§6-5 对称性的利用—力法简化计算
取半结构计算
§6-5 对称性的利用—力法简化计算
对称性的概念
对称结构：几何形状、支承情况、刚度分布均对称的结构。
支承不对称
对称结构
几何对称 支承对称 刚度对称
非对称结构
刚度不对称
对称荷载：作用在对称结构对称轴两侧,大小相等,方向和作用点对称的荷载。 反对称荷载：作用在对称结构对称轴两侧,大小相等，作用点对称,方向
13X 3 23X 3
1 p 2p
0 0
31X1 32 X 2 33 X 3 3 p 0
集美大学船舶结构力学(48学时)第三章 力法(1)2014(2学时)
R
静定基
这时原来仅受均布荷重q作用的静 不定的双跨梁变为受均布荷重q与集中 力R共同作用的静定的单跨梁；
2）比较前后两种梁的变 形情况，根据变形一致 （协调、连续）条件建 立方程式；
原超静定结构
v1 0
静定基
变形一致条件：
v1 0
静定基
变形一致条件：
v1 0
vq1 vR1 0
4
3
Rl 5ql 0 5 6 EI 24 EI R ql 4
P
M图
中点挠度大小
3
端点转角大小
2
m
Pl Pl EI , l 48EI 16EI Pl / 4 2 m ml ml ml 左 右 查单跨梁的弯曲要素表（附录A表A-2），得到： 3EI 6EI 16EI
Q
EI , l
Ql / 8
（力法基本未知数数目与结构的 静不定次数相同。)
2、在去掉约束或截断处， 列出变形一致（连续） 方程式以保证基本结构 的变形与原结构的变形 相同。
（方程数目与基本未知数数目相同。）
3、从变形一致（或连续、 协调）方程式中求出未 知“力”，进一步可求 出结构的其他弯曲要素。
五、三弯矩方程法 1、三弯矩方程式：一般来 说，在用力法的第二种方法 （截面法）解静不定杆系问 题时，列出的变形连续方程 式（或称节点转角连续方程） 是以各断面弯矩为未知数的 方程组，
1 2 M 1 ql 14
3 2 M2 ql 28
7）画弯矩图
求出了 M 1 、M 2 后， 就可以分别对两个单跨 梁1-2、2-3画弯矩图。
其中每一个单跨梁 的弯矩图都可以用叠加 法来画。最后组合起来 得到双跨梁的弯矩图, 图3-7(a)。
静定基
这时原来仅受均布荷重q作用的静 不定的双跨梁变为受均布荷重q与集中 力R共同作用的静定的单跨梁；
2）比较前后两种梁的变 形情况，根据变形一致 （协调、连续）条件建 立方程式；
原超静定结构
v1 0
静定基
变形一致条件：
v1 0
静定基
变形一致条件：
v1 0
vq1 vR1 0
4
3
Rl 5ql 0 5 6 EI 24 EI R ql 4
P
M图
中点挠度大小
3
端点转角大小
2
m
Pl Pl EI , l 48EI 16EI Pl / 4 2 m ml ml ml 左 右 查单跨梁的弯曲要素表（附录A表A-2），得到： 3EI 6EI 16EI
Q
EI , l
Ql / 8
（力法基本未知数数目与结构的 静不定次数相同。)
2、在去掉约束或截断处， 列出变形一致（连续） 方程式以保证基本结构 的变形与原结构的变形 相同。
（方程数目与基本未知数数目相同。）
3、从变形一致（或连续、 协调）方程式中求出未 知“力”，进一步可求 出结构的其他弯曲要素。
五、三弯矩方程法 1、三弯矩方程式：一般来 说，在用力法的第二种方法 （截面法）解静不定杆系问 题时，列出的变形连续方程 式（或称节点转角连续方程） 是以各断面弯矩为未知数的 方程组，
1 2 M 1 ql 14
3 2 M2 ql 28
7）画弯矩图
求出了 M 1 、M 2 后， 就可以分别对两个单跨 梁1-2、2-3画弯矩图。
其中每一个单跨梁 的弯矩图都可以用叠加 法来画。最后组合起来 得到双跨梁的弯矩图, 图3-7(a)。
福建专升本建筑学力法位移法支座位移解析
一、静定结构在支座移动时的位移计算静定结构由于支座移动并不产生内力也无变形，只会发生刚体位移。
因此，静定结构由于支座移动引起的位移计算属于刚体体系问题。
应用虚功方程求解时，虚拟状态的选取同前，因实际状态的变形为零，因此内力虚功为零。
这时结构的位移表达式可以根据式（8-9）改写为（8-28）如果令表示支座移动所引起的位移，为虚拟状态中的支座反力，表示支座位移，则式（8-28）改写为（8-29）式（8-29）就是计算结构由于支座移动所引起的位移表达式。
例8-11 图8-30a 所示为三铰刚架。
支座B 有水平位移a 和竖向位移b ，试求铰C 两边截面的相对转角。
图8-30解：为求C 铰两边截面的相对转角，需在其两边截面施加一对方向相反的单位力偶。
此时因单位力偶的作用产生的支座反力为、、、，如图8-30b 所示。
利用式（8-29），得∑⋅-=c R k K ∆ic ∆R c ∑⋅-=c R ic∆Ax F Ay F Bx F By F ())(h a 0a h 1b F a F c R By Bx C ic 弧度-=⎪⎭⎫⎝⎛-⨯-=⋅-⋅-=⋅-==∆∑ϕ负号表示C处的相对转动的方向与所设的单位力偶的转向相反。
例1 已知简支梁AB跨度为l，右支座B竖直下沉Δ，如图(a)所示。
求梁中点C的竖向位移ΔCV。
解：(1) 在梁中点C处加单位力P=1，如图(b)所示。
(2)计算单位荷载作用下的支座反力:由于A支座无位移，故只需计算B支座反力RB即可。
由对称得B支座反力RB=1/2 (↑)(3) 计算ΔCVΔCV=-∑RC=-(-1/2×Δ)=Δ/2 (↓)例2 图示三铰刚架跨度l=12m，高为h=8m。
已知右支座B发生了竖直沉陷C1=6cm，同时水平移动了C2=4cm (向右)，如图(a)所示。
求由此引起的左支座A处的杆端转角φA。
解: (1) 在A处虚设单位力偶m=1，如图(b)所示。
(2) 计算单位荷载作用下的支座反力由于A支座无位移，故只需计算B支座反力即可。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
l δ11 = 3EI
3
q
A B
∆1P + δ11 X 1 = 0 1P
3 X 1 = ql 8
l
1 2 ql 8 A
原结构 B
求得的未知力X 是正号， 求得的未知力 1是正号，表示 多余力X 多余力 1的方向与原设的方向 相同。 相同。
M图
小结(Summary)
多余未知力求出后， 利用平衡条件绘制基本 多余未知力求出后，可利用平衡条件绘制基本 体系的内力图，亦即原结构的内力图。 体系的内力图，亦即原结构的内力图 根据叠加原理，结构任意截面的弯矩 M 也可 根据叠加原理， 用下列公式表示： 用下列公式表示
1P
l
＋
A B X1
（力法方程 力法方程） + δ11 X 1 = 0 力法方程
∆11
其中，δ11 为柔度系数， 是X1＝1单独作用下沿X1方向产 生的位移； ∆1P 称为自由项。
l
力法方程（Equation of Force Method）
由上式可以看出：若求出 的大小， 由上式可以看出：若求出X1的大小，就可以求得此超静定 结构的内力。 求解 结构的内力。而求解X1，得先求出 ∆1P
M = M1 X1 + M P
小结：力法方程的实质是位移方程， 小结：力法方程的实质是位移方程，之所以 方程 称其为力法，是因为方程的未知量是多余力。 称其为力法，是因为方程的未知量是多余力。
§10.3.1 两次超静定结构的力法方程
原结构
基本体系
基本结构 受X 1 = 1 作用
基本结构 受X 2 = 1 作用qຫໍສະໝຸດ ,δ11； δ11l
B X1 =1
A
B
l
1 2 ql 2
∆1P
A
A
B
MP图
A
B
M 1图
l
ql 4 =− 8 EI
利用图乘法，可以得到： 利用图乘法，可以得到： ∆ 1 P
δ 11
l3 = 3 EI
力法方程（Equation of Force Method）
把 ∆1 P 代入 得
ql 4 =− 8 EI
力法方程（Equation of Force Method） ）
(a) A
q
B
已知：等截面直杆AB，其上有均布荷 已知 载 q ，EI＝常数，求此结构的M 图。 解：分析 分析：原结构与基本体系的区别 分析
l
(b) A 原结构 B
在于B支座 支座处。 支座 原结构中B支座是固定的，没有位移； 原结构中B支座是固定的，没有位移； 基本体系中B为自由端，可以有位移 基本体系中B为自由端，可以有位移；
（1）力法原理概述 （2）力法方程的建立及举例
§10.1 力法原理 （Principle of Force Method)
力法原理概述：
1、基本思路： 、基本思路： 超静定结构 2、基本未知量的确定： 、基本未知量的确定： 力法基本未知量个数＝ 力法基本未知量个数＝结构超静定次数 ＝多余约束数 力法以静定结构为基础， 力法以静定结构为基础，以多余约束力为基本未知量 静定结构为基础 根据变形协调条件建立力法方程并求解多余未知力。 变形协调条件建立力法方程并求解多余未知力 根据变形协调条件建立力法方程并求解多余未知力。
力法原理（Principle of Force Method)
在基本体系中，一方面保留着原结构的外荷 基本体系中 另一方面有相应的约束力X 存在， 载；另一方面有相应的约束力X1存在，只是把它 由原来的被动力（多余约束力）改为主动力。 由原来的被动力（多余约束力）改为主动力 基本体系的受力状态与原结构完全相同 注意：基本体系既是静定结构， 注意 基本体系既是静定结构，又等效于原超静 基本体系既是静定结构 定结构。因此基本体系是静定结构过渡 过渡到超静定 定结构。因此基本体系是静定结构过渡到超静定 结构的一座桥梁。 结构的一座桥梁
基本结构 受荷载作用
■
基本结构的多种选择
§10.3.2 n 次超静定结构的力法方程
主系数均为正值， 主系数均为正值， 副系数互等
柔度矩阵 对称矩阵 叠加法 绘制内力图
变形协调条件
静定结构
力法原理（Principle of Force Method)
MA
q
B
举例： 举例：
XA
MA A XA
q
B
A
(a)
YA 超静定结构 YB
(b)
YA 静定结构
运用两刚片规则，可知 可知图 是具有一个多余约束的几何 ● 运用两刚片规则 可知图 (a)是具有一个多余约束的几何 不变体系；图 (b)是无多余约束的几何不变体系 是无多余约束的几何不变体系； 不变体系 是无多余约束的几何不变体系 对于图(b)静定结构来说 静定结构来说， ● 对于图 静定结构来说， 三个平衡方程式能求出其全部 内力及反力； 对于图(a)超静定结构有四个约束反力 超静定结构有四个约束反力X 内力及反力 ； 对于图 超静定结构有四个约束反力 A、YA、 MA、YB。三个平衡方程不能求出其全部内力及反力。 能求出其全部内力及反力。 。三个平衡方程不能求出其全部内力及反力
第十章
力 法
结构力学(Structural Mechanics)
经典方法(Classical Method)
解超静定结构的基本方法。 力法 ：解超静定结构的基本方法。 解超静定结构的基本方法 超静定结构是有多余约束的几何不变体系， 超静定结构是有多余约束的几何不变体系， 是有多余约束的几何不变体系 其内力和支座反力不能完全用静力学三个平衡 方程式唯一地解出， 方程式唯一地解出，须增加变形协调条件作为 补充方程：力法方程。 补充方程：力法方程。 本节教学内容： 本节教学内容
力法原理（Principle of Force Method)
3、 力法的基本结构与基本体系 、
q
A
B
基本结构
B A B
A 超静定结构
x1
基本体系
A A
q q
力法基本结构：一般为静 力法基本结构 定结构（力法中原结构的 B 基本结构可有多种选择）。 力法基本体系：在力法基 力法基本体系 本结构上用多余未知力代 B X1 替原多余约束与外荷载共 同作用的体系
§10.3 力法方程 （Equation of Force Method）
力法方程的建立： 力法方程的建立：
目的：用力法方程可以解出超静定结构的多余未知 目的 用力法方程可以解出超静定结构的多余未知 力的值，从而得到超静定结构的内力及反力的大小。 力的值，从而得到超静定结构的内力及反力的大小 根据变形协调条件（也称位移条件）建立力法方程。 根据变形协调条件（也称位移条件）建立力法方程。 变形协调条件 位移条件 举例说明如下： 举例说明如下： 说明如下
l
基本结构 (c) A
q
l
基本体系
X1
B
力法方程(Equation of Force Method）
(c) A
q
l
基本体系
X1
q
B
基本体系转化为原来超静定结构的条件 是：基本体系沿多余未知力X1方向的位 移应与原结构相同，即
q
A B
∆ BV = 0
∆1 P
或 即∆
（位移条件 位移条件） 位移条件
∆1P + ∆11 = 0 （补充方程）