八年级不等式培优题
八年级不等式培优提高练习

1.若关于x的不等式组恰好只有四个整数解,则a的取值范围是()A.a B.C.﹣2D.﹣22.设a,b是常数,不等式+>0的解集为x<,则关于x的不等式bx﹣a<0的解集是()A.x>B.x<﹣C.x>﹣D.x<3.若不等式(ax﹣1)(x+2)>0的解集是﹣3<x<﹣2,则a等于()A.B.C.3 D.一34.不等式的解集为x>2,则m的值为()A.4 B.2 C.D.5.若关于x的不等式组的整数解共有3个,则m的取值范围是()A.5<m≤6 B.5≤m<6 C.5≤m≤6 D.5<m<66.已知a>b,c≠0,则下列关系一定成立的是()A.ac>bc B.C.c﹣a>c﹣b D.c+a>c+b 7.下列命题中:①如果a<b,则ac2<bc2;②关于x的不等式(a﹣1)x>1﹣a的解集是x<﹣1,则a<1;③若是自然数,则满足条件的正整数x有4个.正确的命题个数是()A.0 B.1 C.2 D.38.若x是方程2x+m﹣3(m﹣1)=1+x的解为负数,则m的取值范围是()A.m>﹣1 B.m<﹣1 C.m>1 D.m<19.按下面的程序计算:若输入x=100,输出结果是501,若输入x=25,输出结果是631,若开始输入的x值为正整数,最后输出的结果为556,则开始输入的x值可能有()A.1种B.2种C.3种D.4种10.若x为任意实数时,二次三项式x2﹣6x+c的值都不小于0,则常数c 满足的条件是()A.c≥0 B.c≥9 C.c>0 D.c>911.关于x的方程mx﹣1=2x的解为正实数,则m的取值范围是()A.m≥2 B.m≤2 C.m>2 D.m<212.关于x的不等式组的解集为x<3,则m的取值范围为()A.m=3 B.m>3 C.m<3 D.m≥313.已知△ABC的边长分别为2x+1,3x,5,则△ABC的周长L的取值范围是()A.6<L<36 B.10<L≤11 C.11≤L<36 D.10<L<36 14.已知实数x、y同时满足三个条件:①3x﹣2y=4﹣p,②4x﹣3y=2+p,③x>y,则实数p的取值范围是()A.p>﹣1 B.p<1 C.p<﹣1 D.p>115.关于x的不等式组的解集是x>﹣1,则m= .16.若不等式组的解集为﹣1<x<1,则(a+1)(b﹣1)的值等于.17.已知关于x、y的二元一次方程组的解满足x+y>2,则k 的取值范围是.18.若不等式组有解,则a必须满足.19.已知a、b都是实数,且a=,b=,b<<2a,则实数x的取值范围是.20.若关于x、y的二元一次方程组的解满足x+y>0,则m的取值范围是.21.关于x的不等式x﹣3>的解集在数轴上表示如图所示,则a的值是.22.已知关于x的分式方程的解为负数,则字母a的取值范围是.23.求不等式(2x﹣1)(x+3)>0的解集.解:根据“同号两数相乘,积为正”可得:①或②.解①得x>;解②得x<﹣3.∴不等式的解集为x>或x<﹣3.请你仿照上述方法解决下列问题:(1)求不等式(2x﹣3)(x+1)<0的解集.(2)求不等式≥0的解集.24.x取哪些整数值时,不等式5x+2>3(x﹣1)与x﹣1≤7﹣都成立?25.已知关于x的不等式组恰好有两个整数解,求实数a 的取值范围.26.已知一元一次不等式mx﹣3>2x+m.(1)若它的解集是x<,求m的取值范围;(2)若它的解集是x>,试问:这样的m是否存在?如果存在,求出它的值;如果不存在,请说明理由.27.用等号或不等号填空:(1)比较4m与m2+4的大小当m=3时,4m m2+4当m=2时,4m m2+4当m=﹣3时,4m m2+4(2)无论取什么值,4m与m2+4总有这样的大小关系吗?试说明理由.(3)比较x2+2与2x2+4x+6的大小关系,并说明理由.(4)比较2x+3与﹣3x﹣7的大小关系.28.是否存在整数m,使关于x的不等式1+>+与关于x的不等式x+1>的解集相同?若存在,求出整数m和不等式的解集;若不存在,请说明理由.29.已知关于x的不等式(2a﹣b)x+a﹣5b>0的解集为x<,(1)求的值.(2)求关于x的不等式ax>b的解集.30.若不等式组的偶数解a满足方程组,求x2+y2的值.31.小明把三个数﹣1,2﹣a,在数轴上从左到右依次排列在三个对应点上,你能确定a的取值范围吗?请写出你的解答过程.32.阅读下面的例题,并回答问题.【例题】解一元二次不等式:x2﹣2x﹣8>0.解:对x2﹣2x﹣8分解因式,得x2﹣2x﹣8=(x﹣1)2﹣9=(x﹣1)2﹣32=(x+2)(x﹣4),∴(x+2)(x﹣4)>0.由“两实数相乘,同号得正,异号得负”,可得①或②解①得x>4;解②得x<﹣2.故x2﹣2x﹣8>0的解集是x>4或x<﹣2.(1)直接写出x2﹣9>0的解是;(2)仿照例题的解法解不等式:x2+4x﹣21<0;(3)求分式不等式:≤0的解集.。
初中数学培优-八年级数学不等式巩固练习含答案

认识不等式 (巩固练习)姓名 班级第一部分1、选择适当的不等号填空:;(2) 23- 45-;(3) 1a + 1;(4)若分式25x x -+有意义,则x -5; (5) ,,a b c 分别表示三角形的三边, 则b c + a . 2、用适当的不等号填空:⑴-41____0 ;⑵ -1.8_____-431 ;⑶6×4_____6×(-4);(4) 若分式21x x +-有意义,则x 1;(5)y 2-4y+4 0. 3、根据下列数量关系,列出不等式:(1)x 的3倍加上2的和大于-4; (2)4与x 的5倍的和不大于6;(3)y 的12与-10的差小于y 的2倍; (4)正数a 与3的和的算术平方根大于1.4、下列按条件列出的不等式中,正确的是…………………………………………( )A. a 不是负数,则a >0B. a 与3的差不等于1,则a —3<1C. a 是不小于0的数,则a >0D. a 与 b 的和是非负数,则a +b ≥0 5、小李与小王决定把每月省下的零用钱存起来.小李原来存了80元,小王原来存了54元.从这个月开始,小李计划每月存16元,小王计划每月存20元.(1)设x 个月后小王的存款数超过小李,试根据题意列出不等式; (2)6个月后,小王的存款数是否已超过小李?7个月后呢?6、某公交公司年初用120万元购进一批新车,在投入运输后,估计每年的总收入为72万元,需要支出的各种费用为40万元.若设这批新车x 年后开始盈利(盈利即指总收入减去购车费及所有支出费用之差为正值),(1)怎样用不等式表示题中的数量关系?(2)3年后盈利了吗?第二部分1.选择适当的不等号填空:(1)2 -3; (2) 5- 7-.2. 选择适当的不等号填空: (1)2x 0; (2)若x y ≠,则3x 3y . 3. 把“x 与2的和是负数”中的数量关系,列出不等式为 . 4. 根据数量关系列出不等式: x 的3倍大于5: . 5.选择适当的不等号填空:(1)-1 0;(2) 22 7;(3) x - 0;(4) a a 6.若分式3x +不意义,则x 的取值范围是 .7.根据题意列出不等式:y 的一半与3的差是负数 . 8.满足 1.23x -<≤的整数有 个. 9. 将下列不等式分别表示在数轴上: (1)x<3;(2)-2<x≤1.10. 根据下列数量关系,列出不等式:(1)x 的3倍大于x ;(2)m 与1的相反数的和不小于32; (3) a 与-2的差不大于它的3倍; (4) ,a b 两数的平方和不小于它们的积的2倍.参考答案第一部分7个月后, 小王的存款数是54207194+⨯=, 小李的存款数是80167192+⨯=,所以小王的存款数超过了小李.6、某公交公司年初用120万元购进一批新车,在投入运输后,估计每年的总收入为72万元,需要支出的各种费用为40万元.若设这批新车x 年后开始盈利(盈利即指总收入减去购车费及所有支出费用之差为正值),(1)怎样用不等式表示题中的数量关系?(2)3年后盈利了吗?解:(1)72120400x x -->.(2)当x=3时, 7212040240x x --=-<,则还没有盈利.第二部分1.选择适当的不等号填空:(1)2 -3; (2) .答案:> >2. 选择适当的不等号填空: (1)2x 0; (2)若x y ≠,则3x 3y .答案:(1) ≥ (2) ≠3. 把“x 与2的和是负数”中的数量关系,列出不等式为 .答案:x +2<04. 根据数量关系列出不等式: x 的3倍大于5: .答案:3x >55.选择适当的不等号填空:(1)-1 0;(2) ;(3) ;(4) a a 答案:(1)<;(2)<;(3)≤;(4) ≥. 6.不意义,则x 的取值范围是 .答案: x ≠7.根据题意列出不等式:y 的一半与3的差是负数 .答案:1302y -<. 8.满足 1.23x -<≤的整数有 个.答案:5.9. 将下列不等式分别表示在数轴上: (1)x<3;(2)-2<x≤1.解:(1) (2)10. 根据下列数量关系,列出不等式:(1)x 的3倍大于x ;(2)m 与1的相反数的和不小于32; (3) a 与-2的差不大于它的3倍; (4) ,a b 两数的平方和不小于它们的积的2倍. 解: (1) 3x x >;(2) 3(1)2m +-≥;(3) (2)3a a --≤;(4) 222.a b ab +≥01234-1-2-3不等式的基本性质 (巩固练习)姓名 班级第一部分1、如图,天秤中的物体a 、b 、c 使天秤处于平衡状态,则质量最大的物体是 .2、如图,天平右边托盘里的每个砝码的质量都是1千克,则图中显示物体质量的范围是………………( )A. 大于2千克B. 小于3千克C. 大于2千克且.小于3千克D. 大于2千克或.小于3千克 3、若x y >,比较235x -与235y -的大小,并说明理由.4、下列推导过程中竟然推出了0>2的错误结果.请你指出问题究竟出在哪里.已知:m>n.两边都乘2,得:2m>2n ; 两边都减去2m,得:0>2n -2m, 即把:0>2(n -m). 两边都除以n -m,得:0>2.5、某自行车保管站在某个星期日接受保管的自行车共有3500辆次,其中变速车保管费是每辆0.5元,一般车保管费是每辆0.3元.(1) 若设一般车停放的辆次数为x ,总的保管费收入为y 元,试写出y 与x 的关系式. (2) 若估计前来停放的3500辆自行车中,变速车的辆次不小于25%,但不大于40%,试求该保管站这个星期日收入保管费总数的范围.6、某天股票A 的价格比股票B 的价格高,但不到股票B 的2倍.第二天股市大涨,两只股票双双涨停(即都比前一天上涨了10%).问现在股票A 的价格仍比股票B 的价格高,但低于两倍吗?请说明理由.如果每只股票各涨2元呢?第二部分1.若x >y ,则y x .2.若x >y ,则x +3 y +3.3.若x +3>0,两边同时减去3,得 ,根据是 .4.若3y <9,两边同时除以3,得 ,根据是 .5.若3a b <+,且32b c +<,则a 2c .理由是 .6.若1124x ≥-,两边同时乘以2得 ,理由是 . 7.某本书的单价有15元到20元之间(包括15元,20元),买4本这样的书的总价钱a为 (用适当的不等式表示)8.若a b >,则2ax 2ay (填上适当的不等号)9.若x y <,试比较下列各式的大小并说明理由.(1) 31x -与31y -; (2) 263x -+与263y -+.10.某单位为改善办公条件,欲购进20台某品牌电脑.据了解,该品牌电脑的单价大致在6000元至6500元之间.则该单位购买这批电脑应预备多少钱?参考答案第一部分(2) 若估计前来停放的3500辆自行车中,变速车的辆次不小于25%,但不大于40%,试求该保管站这个星期日收入保管费总数的范围.解:(1)由题意,得y=0.3x+0.5(3500-x),y=-0.2x+1750.(2)∵ 变速车停放的辆次不小于3500的25%,但不大于3500的40%. ∴ 一般自行车停放的辆次是在3500×60%与3500×75%之间. 当x=3500×60%=2100时,y=-0.2×2100+1750=1330; 当x=3500×75%=2625时,y=-0.2×2625+1750=1225. ∴ 这个星期天保管费的收入在1225元至1330元之间.6、某天股票A 的价格比股票B 的价格高,但不到股票B 的2倍.第二天股市大涨,两只股票双双涨停(即都比前一天上涨了10%).问现在股票A 的价格仍比股票B 的价格高,但低于两倍吗?请说明理由.如果每只股票各涨2元呢?解:设某天股票A 的价格为x 元,股票B 的价格为y 元.由题意得:x>y,且x<2y.第二天各上张10%后,股票A 的价格为1.1x 元,股票B 的价格为1.1y 元.根据不等式的基本性质3,可知1.1x>1.1y, 1.1x<2.2y,即股票A 的价格仍比股票B 的价格高,但低于2倍.若各上涨2元, 则股票A 的价格为(x+2)元,股票B 的价格为(y+2)元,由不等式的基本性质2,知x+2> y+2, x+2<2 y+2<2(y+2),即上涨2元后股票A 的价格仍比股票B 高,且仍不到股票B 的两倍.第二部分1.若x >y ,则y x .答案:<2.若x >y ,则x +3 y +3.答案:>3.若x +3>0,两边同时减去3,得 ,根据是 .答案:x >-3 不等式基本性质2.4.若3y <9,两边同时除以3,得 ,根据是 .答案:y <3 不等式基本性质3.5.若3a b <+,且32b c +<,则a 2c .理由是 .答案:<,不等式的基本性质1.6.若1124x ≥-,两边同时乘以2得 ,理由是 . 答案: 12x ≥-,不等式的基本性质3.7.某本书的单价有15元到20元之间(包括15元,20元),买4本这样的书的总价钱a为 (用适当的不等式表示) 答案:60≤a ≤80.8.若a b >,则2ax 2ay (填上适当的不等号)答案:≥9.若x y <,试比较下列各式的大小并说明理由.(1) 31x -与31y -; (2) 263x -+与263y -+. 解::(1)∵x y <, ∴33x y <(不等式的基本性质3), ∴3131x y -<-(不等式的基本性质2). (2) ∵x y <, ∴2233x y ->- (不等式的基本性质3), ∴226633x y -+>-+ (不等式的基本性质2). 10.某单位为改善办公条件,欲购进20台某品牌电脑.据了解,该品牌电脑的单价大致在6000元至6500元之间.则该单位购买这批电脑应预备多少钱? 解:设该品牌电脑的单价为x 元,则60006500x ≤≤.∴60002020650020x ⨯≤≤⨯(不等式的基本性质3),即12000020130000x ≤≤. 答:该单位购买这批电脑应预备的钱在120000元至130000元之间.一元一次不等式组在实际生活中的应用一、解答题。
初二数学《不等式分式》提高练习题
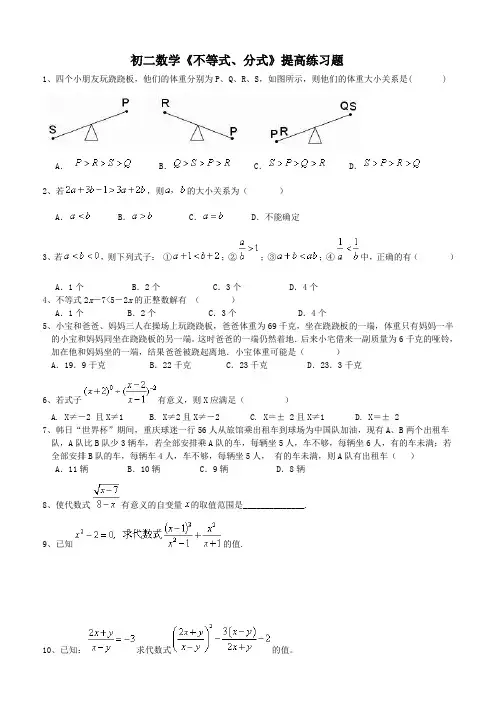
初二数学《不等式、分式》提高练习题1、四个小朋友玩跷跷板,他们的体重分别为P、Q、R、S,如图所示,则他们的体重大小关系是( )A.B. C. D.2、若,则的大小关系为()A. B.C. D.不能确定3、若,则下列式子:①;②;③;④中,正确的有()A.1个 B.2个 C.3个 D.4个4、不等式2x-7<5-2x的正整数解有()A.1个B.2个 C.3个 D.4个5、小宝和爸爸、妈妈三人在操场上玩跷跷板,爸爸体重为69千克,坐在跷跷板的一端,体重只有妈妈一半的小宝和妈妈同坐在跷跷板的另一端。
这时爸爸的一端仍然着地.后来小宅借来一副质量为6千克的哑铃,加在他和妈妈坐的一端,结果爸爸被跷起离地.小宝体重可能是()A.19.9于克 B.22千克 C.23千克 D.23.3千克6、若式子有意义,则X应满足()A. X≠-2 且X≠1B. X≠2且X≠-2C. X=± 2且X≠1D. X=± 27、韩日“世界杯”期间,重庆球迷一行56人从旅馆乘出租车到球场为中国队加油,现有A、B两个出租车队,A队比B队少3辆车,若全部安排乘A队的车,每辆坐5人,车不够,每辆坐6人,有的车未满;若全部安排B队的车,每辆车4人,车不够,每辆坐5人,•有的车未满,则A队有出租车()A.11辆 B.10辆 C.9辆 D.8辆8、使代数式有意义的自变量的取值范围是______________.9、已知的值.10、已知:求代数式的值。
11每户每月用水量不超过10吨(含10吨)超过10吨的部分水费单价 1.30元/吨 2.00元/吨(1(2)若小华家四月份付水费17元,问他家四月份用水多少吨?(3)已知某住宅小区100户居民五月份交水费共1682元,且该月每户用水量均不超过15吨(含15吨),求该月用水量不超过10吨的居民最多可能有多少户?12、县公路局为了对某段公路进行绿化,计划购买A、B两种树共900棵,A、B两种树的相关信息如下表:项目单价(元/棵) 成活率品种A 80 92%B 100 98%设购买A种树x棵,购树所需的总费用为y元.(1)求y与x之间的函数关系式;(2)若购树的总费用不超过82000元,则购A种树不少于多少棵?(3)若希望这批树的成活率不低于94%,且使购树的总费用最低,应选购A、B两种树各多少棵?此时最低费用为多少?13、某公司有型产品40件,型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:型利润型利润甲店200 170乙店160 150(1)设分配给甲店型产品件,这家公司卖出这100件产品的总利润为(元),求关于的函数关系式,并求出的取值范围;(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来;(3)为了促销,公司决定仅对甲店型产品让利销售,每件让利元,但让利后型产品的每件利润仍高于甲店型产品的每件利润.甲店的型产品以及乙店的型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?14、求不等式的整数解。
八年级不等式培优题

不等式提高练习一、选择题(每小题3分,共30分)1..下列不等式一定成立的是( )A.5a >4aB.x +2<x +3C.-a >-2aD.aa 24> 2.不等式-3x +6>0的正整数有( )A.1个B.2个C.3个D.无数多个3. .在数轴上与原点的距离小于8的点对应的x 满足( )A.-8<x <8B.x <-8或x >8C.x <8D.x >84.若不等式组⎩⎨⎧>≤11x m x 无解,则m 的取值范围是( )A.m <11B.m >11C.m ≤11D.m ≥115.要使函数y =(2m -3)x +(3n +1)的图象经过x 、y 轴的正半轴,则m 与n 的取值应为( )A.m >23,n >-31B.m >3,n >-3C.m <23,n <-31D.m <23,n >-31 6. 如右图,当0<y 时,自变量 x 的范围是( )A 、2-<xB 、2->xC 、2<xD 、2>x7. 如果10<<x ,则下列不等式成立的( )A 、x x x 12<<B 、x x x 12<<C 、21x x x <<D 、x x x<<21 8. 若a>b>0, 则下列结论正确的是 ( )(A) -a>-b (B)ba 11> (C)a 3<0 (D)a 2>b 29.某射击运动员在一次比赛中前6次射击共中52环,如果他要打破89环(10次射击)的记录,第七次射击不能少于( )环(每次射击最多是10环)A 、5B 、6C 、7D 、810.初三的几位同学拍了一张合影作留念,已知冲一张底片需要0.80元,洗一张相片需要0.35元.在每位同学得到一张相片、共用一张底片的前提下,平均每人分摊的钱不足0.5元,那么参加合影的同学人数 .A.至多6人 B.至少6人 C.至多5人 D.至少5人11.不等式组⎪⎩⎪⎨⎧≤-->84332x x 的最小整数解为 ( ) (A)–1 (B) 0 (C)1 (D) 412、如果10<<x ,则下列不等式成立的( )A 、x x x 12<<B 、x x x 12<<C 、21x x x <<D 、x x x<<21 13、在平面直角坐标系内,点P (3-m ,5-m )在第四象限,则m 的取值范围是( )A 、35<<-mB 、53<<-mC 、53<<mD 、35-<<-m二、填空题:(每题3分,共15分)1、若11|1|-=--x x ,则x 的取值范围是_______ 2、 如果关于x 的不等式5)1(+<-a x a 和42<x 的解集相同,则a 的值为________.3、若b a <,用“<”或“>”号填空:2a______b a +,33a b -_____. 4、 点A (-5,1y )、B (-2,2y )都在直线x y 2-=上,则1y 与2y 的关系是 。
第3章 一元一次不等式 浙教版数学八年级上册培优试卷(含答案)
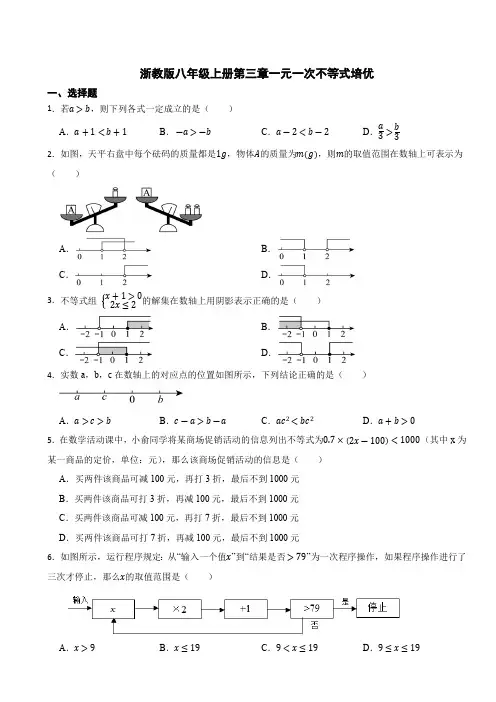
浙教版八年级上册第三章一元一次不等式培优一、选择题1.若a>b,则下列各式一定成立的是( )A.a+1<b+1B.―a>―b C.a―2<b―2D.a3>b32.如图,天平右盘中每个砝码的质量都是1g,物体A的质量为m(g),则m的取值范围在数轴上可表示为( )A.B.C.D.3.不等式组x+1>02x≤2的解集在数轴上用阴影表示正确的是( )A.B.C.D.4.实数a,b,c在数轴上的对应点的位置如图所示,下列结论正确的是( )A.a>c>b B.c―a>b―a C.a c2<b c2D.a+b>05.在数学活动课中,小俞同学将某商场促销活动的信息列出不等式为0.7×(2x―100)<1000(其中x为某一商品的定价,单位:元),那么该商场促销活动的信息是( )A.买两件该商品可减100元,再打3折,最后不到1000元B.买两件该商品可打3折,再减100元,最后不到1000元C.买两件该商品可减100元,再打7折,最后不到1000元D.买两件该商品可打7折,再减100元,最后不到1000元6.如图所示,运行程序规定:从“输入一个值x”到“结果是否>79”为一次程序操作,如果程序操作进行了三次才停止,那么x的取值范围是( )A.x>9B.x≤19C.9<x≤19D.9≤x≤197.若关于x 的不等式组4―(x ―2)≥33x ―a >2x有且只有4个整数解,则a 的取值范围是( )A .―1≤a <0B .―1<a ≤0C .0<a ≤1D .0≤a <18.若x 为实数,则[x ]表示不大于x 的最大整数,例如[1,6]=1,[π]=3,[―2,82]=―3等.[x ]+1是大于x 的最小整数,则方程6x ―3[x ]+9=0的解是( )A .x =―83B .x =―196C .x =―72或x =―3D .x =―83或x =―1969.已知三个实数a ,b ,c 满足a ―2b ―c =0,a +2b ―c <0,则( )A .b <0,b 2+ac ≤0B .b <0,b 2+ac ≥0C .b >0,b 2+ac ≤0D .b >0,b 2+ac ≥010. 已知关于x 的分式方程mx(x ―2)(x ―6)+2x ―2=3x ―6无解,且关于y 的不等式组m ―y >4y ―4≤3(y +4)有且只有三个偶数解,则所有符合条件的整数m 的乘积为( )A .1B .2C .4D .8二、填空题11.若(m ―1)x >(m ―1)的解集是x <1,则m 的取值范围是 ;12.一罐饮料净重300g ,罐上标注有“蛋白质含量≥0.5%”,其中蛋白质的含量至少为 g .13.若关于x 的不等式组x <1x ≤a 的解集是x <1,则a 的值可以是 (写出一个即可).14.关于x 的方程k ―2x =3(k ―2)的解为非负数,且关于x 的不等式x ―2(x ―1)≤32k +x 3≥x 有解,求符合条件的所有整数k 的值的积为 .15.若关于x 的不等式组―6<x <2x ―m <m无解,那么m 的取值范围是 16.对非负实数x“四舍五入”到个位的值记为<x >,即:当n 为非负整数时,如n ﹣12≤x <n+12,则<x >=n .如:<0.48>=0,<3.5>=4.如果<x >=97x ,则x = .三、解答题17.课堂上,老师设计了“接力游戏”,规则:一列同学每人只完成解不等式的一步变形,即前一个同学完成一步,后一个同学接着前一个同学的步骤进行下一步变形,直至解出不等式的解集.请根据下面的“接力游戏”回答问题.接力游戏老师:3x +12―1>5x ―43甲同学:3(3x +1)―6>2(5x ―4)乙同学:9x+3―6>10x―8丙同学:9x―10x>―8―3+6丁同学:―x>―5戊同学:x>5任务一:①在“接力游戏”中,乙同学是根据______进行变形的.A.等式的基本性质B.不等式的基本性质C.乘法对加法的分配律②在“接力游戏”中,出现错误的是______同学,这一步错误的原因是______.任务二:在“接力游戏”中该不等式的正确解集是______.任务三:除纠正上述错误外,请你根据平时的学习经验,针对解不等式时还需要注意的事项给同学们提一条建议.18.解不等式1―x3―x<3―x+24.并把解集表示在数轴上.19.解不等式组:5x―6≤2(x+2) x4―1<x―3320.如图,点A,B均在数轴上,点B在点A的右侧,点A对应的数字是―4,点B对应的数字是m.(1)若AB=2,求m的值;(2)将AB线段三等分,这两个等分点所对应数字从左到右依次是a1,a2,若a2>0,求m的取值范围.21.如图所示的是某大院窗格的一部分,其中“O”代表窗格上所贴的剪纸,设第x个窗格上所贴“O”的个数为y.(1)填写下表.x12345xy581117(用含x的式子表示)(2)若第x个窗格上所贴的“O”的个数大于50,求x的取值范围.22.如图,在平面直角坐标系xOy中,已知A(1,a),B(b,3),E(3―a,0),其中a,b满足|a―5|+b―4=0.平移线AB段得到线段CD,使得C,D两点分别落在y轴和x轴上.(1)①点A的坐标是____________;点B的坐标是____________;②求三角形OCD的面积.(2)将点E向下移动1个单位长度得到点F,连接FC,FD,Q(m,0)是x轴负半轴上一点.若三角形QCD 的面积不小于三角形FCD的面积,求m的取值范围.23.如图,在平面直角坐标系中,三角形ABC的三个顶点的坐标分别为A(a,0),B(0,b),C(2,4),且2a+b+10+|3a―2b+8|=0.(1)求a,b的值;,求t的取值范围;(2)点D(t,0)为x轴上一点,且S三角形ABD≤13S三角形ABC(3)平移三角形ABC到三角形EFG(其中点A,B,C的对应点分别为点E,F,G),设E(m,n),F (p,q),且满足5m―n=43p―q=4,请直接写出点G的坐标.答案解析部分1.【答案】D 2.【答案】A 3.【答案】C 4.【答案】C 5.【答案】C 6.【答案】C 7.【答案】A 8.【答案】C 9.【答案】B 10.【答案】B 11.【答案】m <112.【答案】1.513.【答案】2(答案不唯一)14.【答案】015.【答案】m ≤―316.【答案】0或79或149.17.【答案】任务一:①C ;②戊;不等式的两边同时乘以―1,不等号的方向没有改变任务二:x <5任务三:去括号时,括号前面是“―”,去括号后,括号的每一项都要变号,或移项要变号18.【答案】x >―219.【答案】0<x ≤10320.【答案】(1)―2(2)m >221.【答案】(1)14,3x +2(2)x >16.22.【答案】(1)①A (1,5),B (4,3),②3(2)m ≤―7223.【答案】(1)a 的值为―4,b 的值为―2(2)―10≤t ≤2(3)G(8,10)。
浙教版八年级上册一元一次不等式专题培优(附答案)

浙教版八年级上册一元一次不等式专题培优(附答案)八年级上册一元一次不等式专题培优基础巩固1.不等式 $x+1\geq2x-1$ 的解集在数轴上表示为()。
答案:$[2,+\infty)$2.已知$a>b$,$c\neq0$,则下列关系一定成立的是()。
A。
$ac>bc$B。
$\frac{c}{a}>\frac{c}{b}$C。
$c-a>c-b$D。
$c+a>c+b$答案:A3.若实数 $3$ 是不等式 $2x-a-2<0$ 的一个解,则 $a$ 可取的最小正整数为()。
答案:$5$4.下列命题中:①如果 $a1-a$ 的解集是 $x<-1$,则 $a<1$;③若 $\frac{6-x}{3}$ 是自然数,则满足条件的正整数 $x$ 有$4$ 个。
正确的命题有()。
A。
个B。
$1$ 个C。
$2$ 个D。
$3$ 个答案:C5.若关于$x$,$y$ 的二元一次方程组的解满足$x+y<2$,则 $a$ 的取值范围是()。
A。
$a>2$B。
$a<2$C。
$a>4$D。
$a<4$答案:B6.若 $x$ 的 $3$ 倍大于 $5$,且 $x$ 的一半与 $1$ 的差不大于 $2$,则 $x$ 的取值范围是()。
答案:$[\frac{7}{3},+\infty)$7.若 $ab$ 的解集是 $x<\frac{a}{b}$,则 $a$ 的取值范围是()。
答案:$(-\infty,0)\cup(b,+\infty)$8.若在数轴上表示关于 $x$ 的不等式 $x-3>\frac{2}{3}$ 的解集如图所示,则 $a$ 的值是()。
答案:$a=\frac{11}{3}$9.如图,若开始输入的 $x$ 的值为正整数,最后输出的结果为 $144$,则满足条件的 $x$ 的值为()。
答案:$6$10.解下列不等式,并把解集表示在数轴上。
初二上培优辅导资料10(不等式和不等式组)
初二上培优辅导资料10不等式和不等式组例1.解不等式组,并把解集在数轴上表示出来.⎩⎪⎨⎪⎧ x -32+3≥x +1,1-3(x -1)<8-x .①②例2.如果关于x 的方程a3-2x =4-a 的解大于方程a (x -1)=x (a -2)的解,求a 的取值范围.例3.已知方程组⎩⎪⎨⎪⎧2x +y =2-5a ,x -2y =3a 的解x ,y 的和是负数,求满足条件的最小整数a .例4.若不等式组 ⎩⎪⎨⎪⎧2x -a <1,x -2b >3的解集为−1<x<1,求(a+1)(b −1)的值.例5.x 为何值时,代数式5123--+x x 的值是非负数?例6.已知:关于x 的方程m x m x =--+2123的解的非正数,求m 的取值范围.例7.关于y x ,的方程组⎩⎨⎧-=-+=+131m y x m y x 的解满足x >y ,求m 的最小整数值.例8.试确定实数a 的取值范围,使不等式组⎩⎨⎧x 2+x +13>0,x +5a +43>43(x +1)+a恰有两个整数解.练习:一、选择题:1.已知a >b ,c 为任意实数,则下列不等式中总是成立的是( )A .a +c <b +cB .a -c >b -cC .ac <bcD .ac >bc 2.下列说法中,错误的是( )A .不等式x <2的正整数解中有一个B .-2是不等式2x -1<1的一个解C .不等式-3x >9的解集是x >-3D .不等式x <10的整数解有无数个 3.已知不等式x -1≥0,此不等式的解集在数轴上表示为( )4.已知点M (1-2m ,m -1)关于x 轴的对称点在第一象限,则m 的取值范围在数轴上表示正确的是( )5.不等式⎩⎪⎨⎪⎧2x -1≥x +1,x +8≤4x -1的解集是( )A .x ≥3B .x ≥2C .2≤x ≤3D .空集6.不等式组⎩⎪⎨⎪⎧x -1≥0,4-2x >0的解集在数轴上表示为( )7.如图2-2-2,数轴上表示的是下列哪个不等式组的解集( )图2-2-2 A.⎩⎪⎨⎪⎧ x ≥-5,x >-3 B.⎩⎪⎨⎪⎧ x >-5,x ≥-3 C.⎩⎪⎨⎪⎧ x <5,x <-3 D.⎩⎪⎨⎪⎧x <5,x >-3 8.某校学生志愿服务小组在“学雷锋”活动中购买了一批牛奶到敬老院慰问老人.如果分给每位老人4盒牛奶,那么剩下28盒牛奶;如果分给每位老人5盒牛奶,那么最后一位老人分得的牛奶不足4盒,但至少1盒.则这个敬老院的老人最少有( )A .29人B .30人C .31人D .32人9.不等式组⎩⎪⎨⎪⎧x -1≤0,2x +4>0的解集在数轴上表示为( ).10.不等式-3<x ≤2的所有整数解的代数和是( ).A .0B .6C .-3D .311.已知关于x 的方程ax -3=0的解是x =2,则不等式-⎝⎛⎭⎫a +32x ≤1-2x 的解集是( ). A .x ≥-1B .x ≤-1C .x ≥32D .x ≤3212.已知关于x 的不等式组⎩⎪⎨⎪⎧x -a ≥0,4-x >1的整数解共有5个,则a 的取值范围是( ).A .-3<a <-2B .-3<a ≤-2C .-3≤a ≤-2D .-3≤a <-213.已知关于x 的不等式组⎩⎨⎧+<-≥-122b a x b a x 的解集为3≤x <5,则a b的值是 ( )A .―2B .―21 C .-4 D .―41二、填空题1.不等式x +2>6的解集为______.2.不等式2x -1>12x 的解是______.3.不等式组⎩⎪⎨⎪⎧x +12≤1,1-2x <4的整数解是______.4.小宏准备用50元钱买甲、乙两种饮料共10瓶.已知甲饮料每瓶7元,乙饮料每瓶4元,则小宏最多能买______瓶甲饮料.5.不等式组⎩⎪⎨⎪⎧2x >10-3x ,5+x ≥3x 的解集为________.6.已知关于x 的不等式组⎩⎪⎨⎪⎧x -a >0,1-x >0的整数解共有3个,则a 的取值范围是__________.7.若代数式3x -15的值不小于代数式1-5x6的值,则x 的取值范围是__________.8.若点(1-2m ,m -4)在第三象限内,则m 的取值范围是______.9.若不等式组⎩⎪⎨⎪⎧x >a +2,x <3a -2无解,则a 的取值范围是__________.三、解答题1.解不等式组,并把解集在数轴上表示出来.(1)10(x -3)-4≤2(x -1) (2)x ―2x ―68+x <1-31+x(3) ⎩⎪⎨⎪⎧x -3(x -2)≤4, ①1+2x 3>x -1. ② (4)⎩⎨⎧≤->+423532x x(5)⎪⎩⎪⎨⎧-≤-+>-23722)1(315x x x x (6)3(1)7251.3x x xx --⎧⎪⎨--<⎪⎩≤, ① ②(7)3(1)7251.3x x x x --⎧⎪⎨--<⎪⎩≤,① ②. (8)341221x x +≤--.2.解不等式组331213(1)8x x x x -⎧++⎪⎨⎪--<-⎩,,≥并写出该不等式组的整数解.3.是否存在整数m ,使关于x 的不等式m m x m x 931+>+与321mx x +->+是同解不等式?若存在,求出整数m 和不等式的解集;若不存在,请说明理由.4.三角形的三边长分别是3、(1-2a )、8,求a 的取值范围。
8年级(下)培优课程【2】不等式含参问题、三角形的综合
【2】不等式含参问题、三角形的综合考点一:根据不等式的解集情况求参数例1、若关于x的一元一次不等式组有三个整数解,则m的取值范围是.变式1:若关于x的一元一次不等式组的解集为x>3,那么a的取值范围是.变式2:关于x的不等式组的解集中至少有5个整数解,则正数a的最小值是.考点二:“新定义”在不等式中应用求参数例2、新定义:对非负数x“四舍五入“到个位的值记为<x>,即当n为非负数时,若n﹣≤x<n+,则<x>=n.例如<0>=<0.49>=0,<0.5>=<1.49>=1,<2>=2,<3.5>=<4.23>=4,…试回答下列问题:(1)填空:①<9.6>=;②如果<x>=2,实数x的取值范围是.(2)若关于x的不等式组的整数解恰有4个,求<m>的值;(3)求满足<x>=x的所有非负实数x的值.变式1:.阅读下列材料解答问题:新定义:对非负数x“四舍五入”到个位的值记为<x>,即:当n为非负整数时,如果n﹣≤x<n+,则<x>=n;反之,当n为非负整数时,如果<x>=n,则n﹣≤x<n+.例如:<0.1>=<0.49>=0,<1.51>=<2.48>=2,<3>=3,<4.5>=<5.25>=5,…试解决下列问题:(1)①<π+2.4>=(π为圆周率);②如果<x﹣1>=2,则数x的取值范围为;(2)求出满足<x>=x﹣1的x的取值范围.变式2:若一元一次方程的解也是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.例如:方程2x﹣6=0的解为x=3,不等式组的解集为2<x<5,因为2<3<5,所以方程2x﹣6=0为不等式组的关联方程.(1)在方程①5x﹣3=0,②x﹣3=0中,不等式组的关联方程是.(填序号);(2)若不等式组的一个关联方程的根是整数,则这个关联方程可以是.(写出一个即可);(3)若方程x=2与x=3都是关于x的不等式组的关联方程,求m的取值范围.考点三:与三角形有关的性质及计算1例3、已知等腰三角形的一腰上的高与底边的夹角为40度,那么它的顶角为.变式1:已知等腰三角形的一个内角为50°,则顶角为度.变式2:等腰三角形中有一个内角是70°,则另外两个内角的度数分别为.变式3:如图,在底边BC为2,腰AB为2的等腰三角形ABC中,DE垂直平分AB于点D,交BC于点E,则△ACE的周长.变式4:如图,△ABC中,D是AB的中点,DE⊥AB,∠ACE+∠BCE=180°,EF⊥AC交AC 于F,AC=12,BC=8,则AF=.变式5:如图,△ABC中,AB=AC,AD⊥BC于D点,DE⊥AB于点E,BF⊥AC于点F,DE =3cm,则BF=cm.变式6:如图,在四边形ABCD中,∠ABC=∠ADC=90°,AC=26,BD=24,M、N分别是AC、BD的中点,则线段MN的长为.考点四:与三角形有关的最值问题例4、如图,已知点P是∠AOB角平分线上的一点,∠AOB=60°,PD⊥OA,M是OP的中点,DM=4cm,如果点C是OB上一个动点,则PC的最小值为cm.例5、如图,在锐角三角形ABC中,AB=4,△ABC的面积为10,BD平分∠ABC,若M、N 分别是BD、BC上的动点,则CM+MN的最小值为.例6、如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB 上的动点,∠AOB=30°,则△PMN周长的最小值=.变式1:如图,P是∠AOB的角平分线上的一点,∠AOB=60°,PD⊥OA,M是OP的中点,点C是OB上的一个动点,若PC的最小值为3cm,则MD的长度为cm.变式2:如图,点M是∠AOB平分线上一点,∠AOB=60°,ME⊥OA于E,OE=,如果P是OB上一动点,则线段MP的取值范围是.变式3:如图,∠AOB=30°,点M、N分别是射线OB、OA上的动点,点P为∠AOB内一点,且OP=8,则△PMN的周长的最小值=.变式4:如图,在四边形ABCD中,∠DAB=130°,∠D=∠B=90°,点M,N分别是CD,BC上两个动点,当△AMN的周长最小时,∠AMN+∠ANM的度数为.变式5:如图,在△ABC中,∠C=90°,AC=4,BC=2,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动,在运动过程中,点B到原点的最大距离是.考点五:与三角形有关的证明及计算例7、(1)如图1,已知△ABC,以AB,AC为边向△ABC外做等边△ABD和等边△ACE,连接BE,CD,求证:BE=CD;(2)如图2,已知△ABC,以AB,AC为边向外作正方形ABFD和正方形ACGE,连接BE,CD,BE与CD有什么数量关系?简单说明理由;(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:如图3,要测量池塘两岸相对的两点B,E的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=60米,AC=AE,求BE的长.变式1:(1)问题发现:如图1,△ABC和△DCE均为等边三角形,当△DCA应转至点A,D,E在同一直线上,连接BE,易证△BCE≌△ACD,则①∠BEC=;②线段AD,BE之间的数量关系;(2)拓展研究:如图2,△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=90°,点A,D,E在同一直线上,若AE=12,DE=7,求AB的长度;(3)如图3,P为等边三角形ABC内一点,且∠APC=150°,∠APD=30°,AP=4,CP =3,DP=7,求BD的长.变式2:如图1,在等边△ABC 中,线段AM 为BC 边上的中线,动点D 在直线AM (点D 与点A 重合除外)上时,以CD 为一边且在CD 的下方作等边△CDE ,连接BE . (1)判断AD 与BE 是否相等,请说明理由;(2)如图2,若AB =8,点P 、Q 两点在直线BE 上且CP =CQ =5,试求PQ 的长;(3)在第(2)小题的条件下,当点D 在线段AM 的延长线(或反向延长线)上时.判断PQ 的长是否为定值,若是请直接写出PQ 的长;若不是请简单说明理由.考点五:一次函数综合 如图,直线l 1的解析表达式为112y x =+,且l 1与x 轴交于点D ,直线l 2经过点A 4,0)(、B (1,5)-,直线l 1与l 2交于点C . (1)求直线l 2的函数关系式; (2)求△ADC 的面积;(3)在直线l 2上是否存在一点P ,使得△CDP 的面积为6?若存在,请求出点P 的坐标;若不存在,请说明理由。
完整版八年级不等式培优提高练习
是( )v 0的解集是( )A . x >--B . x v-丄C . x >-丄D . x v 丄5 5553.若不等式(ax - 1) (x+2)> 0的解集是-3v x v- 2,那么a 等于()A . 4B . 2C . 3D .丄2 25.若关于x 的不等式组{;浆畀整数解共有3个,则m的取值范围是()A . 5v m < 6B . 5< m v 6C . 5< m < 6D . 5v m v 66.已知a >b , CM 0,则下列关系一定成立的是()A . ac >beB .丄•一C . C - a >C - bD . c+a >c+bc c7. 下列命题中:① 如果a v b ,那么ae 2v be 2;② 关于x 的不等式(a- 1) x > 1 - a 的解集是x v- 1,贝U a v 1; ③ 若一^是自然数,则满足条件的正整数 x 有4个.6-x 正确的命题个数是() A . 0B . 1C . 2D . 38.若x 是方程2x+m - 3 (m - 1) =1+x 的解为负数,贝U m 的取值范围是( )A . m >-1B . m v-1C . m > 1D . m v 11 •若关于x 的不等式组 2恰好只有四个整数解,则 a 的取值范围2x+2<3(x+a)A- a" '2 .设a , b 是常数,D. - 2 1-—,则关于x 的不等式 bx - aB . 不等式43C .- 2 1 :-— 3>0的解集为x v£54.不等式二了-厂」—:-厂的解集为x >2,则m 的值为(9.按下面的程序计算:若输入x=100,输出结果是501,若输入x=25,输出结果是631,若开始输入的 x 值为正整数,最后输出的结果为 556,则开始输入的x 值可能有( )A . 1种B . 2种C . 3种D . 4种10. 若x 为任意实数时,二次三项式x 2-6x+c 的值都不小于0,则常数c 满足的 条件是( )A . c >0B . c >9C . c >0D . c >911. 关于x 的方程mx -仁2x 的解为正实数,则 m 的取值范围是( )A . m > 2B . m < 2C . m > 2D . m v 2C-1 d ( y —1 }12 .关于x 的不等式组的解集为x v 3,那么m 的取值范围为( ) A . m=3B . m > 3C . m v 3D . m > 313 .已知△ ABC 的边长分别为2x+1,3x ,5,则厶ABC 的周长L 的取值范围是( ) A . 6v L v 36B . 10v L < 11C . 11< L v 36D . 10v L v 3614 .已知实数x 、y 同时满足三个条件:①3x - 2y=4 - p ,②4x - 3y=2+p ,③x > y ,那么实数p 的取值范围是( )A . p >- 1B . p v 1C . p v- 1D . p > 115 .关于x 的不等式组 、 的解集是x >- 1,则m= _________ .x>ir+216 .若不等式组 <2x _a <^ jJ 二 的解集为-1 v x v 1,那么(a+1) (b - 1)的值等 于范围是17 .已知关于x 、y 的二元一次方程组xf2y--2的解满足x+y >2,则k 的取值18 .若不等式组 有解,那么a 必须满足19 .已知a 、b 都是实数,且a=y-,b=—,b v*v 2a ,那么实数x 的取值范围是________20. 若关于x 、y 的二元一次方程组* *于加'1的解满足x+y >0,则m 的取值范x+3y=3 围是 _______ .21.关于x的不等式x - 3>丄一的解集在数轴上表示如图所示,则 a 的值是 _______ ._1~ 1 2 3 4 5 7^22.已知关于x 的分式方程 的解为负数,那么字母 a 的取值范围 R +2 JJ +2是 _______ .23. 求不等式(2x - 1) (x+3)> 0的解集.请你仿照上述方法解决下列问题: (1) 求不等式(2x - 3) (x+1)v 0的解集.解:根据 同号两数相乘,积为正”可得:① r2x-l>0K +3>0r2x-l<0解①得x;解②得x V- 3.•••不等式的解集为x或 x v- 3.(2)求不等式> 0的解集.24. x取哪些整数值时,不等式5x+2>3 (x- 1)与丄x- K 7-一二都成立?25.已知关于x的不等式组恰好有两个整数解, 求实数a的取值范围.26. 已知一元一次不等式mx - 3> 2x+m.(1)若它的解集是XV-—,求m的取值范围;rn-2(2)若它的解集是x>-,试问:这样的m是否存在?如果存在,求出它的值;4如果不存在,请说明理由.27. 用等号或不等号填空:(1)比较4m与m2+4的大小当m=3 时,4m ______ m2+4当m=2 时,4m ______ m2+4当m= - 3 时,4m ____ m2+4(2)无论取什么值,4m与m2+4总有这样的大小关系吗?试说明理由.(3)比较x2+2与2x2+4x+6的大小关系,并说明理由.(4)比较2x+3与-3x- 7的大小关系.28.是否存在整数m ,使关于x 的不等式1七厶—与关于x 的不等式x+1> m m m的解集相同?若存在,求出整数 m 和不等式的解集;若不存在,请说 明理由.29. 已知关于x 的不等式(2a- b ) x+a- 5b >0的解集为x<—, (1) 求丄的值.(2) 求关于x 的不等式ax > b 的解集.值.31. 小明把三个数-1, 2 -a, 丄在数轴上从左到右依次排列在三个对应点上, 你能确定a 的取值范围吗?请写出你的解答过程.32. 阅读下面的例题,并回答问题.30. 若不等式组的偶数解a 满足方程组I" ax-y--7 |2x4-3y=7.求x 2+y 2的【例题】解一元二次不等式:x2- 2x- 8>0.解:对x2- 2x- 8分解因式,得x2- 2x- 8= (x - 1) 2- 9= (x - 1) 2-32= (x+2) (x - 4), •'•(x+2) (x - 4)> 0.由两实数相乘,同号得正,异号得负”,可得解①得x>4;解②得X V- 2.故x2- 2x - 8>0的解集是x>4或x V- 2.(1)_____________________________ 直接写出x2- 9>0的解是;(2)仿照例题的解法解不等式:x2+4x- 21V0;(3)求分式不等式:二一w 0的解集.x-2。
【湘教版】八年级数学上4.1不等式能力培优训练(含答案)
专题列不等式 1.四个小朋友玩跷跷板,他们的体重分别为 P , Q , R , S ,如图所示,则他们的体重大小关P > R >S > Q B . Q >S > P >R C . S >P > Q > R 2. 下列关于 a a 用不等式表示正确的是A. a a 0B. a a 0C. |a a 0D. a a 03. 某工地实施爆破,操作人员点燃导火线后,必须在炸药爆炸前跑到400m 外安全区域, 若导火线燃烧的速度为 1.1cm/秒,人跑步的速度为5m/秒,则导火线的长xcm 应满足的不 等式是: ____________________ .4.辽宁崗部忒冇“半駅之乡 F 勺关称―臬字细织 衲汽乍装运A Ji 阴种苹果到外地硝宙”按规足冊辆乍H 装冋一种 申杲-冃.必须较满”已血每辆仆的运鞍葷型毎吨苹果的获利情况如下表所示1A毎轴1 A 车运4* W ( im ? :<2 审汆抿利E n 儿>5 . y J(1)変求」戏运小苹生节加裝运种 苹 跟的汽乍散M <辆了 z 满足的不等式5 < 3芒荻刑」彳“少 F 12 600丿C ・试"J f I ]隨迖A 种苹果的汽车数 d: J (辆》炖满足的知一伞 不警式.状元笔记【知识要点】不等式:用不等号 >”.N”. “N”“W”“壬连接而成的式子叫作不等式.【温馨提示】注意 不大于“.不小于“.不超过”等字表示不等时要带上 “=号.4. 1 不等式玄阜系疋D . S > P > R >Q【方法技巧】1仔细审题,抓住题中的关键字小于”.大于”.不大于”.不小于”.不超过”列不等式. 2•列不等式时还应掌握常见的数量关系式,如:速度刘寸间=路程,单价W数量=总价,工作效率 >工作时间=工作总量等.参考答案:1. D 解析:观察前两幅图易发现S> P > R,再观察第一幅和第三幅图可以发现R> Q.2. D 解析:分两类讨论:a 0时,|a| a 2a ,显然|a| a 0 ;当a 0时,a a a a 0,故同a 0.x3. 5 4001.14.解:(1) 3x 2(10 x) 26 ;(2) 5x 9(10 x) 126 .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
不等式提高练习一、选择题(每小题3分,共30分)1..下列不等式一定成立的是( )A.5a >4aB.x +2<x +3C.-a >-2aD.aa 24> 2.不等式-3x +6>0的正整数有( )A.1个B.2个C.3个D.无数多个 3. .在数轴上与原点的距离小于8的点对应的x 满足( )A.-8<x <8B.x <-8或x >8C.x <8D.x >8 4.若不等式组⎩⎨⎧>≤11x mx 无解,则m 的取值范围是( )A.m <11B.m >11C.m ≤11D.m ≥115.要使函数y =(2m -3)x +(3n +1)的图象经过x 、y 轴的正半轴,则m 与n 的取值应为( )A.m >23,n >-31B.m >3,n >-3C.m <23,n <-31D.m <23,n >-31 6. 如右图,当0<y 时,自变量 x 的范围是( )A 、2-<xB 、2->xC 、2<xD 、2>x 7. 如果10<<x ,则下列不等式成立的( )A 、x x x 12<< B 、x x x 12<< C 、21x x x << D 、x x x<<21 8. 若a>b>0, 则下列结论正确的是 ( ) (A) -a>-b (B)ba 11> (C)a 3<0 (D)a 2>b 2 9.某射击运动员在一次比赛中前6次射击共中52环,如果他要打破89环(10次射击)的记录,第七次射击不能少于( )环(每次射击最多是10环)A 、5B 、6C 、7D 、810.初三的几位同学拍了一张合影作留念,已知冲一张底片需要0.80元,洗一张相片需要0.35元.在每位同学得到一张相片、共用一张底片的前提下,平均每人分摊的钱不足0.5元,那么参加合影的同学人数 . A.至多6人B.至少6人C.至多5人D.至少5人11.不等式组⎪⎩⎪⎨⎧≤-->84332x x 的最小整数解为 ( )(A)–1 (B) 0 (C)1 (D) 412、如果10<<x ,则下列不等式成立的( )A 、x x x 12<< B 、x x x 12<< C 、21x x x << D 、x x x<<21 13、在平面直角坐标系内,点P (3-m ,5-m )在第四象限,则m 的取值范围是( )A 、35<<-mB 、53<<-mC 、53<<mD 、35-<<-m二、填空题:(每题3分,共15分) 1、若11|1|-=--x x ,则x 的取值范围是_______ 2、 如果关于x 的不等式5)1(+<-a x a 和42<x 的解集相同,则a 的值为________. 3、若b a <,用“<”或“>”号填空:2a______b a +,33ab -_____. 4、 点A (-5,1y )、B (-2,2y )都在直线x y 2-=上,则1y 与2y 的关系是 。
5、若不等式组⎩⎨⎧>-<-3212b x a x 的解集为11<<-x ,那么)3)(3(+-b a 的值等于_______.6、 不等式b ax >的解集是abx <,则a 的取值范围是 。
三、解不等式(组)(每题5分)(1). ⎪⎩⎪⎨⎧-<-+≤-3314)3(265x x x x (2). 0415212<---x x (3).⎩⎨⎧-<-<-2235x x(4)⎪⎩⎪⎨⎧+<-≤+--)1(3151215312x x x x 四、解答题(1)不等式组12,3 5.a x a x -<<+⎧⎨<<⎩的解集是3<x <a +2,则a 的取值范围若关于x 的不等式组211,30x x x k -⎧>-⎪⎨⎪-<⎩的解集为x<2,求k 的取值范围(3)若不等式组1,21x m x m <+⎧⎨>-⎩无解,求m 的取值范围(4)已知关于x ,y 的方程组⎩⎨⎧=+=+3135y x my x 的解为非负数,求整数m 的值(5)画出函数y =3x +12的图象,并回答下列问题:(6分)(1)当x 为什么值时,y >0?(2)如果这个函数y 的值满足-6≤y ≤6,求相应的x 的取值范围. (6)已知方程组⎩⎨⎧=+-=+2212y x my x 的解x 、y 满足x +y >0,求m 的取值范围. (6分【例题1】(1)已知关于x 的不等式组⎩⎨⎧>-≥-0025a x x 无解,则a 的取值范围是是___________。
思路点拨:从数轴上看,原不等式组种两个不等式的解集没有公共部分。
(2)已知不等式03≤-a x 的正整数解恰好是1、2、3,则a 的取值范围是___________。
思路点拨:由题意,结合数轴,理解3a x ≤,作为界点的“3a ”应当3—4之间,即433<≤a【例题2】如果关于x 的不等式组⎩⎨⎧<-≥-0607n x m x 的整数解仅为1、2、3,那么适合这个不等式组的整数对(m ,n )共有_____对。
思路点拨:借助数轴,分别建立m 、n 的不等式,确定整数m 、n 的值。
【例题3】解下列不等式(组)(1)n x m +<+332 (2)1022-≤-x x (3)求不等式321≤-+-x x 的所有整数解。
思路点拨:与方程类似,解含有字母系数的不等式(组)需要对字幕系数进行讨论;解含有绝对值符号的不等式(组)的关键是去掉绝对值符号,化为一般的不等式求解,而“零点分类讨论法”是最有效的方法。
【例题4】已知三个非负数a 、b 、c 满足132523=-+=+c b a bc a 和,若c b a m 73-+=。
求m 的最大值与最小值。
思路点拨:本体综合了方程、不等式组的丰富知识,解题的关键是通过解方程组,用含一个字母的代数式来表示m ,通过解不等式组,确定这个字母的取值范围,在约束条件下,求m 的最大值与最小值。
【课堂练习】1、 若关于不等式组⎪⎩⎪⎨⎧<++>+01456m x xx 的解集为4<x ,则m 的取值范围是______________。
2、 若不等式组⎩⎨⎧>-<-3212b x a x 的解集是11<<-x ,则)1)((-+b a a 的值是_____________。
3、 已知0<a ,且a x a ≤,则262---x x 的最小值是______________。
4、 对于整数a 、b 、c 、d ,符号dcab 表示运算bd ac -,已知3411<<d b ,则b+d 的值是______.。
5、 若01<<<-b a ,则下列式子正确的是____________。
A 、-a<-b B 、ba 11< C 、 b a < D 、22b a >6、若方程组⎩⎨⎧=++=+3414y x k y x 的解满足条件10<+<y x ,则k 的取值范围是__________。
7、已知a 、b 为常数,若0>+b ax 的解集是31<x ,则bx-a<0的解集是_____________。
8、解下列关于x 的不等式(组)。
(1)ab x bb x a +>+22 (2)312≤-x (3)⎪⎩⎪⎨⎧+≥->+<-x x x x x 312113250104 (4)11->-ax ax9、已知方程组⎩⎨⎧=+=-62y mx y x ,若方程组有非负整数解,求正整数m 的的值。
10、如果⎩⎨⎧==21y x 是关于x 、y 的方程08)12(2=+--+--by ax by ax 的解,求不等式组⎪⎩⎪⎨⎧+<-+>--334133x ax b x a x ax 的解集。
11、已知非负实数x 、y ,x 满足433221-=-=-z y x ,记w=3x+4y+5z ,求w 的最大值与最小值。
【能力拓展】12、已知1120<-<x ,则12-x的取值范围是___________。
13、如果关于x 的不等式05)2(>---n m x n m 的解集为710<x ,那么关于x 的不等式mx>n (0≠m )的解集为_______________。
14、已知关于x 、y 的方程组⎩⎨⎧=++=-ay x a y x 523的解满足0>>y x ,化简=-+a a 3________。
15、不等式0)2)((<-+x x x 的解集为______________。
16、关于x 的不等式组⎪⎩⎪⎨⎧+>++-<a x x x x 4231)3(32有四个整数解,则a 的取值范围是________。
17、已知a 为正整数,方程组⎩⎨⎧=+=+62384y x y ax 的解满足0,0<>y x ,则a 的值为__________。
A 卷:基础题一、选择题1.在一次函数y=-2x+8中,若y>0,则( )A.x>4 B.x<4 C.x>0 D.x<02.如下左图是一次函数y=kx+b的图象,当y<2时,x的取值范围是()A.x<1 B.x>1 C.x<3 D.x>33.一次函数y=3x+m-2的图象不经过第二象限,则m的取值范围是()A.m≤2 B.m≤-2 C.m>2 D.m<24.已知函数y=mx+2x-2,要使函数值y随自变量x的增大而增大,则m的取值范围是()A.m≥-2 B.m>-2 C.m≤-2 D.m<-25.直线L1:y=k1x+b与直线L2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b>k2x的解为()A.x>-1 B.x<-1 C.x<-2 D.无法确定二、填空题6.已知y1=3x+2,y2=-x-5,如果y1>y2,则x的取值范围是_____.7.当a取_____时,一次函数y=3x+a+6与y轴的交点在x轴下方.(•在横线上填上一个你认为恰当的数即可)8.已知一次函数y=(a+5)x+3经过第一,二,三象限,则a的取值范围是____.9.一次函数y=kx+2中,当x≥12时,y≤0,则y随x的增大而_____.三、解答题10.一次函数y=2x-a与x轴的交点是点(-2,0)关于y轴的对称点,求一元一次不等式2x-a≤0的解集.11.我边防局接到情报,在离海岸5海里处有一可疑船只A正向公海方向行驶,边防局迅速派出快艇B追赶.图1-5-3中,L A,L B分别表示两船相对于海岸的距离s(海里)与追赶时间t(分)之间的关系.(1)A,B哪个速度快?(2)B能否追上A?12.小华准备将平时的零用钱节约一些储存起来,他已存有62元,•从现在起每个月存12元,小华的同学小丽以前没有存过零用钱,听到小华在存零用钱,•表示从现在起每个月存20元,争取超过小华.(1)试写出小华的存款总数y1与从现在开始的月数x•之间的函数关系式以及小丽存款数y2与与月数x之间的函数关系式;(2)从第几个月开始小丽的存款数可以超过小华?1.(一题多解)已知一次函数y=kx+b中,k<0,则当x1<x2时,x1对应的函数值y1与x2对应的函数值y2之间的大小关系是什么?2.(一题多变题)x为何值时,一次函数y=-2x+3的值小于一次函数y=3x-5的值?(1)一变:x为何值时,一次函数y=-2x+3的值等于一次函数y=3x-5的值;(2)二变:x为何值时,一次函数y=-2x+3的图象在一次函数y=3x-5的图象的上方?(3)三变:已知一次函数y1=-2x+a,y2=3x-5a,当x=3时,y1>y2,求a的取值范围.二、知识交叉题3.(科内交叉题)已知│3a+6│+(a+b+2m)=0,则:(1)当b>0时,求m的取值范围;(2)当b<0时,求m的取值范围;(3)当b=0时,求m的值.4.(科外交叉题)两个物体A,B所受压强分别为P A(帕)与P B(帕)(P A,P B为常数),• 它们所受压力F(牛)与受力面积S(平方米)的函数关系图象分别是射线L A,L B,如图所示,则()A.P A<P B B.P A=P B C.P A>P B D.P A≤P B三、实际应用题5.光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台.•现将这50台联合收割机派往A,B两地区收割小麦,其中30台派往A地区,20台派往B地区.两地区与该农机租赁公司商定的每天的租赁价格见下表:每台甲型收割机的租金每台乙型收割机的租金A地区1800元1600元B地区1600元1200元(1)设派往A地区x台乙型联合收割机,农机租赁公司这50台联合收割机一天获得的租金为y(元),求y与x之间的函数关系式,并写出x的取值范围;(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79600元,•说明有多少种分派方案,并将各种方案设计出来;(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提出一条合理建议.四、经典中考题6.一次函数y=kx+b的图象如图所示,当y<0时,x的取值范围是()A.x>0 B.x<0 C.x>2 D.x<27.李晖到“宁泉牌”服装专卖店做社会调查.了解到商店为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:营业员小俐小花月销售件数(件)200 150月总收入(元)1400 1250假设月销售件数为x件,月总收入为y元,销售1件奖励a元,营业员月基本工资为b元.(1)求a,b的值;(2)若营业员小俐某月总收入不低于1800元,则小俐当月至少要卖服装多少件?C卷:课标新型题1.(条件开放题)当x取______时,一次函数y=-2x+7的函数值为负数.(•在横线上填上一个你认为恰当的数即可)2.(图象信息题)如图,某面粉加工企业急需汽车,但因资金问题无力购买,公司经理想租一辆汽车.一国有公司的条件是每百千米租费110元;•一个体出租车公司的条件是每月付工资1000元,油钱600元,另外每百千米付10元,请问公司经理该根据自己的情况怎样租汽车?3.(最佳方案设计题)某工厂生产某种产品,每件产品的出厂价为1万元,•其原材料成本价(含设备损耗)为0.55万元,同时在生产过程中平均每生产一件产品有1吨废渣产生,为达到国家环保要求,需要对废渣进行脱硫,脱氯等处理,现有两种方案可供选择.方案一:由工厂对废渣直接进行处理,每处理1吨废渣所用的原料费为0.05万元,并且每月设备维护及损耗费为20万元;方案二:工厂将废渣集中到废渣处理厂统一处理,每处理一吨废渣需付0.1•万元的处理费.问:(1)设工厂每月生产x件产品,每月利润为y万元,分别求出方案一和方案二处理废渣时,y 与x之间的关系式(利润=总收入-总支出);(2)若你作为该厂负责人,如何根据月产量选择处理方案,•既可达到环保要求又最合算?3.某学校需刻录一批光盘,若在电脑公司刻录每张需8元(包括空白光盘费);•若学校自制,除租用刻录机需120元外,每张还需成本4元(包括空白光盘费).•问刻录这批电脑光盘到电脑公司刻录费用省,还是自制费用省?请你说明理由.四.应用题某汽车租赁公司要购买轿车和面包车共10辆.其中轿车至少要购买3辆,轿车每辆7万元,面包车每辆4万元,公司可投入的购车款不超过55万元.(10分)(1)符合公司要求的购买方案有哪几种?请说明理由.(2)如果每辆轿车的日租金为200元,每辆面包车的日租金为110元.假设新购买的这10辆车每日都可租出,要使这10 辆车的日租金收入不低于1500元,那么应选择以上哪种购买方案?参考答案A 卷一、1.B 点拨:由题意知-2x+8>0,2x<8,x<4. 2.C 点拨:由图象可知,当y<2时,x<3.3.A 点拨:其图象过第一,三象限或第一,三,四象限. 4.B 点拨:由题意知m+2>0,m>-2. 5.B 二、6.x>-74 点拨:由题意知3x+2>-x -5,4x>-7,x>-74. 7.-7 点拨:当a+6<0,即a<-6时,一次函数y=3x+a+6与y 轴的交点在x 轴的下方,• 此题答案不唯一.8.a>-5 点拨:由题意知a+5>0,a>-59.减小 点拨:由题意可知,直线y=kx+2与x 轴相交于点(12,0),代入表达式求得k=-4<0,y 随x 的增大而减小,也可以通过作图判断.三、10.解:由题意得点(2,0)在y=2x -a 上,所以0=4-a , 所以a=4.当a=4时,2x -4≤0,所以x≤2.11.解:(1)因为直线L A 过点(0,5),(10,7)两点,设直线L A 的解析式为y=k 1x+b ,则15,710b k b =⎧⎨=+⎩,所以1155,k b ⎧=⎪⎨⎪=⎩,所以y=15x+5,因为直线L B 过点(0,0),(10,5)两点, 设直线L B 的解析式为y=k 2x . 当5=10k 2,所以k 2=12,所以y=12x . 因为k 1<k 2,所以B 的速度快. (2)因为k 1<k 2,所以B 能追上A .点拨:根据图象提供的信息,分别求出L A ,L B 的关系式,根据k•值的大小来判断谁的速度快,B 能否追上A .实际上,根据图象就可以直接作出判断. 12.解:(1)y 1=62+12x ,y 2=20x .(2)由20x>62+12x ,得x>7.75,所以从第8个月开始,小丽的存款数可以超过小华.B 卷一、1.解法一:当k<0时,一次函数y=kx+b 中y 随x 的增大而减小,所以当x 1<x 2时,y 1>y 2.解法二:由题意可得1122,y kx b y kx b =+⎧⎨=+⎩,所以1122y b x ky b x k -⎧=⎪⎪⎨-⎪=⎪⎩,由x 1<x 2,得1y b k -<2y bk-,因为k<0,两边同时乘以k ,得y 1-b>y 2-b ,所以y 1>y 2. 点拨:解法一是根据函数性质,判断y 1与y 2的大小,解法二是由方程组得到1122y b x ky b x k -⎧=⎪⎪⎨-⎪=⎪⎩,再由x 1<x 2,得1y b k -<2y bk-,由k<0,得y 1-b>y 2-b ,得y 1>y 2. 2.解:由题意可知-2x+3<3x -5,-5x<-8,x>85.(1)由题意可知-2x+3=3x -5,-5x=-8,x=85.(2)由题意可知-2x+3>3x -5,-5x>-8,x<85.(3)当x=3时,y 1=-6+a ,y 2=9-5a ,因为y 1>y 2, 所以-6+a>9-5a ,6a>15,a>52. 二、3.解:由题意得3a+6=0,a+b+2m=0,由3a+6=0,得a=-2,所以-2+b+2m=0,•即b=2-2m . (1)当b>0时,2-2m>0,2m<2,m<1. (2)当b<0时,2-2m<0,2m>2,m>1. (3)当b=0时,2-2m=0,2m=2,m=1.点拨:由非负数的性质可得到两个方程,由其中一个方程求出a 的值,代入另一个主程,从而得到一个含有b 和m 的方程,用含m 的代数式表示b ,•然后分别代入题目的一个条件中,解不等式或方程即可. 4.A 点拨:在两图象上分别找一点A (S ,F A ),B (S ,F B ),它们的横坐标相同.•由题意知P A =AF S,P B =B F S ,P A -P B =A F S -B F S =A B F F S -,因为F A <F B ,所以F A -F B <0,所以P A -P B =A BF F S-<0,所以P A <P B .三、5.解:(1)派往A 地区的乙型收割机为x 台,则派往A 地区的甲型收割机为(30-x )台,派往B 地区的乙型收割机为(30-x )台,派往B 地区的甲型收割机为(x -10)台,则: y=1600x+1800(30-x )+1200(30-x )+1600(x -10)=200x+74000(10≤x≤30,x•是正整数).(2)由题意得200x+74000≥79600,解得x≥28,由于10≤x≤30,所以x取28,29,30三个值,所以有三种分配方案(方案略).(3)由于一次函数y=200x+74000的值是随着x的增大而增大的,所以当x=30时,•y取最大值.建议农机租赁公司将30台乙型收割机全部派往A地区,20•台甲型收割机全部派往B地区,可使公司获得的租金最高.点拨:根据这50台联合收割机一天获得的租金总额不低于79600元,•得到不等式200x+74000≥79600,解这个不等式,得x的取值范围.注意x为正整数这个条件;•一般情况下,一次函数没有最大(小)值,但根据自变量的取值范围,可求它的最大(小)值.四、6.C 点拨:本题比较容易,考查一次函数的图象,从图象上看y<0时图象在x轴的下方,那么x>2,所以选C.7.解:(1)依题意,得y=ax+b,所以1400200,1250150,a ba b=+⎧⎨=+⎩,解得a=3,b=800.(2)依题意,得y≥1800,即3x+800≥1800,解得x≥33313.答:小俐当月至少要卖服装334件.点拨:列解方程组,求出a,b的值,得到y与x之间的函数关系式,令y≥1800,•得关于x的一元一次不等式,解这个不等式,得x的取值范围,注意x取正整数.C卷1.4 点拨:本题是条件开放题,答案不唯一.2.解:从图象上可以看出:当x<16时,y国有<y个体;当x=16时,y国有=y个体;当x>16时,y国有>y个体.所以若该公司每月业务量小于16百千米时,应选用国有公司的车;若每月业务量等于16百千米时,国有和个体的花费一样多;若每月的业务量大于16百千米时,•应选个体出租车.点拨:数形结合的思想是解决本题的关键.验证结果正确与否,可通过列不等式求解.3.解:(1)y1=x-0.55x-0.05x-20=0.4x-20;y2=x-0.55x-0.1x=0.35x.(2)若y1>y2,0.4x-20>0.35,x>400;若y1=y2,0.4x-20=0.35x,x=400;若y1<y2,0.4x-20<0.35x,x<400.所以当月生产量为400件时,两方案获利一样;当月生产量小于400件时,选择方案二;当月生产量多于400件时,选择方案一.3.解:设需刻录x张光盘,学校自刻的总费用为y1元,电脑公司刻录的总费用为y2元.由题意,得y1=4x+120,y2=8x.(1)当y1>y2时,即4x+120>8x,解得x<30;(2)当y1=y2时,即4x+120=8x,解得x=30;(3)当y1<y2时,即4x+120<8x,解得x>30.所以,当刻录光盘小于30张时,到电脑公司刻录费用省;当刻录光盘等于30张时,两个地方都行;当刻录光盘大于30张时,学校自刻费用省.点拨:本题是经济决策问题,也是近几年中考试题的热点,涉及的知识有函数,不等式,方程等.解决这类问题的关键是先找出相应的数学模型,然后进行抽象,推理,•比较,从而选择最佳的经济方案.。
