电路分析答案第二章
电路的基本分析方法 练习题及答案第2章

第2章 电路的基本分析方法习题答案2-1 在8个灯泡串联的电路中,除4号灯不亮外其它7个灯都亮。
当把4号灯从灯座上取下后,剩下7个灯仍亮,问电路中有何故障?为什么?解:4号灯灯座短路。
如开路则所有灯泡都不亮。
2-2 额定电压相同、额定功率不等的两个白炽灯能否串联使用,那并联呢? 解:不能串联使用,因其电阻值不同,串联后分压不同,导致白炽灯无法正常工作。
在给定的电压等于额定电压的前提下,可以并联使用。
2-3 如图2-34所示,R 1=1Ω,R 2=5Ω,U =6V ,试求总电流强度I 以及电阻R 1、R 2上的电压。
图2-34 习题2-3图解:A 151621=++=R R U I=,V 551= V 111=2211=⨯==⨯=IR U IR U2-4 如图2-35所示,R 1=3Ω,R 2=6Ω,U =6V ,试求总电流I ;以及电阻R 1,R 2上的电流。
图2-35 习题2-4图解:总电阻为:Ω263632121=+⨯+=R R R R R=A 326=∴=R U I=由分流公式得:A 13633A 2363621122121=⨯++=⨯++I=R R R =I I=R R R =I2-5 电路如图2-36(a)~(f)所示,求各电路中a 、b 间的等效电阻R ab 。
(a) (b) (c)(d) (e) (f)2-36 习题2-5图解:(a) Ω4.3)6//4()2//2(ab =+=R(b) Ω2)33//()66//4ab =++(=R (c)Ω2)]6//3()6//3//[(13ab =++)(=R(d) Ω2)6//1)6//3(ab =+)(=R (e) Ω7)10//10(}6//6//]2)8//8{[(ab =++=R (f) Ω6}6//]64)4//4{[()4//4(ab =+++=R2-6 求图2-37所示电路中的电流I 和电压U 。
图2-37 习题2-6电路图解:图2-37等效变换可得:由上图可得;Ω8)816//)]}99//(6[5.7{=+++(总=RA 5.1812==总I 则根据并联电路分流作用可得:A 5.05.1)816()]99//(6[5.7)]99//(6[5.7=1=⨯++++++I则A 15.05.1=13=-=-I I I 总 I 3再次分流可得:A 75.0169999=4=⨯+++IA 25.016996=2=⨯++I所以I =0.75A ,U = U +-U - =9×I 2-8×I 1 = 9×0.25-8×0. 5=-1.75V2-7 电路如图2-38(a)~(g)所示,请用电源等效变换的方法进行化简。
第二章电路的分析方法(答案)

第⼆章电路的分析⽅法(答案)第⼆章电路的分析⽅法本章以电阻电路为例,依据电路的基本定律,主要讨论了⽀路电流法、弥尔曼定理等电路的分析⽅法以及线性电路的两个基本定理:叠加定理和戴维宁定理。
1.线性电路的基本分析⽅法包括⽀路电流法和节点电压法等。
(1)⽀路电流法:以⽀路电流为未知量,根据基尔霍夫电流定律(KCL)和电压定律(KVL)列出所需的⽅程组,从中求解各⽀路电流,进⽽求解各元件的电压及功率。
适⽤于⽀路较少的电路计算。
(2)节点电压法:在电路中任选⼀个结点作参考节点,其它节点与参考节点之间的电压称为节点电压。
以节点电压作为未知量,列写节点电压的⽅程,求解节点电压,然后⽤欧姆定理求出⽀路电流。
本章只讨论电路中仅有两个节点的情况,此时的节点电压法称为弥尔曼定理。
2 .线性电路的基本定理包括叠加定理、戴维宁定理与诺顿定理,是分析线性电路的重要定理,也适⽤于交流电路。
(1)叠加定理:在由多个电源共同作⽤的线性电路中,任⼀⽀路电压(或电流)等于各个电源分别单独作⽤时在该⽀路上产⽣的电压(或电流)的叠加(代数和)。
①“除源”⽅法(a)电压源不作⽤:电压源短路即可。
(b)电流源不作⽤:电流源开路即可。
②叠加定理只适⽤于电压、电流的叠加,对功率不满⾜。
(2)等效电源定理包括戴维宁定理和诺顿定理。
它们将⼀个复杂的线性有源⼆端⽹络等效为⼀个电压源形式或电流源形式的简单电路。
在分析复杂电路某⼀⽀路时有重要意义。
①戴维宁定理:任何⼀个线性含源的⼆端⽹络,对外电路来说,可以⽤⼀个理想电压源和⼀个电阻的串联组合来等效代替,其中理想电压源的电压等于含源⼆端⽹络的开路电压,电阻等于该⼆端⽹络中全部独⽴电源置零以后的等效电阻。
②诺顿定理:任何⼀个线性含源的⼆端⽹络,对外电路来说,可以⽤⼀个理想电流源和⼀个电阻的并联组合来等效代替。
此理想电流源的电流等于含源⼆端⽹络的短路电流,电阻等于该⼆端⽹络中全部独⽴电源置零以后的等效电阻。
3 .含受控源电路的分析对含有受控源的电路,根据受控源的特点,选择相应的电路的分析⽅法进⾏分析。
电路分析基础第二章答案.docx
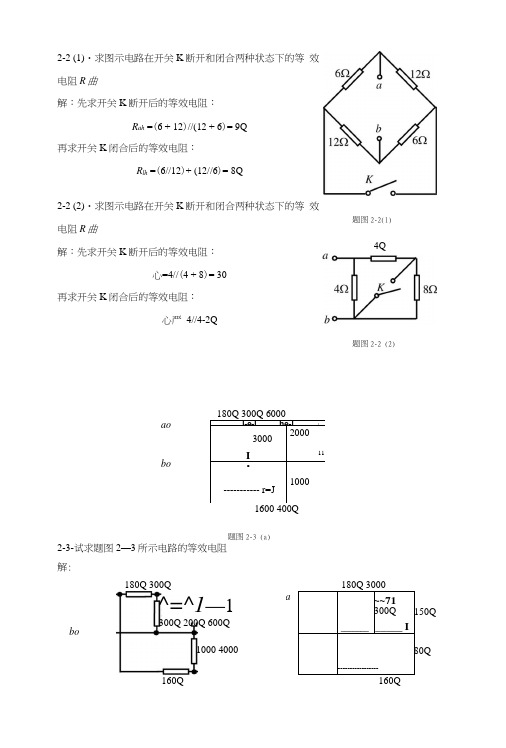
2-2 (1)・求图示电路在开关K 断开和闭合两种状态下的等 效电阻R 曲解:先求开关K 断开后的等效电阻:R ah =(6 + 12)//(12 + 6)= 9Q再求开关K 闭合后的等效电阻:R lh =(6//12)+ (12//6)= 8Q2-2 (2)・求图示电路在开关K 断开和闭合两种状态下的等 效电阻R 曲解:先求开关K 断开后的等效电阻:心=4//(4 + 8)= 30再求开关K 闭合后的等效电阻:心严 4//4-2Q2-3-试求题图2—3所示电路的等效电阻解:bo180Q 300Q 1000 4000^=^1—1300Q 200Q 600Q160Q_______ ~~71300Q_____ I-----------------80Qa150Q160Qaobo_____ l -e-l ____ he-l ____ 卜3000I200011• ----------- r=J1000题图2-2(1)4Q题图2-2 (2)题图2-3 (a)(b)》a300Q_____—450Q9240QI80Qtit -------------360Q240Q心二2400〃3600 = 1440ahbo67 0bo题图2-3 (b)解:60Q20060Qbo180Q180Q240Qt ------- X24()0 360020040Q20040QE—<_Z]_I60Q200200 20Q60Q10Q600bo6003()0心=40Q2-25 (1)・求图示电路a、b两点间的等效电阻R ahO解:在图中画一条垂线,使左右两边对称,参见图中虚线所示。
显然虚线为等位线,没有电流流过,故图中电阻可去掉,其等效电阻为:R ah =[(8 + 8)//(8 + 8)]//8 = 4Q2-25 (2)・求图示电路a、b两点间的等效电阻R ah o题图2-25 (1) 解:此题与上题相同,只是其中电阻的阻值不同,但仍保持其对称性。
电路分析第2章习题解析
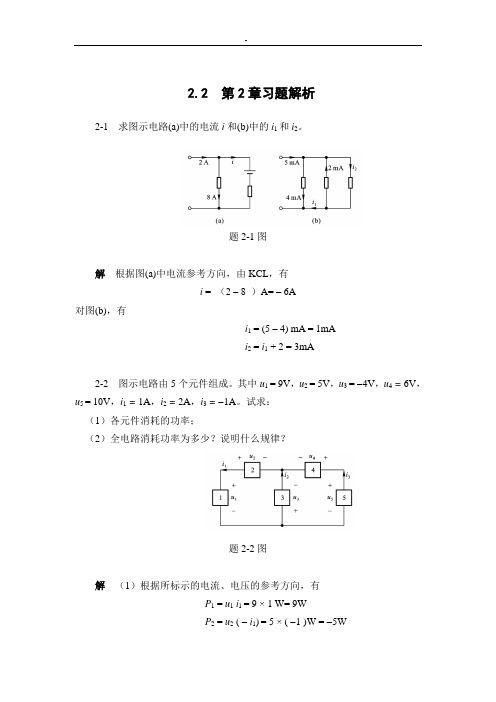
2-10如图示电路,已知R1=100,R2=200,R3=100,R4=50,R5=60,US=12V。求电流IAB。
题2-10图
解由图中R1和R3并联,R2与R4并联关系,可求出电流I
I= = A= 0.08A
再由分流关系,得
I3= I= 0.04A
I4= I= 0.064A
由KCL,得
电池内阻消耗(吸收)的功率P1为
P1=R1i2= 1 × 0.01W= 0.01W
电源产生的功率为
P=USi= 6 ×0.1W= 0.6W
或
P=P1+P2=(0.59 + 0.01)W= 0.6W
2-6图示为电池充电器电路模型。为使充电电流i=2A,试问R应为多少?
题2-6图
解由KVL有
= 2
解之
R= 2.91
所以等效电阻
Rab= =Rb+ ( 1 +)Re
2-21如图所示为一种T形解码网络。它具有将二进制数字量转换为与之成正比的模拟电压的功能,故常称之为数字模拟转换器。
(1)求网络的输入电阻Rin;
(2)求输入电压u1和电位uA、uB、uC、uD及输出电压u2。
题2-21图
解(1)求输入电阻Rin时,应从右端D处向左依次分段利用电阻的串、并联关系求之。观察可得
对于图(b),因为
uAB= 6i3 + 4i+ 5 = 6V
故
i= 0.4A
2-4如图示电路,已知u=6V,求各电阻上的电压。
题2-4图
解设电阻R1、R2和R3上的电压分别为u1、u2和u3,由分压公式得
u1= ·u= × 6V= 1V
u2= ·u= × 6V= 2V
电路的基本分析方法 练习题及答案第2章

第2章 电路的基本分析方法习题答案2-1 在8个灯泡串联的电路中,除4号灯不亮外其它7个灯都亮。
当把4号灯从灯座上取下后,剩下7个灯仍亮,问电路中有何故障?为什么?解:4号灯灯座短路。
如开路则所有灯泡都不亮。
2-2 额定电压相同、额定功率不等的两个白炽灯能否串联使用,那并联呢? 解:不能串联使用,因其电阻值不同,串联后分压不同,导致白炽灯无法正常工作。
在给定的电压等于额定电压的前提下,可以并联使用。
2-3 如图2-34所示,R 1=1Ω,R 2=5Ω,U =6V ,试求总电流强度I 以及电阻R 1、R 2上的电压。
图2-34 习题2-3图解:A 151621=++=R R U I=,V 551= V 111=2211=⨯==⨯=IR U IR U2-4 如图2-35所示,R 1=3Ω,R 2=6Ω,U =6V ,试求总电流I ;以及电阻R 1,R 2上的电流。
图2-35 习题2-4图解:总电阻为:Ω263632121=+⨯+=R R R R R=A 326=∴=R U I=由分流公式得:A 13633A 2363621122121=⨯++=⨯++I=R R R =I I=R R R =I2-5 电路如图2-36(a)~(f)所示,求各电路中a 、b 间的等效电阻R ab 。
(a) (b) (c)(d) (e) (f)2-36 习题2-5图解:(a) Ω4.3)6//4()2//2(ab =+=R(b) Ω2)33//()66//4ab =++(=R (c)Ω2)]6//3()6//3//[(13ab =++)(=R(d) Ω2)6//1)6//3(ab =+)(=R (e) Ω7)10//10(}6//6//]2)8//8{[(ab =++=R (f) Ω6}6//]64)4//4{[()4//4(ab =+++=R2-6 求图2-37所示电路中的电流I 和电压U 。
图2-37 习题2-6电路图解:图2-37等效变换可得:由上图可得;Ω8)816//)]}99//(6[5.7{=+++(总=RA 5.1812==总I 则根据并联电路分流作用可得:A 5.05.1)816()]99//(6[5.7)]99//(6[5.7=1=⨯++++++I则A 15.05.1=13=-=-I I I 总 I 3再次分流可得:A 75.0169999=4=⨯+++IA 25.016996=2=⨯++I所以I =0.75A ,U = U +-U - =9×I 2-8×I 1 = 9×0.25-8×0. 5=-1.75V2-7 电路如图2-38(a)~(g)所示,请用电源等效变换的方法进行化简。
电工学课后答案-第2章-电路的瞬态分析习题及答案
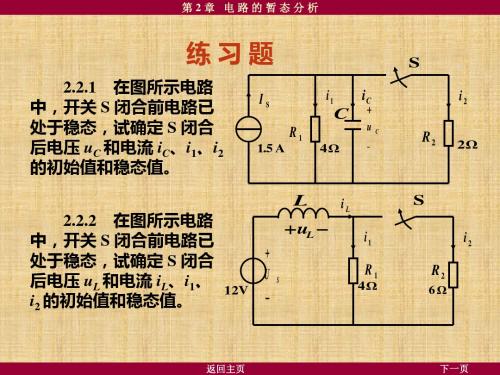
uC、i1、i2 的变化曲线见图
uC / V
i /mA
3.8
12
2.0
0.8
0
t/s
0
i1
i2
t/s
返 回练习题题集
上一页
上一题
下一题
第2章 电路的暂态分析
2.3.4 图所示电路中电容原先未充电。在 t = 0 时将开关
S1 闭合, t = 0.1s 时将开关 S2 闭合,试求 S2 闭合后的响应
换路后电容经 R3 及 R1 与 R2 的并联电阻放电,响应为零输入 响应。电路可简化为图所示,其中等效电阻设
36 R (R 1/R /2)R 3(368)Ω 1Ω 0
电路的时间常数 R 1 C 1 0 1 0 6 s 0 1 4 s 0
iC
所以
uC U0et 30e104t V
始值和稳态值。
R1
2Ω
i1 S
10V
iC
uC C
R2
3Ω
iL
5A IS
uL L
2.3.1 在图所示电路 原已稳定,在 t = 0 时, I S 5 A 将开关 S 闭合,试求 S 闭 合后的 uC 和 iC。
R1
3Ω iC
S
R2
6Ω
R2
8Ω
iC
uC C
10 F
返回
上一页
下一页
第2章 电路的暂态分析
R1
R3
4kΩ iC
R2
6kΩ
1.6kΩ uC
iC
C
2.5F
返回
第2章 电路的暂态分析
2.3.4 图所示电路中 电容原先未充电。在 t = 0 时将开关 S1 闭合, t = 0.1 s 时将开关 S2 闭合,试求 S2闭合后的响应 uR1,并 说明是什么响应。
电路分析基础 上海交通大学出版社 习题答案第二章汇总

2.1 解:对节点列KCL 方程,得① 01=i② 032=+i i③ 0643=++i i i④ 6521i i i i =++⑤ 054=+i i对封闭面列KCL 方程,得②③④节点构成的闭合面:0541=++i i i③④⑤节点构成的闭合面:0321=++i i i②③④⑤节点构成的闭合面:01=i2.2 解:00543164218975645632432631521=+++=+-+=-+-=-+-=-++-=++-=++=++u u u u u u u u u u u u u u u u u u u u u u u u u u u2.3 解:对a 节点列KCL 方程,得A I I I I 123221441=-=-=+=对回路1列KVL 方程,得AI I I I I 45018212125062121255154==+++=+++ 对b 、c 、d 、节点列KCL 方程,得AI I I I I I A I I I I I I AI I I I I I 2)3(1143341623263512125546654=---=-==+-=-=-==+-=-=-=+=对回路2列KVL 方程,可求得UV U I I I U 242611236)3(4123646463=⨯-⨯++-⨯=++=+2.4 解:KCL :00521654431=-+-=++-=+-I I I I I I I I IKVL :23143205652643541=-+=++=--I I I I I I I I I2.5 解:利用支路电流法,对电路列出KCL 、KVL 方程,有 KCL :5644326210i i i i i i i i i =++==++KVL :333554411333222244666i R u i R i R i R u i R i R i R i R u i R s s s +=+=+++=+代入已知条件,解得:A i 956.05-=2.6 解:利用支路电流法,对电路列出KCL 、KVL 方程,有KCL : c b e I I I +=KVL :c c e e c ee b be b b b I R U I R U I R I R I R U ++=++=其中 b c I I β=代入已知条件,解方程得:AI A I AI e c b 3351016.11013.11027.2---⨯=⨯=⨯=2.7 解:假设网孔电流的参考方向如下图所示。
电工学-第二章习题答案
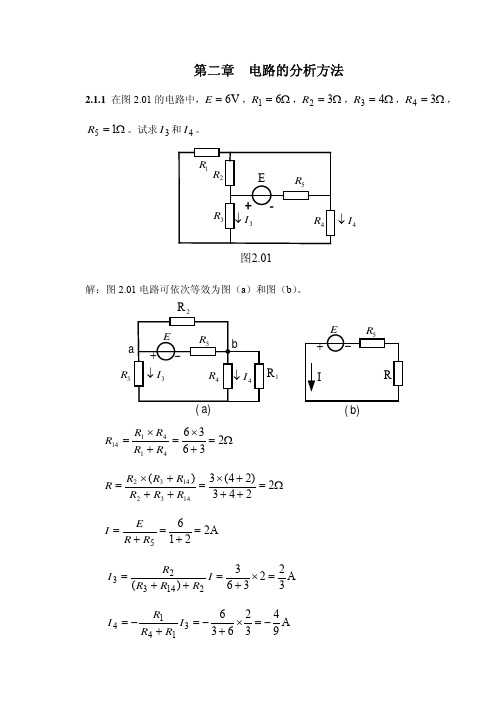
第二章 电路的分析方法2.1.1 在图2.01的电路中,V 6=E ,Ω=61R ,Ω=32R ,Ω=43R ,Ω=34R ,Ω=15R 。
试求3I 和4I 。
4I ↓图2.01解:图2.01电路可依次等效为图(a )和图(b )。
R 3R 1R(b)Ω=+×=+×=23636414114R R R R R Ω=+++×=+++×=2243)24(3)(14321432R R R R R R R A 22165=+=+=R R E IA 322363)(214323=×+=++=I R R R R IA 943263631414−=×+−=+−=I R R R I2.3.3 计算图2.12中的电流3I 。
Ω=1R A2S =图2.12解:根据电压源与电流源的等效变换,图2.12所示电路可依次等效为图(a )和图(b ),由图(b )可求得A 2.15.023=+=I由图(a )可求得:A 6.02.121213=×==I IΩ=1R V22=Ω=14R(b)Ω=12R2.6.1 在图2.19中,(1)当将开关S 合在a 点时,求电流1I ,2I 和3I ;(2)当将开关S 合在b 点时,利用(1)的结果,用叠加定理计算电流321,I I I 和 。
I图2.19I (a)I (b)解:(1)当将开关S 合在a 点时,图2.19所示电路即为图(a ),用支路电流法可得:=+=+=+12042130423231321I I I I I I I 解得:===A 25A 10A 15321I I I(2)开关S 合在b 点时,利用叠加原理图2.19所示电路可等效为图(a )和图(b ),其中图(a )电路中130V 和120V 两个电压源共同作用时所产生的电流已在(1)中求得,即:A 151=,I A 102=,I A 253=,I由图3(b )可求得:A 642422202=+×+=,,I A 464241−=×+−=,,IA26422=×+=则:A 11415111=−=+=,,,I I IA 16610,222=+=+=,,I I IA 27225333=+=+=,,,I I I2.6.2 电路如图2.20(a )所示,V 10ab ,,V 124321=====U R R R R E 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章习题2.1 如题2.1图所示有向拓扑图,试选2种树,并标出2种树所对应的基本(a) 树一1T 如图所示。
基本割集为:c1{1,2,4}, c2{1,3,7}, c3{1,3,6,8}, c4{1,3,6,5,4} 基本回路为:l1{5,6,8}, l2{2,4,5}, l3{3,5,8,7}, l4{1,2,5,8,7}(b) 树二2T 如图所示。
基本割集为:c1{4,5,8}, c2{5,7,8}, c3{1,3,7}, c4{4,2,3,7} 基本回路为:l1{2,4,5}, l2{5,6,8}, l3{1,2,3}, l4{1,2,6,7}2.2 题2.2图示电路,求支路电流1I 、2I 、3I解:列两个KVL 回路方程:051)54211=-+++I I I ( 021)510212=-+++I I I (整理为: 45921=+I I 115521=+I I 解得:A I 5.01= A I 1.02-=而 A I I I 4.0)213-=+-=(2.3 如题2.3图所示电路,已知电流A I 21=解:可列KVL 回路方程: 2I+2+(i-3)R=3已知 i=2A ,代入上式可得: R=3Ω2.4 如题2.4图所示电路,试选一种树,确定基本回路,仅用一个基本回路方程求解电流i 。
解:10(i-6)+5(0.4i+i)+13i=0 解得: i=2A2.5 如题2.5图所示电路,试选一种树,确定基本割集,仅用一个基本割集方程求解电压u 。
若用节点法,你将选择哪一个节点作参考点?试用一个节点方程求电压u 。
解:①② 选3为参考节点,列方程如下: 52018120124-=-+u u )(已知V u 122-=,代入上式,有: 52012812014-=++u )(解得节点点位: V u 324-=又可知 0124=++u u 得: V u u 201232124=-=--=2.6 如题2.6图所示电路,已知电流A i 21=,A i 12=,求电压bc u 、电阻R 及电压源S u 。
解:列三个网孔方程28)6=-+B A Ri i R(①33)43(-=-+++-C B A i i R Ri ②S C B u i i -=++3)323-( ③ 可知: 12==i i B 21==-i i i B A 可得: 32=+=B A i i由①式可得: 283)6=-+R R ( 解得: Ω=5R 由②式有: 33)57(35-=-++⨯-C i 解得: 0=C i 由③式有: S u -=33- 解得: V u S 6= 根据KVL 有: V i u bc 7432-=--=2.7 如题2.7图所示平面电路,各网孔电流如图中所标,试列写出可用来求解该电路的网孔方程。
解:各网孔方程如下:471414)4141--=-+++C B A i i i ( 5725)5214(14--=++++C B A i i i 354)354(54+-=++++-C B A i i i整理得:1041419-=-+C B A i i i 1052114-=++C B A i i i 21254=++-C B A i i i2.8 如题2.8图所示电路,设节点1、2的电位分别为1u 、2u ,试列写出可用来求解该电路的节点方程。
节点方程为: 45131)312131(21-+=-++u u124)4131(3121--=++-u u2.9 如题2.9图所示电路,求电压ab u 。
解:将电压源变换为电流源,列节点 方程如下:2411)3111(-=-+b a u u422)2111(11-+=++-b a u u整理得: 634=-b a u u032=+-b a u u 联解得: V u a 3= V u b 2= 所以有: V u u u b a ab 1=-=2.10 如题2.10图所示电路中,负载电阻L R 是阻值可变的电气设备。
它由一台直流发电机和一串联蓄电池组并联供电。
蓄电组常接在电路。
当用电设备需要大电流(L R 值变小)时蓄电池组放电;当用电设备需要小电流时(L R 值变大)时,蓄电池组充电。
设V U S 401=,阻Ω=5.01S R ,V U S 322=,阻Ω=2.02S R⑴ 如果用电设备的电阻Ω=1L R 时,求负载吸收的功率和蓄电池组所在支路的电流1I 。
这时蓄电池组是充电还是放电?⑵ 如果用电设备的电阻Ω=17L R 时,求负载吸收的功率和蓄电池组所在支路的电流1I 。
这时蓄电池组是充电还是放电?解:⑴ 当Ω=1L R ,设发电机支路电流为2I ,可列两个回路方程:1212120S S S S U I R U I R --+= 21212()0S S LU I R I I R --+=代入数据整理有:210.50.28I I -= 121.232I I +=联立求解得: 110I A = 220I A =所以有: 212()900L L P I I R W =+= 此时蓄电池组放电⑵ 当Ω=17L R ,代入上面方程,可得: 210.50.28I I -= 1217.21732I I +=联立求解得: 110I A =- 212I A =所以有: 212()68L L P I I R W =+= 此时蓄电池组充电2.11 如题2.11图所示电路,求图中受控源产生的功率P 受。
解:如图所示,有三个网孔①、②、③,设定 网孔电流巡回方向一致,列网孔方程:注意到网孔电流 3222A i i i ==,应而只需列网 孔①和②两个方程。
123(100100200)200100142i i i ++--=+ 12200(200300)2i i -++=- 1240040016i i -= 122005002i i -+=-解得: 22100i A =16100i A =受控源两端的电压为: 312146()100(2)100()1002100100u i i i i V =-=-=-=- 所以产生的功率为: 42(2)0.08100A P i u W =⨯=⨯-=受2.12 求如题2.12图所示电路中负载电阻R L 上吸收的功率P L 。
解:由于网孔3的网孔电流已知,为0.5i mA =-3 所以只需列两个网孔方程:123(1.53)3 1.56i i i +--=1233(113)0i i i -+++-= 将0.5i mA =-3代入,整理有:124.53 5.25i i -= 12350.5i i -+=- 联解得: 21i mA =可得: 221L L P i R mW =⨯=2.13 题2.13图示电路为晶体管等效电路,电路中各电阻及β均为已知,求电流放大系数i A (21/i A i i =),电压放大系数u A (21/u A u u =)。
解:设流过b R 的电流为/i ,则有: /1i i i b += 而 bfb be b R R i r i i )1(/β++=所以有: ])1(1[1bfbe b R R r i i β+++=而2i 是b i β的分流,为: LC Cb R R R i i +-=β2可得: fbe b b L C C i R r R R R R R i i A )1(12ββ+++⋅+-==又 LC LC b R R R R i u +-=β2 f b be b s R i r i u )1(β++=可得: fbe L C L C s u R r R R R R u u A )1(12ββ++⋅+-==2.14 如题2.14图所示电路,求电流i 1、i 2。
解:将电压源支路变换为电流源形式, 列一个节点方程:1111()103051110.5u +++=--- 解得 9u V =- 因而有: 291ui mA k ==-Ω154411u Vi mA k k +-===-ΩΩ2.15 求如题2.15图所示电路中电压U 、电流I 和电源U S 产生的功率P S 。
解:将电压源支路变换为电流源形式, 列两个节点方程:12111()22131U U +-=+ 12111()322112U U-++=-+ 联立求解得: 19U V = 28U V = 电压源支路电流为: 222S S U U I A -==- 可得: 28U U V ==1/33I U A ==4(2)8S S s P U I W ==⨯-=-2.16 如题2.16图所示电路,求电压U 。
解:将电压源支路变换为电流源形式, 列节点方程,有:1211111()()6132636U U ++-+=+ 1211111()()2136236U U -++++=-整理有:12214U U -=1222U U -+= 解得: 110U V = 26U V = 所以: 121064U U U V V V =-=-=2.17求如题2.17图所示电路中负载电阻R L 解:选三个节点如图所示,显然有:37U V = 列两个节点方程:1231111()71331U U U +--=-12311111()033212U U U -+++-=将37U V =代入,整理有:1241033U U -= 121117362U U -+=联立求解可得: 22U V =所以有: 22/4L L P U R W ==2.18 试设计一个电路,使其节点方程为如下方程: 12331u u u --= 123531u u u -+-=- 123351u u u --+=-式中,u 1、u 2、u 3分别为节点1、2、3的电位。
解:如图,节点4为参考节点。
2.19 如题2.19图所示电路中。
若/8i i =x ,试求电阻R x 的值。
解:该电路有三个网孔,已知有一个 网孔电流i i A =,所以列网孔方程为:0)15(10=-++-C x B x A i R i R i 0)10(5=++--C x B x A i R i R i已知: C B x i i i -= 和 )(88C B x A i i i i i -=== 带入方程,有0158080=-+++-C x B x B C B i R i R i i i ① 0104040=++-+-C x C B x C B i R i i R i i ② 两式相加,得: 0130105=+-C B i i 可有: 2126105130==C B i i 上面①式可变为: 0)(8065=-++-C B x C B i i R i i 进一步有: 0)1(8065=-++-CB xC B i iR i i 带入2126=C B i i ,解得 Ω=2x R2.20 如题2.20图所示电路,求电压u x 、电流i x2.21 求如题2.21图所示电路中的电流I解:该电路有四个网孔,如图所示, 已知网孔电流A 2=C i ,设1A 电流源上 的电压为/u ,方向与电流方向一致,可 列如下网孔方程:u i i C A -=-12 ① /2u u i B -+= ② 52/+=+-u i i D C ③由②式和③式消去/u ,可得 : u i i i D C B +=+-72 ④ 又已知: 2=C i 代入上式可得:u i A -=32 ⑤ u i i D B +=+92 ⑥由⑤式和⑥式消去u ,可得: 1222=++D B A i i i ⑦ 又已知: 3=-A B i i ⑧ 1=-D B i i ⑨ 联解⑦、⑧、⑨式,可得: A i A 1-= A i B 4= A i D 3= 显然有: A i i D 3==V i u A 523=-=2.22 求如题2.22图所示电路中的电压u x 。
