小半径曲线无缝线路稳定性有限元分析
无缝线路轨道稳定计算

P
EI 2 (
f
f
foe ) l2
4
3
fo2
l2
2
(
4Q
3
t
f
)
fEI
2
4Q
3
t
f
P 两根钢轨计算温度压力(N) E 钢轨弹性模量,2.110(7 N / cm2)
I 两股钢轨对垂直中和轴 的惯惯性矩cm4)
轨道框架刚度系数,取 为1
l 轨道原始弯曲波长(cm)
2、影响无缝线路稳定性的因素
试验研究及运营经验表明,影响无缝线路稳定性的主要因素有:钢轨的温升 幅度、轨道原始不平顺、道床横向阻力以及轨道框架刚度等。前两项是促使 无缝线路轨道失稳的因素,后两项是保持稳定性的因素。另外,道床纵向阻 力和中间扣件的抗扭转作用对无缝线路轨道稳定性影响较小。
钢轨的温升幅度
L T L
钢 轨 的 线 膨 胀 系 数 , 11.810 6 / 0C
t
E
t
E
L L
E
T
E钢 轨 钢 的 弹 性 模 量
E 2.11011 N / m2 2.1107 N / cm2
T Ts - T
Ts-钢轨锁定轨温,又称零应力轨温(℃) T-钢轨计算温度(℃);高温时,取当地气温加
maxPt2=248max△T2F=248×47.9×77.45=
900.5kN
(1)计算模型的建立
无缝线路轨道出现的原始弯曲大多数是单波形的。轨道原始不平顺的总长度 以l0表示,随着钢轨轴向压力的增长,其中l长度范围内将发生新的横向位移 增量,并以虚线表示,其位移变形矢度为f,与之对应的原始弯曲矢度为f0, 线路曲率半径R所对应的矢度是fr。根据力学分析原理可取出l长度范围的一 段轨道作为脱离体,分析无缝线路轨道稳定性,于是得到力学计算模型,并 建立下列基本假定:
无缝线路

摘要伴随着铁路的发展,普通钢轨线路的弊端变得越来越明显,由于钢轨之间的轨缝的存在,铁路提速、保养、旅客舒适度等方面都面临着不小的考验。
在此背景下,无缝线路应运而生。
无缝线路需要克服各种因素带来的危害,所以无缝线路并不是简单的把所有钢轨简单的焊接在一起。
在克服这些困难后无缝线路体现了其无可比拟的优势,大大减少了钢轨街头的数目,提高轨道强度与稳定性,加速实现轨道现代化。
关键词:无缝线路电气化铁路铺设无缝线路的施工特大型长联连续梁桥上无缝线路铺设小半径曲线无缝线路铺设目录绪论———发展现状 (4)高速铁路跨区间无缝线路 (5)一目的和意义 (5)二存在问题 (6)三因果分析 (6)(一)轨条布置 (6)(二)锁定轨温 (6)(三)设计检算 (8)四解决办法 (9)(一) 300m 长轨节基地焊接 (9)(二) 300m 长轨节运输及铺设 (10)(三)轨道整理及钢轨预打磨 (11)电气化铁路铺设无缝线路的施工 (12)一目的和意义 (12)二存在的问题 (12)三解决方案 (12)(一)主要技术标准和要求 (12)(二)长轨的运输组织及质量控制 (14)(三)施工组织安排 (14)(六)安全技术作业要求及注意事项 (16)特大型长联连续梁桥上无缝线路铺设 (18)一目的和意义 (18)二存在问题 (18)三因果分析 (18)(一)计算原理 (18)(二)计算模型 (19)(三)方案分析 (20)1 小阻力扣件铺设范围影响分析 (21)2 桥上铺设钢轨伸缩调节器影响分析 (24)四相应对策 (26)小半径曲线无缝线路铺设 (26)一存在问题 (26)二因果分析 (27)1 “统一公式”的修正 (27)2 铺设无缝线路的规定 (28)参考文献 (29)绪论———发展现状众所周知,对于铁路轨道而言,保证开通时达到设计速度的关键是其高平顺性和高稳定性。
轨道作为铁路固定设备的重要组成部分,其自身的结构特点起着至关重要的作用。
现代有轨电车小半径曲线无缝线路稳定性分析
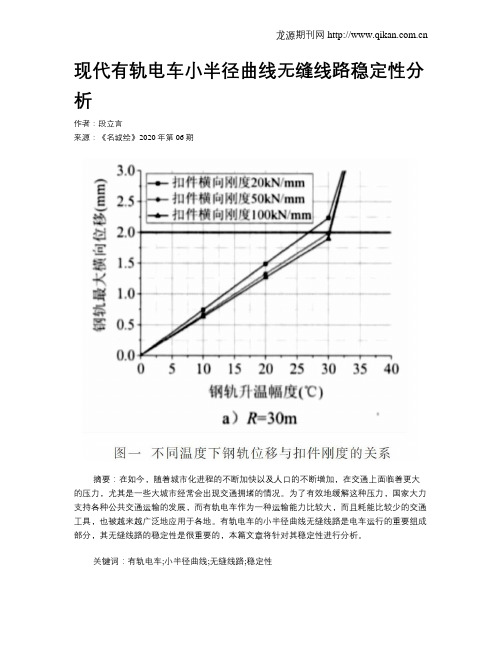
现代有轨电车小半径曲线无缝线路稳定性分析作者:段立言来源:《名城绘》2020年第06期摘要:在如今,随着城市化进程的不断加快以及人口的不断增加,在交通上面临着更大的压力,尤其是一些大城市经常会出现交通拥堵的情况。
为了有效地缓解这种压力,国家大力支持各种公共交通运输的发展,而有轨电车作为一种运输能力比较大,而且耗能比较少的交通工具,也被越来越广泛地应用于各地。
有轨电车的小半径曲线无缝线路是电车运行的重要组成部分,其无缝线路的稳定性是很重要的,本篇文章将针对其稳定性进行分析。
关键词:有轨电车;小半径曲线;无缝线路;稳定性引言现代有轨电车作为环境友好型的交通运输工具之一,在我国的多个地区都已经兴建起了相应的电车线路。
相对于地铁和轻轨,现代有轨电车可以通过的轨道最小平面半径是比较小的,因而在运行过程中其灵活性也更加好。
但是,无论是国内还是国外,在目前对于现代有轨电车的小半径曲线无缝线路稳定性的研究还是不多的,相关的一些规范和标准也没有得到统一和完善。
因此,进行其稳定性的研究和分析具有重要意义。
一、在当前对于无缝线路稳定性研究中的不足首先,在当前比较缺乏针对性的研究。
尽管在目前我国对于小半径曲线无缝线路稳定性的研究并不少,但是在研究其稳定性的时候所针对的对象往往都是国铁和地铁,这二者的曲线半径最小还是250米,但是有轨电车的曲线半径最少是30米,尤其是胶轮导轨的电车,其半径则将近10.5米[1]。
因此,在进行现代有轨电车的无缝线路稳定性研究的时候,不能够直接将现在有的关于无缝线路的研究结果用于有轨电车中。
其次,我国在进行有轨电车的无缝线路研究的时候,并没有统一的规范和标准,在研究过程中通常是借鉴地铁的标准来进行的。
再者,在进行无缝线路研究时,所进行的都是横向稳定性的研究,缺乏垂直稳定性的研究。
二、关于线路的横向稳定性影响因素的分析影响现代有轨电车的小半径曲线无缝线路稳定性的因素有很多,从横向的角度而言,主要有四个因素,分别是曲线半径、扣件的横向刚度、初始不平顺以及道床的横向阻力。
小半径曲线无缝线路稳定性有限元分析

文章编 号 :0 6— 16 2 0 ) 3— 0 8— 5 10 2 0 ( 0 6 0 0 0 0
பைடு நூலகம்
小 半 径 曲线 无 缝 线 路 稳 定 性 有 限 元分 析 。
罗信 伟 ¨ 雷 晓燕 冯 青 松
( 东交通 大 学 , 江西 南昌 3 0 1 ) 华 303
摘要 : 研究 目的 : 利用有限元法解决在温度力作用下 无缝线 路特别是小半径 曲线 的臌 曲失稳 问题 。 研究方法 : 建立了包 含钢轨 、 扣件 、 轨枕和道床阻力为一 体 的轨 道框架模 型 , 导了相应 的数值计算 公式 推 并编制 了有 限元程序 。该模 型还考虑 了横向力对无缝线路稳定性 的影响 。 研究结果 : 到了不 同工况下钢轨横 向位移 一 得 温度 曲线 , 并与“ 统一公式” 进行 了比较 。 研 究结论 : 有限元方法在研究无缝线路稳定性方 面是可行 和有效 的; 有限 元方法能计算 出不 同工况下 的 轨道结构从锁定轨 温直到破坏全过程的横 向位移 , 相对 于“ 统一公 式”, 方法 可考 虑各 种复杂 的工况 , 更 该 能 精确 地反映轨道横向变形的趋势 , 而为铁 路工务部 门养护维修提供理论指 导。 从 关键词 : 无缝线路 ; 稳定性 ; 温度力 ; 小半径 曲线 ; 有限元 ; 统一公 式 中图分类号 : 2 3 U 1 文献标识码 : A
A s at R sa c u p ss T ep pr i e teo igtes blyo c n n o s e e i C b t c : eer hp r oe : h a e m da rsl n t it f o t u u l dr l( WR n e m r a v h a i i w d a )u d re ・ t
小半径曲线无缝线路的稳定性分析及病害整治

钢轨纵 向温度应 , 要保持轨道 的稳定 , 轨道框 架一般不足 以 的 无疑 是机 车 车 辆 作 用 在 小 半 径 曲线 上 的 附加 力 。在 同 等运 营
抵抗轨道变形 , F 常 需要 道 床 的横 向约 束来 保 证 轨 道 的 稳 定 。 条件下, 小半 径 曲线 无 缝 线 路钢 轨将 承 受 更 大 的 径 向力 。如 果 但 由于道床是 由散体介质构 成 , 道 床 结 构 易 于 发 变 化 , 因 而 线 路 局 部 不 平 顺 , 将 加 剧 曲 线 上 股钢 轨 的 磨 耗 和 下 股 钢 轨 的 压 道 床 约 束 阻 力 受 到 削弱 或 被 破 坏 是 轨 道 失 稳 的 直接 原 因 。为保 溃 , 钏 轨 的磨 耗 和 压 溃 会 减 弱 轨 道 的框 架 刚度 并 且 会 使 线 路 轨 证线路稳定性 , 日前 基 本 上 采 用 I I I 型轨枕、 I I 型弹条扣件、 优质 距 扩大 , 不 但 会 加 大 其 他 零 配 件 的磨 损 程 度 , 而 且 会 使 该 处 不 道 砟 并 保 持 足够 的道 床 厚 度 、 加 大道 砟 肩 宽 和 保 持 外 股 1 5 0 mm 平顺程度加剧, 使 轨 道 状 态 恶 化 。 因此 , 保 持 线 路 的平 顺 性 , 以 道砟堆高、 加轨距杆 、 上地 锚 拉 杆 等 措 施 。 二、 小 半径 曲线 无 缝 线 路 的稳 定性 分析
时, 对 钢 轨 的横 向和 竖 向冲 击 作 用 , 使 对 钢 轨 出现 伤 损 异 常 的 曲线 要 做 重 点监 测 。3 ) 小
的变形 , 将导致 列车在 曲线上 的摇摆 , 增加 作用于轨道上 的横 半径 曲线轨距 易变 化 , 需进行常 态化调整 以达到要求 的轨距 。
小半径曲线无缝线路稳定性有限元分析

F in ite Elem en tM ethod for Ana lyz in g the Stab ility of Con tin uousW elded Ra il Track on M in or Rad ius Curve
L UO X i n - we i, L E I X ia o - yan, FENG Q i n g - song ( East China J iaotong University, Nanchang, J iangxi 330013, China ) Abstract: Research purposes: The paper ai m ed at resolving the stability of continuous welded rail ( CWR ) under tem 2 perature forces by the finite elem ent m ethod, especially for m inor - radius - curve CWR. Research m ethods: A track - frame model has been developed, which includes rails, pads, sleepers and ballast resist2 ance, and the finite elem ent p rogram has been exp loited using numerical formulation. The influence of cross force was also considered in this model . Research results: The dependence of the CWR disp lacement on temperature figures in different work conditions were ar2 rived, and the result was compared w ith the result of universal for m ulation. Research conclusion s: Finite element method is effective on analyzing the stability of CWR. And it can analyze the lat2 eral disp lacement of CWR track from locked - in temperature to damage. Compared w ith the universal for m ulation, the method can accurately p resent the trend of the lateral disp lacement of track in several work conditions, and p rovide an evidential m aterial for rail w ay departm ent in p lanning of maintaining the track. Key words: continuous welded rail; stability; temperature stress; m inor radius curve; finite element m ethod; universal for2 mulation
铁路小半径曲线线路病害分析与处理

铁路小半径曲线线路病害分析与处理摘要:随着交通行业的不断发展,铁路已成为当今人们的主要出行方式之一,作为国民经济的大动脉,铁路在提高人民生活质量、加快区域经济发展方面起到了至关重要的作用,而线路的安全与稳定也成为了铁路运输的重中之重。
为减少铁路曲线病害,提高铁路运行安全性、稳定性、可靠性,本文针对线路小半径曲线病害进行分析,为现场病害整治提供一定的参考。
关键字:线路稳定;小半径曲线;病害整治引言为了减少影响铁路线路稳定的问题的出现,对于特殊地势和复杂受力情况的线路区段做出针对性的处理方案成为了铁路养护维修的一个重要话题,其中小半径曲线线路的病害整治也是如今线路维修工作的一个难点,由于其受力条件较为复杂,极易发生各种类型的病害,而为了减少病害的出现频率,我们需要认真分析病害的成因,做出针对性的措施。
一、对小半径曲线的受力情况分析在对铁路线路进行铺设时,会遇到许多复杂的地形条件,受制于铺设成本、时间限制及环境因素等,需要将线路铺设成半径大小不一的曲线,不同于平直线路轨道,曲线需要针对列车的载重量、通过速度、地质条件等对曲线半径、超高、轨距加宽等数据做出不同的调整,而其受力情况则更为复杂,除了在竖直方向上列车通过轮对施加给钢轨的重力外,在水平方向上还会受到列车由于自身向心力带给钢轨的横向压力,随着半径越小、速度越快,列车带给钢轨的横向压力越大。
此外,还有列车在钢轨上爬行时带来的纵向摩擦力,以及温度应力等。
由此可见,小半径曲线是极易出现线路病害的区段。
二、小半径曲线病害分析(一)曲线侧磨、肥边病害在目前曲线线路遇到的病害中,曲线侧磨及钢轨肥边是出现较为频繁的问题,二者都是由于列车在运行时轮对摩擦钢轨产生,而究其原因则是由于轨道几何状态不平顺,进而影响到列车在上下两股钢轨间运行不平稳导致,当曲线实际超高小于设计超高值时,列车受离心力影响挤压摩擦上股钢轨,致使其剥落掉块,磨耗情况见图1所示;反之则列车挤压摩擦下股钢轨,使钢轨极易出现肥边、掉块等病害,磨耗情况见图2所示,严重损耗钢轨使用寿命和线路稳定性,给列车运行带来不良影响。
提速铁路无缝线路稳定性的有限元分析_英文_冯青松

6
Analysis of the Stability of CWR Track on Raising Speed Railway …
LEI Xiao-yan FENG Qing-song
Department of Civil Engineering, East China Jiaotong University, Nanchang 330013, China
Abstract: Computational model for analyzing the stability of continuously welded rail track on raising speed railway is developed by means of the finite element method in this paper, in which track panel including rails, ties, rail fastenings and ballast resistances as a whole system, and non-linear deformation behavior of rails under temperature stress are considered. Based on the model, numerical computational formulas are induced and programmed. Influences of the lateral resistances of the ballast, invalid ties and curved track radius as well as initial flexural deformations on the stability of continuously welded rail track are investigated. Key words: Raising speed railway, continuously welded rail track, stability, temperature stress, finite element method CLC number: U211.2 Document code: A Article ID: 1672-4747(2004)03-0006-08
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
式中 , U 为梁内的应变能 , U 为约束弹簧的应变能 ,
10
e
铁 道 工 程 学 报
2006 年 6 月
T
Uσ 为初应力产生的能量 。
α ΔT 0 0 EA σ ΔT 0 0 = ∑ - EA
e
( 12 )
式 ( 5 )又可写成
U =U +U
e e e e e N e
du
1
B1 +
B1 +
2
3
( 2)
ε=
ε x ε b
=
dx d v 2 dx
2
+
1 du 2 dx
2
+
1 dv 2 dx
2
ε =ε e + N
其中 f — — — 允许变形矢度 ( cm ) ; foe , fop — — — 钢轨初始弹性 、 塑性变形 ( cm ) ; Q — — — 钢轨变形矢度 f = 0. 2 cm 时的等效道床 横向阻力 (N / cm ) 。 [ 1] 1. 2 有限元方法 1. 2. 1 计算模型 无缝线路 60 kg /m 钢轨 ,钢轨弹性模量 E = 2. 1 × - 5 10 M Pa,钢轨的热膨胀系数 α = 1. 18 × 10 / ℃, 两钢 轨间标准轨距 1. 44 m; 配置 1 760 根 / km 预应力钢筋
4 4 4
和养修手段的加强 ,上述限制有所突破 。我国 1987 年 在呼和浩特铁路局最大轨温差 94 ℃ 的条件下在 400 m 半径下成功铺设了无缝线路 , 并采取了增加轨枕配置 数、 加宽并堆高道碴 、 增设防胀挡板等措施 , 取得了较 好的效果 。北京铁路局秦皇岛工务段在半径 350 m , 年最大温差 83 ℃ 的条件下成功铺设了无缝线路 。最 近几年 ,相继有不少铁路局进行了铺设小半径无缝线 路的尝试 ,如上海铁路局就在外福线上铺设了半径为
σ0 x 0 0 = ∑ - σ0 x 0 0
e e
T
( 13 )
e N e
k 为通常的梁单元线性刚度矩阵 , k 是与位移有 关的单元刚度矩阵 , 称大位移矩阵 , kR 是与约束弹簧 刚度有关的矩阵 , 称之为约束刚度矩阵 。式 ( 8 ) 即为 具有初始弯曲的梁在温度力作用下臌曲变形的非线性 平衡方程 。因篇幅有限 ,在此不一一列出推导过程 ,详 见文献 [ 1 ]、 [ 5 ]。 1. 2. 3 轨枕梁单元 轨枕采用考虑剪切变形的弯曲梁单元 , 其单元刚 度矩阵同钢轨梁单元的线性刚度矩阵 。 1. 2. 4 弹簧单元 弹簧单元模拟钢轨与轨枕的扣件连接 , 其刚度矩 阵见式 ( 10 ) 。
铁 道 工 程 学 报 Jun 2006 第 3 期 (总 93 ) JOURNAL OF RA I LWAY ENGI N EER I N G SOC IETY NO. 3 ( Ser . 93 )
2006 年 6 月
文章编号 : 1006 - 2106 ( 2006 ) 03 - 0008 - 05
F in ite Elem en tM ethod for Ana lyz in g the Stab ility of Con tin uousW elded Ra il Track on M in or Rad ius Curve
L UO X i n - we i, L E I X ia o - yan, FENG Q i n g - song ( East China J iaotong University, Nanchang, J iangxi 330013, China ) Abstract: Research purposes: The paper ai m ed at resolving the stability of continuous welded rail ( CWR ) under tem 2 perature forces by the finite elem ent m ethod, especially for m inor - radius - curve CWR. Research m ethods: A track - frame model has been developed, which includes rails, pads, sleepers and ballast resist2 ance, and the finite elem ent p rogram has been exp loited using numerical formulation. The influence of cross force was also considered in this model . Research results: The dependence of the CWR disp lacement on temperature figures in different work conditions were ar2 rived, and the result was compared w ith the result of universal for m ulation. Research conclusion s: Finite element method is effective on analyzing the stability of CWR. And it can analyze the lat2 eral disp lacement of CWR track from locked - in temperature to damage. Compared w ith the universal for m ulation, the method can accurately p resent the trend of the lateral disp lacement of track in several work conditions, and p rovide an evidential m aterial for rail w ay departm ent in p lanning of maintaining the track. Key words: continuous welded rail; stability; temperature stress; m inor radius curve; finite element m ethod; universal for2 mulation
第 3期
罗信伟 : 小半径曲线无缝线路稳定性有限元分析
4
9
维修要求也较高 ,各国铺设无缝线路都规定了禁区 ,但 随着新技术 、 新材料及新设计理论的应用 ,这些禁区正 在逐步缩小 。近 10 年来 , 欧美 、 日本和前苏联在正线 上容许铺设无缝线路的最小曲线半径已有很大突破 。 ( TB 2098 根据《 无缝线路铺设养护维修办法 》 89 )规定 , 我 国铺 设无 缝线 路的 曲 线 半 径 不 能 低 于
小半径曲线无缝线路稳定性有限元分析
罗信伟
ΞΞ
Ξ
雷晓燕 冯青松
(华东交通大学 , 江西 南昌 330013 )
摘要 : 研究目的 : 利用有限元法解决在温度力作用下无缝线路特别是小半径曲线的臌曲失稳问题 。 研究方法 : 建立了包含钢轨 、 扣件 、 轨枕和道床阻力为一体的轨道框架模型 ,推导了相应的数值计算公式 并编制了有限元程序 。该模型还考虑了横向力对无缝线路稳定性的影响 。 研究结果 : 得到了不同工况下钢轨横向位移 - 温度曲线 ,并与“ 统一公式 ” 进行了比较 。 研究结论 : 有限元方法在研究无缝线路稳定性方面是可行和有效的 ; 有限元方法能计算出不同工况下的 轨道结构从锁定轨温直到破坏全过程的横向位移 , 相对于“ 统一公式 ” , 该方法可考虑各种复杂的工况 , 能更 精确地反映轨道横向变形的趋势 ,从而为铁路工务部门养护维修提供理论指导 。 关键词 : 无缝线路 ; 稳定性 ; 温度力 ; 小半径曲线 ; 有限元 ; 统一公式 中图分类号 : U213 文献标识码 : A
无缝线路是铁路轨道结构的一大变革 , 它与有缝 线路相比 ,不仅具有平顺性好 、 轮轨冲击力小 、 列车运
行平稳 、 旅客舒适等优点 ,还可大大降低线路维修费用 和机车车辆的修理费用 。但是无缝线路的铺设及养护
Ξ 收稿日期 : 2005 - 11 - 21 Ξ Ξ 作者简介 : 罗信伟 , 1977 年出生 ,男 ,在读硕士研究生 。
( 6)
Qσ0 = ∑Qσ0 = ∑ B eσ0 dx
e e e e
e
l
∫
T
式中 , U e 为线性应变引起的势能 , UN 为非线性应变引 起的势能 。 由势能驻值原理 ,对式 ( 6 )取一阶变分 e e δ U =δ ∑ ( U e + UN )
e T e e e e e e T e e δ( α ) ( κ α - Qe κ δ( α )κ =∑ σ0 ) + ∑ e T + Rα +Q Nα e
1 目前我国主要采用的研究方法
1. 1 解析法 — — — “ 统一公式 ”
[ 3]
弹性系数则用 kbθ表示 ; 假设初始弯曲的形状是对称 的 ,则可用图 1 表示整个模型的一半 。
1. 2. 2 有限元方程
铁科院和长沙铁道学院为主的课题组提出的“ 统 一无缝线路稳定性计算公式 ” ,简称“ 统一公式 ” , 该法 假设变形曲线为多波正弦曲线 , 分定弦长和定曲率两 种方法 ,其中以定曲率法应用较多 : π2 βE I 2 ( f - foe ) + 43 Q l2 π l P= 2 4l f + foe + 3 π R′ π ( f + foe ) B 1R ′ Q Q 4 βE π I 1 1 8 fop 式中 B 1 = ; = + 2 R′ R′ R l
