伍德里奇计量经济学第6章计算机习题详解STATA
伍德里奇 第六章

R2 = 1−
SSR /(n − k − 1) SSR n − 1 n −1 = 1− ⋅ = 1 − (1 − R 2 ) ⋅ SST /(n − 1) SST n − k − 1 n − k −1
n −1 n − k −1
2
自由度惩罚因子:
在方程中增加一个(组)x,R2 一定增加,但只有该 x 的 t>1(F>1) R 才增加。 ,
2 3
三、含交叉项的模型 粮食产量=β 0 + β1 (施肥量)+β(降水量)+β 3 (施肥量 × 降水量)+随机误差项 2
yi = β 0 + β1 xi + β 2 zi + β3 xi zi + ui
或
E ( y | xi , zi )=β 0 + β1 xi +β 2 zi +β3 xi zi
(B)
将(B)式中的 X 用
yt − yt −1 替换,则(A)式可近似地表示为 yt −1
Δ ln yt ≈
yt − yt −1 yt −1
即表明对数变化相当于变量的变化率(相对变化) 。 该近似计算在系数数值小时比较准确, 但数值大的时候, 不太准确。 准确的变化率: 由于 ln y = β 0 + β1 x1 + β 2 x2 + .... + u ,如果 x1 变化一个绝对单位,其他 x 保持不 变,则有
ji j i
2
2
ˆ βj
ˆ 普通最小二乘回归系数 β j ( j = 1, 2, L , k ) 表示在其它变量不变的情况下,自变量 ˆ x j 每变化一个绝对单位引起的因变量的平均变化量;标准化回归系数 b j 表示在其它变
伍德里奇计量经济学导论第6版笔记和课后习题答案

第1章计量经济学的性质与经济数据1.1复习笔记考点一:计量经济学★1计量经济学的含义计量经济学,又称经济计量学,是由经济理论、统计学和数学结合而成的一门经济学的分支学科,其研究内容是分析经济现象中客观存在的数量关系。
2计量经济学模型(1)模型分类模型是对现实生活现象的描述和模拟。
根据描述和模拟办法的不同,对模型进行分类,如表1-1所示。
(2)数理经济模型和计量经济学模型的区别①研究内容不同数理经济模型的研究内容是经济现象各因素之间的理论关系,计量经济学模型的研究内容是经济现象各因素之间的定量关系。
②描述和模拟办法不同数理经济模型的描述和模拟办法主要是确定性的数学形式,计量经济学模型的描述和模拟办法主要是随机性的数学形式。
③位置和作用不同数理经济模型可用于对研究对象的初步研究,计量经济学模型可用于对研究对象的深入研究。
考点二:经济数据★★★1经济数据的结构(见表1-3)2面板数据与混合横截面数据的比较(见表1-4)考点三:因果关系和其他条件不变★★1因果关系因果关系是指一个变量的变动将引起另一个变量的变动,这是经济分析中的重要目标之计量分析虽然能发现变量之间的相关关系,但是如果想要解释因果关系,还要排除模型本身存在因果互逆的可能,否则很难让人信服。
2其他条件不变其他条件不变是指在经济分析中,保持所有的其他变量不变。
“其他条件不变”这一假设在因果分析中具有重要作用。
1.2课后习题详解一、习题1.假设让你指挥一项研究,以确定较小的班级规模是否会提高四年级学生的成绩。
(i)如果你能指挥你想做的任何实验,你想做些什么?请具体说明。
(ii)更现实地,假设你能搜集到某个州几千名四年级学生的观测数据。
你能得到它们四年级班级规模和四年级末的标准化考试分数。
你为什么预计班级规模与考试成绩成负相关关系?(iii)负相关关系一定意味着较小的班级规模会导致更好的成绩吗?请解释。
答:(i)假定能够随机的分配学生们去不同规模的班级,也就是说,在不考虑学生诸如能力和家庭背景等特征的前提下,每个学生被随机的分配到不同的班级。
伍德里奇《计量经济学导论》(第6版)复习笔记和课后习题详解-多元回归分析:OLS的渐近性【圣才出品】

第5章多元回归分析:OLS 的渐近性5.1复习笔记考点一:一致性★★★★1.定理5.1:OLS 的一致性(1)一致性的证明当假定MLR.1~MLR.4成立时,对所有的j=0,1,2,…,k,OLS 估计量∧βj 是βj 的一致估计。
证明过程如下:将y i =β0+β1x i1+u i 代入∧β1的表达式中,便可以得到:()()()()11111111122111111ˆnni ii i i i n ni i i i xx y n x x u xxnxx ββ-==-==--==+--∑∑∑∑根据大数定律可知上式等式右边第二项中的分子和分母分别依概率收敛于总体值Cov (x 1,u)和Var(x 1)。
假定Var(x 1)≠0,因为Cov(x 1,u)=0,利用概率极限的性质可得:plim ∧β1=β1+Cov(x 1,u)/Var(x 1)=β1。
这就说明了OLS 估计量∧βj 具有一致性。
前面的论证表明,如果假定只有零相关,那么OLS 在简单回归情形中就是一致的。
在一般情形中也是这样,可以将这一点表述成一个假定。
即假定MLR.4′(零均值与零相关):对所有的j=1,2,…,k,都有E(u)=0和Cov(x j1,u)=0。
(2)MLR.4′与MLR.4的比较①MLR.4要求解释变量的任何函数都与u 无关,而MLR.4′仅要求每个x j 与u 无关(且u 在总体中均值为0)。
②在MLR.4假定下,有E(y|x 1,x 2,…,x k )=β0+β1x 1+β2x 2+…+βk x k ,可以得到解释变量对y 的平均值或期望值的偏效应;而在假定MLR.4′下,β0+β1x 1+β2x 2+…+βk x k 不一定能够代表总体回归函数,存在x j 的某些非线性函数与误差项相关的可能性。
2.推导OLS 的不一致性当误差项和x 1,x 2,…,x k 中的任何一个相关时,通常会导致所有的OLS 估计量都失去一致性,即使样本量增加也不会改善。
《计量经济学》第六章精选题及答案

第六章自相关二、问答题1、那些原因可以造成自相关;2、存在自相关时,参数的OLS估计具有哪些性质;3、如何检验是否存在自相关;4、当存在自相关时,如何利用广义差分法进行参数估计;5、当存在自相关时,如何利用广义最小平方估计法进行参数估计;6、异方差与自相关有什么异同;三、计算题1、证明:当样本个数较大时,)d。
≈-1(2ρα2、通过D-W检验,判断下列模型中是否存在自相关,显著性水平%5=(1)样本大小:20;解释变量个数(包括常数项):2;d=0.73;(2)样本大小:35;解释变量个数(包括常数项):3;d=3.56;(3)样本大小:50;解释变量个数(包括常数项):3;d=1.87;(4)样本大小:80;解释变量个数(包括常数项):6;d=1.62;(5)样本大小:100;解释变量个数(包括常数项):5;d=2.41;3、假定存在下表所示的时间序列数据:请回答下列问题:(1)利用表中数据估计模型:t t t x y εββ++=10;(2)利用D-W 检验是否存在自相关?如果存在请用d 值计算估计自相关系数ρ;(3)利用广义差分法重新估计模型:'''1011(1)()t t tt t y y x x ρβρβρε---=-+-+。
第三部分 参考答案二、问答题1、那些原因可以造成自相关?答:造成自相关的原因大致包括以下六个方面:(1)经济变量的变化具有一定的倾向性。
在实际的经济现象中,许多经济变量的现值依赖于他的前期值。
也就是说,许多经济时间序列都有一个明显的相依性特点,这种现象称作经济变量所具有的惯性。
(2)缺乏应有变量的设定偏差。
(3)不正确的函数形式的设定错误。
(4)蛛网现象和滞后效应。
(5)随机误差项的特征。
(6)数据拟合方法造成的影响。
2、存在自相关时,参数的OLS 估计具有哪些性质?答:当存在自相关,即I D ≠ΩΩ=,)(2σε时,OLS 估计的性质有:(1)βˆ是观察值Y 和X 的线性函数;(2)βˆ是β的无偏估计;(3)βˆ的协方差矩阵为112)()()ˆ(--'Ω''=X X X X X X D σβ;(4)βˆ不是β的最小方差线性无偏估计;(5)如果nX X n Ω'∞→lim存在,那么βˆ是β的一致估计;(6)2σ 不是2σ的无偏估计;(7)2σ不是2σ的一致估计。
伍德里奇《计量经济学导论》(第6版)复习笔记和课后习题详解-第一篇(第4~6章)【圣才出品】

考点五:对多个线性约束的检验:F 检验 ★★★★★
1.对排除性约束的检验 对排除性约束的检验是指检验一组自变量是否对因变量都没有影响,该检验不适用于不 同因变量的检验。F 统计量通常对检验一组变量的排除有用处,特别是当变量高度相关的时 候。 含有 k 个自变量的不受约束模型为:y=β0+β1x1+…+βkxk+u,其中参数有 k+1 个。 假设有 q 个排除性约束要检验,且这 q 个变量是自变量中的最后 q 个:xk-q+1,…,xk, 则受约束模型为:y=β0+β1x1+…+βk-qxk-q+u。 虚拟假设为 H0:βk-q+1=0,…,βk=0,对立假设是列出的参数至少有一个不为零。 定义 F 统计量为 F=[(SSRr-SSRur)/q]/[SSRur/(n-k-1)]。其中,SSRr 是受约束模型 的残差平方和,SSRur 是不受约束模型的残差平方和。由于 SSRr 不可能比 SSRur 小,所以 F 统计量总是非负的。q=dfr-dfur,即 q 是受约束模型与不受约束模型的自由度之差,也是 约束条件的个数。n-k-1=分母自由度=dfur,且 F 的分母恰好就是不受约束模型中σ2= Var(u)的一个无偏估计量。 假设 CLM 假定成立,在 H0 下 F 统计量服从自由度为(q,n-k-1)的 F 分布,即 F~ Fq,n-k-1。如果 F 值大于显著性水平下的临界值,则拒绝 H0 而支持 H1。当拒绝 H0 时,就 说,xk-q+1,…,xk 在适当的显著性水平上是联合统计显著的(或联合显著)。
∧
∧
∧
∧
注:β1,β2,…,βk 的任何线性组合也都符合正态分布,且βj 的任何一数检验:t 检验 ★★★★
1.总体回归函数 总体模型的形式为:y=β0+β1x1+…+βkxk+u。假定该模型满足 CLM 假定,βj 的 OLS 量是无偏的。
伍德里奇---计量经济学第6章部分计算机习题详解(STATA)
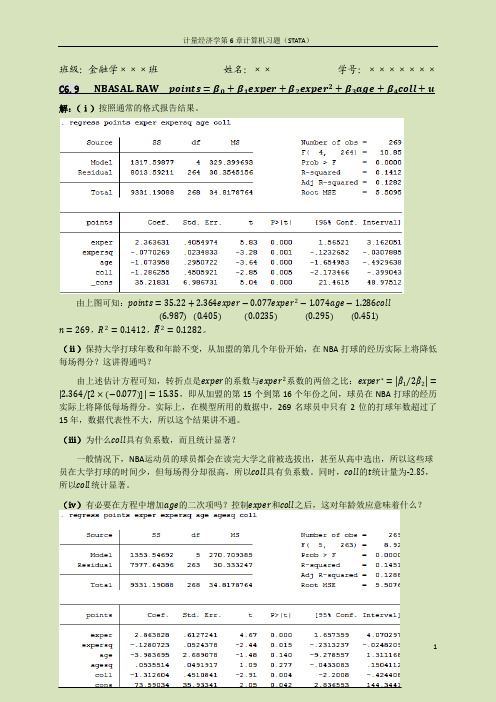
班级:金融学×××班姓名:××学号:×××××××C6.9 NBASAL.RAW points=β0+β1exper+β2exper2+β3age+β4coll+u 解:(ⅰ)按照通常的格式报告结果。
由上图可知:points=35.22+2.364exper−0.077exper2−1.074age−1.286coll6.9870.4050.02350.295 (0.451)n=269,R2=0.1412,R2=0.1282。
(ⅱ)保持大学打球年数和年龄不变,从加盟的第几个年份开始,在NBA打球的经历实际上将降低每场得分?这讲得通吗?由上述估计方程可知,转折点是exper的系数与exper2系数的两倍之比:exper∗= β12β2= 2.364[2×−0.077]=15.35,即从加盟的第15个到第16个年份之间,球员在NBA打球的经历实际上将降低每场得分。
实际上,在模型所用的数据中,269名球员中只有2位的打球年数超过了15年,数据代表性不大,所以这个结果讲不通。
(ⅲ)为什么coll具有负系数,而且统计显著?一般情况下,NBA运动员的球员都会在读完大学之前被选拔出,甚至从高中选出,所以这些球员在大学打球的时间少,但每场得分却很高,所以coll具有负系数。
同时,coll的t统计量为-2.85,所以coll统计显著。
(ⅳ)有必要在方程中增加age的二次项吗?控制exper和coll之后,这对年龄效应意味着什么?增加age的二次项后,原估计模型变成:points=73.59+2.864exper−0.128exper2−3.984age+0.054age2−1.313coll35.930.610.05 2.690.05 (0.45)n=269,R2=0.1451,R2=0.1288。
最新计量经济学第六章习题答案讲课教案

3解:(1)样本回归方程为998792.00170.1226.793261-176283.0454750.12^t r X Y t,(2)残差图(3)DW 统计量的值734726.0DW(4)BG LM 自相关检验辅助回归式估计结果是t t t tX e e 000420.0060923.0638831.01因为84.3998223.7,84.31205.0LM ,所以LM 检验量也说明样本回归方程的误差项存在一阶正自相关。
首先估计自相关系数^,得632637.02734726.0121^DW 对原变量做广义差分变换。
令1t 632637.0t t Y Y GDY ,1t 632637.0t t X X GDX 以年1994~1975,,t t GDX GDY 为样本再次回归,得tGDX GDY 173740.0391490.0t 回归方程拟合的效果仍然比较好,651914.1DW 对于给定05.0,查表得,。
43.1,24.1U L d d 因为75.243.11651914.1DW ,依据判别规则,误差项已消除自相关。
由391490.0^*0,得06568.1632637.01/391490.01/^^*0^0则原模型的广义最小二乘估计结果是t X Y 173470.006568.1^t 。
4解:(1)样本回归方程为tGDP Y 694454.0674.2816^t(2)残差图(3)3397.0DW(4)BG LM 自相关检验辅助回归式估计结果是t t t tGDP e e 029062.07871.334985257.01因为84.309615.30,84.31205.0LM ,所以LM 检验量也说明样本回归方程的误差项存在一阶正自相关。
首先估计自相关系数^,得83015.023397.0121^DW对原变量做广义差分变换。
令1t 83015.0t t Y Y GDY ,183015.0t t tGDGDP GDP GDGDP ,以年1994~1975,,t t GDGDP GDY 为样本再次回归,得。
伍德里奇计量经济学导论第6版笔记和课后习题详解

伍德里奇计量经济学导论第6版笔记和课后习题详解伍德里奇所著的《计量经济学导论》(第6版)是我国许多高校采用的计量经济学优秀教材,也被部分高校指定为“经济类”专业考研考博参考书目。
作为该教材的学习辅导书,(1)整理名校笔记,浓缩内容精华。
每章的复习笔记以伍德里奇所著的《计量经济学导论》(第6版)为主,并结合国内外其他计量经济学经典教材对各章的重难点进行了整理,因此,(2)解析课后习题,提供详尽答案。
(3)补充相关要点,强化专业知识。
一般来说,国外英文教材的中译本不太符合中国学生的思维习惯,有些语言的表述不清或条理性不强而给学习带来了不便,因此,对每章复习笔记的一些重要知识点和一些习题的解答,我们在不违背原书原意的基础上结合其他相关经典教材进行了必要的整理和分析。
第1章计量经济学的性质与经济数据1.1复习笔记考点一:计量经济学★||计量经济学的含义计量经济学,又称经济计量学,是由经济理论、统计学和数学结合而成的一门经济学的分支学科,其研究内容是分析经济现象中客观存在的数量关系。
计量经济学模型(1)模型分类模型是对现实生活现象的描述和模拟。
根据描述和模拟办法的不同,对模型进行分类,如表1-1所示。
表1-1模型分类(2)数理经济模型和计量经济学模型的区别①研究内容不同数理经济模型的研究内容是经济现象各因素之间的理论关系,计量经济学模型的研究内容是经济现象各因素之间的定量关系。
②描述和模拟办法不同数理经济模型的描述和模拟办法主要是确定性的数学形式,计量经济学模型的描述和模拟办法主要是随机性的数学形式。
③位置和作用不同数理经济模型可用于对研究对象的初步研究,计量经济学模型可用于对研究对象的深入研究。
拓展: 计量经济模型的检验(见表1・2)表1-2计量经济模型的检验考点二:经济数据★★★经济数据的结构(见表1-3)表1-3经济数据的结构面板数据与混合横截面数据的比较(见表1-4)表1-4面板数据与混合横截面数据的比较考点三:因果关系和其他条件不变★★因果关系因果关系是指一个变量的变动将引起另一个变量的变动,这是经济分析中的重要目标之一。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
伍德里奇计量经济学第6章计算机习题详解 STATA
引言
本文档旨在对伍德里奇计量经济学第6章的计算机习题进
行详解和解答,使用计量经济学软件STATA进行操作和分析。
本文档将逐步解答各个习题,并给出相应的STATA代码和结
果展示。
习题1
假设我们有一个数据集data.dta,其中包含了变量y和x。
现在我们想要估计下列回归模型的系数:
$$y = \\beta_0 + \\beta_1 x + \\beta_2 x^2 + u$$
使用STATA进行分析,首先加载数据集:
use data.dta
然后我们可以采用如下代码进行回归分析:
reg y x c.x#c.x
这里的c.x#c.x表示将变量x进行平方。
执行上述代码后,STATA将输出回归结果。
习题2
在第6章的习题2中,我们需要进行假设检验。
假设我们想要检验系数$\\beta_1=0$和$\\beta_2=0$的原假设。
我们可以使用STATA进行对应的假设检验。
首先,我们需要执行回归分析,并保存回归结果:
reg y x c.x#c.x
estimates store reg1
然后,我们可以使用如下代码进行假设检验:
test x#c.x=0
执行上述代码后,STATA将输出相应的假设检验结果。
习题3
在第6章的习题3中,我们需要计算残差的平方和(Sum of Squared Residuals)。
我们可以使用STATA来计算残差的平方和。
首先,我们需要执行回归分析,并保存回归结果:
reg y x c.x#c.x
estimates store reg1
然后,我们可以使用以下代码计算残差的平方和:
predict u, resid
egen ssr = sum(u^2)
scalar ssr_sum = r(ssr)
执行上述代码后,STATA将输出残差的平方和。
习题4
在第6章的习题4中,我们需要计算拟合度(Goodness of Fit)度量指标,如R2,调整后R2等。
我们可以使用STATA计算拟合度指标。
执行回归分析后,我们可以使用以下代码计算R2和调整后R2:
scalar R2 = e(r2)
scalar R2_adj = e(r2_a)
执行上述代码后,STATA将输出R2和调整后R2的值。
结论
本文档对伍德里奇计量经济学第6章的计算机习题进行了详解和解答。
通过使用STATA软件进行分析和操作,我们解答了习题1到习题4,并给出了相应的STATA代码和结果。
使用STATA进行计量经济学分析可以方便地进行回归分析、假设检验以及计算拟合度指标,帮助我们更好地理解和应用计量经济学的知识。
