地月二体轨道模型
月地转移轨道快速设计与特性分析

tnR p sn法求解 函数 ( ) o — a ho 1 ,以 作 为迭 代变 量 ,迭代 格式 为
l 一 + ( 一 L( ) y () 2
『acf翠) f 一 ) 降 再 一r。 \ 号 段 入 csl / / \n 一厂 z , S
6 一 0 ( 4)
分布 等特性 进行 了分 析 。仿 真 结果验 证 了所提 出方 法的有 效性 。
关 键 词 采 样 返 回 轨 道 设 计 月
DOI 0 3 8 /. s n 1 0 — 5 X. 0 1 0 . 1 :1 . 7 0 iis . 0 0 7 8 2 1 . 3 0 0
【c( 一 。号,段 入 a。 )(一 )升 再 rs c詈
收 稿 日期 :2 1 —8 0 。收 修 改 稿 日期 :2 1 1 0 0 0 9 O 0 1 1 9
2l年 6 01 月
中 国 空 间 科 学 技 术
2 2 双 二 体 模 型 下 月 地 转 移 轨 道 的 求 解 .
通 过 引入 月球影 响球 的定义 ,可 以将地 一 器 限制 性 三体 模 型 近似 和 简 化 为地_ 和 月一 月一 器 器两 个 二 体模 型 ,称 为双 二体模 型 。在 月球 影 响球 内 ,探 测器 仅 受 月 球 中心 引 力作 用 ;在 月 球影 响球 外 ,
心段轨 道倾 角 。
( )地 心段 轨 道求解 1
已知 月球影 响球 出 口点 S的地 心 距 、再 入 点 N 的地 心 距 r 、再 入 角 y 、地 心 段 飞 行 时 间 T ,可 以求 得 地心 段轨 道 的半长 轴 a 和偏 心率 e。引入 函数
y— L( , r r , T , ) ( 1)
探 测器 仅 受地球 中心引力 作 用 。在双 二体模 型 下对 月地 转移 轨道 的求解 ,实际上 是分 别求解 满 足约
新人教版选修1:2.2 月球和地月系 课件 (人教版选修1)
黄昏 半夜 清晨 通宵见月
上弦月 90º 迟升后落 下弦月 270º 早升先落
正午 黄昏 半夜 上半夜西天 半夜 清晨 正午 下半夜东天
v 月亮愈圆见月时间越长;月牙愈窄,见月时间愈短。 满月通宵可见,弦月半夜可见,新月则不见。
q 几个概念
v 恒星月:月球在白道上连续两次通过同一恒 星(无明显自行)所需的时间:27.3217日。
v 朔望月:从这一次新月(或满月)到下一次新 月(或满月)所经历的时间:29.5306日。
v 近点月:以月球近地点为参考点,月球的公 转周期:27.5546日。
v 交点月:以月球升交点(或降交点)为参考 点,月球的公转周期:27.2122日。
上所见的月相)
上图:旧历上半月 傍晚所见的月亮; 下图:旧历下半月 清晨所见的月亮
图2-20 月相的变化(二)
q 月相变化周期:29.5306日(朔望月) q 月相、方位和时刻
月相 新月
距角 与太阳出没 比较
0º 同升同落
月出 中天 月落 见月时间 清晨 正午 黄昏 彻夜无月
满月 180º 此起彼落
v 月球自转与其公 转同步,即方向 相同,周期相等。 因此称同步自转;
v 大体上只看到相 同的半个月面。
二、 月相和朔望月
q 月相变化的因素:太阳照射方向;地球 观测方向 v 方向相反,新月; v 方向相同,满月; v 方向垂直,上下。
月相变化动态演示
图2-20 月相的变化(一) 上半月由亏转盈,凸面向西,下半月 由盈转亏,凸面向东(外圈表示地球
第二节 月球和地月系
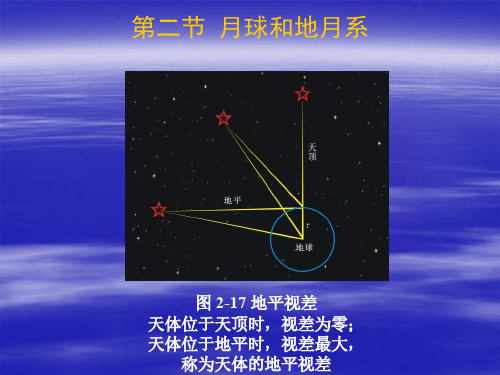
图 2-17 地平视差 天体位பைடு நூலகம்天顶时,视差为零; 天体位于地平时,视差最大,
称为天体的地平视差
基于双二体模型的月球探测器返回轨道初步设计及特性分析

Abstract:Idealized double two—body model is the universal hypothesis in the preliminary trajectory design of deep space.Based on this hypothesis,a return trajectory model with six independent parameters of lu— nar spacecraft from parking moon orbit including direct return trajectory and indirect return trajectory is
ZH OU Liang 一. HU Jun’'。
( .Beijing Institute of Control Engineering,Beijing 1 001 90,China; 2.Science and Technology on space Intelligent Control Laboratory,Beijing 1 001 90,China)
本 文在 文献 [4]的基 础 上 ,针 对 直 接 返 回型 轨
收 稿 日期 :2011—09—14
· 2 ·
空 间控 制 技 术 与 应 用
道和 间接返 回型 轨道 ,采 用双 二体 理论模 型 ,提 出 了 直观六 参数 返 回轨道 初 步设 计 方 法 .新 选 择六 个 独 立参 数 ,物 理 意 义 明 晰 ,可 直接 得 到 月 心 段 轨 道 参 数 ,方便 在 出 口点轨道 拼接 .利用 简单且解 析 的计算 公式 ,可初 步设计 返 回轨道 ,并分 析直 观六参 数 以及 出 口点 时刻对 轨道 特性 的影 响 ,得 到一 些 定 性 的结 论 .针对提 出 的方 法 ,对 应 两 种返 回轨 道 类 型 ,分 别 给出较节 省燃 料 的返 回轨 道 初 步设 计 算 例 ,并 进行 了 比较 .
二体问题与行星的运动轨迹

二体问题与行星的运动轨迹在天文学中,二体问题是指两个物体之间的相互作用。
这两个物体可以是恒星、行星、卫星等。
而行星的运动轨迹是由二体问题所决定的。
二体问题最早由牛顿在17世纪提出。
他的万有引力定律为我们解决了二体问题提供了基础。
根据牛顿的定律,两个物体之间的引力与它们的质量成正比,与它们之间的距离的平方成反比。
这个引力的方向始终指向两个物体之间的连线上。
当我们考虑一个行星绕着太阳运动时,可以将太阳看作是一个质量非常大的物体,而行星则是一个质量相对较小的物体。
根据牛顿的定律,太阳对行星的引力将使其绕太阳运动。
行星的运动轨迹可以是椭圆、抛物线或者双曲线。
这取决于行星的初始速度。
如果行星的初始速度足够大,它将离开太阳,形成一个双曲线轨道。
如果初始速度恰好等于逃逸速度,行星将运动到无穷远处,形成一个抛物线轨道。
而如果初始速度小于逃逸速度,行星将绕太阳运动,并形成一个椭圆轨道。
椭圆轨道是最常见的行星轨道。
地球绕太阳运动的轨道就是一个椭圆。
椭圆轨道有两个焦点,太阳位于其中一个焦点上。
行星在椭圆轨道上运动时,距离太阳的距离是不断变化的。
当行星离太阳较远时,它的速度较慢;当行星离太阳较近时,它的速度较快。
这就是著名的开普勒第二定律,也被称为面积定律。
根据这个定律,行星在相同时间内扫过的面积是相等的。
另一个重要的定律是开普勒第一定律,也被称为椭圆定律。
根据这个定律,行星的轨道是一个椭圆,太阳位于椭圆的一个焦点上。
这就解释了为什么行星绕太阳运动而不是绕其他物体运动。
除了椭圆轨道,行星也可以有其他类型的轨道。
例如,哈雷彗星的轨道是一个椭圆,但它的轨道非常扁平,接近于一个抛物线。
这意味着哈雷彗星只会经过太阳一次,然后再离开太阳系。
总的来说,二体问题和行星的运动轨迹是天文学中非常重要的研究课题。
通过研究二体问题,我们可以了解行星的运动规律,揭示宇宙中的奥秘。
而行星的运动轨迹也是天文学家们观测和研究行星的重要依据。
通过观测行星的轨道,我们可以了解行星的运动速度、轨道周期等信息,进一步研究行星的性质和演化过程。
载人登月地月转移轨道快速设计及特性分析_彭祺擘

轨道高度,又不能距离月球太远,以便于通过合适的
变轨策略将飞船送入预定环月轨道,见式(3)。
rLC ∈(rLmin ,rLmax)
(3)
其中,rLC 为地月转移轨道的近月距,rLmin 为目标环
月轨道高度,rLmax 为地月转移轨道近月距允许的最
大值。
(2)轨道倾角约束
要求到达环月轨道倾角大于着陆点纬度,即
月轨道。
(1)位置条件
假设在某时刻 t,航天器运行到 B 点。要使 B 点
成为入口点,首先在位置条件上要求 B 点在所形成
的穿越区内。设在轨道坐标系中,满足条件的 B 点位
姨 姨 E
置矢量为 R1B =
E
X1B
E
Y1B
0
,则在地心白道坐标系
B 点的位置矢量为:
第3期
彭祺擘 等:载人登月地月转移轨道快速设计及特性分析
21
L L E
R1B =
E
x1B
E
y1B
E
z1B
T
LE
=Mx(-iE)R1B
(8)
此外还要求 B 点在月球影响球的边界上,因此
这就要求在航天器到达 B 时,月球在该时刻的位置
满足式(9)。
L2 2
2
xL
LL
+y
=REL
L
2
L
E2
E2 E
2
(LLL x-x1B) +(y-y1B) +z1B =ρL
(9)
工程约束主要包括飞行时间约束和能量约束。
和无人月球探测不同,受到整个工程规模的限制,以
及为了保证航天员的安全,要求地月转移时间 t1 不
能太长,一般不多于三天左右。同时受推进剂限制,
描述轨道

第5章描述轨道本章中你将学到……经典轨道根数定义,描述轨道的大小、形状和方向,以及航天器在轨道上的位置利用航天器在轨道上某一点的位置矢量R r和速度V r确定经典轨道根数解释并利用轨道地面轨迹你应该已经掌握……二体运动方程及其假设(第4 章)轨道比机械能ε (第4 章)轨道比角动量h r(第4 章)矢量的定义及矢量的运算,包括点积和叉积(附录A.2)反三角函数cos−1 和sin−1 (附录A.2)内容安排5.1轨道根数定义经典轨道根数备用轨道根数5.2计算轨道根数半长轴偏心率轨道倾角升交点赤经近地点幅角真近点幅角5.3航天器地面轨迹航天器任务操控系统任务管理与操控弹道和轨道航天任务运载工具航天任务结构。
本章学习图1-20 所示的航天任务结构中的轨迹和轨道部分。
上一章学习了二体运动问题,推导出运动方程,并用严格的数学术语描述了航天器如何在空间运动。
但是很多情况下,只给出航天器在惯性空间的位置和速度是不够的。
通常还需要知道轨道与地球上相对应的轨迹(在地面上的投影)。
例如,想知道一颗遥感卫星什么时候经过洪水灾区(图5-1)。
图5-1.密西西比河洪水泛滥。
这是对地观测卫星1993 年拍摄的密苏里州圣路易斯洪水泛滥的图片。
(由NASA/戈达德航天中心许可)这一章将学习两个能够帮助我们了解航天器运动的有用工具——经典轨道根数和地面轨迹。
一旦你熟悉了它,就可以利用这些经典轨道根数来直观地描述轨道在空间中的样子。
地面轨迹可以确定地球上某一区域什么时候进入航天器的视野,什么时候地球上的观察者可以看到航天器。
5.1轨道根数本小节的主要内容是……定义经典轨道根数用经典轨道根数描述轨道的大小、形状和方位以及航天器在轨道上的位置如果一些特定的经典轨道根数没有定义,需要用哪些替换根数来代替如果你驾驶一架飞机,地面的控制人员通过无线电信号询问你在哪里,准备去哪里,你必须告诉他们6 个关于飞机的参数高度纬度经度水平速度机头方向(南北等等)垂直速度(上升还是下降)知道了这些参数,控制人员就能预见你的下一个位置。
地-月系平动点轨道的特征及其相关问题
地-月系平动点轨道的特征及其相关问题刘林;汤靖师;侯锡云【摘要】当探测器定点在地-月系共线平动点L1、L2附近的halo轨道或Lissajous轨道时,由于其固有的动力学特征,通常是被人们置于地-月系质心旋转坐标系中展现其几何特征.其实,它们同样是环绕地球运行的Kepler轨道,这类探测器实为地球的远地卫星.但由于其自身所具有的不稳定性特征,在轨道外推中,初值误差的传播程度远比一般的环绕型探测器轨道外推显著.这在轨道设计、运行控制和地面测控等领域都是需要重视的问题.尽管如此,除在构造这类轨道变化的受摄分析解时遇到困难外,对其定轨等问题,与一般远地卫星类似,并无其他特殊要求.将具体给出该类轨道由于不稳定特性引起误差快速传播的定量状态和相应的理论分析,以及实际应用中的短弧定轨和相应的高精度轨道预报方法,并附有实测资料进行定轨结果的检验.【期刊名称】《天文学报》【年(卷),期】2018(059)003【总页数】12页(P84-95)【关键词】天体力学;地球;月球;轨道预报【作者】刘林;汤靖师;侯锡云【作者单位】南京大学天文与空间科学学院南京 210046;南京大学空间环境与航天动力学研究所南京 210093;南京大学天文与空间科学学院南京 210046;南京大学空间环境与航天动力学研究所南京 210093;南京大学天文与空间科学学院南京210046;南京大学空间环境与航天动力学研究所南京 210093【正文语种】中文【中图分类】P1351 引言关于定点在地-月系共线平动点附近的探测器轨道外推(或称预报)问题,并不是一个新问题,该类型的飞行器,实际上就是一颗带有一定轨道特征的远地卫星.但是,尽管理论上绕地运行周期与月球一致,但它受到的月球引力影响却不是一个小扰动,而是一个几乎与地球引力作用同等重要的外力源.因此,该问题也无法处理成一个简单的受摄二体问题.如果仍然像构造平动点特殊轨道(如晕轨道)问题那样,在地-月系中来处理该问题,也无法像卫星运动那样处理成一个简单的受摄二体问题,其难点有如下两个方面:(1)即使基本模型采用简单的圆型限制性三体问题[1−3],其基本解也较复杂.如果考虑月球轨道偏心率,处理成椭圆型限制性三体问题,不仅基本解更复杂,而且无济于事.因为太阳引力摄动影响与月球轨道偏心率的效应相当,无论采用上述哪类基本模型,要在此基础上构造摄动解,都不可能像一般受摄二体问题那样简单,无法满足实际应用的需求.(2)即使形式上处理成一般的受摄二体问题,但由于探测器到月球的距离与探测器到地球的距离相当,这是处理第三体摄动问题的一个难点.鉴于上述分析,对于地面测控而言,宜在J2000地心天球坐标系中采用数值方法实现地-月系平动点探测器的轨道外推,其数学模型就是一个表面形式上的受摄二体问题,状态运动方程如下:该式中表示探测器加速度,r为探测器和摄动天体到地球的距离,µ=G(E+m)中,G为引力常数,探测器的质量m取为零,E为地球质量,mj(j=1,2,···)是摄动天体月球、太阳等第三体的质量,其中主要是月球和太阳,对应m1和m2,表示第三体摄动加速度,N表示第三体的总数.另外,(ε)是其他外力因素(包括各天体的非球形引力,太阳光压等)对应的摄动加速度,ε是摄动小量.2 外力分析对于航天器的轨道外推问题,实为一个定量问题,因涉及的各物理量有不同的量纲和大小,不便于问题的分析和表达,拟采用无量纲单位(可简称为归一化单位)来处理问题.以地球卫星的轨道运动为背景,包括月球之类的远地卫星(如地-月系的L1或L 2点探测器)轨道,通常采用的归一化单位系统,即长度单位[L]、质量单位[M]和时间单位[T]如下:其中,GE是地心引力常数,a e是地球参考椭球体的赤道半径,时间单位[T]是导出单位,目的是使该计算单位系统中,引力常数G=1和中心天体引力常数µ=GE=1.如果地球引力模型采用当今地固坐标系所对应的WGS-84系统,则相应的地球动力学扁率为J2=1.082636022×10−3.在采用上述归一化单位后,状态运动方程(1)式变为下列形式:该式中的是月球、太阳等第三体的无量纲质量,即其中,GM和GS分别为月心和日心引力常数.在上述处理下,运动方程(3)式中的第三体引力加速度为其中,是航天器到第j个天体的位置矢量,是航天器到第j个天体的距离,是地心天球坐标系中月球、太阳等第三体坐标矢量.2.1 各大天体的引力摄动量级估计地球的引力常数即GE=398600.4418 km3/s2,而月球、太阳、水星、金星、火星、木星和土星的引力常数相对地球的大小依次分别为0.0123000383、332946.050895、0.055273598、0.814998108、0.107446732、317.8942053和95.1574041.摄动量级的近似估计式为该式中的即各大天体相对地球的质量比,其值即上面给出的引力常数比,r和分别为探测器和摄动天体到地球的距离,估计中可取的平均值,但因水星轨道的偏心率较大(e>0.2),对应的r′值将分别按近日点和远日点两种状态设定平均距离.考虑定点在地-月系共线平动点L1和L 2的探测器到地球的距离r分别为其中是地-月平均距离.由(6)式给出上述各大天体对L1和L 2点探测器轨道的摄动量级分别如下:2.2 地球非球形引力摄动量级主项(扁率J2)的摄动量级估计2.3 太阳光压的摄动量级定点在地-月系共线平动点L1和L 2的一个通常尺度(包括质量和承受光压的等效截面)的探测器,太阳光压摄动的量级估计如下:其中,κ=1.44,面质比S/m=109,ρ⊙为1 au处的太阳辐射压强,ρ⊙=0.3169×10−17.根据上述对外力因素的量级估计,对于定点在地-月系共线平动点L1和L 2或其附近的探测器轨道,若考虑10−6以上的摄动因素,相应的力模型中只需要考虑如下摄动源:月球、太阳和金星的质点引力,地球非球形引力位的扁率J2和太阳光压,其中最主要的是月球和太阳的质点引力.3 定点在地-月系L1和L2点的探测器轨道概貌这里给出地-月系圆型限制性三体问题模型下两个简单的算例,初始历元为2016-09-30UTC0:00:0.0,对应的TDT(地球力学时)是57661.0007891667(MJD),探测器定点在地-月系L1和L 2点的各一条轨道上.经简单坐标转换,即可获得J2000.0地心天球坐标系中相应的两条轨道的初始位置(x,y,z)、速度(˙x,˙y,˙z)和相应的轨道根数,分别列于表1和表2.表1L 1点和L 2点的位置和速度Table 1 The positions and velocities of the points L1 and L2pointx/kmy/kmz/km˙x/(km/s)˙y/(km/s)˙z/(km/s)L1–337774.810825 –337774.810825 16503.725924 –0.08734133 –0.793809190 –0.262191839L 2–464586.522898 27663.672934 22699.764448 –0.120132126 –1.091831124 –0.360627231表2L 1点和L 2点的轨道根数Table 2 The orbital elements of the points L1 and L2po inta/kme i/◦Ω/◦ ω/◦ M/◦L1242063.297 0.40063038 18.507748 4.970405 353.948868 353.948868L 21064951.700 0.56309178 18.507748 4.970405 166.026309 1.189763两条轨道的图像见图1–2,这表明在初始时刻瞬间,实际上都是一条偏心率较大的环绕地球的椭圆轨道,探测器均处于该轨道的远地点和近地点(对读者而言,这一特点是容易理解的,无需做过多解释),两图中的坐标单位a e是地球参考椭球体的赤道半径.就地-月+探测器系统而言,这都是初始瞬时轨道,而在月球的引力作用下,探测器与月球轨道“同步”做相同的圆轨道运动.4 平动点轨道外推问题的相关分析4.1 平动点轨道分析采用的数学模型第1节引言中已指出,应在J2000地心天球坐标系中处理其轨道运动问题,并采用数值方法实现相应的轨道外推.为了定量显示这类轨道外推中误差传播状态的主要特征,显然应选择地-月-日+探测器的质点引力系统,相应的状态运动方程即其中是地球引力加速度:而和分别为月球和太阳的无量纲质量,见前面的(4)式.相应的月球和太阳引力摄动加速度、的具体形式分别为图1L1点初始轨道在J2000地心天球坐标系中(赤道面内)的图像Fig.1 The figure(in the equatorial plane)of point L1initial orbit in the J2000 reference system图2L 2点初始轨道在J2000地心天球坐标系中(赤道面内)的图像Fig.2 The figure(in the equatorial plane)of pointL 2initial orbit in the J2000 reference system4.2 平动点轨道类型的选择这里考查的平动点轨道,包括如下3种类型:(1)初始时刻定点在地-月系的L1点或L 2点处的平动点轨道,以下简称该类型轨道为L1点轨道或L 2点轨道;(2)初始时刻定点在地-月系的L1点或L 2点附近的halo轨道上,以下简称该类型轨道为L1点晕轨道或L 2点晕轨道;(3)初始时刻定点在地-月系的L1点或L 2点附近的Lissajous轨道上,以下简称该类型轨道为L1点Lissajous轨道或L 2点Lissajous轨道.经初步设计(对应所采用的质点引力系统)分别给出6条轨道,在J2000地心天球坐标系中各对应的轨道初值如下:所有初始时刻对应历元为2016-09-30UTC0:00:0.0(相应TDT的MJD为57661.0007891667),位置、速度和相应的轨道根数分别列于表3和表4.表中的轨道类型1、2、···、6依次为L1点轨道、L1点晕轨道、L1点Lissajous轨道、L 2点轨道、L 2点晕轨道、L 2点Lissajous轨道,表4–8类同.表3 6条轨道的位置和速度Table 3 The positions and velocities of 6 oribitstypex/kmy/kmz/km˙x/(km/s)˙y/(km/s)˙z/(km/s)1 –337774.812386 20112.705545 16503.726001 –0.060238672 –0.795423014 –0.263516080 2 –345532.034293 23412.210001 18744.897406 18744.897406 –0.681345631 –0.223235504 3 –339800.358749 18612.308488 17838.793255 –0.084919606 –0.758511545 –0.244765666 4 –464586.522898 27663.672934 22699.764448 –0.120132126 –1.091831124 –0.360627231 5 –474559.546159 30334.673645 24471.171450 –0.108738242 –0.966961696 –0.318679777 6 –468100.537842 27030.333913 27058.570893 –0.116389398 –1.050980229 –0.346236851表4 6条轨道的轨道根数Table 4 The orbital elements of 6 oribitstypea/kme i/◦Ω/◦ ω/◦ M/◦1 2419 54.728 0.40015996 18.507748 4.970405 351.172034 180.000000 2 224124.112 0.54793918 18.406015 5.484455 351.389485 176.433825 3 234898.998 0.45201084 18.179965 6.049772 352.984029 173.757384 4 1064951.700 0.56309178 18.507748 4.970405 166.026309 1.189763 5 636901.958 0.25401430 18.487234 5.196394 162.2609384.846848 6 867630.708 0.45956498 18.568585 6.587056 163.7559041.916194下面首先对上述6类轨道作7d和27d的轨道外推,给出一个误差传播的定量轮廓,在此基础上再作定性分析.4.3 6条平动点轨道外推7d的状态为简单起见(也不失一般性),在考查误差传播中,将初始误差全部集中在最重要的轨道半长径上(根据目前定轨的实际状况,轨道半长径的精度为10 m量级),7d的轨道外推结果列于表5–6.表5 平动点轨道外推7d的轨道状态Table 5 The states of the libration point orbits propagated for 7daystype mo del a/km e i/◦Ω/◦λ/◦1 standard 220999.515 0.415332 18.520032 5.002991 313.907599∆a0=10 m 220999.532 0.415332 18.520032 5.002991 313.907501 2 standard 266442.683 0.267042 18.718604 4.923182 256.745900∆a0=10 m 266443.184 0.267041 18.718603 4.923173 256.745426 3 standard 249439.450 0.364272 18.916482 5.301399 257.378240∆a0=10 m 249439.933 0.364271 18.916479 5.301379 257.377737 4 standard 980939.283 0.536729 18.534082 5.083138 265.994812∆a0=10 m 980939.634 0.536729 18.534082 5.083138 265.994765 5 standard 2623047.427 0.826111 18.614129 5.248427 257.032873∆a0=10 m 2623040.349 0.826110 18.614129 5.248428 257.032827 6 standard 1223545.852 0.619375 19.078832 6.073193 257.502177∆a0=10 m 1223545.763 0.619375 19.078833 6.073195 257.502134表6 平动点轨道外推7d的空间位置状态Table 6 The positions of the libration point orbits prop a gated for 7daystype model x/km y/km z/km r/km1 standard 17349.352 –235429.496 –79071.509 248958.533∆a0=10 m 17349.130 –235429.732 –79071.581 248958.763 2 standard –52603.690 –316406.575 –105287.004 337587.947∆a0=10 m –52604.014 –316407.100 –105287.168 337588.541 3 standard –61169.892 –317191.268 –106298.963 340075.765∆a0=10 m –61170.234 –317191.785 –106299.122 340076.358 4 standard –75890.039 –430172.798 –141396.957 459130.737∆a0=10 m –75890.082 –430172.853 –141396.974 459130.801 5 standard –96023.763 –424222.928 –139325.760 456724.559∆a0=10 m –96023.848 –424222.971 –139325.772 456724.621 6 standard –89282.870 –433942.578 –145977.148 466462.131∆a0=10 m –89282.927 –433942.628 –145977.163 466462.193 4.4 6条轨道外推27d的状态尽管探测器的定点只是近似的,实际运行过程中必须通过不断轨控才能保持这类轨道,外推弧段增长至27d,只是为了进一步了解这类特殊轨道的动力学特征及其相应的误差传播规律.初始误差仍全部集中在轨道半长径上,27d的轨道外推结果列于表7–8,其中,第2和3两类轨道(即L1点晕轨道和L1点Lissajous轨道)只外推了22 d,其原因将在4.5小节中具体说明.表7 平动点轨道外推27d的轨道状态Table 7 The states of the libration point orbits propagat ed for 27daystype modela/kme i/◦Ω/◦ λ/◦1 standard 212685.965 0.442498 18.517044 5.009819 211.007387∆a0=10 m 212685.969 0.442498 18.517044 5.009819 211.007270 2 standard 222801.427 0.515663 18.570547 6.333758 88.715061∆a0=10 m 247840.427 0.595452 18.616593 6.037248 56.512170 3 standard 235375.045 0.425546 18.494325 7.675744 85.777531∆a0=10 m 378708.222 0.532445 18.639545 6.508178 37.783963 4 standard 1187150.224 0.614869 18.614143 5.245764 164.740828∆a0=10 m 1187149.042 0.614869 18.614143 5.245764 164.740913 5 standard 690495.272 0.333894 18.560056 5.215658 162.442776∆a0=10 m704825.483 0.346515 18.560165 5.213139 161.458414 6 standard 860189.818 0.462166 17.811203 6.065852 165.371342∆a0=10 m 875504.051 0.469931 17.813259 6.041064 164.128126对于探测器的轨道运动而言,通常所说的长期位置预报和短期位置预报中的长期或短期并不是简单的时间间隔,而是运行弧段的长短.因此,为了比较上述各条轨道之间外推误差传播的定量大小,需要了解它们的轨道运行周期,这6条特殊轨道的初始运行周期T S值依次为L1类:T S=13.708768 d,12.221658 d,13.113512 d;L 2类:T S=126.58784 d,58.847196 d,93.089267d.由此便于了解轨道外推7d和27d对上述6条轨道所对应的弧段长短.在已知6条轨道自身的动力学特性和轨道外推弧段长短的前提下,不难看出表5所列出的外推位置误差所反映的一些动力学规律,基本上可归纳如下:(1)轨道外推7d均为短弧,位置误差都在1 km以内;(2)对于L1点轨道和L 2点轨道,外推7d或27d,位置误差的累积仍不严重,其误差传播的特征就是一般Kepler运动特征的反映.由于初值误差(∆a0=10 m)较小,实为小扰动,既不会激发其初值不稳定的固有特征,又不会明显改变短弧段误差累积的效果,反而周期性的效果比长期累积效应更明显,见表5中轨道1(即L1点轨道)的误差定量状态.(3)对于L1点和L 2点的halo轨道和Lissajous轨道而言,由于其位置已经“远离”不稳定平动点L1和L 2,而严格的halo轨道和Lissajous轨道设计又无法实现,探测器的定点只是近似的,在同样是∆a0=10 m的初值误差情况下,已不能再简单地只看作对halo轨道和Lissajous轨道的小扰动,而更重要的是对平动点的大扰动起作用,在不太长的外推弧段内,其平动点本身的不稳定特征即显现无遗.见表5中的轨道2、轨道3、轨道5和轨道6,特别是轨道2和3,相对而言,27d的弧段显得更长,外推弧段超过22 d后,其轨道偏心率很快就会达到e≈1.0的状态.表8 平动点轨道外推27d的空间位置状态Table 8 The positions of the libration point orbits propagated for 27daystypemodelx/kmy/kmz/kmr/km 1 standard –231950.200 –191657.303 –57161.753 306269.298∆a0=10 m –231950.225 –191657.248 –57161.734 306269.280 2 standard –115564.838 294821.738 102728.456332908.733∆a0=10 m –110340.192 314798.221 109363.932 351046.076 3 standard –106522.282 294300.982 102316.285 329285.115∆a0=10 m –106322.537 324499.131 112814.962 359626.728 4 standard –452814.170 55918.600 32699.152 457424.089∆a0=10 m –452813.996 55918.681 32699.174 457423.928 5 standard –464361.937 21794.997 21461.005 465368.247∆a0=10 m –465954.469 22340.406 21685.299 466993.482 6 standard –460599.098 39263.652 28181.440 463127.798∆a0=10 m –462359.879 40264.443 28501.149 464984.0844.5 平动点轨道运行中误差传播状态的基本特征从上述6条轨道的外推计算结果已能看出拉格朗日点轨道外推中位置误差传播的基本特征,首先将由∆a0=10 m导致的位置误差集中列于表9.表9 拉格朗日点轨道外推位置误差的定量状态(单位:km)Table 9 The quantitative state of position error s of the Lagrange point orbit propagation(unit:km)propagating arc/d type 1 2 3 4 5 6 7 0.322 0.638 0.640 0.072 0.096 0.077 22 – 186181.8–47023.6 –––27 0.063––0.193 1698.216 2050.401综上几小节,就平动点探测器轨道运行误差传播状态的简单计算和分析,可以表明:在地-月系L1和L 2平动点轨道设计中,确实很难实现较长弧段的无动力控制运行轨道,而不是设计者本身的问题.那么,在这样较短的弧段内,就轨道预报而言,要达到较高的精度是容易实现的,本节最后一小节将会给出具体算例,并有实测结果的检验.4.6L1点晕轨道的运行状态为了进一步揭示平动点飞行器轨道外推中误差传播的动力学机制,这里再给出一条与上述L1点晕轨道相近的环绕地球运行的大椭圆逆行轨道,同样对应一远地卫星.初始时刻仍为2016-09-30UTC0:00:0.0,初始位置和速度及相应的轨道根数分别列于表10和表11.该轨道的初始运行周期为12.208831 d.对此轨道同作27d的外推,计算结果列于表12–13.表10L1点晕轨道的位置和速度Table 10 The position and velocity of the halo orbit at pointL 1x/kmy/kmz/km˙x/(km/s)˙y/(km/s)˙z/(km/s)–345307.466263 21904.224767 19425.079239 –0.077571217 0.681599717 –0.223818048表11L 1点晕轨道的轨道根数Table 11 The orbital elements of the halo or bit at pointL 1a/kme i/◦Ω/◦ ω/◦ M/◦223967.268 0.56141578 160.912742 160.912742 356.972610 356.972610表12L 1点晕轨道外推27d的轨道状态Table 12 The states of the halo orbit prop a gated for 27days at pointL 1modela/kme i/◦Ω/◦ λ/◦standard 213214.203 0.653838 162.168040 350.586870 267.258205∆a0=10 m 213214.209 0.653838 162.168042 347.586870 267.258158表13L 1点晕轨道外推27d的空间位置状态Table 13 The positions of the halo orbit prop a gated for 27days at pointL 1modelx/kmy/kmz/kmr/km standard –229245.266 186181.824 –47023.643 299045.626∆a0=10 m –229245.393 186181.802 –47023.625 299045.707这样一条有别于L1点晕轨道绕地运行的大椭圆逆行轨道,本质上就是一条普通的Kepler轨道,其固有的初值不稳定性在绕地运行27d(仅2圈)的短弧内不会有明显体现,这是一个常规问题,本文引进这一算例的目的,是从另一角度体现地-月系平动点轨道误差快速传播的固有不稳定性特征.至于逆行轨道自身的运动规律及其动力学特征,已超出本文论述的范畴,不再介绍,如有需要,可见文献[4]及其有关作者的研究工作.4.7 平动点轨道的定轨和短弧预报精度的检验既然严格的拉格朗日点轨道设计无法实现,探测器的定点只是近似的,运行过程中必须通过不断的轨控才能保持,那么,对于地面测控和星上控制,只能从短弧角度来考虑问题.对于平动点轨道的短弧定轨和轨道预报而言,相对地球低轨或高轨卫星的同类问题,实无任何特殊困难和特别需要处理的难题.采用南京大学空间环境与航天动力学研究所自主编写的定轨软件和利用国内的USB(Unified S-band)测量数据,在没有任何其他辅助信息的前提下,对嫦娥3号的相关任务探测器进行了定轨,并与北京航天飞行控制中心的事后定轨结果作了对比.在此定轨的基础上,采用非常简单的数值外推方法(只考虑地、月、日三体的质点引力和简单的光压模型,外推中的6个轨道初值采用相关任务的定轨结果)进行了轨道预报,毫无困难地达到了较高精度.略去不必要的细节说明,将有关结果一并列于表14–15.表14L 2点晕轨道短弧外推3 d与事后精密定轨结果的比较Table 14 The comparison of two precise orbit determination method s for the pointL2orbit after propagating 3daysmethodx/kmy/kmz/km˙x/(km/s)˙y/(km/s)˙z/(km/s)orbi t determination A –451897.422 138113.307 36463.951 –0.237782 –0.978285 –0.204902 orbit determination B –451897.388 138112.927 36463.914 –0.237782 –0.978287 –0.204900 short arc propagation A –451897.458 138113.145 36463.888 –0.237783 –0.978286 –0.204902 short arc propagation B –451897.346 138112.816 36463.866 –0.237782 –0.978288 –0.204900表15L 2点晕轨道短弧外推7d与事后精密定轨结果的比较Table 15 The comparison of two precise orbit determination methods for the pointL2orbit after prop a gating 7days?表14–15中的精密定轨A和B分别对应北京航天飞行控制中心和南京大学空间环境与航天动力学研究所的结果,表中的结果基本上已能说明问题,但为了让读者对这类探测器的定轨和外推精度有更清晰的了解,下面进一步作些必要的说明.(1)关于光压模型,在不了解探测器的具体细节情况下,作者们根据独立定轨中获得的有关估计值,获得了包括卫星表面热性能在内的等效面质比,从而给出了相应的经验模型:一个等效的平面模型.(2)尽管没有具体给出两个单位的定轨(包括测量数据)细节,但表14–15所给出的计算结果,已能说明本文要体现的这类特殊轨道的定轨和外推精度了.因为表中的结果是外推3 d和7d与事后精密定轨结果的比较,且两个单位的定轨结果之差基本上在500 m之内,这样的比较更能体现两个单位定轨结果的真实性以及本文所采用的力模型的合理性.上述计算结果和两点补充说明充分表明:尽管这类探测器的轨道特殊,初值误差的传播程度远比一般的环绕型探测器的轨道显著,但相应的短弧定轨和高精度轨道预报并无特殊困难.4.8 关于两种坐标系中平动点探测器轨道形式的转换问题就定轨和预报的需求,显然是在J2000地心天球坐标系中进行相关问题的处理,而对这类具有特殊性质的轨道,轨控又必须通过相应的地-月系旋转坐标系来处理.这就涉及到两种坐标系之间的转换问题,其本身是容易实现的,而在具体的航天任务中,各有关部门根据实际需求,对相应的地-月系旋转坐标系实有不同取法,故这里不再做相应讨论.参考文献【相关文献】[1]刘林,汤靖师.卫星轨道理论与应用.北京:电子工业出版社,2015[2]Gmez G,Llibre J,Mart´ınez R,et al.Dynamics and Mission Design Near Libration Points.Singapore,New Jersey,London,Hong Kong:World Scientific,2001[3]刘林,侯锡云.深空探测轨道理论与应用.北京:电子工业出版社,2015[4]赵长印,刘林.天文学报,1994,35:434。
基于不变流形的地月L2点Halo轨道转移轨道设计
Manned Spaceflight
载 人 航 天
Vol. 22 No. 6 Dec. 2016
基于不变流形的地月 L2 点 Halo 轨道转移轨道设计
彭 坤 \ 李 明 涛 2 ,王 平 1, 田 林 、果 琳 Байду номын сангаас 、杨 雷 1
( 1 . 中国空间技术研究院载人航天总体部, 北 京 100094;2. 中国科学院空间科学与应用研究中心, 北 京 100190)
Transfer Trajectory Design for EML2 Halo Orbit Based on Invariant Manifolds
(1. Institute of Manned Space System Engineering, China Academy of Space Technology, Beijing 100094, China ; 2. Technology and Engineering Center for Space Utilization, Chinese Academy of Sciences, Beijing 100190, China)
摘要: 针 对 Halo 轨 道 转 移 轨 道 设 计 不 易 收 敛 的 问 题 , 结合月球探测背景, 分 析 了 地 月 L2 点
Halo轨 道 及 其 不 变 流 形 可 靠 近 月 球 的 运 动 轨 迹 特 性 , 给出基于二分法的先粗选后精选的零消 耗 转 移 轨 道 搜 索 方 法 并 研 究 得 出 Halo轨 道 全 相 位 点 入 轨 的 零 消 耗 转 移 轨 道 不 超 过 2 条 , 提出 一 种 最 小 x 轴约束的近月点终止条件和自适应退步搜索的改进微分修正算法, 对 Halo轨道全 相 位 点 入 轨 的 转 移 轨 道 设 计 进 行 求 解 。仿 真 结 果 表 明 , 该改进微分修正算法收敛速度快, 能有 效避免奇异, 且适应性强, 能 搜索 出 全 相 位 点 入 轨 的 所 有 转 移 轨 道 。 关键词 : 月球探测; 平动点; Halo轨 道 ; 不变流形; 转移轨道 中图分类号 : V 412. 4 文献标识码 : A 文章编号 =1674-5825(2016 ) 06-0673-07
月地返回轨道参数的初步分析
Ke od : iu a a co ; aa t a s ; rl nr ein Smua o m uain y W rs C s n t j tr P me r l i Pei ay s ; i lt nc p t o l rr e y r ea y s n i m d g i o t
月地 返 回轨 道 参 数 的初 步 分析
刘 银 ,茹 家欣 ,朱永贵 ,容 易
( 京 宇航 系 统 工 程 研 究 所 ,北 京 ,10 7 ) 北 0 0 6
摘要:对月球探测 器的返 回轨 道进行 建模与参数分析 。基 于双二体假设 ,在三 维空间中建立返回轨道的数学模型;根据 模型计算给 出初步设计轨道的算例 ,并以此结果为初值 ,在 已有 高精度 动力学模 型下搜 索计算,较快地得到 了精确轨道参数; 通过 两条轨道参数 的对 比,证 明文 中初步设计解析 方法的正确性 ;通 过对模型 进行 仿真计算 ,得到 落区位置等 因素对近 月点
Li i RuJ a n, u y n, ixi ZhuYo g i Ro g y ng u , n i
e ig n tue f t n ui l yt n ier g B in , 0 0 6 On stto r at a S s ms gn e n , e ig 10 7 ) I i As o c e E i j A src:Ma e t a mo e n aa ee n yi o iu n r etr es de . crigt ed u l t —o y bt t a t ma c dlad prm t a a s fcs art jcoy a t i Acodn ot o be wob d h il r l s l a r u d h asmp o , t ma cl d l f i u a a co s bi e D saeadpe miaytjco aa ees e a ua d su t n ma e t a mo e o s n t j tr iet lh di 3 c rl n r aetr p m tr a l lt . i h i c l rr e y s a s n p n i r y r c c e r
地月空间飞行轨道分层搜索设计
般 来 讲 , 月空 间轨 道设 计 是 解 两点 边 值 问 地
例, 描述 如 下 :
, +A , ( x Y+△ , ) )= A g +△ ) + A ): B ( , , y … 1 )
高 玉 东 ,郗 晓 宁 ,王 威
( 防科 技 大 学 航 天 与 材 料 工 程 学 院 ,长 沙 407 ) 国 103
摘 要 :通 过 对 地 月 间 飞行 轨 道 特 征 进 行 分 析 , 据 不 同 的终 端 约 束条 件 , 出 了 分 层 搜 索 的 轨 道 设 计 方 法 。 根 提 其 基本 思 想 首先 是 将 月 球 视 为 质 点 , 决 空 间 两 质 点 的 相 遇 问 题 , 次 进 一 步 视 月 球 为 球 体 , 成 二 体 假 设 下 的 B 解 其 完 平 面 瞄 准 , 后 在 前 两 步 基 础 之 上 , 据 具 体 目标 条 件 约 束 得 到 精 确 的 轨 道 。本 文 详 细 清 晰 地 给 出该 方 法 的 设 计 最 根 过 程 , 好 地 解 决 了 地 月 空 间 轨 道 搜 索 的 快 速 收 敛 性 问 题 , 深 空探 测 器 轨 道 设计 有借 鉴 意 义 。 很 对 关 键 词 :地 月 空 间 轨 道 ;分 层 搜 索 ;B平 面 瞄 准 ;微 分 改 正 法
维普资讯
第2 7卷第 6期
20 0 6年 1 1月
字 学 报
J u n lo to a tc o r a fAsr n u is
V0 . 7 12
No e  ̄r v ml
No. 6
2 o6 0
地 月 空 间飞行 轨道 分 层 搜 索设 计
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3. 2地月二体轨道模型
假定卫星在地球中心引力场运动,忽略各种摄动力因素影响的卫星轨道称为二体轨道。
此时,卫星的运动轨迹是一个不变的椭圆轨道,分析这种轨道的特性称为二体问题。
其相应的运动方程为:
223d dt r
μ
=-r r
(1)
称之为开普勒方程[4],其中μ(32398601.19/km s μ=)为地心引力常数。
为仿真计算的需要,下面把各摄动力在地心惯性坐标系下用力的分量形式表示出来,并用下标,,x y z 分别表示力在i F 坐标系中的三个坐标方向上的三个分量。
由(1)式可以直接得到0F 的分量表示:
0003
3
3
,,x y z F x F y F z r r
r
μ
μ
μ
=-
=-
=-
(2)
3. 3理想模型
假定月球在地球中心引力场运动,忽略各种摄动力因素影响,地球为圆形球体,那么月球在地心惯性坐标系中的位置和速度分别为[4] :
20cos cos()sin sin()cos (1)sin cos()cos sin()cos 1cos sin()sin x f f i a e y f f i e f z f i ωωωωωΩ+-Ω+⎡⎤
⎡⎤
-⎢⎥⎢⎥==
Ω++Ω+⎢⎥⎢⎥+⎢⎥⎢⎥+⎣⎦
⎣⎦
r
(3)
]0sin (cos )(1f e f a μ⎡⎤
⎢⎥==-++⎢⎥-⎢⎥⎣⎦
x v y z E Q
(4)
cos cos sin sin cos cos sin sin cos cos sin sin i i i ωωωωωΩ-Ω⎡⎤
⎢⎥=Ω+Ω⎢⎥
⎢⎥⎣⎦
E
(5)
sin cos cos sin cos sin sin cos cos cos cos sin i i i ωωωωω-Ω-Ω⎡⎤
⎢⎥=-Ω+Ω⎢⎥
⎢⎥⎣⎦
Q
(6)
由上面四个公式可得月球在地心惯性坐标系中假设初始点的位置r 和速度v (参看附录1)分别为
(
-173450,72740,-311210)
(7)
和
(
0.2011,-0.9981,-0.3454)
(8)
记0000(,,)x y z =r 和0000(,,)x y z v v v =v 分别为月球的位置矢量和速度矢量。
由于(1)式等价于[5]: 00x dx v dt = 00y dy v dt = 00z dz
v dt
= 003x dv x dt r μ=- 003y dv y dt r μ=- 003z dv z
dt r
μ=- 记300000(,),(,)(,/)f t r μ==-r v v r X X ,则上面6个方程构成的方程组等价于:
()
00/,d dt f t =X X
(9)
取采样周期(采样时间间隔)为N ,把(10)式离散化得:
001011[]
(,)
k k k k f t N ----=X X X
(10)
即:
0010101(,)k k k k f t N
---=+X X X
(11)
其中00()k k t =X X 为k t 时刻位置速度向量。
利用(11)式和初始时刻的位置和速度就可以求出以后各时刻的位置和速度,从而确定月球轨道。
已知月球的轨道平均周期为29.53天,使用MATLAB 软件编程[6]计算出任一周期的各个时刻的月球在地心坐标系下的位置矢量,自探月卫星发射时刻开始的以1秒为间隔的各时刻月球位置坐标参看表1.
表1 各时刻月球位置坐标
图2是自探月卫星发射时刻开始的以1秒为间隔模拟的一个周期的月球轨道示意图:
附录
附录2 计算月球初始位置和速度
f=0;
图2 月球绕地进动轨道示意图
5
u=398601.19;
r=a*(1-e^2)/(1+e*cos(f))*[cos(ou)*cos(w+f)-sin(ou)*sin(w+f)*cos(i);si n(ou)*cos(w+f)+cos(ou)*sin(w+f)*cos(i);sin(w+f)*sin(i)];
E=[cos(w)*cos(ou)-sin(w)*sin(ou)*cos(i);cos(w)*sin(ou)+sin(w)*cos(ou) *cos(i);sin(w)*sin(i)];
Q=[-sin(w)*cos(ou)-cos(w)*sin(ou)*cos(i);-sin(w)*sin(ou)+cos(w)*cos(o u)*cos(i);cos(w)*sin(i)];
v=sqrt(u/a/(1-e^2))*((-sin(f)*E)+(e+cos(f))*Q);
r
v
附录3(画出月球轨道并求出各个时刻月球位置与速度)
clear
clc
u=398601.19;
u2=u/81;
rs2=rs*9/10;
vs2=[-0.8563,4.5805,-1.7957];
x0=[rs2,vs2];
r2=sqrt((rs2(1)+rs(1))^2+(rs2(2)++rs(2))^2+(rs2(3)++rs(3))^2);
N=60;
n=29.53*24*60;
for k=1:n-1;
a(k)=(X(k+1)-X(k))/N; b(k)=(Y(k+1)-Y(k))/N;c(k)=(Z(k+1)-Z(k))/N; vs(k,:)=[a(k),b(k),c(k)];
end
for k=1:n-2;
a1(k)=(a(k+1)-a(k))/N;
b1(k)=(b(k+1)-b(k))/N;c1(k)=(c(k+1)-c(k))/N;
vs1(k,:)=[a1(k),b1(k),c1(k)];
end
for k=1:n-2;
x=x0+[vs2,(-u/r2^3-u2/r2^3)/2*rs2-u2/r2^3/2*rs-vs1(k,:)]*N; X2(k)=x(1); Y2(k)=x(2); Z2(k)=x(3);
x0=x;
r2=sqrt((rs2(1)+rs(1))^2+(rs2(2)++rs(2))^2+(rs2(3)++rs(3))^2); rs2=x0(1:3);
vs2=x0(4:6);
end
plot3(X2,Y2,Z2)
hold on
comet3(X2,Y2,Z2)。
