《电路基础》第20讲 正弦量与相量法的基本概念

例1. 已知 i = 141.4cos(314t + 30o )A u = 311.1cos(314t 60o )V
试用有效值相量表示 i, u 。解：•I源自= 10030o A•
U = 220 60o V
振幅相量:
•
Um
= Ume ju
= Umu
=
•
2U
15
u 错误的写法：
U
i
I
例2.
•
已知I = 5015o A,
u=Umcos(t + u) i = Imcos(t + i )
(1) Um(Im )：正弦量的振幅。是正弦量在整个振荡过程中 达到的最大值。
(2) (t + u)和(t + i)：相位角或相位。它反映了正弦量
变化的进程。
（3）u(i)称为正弦电压(电流)的初相角, 简称初相, 它是正
弦量t =0时刻的相角。
f = 50Hz .
试写出电流的瞬时值表达式。
解： i = 50 2cos(314t + 15o ) A
3、 相量图
i(t) = 2Icos(ω t + i ) I= Ii u(t) = 2Ucos(t + u ) U= Uu
•
U
•
I u i
16
4、 相量运算 (1) 同频率正弦量相加减
u1(t ) = 2 U1 cos(t + 1) = Re(
复常数
A(t)包含了三要素：I， y ， 复常数包含了I , 。
•
称 I = I 为正弦量 i(t) 对应的有效值相量。
14
•
i(t) = 2I cos(t + ) I = I
正弦量的有效值相量表示:
以正弦量的有效值作为相量的模 正弦量的初相位作为相量的幅角
•
u(t) = 2U cos(t + ) U = U
2
•
U
1
e
j
t
)
u2 (t ) =
2 U2 cos(t + 2) = Re(
2
•
U
2
e
j
t
)
u(t) = u1(t)+ u2(t)
= Re(
2
•
U
1
e
j
t
)
+
Re(
2
•
U
2
e
j
t
)
= Re(
•
2U1
e jt
+
2
•
U
2
e
j
t
)
= Re[
2
•
(U
1
+
•
U
2
)e
j
t
]
U
得：
U= U1 + U2
17
（2） 正弦量的微分、积分运算
2
N
线性
非
线性
不适用 ③ 相量法可以用来求强迫响应是正弦量的任意常系数线
性微分方程的特解，即可用来分析正弦稳态电路。
19
例 1 如有两个同频率的正弦电压分别为
u1(t) = 2220cos t (V) u2(t) = 2220cos(t 120) (V)
求 u1+u2 和 u1u2。 解：
•
U1
22
L
d dt
•
[I
m
e
jt
]+
R
•
Re[I
m
e
jt
]
=
•
Re[U
Sm
e
jt
]
•
•
•
Re[ jL I m e jt ] + Re[R I m e jt ] = Re[U Sm e jt ]
•
•
Re[(R + jL) I m e jt ] = Re[U Sm e jt ]
•
•
(R + jL) I m = U Sm
13
2、 正弦量的相量表示
复函数 A(t ) = 2Iej(t+ )
= 2Icos(t + ) + j 2Isin(t + ) 若对A(t)取实部：
Re[ A(t )] = 2Icos(t + )
i = 2Icos(t + ) A(t ) = 2Iej(t+ )
A(t)还可以写成
A(t ) = 2 I ej ej t = 2 Ie j t
u1(t ) u2 (t ) = 2 381cos(t + 30 )
•
U2
•
U1
•
•
U1 U2
-120o
•
U2
•
•
U1+ U2
21
例 2 如图所示电路, 已知R = 2 Ω, L = 1H, 激励uS(t) = 8 cos ωt (V), ω=2rad/s, 求电流i(t)的稳态响应。
解： 列KVL方程为
第20讲 正弦量与相量法的基本概念
学习重点: 1、正弦量三要素的概念，周期、频率与角频率的关系； 2、相位差及其物理含义； 3、正弦量的有效值及其物理含义； 4、振幅相量、有效值相量的概念； 5、正弦量的相量运算。
1
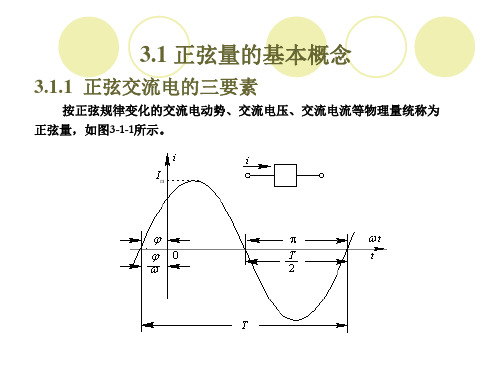
一. 正 弦量(P145)
电路中凡是按正弦(余弦)规律随时间作周期变化的电压或电 流称为正弦电压或正弦电流，统称为正弦量。它可以用正弦函 数表示，也可以用余弦函数表示。本课程用余弦函数表示，即
L
di dt
+
Ri
=
us
当激励uS为正弦量时,方程的特解是与uS同频率的正弦量。
设
i(t) = Im cos(ωt+i) = Re[Imejωt］
uS(t) = USm cosωt =Re［ USme jωt］
代入微分方程得：
L
d dt
•
[I
m
e
jt
]+
R
•
Re[I
m
e
jt
]
=
•
Re[U
Sm
e
jt
]
F1·F2=F ej
F逆时针旋转一个角度 ，模不变
ej 称为旋转因子。
j
e2
= cos
+
j sin
=+j
2
2
e j(
2
)
=
c o s (
2
)
+
j
s i n (
2
)
=
j
Im
+ j I
0
I
Re
e j = cos( ) + j sin( ) = 1
I jI
+j , –j , -1 都可以看成旋转因子。
注意:只适用正弦量
Im = 2I
i(t) = Im cos(t + ) = 2I cos(t + )
同理: u(t ) = Um cos(t + ) = 2U cos(t + )
★ 正弦量的有效值与最大值之间有固定的 2 关系，即
Im = 2I Um = 2U
11
二、 相 量 法 的 基 本 概 念（P149）
-120o
•
U 1 = 220
0 ,
•
U 2 = 220
120
•
U2
+ •
•
U 1 + U2 = 220
0
220
120
•
•
U1+ U2
= 220 (cos0 + j sin 0) + 220[cos(120) + j sin(120)] = 110 j190.5 = 1102 + (190.5)2 arctan 190.5 = 220 60
L
di dt
+
Ri
=
us
•
•
(R + jL) I m = U Sm
24
第20讲 正弦量与相量法的基本概念
结束
作业：P266 4-2 预习: 电路定律的相量形式、阻抗与导 纳
25
i I
证明：
di jI
dt
di = d Re[ 2Ie j t ] dt dt
= Re d [ 2Ie j t ] dt
= Re[ 2 Ij e j t ]
i I
idt
1
j
I
18
小结
① 正弦量
正弦波形图
相量
有效值相量 振幅相量
相量图
② 相量法只适用于激励为同频正弦量的线性时不变电路。
N
线性
1
3
正弦电压与电流
4
初相角的单位为弧度(rad)或度(°)。通常在-π≤ φu (或φi)≤π 的主值范围内取值。
初相角的大小与计时起点有关。因本课程用余弦函数表示正
弦量，因而用最大值发生的时刻与t=0时相比较。如果正弦量的正
最大值发生在计时起点(t = 0)之前 , 则φu (φi)>0, 如图(a)所示; 如
设 i(t)=Imcos( t + )
def
I=
1 T i 2 (t )dt
T0
I =
1 T
T 0
I
2 m
cos2
(
t
+
)
dt
T cos2( t + ) dt = T 1 + cos 2(t + ) dt = 1 t T = 1 T