数学-初三-圆的相关概念与垂径定理
初三下册数学圆知识点定理总结

1.垂径定理及推论:如图:有五个元素,“知二可推三”;需记忆其中四个定理,即“垂径定理”“中径定理”“弧径定理”“中垂定理”.几何表达式举例:∵ CD过圆心∵CD⊥AB2.平行线夹弧定理:圆的两条平行弦所夹的弧相等.几何表达式举例:3.“角、弦、弧、距”定理:(同圆或等圆中)“等角对等弦”;“等弦对等角”;“等角对等弧”;“等弧对等角”;“等弧对等弦”;“等弦对等(优,劣)弧”;“等弦对等弦心距”;“等弦心距对等弦”.几何表达式举例:(1) ∵∠AOB=∠COD∴ AB = CD(2) ∵ AB = CD∴∠AOB=∠COD4.圆周角定理及推论:(1)圆周角的度数等于它所对的弧的度数的一半;(2)一条弧所对的圆周角等于它所对的圆心角的一半;(如图)(3)“等弧对等角”“等角对等弧”;(4)“直径对直角”“直角对直径”;(如图)(5)如三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.(如图)(1)(2)(3)(4)几何表达式举例:(1)∵∠ACB=∠AOB∴……………(2)∵ AB是直径∴∠ACB=90°(3)∵∠ACB=90°∴ AB是直径(4)∵ CD=AD=BD∴ΔABC是RtΔ5.圆内接四边形性质定理:圆内接四边形的对角互补,并且任何一个外角都等于它的内对角.几何表达式举例:∵ ABCD是圆内接四边形∴∠CDE =∠ABC∠C+∠A =180°6.切线的判定与性质定理:如图:有三个元素,“知二可推一”;需记忆其中四个定理.(1)经过半径的外端并且垂直于这条半径的直线是圆的切线;(2)圆的切线垂直于经过切点的半径;※(3)经过圆心且垂直于切线的直线必经过切点;※(4)经过切点且垂直于切线的直线必经过圆心.几何表达式举例:(1)∵OC是半径∵OC⊥AB∴AB是切线(2)∵OC是半径∵AB是切线∴OC⊥AB(3)……………7.切线长定理:从圆外一点引圆的两条切线,它们的切线长相等;圆心和这一点的连线平分两条切线的夹角.几何表达式举例:∵ PA、PB是切线∴ PA=PB∵PO过圆心∴∠APO =∠BPO8.弦切角定理及其推论: 几何表达式举例:(1)弦切角等于它所夹的弧对的圆周角;(2)如果两个弦切角所夹的弧相等,那么这两个弦切角也相等;(3)弦切角的度数等于它所夹的弧的度数的一半.(如图)(1)∵BD是切线,BC是弦∴∠CBD =∠CAB(2)∵ ED,BC是切线∴∠CBA =∠DEF9.相交弦定理及其推论:(1)圆内的两条相交弦,被交点分成的两条线段长的乘积相等;(2)如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段长的比例中项. 几何表达式举例:(1)∵PA·PB=PC·PD∴………(2)∵AB是直径∵PC⊥AB∴PC2=PA·PB10.切割线定理及其推论:(1)从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项;(2)从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等.几何表达式举例:(1)∵PC是切线,PB是割线∴PC2=PA·PB (2)∵PB、PD是割线∴PA·PB=PC·PD11.关于两圆的性质定理:(1)相交两圆的连心线垂直平分两圆的公共弦;(2)如果两圆相切,那么切点一定在连心线上.(1)(2)几何表达式举例:(1)∵O1,O2是圆心∴O1O2垂直平分AB (2)∵⊙1 、⊙2相切∴O1 、A、O2三点一线12.正多边形的有关计算:(1)中心角αn ,半径R N ,边心距r n ,边长a n ,内角βn ,边数n;(2)有关计算在RtΔAOC中进行. 公式举例:(1) αn =;(2)几何B级概念:(要求理解、会讲、会用,主要用于填空和选择题)一基本概念:圆的几何定义和集合定义、弦、弦心距、弧、等弧、弓形、弓形高三角形的外接圆、三角形的外心、三角形的内切圆、三角形的内心、圆心角、圆周角、弦切角、圆的切线、圆的割线、两圆的内公切线、两圆的外公切线、两圆的内(外)公切线长、正多边形、正多边形的中心、正多边形的半径、正多边形的边心距、正多边形的中心角.二定理:1.不在一直线上的三个点确定一个圆.2.任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆.3.正n边形的半径和边心距把正n边形分为2n个全等的直角三角形.三公式:1.有关的计算:(1)圆的周长C=2πR;(2)弧长L=;(3)圆的面积S=πR2.(4)扇形面积S扇形=;(5)弓形面积S弓形=扇形面积S AOB±ΔAOB的面积.(如图)2.圆柱与圆锥的侧面展开图:(1)圆柱的侧面积:S圆柱侧 =2πrh; (r:底面半径;h:圆柱高)(2)圆锥的侧面积:S圆锥侧 =. (L=2πr,R是圆锥母线长;r是底面半径)四常识:1.圆是轴对称和中心对称图形.2.圆心角的度数等于它所对弧的度数.3.三角形的外心⇔两边中垂线的交点⇔三角形的外接圆的圆心;三角形的内心⇔两内角平分线的交点⇔三角形的内切圆的圆心.4.直线与圆的位置关系:(其中d表示圆心到直线的距离;其中r表示圆的半径)直线与圆相交⇔ d<r ;直线与圆相切⇔ d=r ;直线与圆相离⇔ d>r.5.圆与圆的位置关系:(其中d表示圆心到圆心的距离,其中R、r表示两个圆的半径且R≥r)两圆外离⇔ d>R+r;两圆外切⇔ d=R+r;两圆相交⇔ R-r<d<R+r;两圆内切⇔ d=R-r;两圆内含⇔ d<R-r.6.证直线与圆相切,常利用:“已知交点连半径证垂直”和“不知交点作垂直证半径”的方法加辅助线.7.关于圆的常见辅助线:已知弦构造弦心距.已知弦构造RtΔ. 已知直径构造直角.已知切线连半径,出垂直.圆外角转化为圆周角. 圆内角转化为圆周角. 构造垂径定理. 构造相似形.两圆内切,构造外公切线与垂直.两圆内切,构造外公切线与平行.两圆外切,构造内公切线与垂直.两圆外切,构造内公切线与平行.两圆同心,作弦心距,可证得AC=DB.两圆相交构造公共弦,连结圆心构造中垂线. PA、PB是切线,构造双垂图形和全等.相交弦出相似.一切一割出相似, 并且构造弦切角.两割出相似,并且构造圆周角.双垂出相似,并且构造直角.规则图形折叠出一对全等,一对相似.圆的外切四边形对边和相等. 若AD ∥BC都是切线,连结OA、OB可证∠AOB=180°,即A、O、B三点一线.等腰三角形底边上的的高必过内切圆的圆心和切点,并构造相似形.RtΔABC的内切圆半径:r=.补全半圆.AB=. AB=.PC过圆心,PA是切线,构造双垂、RtΔ.O是圆心,等弧出平行和相似. 作AN⊥BC,可证出:.。
初三数学圆的知识点

初三数学圆的知识点1.圆的定义(1)在一个平面内,线段OA绕它的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫做圆。
固定的端点O 叫做圆心,线段OA叫做半径,如右图所示。
(2)圆可以看作是平面内到定点的距离等于定长的点的集合,定点为圆心,定长为圆的半径。
说明:圆的位置由圆心确定,圆的大小由半径确定,半径相等的两个圆为等圆。
2.圆的有关概念(1)弦:连结圆上任意两点的线段。
(如右图中的CD)。
(2)直径:经过圆心的弦(如右图中的AB)。
直径等于半径的2倍。
(3)弧:圆上任意两点间的部分叫做圆弧。
(如右图中的CD、CAD)其中大于半圆的弧叫做优弧,如CAD,小于半圆的弧叫做劣弧。
(4)圆心角:如右图中∠COD就是圆心角。
3.圆心角、弧、弦、弦心距之间的关系。
(1)定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦的弦心距相等。
(2)推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等。
4.过三点的圆。
(1)定理:不在同一条直线上的三点确定一个圆。
(2)三角形的外接圆圆心(外心)是三边垂直平分线的交点。
5.垂径定理。
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
推论:(1)①平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;②弦的垂直平分线经过圆心,并且平分弦所对的两条弧;③平分弦所对的一条弦的直径,垂直平分弦,并且平分弦所对的另一条弧。
(2)圆的两条平行弦所夹的弧相等。
6.与圆相关的角(1)与圆相关的角的定义①圆心角:顶点在圆心的角叫做圆心角②圆周角:顶点在圆上且两边都和圆相交的角叫做圆周角。
③弦切角:顶点在圆上,一边和圆相交,另一连轴和圆相切的角叫做弦切角。
(2)与圆相关的角的性质AB①圆心角的度数等于它所对的弦的度数;②一条弧所对的圆周角等于它所对的圆心角的一半;③同弧或等弧所对的圆周角相等;④半圆(或直径)所对的圆周角相等;⑤弦切角等于它所夹的弧所对的圆周角;⑥两个弦切角所夹的弧相等,那么这两个弦切角也相等;⑦圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角。
九年级圆垂径定理知识点

九年级圆垂径定理知识点圆垂径定理是数学中的一个重要定理,它是研究圆的性质和应用的基础。
本文将详细介绍九年级圆垂径定理的相关知识点,帮助你更好地理解和应用这一定理。
一、圆垂径定理的概述圆垂径定理是指:在一个圆中,如果一条直径垂直于另一条弦,那么它一定是这条弦的垂直平分线。
二、圆垂径定理的证明为了证明圆垂径定理,我们可以采用几何证明和代数证明两种方法。
1. 几何证明假设圆的中心为O,半径为r,直径AB垂直于弦CD。
我们需要证明AO = BO。
首先,连接AC和BC,并设AC = x,BC = y。
根据圆的性质,我们知道AO = r,BO = r,AC = BC = r。
又因为AO垂直于CD,所以∠ACO = ∠BCO = 90°。
由三角形的性质可知,AO² = AC² - CO²,BO² = BC² - CO²。
代入已知条件,我们可以得到r² = x² - CO²,r² = y² - CO²。
通过这两个等式,我们可以得到x² - CO² = y² - CO²,即x² = y²。
进而,我们可以得知x = y,即AC = BC。
所以,根据直角三角形的特性,AO = BO,也就是说AO = BO = r。
因此,根据圆的定义,我们可以得出圆垂径定理的结论。
2. 代数证明我们也可以采用代数方法证明圆垂径定理。
设圆的方程为x² + y² = r²(其中,O为坐标原点)。
直径AB垂直于弦CD,且AB的斜率k存在。
根据直线的斜率公式,可以得到直线AB的方程为y = kx。
将直线AB的方程代入圆的方程中,我们可以得到x² + (kx)² =r²。
简化这个方程,可以得到x² + k²x² = r²。
人教版初中数学九年级上册第24章知识复习第一部分圆的有关概念和性质

在上图中,
D
若∠COD=∠AOB,则 CD=AB,CD=AB ;
若CD=AB,则 ∠COD=∠AOB,CD=AB;
若CD=AB,则 ∠COD=∠AOB,CD=AB,.
CAD=ACB.
(二)圆的有关性质 3、垂径定理:
•
垂直于弦的直径平分这条弦,并且平分弦 所对的两条弧。 推论:①平分弦(非直径)的直径垂直于这条弦,
(二)圆的有关性质 Q
A•
O•
•B
P
C
4、②在同圆或等圆中,同弧或等弧所对的 圆周角相等,都等于该弧所对的圆心角的 一半;相等的圆周角所对的弧相等。
如图:∠BOC=2∠BAC=2∠BPC=2∠BQC.
(二)圆的有关性质
PQ
O •
D
A C
B
如图:若AB=CD, 则∠AOB=∠COD=2∠APB=2∠CQD.
反之,若∠APB=∠CQD,则AB=CD.
【及时巩固】
d P
P
d
O
•
r
d
P
1、设⊙O的半径为r,点P到圆心的而距离为d,
则 ①点P在⊙O上 d = r;
②点P在⊙O内 d< r;
③点P在⊙O外 d >r.
【及时巩固】
2、“经过三角形各顶点的圆叫三角形的外接圆. 外接圆的圆心叫做三角形的外心(即三角形三边 中垂线的交点),这个三角形叫圆的内接三角形.” 先分别作出锐角三角形、钝角三角形、直角三 角形的外接圆,再观察图形,填空:
并且平分弦所对的弧; ②平分弧的直径垂直平分这条弧所对的弦;...
(二)圆的有关性质
•
垂径定理及推论可归纳为: 一条直线若具有“①经过圆心; ②垂直于弦;③平分弦;④平分弦所对的 优弧;⑤平分弦所对的劣弧”这五个性质 中的两个,这条直线就具有其余三个性质. 注意:①③组合有限制.
圆的基本概念和垂径定理

【练】某地有一座圆弧形拱桥,桥下水面宽度为 7.2 米,拱顶高出水面 2.4 米。现有一艘宽 3 米、船舱顶部为方形并高出水面 2 米的货船要经过这里,此货船能顺利通过这座拱桥吗? M C N
A
3
E
D
B F
【作业】 1、一条排水管的截面如图所示.已知排水管的截面圆半径 OB=10,截面圆圆心 O 到水面的 距离 OC 是 6,则水面宽 AB 是( ) A、16 B、10 C、8 D、6 2、如图,⊙O 的弦 AB 垂直平分半径 OC,若 AB= 6,则⊙O 的半径为( A、 2 的弦,半径 OC、OD 分别交 AB 于点 E、F,且 AE=BF,请 你找出线段 OE 与 OF 的数量关系,并给予证明.
【练】如图,已知 AB 是⊙O 的弦,半径 OA=20cm,∠AOB=120° ,求△AOB 的面积.
【例 4】如图所示,⊙O 表示一个圆形工件,图中标注了有关尺寸,并且 MB:MA=1:4,求 工件的半径的长。
A
中任意 2 个条件推出其他 3 个结论。 推论 2:圆的两条平行弦所夹的弧相等。 即:在⊙ O 中,∵ AB ∥ CD ∴弧 AC 弧 BD
C O A B
C B
D
O E D
【例题解析】 【例 1】 如图所示, P 为弦 AB 上一点, CP⊥OP 交⊙O 于点 C, AB=8, AP:PB=1:3,求 PC 的长。 P O B
4
10、 如图, ⊙O 的直径 AB 与弦 CD 交于点 E, AE=5, BE=1, CD=4 2, 则∠AED=
_________ .
11、如图,已知 AB 是⊙O 的弦,半径 OA=6cm,∠AOB=120° ,则 AB= _________ cm.
数学-初三-圆的相关概念与垂径定理

精锐教育1对1辅导讲义学员: 学科教师:年级: 辅导科目:主题:圆基本概念与垂径定理授课时间:学习目标1、掌握圆的相关基本概念2、运用垂径定理解决问题教学容1、 圆是如何确定的?大小怎么判定?2、 圆中有哪些概念?3、 垂径定理如何应用?【知识梳理1】圆的确定定理 同圆或等圆中半径相等1.点与圆的位置关系圆是到定点(圆心)的距离等于定长(半径)的点的集合。
圆的部是到圆心的距离小于半径的点的集合。
圆的外部是到圆心的距离大于半径的点的集合。
点P 与圆心的距离为d ,则点P 在直线外⇔r d >;点P 在直线上⇔r d =;点P 在直线⇔r d <。
【例题精讲】例1.如图,圆O 的半径为15,O 到直线l 的距离OH =9,P 、Q 、R 为l 上的三点.PH =9,QH =12,RH =15,请分别说明点P 、Q 、R 与圆O 的位置关系.【试一试】1.矩形ABCD 中,AB =8,35BC =,点P 在边AB 上,且BP =3AP ,如果圆P 是以点P 为圆心,PD 为半径的圆,那么下列判断正确的是( ).(A) 点B 、C 均在圆P 外; (B) 点B 在圆P 外、点C 在圆P ; (C) 点B 在圆P 、点C 在圆P 外; (D) 点B 、C 均在圆P .2.如图所示,已知ABC ∆,90ACB ∠=o,12AC =,13AB =,CD AB ⊥于点D ,以C 为圆心,5为半径作圆C ( )A .点D 在圆,B A 、在圆外 B .点D 在圆,点B 在圆上,点A 在圆外C .点B 、D 在圆,A 在圆外 D .点D 、B A 、都在圆外2. 过三点的圆1.不在同一直线上的三点确定一个圆。
2.经过三角形的三个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,三角形叫做圆的接三角形。
例2.如图,作出»AB所在圆的圆心,并补全整个圆.【试一试】1.小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图示,为配到与原来大小一样的圆形玻璃,小明带到商定去的一块玻璃片应该是()A.第①快B.第②快C.第③快D.第④快2.三角形的外心一定在该三角形上的三角形是()A.锐角三角形B.钝角三角形C.直角三角形D.等腰三角形【知识梳理2】圆心角、弧、弦、弦心距之间的关系1.圆心角:顶点在圆心的角。
(一) 圆的相关概念及垂径定理

AODBCAO(一) 圆的相关概念及垂径定理一、知识梳理(一)圆的有关概念1.圆的基本概念:在一个平面内,线段OA 绕它固定的一个端点O 旋转一周,另一个端点A 所形成的图形叫做圆。
固定点O 叫做圆心;线段OA 叫做半径;圆上各点到定点(圆心O )的距离都等于定长(半径r);反之,到定点的距离等于定长的点都在同一个圆上(另一定义); 以O 为圆心的圆,记作“⊙O ”,读作“圆O ”2.圆的对称性及特性:(1)圆是轴对称图形,圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴; (2)圆也是中心对称图形,它的对称中心就是圆心.(3)一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合.这是圆特有的一个性质:圆的旋转不变性 3.弦:连接圆上任意两点的线段叫做弦。
4.弦心距:圆心到弦的距离叫做弦心距. 5.直径:经过圆心的弦叫直径。
注:圆中有无数条直径6.圆弧:(1)圆上任意两点间的部分,也可简称为“弧”以A,B 两点为端点的弧.记作AB ⋂,读作“弧AB”. (2)圆的任意一条直径的两个端点把圆分成两条弧,其中每一条弧都叫半圆。
如弧AD. (3)小于半圆的弧叫做劣弧,如记作AB ⋂(用两个字母). 7.圆心角:顶点在圆心,两边和圆相交的角叫做圆心角。
说明:(1)直径是弦,但弦不一定是直径,直径是圆中最长的弦。
(2)半圆是弧,但弧不一定是半圆。
(3)等弧只能是同圆或等圆中的弧,离开“同圆或等圆”这一条件不存在等弧。
(4)等弧的长度必定相等,但长度相等的弧未必是等弧。
(二)弦、弧、弦心距、圆心角的关系定理:在同圆或等圆中,弦、弧、弦心距、圆心角四组量中只要有一组量相等,则其余三组量也相等。
(三)和圆有关的角:1、圆周角:顶点在圆上,它的两边和圆还有另一个交点的角叫做圆周角。
2、圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半。
推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等。
推论2:圆的两条平行弦所夹的弧相等。
初三数学圆——圆的认识及垂径定理(教案)
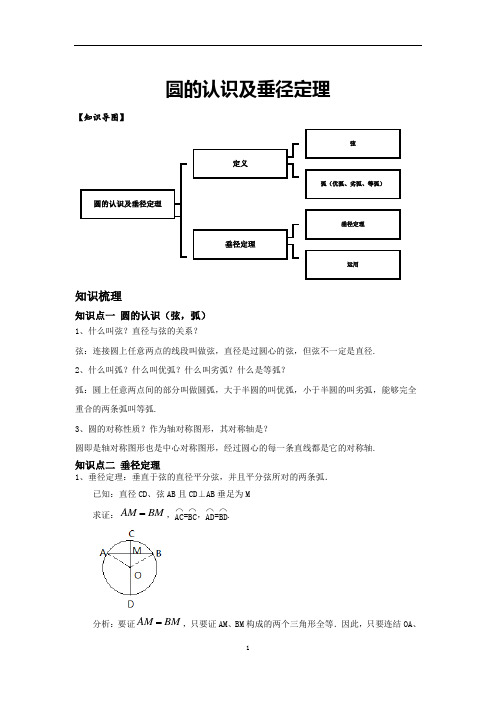
圆的认识及垂径定理【知识导图】知识梳理知识点一 圆的认识(弦,弧)1、什么叫弦?直径与弦的关系?弦:连接圆上任意两点的线段叫做弦,直径是过圆心的弦,但弦不一定是直径.2、什么叫弧?什么叫优弧?什么叫劣弧?什么是等弧?弧:圆上任意两点间的部分叫做圆弧,大于半圆的叫优弧,小于半圆的叫劣弧,能够完全重合的两条弧叫等弧.3、圆的对称性质?作为轴对称图形,其对称轴是?圆即是轴对称图形也是中心对称图形,经过圆心的每一条直线都是它的对称轴.知识点二 垂径定理1、垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.已知:直径CD 、弦AB 且CD ⊥AB 垂足为M求证:,⌒AC =⌒BC ,⌒AD =⌒BD.分析:要证,只要证AM 、BM 构成的两个三角形全等.因此,只要连结OA、BM AM=BM AM =OB 或AC 、BC 即可.证明:如图,连结OA 、OB ,则OA=OB在和中∴∴∴点A 和点B 关于CD 对称∵⊙O 关于直径CD 对称∴当圆沿着直线CD 对折时,点A 与点B 重合,⌒AC 与⌒BC 重合,⌒AD 与⌒BD 重合.∴⌒AC =⌒BC ,⌒AD =⌒BD进一步,我们还可以得到结论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.垂径定理推论:1、推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.推论扩展推论1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
(3)平分弦所对的一条弧的直径垂直平分弦,并且平分弦所对的另一条弧。
推论2:圆的两条平行弦所夹的弧相等。
2、垂径定理及其推论可概括为OAM Rt ∆OBM Rt ∆⎩⎨⎧==OM OM OB OA OBM Rt OAM Rt ∆≅∆BM AM=考点解析类型一圆的认识(弦、弧)【例题1】下列五个命题:(1)平分弦的直径必垂直于弦(2)圆是轴对称图形,对称轴是直径(3)圆中两点之间的部分叫做弧(4)长度相等的两条弧叫等弧(5)直径是过圆心的弦,但弦不一定是直径其中真命题有()A.1个B.2个C.3个D.4个【解析】(1)平分弦(不是直径)的直径必垂直于弦,故原命题是假命题,(2)圆的对称轴是直径所在的直线,故原命题是假命题,(3)圆上两点之间的部分叫做弧,故原命题是假命题,(4)能够完全重合的两条弧叫等弧,故原命题是假命题,(5)直径是过圆心的弦,但弦不一定是直径,原命题是真命题,其中真命题有1个.故选;A.【总结与反思】本题考查圆的相关概念及垂径定理,理解概念及定理即可解决,要求学生掌握圆的相关概念及垂径定理内容。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精锐教育1对1辅导讲义棗互钠探索1、圆是如何确定的?大小怎么判定?2、圆中有哪些概念?3、垂径定理如何应用?*曲需提#【知识梳理1】圆的确定定理同圆或等圆中半径相等1•点与圆的位置关系圆是到定点(圆心)的距离等于定长(半径)的点的集合。
圆的内部是到圆心的距离小于半径的点的集合。
圆的外部是到圆心的距离大于半径的点的集合。
点P与圆心的距离为d,则点P在直线外二d r ;点P在直线上=d = r ;点P在直线内=d :::r。
【例题精讲】例1•如图,圆0的半径为15,O到直线I的距离0H=9,P、Q、R为I上的三点.PH=9,QH=12,RH=15,请分别说明点P、Q、R与圆0的位置关系【试一试】1•矩形ABCD中,AB= 8, BC=3.5,点P在边AB上,且BP = 3AP,如果圆P是以点P为圆心,PD为半径的圆,那么下列判断正确的是( ).(A) 点B、C均在圆P夕卜;(B)点B在圆P夕卜、点C在圆P内;(C)点B在圆P内、点C在圆P夕卜;(D)点B、C均在圆P内.2•如图所示,已知丄ABC ,乙ACB=90, AC=12, AB “3, CD _ AB于点D,以C为圆心,5为半径作圆C ( )A.点D在圆内,B、A在圆外B.点D在圆内,点B在圆上,点A在圆外C.点B、D在圆内,A在圆外D.点D、B、A都在圆外2. 过三点的圆1. 不在同一直线上的三点确定一个圆。
2. 经过三角形的三个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,三角形叫做圆的内接三角形。
例2•如图,作出AB所在圆的圆心,并补全整个圆.【试一试】1. 小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图示,为配到与原来大小一样的圆形玻璃,小明带到 商定去的一块玻璃片应该是 ( )2.三角形的外心一定在该三角形上的三角形是( ) A.锐角三角形 B.钝角三角形 C.直角三角形 D.等腰三角形【知识梳理2】圆心角、弧、弦、弦心距之间的关系1. 圆心角:顶点在圆心的角。
2. 弧:圆上任意两点之间的部分。
大于半圆的弧叫优弧,小于半圆的弧叫劣弧,能够重合的弧叫等弧。
3. 弦:联结圆上任意两点的线段。
直径是一条特殊的弦,并且是圆中最大的弦。
4. 弦心距:从圆心到弦的距离。
定理1在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对弦的弦心距相等【例题精讲】 例1•已知,如图,ABCD 是O O 的直径,弦 AE // CD ,联结CEBC.求证:BC=DE.A .第①快B .第②快C .第③快D .第④快定理2在同圆或等圆中,如果两个圆心角、两个圆周角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等•例2.如图,O O是厶ABC的外接圆,AO平分/ BAC,/ AOB= / BOC,探究△ ABC的形状,并说明理由【巩固练习】1.如图,AB=CD,OE L AB OFl CD / OEF25°,求/ EOF的度数.2.如图,点P是O O外的一点,PB与O O相交于点AB PD与O O相交于C D, AB=CD 例3.如图,在OO中,弦AB的长是半径0A的J3倍,C为AB的中点,AB 0C相交于P求证:四边形OACB为菱形.【巩固练习】1.如图,弦AB和CD相交于圆0内一点P,且/ OPB= / OPD,求证;AB =CD求证:(1)PO平分/ BPD(2) AE =EC【知识梳理3】垂径定理定理垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧推论1 一条直线,如果具有①过圆心;②垂直于弦;③平分弦(非直径) :④平分弦所对的劣弧;⑤平分弦所对的优弧•这五个性质中的任何两个性质这条直线就具有其余的三条性质.推论2圆的平行弦所夹的弧相等【例题精讲】例1.已知ABC中,AD _BC,垂足为D,且AD =4,以AD为直径作圆0,交AB边于点G,交AC边于点F,如果点F恰好是AD的中点.(1)求CD的长度;(2)当BD =3时,求BG的长度.【试一试】1•如图,已知O 0的半径为5,弦AB的长等于8, 0D丄AB,垂足为点D , D0的延长线与O 0相交3于点C,点E在弦AB的延长线上,CE与O O相交于点F, cosC二,5求:(1) CD的长(5分);(2) EF的长(7分).例2•如图,AB是O O的直径,弦CD与AB相交,过点A、B向CD引垂线,垂足分别为E、F.求证:CE=DF【试一试】1.如图,CD为O O的弦,EF在直径AB上,EC丄CD, DF丄CD.求证:AE=DF置达絲检测1.下列命题中假命题是( )(A)平分弦的半径垂直于弦;(B)垂直平分弦的直线必经过圆心;(C)垂直于弦的直径平分这条弦所对的弧;(D)平分弧的直径垂直平分这条弧所对的弦.2.如图,EF是O O的直径,CD交O O于M、N , H为MN的中点,EC _ CD于点C , FD _ CD于点D , 则下列结论错误的是()A. CM =DN ;B . CH =HD ;C . OH _CD ;D . EC=OH OH FD3. 我们把两个三角形的外心之间的距离叫做外心距.如图4,在Rt △ ABC和Rt △ ACD中,•_ACB = • ACD =90,点D在边BC的延长线上,如果BC = DC = 3,那么△ ABC和厶ACD的外心距是4•如图,已知在L O中,弦CD垂直于直径AB,垂足为点E,如果.BAD =30 , OE =2,那么CD = . 5点P为。
O内一点,过点P的最长的弦长为10cm ,最短的弦长为8cm ,那么OP的长等于_________________ cm 6•如图,CD为O O的直径,以D为圆心,DO长为半径作弧,交O O于AB两点,求证:AC =BC = BA7•已知:如图,在△ ABC中,D是边BC上一点,以点D为圆心、CD为半径作半圆,分别与边AC、BC相交4于点 E 和点F.如果AB=AC=5, cosB= , AE=1 .5求:(1)线段CD的长度;(2)点A和点F之间的距离.1•下列说法中,结论错误的是(A •直径相等的两个圆是等圆;B •长度相等的两条弧是等弧;C •圆中最长的弦是直径;D •一条弦把圆分成两条弧,这两条弧可能是等弧.2•已知00是以坐标原点0为圆心,5为半径的圆,点M 的坐标为(-3,4),则点M 与00的位置关系为()围是( )5•如图,圆0过点B 、C ,圆心0在等腰直角三角形 ABC 内部,/ BAC = 90° 0A=1,BC = 6,那么圆0的半径 为A. M 在O O 上;B. M 在00内;C. M 在00夕卜;D. M 在00右上方; 3•如图,两个同心圆,大圆的半径为5,小圆的半径为3, 若大圆的弦AB 与小圆有公共点,则弦 AB 的取值范A • 8*B W 10 B . 8v AB < 10C • 4^AB < 5D • 4V AB W54•如图,L 0的直径AB 垂直弦CD 于M ,且M 是半径 0B 的中点,CD 6,则直径AB 的长3交O O 于点D , sin . BPC ,求CD 的长;5 7•如图,在△ ABC 中,AB=AC=10, BC =12, AD _ BC 于 D ,且 AG = AD ; 下列结论正确的是()(A) DE J FG 4 DF EG(B) 1 FB GC (C) AD = 3 . 2 FB AD 2(D) DB = 22.如图,点D 、E 位于△ ABC 的两边上,下列条件能判定 DE II BC 的是( )A. AD DB 二 AE ECB. AD AE 二 BD ECC. AD CE =AE BDD. AD BC =AB DE3.已知非零向量a 、b 、c ,下列命题中是假命题的是( ) OP=10,点 C 是O O 上一点,PC6•如图,已知AB 是O O 的直径,AB =16,点P 是AB 所在直线上一点, O 为AD 上一点,以O 为圆心,OA1.如图,点 D E F 、G 为 MBC 两边上的点,且 DE II FG II BC ,若DE FG 将 MBC 的面积三等分,那么为半径的圆交AB 于G ,交BC 于E 、F ,(1)求EF 的长;(2)求 tan BDG 的值;A.如果a = 2b,那么a // b ;B. 如果a = —2b,那么a // b ;4 4 4 4 4^44 ddC.如果| a |=| b |,那么a // b ;D. 如果a = 2b , b = 2c ,那么a // c;4. 如图,已知人0是厶ABC勺中线(是厶ABC勺重心,联结BG并延长交AC于点E,联结DE则S ABC : S GED的值为•5. 已知在△ ABC中,AB = AC = m , Z B = :•,那么边BC的长等于()A. 2m sin:;B. 2m cos:;C. 2m tan:;D. 2m cot:;6. 抛物线y =x2 -2x在直线x =1右侧的部分是 ______________ .(从“上升的”或“下降的”中选择).7. 已知抛物线y=ax2-4ax与x轴交于点A、B,顶点C的纵坐标是一2,那么a= ________________8. 下列说法正确的是()(A)相切两圆的连心线经过切点(B)长度相等的两条弧是等弧(C)平分弦的直径垂直于弦(D)相等的圆心角所对的弦相等9. 已知O的半径长为3,0。
2的半径长r (r >0 ),如果0Q2 =3,那么O与O 0?不可能存在的位置关系是()A.两圆内含;B. 两圆内切;C. 两圆相交;D. 两圆外切;。
