7、圆的培优专题：与切线有关的计算
教案标题初中数学知识点球的切线与切圆的计算
教案标题初中数学知识点球的切线与切圆的计算初中数学知识点：球的切线与切圆的计算球的切线与切圆是初中数学中的一个重要知识点，它与几何图形和立体图形的计算息息相关。
本文将为您详细介绍球的切线与切圆的计算方法。
一、切线的定义与性质在数学中，切线是指与圆或球相切于一点且仅有一个交点的直线。
对于球体来说，相切的切线与球体的切点处的切平面是相切的。
给定一个球体和球外一点P，我们来计算球体与点P处的切线。
首先，连接球心O与点P，并做球心O到点P的垂线段。
球心O到点P的距离为r（r为球的半径），垂线段与切线的交点为A。
连接点P与切点A，可以得到切线。
根据勾股定理，我们可以得出以下关系式：OP² = OA² + AP²由此，可以得到切线PA的长度为：AP = √(OP² - OA²)二、切线与切圆的计算对于球体上的任意一点M，我们来计算球的切线与圆的关系。
首先，连接点M与球心O，并做球心O到点M的垂线段。
球心O到点M的距离为r（r为球的半径），垂线段与切线的交点为B。
我们可以将球切面看作一个圆，在切面上点B与切点A之间的弦与切线PA相等。
根据这一性质，我们可以得到切线与切圆的关系。
对于圆上的任意一点N，连接点N与切点A，并做点N与圆心O的垂线段。
圆心O到点N的距离为r'（r'为切圆的半径），垂线段与切线PA的交点为B'。
根据勾股定理，我们可以得到以下关系式：OA² = ON² + AN²OB² = ON² + NB²因为切线PA与切圆相切，所以OB'与切线PA也垂直。
根据上述关系式，可以得到切线PA的长度为：AP = √(OA² - ON²)B'P = √(OB'² - ON²)对于切点A与切点B'之间的弦AB'，可以得到以下关系式：AB' = 2 √(ON² - OA²)综上所述，我们可以通过计算球心到切线的距离来得到切线的长度，进而计算切线与切圆的关系。
2020年中考数学提优专题：《圆：切割线定理》(含答案)
《圆：切割线定理》知识梳理：（1）切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项．几何语言：∵PT切⊙O于点T，PBA是⊙O的割线∴PT的平方=PA•PB（切割线定理）（2）推论：从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等．几何语言：∵PBA，PDC是⊙O的割线∴PD•PC=PA•PB（切割线定理推论）（割线定理）由上可知：PT2=PA•PB=PC•PD．一．选择题1．如图，P是⊙O的直径BC延长线上一点，PA切⊙O 于点A，若PC＝2，BC＝6，则切线PA的长为（）A．无限长B．C．4 D．2．如图，PT是⊙O的切线，T为切点，PBA是割线，交⊙O于A、B两点，与直径CT交于点D，已知CD＝2，AD＝3，BD＝4，那么PB等于（）A．6 B．C．7 D．203．设H为锐角△ABC的三条高AD、BE、CF的交点，若BC＝a，AC＝b，AB＝c，则AH•AD+BH•BE+CH•CF 等于（）A．（ab+bc+ca）B．（a2+b2+c2）C．（ab+bc+ca） D．（a2+b2+c2）4．如图，MN切⊙O于A点，AC为弦，BC为直径，那么下列命题中假命题是（）A．∠MAB和∠ABC互余B．∠CAN＝∠ABC C．OA＝BC D．MA2＝MB•BC5．如图，以OB为直径的半圆与半圆O交于点P，A、O、C、B在同一条直线上，作AD⊥AB与BP的延长线交于点D，若半圆O的半径为2，∠D的余弦值是方程3x2﹣10x+3＝0的根，则AB的长等于（）A．B．C．8 D．56．如图，AB是⊙O直径，AC是⊙O的弦，过弧BC 的中点D作AC的垂线交AC的延长于E，若DE＝2，EC＝1，则⊙O的直径为（）A． B．C．5 D．47．如图，过点P作⊙O的两条割线分别交⊙O于点A、B和点C、D，已知PA＝3，AB＝PC＝2，则PD的长是（）A．3 B．7.5 C．5 D．5.58．如图，已知⊙O的弦A B、CD相交于点P，PA＝4cm，PB＝3cm，PC＝6cm，EA切⊙O于点A，AE与CD的延长线交于点E，若AE＝cm，则PE的长为（）A．4cm B．3cm C．5cm D．cm9．如图，⊙O1与⊙O2相交于A、B两点，PQ切⊙O1于点P，交⊙O2于点Q、M，交AB的延长线于点N．若MN＝1，MQ＝3，则NP等于（）A．1 B．C．2 D．310．同心圆O中，大圆的弦EF切小圆于K，EP切小圆于P，FQ切小圆于Q，G为小圆上一点，GE、GF 分别交小圆于M、N两点，下列四个结论：①EM＝MG；②FQ2＝FN•NG；③EP＝FQ；④FN•FG＝EM•EG．正确的结论为（）A．①③B．②③C．③④D．②④二．填空题11．如图，AB为⊙O的直径，P点在AB的延长线上，PM切⊙O于点M．若OA＝a，PM＝，那么△PMB 的周长是．12．已知：如图，PC切⊙O于点C，割线PAB经过圆心O，弦CD⊥AB于点E，PC＝4，PB＝8，则PA ＝，sin∠P＝，CD＝．13．如图，PA、PB与⊙O分别相切于点A、点B，AC 是⊙O的直径，PC交⊙O于点D，已知∠APB＝60°，AC＝2，那么CD的长为．14．如图，PA切⊙O于点A，割线PBC交⊙O于点B、C，若PA＝6，PB＝4，弧AB的度数为60°，则BC ＝，∠PCA＝度，∠PAB＝度．15．如图，已知ABCD是一个半径为R的圆内接四边形，AB＝12，CD＝6，分别延长AB和DC，它们相交于点P，且BP＝8，∠APD＝60°，则R＝．16．如图，AC为⊙O的直径，PA是⊙O的切线，切点为A，PBC是⊙O的割线，∠BAC的平分线交BC于D 点，PF交AC于F点，交AB于E点，要使AE＝AF，则PF应满足的条件是（只需填一个条件）．17．由⊙O外一点F作⊙O的两条切线，切点分别为B、D，AB是⊙O的直径，连接AD、BD，线段OF交⊙O 于E，交BD于C，连接DE、BE．有下列序号为①～④的四个结论：①BE＝DE；②∠EBD＝∠EDB；③DE∥AB；④BD2＝2AD•FC其中正确的结论有．（把你认为正确结论的序号全部填上）三．解答题18．已知：如图，在△ABC中，∠C＝90°，BE是角平分线，DE⊥BE交AB于D，⊙O是△BDE的外接圆．（1）求证：AC是⊙O的切线；（2）若AD＝6，AE＝6，求DE的长．19．如图，圆O是以AB为直径的△ABC的外接圆，D 是劣弧的中点，连AD并延长与过C点的切线交于点P，OD与BC相交于E；（1）求证：OE＝AC；（2）求证：；（3）当AC＝6，AB＝10时，求切线PC的长．20．如图，OB是以（O，a）为圆心，a为半径的⊙O1的弦，过B点作⊙O1的切线，P为劣弧上的任一点，且过P作OB、AB、OA的垂线，垂足分别是D、E、F．（1）求证：PD2＝PE•PF；（2）当∠BOP＝30°，P点为的中点时，求D、E、F、P四个点的坐标及S△DEF．参考答案一．选择题1．解：∵PC＝2，BC＝6，∴PB＝8，∵PA2＝PC•PB＝16，∴PA＝4．故选：C．2．解：∵TD•CD＝AD•BD，CD＝2，AD＝3，BD＝4，∴TD＝6，∵PT2＝PD2﹣TD2，∴PT2＝PB•PA＝（PD﹣BD）（PD+AD），∴PD＝24，∴PB＝PD﹣BD＝24﹣4＝20．故选：D．3．解：AH•AD＝AC•AE＝AC•AB•cos∠BAE＝（b2+c2﹣a2），同理BH•BE＝（a2+c2﹣b2），CH•CF＝（a2+b2﹣c2），故AH•AD+BH•BE+CH•CF＝（a2+b2+c2）．故选：B．4．解：∵BC是⊙O的直径，∴∠BAC＝90°，∴∠MAB+∠CA N＝90°；∵MN切⊙O于A，∴MA2＝MB•MC，（故D错误）∠CAN＝∠CBA，（故B正确）∴∠MAB+∠CBA＝90°；（故A正确）∵OA是⊙O的半径，BC是⊙O的直径，∴BC＝2OA；（故C正确）故选：D．5．解：∵3x2﹣10x+3＝0，∴x＝3（不合题意，舍去）或x＝．∴cosD＝AD：BD＝1：3，设A D＝x，则BD＝3x．∴AB＝＝2x，BC＝2x﹣4．∴（2x）2＝（2x﹣4）•x．∴x＝0（舍去），或x＝2．∴AB＝2×2＝8．故选：C．6．解：连接OD，∵点D是弧BC的中点，∴OD⊥BC，∠OFC＝90°，AB是直径，∴∠ACB＝90°，DE⊥AE，∴∠E＝90°，∴四边形CFDE是矩形，∴∠ODE＝90°，∴ED是圆的切线．作OG⊥AC，则OG＝CF＝ED＝2．∵DE2＝EC•AE，∴AE＝4，AC＝3，AG＝，∴AO＝，∴AB＝5．故选：C．7．解：∵PA＝3，AB＝PC＝2，∴PB＝5，∵PA•PB＝PC•PD，∴PD＝7.5，故选：B．8．解：∵PA•PB＝PC•PD，PA＝4cm，PB＝3cm，PC＝6cm，∴PD＝2；设DE＝x，∵AE2＝ED•EC，∴x（x+8）＝20，∴x＝2或x＝﹣10（负值舍去），∴PE＝2+2＝4．故选：A．9．解：∵PN2＝NB•NA，NB•NA＝NM•NQ，∴PN2＝NM•NQ＝4，∴PN＝2．故选：C．10．解：连接OK，∵EF切小圆于K，∴OK⊥EF，根据垂径定理得EK＝FK，∵EP切小圆于P，FQ切小圆于Q，∴EP＝EK，FQ＝FK，∴EP＝FQ，故③正确；∴由切割线定理得，FK2＝FN•FG，EK2＝EM•EG，∴FN•FG＝EM•EG，故④正确；故选：C．二．填空题（共7小题）11．解：连接OM；∵PM切⊙O于点M，∴∠OMP＝90°，∵OA＝OM＝a，PM＝，∴tan∠MOP＝MP：OM＝，∴∠MOP＝60°，∴OP＝2a，∴PB＝OP﹣OB＝a；∵OM＝OB，∴△OMB是等边三角形，MB＝OB＝a，∴△PMB的周长是（+2）a．12．解：∵PC切⊙O于点C，割线PAB经过圆心O，PC＝4，PB＝8，∴PC2＝PA•PB．∴PA＝＝2．∴AB＝6．∴圆的半径是3．连接OC．∵OC＝3，OP＝5，∴sin∠P＝．∴CE＝，∴CD＝．13．解：连接AD，OB，OP；∵PA、PB与⊙O分别相切于点A、点B，∴∠OAP＝∠OBP＝90°，∠AOB＝180°﹣∠P＝120°，∴∠AOP＝60°，AP＝AOtan60°＝，∴PC＝；∵PA2＝PD•PC，∴PD＝，∴CD＝．14．解：∵PA2＝PB•PC，PA＝6，PB＝4；∴PC＝9，∴BC＝5；∵弧AB的度数为60°，∴∠PCA＝30°，∴∠PAB＝30°．15．解：由切割线定理得PB•PA＝PC•PD，则有8×20＝PC（PC+6）．解得PC＝10．在△PAC中，由PA＝2PC，∠APC＝60°，得∠PCA＝90°．从而AD是圆的直径．由勾股定理，得AD2＝AC2+CD2＝（PA2﹣PC2）+CD2＝202﹣102+62＝336．∴AD＝＝4∴R＝AD＝2．故答案为2．16．解：∵∠PAC＝90°，∠ABC＝90°，∴90°﹣∠AFP＝90°﹣∠BEP，∴∠APF＝∠CPF，∴PF平分∠APC．17．解：∵BF，DF是⊙O的两条切线∴OF是∠DFB的角平分线，DF＝FB，FO⊥BD，CD＝CB∴＝∴BE＝DE（①正确）∵＝∴∠EBD＝∠EDB（②正确）∵FB切⊙O于B∴FB⊥OB∵BC⊥OF∵BC2＝OC•FC∴（BD）2＝OC•CE∵OC为△ABD的中位线∴OC＝AD∴（BD）2＝AD•CE∴BD2＝2AD•FC（④正确）故其中正确的结论有①②④．三．解答题（共3小题）18．（1）证明：连接OE；（1分）∵⊙O是△BDE的外接圆，∠DEB＝90°，∴BD是⊙O的直径，（不证直径，不扣分）∵BE平分∠ABC，∴∠CBE＝∠OBE，∵OB＝OE，∴∠OBE＝∠OEB，（2分）∴∠OEB＝∠CBE，∴OE∥BC，（3分）∵∠C＝90°，∴∠AEO＝90°，∴AC是⊙O的切线；（4分）（2）解：∵AE是⊙O的切线，AD＝6，AE＝6，∴AE2＝AD•AB，（5分）∴AB＝＝＝12，∴BD＝AB﹣AD＝12﹣6＝6；∵∠AED＝∠ABE，∠A＝∠A，∴△AED∽△ABE，（6分）∴；设DE＝x，BE＝2x，∵DE2+BE2＝BD2，（7分）∴2x2+4x2＝36，解得x＝±（负的舍去），∴DE＝2．（8分）19．（1）证明：∵AB为直径∴∠ACB＝90°∴AC⊥BC又D为中点，∴OD⊥BC，OD∥AC，又O为AB中点，∴；（4分）（2）证明：连接CD，PC为切线，由∠PCD＝∠CAP，∠P为公共角，∴△PCD∽△PAC，（6分）∴，又CD＝BD，∴；（8分）（3）解：∵AC＝6，AB＝10，∴BC＝8，BE＝4，OE＝3，∴DE＝2，∴BD2＝DE2+BE2＝20，（9分）∴AD2＝AB2﹣BD2＝80，∴AD＝4，（10分）CD＝BD＝2，由（2），∴，（11分）∴CP2＝DP•AP＝45×5，∴切线PC＝15．（12分）20．（1）证明：连接PB，OP，∵PE⊥AB，PD⊥OB，∴∠BEP＝∠PDO＝90°，∵AB切⊙O1于B，∠ABP＝∠BOP，∴△PBE∽△POD，∴＝，同理，△OPF∽△BPD∴＝，∴＝，∴PD2＝PE•PF；（2）解：连接O1B，O1P，∵AB切⊙O1于B，∠POB＝30°，∴∠ABP＝30°，∴∠O1BP＝90°﹣30°＝60°，∵O1B＝O1P，∴△O1BP为等边三角形，∴O1B＝BP，∵P为弧BO的中点，∴BP＝OP，即△O1PO为等边三角形，∴O1P＝OP＝a，∴∠O1OP＝60°，又∵P为弧BO的中点，∴O1P⊥OB，在△O1DO中，∵∠O1OP＝60°O1O＝a，∴O1D＝a，OD＝a，过D作DM⊥OO1于M，∴DM＝OD＝a，OM＝DM＝a，∴D（﹣a，a），∵∠O1OF＝90°，∠O1OP＝60°∴∠POF＝30°，∵PE⊥OA，∴PF＝OP＝a，OF＝a，∴P（﹣a，），F（﹣a，0），∵AB切⊙O1于B，∠POB＝30°，∴∠ABP＝∠BOP＝30°，∵PE⊥AB，PB＝a，∴∠EPB＝60°∴PE＝a，BE＝a，∵P为弧BO的中点，∴BP＝PO，∴∠PBO＝∠BOP＝30°，∴∠BPO＝120°，∴∠BPE+∠BPO＝120°+60°＝180°，即OPE三点共线，∵OE＝a+a＝a，过E作EM⊥x轴于M，∵AO切⊙O1于O，∴∠EOA＝30°，∴EM＝OE＝a，OM＝a，∴E（﹣a，a），∵E（﹣a，a），D（﹣a，a），∴DE＝﹣a﹣（﹣a）＝a，DE边上的高为：a，∴S△DEF＝×a×a＝a2．故答案为：D（﹣a，a），E（﹣a，a），F（﹣a，0），P（﹣a，）；S△DEF＝a2．。
中考数学专题复习：与圆切线有关的线段计算
中考数学专题复习：与圆的切线有关的线段计算斗门区第四中学卢燕英教学目标：1、掌握圆的切线证明的技巧．2、会选择适当的作辅助线的方法．3、学会计算与圆的切线有关的线段．教学重点：1、圆的切线的证明 2、与圆的切线有关的线段的计算．教学难点：灵活运用勾股定理、相似三角形对应边成比例、三角函数等建立方程进行有关线段的计算．教学方法:启发引导与归纳讨论相结合．教学过程：一、复习：1．切线的性质定理：圆的切线垂直于经过切点的半径．（解决与圆的切线有关题目）解题技巧是：圆心与切点的连线是常用的辅助线．2．切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆切线．证圆的切线技巧：（1）如果直线与圆有交点，连接圆心与交点的半径，证明直线与该半径垂直，即“有交点，连半径，证垂直”．（2）如果直线与圆没有明确的交点，则过圆心作该直线的垂线段，证明垂线段等于半径，即“无交点，作垂直，证半径”．二、运用技巧类型一：“有交点，连半径，证垂直”．【难点在于如何证明两线垂直】1.如图，AB=AC，AB为⊙O的直径，⊙O交BC于D，DM⊥AC于M，求证：DM与⊙O相切．【说明】：此题可以引导学生通过证明平行来证明垂直，也可通过证明两角互余，来证明垂直，解题中要注意知识的综合运用。
（还有的题目也可证明三角形全等来证明垂直，这里就没去举例）类型二：“无交点，作垂直，证半径”．【难点在于作出的垂线段，如何证明该垂线段等于半径】2．如图，已知OC平分∠AOB，D是OC上任一点，⊙D与OA相切于点E，求证：OB与⊙D相切．小结：切线证明的步骤及方法：①审题；②根据题意选择适当的添辅助线方法；③证垂直或证半径．三、实战中考例：如图，点O在∠APB的平分线上，⊙O与PA相切于点C．（1）求证：直线PB与⊙O相切；（2）PO的延长线与⊙O交于点E．若⊙O的半径为3，PC=4．求弦CE的长．变式训练：如图,点D为⊙O上的一点,点C在直径BA的延长线上,并且∠CDA=∠CBD．（1）求证：CD是⊙O的切线；（2）过点B作O的切线,交CD的延长线于点E,若BC=12,tan∠CDA=，求BE的长．A B【解题的关键】构造思想——运用相似三角形对应边成比例，或三角函数边角的关系、勾股定理等找出隐藏的线段之间的数量关系，建立数学模型，利用方程的思想，设出未知数表示关键的线段，再运用线段之间的数量关系建立方程来解决问题。
（完整版）圆的切线问题
（完整版）圆的切线问题圆的切线问题1. 自一点引圆的切线的条数（1）若点在圆外，则过此点可以作圆的两条切线；（2）若点在圆上，则过此点可以作圆的一条切线，切此点是切点；（3）若点在圆内，则过此点不能作圆的切线。
2. 切线方程的几个重要结论（1）经过圆222r y x =+上一点),(00y x P 的切线方程为200r y y x x =+；（2）经过圆222)()(r b y a x =-+-上一点),(00y x P 的切线方程为 200))(())((r b y b y a x a x =--+--；（3）经过圆022=++++F Ey Dx y x 上一点),(00y x P 的切线方程为0220000=++?++?++F y y E x x D y y x x ；（4）已知圆222r y x =+的切线方程的斜率为k ，则圆的切线方程为12+±=k r kx y 。
3. 切线长公式过圆外一点),(00y x P 引圆的两条切线，则切线的长为22020002020)()(r b y a x F Ey Dx y x --+-=++++。
4. 切点弦方程过圆222r y x =+外一点),(00y x P 引圆的两条切线，切点分别是B A 、，则过两切点BA 、的弦所在直线的方程为200r y y x x =+。
（即此弦所在的直线方程的求法为：以圆心)0,0(O 和),(00y x P 的为直径两端点的圆的方程为0)()(00=-+-y y y x x x ，两圆方程联立方程组=-+-=+,0)()( ,00222y y y x x x r y x ，同时消去22y x 、项得直线方程就是切点弦虽在的直线方程。
）。
九年级中考复习专题七圆切线证明及计算
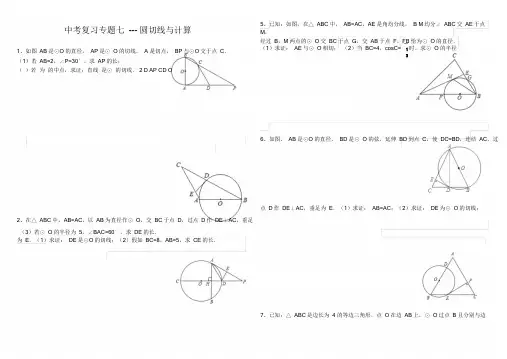
中考复习专题七--- 圆切线与计算5、已知：如图，在△ABC中，AB=AC，AE是角均分线，B M均分∠ABC交AE于点M，经过B，M两点的⊙O交BC于点G，交AB于点F，FB恰为⊙O的直径．1、如图AB是⊙O的直径，AP是⊙O的切线，A 是切点，BP与⊙O交于点C．（1）若AB=2，∠P=30°，求AP的长；（）若为的中点，求证：直线是⊙的切线． 2 D AP CD O （1）求证：AE与⊙O相切；（2）当BC=4，cosC= 1时，求⊙O的半径36、如图，AB是⊙O的直径，BD是⊙O的弦，延伸BD到点C，使DC=BD，连结AC，过点D作DE⊥AC，垂足为E．（1）求证：AB=AC；（2）求证：DE为⊙O的切线；2、在△ABC中，AB=AC，以AB为直径作⊙O，交BC于点D，过点D作DE⊥AC，垂足（3）若⊙O的半径为5，∠BAC=60°，求DE的长．为E．（1）求证：DE是⊙O的切线；（2）假如BC=8，AB=5，求CE的长．7、已知：△ABC是边长为4 的等边三角形，点O在边AB上，⊙O过点B且分别与边AB，BC订交于点D，E，EF⊥AC，垂足为F．4、如图，AB为⊙O内垂直于直径的弦，AB、CD相于点H，△AED与△AHD对于直线（1）求证：直线EF 是⊙O的切线；（2）当直线DF与⊙O相切时，求⊙O的半径．AD成轴对称．（1）试说明：AE为⊙O的切线；（2）延伸AE与CD交于点P，已知PA=2，PD=1，求⊙O的半径和DE的长．8、如图，已知⊙O是△ABC的外接圆，AB是⊙O的直径，D是AB延伸线上的一点，14、如图，△ABC内接于半圆，AB是直径，过A作直线MN，∠MAC=∠ABC，D是弧ACA E⊥C D交DC的延伸线于E，C F⊥AB于F，且CE=CF．的中点，连结BD交AC于G，过D作DE⊥AB于E，交AC于F．（1）判断DE与⊙O的地点关系，并说明原因；（1）求证：MN是半圆的切线；（2）若AB=6，BD=3，求BC和AE的长．（2）求证：FD=FG．（3）若△DFG的面积为 4.5 ，且DG=3，GC=4，试求△BCG的面积．15、如图，AB=AC，D为BC中点，⊙D与AB切于E 点。
圆的切线方程公式推导过程
圆切线方程公式推导过程
圆的切线方程公式推导过程如下：
1. 设圆的标准方程为(x - a)^{2} + (y - b)^{2} = r^{2}，其中(a, b) 是圆心，r 是半径。
2. 设切线的斜率为k，则切线方程可以表示为y = kx + m。
3. 将切线方程y = kx + m 代入圆的方程(x - a)^{2} + (y - b)^{2} = r^{2}，得到：(x - a)^{2} + (kx + m - b)^{2} = r^{2}
4. 展开并整理上述方程，得到：
(1 + k^{2})x^{2} + 2(km - b)x + m^{2} - 2bm + b^{2} - r^{2} = 0
5. 由于切线与圆只有一个交点，因此上述方程应该只有一个解，即判别式Delta 应该等于0：
Delta = [2(km - b)]^{2} - 4(1 + k^{2})(m^{2} - 2bm + b^{2} - r^{2}) = 0
6. 展开并整理上述方程，得到：
k^{2}m^{2} - 2kbm + b^{2} - k^{2}m^{2} + 2kbm - b^{2} + r^{2} = 0
r^{2} = 0
7. 由于r^{2} 显然不为0，因此上述方程可以简化为：
2kbm - 2kbm = 0
8. 由于上述方程对所有的k 和m 都成立，因此我们可以得到切线的斜率k 与圆的半径r、圆心(a, b) 和切线在y 轴上的截距m 无关。
9. 最后，我们可以得到圆的切线方程为y = kx + m，其中k 是任意实数，m 是切线在y 轴上的截距。
由于切线与圆只有一个交点，因此m 可以是任意实数。
圆形切线经典习题
圆形切线经典习题1. 切线定义在数学中，一条切线是一条与圆的曲线相切，且切点与圆心连线垂直的直线。
切线的长度与半径相等。
2. 切线性质- 切线与圆的交点处，切线的斜率是切点处切线的斜率的负倒数。
- 切线与半径在交点处构成直角。
3. 切线计算设圆的方程为 x^2 + y^2 = r^2，圆心为 (a, b)，切线的斜率为 k，则切线方程为：y - b = k(x - a)4. 经典题题1已知圆的方程为 x^2 + y^2 = 4 和点 P(1, -1) 是圆上的一点，求通过点 P 切圆的切线方程。
题2已知圆的方程为 x^2 + y^2 = 9 和切点为 A(3, -2)，求通过切点A 切圆的切线方程。
题3已知圆的方程为 x^2 + y^2 = 25 和切线方程为 y = 2x + 1，求切点坐标。
题4已知圆的方程为 (x - 2)^2 + (y - 3)^2 = 25，求与圆相切且斜率为 3 的切线方程。
5. 解答题1通过点 P 切圆的切线方程为：y - (-1) = k(x - 1)题2通过切点 A 切圆的切线方程为：y - (-2) = k(x - 3)题3设切点坐标为 (x1, y1)，代入切线方程得：2x1 + 1 = y1代入圆的方程得：x1^2 + y1^2 = 25联立解方程得切点坐标。
题4斜率为 3 的切线方程为：y - 3 = 3(x - 2)解得切点坐标。
以上是圆形切线的经典习题及解答。
通过这些习题的练习，可以加深对圆形切线的理解与掌握。
圆的切线证明及有关计算
能力提升
3. （14.贺州 九下P102 第11题变式）
如图，ＡＢ，ＢＣ，ＣＤ分别与⊙Ｏ相切于Ｅ，Ｆ，Ｇ， 且ＡＢ∥ＣＤ，ＢＯ＝６ｃｍ，ＣＯ＝８ｃｍ．
（１）求证：ＢＯ⊥ＣＯ；
（２）求ＢＥ和ＣＧ的长．
能力提升
4. （13.南宁）如图，在△ABC中，∠BAC=90°， AB=AC，AB是⊙ O的直径，⊙O交BC于点D，
A．8 B．6 C．5 D．4
类型二 与切线判定有关的证明
3.已知如图,AB是⊙O的直径,⊙O过BC的中点D, 且
DE⊥AC于点E.
C
(1)求证:DE是⊙O的切线； (2)若∠C＝30°,CD＝10 cm,
求⊙O的直径．
D
E
A
·
O
B
分析： (1)若所证直线与圆的交点字母标出,则连接这条半径, 证明这条半径________所证直线；
两点，且∠P=70°，则∠C=__5__5_°__.
（变式） （12.贵港）如图，PA、PB切⊙O于A、B两点，点C
在⊙O上，且∠ACB=50°，则∠P=__8_0__°__.
2.如图，在等腰直角三角形ABC中，AB=AC=8，O为BC 的中点，以O为圆心作半圆，使它与AB，AC都相切，
切点分别为D，E，则⊙O的半径为（ Ｄ ）
(2)利用等腰三角形和直角三角形知识可求．
解：(1)连接OD，OD是半径， C
∵O是AB的中点,D是BC的中点，
D
∴OD是△ABC 中_位__线__, 即OD∥_A__C_.
E
A
·
O
B
∵DE⊥AC ,则DE_⊥__OD，
高考数学培优---圆的“双切线”问题
高考数学培优---圆的“双切线”问题【方法点拨】1.涉及从圆外一点向圆引两条切线的相关线段长计算问题，根据对称性,常将双切线问题转化为一条切线问题，抓住“特征直角三角形”(切点、圆心、圆外点为顶点)，向点与圆心的距离问题转化.2.圆上存在一点、圆心与圆外一点（或圆上存在两点与圆外一点）的张角有最大值，张角最大时，直线与圆相切，转化为点与圆心的距离问题.【典型题示例】例1已知⊙M ：222220x y x y +---=，直线l ：220x y ++=，P 为l 上的动点，过点P 作⊙M 的切线,PA PB ，切点为,A B ，当||||PM AB ⋅最小时，直线AB 的方程为（ ）A. 210x y --=B. 210x y +-=C. 210x y -+=D. 210x y ++=【答案】D【分析】由题意可判断直线与圆相离，根据圆的知识可知，四点,,,A P B M 共圆，且AB MP ⊥，根据22PAM PM AB S PA ⋅==△可知，当直线MP l ⊥时，PM AB ⋅最小，求出以MP 为直径的圆的方程，根据圆系的知识即可求出直线AB 的方程．【解析】圆的方程可化为()()22114x y -+-=，点M 到直线l的距离为2d ==>，所以直线l 与圆相离．依圆的知识可知，四点,,,A P B M 四点共圆，且AB MP ⊥，所以12222PAM PM AB S PA AM PA ⋅==⨯⨯⨯=△，而PA = 当直线MP l ⊥时，min MP =，min 1PA =，此时PM AB ⋅最小． ∴()1:112MP y x -=-即1122y x =+，由1122220y x x y ⎧=+⎪⎨⎪++=⎩解得，10x y =-⎧⎨=⎩．所以以MP 为直径的圆的方程为()()()1110x x y y -++-=，即2210x y y +--=，两圆的方程相减可得：210x y ++=，即为直线AB 的方程．例2 在平面直角坐标系xOy 中，已知直线l :y =kx +6上存在点P ，过点P 作圆O : x 2+ y 2=4的切线，切点分别为A (x 1，y 1)，B (x 2，y 2)，且x【答案】(－∞，－52]∪[52，＋∞) 【分析】由x 1 x 2+ y 1y 2=－2直线l :y =kx +6上的点P 只需满足PC 以垂线段最短，故只需C 【解析】由x 1 x 2+ y 1y 2=－2得： 1212=cos x x y y OA OB OA OB +=⋅在△P AC ，∠APC =300，PC =4，当直线l 上的点 P 满足PC =4又因为点C 与直线上点间的距离，以垂线段最短，故只需C 到直线的距离不大于4.4≤，解之得22k k ≤-≥ 所以k 的取值范围为(－∞，－52]∪[52，＋∞).例 3 过点)1,1(-P 作圆C :)(1)2()(22R t t y t x ∈=+-+- 的切线,切点分别为B A ,,则PA PB ⋅ 的最小值为__________.【答案】214【分析】为了求出PA PB ⋅的最小值，需建立目标函数，这里选择使用数量积的定义作为突破口，选择线段PC 长为“元”.设∠APC =θ，则1sin PC θ=，222cos 212sin 1PC θθ=-=-， 故222222cos 2(1)(1)3PA PB PA PB PC PC PC PCθ⋅==--=+- 又点(,2)C t t -在直线20x y --=，故22PC ≥即28PC ≥所以2218384PA PB ⋅≥+-=，故PA PB ⋅ 的最小值为214. 点评：（1）求最值问题要牢固树立建立目标函数的意识；（2）涉及从圆外一点向圆引两条切线的相关线段长计算问题，常将双切线问题转化为一条切线问题，抓住“特征直角三角形”，向点与圆心的距离问题转化.例4 已知圆O ：x 2＋y 2＝1，圆M ：(x ＋a ＋3)2＋(y －2a )2＝1(a 为实数)．若圆O 与圆M 上分别存在点P ，Q ，使得∠OQP ＝30︒，则a 的取值范围为 ．【答案】[－65，0] 【分析】双动点问题先转化为一点固定不动，另一点动.这里，先将Q 固定不动，则点P 在圆O 运动时，当PQ 为圆O 的切线时，∠OQP 最大，故满足题意，需∠OQP ≥30︒，再将角的范围转化为O 、Q 间的距离问题，即需OQ ≤2.再固定P 不动，易得只需OM ≤3即可，利用两点间距离公式(a ＋3)2＋(2a )2≤9，解得－65 ≤a ≤ 0.点评：圆上存在一点（或两点）与圆外一点的张角问题，张角最大时，直线与圆相切，转化为点与圆心的距离问题.例5 平面直角坐标系xOy 中，点P 在x 轴上，从点P 向圆C 1：x 2＋(y －3)2＝5引切线，切线长为d 1，从点P 向圆C 2：(x －5)2＋(y ＋4)2＝7引切线，切线长为d 2，则d 1＋d 2的最小值为_____．【答案】52【分析】求切线长问题再利用数形结合思想解决最值问题.【解析】设点P (x ，0)，则d 1＝x 2＋(－3)2－5，d 2＝(x －5)2＋42－7，d 1＋d 2＝x 2＋4＋(x －5)2＋9，几何意义：点P (x ，0)到点M (0，2)，N (5，－3)的距离和．当M，P，N三点共线时，d1＋d2有最小值52，此时P(2，0).【巩固训练】1.在平面直角坐标系xOy 中，已知圆C ：x 2＋(y －3)2＝2，点A 是x 轴上的一个动点，AP ，AQ 分别切圆C 于P ，Q 两点，则线段PQ 的长的取值范围是________．2.已知圆M ：(x －1)2＋(y －1)2＝4，直线l ：x ＋y －6＝0，A 为直线l 上一点．若圆M 上存在两点B ，C ，使得∠BAC ＝60°，则点A 横坐标的取值范围是__________．3.已知椭圆C 1：22221x y a b +=（a ＞b ＞0）与圆C 2：22234b x y +=，若在椭圆C 1上不存在点P ，使得由点P 所作的圆C 2的两条切线互相垂直，则椭圆C 1的离心率的取值范围是_______4.在平面直角坐标系xOy 中，已知圆O : x 2+ y 2= r 2 (r ＞0) 与圆C : (x －6)2+ (y －8)2=4，过圆O 上任意一点P 作圆C 的切线，切点分别为A ，B ，6PA PB +≥，则实数r 的取值范围为 .5.在平面直角坐标系xOy 中，已知圆C ：22(3)(4)16x y +++=，若对于直线10x my ++= 上的任意一点P ，在圆C 上总存在Q 使∠PQC ＝2π，则实数m 的取值范围为 ． 6.在平面直角坐标系xOy 中，已知圆O ：x 2＋y 2＝1，直线l ：x ＋ay －3＝0(a >0)，过直线l 上一点P 作圆O的两条切线，切点分别为M ，N .若PM →·PN →＝23，则正实数a 的取值范围是________． 7. 过直线l ：y ＝x －2上任意一点P 作圆C ：x 2＋y 2＝1的两条切线，切点分别为A ，B ，当切线最短时，△P AB 的面积为________．8. 已知圆C ：(x －1)2＋(y －4)2＝10上存在两点A ，B ，P 为直线x ＝5上的一个动点．且满足AP ⊥BP ，那么点P 的纵坐标的取值范围是________．。
圆中与切线有关的解题策略
圆中与切线有关的解题策略知识精解一、切线的三种判定方法：（1）和圆只有一公共点的直线是圆的切线；（2）圆心到直线的距离等于半径的直线是圆的切线；（3）经过半径外端且与半径垂直的直线是圆的切线；证题中常用后两种方法，且往往需要添加辅助线。
常见证明切线的方法(添加辅助线)：（1）如果已知直线经过圆上一点，那么连结这点和圆心得到半径再证所作半径与这条直线垂直。
即“连半径，证_______”（2）如果已知条件中不知直线与圆是否有公共点，那么过圆心作直线的垂线段，再证明垂线段的长等于半径，即“作垂直，证_______”。
自主学习例1. 如图，△ABC中，∠ACB=90°，以AC为直径的⊙O交AB于D，E为BC中点。
求证：DE是⊙O切线。
例2. 如图，梯形ABCD中，AD∥BC，∠C=∠D=90°，且AD+BC=AB。
求证：以AB为直径的⊙O与CD相切。
练习1：直线MN∥PQ，点A在MN上，点B在PQ上，O是AB的中点，⊙O与MN相切于于K．求证：⊙O与PQ也相切．练习2：已知△ABC 中，=∠90 C ，=AC BC ，，D E 分别是，AC BC 的中点，⊙O 是△DCE 的外接圆． 求证：AB 是⊙O 的切线．练习3：已知：∠MAN=30°，O 为边AN 上一点，以O 为圆心、2为半径作⊙O ，交AN 于D 、E 两点，设AD=x ，⑴如图⑴当x 取何值时，⊙O 与AM 相切；⑵如图⑵当x 为何值时，⊙O 与AM 相交于B 、C 两点，且∠BOC=90°．二. 切线长定理：从圆外一点引圆的两条切线，它们的切线长相等且这点和圆心连线平分两条切线的夹角。
如图，已知：P 是⊙O 外一点，PA 、PB 是⊙O 的切线，A 、B 为切点；结论：(1)PA____PB ；(2)OP______∠APB 。
由切线长定理，可以推得如下重要结论：(1)圆外切四边形的对边和相等；(2)圆的两条平行切线的切点连线是圆的______。
圆的切线证明及相关计算
与圆的切线相关的线段计算学习目标1、利用圆的切线性质计算圆的相关线段；2、会选择适当的做辅助线的方法；学习过程：切线的性质： ； 与圆相关切线的辅助线常见做法： ；一、圆与切线有关的角度计算例.如图，AB 是⊙O 的弦，AC 是⊙O 的切线，A 为切点，BC 经过圆心。
若∠B=20°，则∠C 的大小等于A.20°B.25°C.40°D.50°练习.如图，PA 、PB 分别与⊙O 相切于A 、B 两点，若∠C=65°，则∠P 的度数为A. 65°B. 130°C. 50°D. 100°二、圆与切线有关的长度计算1.如图， 中，AB=5，BC=3，AC=4，以点C 为圆心的圆与AB 相切于点D ，则☉C 的半径为（）（A ）2.3（B ）2.4 （C ）2.5（D ）2.6第8题图2.如图，已知，AB是⊙O的一条直径，延长AB至C点，使AC3BC=,CD与⊙O相切于D点，若CD,则劣弧AD的长为 .3.如图，AB是⊙O的直径，点C在⊙O上，点D在AB延长线上，CD与圆O相切于点C，∠A＝30°，AC＝23，图中阴影部分的面积是；．例.已知，如图，AB是⊙O的直径，⊙O过AC的中点D，过D作DE⊥BC交BC于点E。
（1）求证：DE是⊙O的切线；（2）如果CD＝4，CE＝3，求⊙O的半径。
C三、练习题1．如图，已知AB是⊙O的直径，点C、D在⊙O上，点E在⊙O外，∠EAC=∠D=60°．（1）求∠ABC的度数；（2）求证：AE是⊙O的切线；（3）当BC=4时，求劣弧AC的长．2.如图，在△ABC中，AB=AC，点D是边BC的中点．以BD为直径作圆O，交边AB于点P，连接PC，交AD于点E．（1）求证：AD是圆O的切线；（2）若PC是圆O的切线，BC=8，求DE的长课后作业：1.如图，等腰三角形ABC中，AC＝BC＝10，AB＝12。
中考数学复习指导：巧用口诀妙解圆中切线问题
巧用口诀妙解圆中切线问题与切线有关的问题是圆中十分重要的内容之一，在解决此类问题时，可灵活运用这样的口诀：“遇切线，连半径；连半径，证垂直；作垂线，证半径”，常常能取得较好的效果．下面举例说明其用法，供参考．一、遇切线，连半径已知圆的切线进行运算或证明时，通常要把切点与圆心连结起来，充分利用“垂直”来解决问题．例1 如图1，在同心圆⊙O中，大圆的弦AB切小圆于点C，且AB＝6cm，求圆环的面积．思路点拨因为大圆的弦AB切于小圆C点，所以连结OC，可得OC⊥AB，进而根据垂径定理求得AC＝12AB＝3．圆环的面积是大圆面积与小圆面积的差，连结OA，此时OA为大圆半径，OC为小圆半径．在Rt△AOC中，利用勾股定理可求出（OA2－OC2）的值，就可求出圆环的面积．例2 如图2，在△ABC中，AB＝AC，以AB为直径的⊙O交BC于点D，DE是⊙O的切线交AC于点E，求证：DE⊥AC．思路点拨连结OD，利用切线的性质可得OD⊥DE，再利用“等边对等角”可证得∠ODB＝∠ACB，可得OD∥AC即可．证明连结OD．二、连半径，证垂直已知直线经过圆上的一点，其证法是连接这点和圆心，然后证明这个辅助半径与这条直线垂直即可．例3 如图3，已知AB是⊙O的直径，P是⊙O的切线，在BP上取一点P，连结OP，过点A作OP的平行线交⊙O于点C，连结PC．求证：PC是⊙O的切线．思路点拨点C在O上，连结半径OC，PC经过半径OC的外端C这个条件就已具备，只要再证OC⊥PC即可．又因为PB为圆的切线，由切线的性质，可知∠PBO＝90°，利用全等三角形可证得∠PCO＝∠PBO＝90°，即可得OC⊥PC．证明连结OC．∵OA＝OC，∴∠1＝∠A．又∵OP∥AC，即OC⊥PC，∴PC是⊙O的切线．三、作垂线，证半径如果已知条件中，不知道直线与圆的公共点，其证法是过圆心作该直线的垂线段，再证明这条垂线段的长度等于此圆的半径即可．例4 如图4，在梯形ABCD中，AB∥CD，∠B＝90°，AD＝AB＋DC，AD是⊙O 的直径．求证：BC与⊙O相切．思路点拨由条件不易判断直线BC与⊙O有没有公共点，所以不便利用切线的判定定理来证明，联想到“到圆心的距离等于半径的直线是圆的切线”，考虑作OE⊥BC，垂足为E，只要证明OE等于⊙O的半径（12AD）即可，根据梯形中位线定理可达到这一目的．证明作OE⊥BC于点E．。
圆的切线方程公式
圆的切线方程公式圆是几何学中的重要概念之一，其切线的求解在数学中也有很大的应用价值。
在本文中，我将为您介绍圆的切线方程公式，并按照列表划分，详细解释其求解步骤和性质。
一、什么是切线？切线是指与给定曲线在某一点相切，并且只与该点产生相切关系的直线。
对于圆而言，切线即与圆相交于一个点，并且只与该点产生相切关系的直线。
二、圆的切线方程公式1. 已知圆的方程和切点坐标的情况下，可以使用圆的切线方程公式进行求解。
2. 设圆的方程为：(x-a)² + (y-b)² = r²，其中(a, b)为圆心坐标，r为圆的半径。
3. 假设切点坐标为(x₁, y₁)，切线方程的一般形式为：y = kx + c，其中k为斜率，c为截距。
4. 求解圆的切线方程的步骤如下：(1) 计算圆心到切点的距离，记为d，即：d = √((x₁-a)² + (y₁-b)²)(2) 计算切线的斜率k，即：k = -((x₁-a)/(y₁-b))(3) 计算切线的截距c，即：c = y₁ - kx₁(4) 则切线的方程为：y = kx + c。
三、切线方程的性质1. 切点：切线与圆相切的点称为切点，切线方程公式中的切点坐标即为切点的位置。
2. 相切条件：当切线方程的切点坐标与圆的方程满足时，切线才与圆相切。
3. 斜率关系：切线与圆相切的切点与圆心的连线垂直于切线，即切线的斜率与圆心到切点的线段的斜率的乘积为-1。
4. 切线的数量：对于圆而言，切线的数量不止一条，具体数量取决于切点的位置。
四、实例应用圆的切线方程公式在实际问题中有广泛的应用，例如：1. 建筑设计中，圆形窗户的设计需要确定切线的位置，以确保窗户与建筑物的完美结合。
2. 制造业中，机械零件的加工需要计算切线方程，来确定切削工具的位置和角度。
3. 车辆运动的轨迹研究，有时需要计算车辆在弯道上的切线方程，以确定行车路线和速度控制。
综上所述，圆的切线方程公式是一种重要的数学工具，在几何学和应用数学中起到了重要的作用。
圆的切线与相关计算
1、（09广安）已知：如图，AB 是⊙O 的直径，AD 是弦，OC 垂直AD 于F 交⊙O 于E ，连结DE 、BE ，且∠C =∠BED ．（1）求证：AC 是⊙O 的切线； （2）若OA =10，AD =16，求AC 的长．2、（09泸州）如图11，在△ABC 中，AB=BC ，以AB 为直径的⊙O 与AC 交于点D ，过D 作D F ⊥BC ，交AB 的延长线于E ，垂足为F ． (1)求证：直线DE 是⊙O 的切线；(2)当AB=5，AC=8时，求cosE 的值． 3、（09达州）如图，⊙O 的弦AD ∥BC,过点D 的切线交BC 的延长线于点E ，AC ∥DE 交BD 于点H ，DO 及延长线分别交AC 、BC 于点G 、F. (1)求证：DF 垂直平分AC ；（2）求证：FC ＝CE ；（3）若弦AD ＝5㎝，AC ＝8㎝，求⊙O 的半径.C ED A F OB4.（本题满分9分）( 恩施自治州2008年)如图，AB 是⊙O 的直径，BD 是⊙O 的弦，延长BD 到点C ，使DC =BD ，连结AC ，过点D 作DE ⊥AC ，垂足为E . （1）求证：AB =AC ；（2）求证：DE 为⊙O 的切线；（3）若⊙O 的半径为5,∠BAC =60°,求DE 的长.5（本小题满分10分）如图所示，ABC △是直角三角形，90ABC ∠= ，以AB 为直径的O 交AC 于点E ，点D 是BC 边的中点，连结DE ． （1）求证：DE 与O 相切；（2）若O3DE =，求AE ．（第5题）6．（本题满分10分）(孝感市2008年)如图，AB 为O 的直径，PQ 切O 于T ，AC PQ ⊥于C ，交O 于D ．（1）求证：AT 平分BAC ∠；（5分） （2）若2AD =，TC =O 的半径．（5分）7（本题满分8分）(2008年陕西省中考)如图，在Rt △ABC 中，∠ACB ＝90°，AC ＝5，CB ＝12，AD 是△ABC 的角平分线，过A 、C 、D 三点的圆与斜边AB 交于点E ，连接DE 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
则大圆的 的度数为.
8、如图，⊙O1和⊙O2交于A、B两点，且点O1在⊙O2上，若 D＝ ，则 C＝
9、如图，⊙O1和⊙O2外切于D，AB过点D，若 AO2D＝ ，C为优弧 上任一点，
则 DCB＝.答案：7、 ；8、40 ；9、 （过点D作两圆的切线）
4、如图，PA、PB为⊙Байду номын сангаас的切线，C为 上一点，
若 BCA＝ ，则 APB＝.
5、如图，点O是△ABC的内切圆的的圆心，若
BAC＝ ，则 BOC＝.
6、如图，PA切⊙O于A，若PA＝AB，PD平分
APB交AB于D，则 ADP＝.（设元，列方程）
二 切线与两个圆
7、如图，两同心圆的圆心为O，大圆的弦AB、AC
圆的培优专题7——与切线有关的角度计算
一 切线与一个圆答案：1、 ；2、 ；3、 ；4、 ；5、 ；6、
1、如图，AD切⊙O于A，BC为直径，若 ACB＝ ，则 CAD＝.
2、如图，AP切⊙O于P，PB过圆心，B在⊙O上，若 ABP＝ ，则 APB＝.
3、如图，PA、PB为⊙O的切线，C为 上一点，若 BCA＝ ，则 APB＝.