高二文科数学每日一练4
试题君之每日一题君2016-2017学年高二文数人教A版选修

4月17日 二维形式的柯西不等式高考频度:★★☆☆☆ 难易程度:★★☆☆☆(1)若,b +∈R ,且1a b +=A .2+B .C .D(2)函数y =______________.【参考答案】(1)D ;(2)【试题解析】(1)因为,b +∈R ,且1a b +=,所以2212a b ab +=-, 又22256262()22a b ab ab ab =+++≥-+=-++10=,≥,当且仅当12a b =时,等号成立,D .(2)因为222(34)(11)50x x ≤+++-=,所以||2y ≤.故函数y =.1.已知1=,则以下式子成立的是A .221a b +>B .221a b +=C .221a b +<D .221a b =2.设向量(,)a b =α,(,)c d =β,其中,,,d ∈R ,由不等式||||||⋅≤αβαβ恒成立,可以证明柯西不等式22222()()()a b c d ac bd ≥+++(当且仅当k =αβ,即ad bc =时等号成立).己知,y +∈R 值范围为______________.3.已知,,,d 均为正数,且224a b +=,1cd =,则22222222()()a c b d b c a d ++的最小值为______________.1.B 【解析】由柯西不等式,可得222221([(1)][(1)]1a a b b =≤+--+=,当且仅当=时,上式取等号,所以ab =,即2222(1)(1)a b a b =--,故 221a b +=.故选B .2.)+∞【解析】因为22222()()()a b c d a c b d≥+++,所以222)(13)()y x y ≤++,所以,因为,y +∈R ,<k >.故填)+∞.3.16 【解析】因为,,,d 均为正数,且224a b +=,1cd =,则2222222()()a c b d b c a d++=2222()b d ac +222222222()()()16b c a d b c d a c d b a +≥+=+=,故22222222()()a c b d b c a d ++的最小值为16.4月18日 一般形式的柯西不等式高考频度:★★★☆☆ 难易程度:★★★☆☆已知1a b c ++=.(1)求22232c b a S ++=的最小值及取最小值时,,的值. (2)若132222=++c b a ,求实数的取值范围.【参考答案】(1)最小值为116,116,112,113===c b a ;(2【思路分析】(1)根据柯西不等式的一般形式可得))(()(2322212322212332211b b b a a a b a b a b a ++++≤++,把已知条件可化为c b a c b a ⋅+⋅+⋅=++=13312211,即可求出22232c b a S ++=的最小值,注意等号成立的条件;(2)由柯西不等式得到不等式,再利用等量代换转化为关于的不等式即可求解. 【试题解析】(1)根据柯西不等式可得:≤⋅+⋅+⋅=++=c b a c b a 133122112122221)32()13121(c b a ++++S ⋅=611, 即1611≥⋅S ,所以116≥S ,易知等号成立时116,112,113===c b a ,116min =S .(2)根据条件可得2221231a b ca b c +=-⎧⎨+=-⎩,根据柯西不等式得23,,n a ,1,,n b b 是实2)n a ++221122)()n n n b a b a b a b ++≥+++,当且仅当,2,3,,)n 或存在一个数,使得i i a kb =(1,2,3,,)i n =时,等号成立.1.已知,,x y z ∈R ,且522=+-z y x ,则222)3()1()5(++-++z y x 的最小值是 A .20B .25C .36D .472.已知实数,,,d ,满足8a b c d e ++++=,2222216a b c d e ++++=,则实数的取值范围为______________.3.已知在ABC △中,角A ,B ,C 所对的边分别为,,. (1)证明:333111abc a b c +++≥; (2)若231a b c ++=,且222a b ck ++>恒成立,求实数的最小值.1.C【解析】由于22222[(5)(1)(3x y z x y ++-+++-+324,所以222(5)(1)(3)36x y z ++-++≥,当且仅当513122x y z +-+==-,即331x y z =-⎧⎪=-⎨⎪=⎩时取等号.故选C . 2.16[0,]5【解析】由柯西不等式得22222(1111)()()a b c d a b c d ++++++≥+++,即24(16)e -≥2(8)e -,解得1605e ≤≤,所以实数的取值范围为16[0,]5.【名师点睛】本题主要考查不等式的证明问题,其中涉及柯西不等式的应用问题,有一定的技巧性,需要同学们对一般形式的柯西不等式非常熟练.3.【思路分析】本题主要考查不等式的证明、均值不等式等基础知识,意在考查考生的分析问题解决问题的能力、运算求解能力.(1)先利用均值不等式3331113a b c abc++≥,再化简得abc ,再次利用均值不等式3abc abc +≥,最后验证等号是否成立即可;(2)由231a b c ++=及222a b c ++的形式,联想到柯西不等式,构造222(123)++作为一个因式进行求解.【解析】(1)因为,, 错误!未找到引用源。
人教A版数学必修四高二文科数学周练试题

高中数学学习材料金戈铁骑整理制作常宁二中高二文科数学周练试题2012-4-28晚7:15—9:15一、选择题(本大题共8小题,每小题5 分,满分40分.) 1 i 是虚数单位,若集合}0,1{-=S ,则( )A .S i ∈B .S i ∈2C .S i ∈3D .S i ∈42.为了评价某个电视栏目的改革效果,在改革前后分别从居民点抽取了100位居民进行调查,经过计算99.02≈K ,根据这一数据和P(2k≥6.635)=0.01分析,下列说法正确的是( ) A .有的人认为该栏目优秀B .有%99的人认为该栏目是否优秀与改革有关系C .有%99的把握认为电视栏目是否优秀与改革有关系D .没有理由认为电视栏目是否优秀与改革有关系3、抛物线 22y x -=的准线方程是 ( )A .21=y B .81=y C .41=x D .81=x 4.已知等差数列{}n a 的通项公式为32n a n =- , 则它的公差为( ) A .2 B .3 C . 2- D.3- 5.给出结论:①命题“(x -1)(y -2)=0,则(x -1)2+(y -3)2=0”的逆命题为真; ②命题“若x >0,y >0,则xy >0”的否命题为假;③命题“若a <0,则x 2-2x +a =0有实根”的逆否命题为真;④“33x x -=-”是“x =3或x =2”的充分不必要条件.其中结论正确的个数为( ) A .4B .3C .2D .16.如图,函数()y f x =的图象在点P 处的切线方程是8y x =-+,则()()55f f '+=( )A .12 B .1 C .2D .07.盒子中有大小相同的3只白球,1只黑球,若从中随机地摸出两只球,两只球颜色不同的概率是( )A 14B 12C 18D 无法确定8.设函数1()ln (0),3f x x x x =->则()y f x =( )A .在区间1(,1),(1,)e e 内均有零点。
高二数学基础题练习题大全

高二数学基础题练习题大全在高中数学学习过程中,基础是非常重要的。
高二是数学知识进一步深化和拓展的阶段,因此,掌握基础题是非常重要的。
本文将提供一些适用于高二学生的数学基础题练习题大全,供同学们进行复习和巩固。
一、函数与方程1. 求方程的解:求解方程2x + 3 = 11的解。
2. 函数的求值:已知函数y = 2x + 1,求当x = 3时,函数的值y为多少?3. 二次方程的求解:解方程x^2 - 2x - 3 = 0。
4. 函数的图像:画出函数f(x) = x^2 - 2x + 1的图像,并指出其顶点和对称轴。
5. 求方程组的解:求解方程组{2x + y = 5,x - y = 1}的解。
二、数列与级数1. 等差数列:已知数列{an}的首项为a1 = 2,公差d = 3,求第10项an的值。
2. 等比数列:已知数列{bn}的首项b1 = 0.5,公比q = 2,求第5项bn的值。
3. 数列求和:已知等差数列{sn}的前n项和为Sn = 3n^2 - 2n,求第10项s10的值。
4. 级数求和:已知等比数列{an}的前n项和为Sn = 5(1 - 2^n),求前10项的和S10的值。
5. 递归数列:已知数列{cn}满足c1 = 2,cn = 2cn-1 - 1,求第5项c5的值。
三、几何图形与空间几何1. 三角形性质:已知三角形ABC,AB = 3,AC = 4,BC = 5,判断三角形ABC的形状。
2. 圆的性质:已知半径r = 2的圆O,求圆O的周长和面积。
3. 直角三角形:已知直角三角形ABC,∠C = 90°,AB = 3,BC = 4,求斜边AC的长度。
4. 空间直线与平面:已知直线l过点A(1, 2, 3)且与平面P:x + 2y - z= 5平行,求直线l的方程。
5. 空间几何体积:已知正方体的体积为27,求正方体的边长。
四、概率与统计1. 概率计算:有一只装有红、蓝、黄三种颜色球的袋子,红球2个,蓝球3个,黄球5个,从袋子中随机抽取一个球,求抽到红球的概率。
人教A版数学必修四高二文科数学周练试题

常宁二中高二文科数学周练试题2012-4-28晚7:15—9:15一、选择题(本大题共8小题,每小题5 分,满分40分.) 1 i 是虚数单位,若集合}0,1{-=S ,则( )A .S i ∈B .S i ∈2C .S i ∈3D .S i ∈42.为了评价某个电视栏目的改革效果,在改革前后分别从居民点抽取了100位居民进行调查,经过计算99.02≈K ,根据这一数据和P(2k≥6.635)=0.01分析,下列说法正确的是( ) A .有的人认为该栏目优秀B .有%99的人认为该栏目是否优秀与改革有关系C .有%99的把握认为电视栏目是否优秀与改革有关系D .没有理由认为电视栏目是否优秀与改革有关系3、抛物线 22y x -=的准线方程是 ( )A .21=y B .81=y C .41=x D .81=x 4.已知等差数列{}n a 的通项公式为32n a n =- , 则它的公差为( ) A .2 B .3 C . 2- D.3- 5.给出结论:①命题“(x -1)(y -2)=0,则(x -1)2+(y -3)2=0”的逆命题为真;②命题“若x >0,y >0,则xy >0”的否命题为假;③命题“若a <0,则x 2-2x +a =0有实根”的逆否命题为真; ④“33x x -=-”是“x =3或x =2”的充分不必要条件.其中结论正确的个数为( ) A .4B .3C .2D .16.如图,函数()y f x =的图象在点P 处的切线方程是8y x =-+,则()()55f f '+=( )A .12B .1C .2D .07.盒子中有大小相同的3只白球,1只黑球,若从中随机地摸出两只球,两只球颜色不同的概率是( )A 14B 12C 18D 无法确定8.设函数1()ln (0),3f x x x x =->则()y f x =( )A .在区间1(,1),(1,)e e 内均有零点。
最新版2020年高二数学第二学期期末模拟试卷及答案(四)(文科)

2020年高二数学第二学期期末模拟试卷及答案(四)(文科)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的.1.若i是虚数单位,则复数=()A.﹣1 B.1 C.﹣i D.i2.设集合M={x|0<x≤3},N={x|0<x≤2},那么“a∈M”是“a∈N”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件3.已知命题P:∃x∈R,x2+2ax+a≤0.若命题P是假命题,则实数a的取值范围是()A.(0,1)B.(﹣∞,0)∪(1,+∞)C.[0,1]D.(﹣∞,0)∪[1,+∞)4.若函数f(x)=x3+ax2+3x﹣6在x=﹣3时取得极值,则a=()A.2 B.3 C.4 D.55.若log6a=log7b,则a、b、1的大小关系可能是()A.a>b>1 B.b>1>a C.a>1>b D.1>a>b6.函数y=x2﹣2lnx的单调增区间为()A.(﹣∞,﹣1)∪(0,1)B.(1,+∞)C.(﹣1,0)∪(1,+∞)D.(0,1)7.已知函数f(x)的定义域为R,f(﹣1)=2,对任意x∈R,f′(x)>2,则f(x)>2x+4的解集为()A.(﹣1,1)B.(﹣1,+∞)C.(﹣∞,﹣1)D.(﹣∞,+∞)8.设f(x)=3x+3x﹣8,用二分法求方程3x+3x﹣8=0在x∈(1,2)内近似解的过程中得f(1)<0,f(1.5)>0,f(1.25)<0,则方程的根落在区间()A.(1,1.25)B.(1.25,1.5)C.(1.5,2) D.不能确定9.函数f(x)=,若f(a)=0,则a的所有可能值组成的集合为()A.{0}B.{0, } C.{0,﹣ }D.{﹣,﹣ } 10.已知定义在R上的函数f(x)满足:y=f(x﹣1)的图象关于(1,0)点对称,且当x≥0时恒有f(x﹣)=f(x+),当x∈[0,2)时,f(x)=e x﹣1,则f=()A.1﹣e B.﹣1﹣e C.e﹣1 D.e+111.设是奇函数,则()A.,且f(x)为增函数B.a=﹣1,且f(x)为增函数C.,且f(x)为减函数D.a=﹣1,且f(x)为减函数12.若存在两个正实数m、n,使得等式a(lnn﹣lnm)(4em﹣2n)=3m成立(其中e为自然对数的底数),则实数a的取值范围是()A.(﹣∞,0)B.(0,]C.[,+∞)D.(﹣∞,0)∪[,+∞)二、填空题:本大题共4小题,每小题5分,共20分).13.函数f(x)=x3﹣ax2+3x+4在(﹣∞,+∞)上是增函数,则实数a的取值范围是.14.曲线y=xlnx+1在点(1,1)处的切线方程是.15.函数f(x)=x3+sinx,(﹣1<x<1),若f(x2)+f(﹣x)>0,则实数x的取值范围是:.16.下列4个命题:①“若a、G、b成等比数列,则G2=ab”的逆命题;②“如果x2+x﹣6≥0,则x>2”的否命题;③在△ABC中,“若A>B”则“sinA>sinB”的逆否命题;④当0≤α≤π时,若8x2﹣(8sinα)x+cos2α≥0对∀x∈R恒成立,则α的取值范围是0≤α≤.其中真命题的序号是.三、解答题:本大题共6小题,共48分.解答写出文字说明、证明过程或演算过程.17.求函数f(x)=﹣x3+4x﹣1在[0,3]上的最大值和最小值.18.已知函数f(x)=x3﹣3x.(Ⅰ)求函数f(x)的极值;(Ⅱ)若关于x的方程f(x)=k有3个实根,求实数k的取值范围.19.已知p:﹣x2+4x+12≥0,q:x2﹣2x+1﹣m2≤0(m>0).(Ⅰ)若p是q充分不必要条件,求实数m的取值范围;(Ⅱ)若“¬p”是“¬q”的充分条件,求实数m的取值范围.20.已知函数f(x)=.(Ⅰ)求函数f(x)的定义域;(Ⅱ)判定f(x)的奇偶性并证明;(Ⅲ)用函数单调性定义证明:f(x)在(1,+∞)上是增函数.21.某土特产销售总公司为了解其经营状况,调查了其下属各分公司月销售额和利润,得到数据如下表:分公司名称雅雨雅雨雅女雅竹雅茶35679月销售额x(万元)23345月利润y(万元)在统计中发现月销售额x和月利润额y具有线性相关关系.(Ⅰ)根据如下的参考公式与参考数据,求月利润y与月销售额x之间的线性回归方程;(Ⅱ)若该总公司还有一个分公司“雅果”月销售额为10万元,试求估计它的月利润额是多少?(参考公式:=,=﹣,其中:=112,=200).22.已知函数f(x)=px﹣﹣2lnx.(Ⅰ)若p=2,求曲线f(x)在点(1,f(1))处的切线方程;(Ⅱ)若函数f(x)在其定义域内为增函数,求正实数p的取值范围;(Ⅲ)设函数g(x)=(e为自然对数底数),若在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立,求实数p的取值范围.参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的.1.若i是虚数单位,则复数=()A.﹣1 B.1 C.﹣i D.i【考点】A5:复数代数形式的乘除运算.【分析】直接由复数代数形式的乘除运算化简得答案.【解答】解:=,故选:D.2.设集合M={x|0<x≤3},N={x|0<x≤2},那么“a∈M”是“a∈N”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【考点】2L:必要条件、充分条件与充要条件的判断.【分析】由题意N⊆M,由子集的定义可选.【解答】解:设集合M={x|0<x≤3},N={x|0<x≤2},M⊇N,所以若“a∈M”推不出“a∈N”;若“a∈N”,则“a∈M”,所以“a∈M”是“a∈N”的必要而不充分条件,故B.3.已知命题P:∃x∈R,x2+2ax+a≤0.若命题P是假命题,则实数a的取值范围是()A.(0,1)B.(﹣∞,0)∪(1,+∞)C.[0,1]D.(﹣∞,0)∪[1,+∞)【考点】2K:命题的真假判断与应用.【分析】根据命题P是假命题得到命题¬P是真命题,然后建立条件即可求出a的取值范围.【解答】解:∵命题P是假命题,∴命题¬P是真命题,即∀x∈R,x2+2ax+a>0恒成立,即△=4a2﹣4a<0,解得0<a<1,故选:A.4.若函数f(x)=x3+ax2+3x﹣6在x=﹣3时取得极值,则a=()A.2 B.3 C.4 D.5【考点】6D:利用导数研究函数的极值.【分析】先对函数进行求导,根据函数f(x)在x=﹣3时取得极值,可以得到f′(﹣3)=0,代入求a值.【解答】解:对函数求导可得,f′(x)=3x2+2ax+3∵f(x)在x=﹣3时取得极值,∴f′(﹣3)=0⇒a=5故选:D.5.若log6a=log7b,则a、b、1的大小关系可能是()A.a>b>1 B.b>1>a C.a>1>b D.1>a>b【考点】4H:对数的运算性质.【分析】利用换底公式、对数函数的单调性即可得出.【解答】解:log6a=log7b,∴,∴1<a<b,或0<b<a<1.故选:D.6.函数y=x2﹣2lnx的单调增区间为()A.(﹣∞,﹣1)∪(0,1)B.(1,+∞)C.(﹣1,0)∪(1,+∞)D.(0,1)【考点】6B:利用导数研究函数的单调性.【分析】利用导数判断单调区间,导数大于0的区间为增区间,导数小于0的区间为减区间,所以只需求导数,再解导数大于0即可.【解答】解:函数y=x2﹣2lnx的定义域为(0,+∞),求函数y=x2﹣2lnx的导数,得,y′=2x﹣,令y'>0,解得x<﹣1(舍)或x>1,∴函数y=x2﹣2lnx的单调增区间为(1,+∞)故选:B.7.已知函数f(x)的定义域为R,f(﹣1)=2,对任意x∈R,f′(x)>2,则f(x)>2x+4的解集为()A.(﹣1,1)B.(﹣1,+∞)C.(﹣∞,﹣1)D.(﹣∞,+∞)【考点】6B:利用导数研究函数的单调性.【分析】构造函数g(x)=f(x)﹣2x﹣4,利用导数研究函数的单调性即可得到结论.【解答】解:设g(x)=f(x)﹣2x﹣4,则g′(x)=f′(x)﹣2,∵对任意x∈R,f′(x)>2,∴对任意x∈R,g′(x)>0,即函数g(x)单调递增,∵f(﹣1)=2,∴g(﹣1)=f(﹣1)+2﹣4=4﹣4=0,则∵函数g(x)单调递增,∴由g(x)>g(﹣1)=0得x>﹣1,即f(x)>2x+4的解集为(﹣1,+∞),故选:B8.设f(x)=3x+3x﹣8,用二分法求方程3x+3x﹣8=0在x∈(1,2)内近似解的过程中得f(1)<0,f(1.5)>0,f(1.25)<0,则方程的根落在区间()A.(1,1.25)B.(1.25,1.5)C.(1.5,2) D.不能确定【考点】56:二分法求方程的近似解.【分析】由已知“方程3x+3x﹣8=0在x∈(1,2)内近似解”,且具体的函数值的符号也已确定,由f(1.5)>0,f(1.25)<0,它们异号.【解答】解析:∵f(1.5)•f(1.25)<0,由零点存在定理,得,∴方程的根落在区间(1.25,1.5).故选B.9.函数f(x)=,若f(a)=0,则a的所有可能值组成的集合为()A.{0}B.{0, } C.{0,﹣ }D.{﹣,﹣ }【考点】3T:函数的值.【分析】当﹣1<a<0时,f(a)=cos(π•a2)=0,当a≥0时,f(a)=e a﹣1=0,由此能求出a的所有可能值组成的集合.【解答】解:∵f(x)=,f(a)=0,∴当﹣1<a<0时,f(a)=cos(π•a2)=0,由﹣1<a<0,解得a=﹣;当a≥0时,f(a)=e a﹣1=0,解得a=0.综上,a的所有可能值组成的集合为{0,﹣ }.故选:C.10.已知定义在R上的函数f(x)满足:y=f(x﹣1)的图象关于(1,0)点对称,且当x≥0时恒有f(x﹣)=f(x+),当x∈[0,2)时,f(x)=e x﹣1,则f=()A.1﹣e B.﹣1﹣e C.e﹣1 D.e+1【考点】3T:函数的值.【分析】根据图象的平移可知y=f(x)的图象关于(0,0)点对称,可得函数为奇函数,由题意可知当x≥0时,函数为周期为2的周期函数,可得f=f(1)﹣f(0),求解即可.【解答】解:∵y=f(x﹣1)的图象关于(1,0)点对称,∴y=f(x)的图象关于(0,0)点对称,∴函数为奇函数,∵当x≥0时恒有f(x+2)=f(x),∴函数为周期为2的周期函数,当x∈[0,2)时,f(x)=e x﹣1,∴f=f=f(1)﹣f(0)=(e﹣1)﹣0=e﹣1.故选:C.11.设是奇函数,则()A.,且f(x)为增函数B.a=﹣1,且f(x)为增函数C.,且f(x)为减函数D.a=﹣1,且f(x)为减函数【考点】3L:函数奇偶性的性质;3E:函数单调性的判断与证明.【分析】由于f(x)为R上的奇函数,故f(0)=0,从而可求得a,再结合其单调性即可得到答案.【解答】解:∵f(x)=a﹣是R上的奇函数,∴f(0)=a﹣=0,∴a=;又y=2x+1为R上的增函数,∴y=为R上的减函数,y=﹣为R上的增函数,∴f(x)=﹣为R上的增函数.故选A.12.若存在两个正实数m、n,使得等式a(lnn﹣lnm)(4em﹣2n)=3m成立(其中e为自然对数的底数),则实数a的取值范围是()A.(﹣∞,0)B.(0,]C.[,+∞)D.(﹣∞,0)∪[,+∞)【考点】3R:函数恒成立问题.【分析】根据函数与方程的关系将方程进行转化,利用换元法转化为方程有解,构造函数求函数的导数,利用函数极值和单调性的关系进行求解即可.【解答】解:由3m+a(2n﹣4em)(lnn﹣lnm)=0,得3m+2a(n﹣2em)ln=0,即3+2a(﹣2e)ln=0,即设t=,则t>0,则条件等价为3+2a(t﹣2e)lnt=0,即(t﹣2e)lnt=﹣有解,设g(t)=(t﹣2e)lnt,g′(t)=lnt+1﹣为增函数,∵g′(e)=lne+1﹣=1+1﹣2=0,∴当t>e时,g′(t)>0,当0<t<e时,g′(t)<0,即当t=e时,函数g(t)取得极小值为:g(e)=(e﹣2e)lne=﹣e,即g(t)≥g(e)=﹣e,若(t﹣2e)lnt=﹣有解,则﹣≥﹣e,即≤e,则a<0或a≥,故实数a的取值范围是(﹣∞,0)∪[,+∞).故选:D.二、填空题:本大题共4小题,每小题5分,共20分).13.函数f(x)=x3﹣ax2+3x+4在(﹣∞,+∞)上是增函数,则实数a的取值范围是[﹣,] .【考点】3F:函数单调性的性质.【分析】利用函数的单调性和导数的关系,求得实数a的取值范围.【解答】解:∵函数f(x)=x3﹣ax2+3x+4在(﹣∞,+∞)上是增函数,∴f′(x)=x2﹣2ax+3≥0恒成立,∴△=4a2﹣12≤0,求得﹣≤a≤,故答案为:[﹣,].14.曲线y=xlnx+1在点(1,1)处的切线方程是y=x.【考点】6H:利用导数研究曲线上某点切线方程.【分析】求出函数的导数,可得切线的斜率,由点斜式方程即可得到所求切线的方程.【解答】解:y=xlnx+1的导数为y′=lnx+1,曲线y=xlnx+1在点(1,1)处的切线斜率为k=1,可得曲线y=xlnx+1在点(1,1)处的切线方程为y﹣1=x﹣1,即为y=x.故答案为:y=x.15.函数f(x)=x3+sinx,(﹣1<x<1),若f(x2)+f(﹣x)>0,则实数x的取值范围是:(﹣1,0).【考点】3N:奇偶性与单调性的综合.【分析】根据题意,分析可得函数f(x)为奇函数且在(﹣1,1)上增函数,由此可以将f(x2)+f(﹣x)>0转化为,解可得x的取值范围,即可得答案.【解答】解:根据题意,函数f(x)=x3+sinx,f(﹣x)=(﹣x)3+sin (﹣x)=﹣(x3+sinx)=﹣f(x),故函数f(x)为奇函数,其导数f′(x)=3x2+cosx,又由﹣1<x<1,则有f′(x)=3x2+cosx≥0,故函数f(x)为增函数,f(x2)+f(﹣x)>0⇒f(x2)>﹣f(﹣x)⇒f(x2)>f(x)⇒,解可得:﹣1<x<0,即x的取值范围是(﹣1,0);故答案为:(﹣1,0)16.下列4个命题:①“若a、G、b成等比数列,则G2=ab”的逆命题;②“如果x2+x﹣6≥0,则x>2”的否命题;③在△ABC中,“若A>B”则“sinA>sinB”的逆否命题;④当0≤α≤π时,若8x2﹣(8sinα)x+cos2α≥0对∀x∈R恒成立,则α的取值范围是0≤α≤.其中真命题的序号是②③.【考点】2K:命题的真假判断与应用.【分析】由a=G=b=0,则a、G、b不成等比数列,即可判断①;写出命题的否命题,由二次不等式的解法,即可判断②;运用三角形的边角关系和正弦定理,即可判断③;由二次不等式恒成立可得判别式不大于0,解不等式,结合二倍角公式和余弦函数的图象,即可判断④.【解答】解:①“若a、G、b成等比数列,则G2=ab”的逆命题为“若G2=ab,则a、G、b成等比数列”,不正确,比如a=G=b=0,则a、G、b不成等比数列,故①错;②“如果x2+x﹣6≥0,则x>2”的否命题为“②“如果x2+x﹣6<0,则x ≤2”的否命题”,由x2+x﹣6<0,可得﹣3<x<2,推得x≤2,故②对;③在△ABC中,“若A>B”⇔“a>b”⇔“2RsinA>2RsinB”⇔“sinA>sinB”(R为外接圆的半径)则其逆否命题正确,故③对;④当0≤α≤π时,若8x2﹣(8sinα)x+cos2α≥0对∀x∈R恒成立,即有△=64sin2α﹣32cos2α≤0,即有1﹣2cos2α≤0,即为cos2α≥,可得0≤2α≤或≤2α≤2π,解得0≤α≤或≤α≤π,故④错.故答案为:②③.三、解答题:本大题共6小题,共48分.解答写出文字说明、证明过程或演算过程.17.求函数f(x)=﹣x3+4x﹣1在[0,3]上的最大值和最小值.【考点】6E:利用导数求闭区间上函数的最值.【分析】求出函数的导数,解关于导函数的方程,求出函数的单调区间,从而求出函数的最值即可.【解答】解:由f(x)=﹣x3+4x﹣4,得f′(x)=﹣x2+4,令f′(x)=0,则x=﹣2或x=2,当x变化时,f′(x)和f(x)变化如下表:x0(0,2)2(2,3)3f′(x)+0﹣f(x)﹣4增减﹣1故函数f(x)在[0,3]上有最大值,最大值为f(2)=,最小值为f(0)=﹣4.18.已知函数f(x)=x3﹣3x.(Ⅰ)求函数f(x)的极值;(Ⅱ)若关于x的方程f(x)=k有3个实根,求实数k的取值范围.【考点】6D:利用导数研究函数的极值;6B:利用导数研究函数的单调性.【分析】(Ⅰ)求出函数的导数,解关于导函数的方程,求出函数的单调区间,从而求出函数的极值即可;(Ⅱ)问题转化为y=f(x)和y=k有3个交点,根据f(x)的极大值和极小值求出k的范围即可.【解答】解:(I)∵f(x)=x3﹣3x,∴f′(x)=3(x﹣1)(x+1),令f′(x)=0,解得x=﹣1或x=1,列表如下:x(﹣∞,﹣1)﹣1(﹣1,1)1(1,+∞)f′(x)+0﹣0+f(x)增极大值减极小值增当x=﹣1时,有极大值f(﹣1)=2;当x=1时,有极小值f(1)=﹣2.(II)要f(x)=k有3个实根,由(I)知:f(1)<k<f(﹣1),即﹣2<k<2,∴k的取值范围是(﹣2,2).19.已知p:﹣x2+4x+12≥0,q:x2﹣2x+1﹣m2≤0(m>0).(Ⅰ)若p是q充分不必要条件,求实数m的取值范围;(Ⅱ)若“¬p”是“¬q”的充分条件,求实数m的取值范围.【考点】2L:必要条件、充分条件与充要条件的判断.【分析】(Ⅰ)求出p,q的等价条件,结合充分不必要条件的定义建立集合关系进行求解即可.(Ⅱ)根据逆否命题的等价性进行转化,结合充分条件和必要条件的定义进行转化解不等式组即可.【解答】解:由题知:p为真时,由﹣x2+4x+12≥0得﹣2≤x≤6,q为真时,由x2﹣2x+1﹣m2≤0(m>0).得1﹣m≤x≤1+m,令P=[﹣2,6],Q=[1﹣m,1+m],m>0…(Ⅰ)∵p是q的充分不必要条件,∴P⊊Q,∴,等号不能同时取,得,解得m≥5,故p是q充分不必要条件时,m取值范围是[5,+∞)…(Ⅱ)∵“¬p”是“¬q”的充分条件,∴“p”是“q”的必要条件,∴Q⊆P,∴,解得0<m≤3,∴m的取值范围是(0,3]…20.已知函数f(x)=.(Ⅰ)求函数f(x)的定义域;(Ⅱ)判定f(x)的奇偶性并证明;(Ⅲ)用函数单调性定义证明:f(x)在(1,+∞)上是增函数.【考点】3K:函数奇偶性的判断;3E:函数单调性的判断与证明.【分析】(Ⅰ)根据函数成立的条件进行求解即可.(Ⅱ)根据函数奇偶性的定义进行证明.(Ⅲ)根据函数单调性的定义进行证明.【解答】解:(Ⅰ)由1﹣x2≠0,得x≠±1,即f(x)的定义域{x|x ≠±1}…;(Ⅱ)f(x)为偶函数.∵f(x)定义域关于原点对称,且f(﹣x)=f(x)∴f(x)为偶函数;…(III)证明:f(x)===﹣1,设1<x1<x2,则f(x1)﹣f(x2)=﹣=2(),∵1<x1<x2,∴x1﹣x2<0,1﹣x2<0,1﹣x1<0,则f(x1)﹣f(x2)<0,即f(x1)<f(x2),则函数f(x)在(1,+∞)上是增函数.21.某土特产销售总公司为了解其经营状况,调查了其下属各分公司月销售额和利润,得到数据如下表:分公司名称雅雨雅雨雅女雅竹雅茶35679月销售额x(万元)23345月利润y(万元)在统计中发现月销售额x和月利润额y具有线性相关关系.(Ⅰ)根据如下的参考公式与参考数据,求月利润y与月销售额x之间的线性回归方程;(Ⅱ)若该总公司还有一个分公司“雅果”月销售额为10万元,试求估计它的月利润额是多少?(参考公式:=,=﹣,其中:=112,=200).【考点】BK:线性回归方程.【分析】(Ⅰ)根据已知数据计算、,求出回归系数、,写出回归方程;(Ⅱ)把x=10代入线性回归方程中计算的值即可.【解答】解:(Ⅰ)根据已知数据,计算=×(3+5+6+7+9)=6,=×(2+3+3+4+5)=3.4,回归系数为===0.5,=﹣=3.4﹣0.5×6=0.4,∴y与x的线性回归方程为=0.5x+0.4;(Ⅱ)把x=10代入线性回归方程中,计算=0.5x+0.4=0.5×10+0.4=5.4,∴估计它的月利润额是5.4万元.22.已知函数f(x)=px﹣﹣2lnx.(Ⅰ)若p=2,求曲线f(x)在点(1,f(1))处的切线方程;(Ⅱ)若函数f(x)在其定义域内为增函数,求正实数p的取值范围;(Ⅲ)设函数g(x)=(e为自然对数底数),若在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立,求实数p的取值范围.【考点】6E:利用导数求闭区间上函数的最值;6H:利用导数研究曲线上某点切线方程.【分析】(I)求出函数在x=1处的值,求出导函数,求出导函数在x=1处的值即切线的斜率,利用点斜式求出切线的方程.(II)求出函数的导函数,令导函数大于等于0恒成立,构造函数,求出二次函数的对称轴,求出二次函数的最小值,令最小值大于等于0,求出p的范围.(III)通过g(x)的单调性,求出g(x)的最小值,通过对p的讨论,求出f(x)的最大值,令最大值大于等于g(x)的最小值求出p的范围.【解答】解:(I)当p=2时,函数f(x)=2x﹣﹣2lnx,f(1)=2﹣2﹣2ln1=0,f′(x)=2+﹣,曲线f(x)在点(1,f(1))处的切线的斜率为f'(1)=2+2﹣2=2.从而曲线f(x)在点(1,f(1))处的切线方程为y﹣0=2(x﹣1)即y=2x﹣2.(II)f′(x)=p+﹣=,令h(x)=px2﹣2x+p,要使f(x)在定义域(0,+∞)内是增函数,只需h(x)≥0在(0,+∞)内恒成立,由题意p>0,h(x)=px2﹣2x+p的图象为开口向上的抛物线,对称轴方程为x=∈(0,+∞),∴h(x)min=p﹣,只需p﹣≥0,即p≥1时,h(x)≥0,f'(x)≥0∴f(x)在(0,+∞)内为增函数,正实数p的取值范围是[1,+∞).(III)∵g(x)=在[1,e]上是减函数,∴x=e时,g(x)min=2;x=1时,g(x)max=2e,即g(x)∈[2,2e],当p<0时,h(x)=px2﹣2x+p,其图象为开口向下的抛物线,对称轴x=在y轴的左侧,且h(0)<0,所以f(x)在x∈[1,e]内是减函数.当p=0时,h(x)=﹣2x,因为x∈[1,e],所以h(x)<0,f′(x)=﹣<0,此时,f(x)在x∈[1,e]内是减函数.∴当p≤0时,f(x)在[1,e]上单调递减⇒f(x)max=f(1)=0<2,不合题意;当0<p<1时,由x∈[1,e]⇒x﹣≥0,所以f(x)=p(x﹣)﹣2lnx≤x﹣﹣2lnx.又由(2)知当p=1时,f(x)在[1,e]上是增函数,∴x﹣﹣2lnx≤e﹣﹣2lne=e﹣﹣2<2,不合题意;当p≥1时,由(2)知f(x)在[1,e]上是增函数,f(1)=0<2,又g(x)在[1,e]上是减函数,故只需f(x)max>g(x)min,x∈[1,e],而f(x)max=f(e)=p(e﹣)﹣2lne,g(x)min=2,即p(e﹣)﹣2lne>2,解得p>,综上所述,实数p的取值范围是(,+∞).。
人教A版数学选修4第二学期高二文科数学第四次周练试题.docx

第二学期高二文科数学第四次周练试题一、选择题1.若不等式4104822<<>---x a x x 在内有解,则实数a 的取值范围是( )A 4-<aB 4->aC .12->aD .12-<a2.若不等式m x x ≥-42对任意]1,0[∈x 恒成立,则m 的取值范围是( )A .3-≤mB .3-≥mC .03≤≤-mD .03≥-≤m m 或 3.当x >1时,不等式x +11-x ≥a 恒成立,则实数a 的取值范围是 ( )A(-∞,2] B[2,+∞) C[3,+∞) D(-∞,3]4.设a >0,b >0.若3是3a 与3b 的等比中项,则1a +1b的最小值为( )A .8B .4C .1 D.145.若x >0,y >0,则221+)(y x +221+)(xy 的最小值是( ). A .3B .27C .4D .296.设x 、y 均为正实数,且32+x +32+y=1,则xy 的最小值为( ) A .4 B .4 3 C .9 D .167.已知x >0,y >0,x +2y +2xy =8,则x +2y 的最小值是( )A .3B .4 C.92D.112二、填空题:8、当0>x 时,()122+=x xx f 的值域是 。
9.已知0<x <34,则函数y =5x (3-4x )的最大值为________.10.若正数a ,b 满足ab =a +b +3,则ab 的取值范围是 . 11.设a ,b 均为正的常数且x >0,y >0,xa+y b =1,则x +y 的最小值为 .12.若点A (-2,-1)在直线mx +ny +1=0上,其中mn >0,则m 1+n2的最小值为 . 13.已知关于x 的不等式2x +2x -a≥7在x ∈(a ,+∞)上恒成立,则实数a 的最小值为______. 14.求函数12++=x x xy (x >0)的值域为 . 15.当x =________时,28(1)1x y x x +=>-有最小值为 .河北省张家口市康保县第一中学2016—2017学年第二学期高二文科数学第四次周练答题纸一、选择题 二、填空题 8______________9___________10____________11_____________12_____________13__________14____________15________、______ 三、解答题16.求函数y =1+10+7+2x x x (x >-1)的最小值.17.若,x y 是正数,且1222=+y x ,求21y x +的最大值 班级_______姓名___________考号____________成绩___________ 18.已知不等式(x +y )(1x +ay)≥9对任意的正实数x 、y 恒成立,求正数a 的最小值.19、正数a ,b ,c 满足a+b+c=1,求证:(1-a)(1-b)(1-c)≥8abc 。
高二文科数学每日一练4

高二文科数学每日一练
1. 函数()ln f x x x =的单调递减区间是 A. 1(0,)e B. 1(,)e +∞ C. (0,)e D. (,)e +∞
2.下面几种推理是类比推理的是
(A )两条直线平行,同旁内角互补,如果∠A 和∠B 是两条平行直线的同旁内角,则∠A +∠B =1800
(B )由平面三角形的性质,推测空间四边形的性质
(C )某校高二级有20个班,1班有51位团员,2班有53位团员,3班有52位团员,由此可以推测各班都超过50位团员.
(D )一切偶数都能被2整除,1002是偶数,所以1002能被2整除.
3. 函数3y x bx c =++在1x =与1x =-处取得极值,则b =.
4.(几何证明选做题)如图,P A 切⊙O 于点A ,割线PBC
经过圆心O ,PB =3, P A OA 绕点O 逆时针旋转60︒
到OD ,则PD 的长为.
5.阅读下文,然后画出该章的知识结构图.
推理与证明这一章介绍了推理与证明这两个知识点. 推理这节包括合情推理和演绎推理;证明这节包括直接证明和间接证明
合情推理中有两种常用推理:归纳推理和类比推理;
直接证明有综合法和分析法;间接证明通常用反证法.。
人教A版数学必修四高二国庆中秋双节假期每日一测文科数学试卷四.doc
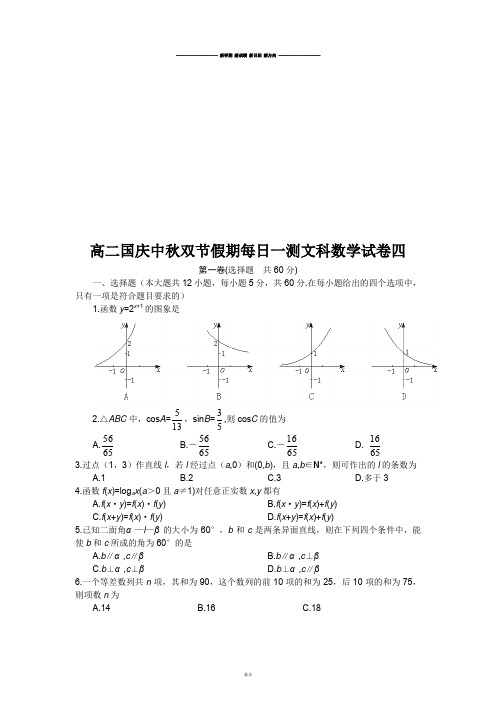
高二国庆中秋双节假期每日一测文科数学试卷四第一卷(选择题 共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.函数y =2x +1的图象是2.△ABC 中,cos A =135,sin B =53,则cos C 的值为 A.6556B.-6556C.-6516D.65163.过点(1,3)作直线l ,若l 经过点(a ,0)和(0,b ),且a ,b ∈N *,则可作出的l 的条数为A.1B.2C.3D.多于3 4.函数f (x )=log a x (a >0且a ≠1)对任意正实数x ,y 都有A.f (x ·y )=f (x )·f (y )B.f (x ·y )=f (x )+f (y )C.f (x +y )=f (x )·f (y )D.f (x +y )=f (x )+f (y )5.已知二面角α—l —β的大小为60°,b 和c 是两条异面直线,则在下列四个条件中,能使b 和c 所成的角为60°的是A.b ∥α,c ∥βB.b ∥α,c ⊥βC.b ⊥α,c ⊥βD.b ⊥α,c ∥β6.一个等差数列共n 项,其和为90,这个数列的前10项的和为25,后10项的和为75,则项数n 为A.14B.16C.18D.207.某城市的街道如图,某人要从A 地前往B 地,则路程最短的走法有A.8种B.10种C.12种D.32种 8.若a ,b 是异面直线,a ⊂α,b ⊂β,α∩β=l ,则下列命题中是真命题的为A.l 与a 、b 分别相交B.l 与a 、b 都不相交C.l 至多与a 、b 中的一条相交D.l 至少与a 、b 中的一条相交9.设F 1,F 2是双曲线42x -y 2=1的两个焦点,点P 在双曲线上,且1PF ·2PF =0,则|1PF |·|2PF |的值等于 A.2B.22C.4D.810.f (x )=(1+2x )m +(1+3x )n (m ,n ∈N *)的展开式中x 的系数为13,则x 2的系数为A.31B.40C.31或40D.71或8011.从装有4粒大小、形状相同,颜色不同的玻璃球的瓶中,随意一次倒出若干粒玻璃球(至少一粒),则倒出奇数粒玻璃球的概率比倒出偶数粒玻璃球的概率A.小B.大C.相等D.大小不能确定 12.如右图,A 、B 、C 、D 是某煤矿的四个采煤点,l 是公路,图中所标线段为道路,ABQP 、BCRQ 、CDSR 近似于正方形.已知A 、B 、C 、D 四个采煤点每天的采煤量之比约为5∶1∶2∶3,运煤的费用与运煤的路程、所运煤的重量都成正比.现要从P 、Q 、R 、S 中选出一处设立一个运煤中转站,使四个采煤点的煤运到中转站的费用最少,则地点应选在A.P 点B.Q 点C.R 点D.S 点第二卷(非选择题 共90分)二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中横线上) 13.抛物线y 2=2x 上到直线x -y +3=0距离最短的点的坐标为_________.14.一个长方体共一顶点的三个面的面积分别是2,3,6,这个长方体对角线的长是_________.15.设定义在R 上的偶函数f (x )满足f (x +1)+f (x )=1,且当x ∈[1,2]时,f (x )=2-x ,则f (8.5)=_________.16.某校要从甲、乙两名优秀短跑选手中选一名选手参加全市中学生田径百米比赛,该校预先对这两名选手测试了8次,测试成绩如下:第1次 第2次 第3次 第4次 第5次 第6次 第7次 第8次 甲成绩(秒) 12.1 12.2 13 12.5 13.1 12.5 12.4 12.2 乙成绩(秒)1212.412.81312.212.812.312.5根据测试成绩,派_________(填甲或乙)选手参赛更好,理由是____________________.三、解答题(本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分12分)甲、乙、丙三位同学独立完成6道数学自测题,他们答及格的概率依次为54,53,107. 求(1)三人中有且只有2人答及格的概率; (2)三人中至少有一人不及格的概率.18.(本小题满分12分)如图,函数f (x )的图象为单位圆上的两段弧,求不等式f (x )-f (-x )>x 的解集.19.(本小题满分12分)已知PA ⊥平面ABCD ,ABCD 为矩形,M ,N 分别是AB ,PC 的中点. (1)求证MN ⊥AB ;(2)若平面PDC 与平面ABCD 所成的二面角为θ,能否确定θ,使直线MN 是异面直线AB 与PC 的公垂线,若可以确定,试求θ的值,若不可以,请说明理由.20.(本小题满分12分)已知向量a =(-2,sin θ),b =(cos θ,1),其中θ∈(-2π,2π). (1)若a ⊥b ,求θ的值;(2)令c =a -b ,求|c |的最大值.21.(本小题满分12分) 已知曲线C :⎩⎨⎧==θθsin cos 2y x (θ为参数),若A 、B 是曲线C 上关于坐标轴不对称的任意两点.(1)求AB 的垂直平分线l 在x 轴上截距的取值范围;(2)设过点M (1,0)的直线l 是曲线C 上A ,B 两点连线的垂直平分线,求l 的斜率k 的取值范围.22.(本小题满分14分)已知函数y =ax 2+bx +c (a ≠0)图象上有两点A 1(m 1,y 1),A 2(m 2,y 2),满足a 2+(y 1+y 2)a +y 1·y 2=0,求证:(1)存在i ∈{1,2},使y i =-a ;(2)抛物线y =ax 2+bx +c 与x 轴总有两个不同的交点;(3)若使该图象与x 轴交点为(x 1,0)(x 2,0),(x 1<x 2),则存在i ∈{1,2},使x 1<m i <x 2.答案一、1.A 2.D 3.B 4.B 5.C 6.C 7.B 8.D 9.A 10.C 11.B 12.B二、13.(21,1) 14.6 15. 21 16.因为x 甲=x 乙=12.5,S 甲2=0.12,S 乙2=0.10,所以乙选手成绩比甲选手成绩稳定,派乙选手参赛更好.三、17.设甲、乙、丙答题及格分别为事件A ,B ,C ,则事件A ,B ,C 相互独立. (1)三人中有且只有2人答及格的概率为:P 1=P (AB C )+P (A B C )+P (A BC )=P (A )P (B )P (C )+P (A )P (B )P (C )+P (A )·P (B )P (C )=54×53×(1-107)+54×(1-53)×107+(1-54)×53×107=250113.6分(2)三人中至少有1人不及格的概率为P 2=1-P (ABC )=1-P (A )P (B )P (C )=1-54×53×107=12583. 12分18.f (x )=21||x x x- =⎪⎩⎪⎨⎧<≤--≤<-0)(-1 ,11)(0,122x x x x(1)当0<x ≤1时,f (x )=21x -,f (-x )=221)(1x x --=---.由f (x )-f (-x )>x .则221x ->x >0.4-4x 2>x 2,x 2<54.∵0<x ≤1.∴0<x <552 6分(2)当-1≤x <0时,f (x )=-21x -,f (-x )= 221)(1x x -=--,f (x )-f (-x )>x ,-221x ->x ,221x -<-x ,4-4x 2<x 2,x 2>54. ∵-1≤x <0,∴-1≤x <-552. 由(1)(2)知原不等式的解集为{x |-1≤x <-552,或0<x <552}. 12分19.(1)连结AC 取AC 中点E .连结EM ,EN .∵M ,N ,E 分别为AB ,PC ,AC 的中点,∴ME ∥BC .ME ⊥AB ,NE ∥PA ,NE ⊥面ABCD . ∴MN ⊥AB . 6分 (2)若MN ⊥P C.∵MN ⊥CD∴有MN ⊥面PCD .延长ME 交CO 于F . ∵ME ∥BC .∴F 为CD 中点,连结NF .则NF ⊥CD ,∴∠NFM 为面PDC 与面ABCD 所在二面角的平面角. 8分 ∠NFM =θ,又∵MN ⊥面PCD ,∴MN ⊥NF ,∴△MNF 为Rt △,且E 为MF 的中点,NE ⊥MF ,∴MN =NF ,∠MFN =45°. 12分20.(1)因为a =(-2,sin θ),b =(cos θ,1),a ⊥b , 所以(-2,sin θ)·(cos θ,1)=0. 2分 即-2cos θ+sin θ=0. 所以tan θ=2. 4分又因为θ∈(-2π,2π),所以θ=arctan2. 6分(2)因为c =a -b =(-2-cos θ,sin θ-1), 所以|c |=22)1(sin )cos 2(-+--θθ =θθcos 4sin 26+- =)2arctan sin(526--θ,8分因为θ∈(-2π, 2π), 所以θ-arctan2∈(-2π-arctan2, 2π-arctan2).10分所以当θ=-2π+arctan2时,|c |的最大值为5+1. 12分21.(1)曲线C :42x +y 2=1,设A (x 1,y 1),B (x 2,y 2),AB 的中点M (x 0,y 0),421x +y 12=1①422x +y 22=1②由①-②可得42221x x -+y 12-y 22=0.k AB =000212121214242)(4y x y x y y x x x x y y -=⋅-=++-=--.2分l 的方程y -y 0=004x y (x -x 0),令y =0,x =43x 0.4分∵-2<x 0<2,∴x ∈(-23,23). 6分(2)设直线l 的方程为y =k (x -1),AB 的中点M (x 0,y 0).由(1)可知k AB =-4y x ,∴k =4x y . ∵M 在直线l 上,∴y 0=4x y (x 0-1). ∵y 0≠0.∴x 0=34.8分∵M (x 0,y 0)在椭圆内部.∴420x+y 02<1即4916+y 02<1.10分-35<y 0<35且y 0≠0. k =04x y =3440y =3y 0.∴-5<k <5且k ≠0.12分22.(1)由a 2+(y 1+y 2)a +y 1y 2=0有 (y 1+a )(y 2+a )=0. 2分 ∴y 1=-a 或y 2=-a ,即存在i ∈{1,2},使得y i =-a . 4分(2)由(1)知存在i ∈{1,2},使得y i =-a ,则有-a =ax 2+bx +c ,即ax 2+bx +a +c =0,由Δ=b 2-4a (a +c )≥0.∴b 2-4ac ≥4a 2>0.∴b 2-4ac >0.∴抛物线y =ax 2+bx +c 与x 轴总有两个不同的交点. 8分(3)方程ax 2+bx +c =0有两个实数根x 1、x 2,x 1+x 2=-a b ,x 1x 2=ac . 10分∴(m i -x 1)(m i -x 2)=m i 2-(x 1+x 2)m i +x 1x 2=m i 2+a b m i +a c =a 1(am i 2+bm i +c )= a1y i ,由(1)可知a1y i =-1<0,∴x 1<m i <x 2.14分.。
