中考数学“动态型”问题专题
中考数学专题复习——动态变化问题(经典题型)

中考数学专题复习——动态变化问题(经典题型)【专题点拨】动态型问题一般是指以几何知识和图形为背景,渗透运动变化观点的一类试题,常见的运动对象有点动、线动和面动;其运动形式而言就是平移、旋转、翻折和滚动等。
动态型试题其特点是集几何、代数知识于一体,数形结合,有较强的综合性,题目灵活,多变,动中有静,动静结合,能够在运动变化中发展同学们的空间想象能力。
解答动态型试题的策略是:(1)动中求静,即在运动变化中探索问题中的不变性;(2)动静互化,抓住静的瞬间。
找到导致图形或者变化规律发生改变的特殊时刻,同时在运动变化的过程中寻找不变性及其变化规律。
【典例赏析】【例题1】(2017黑龙江佳木斯)如图,在边长为4的正方形ABCD中,E、F是AD边上的两个动点,且AE=FD,连接BE、CF、BD,CF与BD交于点G,连接AG 交BE于点H,连接DH,下列结论正确的个数是()①△ABG∽△FDG ②HD平分∠EHG ③AG⊥BE ④S△HDG :S△HBG=tan∠DAG ⑤线段DH的最小值是2﹣2.A.2 B.3 C.4 D.5【考点】S9:相似三角形的判定与性质;KD:全等三角形的判定与性质;LE:正方形的性质;T7:解直角三角形.【分析】首先证明△ABE≌△DCF,△ADG≌△CDG(SAS),△AGB≌△CGB,利用全等三角形的性质,等高模型、三边关系一一判断即可.【解答】解:∵四边形ABCD是正方形,∴AB=CD,∠BAD=∠ADC=90°,∠ADB=∠CDB=45°,在△ABE和△DCF中,,∴△ABE≌△DCF(SAS),∴∠ABE=∠DCF,在△ADG和△CDG中,,∴△ADG≌△CDG(SAS),∴∠DAG=∠DCF,∴∠ABE=∠DAG,∵∠DAG+∠BAH=90°,∴∠BAE+∠BAH=90°,∴∠AHB=90°,∴AG⊥BE,故③正确,同法可证:△AGB≌△CGB,∵DF∥CB,∴△CBG∽△FDG,∴△ABG∽△FDG,故①正确,∵S△HDG :S△HBG=DG:BG=DF:BC=DF:CD=tan∠FCD,又∵∠DAG=∠FCD,∴S△HDG :S△HBG=tan∠FCD,tan∠DAG,故④正确取AB的中点O,连接OD、OH,∵正方形的边长为4,∴AO=OH=×4=2,由勾股定理得,OD==2,由三角形的三边关系得,O、D、H三点共线时,DH最小,DH最小=2﹣2.无法证明DH平分∠EHG,故②错误,故①③④⑤正确,故选C.【例题2】(2017黑龙江佳木斯)已知:△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°.连接AD,BC,点H为BC中点,连接OH.(1)如图1所示,易证:OH=AD且OH⊥AD(不需证明)(2)将△COD绕点O旋转到图2,图3所示位置时,线段OH与AD又有怎样的关系,并选择一个图形证明你的结论.【考点】R2:旋转的性质;KD:全等三角形的判定与性质;KW:等腰直角三角形.【分析】(1)只要证明△AOD≌△BOC,即可解决问题;(2)①如图2中,结论:OH=AD,OH⊥AD.延长OH到E,使得HE=OH,连接BE,由△BEO≌△ODA即可解决问题;②如图3中,结论不变.延长OH到E,使得HE=OH,连接BE,延长EO交AD于G.由△BEO≌△ODA即可解决问题;【解答】(1)证明:如图1中,∵△OAB与△OCD为等腰直角三角形,∠AOB=∠COD=90°,∴OC=OD,OA=OB,∵在△AOD与△BOC中,,∴△AOD≌△BOC(SAS),∴∠ADO=∠BCO,∠OAD=∠OBC,∵点H为线段BC的中点,∴OH=HB,∴∠OBH=∠HOB=∠OAD,又因为∠OAD+∠ADO=90°,所以∠ADO+∠BOH=90°,所以OH⊥AD(2)解:①结论:OH=AD,OH⊥AD,如图2中,延长OH到E,使得HE=OH,连接BE,易证△BEO≌△ODA∴OE=AD∴OH=OE=AD由△BEO≌△ODA,知∠EOB=∠DAO∴∠DAO+∠AOH=∠EOB+∠AOH=90°,∴OH⊥AD.②如图3中,结论不变.延长OH到E,使得HE=OH,连接BE,延长EO交AD于G.易证△BEO≌△ODA∴OE=AD∴OH=OE=AD由△BEO≌△ODA,知∠EOB=∠DAO∴∠DAO+∠AOF=∠EOB+∠AOG=90°,∴∠AGO=90°∴OH⊥AD.【例题3】(2017湖北江汉)如图,在平面直角坐标系中,四边形ABCD的边AD 在x轴上,点C在y轴的负半轴上,直线BC∥AD,且BC=3,OD=2,将经过A、B 两点的直线l:y=﹣2x﹣10向右平移,平移后的直线与x轴交于点E,与直线BC 交于点F,设AE的长为t(t≥0).(1)四边形ABCD的面积为20 ;(2)设四边形ABCD被直线l扫过的面积(阴影部分)为S,请直接写出S关于t的函数解析式;(3)当t=2时,直线EF上有一动点,作PM⊥直线BC于点M,交x轴于点N,将△PMF沿直线EF折叠得到△PTF,探究:是否存在点P,使点T恰好落在坐标轴上?若存在,请求出点P的坐标;若不存在,请说明理由.【考点】FI:一次函数综合题.【分析】(1)根据函数解析式得到OA=5,求得AC=7,得到OC=4,于是得到结论;(2)①当0≤t≤3时,根据已知条件得到四边形ABFE是平行四边形,于是得到S=AE•OC=4t;②当3≤t<7时,如图1,求得直线CD的解析式为:y=2x﹣4,直线E′F′的解析式为:y=﹣2x+2t﹣10,解方程组得到G(,t﹣7),于是得到S=S四边形ABCD ﹣S△DE′G=20﹣×(7﹣t)×(7﹣t)=﹣t2+7t﹣,③当t≥7时,S=S四边形ABCD=20,(3)当t=2时,点E,F的坐标分别为(﹣3,0),(﹣1,﹣4),此时直线EF 的解析式为:y=﹣2x﹣6,设动点P的直线为(m,﹣2m﹣6),求得PM=|(﹣2m ﹣6)﹣(﹣4)|=2|m+1|,PN=(﹣2m﹣6|=2(m+3|,FM=|m﹣(﹣1)|=|m+1,①假设直线EF上存在点P,使点T恰好落在x轴上,如图2,连接PT,FT,②假设直线EF上存在点P,使点T恰好落在y轴上,如图3,连接PT,FT,根据全等三角形的判定性质和相似三角形的判定和性质即可得到结论.【解答】解:(1)在y=﹣2x﹣10中,当y=0时,x=﹣5,∴A(﹣5,0),∴OA=5,∴AC=7,把x=﹣3代入y=﹣2x﹣10得,y=﹣4∴OC=4,∴四边形ABCD的面积=(3+7)×4=20;故答案为:20;(2)①当0≤t≤3时,∵BC∥AD,AB∥EF,∴四边形ABFE是平行四边形,∴S=AE•OC=4t;②当3≤t<7时,如图1,∵C(0,﹣4),D(2,0),∴直线CD的解析式为:y=2x﹣4,∵E′F′∥AB,BF′∥AE′∴BF′=AE=t,∴F′(t﹣3,﹣4),直线E′F′的解析式为:y=﹣2x+2t﹣10,解得,∴G(,t﹣7),∴S=S四边形ABCD ﹣S△DE′G=20﹣×(7﹣t)×(7﹣t)=﹣t2+7t﹣,③当t≥7时,S=S四边形ABCD=20,综上所述:S关于t的函数解析式为:S=;(3)当t=2时,点E,F的坐标分别为(﹣3,0),(﹣1,﹣4),此时直线EF的解析式为:y=﹣2x﹣6,设动点P的直线为(m,﹣2m﹣6),∵PM⊥直线BC于M,交x轴于n,∴M(m,﹣4),N(m,0),∴PM=|(﹣2m﹣6)﹣(﹣4)|=2|m+1|,PN=(﹣2m﹣6|=2(m+3|,FM=|m﹣(﹣1)|=|m+1,①假设直线EF上存在点P,使点T恰好落在x轴上,如图2,连接PT,FT,则△PFM≌△PFT,∴PT=PM=2|m+1|,FT=FM=|m+1|,∴=2,作FK⊥x轴于K,则KF=4,由△TKF∽△PNT得, =2,∴NT=2KF=8,∵PN2+NT2=PT2,∴4(m+3)2+82=4(m+1)2,解得:m=﹣6,∴﹣2m﹣6=﹣6,此时,P(﹣6,6);②假设直线EF上存在点P,使点T恰好落在y轴上,如图3,连接PT,FT,则△PFM≌△PFT,∴PT=PM=2|m+1|,FT=FM=|m+1|,∴=2,作PH⊥y轴于H,则PH=|m|,由△TFC∽△PTH得,,∴HT=2CF=2,∵HT2+PH2=PT2,即22+m2=4(m+1)2,解得:m=﹣,m=0(不合题意,舍去),∴m=﹣时,﹣2m﹣6=﹣,∴P(﹣,﹣),综上所述:直线EF上存在点P(﹣6,6)或P(﹣,﹣)使点T恰好落在y轴上.【能力检测】1.(2017乌鲁木齐)如图,在矩形ABCD中,点F在AD上,点E在BC上,把这个矩形沿EF折叠后,使点D恰好落在BC边上的G点处,若矩形面积为4且∠AF G=60°,GE=2BG,则折痕EF的长为()A.1 B.C.2 D.【考点】PB:翻折变换(折叠问题);LB:矩形的性质.【分析】由折叠的性质可知,DF=GF、HE=CE、GH=DC、∠DFE=∠GFE,结合∠AFG=60°即可得出∠GFE=60°,进而可得出△GEF为等边三角形,在Rt△GHE中,通过解含30度角的直角三角形及勾股定理即可得出GE=2EC、DC=EC,再由GE=2BG 结合矩形面积为4,即可求出EC的长度,根据EF=GE=2EC即可求出结论.【解答】解:由折叠的性质可知,DF=GF,HE=CE,GH=DC,∠DFE=∠GFE.∵∠GFE+∠DFE=180°﹣∠AFG=120°,∴∠GFE=60°.∵AF∥GE,∠AFG=60°,∴∠FGE=∠AFG=60°,∴△GEF为等边三角形,∴EF=GE.∵∠FGE=60°,∠FGE+∠HGE=90°,∴∠HGE=30°.在Rt△GHE中,∠HGE=30°,∴GE=2HE=CE,∴GH==HE=CE.∵GE=2BG,∴BC=BG+GE+EC=4EC.∵矩形ABCD的面积为4,∴4EC•EC=4,∴EC=1,EF=GE=2.故选C.2.(2017乌鲁木齐)如图,点A(a,3),B(b,1)都在双曲线y=上,点C,D,分别是x轴,y轴上的动点,则四边形ABCD周长的最小值为()A.B.C.D.【考点】G6:反比例函数图象上点的坐标特征;PA:轴对称﹣最短路线问题.【分析】先把A点和B点的坐标代入反比例函数解析式中,求出a与b的值,确定出A与B坐标,再作A点关于y轴的对称点P,B点关于x轴的对称点Q,根据对称的性质得到P点坐标为(﹣1,3),Q点坐标为(3,﹣1),PQ分别交x 轴、y轴于C点、D点,根据两点之间线段最短得此时四边形PABQ的周长最小,然后利用两点间的距离公式求解可得.【解答】解:分别把点A(a,3)、B(b,1)代入双曲线y=得:a=1,b=3,则点A的坐标为(1,3)、B点坐标为(3,1),作A点关于y轴的对称点P,B点关于x轴的对称点Q,所以点P坐标为(﹣1,3),Q点坐标为(3,﹣1),连结PQ分别交x轴、y轴于C点、D点,此时四边形ABCD的周长最小,四边形ABCD周长=DA+DC+CB+AB=DP+DC+CQ+AB=PQ+AB=+=4+2=6,故选:B.3.(2017黑龙江鹤岗)如图,边长为4的正方形ABCD,点P是对角线BD上一动点,点E在边CD上,EC=1,则PC+PE的最小值是 5 .【考点】PA:轴对称﹣最短路线问题;LE:正方形的性质.【分析】连接AC、AE,由正方形的性质可知A、C关于直线BD对称,则AE的长即为PC+PE的最小值,再根据勾股定理求出AE的长即可.【解答】解:连接AC、AE,∵四边形ABCD是正方形,∴A、C关于直线BD对称,∴AE的长即为PC+PE的最小值,∵CD=4,CE=1,∴DE=3,在Rt△ADE中,∵AE===5,∴PC+PE的最小值为5.故答案为:5.4.(2017黑龙江鹤岗)在四边形ABCD中,对角线AC、BD交于点O.若四边形ABCD是正方形如图1:则有AC=BD,AC⊥BD.旋转图1中的Rt△COD到图2所示的位置,AC′与BD′有什么关系?(直接写出)若四边形ABCD是菱形,∠ABC=60°,旋转Rt△COD至图3所示的位置,AC′与BD′又有什么关系?写出结论并证明.【考点】LE:正方形的性质;KD:全等三角形的判定与性质;L8:菱形的性质;R2:旋转的性质.【分析】图2:根据四边形ABCD是正方形,得到AO=OC,BO=OD,AC⊥BD,根据旋转的性质得到OD′=OD,OC′=OC,∠D′OD=∠C′OC,等量代换得到AO=BO,OC′=OD′,∠AOC′=∠BOD′,根据全等三角形的性质得到AC′=BD′,∠OAC′=∠OBD′,于是得到结论;图3:根据四边形ABCD是菱形,得到AC⊥BD,AO=CO,BO=DO,求得OB=OA,OD=OC,根据旋转的性质得到OD′=OD,OC′=OC,∠D′OD=∠C′OC,求得OD′=OC′,∠AOC′=∠BOD′,根据相似三角形的性质得到BD′=AC′,于是得到结论.【解答】解:图2结论:AC′=BD′,AC′⊥BD′,理由:∵四边形ABCD是正方形,∴AO=OC,BO=OD,AC⊥BD,∵将Rt△COD旋转得到Rt△C′OD′,∴OD′=OD,OC′=OC,∠D′OD=∠C′OC,∴AO=BO,OC′=OD′,∠AOC′=∠BOD′,在△AOC′与△BOD′中,,∴△AOC′≌△BOD′,∴AC′=BD′,∠OAC′=∠OBD′,∵∠AO′D′=∠BO′O,∠O′BO+∠BO′O=90°,∴∠O′AC′+∠AO′D′=90°,∴AC′⊥BD′;图3结论:BD′=AC′,AC′⊥BD’理由:∵四边形ABCD是菱形,∴AC⊥BD,AO=CO,BO=DO,∵∠ABC=60°,∴∠ABO=30°,∴OB=OA,OD=OC,∵将Rt△COD旋转得到Rt△C′OD′,∴OD′=OD,OC′=OC,∠D′OD=∠C′OC,∴OD′=OC′,∠AOC′=∠BOD′,∴=,∴△AOC′∽△BOD′,∴==,∠OAC′=∠OBD′,∴BD′=AC′,∵∠AO′D′=∠BO′O,∠O′BO+∠BO′O=90°,∴∠O′AC′+∠AO′D′=90°,∴AC′⊥BD′.5.如图,矩形AOCB的顶点A、C分别位于x轴和y轴的正半轴上,线段OA、OC 的长度满足方程|x﹣15|+=0(OA>OC),直线y=kx+b分别与x轴、y轴交于M、N两点,将△BCN沿直线BN折叠,点C恰好落在直线MN上的点D处,且tan∠CBD=(1)求点B的坐标;(2)求直线BN的解析式;(3)将直线BN以每秒1个单位长度的速度沿y轴向下平移,求直线BN扫过矩形AOCB的面积S关于运动的时间t(0<t≤13)的函数关系式.【考点】FI:一次函数综合题.【分析】(1)由非负数的性质可求得x、y的值,则可求得B点坐标;(2)过D作EF⊥OA于点E,交CB于点F,由条件可求得D点坐标,且可求得=,结合DE∥ON,利用平行线分线段成比例可求得OM和ON的长,则可求得N 点坐标,利用待定系数法可求得直线BN的解析式;(3)设直线BN平移后交y轴于点N′,交AB于点B′,当点N′在x轴上方时,可知S即为▱BNN′B′的面积,当N′在y轴的负半轴上时,可用t表示出直线B′N′的解析式,设交x轴于点G,可用t表示出G点坐标,由S=S﹣S四边形BNN′B′,可分别得到S与t的函数关系式.△OGN′【解答】解:(1)∵|x﹣15|+=0,∴x=15,y=13,∴OA=BC=15,AB=OC=13,∴B(15,13);(2)如图1,过D作EF⊥OA于点E,交CB于点F,由折叠的性质可知BD=BC=15,∠BDN=∠BCN=90°,∵tan∠CBD=,∴=,且BF2+DF2=BD2=152,解得BF=12,DF=9,∴CF=OE=15﹣12=3,DE=EF﹣DF=13﹣9=4,∵∠CND+∠CBD=360°﹣90°﹣90°=180°,且∠ONM+∠CND=180°,∴∠ONM=∠CBD,∴=,∵DE∥ON,∴==,且OE=3,∴=,解得OM=6,∴ON=8,即N(0,8),把N、B的坐标代入y=kx+b可得,解得,∴直线BN的解析式为y=x+8;(3)设直线BN平移后交y轴于点N′,交AB于点B′,当点N′在x轴上方,即0<t≤8时,如图2,由题意可知四边形BN N′B′为平行四边形,且NN′=t,∴S=NN′•OA=15t;当点N′在y轴负半轴上,即8<t≤13时,设直线B′N′交x轴于点G,如图3,∵NN′=t,∴可设直线B′N′解析式为y=x+8﹣t,令y=0,可得x=3t﹣24,∴OG=24,∵ON=8,NN′=t,∴ON′=t﹣8,∴S=S四边形BNN′B′﹣S△OGN′=15t﹣(t﹣8)(3t﹣24)=﹣t2+39t﹣96;综上可知S与t的函数关系式为S=.。
中考动态问题专题讲解

中考几何动态问题专题一、概述:所谓“动态问题”一般是指以几何知识和图形为背景,渗透运动变化观点的一类问题。
二、考查内容:这类问题主要是考查运动中图形的位置、数量关系。
三、问题展开方式:点动:线动:形动。
(“动”指三种形式:平移、旋转、对折或其几种综合) 四、常用知识:几何方面:全等三角形、直角三角形(勾股定理)、特殊四边形、等腰三角形(等边三角形)、相似及三角函数;代数方面:方程、函数解析式;运动中路程、时间、速度关系式:S=VT 、T=S/V 等。
五、解题策略:1.动中觅静:这里的“静”是指问题中的不变量、不变关系。
2.动静互化:抓住“静”的瞬间,使一般转化为特殊,建立等量关系,3.以动定动:建立两个变量的函数关系,通过函数关系找到变动元素的关系。
六、解题方法:第一全面仔细阅读题目,明确运动方式,全方位考察运动中的变与不变的量及其位置关系,;第二应用分类讨论思想,将在运动过程中导致图形本质发生变化的各种时刻的图形分类画出,化“动”为“静”;第三在各种“静态位置”上结合三角形、四边形进行探索,通过全等、相似及其它知识寻找各个相关量之间的数量关系,建立方程或函数解析式求解。
七、中考位置:重庆市中考热点、难点。
在压轴题第26题中出现。
八、命题目的:甄选优生。
九、解答效果:解答压轴题第26题中,得2分者,顺利进入职教中心学习;得4分者,可读松树桥中学、暨华中学和南华中学;得6分者,读渝北中学;得8分者可“拨打138”了;得8分以上者所有优秀学校的所有优秀班级你自己选吧!特别提醒:认真解读上面“二至六”,才做后面的题目;每做一道题,又结合上面“二至六”来积淀方法,提升能力。
(一)点动问题.1. (2007 江苏省连云港市变式题) 如图,在矩形OABC 中, 60cm OA =,80cm OC =.动点P 从点O 出发,以5cm/s 的速度沿O C 方向运动,到达点C 即停止.设点P 运动的时间为s t .(1)过点P 作对角线OB 的垂线,垂足为点T .求PT 的长y 与时间t 的函数关系式,并写出自变量t 的取值范围;(2)在点P 运动过程中,当点O 关于直线AP 的对称点O '恰好落在对角线OB 上时,求此的运动时间t (3)探索:以A P T ,,三点为顶点的APT △的面积能否达到矩形OABC 面积的14?请说明理由.2. (2008 黑龙江省哈尔滨市) 在矩形ABCD 中,点E 是AD 边上一点,连接BE ,且∠ABE =30°,BE =DE ,连接BD .点P 从点E 出发沿射线ED 运动,过点P 作PQ ∥BD 交直线BE 于点Q . (1) 当点P 在线段ED 上时(如图1),求证:BE =PD +33PQ ; (2)若 BC =6,设PQ 长为x ,以P 、Q 、D 三点为顶点所构成的三角形面积为y ,求y 与 x 的函数关系式(不要求写出自变量x 的取值范围);(3)在②的条件下,当点P 运动到线段ED 的中点时,连接QC ,过点P 作PF ⊥QC ,垂足为F ,PF 交对角线BD 于点G (如图2),求线段PG 的长.3. (2011江苏淮安)如图,在Rt △ABC 中,∠C=90°,AC=8,BC=6,点P 在AB 上,AP=2.点E 、F 同时从点P 出发,分别沿PA 、PB 以每秒1个单位长度的速度向点A 、B 匀速运动,点E 到达点A 后立即以原速度沿AB 向点B 运动,点F 运动到点B 时停止,点E 也随之停止.在点E 、F 运动过程中,以EF 为边作正方形EFGH ,使它与△ABC 在线段AB 的同侧,设E 、F 运动的时间为t 秒(t >0),正方形EFGH 与△ABC 重叠部分面积为S .(1)当t=1时,正方形EFGH 的边长是 ;当t=3时,正方形EFGH 的边长是 ; (2)当0<t ≤2时,求S 与t 的函数关系式;(3)直接答出:在整个运动过程中.......,当t 为何值时,S 最大?最大面积是多少?考点:相似三角形的判定与性质;二次函数的最值;勾股定理;正方形的性质。
中考专题复习动态问题

中考专题复习:动态问题一、专题分析图形中的点、线的运动,构成了数学中的一个新问题——动态问题。
它通常分为三种类型:动点问题、动线问题、动形问题。
此类问题常集代数、几何知识于一体,数形结合,有很强的综合性。
动点问题是近年来在中考试卷压轴题中出现频率较高的一类问题,以函数与三角形和四边形结合的题目为主。
二、学情分析1、这类问题无论教师做了多大的努力,对学生来说都比较困难,所以一部分学生放弃作答。
2、一部分学生对动点问题从根本上不理解,勉强照猫画虎,写了不少但不得分。
3、一部分学生对动点问题有一定认识,对分类能进行简单尝试, 但不完整。
三、教法分析1、教师在教学时引导学生把动态问题变为静态问题来解,抓住变化中的“不变量”。
并从特殊位置点着手确定自变量取值范围, 对基本图形进行充分的分析,画出符合条件的各种草图分散难点、降低难度,将复杂问题简单化。
2、专题化,少而精。
如动点问题有等腰三角形分类、直角三角形分类、三角形相似分类、四边形存在性等问题,分小专题复习效果更好。
四、复习设计本节课重点来探究动态几何中的第一类型----动点问题(等腰三角形分类讨论问题)。
(一)自主解决1、在平面直角坐标系中,已知点P(-2,-1).点T(t,0)是x轴上的一个动点。
当t 取何值时,△TOP是等腰三角形?P情况一:OP=OT情况二:PO=PT T3(-4,0)情况三:TO=TP(设计意图:引导学生总结以已知线段为边作等腰三角形时,通常要分三种情况讨论:以已知线段为腰或为底。
且以已知线段为腰时,以该腰不同顶点为顶角顶点有两种情况。
)2、如图:已知ABCD 中,AB=7,BC=4,∠A=30°(1)点P 从点A 沿AB 边向点B 运动,速度为1cm/s 。
若设运动时间为t(s),连接PC,当t 为何值时,△PBC 为等腰三角形?)0,5();0,5(21T T -)0,45(4-TDCBA解:若△PBC 为等腰三角形 则PB=BC ∴t=3(设计意图:此题起抛砖引玉的作用,体现了从特殊到一般的数学思想。
中考数学专题——动态问题(非常全面)

(中考数学专题3) 动态几何问题【例1】如图,在梯形ABCD 中,AD BC ∥,3AD =,5DC =,10BC =,梯形的高为4.动点M 从B 点出发沿线段BC 以每秒2个单位长度的速度向终点C 运动;动点N 同时从C 点出发沿线段CD 以每秒1个单位长度的速度向终点D 运动.设运动的时间为t (秒).D NCM B A(1)当MN AB ∥时,求t 的值;(2)试探究:t 为何值时,MNC △为等腰三角形.【例3】在△ABC 中,∠ACB=45º.点D (与点B 、C 不重合)为射线BC 上一动点,连接AD ,以AD 为一边且在AD 的右侧作正方形ADEF .(1)如果AB=AC .如图①,且点D 在线段BC 上运动.试判断线段CF 与BD 之间的位置关系,并证明你的结论.(2)如果AB ≠AC ,如图②,且点D 在线段BC 上运动.(1)中结论是否成立,为什么?(3)若正方形ADEF 的边DE 所在直线与线段CF 所在直线相交于点P ,设AC =42,3=BC ,CD=x ,求线段CP 的长.(用含x 的式子表示)【例4】已知如图,在梯形ABCD 中,24AD BC AD BC ==∥,,,点M 是AD 的中点,MBC △是等边三角形.(1)求证:梯形ABCD 是等腰梯形;(2)动点P 、Q 分别在线段BC 和MC 上运动,且60MPQ =︒∠保持不变.设PC x MQ y ==,,求y与x 的函数关系式; (3)在(2)中,当y 取最小值时,判断PQC △的形状,并说明理由.【例5】已知正方形ABCD 中,E 为对角线BD 上一点,过E 点作EF BD ⊥交BC 于F ,连接DF ,G 为DF 中点,连接EG CG ,. (1)直接写出线段EG 与CG 的数量关系;(2)将图1中BEF ∆绕B 点逆时针旋转45︒,如图2所示,取DF 中点G ,连接EG CG ,,. 你在(1)中得到的结论是否发生变化?写出你的猜想并加以证明.(3)将图1中BEF ∆绕B 点旋转任意角度,如图3所示,再连接相应的线段,问(1)中的结论是否仍然成立?(不要求证明)A DC B P M Q 60图3图2图1FEABCDABC DEFGGFED C BA【总结】 通过以上五道例题,我们研究了动态几何问题当中点动,线动,乃至整体图形动这么几种可能的方式。
初中数学_中考专题复习 动态探究型问题教学设计学情分析教材分析课后反思
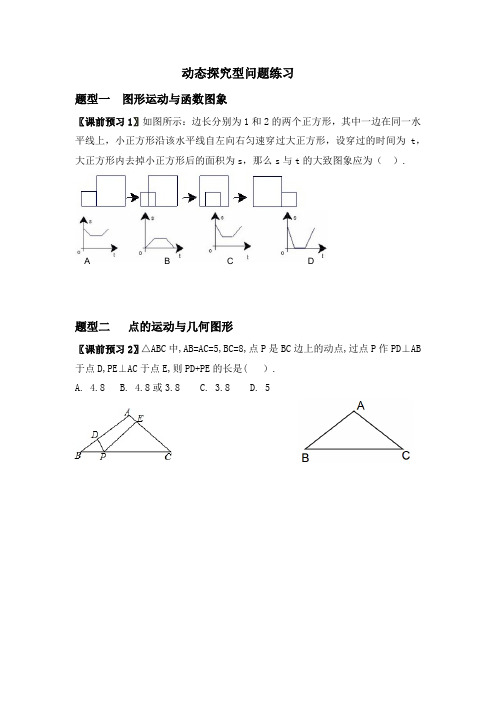
动态探究型问题练习题型一图形运动与函数图象〖课前预习1〗如图所示:边长分别为1和2的两个正方形,其中一边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形,设穿过的时间为t,.大正方形内去掉小正方形后的面积为s,那么s与t的大致图象应为()题型二点的运动与几何图形〖课前预习2〗△ABC中,AB=AC=5,BC=8,点P是BC边上的动点,过点P作PD⊥AB 于点D,PE⊥AC于点E,则PD+PE的长是( ).A. 4.8B. 4.8或3.8C. 3.8D. 5题型 三 动态问题中存在探究〖课前预习3〗如图,在平面直角坐标系中,点C(−3,0),点A,B 分别在x 轴,y 轴的正半轴上,且满足0132=-+-OA OB .(1) 求点A ,点B 的坐标.(2)若点P 从C 点出发,以每秒1个单位的速度沿射线CB 运动,连结AP.设△ABP 的面积为S ,点P 的运动时间为t 秒,求S 与t 的函数关系式,并写出自变量的取值范围.(3)在(2)的条件下,是否存在点P ,使以点A ,B ,P 为顶点的三角形与△AOB 相似?若存在,请直接写出点P 的坐标;若不存在,请说明理由.〖举一反三1〗如图,点P是▱ABCD边上一动点,沿A→D→C→B的路径移动,设P点经过的路径长为x,△BAP的面积是y,则下列能大致反映y与x的函数关系的图象是( ).〖举一反三2〗如图,Rt△ABC中,∠ACB=90∘,∠ABC=60∘,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为().A 2 B2.5或3.5C3.5或4.5 D2或3.5或4.5中考链接达标检测1.(2017.济宁)如图,A,B是半径为1的⊙O上两点,且OA⊥OB,点P从点A出发,在⊙O上以每秒一个单位长度的速度匀速运动,回到点A运动结束,设运动时间为x(单位:s),弦BP的长为y,那么下列图象中可能表示y与x函数关系的是( ).)0(62>+-=a c ax ax y 2721+-=x y2.(2016•济宁)如图,已知抛物线m :的顶点A 在x 轴上,并过点B (0,1),直线n : 与x 轴交于点D ,与抛物线m 的对称轴L 交于点F ,过B 点的直线BE 与直线n 相交于点E (﹣7,7).(1)求抛物线m 的解析式.(2)P 是对称轴L 上的一个动点,若以B ,E ,P 为顶点的三角形的周长最小,求点P 的坐标.(3)抛物线m 上是否存在一动点Q ,使以线段FQ 为直径的圆恰好经过点D ?若存在,求点Q 的坐标;若不存在,请说明理由.《动态探究型问题》学情分析动态探究型问题这类题目多出现在压轴题题目中,题目难度较大,试题信息量大,对同学们获取信息和处理信息的能力要求较高,是近年来中考数学的热点题型,学生遇到这类题目时都会感到恐惧。
中考数学试题分类动态问题
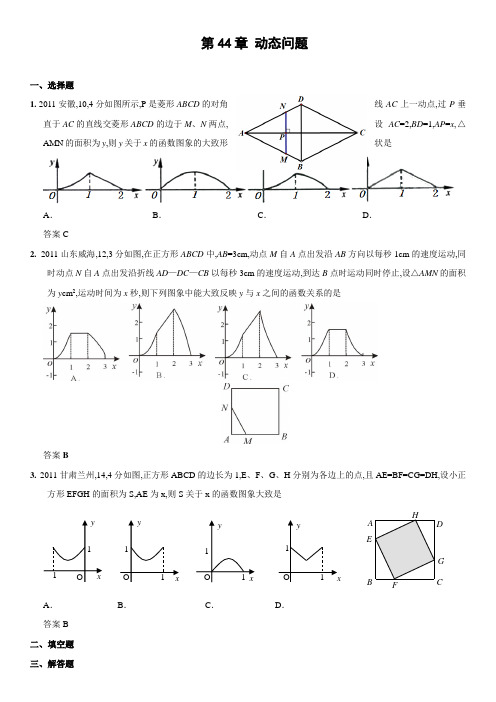
第44章 动态问题一、选择题1. 2011安徽,10,4分如图所示,P 是菱形ABCD 的对角线AC 上一动点,过P 垂直于AC 的直线交菱形ABCD 的边于M 、N 两点,设AC =2,BD =1,AP =x ,△AMN 的面积为y ,则y 关于x 的函数图象的大致形状是A .B .C .D .答案C2. 2011山东威海,12,3分如图,在正方形ABCD 中,AB =3cm,动点M 自A 点出发沿AB 方向以每秒1cm 的速度运动,同时动点N 自A 点出发沿折线AD —DC —CB 以每秒3cm 的速度运动,到达B 点时运动同时停止,设△AMN 的面积为y cm 2,运动时间为x 秒,则下列图象中能大致反映y 与x 之间的函数关系的是答案B3. 2011甘肃兰州,14,4分如图,正方形ABCD 的边长为1,E 、F 、G 、H 分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH 的面积为S,AE 为x,则S 关于x 的函数图象大致是A .B .C .D .答案B 二、填空题 三、解答题A BC DEFGHx y -1 O 1x y1 O 1 x yO 1 xy1O 1 11. 2011浙江省舟山,24,12分已知直线3+=kx y k <0分别交x 轴、y 轴于A 、B 两点,线段OA 上有一动点P 由原点O 向点A 运动,速度为每秒1个单位长度,过点P 作x 轴的垂线交直线AB 于点C ,设运动时间为t 秒.1当1-=k 时,线段OA 上另有一动点Q 由点A 向点O 运动,它与点P 以相同速度同时出发,当点P 到达点A 时两点同时停止运动如图1.① 直接写出t =1秒时C 、Q 两点的坐标;② 若以Q 、C 、A 为顶点的三角形与△AOB 相似,求t 的值. 2当43-=k 时,设以C 为顶点的抛物线n m x y ++=2)(与直线AB 的另一交点为D 如图2, ① 求CD 的长;② 设△COD 的OC 边上的高为h ,当t 为何值时,h 的值最大答案1①C 1,2,Q 2,0.②由题意得:Pt ,0,Ct ,-t+3,Q 3-t ,0, 分两种情形讨论:情形一:当△AQC ∽△AOB 时,∠AQC=∠AOB =90°,∴CQ ⊥OA , ∵CP ⊥OA ,∴点P 与点Q 重合,OQ =OP ,即3-t =t ,∴t=.情形二:当△ACQ ∽△AOB 时,∠ACQ=∠AOB =90°,∵O A=O B=3,∴△AOB 是等腰直角三角形,∴△ACQ 是等腰直角三角形,∵CQ ⊥OA ,∴AQ=2CP ,即t =2-t +3,∴t=2.∴满足条件的t 的值是秒或2秒. 2 ①由题意得:Ct ,-34t +3,∴以C 为顶点的抛物线解析式是23()34y x t t =--+, 由233()3344x t t x --+=-+,解得x 1=t ,x 2=t 34-;过点D 作DE ⊥CP 于点E ,则∠DEC=∠AOB =90°,DE ∥OA ,∴∠EDC=∠OAB ,∴△DEC ∽△AOB ,∴DE CDAO BA=, ∵AO =4,AB =5,DE =t -t-34=34.∴CD =35154416DE BA AO ⨯⨯==.②∵CD =1516,CD 边上的高=341255⨯=.∴S △COD =11512921658⨯⨯=.∴S △COD 为定值; 要使OC 边上的高h 的值最大,只要OC 最短.第24题图2第24题图1因为当OC ⊥AB 时OC 最短,此时OC 的长为125,∠BCO =90°,∵∠AOB =90°,∴∠COP =90°-∠BOC =∠OBA ,又∵CP ⊥OA ,∴Rt △PCO ∽Rt △OAB ,∴OP OC BO BA =,OP =123365525OC BO BA ⨯⨯==,即t =3625, ∴当t 为3625秒时,h 的值最大.2. 2011广东东莞,22,9分如图,抛物线2517144y x x =-++与y 轴交于点A ,过点A 的直线与抛物线交于另一点B ,过点B 作BC ⊥x 轴,垂足为点C 3,0. 1求直线AB 的函数关系式;2动点P 在线段OC 上,从原点O 出发以每钞一个单位的速度向C 移动,过点P 作⊥x 轴,交直线AB 于点M ,抛物线于点N ,设点P 移动的时间为t 秒,MN 的长为s 个单位,求s 与t 的函数关系式,并写出t 的取值范围;3设2的条件下不考虑点P 与点O ,点G 重合的情况,连接CM ,BN ,当t 为何值时,四边形BCMN 为平等四边形问对于所求的t 的值,平行四边形BCMN 是否为菱形说明理由.解1把x=0代入2517144y x x =-++,得1y = 把x=3代入2517144y x x =-++,得52y =,∴A 、B 两点的坐标分别0,1、3,52设直线AB 的解析式为y kx b =+,代入A 、B 的坐标,得1532b k b =⎧⎪⎨+=⎪⎩,解得112b k =⎧⎪⎨=⎪⎩所以,112y x =+2把x=t 分别代入到112y x =+和2517144y x x =-++ 分别得到点M 、N 的纵坐标为112t +和2517144t t -++∴MN=2517144t t -++-112t +=251544t t -+即251544s t t =-+∵点P 在线段OC 上移动, ∴0≤t ≤3.3在四边形BCMN 中,∵BC ∥MN∴当BC=MN 时,四边形BCMN 即为平行四边形 由25155442t t -+=,得121,2t t == 即当12t =或时,四边形BCMN 为平行四边形 当1t =时,PC=2,PM=32,PN=4,由勾股定理求得CM=BN=52, 此时BC=CM=MN=BN,平行四边形BCMN 为菱形; 当2t =时,PC=1,PM=2,由勾股定理求得CM=5, 此时BC ≠CM,平行四边形BCMN 不是菱形; 所以,当1t =时,平行四边形BCMN 为菱形.3. 2011江苏扬州,28,12分如图,在Rt △ABC 中,∠BAC=90o,AB<AC,M 是BC 边的中点,MN ⊥BC 交AC 于点N,动点P 从点B 出发沿射线BA 以每秒3厘米的速度运动;同时,动点Q 从点N 出发沿射线NC 运动,且始终保持MQ ⊥MP;设运动时间为t 秒t>01△PBM 与△QNM 相似吗以图1为例说明理由; 2若∠ABC=60o,AB=43厘米; ① 求动点Q 的运动速度;② 设Rt △APQ 的面积为S 平方厘米,求S 与t 的函数关系式; 3探求BP 2、PQ 2、CQ 2三者之间的数量关系,以图1为例说明理由;答案解:1△PBM 与△QNM 相似;∵MN ⊥BC MQ ⊥MP ∴ ∠NMB=∠PMQ=∠BAC =90o ∴∠PMB=∠QMN, ∠QNM=∠B =90o -∠C ∴ △PBM ∽△QNM2①∵∠ABC=60o,∠BAC =90o,AB=43,BP=3t ∴AB=BM=CM=43,MN=4 ∵ △PBM ∽△QNM ∴MN BM NQ BP = 即:3434==NQ BP ∵P 点的运动速度是每秒3厘米, ∴ Q 点运动速度是每秒1厘米; ② ∵ AC=12,CN=8∴ AQ=12-8+t=4+t, AP=43-3t∴ S=)334()4(21t t -⨯+⨯=)16(232--t 3 BP 2+ CQ 2 =PQ 2证明如下: ∵BP=3t, ∴BP 2=3t 2 ∵CQ=8-t ∴CQ 2=8-t 2=64-16t+t 2 ∵PQ 2=4+t 2+34-t 2=4t 2-16t+64 ∴BP 2+ CQ 2 =PQ 24. 2011山东德州23,12分在直角坐标系xoy 中,已知点P 是反比例函数)>0(32x xy =图象上一个动点,以P 为圆心的圆始终与y 轴相切,设切点为A .1如图1,⊙P 运动到与x 轴相切,设切点为K ,试判断四边形OKP A 的形状,并说明理由. 2如图2,⊙P 运动到与x 轴相交,设交点为B ,C .当四边形ABCP 是菱形时: ①求出点A ,B ,C 的坐标.②在过A ,B ,C 三点的抛物线上是否存在点M ,使△MBP 的面积是菱形ABCP 面积的21.若存在,试求出所有满足条件的M 点的坐标,若不存在,试说明理由.答案解:1∵⊙P分别与两坐标轴相切,∴P A⊥OA,PK⊥OK.∴∠P AO=∠OKP=90°.又∵∠AOK=90°,∴∠P AO=∠OKP=∠AOK=90°.∴四边形OKP A是矩形.又∵OA=OK,∴四边形OKP A是正方形.……………………2分2①连接PB,设点P的横坐标为x,则其纵坐标为x 32.过点P作PG⊥BC于G.∵四边形ABCP为菱形,∴BC=P A=PB=PC.∴△PBC为等边三角形.在Rt△PBG中,∠PBG=60°,PB=P A=x,PG=x 32.AP 23yx=xyKO图1OA P 23yx=xyB C图2GMsin ∠PBG =PBPG,即2x x =. 解之得:x =±2负值舍去.∴ PG,P A =B C=2.……………………4分 易知四边形OGP A 是矩形,P A =OG =2,BG =CG =1, ∴OB =OG -BG =1,OC =OG +GC =3.∴ AB 1,0C 3,0.……………………6分 设二次函数解析式为:y =ax 2+bx +c .据题意得:0930a b c a b c c ⎧++=⎪++=⎨⎪=⎩解之得:a=3, b=3-, c∴二次函数关系式为:233y x x =-9分 ②解法一:设直线BP 的解析式为:y =ux +v ,据题意得:2u v u v +=⎧⎪⎨+=⎪⎩解之得:uv=-∴直线BP的解析式为:y =-.过点A 作直线AM ∥PB ,则可得直线AM的解析式为:y =+解方程组:233y y x x ⎧=+⎪⎨=-⎪⎩得:110x y =⎧⎪⎨=⎪⎩;227x y =⎧⎪⎨=⎪⎩ 过点C 作直线CM ∥PB ,则可设直线CM的解析式为:y t =+. ∴0=t .∴t =-∴直线CM的解析式为:y =-.解方程组:2y y x x ⎧=-⎪⎨=⎪⎩得:113x y =⎧⎨=⎩ ;224x y =⎧⎪⎨=⎪⎩. 综上可知,满足条件的M 的坐标有四个,分别为:12分 解法二:∵12PAB PBC PABCS S S ∆∆==,∴AC 3,0显然满足条件.延长AP 交抛物线于点M ,由抛物线与圆的轴对称性可知,PM =P A . 又∵AM ∥BC , ∴12PBM PBA PABCS S S ∆∆==.∴点M又点M 的横坐标为AM =P A +PM =2+2=4. ∴点M点7,综上可知,满足条件的M 的坐标有四个,分别为:12分解法三:延长AP 交抛物线于点M ,由抛物线与圆的轴对称性可知,PM =P A . 又∵AM ∥BC , ∴12PBM PBA PABCS S S ∆∆==.∴点M2x x =. 解得:10x =舍,24x =. ∴点M 的坐标为点7,综上可知,满足条件的M 的坐标有四个,分别为:12分 5. 2011山东菏泽,21,9分如图,抛物线y =12x 2+bx -2与x 轴交于A ,B 两点,与y 轴交于C 点,且A -1,0. 1求抛物线的解析式及顶点D 的坐标; 2判断△ABC 的形状,证明你的结论;3点Mm ,0是x 轴上的一个动点,当MC +MD 的值最小时,求m 的值.解:1把点A -1,0的坐标代入抛物线的解析式y =12x 2+bx -2, 整理后解得32b =-, 所以抛物线的解析式为 213222y x x =--. 顶点D 325,28⎛⎫- ⎪⎝⎭.2∵AB =5,AC 2=OA 2+OC 2=5,BC 2=OC 2+OB 2=20,∴AC 2+BC 2=AB 2.∴△ABC 是直角三角形. 3作出点C 关于x 轴的对称点C′,则C′ 0,2,OC′=2. 连接C′D 交x 轴于点M ,根据轴对称性及两点之间线段最短可知,MC +MD 的值最小. 设抛物线的对称轴交x 轴于点E . △C′OM ∽△DEM . ∴OM OC EM ED '=.∴232528m m =-.∴m =2441. 6. 2011山东济宁,23,10分如图,在平面直角坐标系中,顶点为4,1-的抛物线交y 轴于A 点,交x 轴于B ,C 两点点B 在点C 的左侧. 已知A 点坐标为0,3.1求此抛物线的解析式;2过点B 作线段AB 的垂线交抛物线于点D , 如果以点C 为圆心的圆与直线BD 相切,请判断抛物线的对称轴l 与⊙C 有怎样的位置关系,并给出证明;3已知点P 是抛物线上的一个动点,且位于A ,C 两点之间,问:当点P 运动到什么位置时,PAC ∆的面积最大并求出此时P 点的坐标和PAC ∆的最大面积.答案1解:设抛物线为2(4)1y a x =--. ∵抛物线经过点A 0,3,∴23(04)1a =--.∴14a =. ∴抛物线为2211(4)12344y x x x =--=-+. ……………………………3分 2 答:l 与⊙C 相交. …………………………………………………………………4分 证明:当21(4)104x --=时,12x =,26x =. ∴B 为2,0,C 为6,0.∴AB =设⊙C 与BD 相切于点E ,连接CE ,则90BEC AOB ∠=︒=∠. ∵90ABD ∠=︒,∴90CBE ABO ∠=︒-∠.又∵90BAO ABO ∠=︒-∠,∴BAO CBE ∠=∠.∴AOB ∆∽BEC ∆. ∴CE BCOB AB =.∴2CE =.∴2CE =>.…………………………6分 ∵抛物线的对称轴l 为4x =,∴C 点到l 的距离为2.∴抛物线的对称轴l 与⊙C 相交. ……………………………………………7分 3 解:如图,过点P 作平行于y 轴的直线交AC 于点Q .可求出AC 的解析式为132y x =-+.…………………………………………8分 设P 点的坐标为m ,21234m m -+,则Q 点的坐标为m ,132m -+.∴2211133(23)2442PQ m m m m m =-+--+=-+.∵22113327()6(3)24244PAC PAQ PCQ S S S m m m ∆∆∆=+=⨯-+⨯=--+,∴当3m =时,PAC ∆的面积最大为274.x第23题此时,P 点的坐标为3,34-. ……………………………10分7. 2011山东威海,25,12分如图,抛物线2y ax bx c =++交x 轴于点(3,0)A -,点(1,0)B ,交y 轴于点(0,3)E -.点C 是点A 关于点B 的对称点,点F 是线段BC 的中点,直线l 过点F 且与y 轴平行.直线y x m =-+过点C ,交y 轴于点D .1求抛物线的函数表达式;2点K 为线段AB 上一动点,过点K 作x 轴的垂线与直线CD 交于点H ,与抛物线交于点G ,求线段HG 长度的最大值;3在直线l 上取点M ,在抛物线上取点N ,使以点A ,C ,M ,N 为顶点的四边是平行四边形,求点N 的坐标.图① 备用图答案 解:1设抛物线的函数表达式(1)(3)y a x x =-+ ∵抛物线与y 轴交于点(0,3)E -,将该点坐标代入上式,得1a =. ∴所求函数表达式(1)(3)y x x =-+,即223y x x =+-. 2∵点C 是点A 关于点B 的对称点,点(3,0)A -,点(1,0)B , ∴点C 的坐标是(5,0)C .将点C 的坐标是(5,0)C 代入y x m =-+,得5m =. ∴直线CD 的函数表达式为5y x =-+.AxyBOCD第23题EPQ设K 点的坐标为(,0)t ,则H 点的坐标为(,5)t t -+,G 点的坐标为2(,23)t t t +-. ∵点K 为线段AB 上一动点, ∴31t -≤≤.∴222341(5)(23)38()24HG t t t t t t =-+-+-=--+=-++. ∵3312-≤-≤, ∴当32t =-时,线段HG 长度有最大值414.3∵点F 是线段BC 的中点,点(1,0)B ,点 (5,0)C , ∴点F 的坐标为(3,0)F . ∵直线l 过点F 且与y 轴平行, ∴直线l 的函数表达式为3x =. ∵点M 在直线l 上,点N 在抛物线上 ,∴设点M 的坐标为(3,)M m ,点N 的坐标为2(,23)N n n n +-. ∵点(3,0)A -,点 (5,0)C ,∴8AC =. 分情况讨论: ①若线段AC 是以点A ,C ,M ,N 为顶点的四边是平行四边形的边,则须MN ∥AC ,且MN =AC =8.当点N 在点M 的左侧时,3MN n =-. ∴38n -=,解得5n =-. ∴N 点的坐标为(5,12)N -.当点N 在点M 的右侧时,3MN n =-. ∴38n -=,解得11n =. ∴N 点的坐标为(11,40)N .②若线段AC 是以点A ,C ,M ,N 为顶点的平行四边形的对角线,由“点C 与点A 关于点B 中心对称”知:点M 与点N 关于点B 中心对称.取点F 关于点B 对称点P ,则点P 的坐标为(1,0)P -.过点P 作NP ⊥x 轴,交抛物线于点N .将1x =-代入223y x x =+-,得4y =-. 过点N ,B 作直线NB 交直线l 于点M . 在△BPN 和△BFM 中,∵90NPB MBF BF BP BPN BFM ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩∴△BPN ≌△BFM . ∴NB =MB .∴四边形点ANCM 为平行四边形. ∴坐标为(1,4)--的点N 符合条件.∴当点N 的坐标为(5,12)-,(11,40),(1,4)--时,以点A ,C ,M ,N 为顶点的四边是平行四边形.8. 2011山东烟台,26,14分如图,在直角坐标系中,梯形ABCD 的底边AB 在x 轴上,底边CD 的端点D 在y 轴上.直线CB 的表达式为y =-43x +163,点A 、D 的坐标分别为-4,0,0,4.动点P 自A 点出发,在AB 上匀速运行.动点Q 自点B 出发,在折线BCD 上匀速运行,速度均为每秒1个单位.当其中一个动点到达终点时,它们同时停止运动.设点P 运动t 秒时,△OPQ 的面积为s 不能构成△OPQ 的动点除外. 1求出点B 、C 的坐标; 2求s 随t 变化的函数关系式;3当t 为何值时s 有最大值并求出最大值.答案解:1把y =4代入y =-43x +163,得x =1. ∴C 点的坐标为1,4. 当y =0时,-43x +163=0, ∴x =4.∴点B 坐标为4,0.2作CM ⊥AB 于M ,则CM =4,BM =3. ∴BC =22CM BM +=2234+=5. ∴sin ∠ABC =CM BC =45. ①当0<t <4时,作QN ⊥OB 于N , 则QN =BQ ·sin ∠ABC =45t. 备用图2O xyABCDO xyABCD备用图1 OxyABCD PQ∴S=12OP·QN=124-t×45t=-25t2+85t0<t<4.②当4<t≤5时,如备用图1, 连接QO,QP,作QN⊥OB于N.同理可得QN=4 5 t.∴S=12OP·QN=12×t-4×45t. =25t2-85t4<t≤5.③当5<t≤6时,如备用图2, 连接QO,QP.S=12×OP×OD=12t-4×4=2t-85<t≤6.3①在0<t<4时,当t=8522()5⨯-=2时,S最大=28()524()5-⨯-=85.②在4<t≤5时,对于抛物线S=25t2-85t,当t=-85225-⨯=2时,S最小=25×22-85×2=-85.∴抛物线S=25t2-85t的顶点为2,-85.∴在4<t≤5时,S随t的增大而增大.∴当t =5时,S 最大=25×52-85×5=2. ③在5<t ≤6时,在S =2t -8中,∵2>0,∴S 随t 的增大而增大. ∴当t =6时,S 最大=2×6-8=4.∴综合三种情况,当t =6时,S 取得最大值,最大值是4.说明:3中的②也可以省略,但需要说明:在2中的②与③的△OPQ ,③中的底边OP 和高CD 都大于②中的底边OP 和高.所以③中的△OPQ 面积一定大于②中的△OPQ 的面积.9. 2011四川南充市,22,8分抛物线y =ax 2+bx+c 与x 轴的交点为A m -4,0和B m ,0,与直线y =-x +p 相交于点A 和点C2m -4,m -6.1求抛物线的解析式;2若点P 在抛物线上,且以点P 和A,C 以及另一点Q 为顶点的平行四边形ACQP 面积为12,求点P,Q 的坐标; 3在2条件下,若点M 是x 轴下方抛物线上的动点,当⊿PQM 的面积最大时,请求出⊿PQM 的最大面积及点M 的坐标;答案解:1∵点Am-4,0和C2m-4,m-6在直线y =-x +p 上 ∴0(4)6(24)m p m m p =--+⎧⎨-=--+⎩解得:31m p =⎧⎨=-⎩∴A-1,0 B3,0, C2,-3 设抛物线y =ax 2+bx+c =ax-3x+1, ∵C2,-3 ∴a=1∴抛物线解析式为:y =x 2-2x-32AC=32,AC 所在直线的解析式为:y =-x -1,∠BAC=450∵平行四边形ACQP 的面积为12. ∴平行四边形ACQP 中AC 边上的高为2312=22过点D 作DK ⊥AC 与PQ 所在直线相交于点K,DK= 22,∴DN=4 ∵ACPQ,PQ 所在直线在直线ACD 的两侧,可能各有一条, ∴PQ 的解析式或为y =-x +3或y =-x -5∴2233y x x y x ⎧=--⎨=-+⎩解得:1130x y =⎧⎨=⎩或2225x y =-⎧⎨=⎩2235y x x y x ⎧=--⎨=--⎩,此方程组无解. 即P 13,0, P 2-2,5∵ACPQ 是平行四边形 ,A-1,0 C2,-3 ∴当P3,0时,Q6,-3 当P-2,5时,Q1,2∴满足条件的P,Q 点是P 13,0, Q 16,-3或 P 2-2,5,Q 21,2 (1)设M t ,t 2-2t-3,-1<t <3,过点M 作y 轴的平行线,交PQ 所在直线雨点T,则Tt,-t+3MT=-t+3- t 2-2t-3=- t 2+t+6过点M 作M S ⊥PQ 所在直线于点S, MS=22MT=22 - t 2+t+6=- 22t-212+8225∴当t=21时,M 21,-415,⊿PQM 中PQ 边上高的最大值为822510.2011 浙江杭州,24, 12图形既关于点O 中心对称,又关于直线AC ,BD 对称,AC =10,BD =6,已知点E ,M 是线段AB 上的动点不与端点重合,点O 到EF ,MN 的距离分别为1h ,2h .△OEF 与△OGH 组成的图形称为蝶形. 1求蝶形面积S 的最大值;2当以EH 为直径的圆与以MQ 为直径的圆重合时,求1h 与2h 满足的关系式,并求1h 的取值范围.答案1 如图,设EF 与AC 交于点K,由△OEF ∽△ABD,得AK EF AO BD =,1556h EF-=, O DCBAyxLK SEROABM16(5)5EF h =-,1111622(5)225S OK EF h h =⨯•=⨯•-,整理得216515()522S h =--+,当152h =时,蝶形面积S 的最大,最大值为152.2 如图,设MN 与AC 交于点L,由1得16(5)5EF h =-,则13(5)5EK h =-,23(5)5ML h =-由OK 2+EK 2=OE 2,OL 2+ML 2=OM 2,得OK 2+EK 2=OL 2+ML 2,2222112233(5)(5)55h h h h ⎡⎤⎡⎤+-=+-⎢⎥⎢⎥⎣⎦⎣⎦,整理得[]1212()17()450h h h h -+-=,当点E,M 不重合时,120h h -≠,124517h h +=.当OE ⊥AB 时,14534h =,所以145017h << 2当点,E M 重合时,则12h h =,此时1h 的取值范围为105h <<.解法二:1由题意,得四边形ABCD 是菱形. 由//EF BD ,得ABDAEF ∆∆,1565h EF -∴=,即()1655EF h =- ()2111166515255522OEFS S EF h h h h ∆⎛⎫∴==⨯=-⨯=--+ ⎪⎝⎭所以当152h =时,max 152S =. 2根据题意,得OE OM =.如图,作OR AB ⊥于R , OB 关于OR 对称线段为OS ,1当点,E M 不重合时,则,OE OM 在OR 的两侧,易知RE RM =.225334AB =+=,34OR ∴=221533434BR ⎛⎫∴=-= ⎪⎝⎭由////ML EK OB ,得,OK BE OL BMOA AB OA AB== 2OK OL BE BM BR OA OA AB AB AB ∴+=+=,即1295517h h +=124517h h ∴+=,此时1h 的取值范围为145017h <<且14534h ≠ 2当点,E M 重合时,则12h h =,此时1h 的取值范围为105h <<.11. 2011 浙江湖州,24,14如图1.已知正方形OABC 的边长为2,顶点A 、C 分别在x 、y 轴的正半轴上,M 是BC 的中点.P 0,m 是线段OC 上一动点C 点除外,直线PM 交AB 的延长线于点D . 1 求点D 的坐标用含m 的代数式表示; 2 当△APD 是等腰三角形时,求m 的值;3 设过P 、M 、B 三点的抛物线与x 轴正半轴交于点E ,过点O 作直线ME 的垂线,垂足为H 如图2.当点P 从点O 向点C 运动时,点H 也随之运动.请直接写出点H 所经过 的路径长.不必写解答过程答案解:1由题意得CM=BM ,∵∠PMC =∠DMB ,∴Rt △PMC ≌Rt △DMB ,∴DB =PC ,∴DB =2-m,AD =4-m,∴点D 的坐标为2,4-m.2分三种情况:①若AP =AD ,则224(4)m m +=-,解得32m =. ② 若PD =P A ,过P 作PF ⊥AB 于点F 如图,则AF =FD,11(4)22AF FD AD m ===-,又OP =AF ,∴1(4)2m m =-,解得43m =, ③ 若DP =DA ,∵△PMC ≌△DMB ,∴11(4)22PM PD m ==-,∵222PC CM PM +=,∴221(2)1(4)4m m -+=-, 解得122,23m m ==(舍去). 综上所述,当△APD 是等腰三角形时,过m 的值为342233或或. 3点H 5. 12. 2011宁波市,26,10分如图.平面直角坐标系xOy 中,点B 的坐标为-2,2,点B 的坐标为6,6,抛物线经过A 、O 、B 三点,线段AB 交y 轴与点E . 1求点E 的坐标; 2求抛物线的函数解析式;3点F 为线段OB 上的一个动点不与O 、B 重合,直线EF 与抛物线交与M 、N 两点点N 在y 轴右侧,连结ON 、BN ,当点F 在线段OB 上运动时,求∆BON 的面积的最大值,并求出此时点N 的坐标;4连结AN ,当∆BON 的面积的最大时,在坐标平面内使得∆BOP 与∆OAN 相似点B 、O 、N 对应的点P 的坐标.答案26.解:1设直线AB的函数解析式为y=mx+n将点A-2,2,B6,6代入得:错误!得m=错误!,n=3∴y=错误!x+3当x=0时y=3 ∴E0,3设抛物线的函数解析式为y=ax+bx将A-2,2B6,6代入得错误!解得a=错误!,b=-错误!∴抛物线的解析式为y=错误!x2-错误!x3过点N做x轴的垂线NG,垂足为G,交OB于点Q,过B作BH⊥x轴于H,设Nx, 错误!x2-错误!x 则Qx,x则S∆BON=S∆BON+S∆BON=错误!×QN×OG+错误!×QN×HG=错误!×QN×OG+HG=错误!×QN×OH=错误!〔x-错误!x2-错误!x〕×6=-错误!x2+错误!x=-错误!x-32+错误!0<x<6∴当x =3时,∆BON 面积最大,最大值为错误! 此时点N 的坐标为3, 错误! 4过点A 作AS ⊥GQ 于S ∵A -2,2,B 6,6,N 3, 错误!∴∠AOE =∠OAS =∠BOH =45°,OG =3,NG =错误!,NS =错误!,AS =5 在Rt ∆SAN 和Rt ∆NOG 中 ∴tan ∠SAN = tan ∠NOG =错误! ∴∠SAN =∠NOG∴∠OAS -∠ASN =∠BOG -∠NOG ∴∠OASN =∠BON∴ON 的延长线上存在一点P ,使∆BOP ~∆OAN ∵A -2,2, N 3, 错误! 在Rt ∆ASN 中 AN =错误!=错误!当∆BOP ~∆OAN 时 错误!=错误! ∴错误!=错误! ∴OP =错误! 过点P 作PT ⊥x 轴于点T∴∆OPT ~∆ONG ∴错误!=错误!=错误! 设P 4t ,t 在在Rt ∆POT 中,有4t 2+t 2=错误!2 ∴t 1=错误! ,t 2=-错误!舍 ∴点P 的坐标为15,错误!将∆OBP 沿直线OB 返折,可得出另一个满足条件的点P '错误!,15,由以上推理可知,当点P 的坐标为15,错误!或错误!,15时∆BOP 与∆OAN 相似.13. 2011浙江衢州,24,12分已知两直线12l l 、分别经过点()1,0A ,点()3,0B -,并且当两条直线同时相交于y 轴正半轴的点C 时,恰好有12l l ⊥,经过点A B C 、、的抛物线的对称轴于直线1l 交于点K ,如图所示. 求点C 的坐标,并求出抛物线的函数解析式.抛物线的对称轴被直线1l ,抛物线,直线2l 和x 轴依次截得三条线段,问这三条线段有何数量关系请说明理由. 当直线2l 绕点C 旋转时,与抛物线的另一个交点为M .请找出使MCK 为等腰三角形的点M .简述理由,并写出点M 的坐标.答案1解法1:由题意易知(1,.3C 0BOC COA CO AO CO BO CO COCO ∴==∴=∴即点的坐标是~由题意,可设抛物线的函数解析式为2y ax bx =++把(1,0),(3,0)A B -的坐标分别代入2y ax bx =++得{0930.a b a b +-解这个方程组,得a b ⎧⎪⎨⎪⎩∴抛物线的函数解析式为233y x x =--+ 解法2:由勾股定理,得2222222()().OC OB OC OA BC AC AB +++=+= 又314OB OA AB ===,,(.OC C ∴=∴点的坐标是由题意可设抛物线的函数解析式为()()13.y a x x =-+把(C 0代入函数解析式得a =所以抛物线的函数解析式为)()13.y x x =-+ 2解法1:截得三条线段的数量关系为.KD DE EF == 理由如下:可求得直线1l的解析式为y =+直线2l的解析式为3y x =,抛物线的对称轴为直线1x =-.由此可求得点K的坐标为(-,点D的坐标为1,3⎛⎫- ⎪ ⎪⎝⎭,点E的坐标为1,3⎛- ⎝⎭,点F 的坐标为()1,0-. ,333.KD DE EF KD DE EF ∴===∴==解法2:截得三条线段的数量关系为.KD DE EF == 理由如下:由题意可知Rt 3060ABC ABC CAB ∠=︒∠=︒中,,,则可得tan 30=tan 603EF BF KF AF =⨯︒=⨯︒. 由顶点D的坐标为1,3⎛⎫- ⎪ ⎪⎝⎭得3DF =, 3KD DE EF ∴===3解法1:i 以点K 为圆心,线段KC 长为半径画圆弧,交抛物线于点1M ,由抛物线的对称性可知点1M 为点C 关于直线1x =-的对称点.∴所以点1M的坐标为(-,此时,1M CK 为等腰三角形.ii 当以点C 为圆心,线段KC 长为半径画圆弧时,与抛物线交点为点1M 和点A ,而三点A C K 、、在同一直线上,不能构成三角形.iii 作线段KC 的中垂线l ,由点D 是KE 的中点,且12l l ⊥,可知l 经过点D ,.KD DC ∴=此时,有点2M 即点D坐标为(1,3-,使2M CK 为等腰三角形. l 与抛物线的另一交点即为1M综上所述,当点M 的坐标为(1,3--时,MCK 为等腰三角形 解法2:当点M 的坐标分别为 理由如下:i 链接BK ,交抛物线于点G ,易知点G的坐标为(- .又点C的坐标为,则//.GC AB可求得4AB BK ==,且60ABK ∠=︒,即ABK ∆为正三角形.CGK ∴∆为正三角形∴当2l 与抛物线交于点G ,即2//l AB 时,符合题意,此时点1M的坐标为(- ii 连接CD ,由230KD CK CG CKD ===∠=︒,,易知KDC ∆为等腰三角形 当2l 过抛物线顶点于点D 时,符合题意,此时点2M 的坐标为(1,)3-. iii 当点M 在抛物线对称轴右边时,只有点M 与点A 重合时,满足CM CK =,但此时,三点A C K 、、在同一直线上,不能构成三角形.综上所述,当点M的坐标分别为(1,3--时,MCK ∆为等腰三角形. 14. 2011浙江绍兴,24,14分抛物线21(1)34y x =--+与y 轴交于点A ,顶点为B ,对称轴BC 与x 轴交于点C . 1如图1,求点A 的坐标及线段OC 的长;2点P 在抛物线上,直线//PQ BC 交x 轴于点Q ,连接BQ .①若含45°角的直线三角板如图2所示放置,其中,一个顶点与C 重合,直角顶点D 在BQ 上,另一顶点E 在PQ 上,求直线BQ 的函数解析式;②若含30°角的直角三角板一个顶点与点C 重合,直角顶点D 在直线BQ 上,另一个顶点E 在PQ 上,求点P 的坐标.答案解:1把0x=代入21(1)34y x =--+得114y =, ∴点11(0,)4A , BC 为对称轴,(1,3)B ,1OC ∴=.2①如图1,过点D 作DM x ⊥轴,交x 轴于点M , 过点D 作DN PQ ⊥,交PQ 于点N ,//PQ BC90DMQ DNQ MDN ∴∠=∠=∠=︒ ∴四边形MDNQ 为矩形,90,,,,,CDE MDN CDM EDN DC DE DCM DEN DM DN ∠=∠=︒∴∠=∠=∴∆≅∆∴=∴四边形MDNQ 为正方形,45DQC ∴∠=︒,BCQ ∴∆为等腰直角三角形, 34CQ BC OQ ∴==∴=,,设直线BQ 的函数解析式为y kx b =+, 直线上两点的坐标为(1,3),(4,0)B Q , 代入求得1,4k b =-=,∴直线BQ 的函数解析式为4y x =-+.②当点P D DM x ⊥x M D DN PQ ⊥PQ N (,0)Q m 90,Rt Rt ,,,,//,,31,CDM MDE EDN MDE CDM EDN CD DMCDM EDN DE DNCD DMDN MQ DE MQ DM BCPQ BC MQ CQCD DE m ∠+∠=∠+∠=︒∴∠=∠∴∆∆∴==∴=∴=∴=-, 15. 2011浙江台州,24,14分已知抛物线n m x a y +-=2)(与y 轴交于点A,它的顶点为B,点A 、B 关于原点O 的对称点分别是点C 、D;若点A 、B 、C 、D 中任何三点都不在一直线上,则称四边形ABCD 为抛物线的伴随四边形,直线AB 为抛物线的伴随直线;1如图1,求抛物线1)2(2+-=x y 的伴随直线的解析式;2如图2,若n m x a y +-=2)(m>0的伴随直线是y=x -3,伴随四边形的面积为12,求此抛物线的解析式; 3如图3,若抛物线n m x a y +-=2)(的伴随直线是y =-2x+bb>0,且伴随四边形ABCD 是矩形; ① 用含b 的代数式表示m,n 的值;② 在抛物线的对称轴上是否存在点P,使得△PBD 是一个等腰三角形若存在,请直接写出点P 的坐标用含b 的代数式;若不存在,请说明理由;答案解:1设直线AB 的解析式为y=kx+b.由题意,得:A0,5,B2,1 ∴⎩⎨⎧=+=125b k b ∴k=-2 ,b=5∴直线AB 的解析式为y=-2x+52 由伴随直线是y=x -3,得:A0,-3,C0,3 ∴ AC=6 由伴随四边形的面积为12,得:△ABC 的面积为6=m AC ⨯⨯21∴m=±2 ∵m>0 ∴m=2当m=2时,y=-1,顶点为2,-1, 且过点C0,3 ∴抛物线的解析式为y=1)2(212---x ; 3 ① 如图,作BE ⊥x 轴,由题意,得:A0,b,C 0,-b∵抛物线的顶点Bm,n 在y=-2x+bb>0上, ∴n=-2m+b Bm, -2m+b 在矩形ABCD 中,OC=OB ∴OC 2=OB 2即:222)b -2m (++=m b ∴m5m-4b=0 ∴m 1=0舍去,m 2=b 54 ∴n=-2m+b=b 53∴ b m 54=,b n 53=; ② 存在,有4个点:b 54,b 57, b 54,b 59, b 54,b 1516, b 54,b 513-16. 2011浙江义乌,24,12分已知二次函数的图象经过A 2,0、C 0,12 两点,且对称轴为直线x =4. 设顶点为 点P ,与x 轴的另一交点为点B .1求二次函数的解析式及顶点P 的坐标;2如图1,在直线 y=2x 上是否存在点D ,使四边形OPBD 为等腰梯形若存在,求出点D 的坐标;若不存在,请说明理由;3如图2,点M 是线段OP 上的一个动点O 、P 两点除外,以每秒2个单位长度的速度由点P 向点O 运动,过点M 作直线MN ∥x 轴,交PB 于点N. 将△PMN 沿直线MN 对折,得到△P 1MN. 在动点M 的运动过程中,设△P 1MN 与梯形OMNB 的重叠部分的面积为S ,运动时间为t 秒. 求S 关于t 的函数关系式.答案1设二次函数的解析式为y =ax 2+bx +c由题意得⎪⎪⎩⎪⎪⎨⎧=++==-0241242c b a c a b 解得⎪⎩⎪⎨⎧=-==1281c b a∴二次函数的解析式为y = x 2-8x +12 点P 的坐标为4,-42存在点D ,使四边形OPBD 为等腰梯形. 理由如下:当y =0时,x 2-8x +12=0 ∴x 1=2 , x 2=6 ∴点B 的坐标为6,0设直线BP 的解析式为y =kx +m 则⎩⎨⎧-=+=+4406m k m k 解得⎩⎨⎧-==122m k∴直线BP 的解析式为y =2x -12D xA OBCPyO PC BAxy图1图2MOAxPNCBy∴直线OD ∥BP∵顶点坐标P 4, -4 ∴ OP =42 设Dx ,2x 则BD 2=2x 2+6-x 2当BD =OP 时,2x 2+6-x 2=32解得:x 1=52,x 2=2 当x 2=2时,OD =BP =52,四边形OPBD 为平行四边形,舍去∴当x =52时四边形OPBD 为等腰梯形 ∴当D 52,54时,四边形OPBD 为等腰梯形3① 当0<t ≤2时,∵运动速度为每秒2个单位长度,运动时间为t 秒, 则MP =2t ∴PH =t ,MH =t ,HN =21t ∴MN =23t ∴S =23t ·t ·21=43t 2 ② 当2<t <4时,P 1G =2t -4,P 1H =txP 1 MAO BCPNyH∵MN ∥OB ∴ EF P 1∆∽MN P 1∆∴211)(11H P G P S S MNP EF P =∆∆ ∴22)42(431t t t S EF P -=∆ ∴ EF P S 1∆=3t 2-12t +12∴S =43t 2-3t 2-12t +12= -49t 2+12t -12 ∴ 当0<t ≤2时,S=43t 2当2<t <4时,S =-49t 2+12t -12 ;17. 2011四川重庆,26,12分如图,矩形ABCD 中,AB =6,BC =2错误!,点O 是AB 的中点,点P 在AB 的延长线上,且BP =3.一动点E 从O 点出发,以每秒1个单位长度的速度沿OA 匀速动动,到达A 点后,立即以原速度沿AO 返回;另一动点F 从P 点出发,以每秒1个单位长度的速度沿射线P A 匀速动动,点E 、F 同时出发,当两点相遇时停止运动.在点E 、F 的运动过程中,以EF 为边作等边△EFG ,使△EFG 和矩形ABCD 在射线P A 的同侧,设动动的时间为t 秒t ≥0. 1当等边△EFG 的边FG 恰好经过点C 时,求运动时间t 的值;2在整个运动过程中,设等边△EFG 和矩形ABCD 重叠部分的面积为S ,请直接写出S 与t 之间的函数关系式和相应的自变量t 的取值范围;3设EG 与矩形ABCD 的对角线AC 的交点为H ,是否存在这样的t ,使△AOH 是等腰三角形若存在,求出对应的t 的值;若不存在,请说明理由.xP 1M A OB CPNG HE F y答案1当等边△EFG的边FG恰好经过点C时如图,∠CFB=60°,BF=3-t,在Rt△CBF中,BC=2错误!,∴tan∠CFB =错误!,∴tan 60°=错误!,∴BF=2,∴t=3-t =2,∴t=1.2当0≤t<1时,S= 2错误!t+4错误!;当1≤t<3时,S=错误!t 2+3错误!t+错误!;当3≤t<4时,S= -4错误! t+20错误!;当4≤t<6时,S= 错误!t2-12错误!t+36错误!.3存在,理由如下:在Rt△ABC中,tan∠CAB=错误!=错误!,∴∠CAB=30°.又∵∠HEO=60°,∴∠HAE=∠AHE=30°.∴AE=HE=3-t或t-3.ⅰ当AH=AO=3时如图②,过点E作EM⊥AH于M,则AM=错误!AH=错误!.在Rt△AME中,cos∠MAE=错误!,即cos 30°=错误!,∴AE=错误!,即3-t=错误!或t-3=错误!,t=3-错误!或3+错误!.ⅱ当HA=HO时如图③,则∠HOA=∠HAO=30°,又∵∠HEO=60°,∴∠EHO=90°.∴EO=2HE=2AE.又∵AE+EO=3,∴AE+2AE=3.∴AE=1.即3-t=1或t-3=1,t=2或4.ⅲ当OH=OA时如图④,则∠OHA=∠OAH=30°,∴∠HOB=60°=∠HEB.∴点E和O重合,∴AE=3.即3-t=3或t-3=3,t=6舍去或t=0.综上所述,存在5个这样的值,使△AOH是等腰三角形,即:t=3-错误!或t=3+错误!或t=2或t=4或t=0.18. 2011浙江省嘉兴,24,14分已知直线3+=kx y k <0分别交x 轴、y 轴于A 、B 两点,线段OA 上有一动点P 由原点O 向点A 运动,速度为每秒1个单位长度,过点P 作x 轴的垂线交直线AB 于点C ,设运动时间为t 秒.1当1-=k 时,线段OA 上另有一动点Q 由点A 向点O 运动,它与点P 以相同速度同时出发,当点P 到达点A 时两点同时停止运动如图1.① 直接写出t =1秒时C 、Q 两点的坐标;② 若以Q 、C 、A 为顶点的三角形与△AOB 相似,求t 的值. 2当43-=k 时,设以C 为顶点的抛物线n m x y ++=2)(与直线AB 的另一交点为D 如图2, ① 求CD 的长;② 设△COD 的OC 边上的高为h ,当t 为何值时,h 的值最大答案1①C 1,2,Q 2,0.②由题意得:Pt ,0,Ct ,-t+3,Q 3-t ,0, 分两种情形讨论:情形一:当△AQC ∽△AOB 时,∠AQC=∠AOB =90°,∴CQ ⊥OA , ∵CP ⊥OA ,∴点P 与点Q 重合,OQ =OP ,即3-t =t ,∴t=.情形二:当△ACQ ∽△AOB 时,∠ACQ=∠AOB =90°,∵O A=O B=3,∴△AOB 是等腰直角三角形,∴△ACQ 是等腰直角三角形,∵CQ ⊥OA ,∴AQ=2CP ,即t =2-t +3,∴t=2.∴满足条件的t 的值是秒或2秒. 2 ①由题意得:Ct ,-34t +3,∴以C 为顶点的抛物线解析式是23()34y x t t =--+, 由233()3344x t t x --+=-+,解得x 1=t ,x 2=t 34-;过点D 作DE ⊥CP 于点E ,则∠DEC=∠AOB =90°,DE ∥OA ,∴∠EDC=∠OAB ,∴△DEC ∽△AOB ,∴DE CDAO BA=, ∵AO =4,AB =5,DE =t -t-34=34.∴CD =35154416DE BA AO ⨯⨯==.②∵CD =1516,CD 边上的高=341255⨯=.∴S △COD =11512921658⨯⨯=.∴S △COD 为定值; 要使OC 边上的高h 的值最大,只要OC 最短. 因为当OC ⊥AB 时OC 最短,此时OC 的长为125,∠BCO =90°,∵∠AOB =90°,∴∠COP =90°-∠BOC =∠OBA ,第24题图2第24题图1又∵CP ⊥OA ,∴Rt △PCO ∽Rt △OAB ,∴OP OC BO BA =,OP =123365525OC BO BA ⨯⨯==,即t =3625, ∴当t 为3625秒时,h 的值最大.19. 2011福建泉州,25,12分在直角坐标系xoy 中,已知点P 是反比例函数)>0(32x xy =图象上一个动点,以P 为圆心的圆始终与y 轴相切,设切点为A .1如图1,⊙P 运动到与x 轴相切,设切点为K ,试判断四边形OKP A 的形状,并说明理由. 2如图2,⊙P 运动到与x 轴相交,设交点为B ,C .当四边形ABCP 是菱形时: ①求出点A ,B ,C 的坐标.②在过A ,B ,C 三点的抛物线上是否存在点M ,使△MBP 的面积是菱形ABCP 面积的21.若存在,试求出所有满足条件的M 点的坐标,若不存在,试说明理由.答案解:1∵⊙P 分别与两坐标轴相切, ∴ P A ⊥OA ,PK ⊥OK . ∴∠P AO =∠OKP =90°. 又∵∠AOK =90°,∴ ∠P AO =∠OKP =∠AOK =90°. ∴四边形OKP A 是矩形. 又∵OA =OK ,∴四边形OKP A 是正方形.……………………2分 2①连接PB ,设点P 的横坐标为x ,则其纵坐标为x32. 过点P 作PG ⊥BC 于G .AP23y x=xyKO第25题 图1∵四边形ABCP 为菱形, ∴BC =P A =PB =PC . ∴△PBC 为等边三角形.在Rt △PBG 中,∠PBG =60°,PB =P A =x , PG =x32. sin ∠PBG =PBPG,即2332x x =. 解之得:x =±2负值舍去.∴ PG =3,P A =B C=2.……………………4分 易知四边形OGP A 是矩形,P A =OG =2,BG =CG =1, ∴OB =OG -BG =1,OC =OG +GC =3.∴ A 0,3,B 1,0 C 3,0.……………………6分 设二次函数解析式为:y =ax 2+bx +c .据题意得:09303a b c a b c c ⎧++=⎪++=⎨⎪=⎩解之得:a =33, b =433-, c =3. ∴二次函数关系式为:2343333y x x =-+.……………………9分 ②解法一:设直线BP 的解析式为:y =ux +v ,据题意得:23u v u v +=⎧⎪⎨+=⎪⎩解之得:u =3, v =33-.∴直线BP 的解析式为:333y x =-.过点A 作直线AM ∥PB ,则可得直线AM 的解析式为:33y x =+.解方程组:233343333y x y x x ⎧=+⎪⎨=-+⎪⎩O AP 23y x=xyB C图2GM。
中考数学专题第9课时-动态型问题(含答案)

第9课时动态型问题动态型试题比较侧重图形的旋转、平移、对称、翻折,在这里重点考察学生几何图形的认识,对称、全等、相似,是对数学综合能力的考察动态型试题.对学生的思维要求比较高,对题目的理解要清晰,明确变化的量之间的关系,同时还要明确不变的量有那些,抓住关键,理清思路。
动态几何型问题体现的数学思想方法是数形结合思想,这里常把函数与方程、函数与不等式联系起来,实际上是一般化与特殊化方法.当求变量之间关系时,通常建立函数模型或不等式模型求解;当求特殊位置关系和值时,常建立方程模型求解.类型之一探索性的动态题探索性问题是指命题中缺少一定的条件或无明确的结论,需要经过推断。
探索型问题一般没有明确的结论,没有固定的形式和方法,需要学生自己通过观察、分析、比较、概括、推理、判断等探索活动来确定所需要的结论或方法或条件,用考察学生的分析问题和解决问题的能力和创新意识。
1.(宜昌市)如图,在Rt△ABC中,AB=AC,P是边AB(含端点)上的动点,过P作BC的垂线PR,R为垂足,∠PRB的平分线与AB相交于点S,在线段RS上存在一点T,若以线段PT为一边作正方形PTEF,其顶点E、F恰好分别在边BC、AC上.(1)△ABC与△SBR是否相似?说明理由;(2)请你探索线段TS与PA的长度之间的关系;(3)设边AB=1,当P在边AB(含端点)上运动时,请你探索正方形PTEF的面积y的最小值和最大值.2.(南京市)如图,已知O的半径为6cm,射线PM经过点O,O A CBxy 10cm OP =,射线PN 与O 相切于点Q .A B ,两点同时从点P 出发,点A 以5cm/s 的速度沿射线PM 方向运动,点B 以4cm/s 的速度沿射线PN 方向运动.设运动时间为t s .(1)求PQ 的长;(2)当t 为何值时,直线AB 与O 相切?类型之二 存在性动态题存在性动态题运用几何计算进行探索的综合型问题,要注意相关的条件,可以先假设结论成立,然后通过计算求相应的值,再作存在性的判断.3.如图,直线434+-=x y 和x 轴、y 轴的交点分别为B 、C ,点A 的坐标是(-2,0). (1)试说明△ABC 是等腰三角形;(2)动点M 从A 出发沿x 轴向点B 运动,同时动点N 从点B 出发沿线段BC 向点C 运动,运动的速度均为每秒1个单位长度.当其中一个动点到达终点时,他们都停止运动.设M 运动t 秒时,△MON 的面积为S .① 求S 与t 的函数关系式;② 设点M 在线段OB 上运动时,是否存在S =4的情形?若存在, 求出对应的t 值;若不存在请说明理由;③在运动过程中,当△MON 为直角三角形时,求t 的值.4.(湖州市) 已知:在矩形AOBC 中,4OB =,3OA =.分别以OB OA ,所在直线为x 轴和y 轴,建立如图所示的平面直角坐标系.F 是边BC 上的一个动点(不与B C ,重合),过F 点的反比例函数(0)ky k x=>的图象与AC 边交于点E . (1)求证:AOE △与BOF △的面积相等;(2)记OEF ECF S S S =-△△,求当k 为何值时,S 有最大值,最大值为多少?(3)请探索:是否存在这样的点F ,使得将CEF △沿EF 对折后,C 点恰好落在OB 上?若存在,求出点F 的坐标;若不存在,请说明理由.5.(白银市)如图,在平面直角坐标系中,四边形OABC 是矩形,点B 的坐标为(4,3).平行于对角线AC 的直线m 从原点O 出发,沿x 轴正方向以每秒1个单位长度的速度运动,设直线m 与矩形OABC 的两边..分别交于点M 、N ,直线m 运动的时间为t (秒). (1) 点A 的坐标是__________,点C 的坐标是__________; (2) 当t = 秒或 秒时,MN =21AC ; (3) 设△OMN 的面积为S ,求S 与t 的函数关系式;(4) 探求(3)中得到的函数S 有没有最大值?若有,求出最大值;若没有,要说明理由.类型之三 开放性动态题开放性问题的条件或结论不给出,即条件开放或结论开放,需要我们充分利用自己的想像,大胆猜测,发现问题的结论,寻找解决问题的方法,正确选择解题思路。
中考数学复习专题--动态型问题

1)当点P沿A-D-A运动时,求AP的长(用含 t的代数式表示).
解:(1)当点P沿A-D运动时,AP=8(t-1)=8t-8. 当点P沿D-A运动时,AP=50×2-8(t-1)=108-8t.
(2)连结AQ,在点P沿B-A-D运动过程中,当点P 与点B、点A不重合时,记△APQ的面积为S.求S
时t的值
当点P与点R重合时, AP=BQ,8t-8=5t,t=
8
.
当0<t≤1时,如图③. 3
∵S△BPM=S△BQM, ∴PM=QM.
∵AB∥QR,
∴∠PBM=∠QRM,
∠BPM=∠MQR
在△BPM和△RQM中
PBM QRM
B
P
M
MQR
PM Q M
∴△BPM≌△RQM. ∴BP=RQ, ∵RQ=AB, ∴BP=AB ∴13t=13, 解得:t=1
(2)S=-7t2+16t;
(3)S=-14t+32. ;
(3)试求(2)中当t为何值时,考区查 间了 上指 的定 函 S的值最大,并求出S的最大值; 数极值
①当0<t≤1时, (1)S=-5t2+14t;
②当1<t≤2时, (2)S=-7t2+16t;
③当2<t< 1 6
7
时,(3)S=-14t+32. ;
(1)当t=1时,S有最大值,最大值为9;
(2)当t= 8 时,S有最大值,最大值为 6 4 ;
7
7
(3)0<S<4
(4)随着P,Q两点的运动,当点M在线段 DC上运动时,设PM的延长线与直线l相交于 点N,试探究:当t为何值时,△QMN为等腰
三角形?请直接写出t的值
如答图4所示,点M在线段 CD上,与Q相遇前时, MQ=CD-DM-CQ=7-(2t4)-(5t-5)=16-7t, MN=DM=2t-4, 由MN=MQ,得16-7t=2t-4, 解得t= 2 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考数学“动态型”问题专项检测一、选择题1,将直线y =2x 向右平移2个单位所得的直线的解析式是( ) A.y =2x +2 B.y =2x -2 C.y =2(x -2) D.y =2(x +2) 2.如图1,△ACD 和△AEB 都是等腰直角三角形,∠CAD =∠EAB =90°,四边形ABCD 是平行四边形,下列结论中错误的是( )A.△ACE 以点A 为旋转中心,逆时针方向旋转90°后与△ADB 重合B.△ACB 以点A 为旋转中心,顺时针方向旋转270°后与△DAC 重合C.沿AE 所在直线折叠后,△ACE 与△ADE 重合D.沿AD 所在直线折叠后,△ADB 与△ADE 重合3,如图2,四边形ABCD 为矩形纸片.把纸片ABCD 折叠,使点B 恰好落在CD 边的中点E 处,折痕为AF .若CD =6,则AF 等于( )D.84,(20XX 年重庆市)如图4,在矩形ABCD 中,AB =3,BC =4,点P 在BC 边上运动,连结DP ,过点A 作AE ⊥DP ,垂足为E ,设DP =x ,AE =y ,则能反映y 与x 之间函数关系的大致图象是( )5.如图4,MN是⊙O 的直径,MN =2,点A 在⊙O 上,∠AMN =30°,B 为AN 的中点,P 是直径MN 上一动点,则P A +PB 的最小值为( )C.1D.26, 如图5,在等腰梯形ABCD 中,AB ∥DC ,AD =BC =5,DC =7,AB =13,点P 从点A 出发,以3个单位/s 的速度沿AD →DC 向终点C 运动,同时点Q 从点B 出发,以1个单位/s 的速度沿BA 向终点A 运动.在运动期间,当四边形PQBC 为平行四边形时,运动时间为( )A.3sB.4sC.5sD.6s图4B FC ED A 图2 图1E DCB A A BC D图3E P DC B A 10 题图ABQ图57.如图6,在直角梯形ABCD 中,∠ABC =90°,DC ∥AB ,BC =3,DC =4,AD =5.动点P 从B 点出发,由B →C →D →A 沿边运动,则△ABP 的最大面积为( )A.10B.12C.14D.168.如图7,已知EF 是⊙O 的直径,把∠A 为60°的直角三角板ABC 的一条直角边BC 放在直线EF 上,斜边AB 与⊙O 交于点P ,点B 与点O 重合;将三角形ABC 沿OE 方向平移,使得点B 与点E 重合为止.设∠POF =x °,则x 的取值范围是( )A.60≤x ≤120B. A.30≤x ≤60C. A.30≤x ≤90D. A.30≤x ≤120二、填空题9, 将一块含30°角的三角尺绕较长直角边旋转一周得一圆锥.设较短直角边的边长为1,则这个圆锥的侧面积为 .10, 如图8,将正方形ABCD 中的△ABP 绕点B 顺时针旋转能与△CBP 重合,若BP =4,则点P 所走过的路径长为______.11, 如图9,在等腰△ACB 中,AC =BC =5,AB =8,D 为底边AB 上一动点(不与点A ,B 重合),DE ⊥AC ,DF ⊥BC ,垂足分别为E ,F ,则DE +DF = .12, 如图10所示的圆柱体中底面圆的半径是2π,高为2,若一只小虫从A 点出发沿着圆柱体的侧面爬行到C 点,则小虫爬行的最短路程是 (结果保留根号)13,如图12,小正六边形沿着大正六边形的边缘顺时针滚动,小正方形的边长是大正六边形边长的一半,当小正六边形由图①位置滚动到图②位置时,线段OA 绕点O 顺时针转过的角度为_______度.y 轴于点A (4,0)与 B (0,-3),现有一半径为1的动圆的圆心AB 相切.D C P B A 图6 OF C A P E (B ) 图7 图8 A B C DEF 图9 D C A B 图10图12 ① ②B(0,-3)(4,0)Ao x(4y图1415.如图14所示,直线l 1⊥l 2,垂足为点O ,A 、B 是直线l 1上的两点,且OB =2,AB.直线l 1绕点O 按逆时针方向旋转,旋转角度为α(0°<α<180°).(1)当α=60°时,在直线l 2上找点P ,使得△BP A 是以∠.B .为顶角...的等腰三角形,此时OP =_____.(2)当α在什么范围内变化时,直线l 2上存在点P ,使得△BP A 是以∠.B .为顶角...的等腰三角形,请用不等式表示α的取值范围:______. 三、解答题16,如图15,⊙O 的直径AB =6cm ,P 是AB 延长线上的一点,过P 点作⊙O 的切线,切点为C ,连接AC .(1)若∠CP A =30°,求PC 的长;(2)若点P 在AB 的延长线上运动,∠CP A 的平分线交AC 于点M ,你认为∠CMP 的大小是否发生变化?若变化,请说明理由;若不变,求出∠CMP 的值.17.如图16①,OABC 是一张放在平面直角坐标系中的矩形纸片,O 为原点,点A 在x 轴的正半轴上,点C 在y 轴的正半轴上,OA =5,OC =4.(1)在OC 边上取一点D ,将纸片沿AD 翻折,使点O 落在BC 边上的点E 处,求D 、E 两点的坐标; (2)图②,若AE 上有一动点P (不与A 、E 重合)自A 点沿AE 方向向E 点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为t 秒(0<t <5),过P 点作ED 的平行线交AD 于点M ,过点M 作AE 的平行线交DE 于点N .求四边形PMNE 的面积S 与时间t 之间的函数关系式;当t 取何值时,S 有最大值?最大值是多少?(3)在(2)的条件下,当t 为何值时,以A 、M 、E 为顶点的三角形为等腰三角形,并求出相应时刻点M 的坐标.C P A B O· 图1518.已知:∠MAN =60°,点B 在射线AM 上,AB =4(如图17).P 为直线AN 上一动点,以BP 为边作等边三角形BPQ (点B ,P ,Q 按顺时针排列),O 是△BPQ 的外心.(1)当点P 在射线AN 上运动时,求证:点O 在∠MAN 的平分线上;(2)当点P 在射线AN 上运动(点P 与点A 不重合)时,AO 与BP 交于点C ,设AP =x ,AC ·AO =y ,求y 关于x 的函数解析式,并写出函数的定义域;(3)若点D 在射线AN 上,AD =2,圆I 为△ABD 的内切圆.当△BPQ 的边BP 或BQ 与圆I 相切时,请直接写出点A 与点O 的距离.19.如图19,在等腰梯形ABCD 中,AD ∥BC ,AB =DC =50,AD =75,BC =135.点P 从点B 出发沿折线段BA →AD →DC 以每秒5个单位长的速度向点C 匀速运动;点Q 从点C 出发沿线段CB 方向以每秒3个单位长的速度匀速运动,过点Q 向上作射线QK ⊥BC ,交折线段CD →DA →AB 于点E .点P 、Q 同时开始运动,当点P 与点C 重合时停止运动,点Q 也随之停止.设点P 、Q 运动的时间是t 秒(t >0).(1)当点P 到达终点C 时,求t 的值,并指出此时BQ 的长; (2)当点P 运动到AD 上时,t 为何值能使PQ ∥DC ?(3)设射线QK 扫过梯形ABCD 的面积为S ,分别求出点E 运动到CD 、DA 上时,S 与t 的函数关系式;(不必写出t 的取值范围)(4)△PQE 能否成为直角三角形?若能,写出t 的取值范围;若不能,请说明理由.M 图17 图18备用图19参考答案:一、1,B ;2,B ;3,A ;4,C ;5,B ;6,A ;7,B ;8,B . 二、9,2π;10,2π;11,524;12,;13,240°;14,73或173;15,(1-1(2)45°<α<90°或90°<α<135°.三、16,(1)连接OC ,PC 是⊙O 的切线,所以∠OCP =Rt ∠.因为∠CP A =30°,OC =2AB=3,所以tan30°=3PC,即PC =.2)∠CMP 的大小不发生变化.因为PM 是∠CP A 的平分线,所以∠CPM =∠MP A .因为OA =OC ,所以∠A =∠ACO .在△APC 中,因为∠A +∠ACP +∠CP A =180°,所以2∠A +2∠MP A =90°,∠A +∠MP A =45°.所以∠CMP =∠A +∠MP A =45°.即∠CMP 的大小不发生变化.17,(1)依题意可知,折痕AD 是四边形OAED 的对称轴,所以在Rt △ABE 中,AE =AO =5,AB =4,所以BE3,所以CE =2,E 点坐标为(2,4).在Rt △DCE 中,DC 2+CE 2=DE 2,又因为DE =OD ,所以(4-OD )2+22=OD 2,解得OD =52,所以D 点坐标为(0,52).(2)因为PM ∥ED ,所以△APM ∽△AED ,所以PM ED =AP AE ,又知AP =t ,ED =52,AE =5,所以PM =5t ×52=2t,又因为PE =5-t , 而显然四边形PMNE 为矩形,所以S PMNE =PM ×PE =2t ×(5-t )=12t 2+52t .所以S PMNE =12(t-52)2+258 又因为0<52<5,所以当t =52时,S PMNE 有最大值258(面积单位).(3)(i )若ME =MA ,在Rt △AED 中,ME =MA ,因为PM ⊥AE ,所以P 为AE 的中点.又因为PM ∥ED ,所以M 为AD 的中点,所以AP =12AE =52,所以AP =t =52,所以PM =12t =54,又因为P 与F 是关于AD 对称的两点,所以x M =52,y M =54,所以当t =52时(0<52<5),△AME 为等腰三角形,此时M 点坐标为(52,54).(ii )若AM =AE =5,在Rt △AOD 中,AD52因为PM ∥ED ,所以△APM∽△AED ,所以AP AE =AM AD ,所以t =AP =AM AE AD ⋅=555⨯PM =12tx M =5-y Mt =0<5),此时M 点坐标为(5-综合(i )、(ii )可知:t =52或t =A 、M 、E 为顶点的三角形为等腰三角形,相应M 点的坐标为(52,54)或(5-18,(1)证明:如图1,连结OB OP ,,O 是等边三角形BPQ 的外心,OB OP ∴=,圆心角3601203BOP ∠==.当OB 不垂直于AM 时,作OH AM ⊥,OT AN ⊥,垂足分别为H T ,.由360HOT A AHO ATO ∠+∠+∠+∠=,且60A ∠=,90AHO ATO ∠=∠=,120HOT ∴∠=.BOH POT ∴∠=∠.Rt Rt BOH POT ∴△≌△.OH OT ∴=.∴点O 在MAN ∠的平分线上.当OB AM ⊥时,36090APO A BOP OBA ∠=-∠-∠-∠=.即OP AN ⊥,∴点O 在MAN ∠的平分线上.综上所述,当点P 在射线AN 上运动时,点O 在MAN ∠的平分线上.(2)如图2,AO 平分MAN ∠,且60MAN ∠=,30BAO PAO ∴∠=∠=.由(1)知,OB OP =,120BOP ∠=,30CBO ∴∠=,CBO PAC∴∠=∠.BCO PCA∠=∠,AOB APC ∴∠=∠.ABO ACP ∴△∽△.AB AOAC AP∴=.AC AO AB AP ∴=,4y x ∴=.定义域为:0x >.(3)解:①如图3,当BP 与圆I相切时,AO =②如图4,当BP 与圆I相切时,AO =;③如图5,当BQ 与圆I 相切时,0AO =.19,(1)t =(50+75+50)÷5=35(秒)时,点P 到达终点C . 此时,QC =35×3=105,∴BQ 的长为135-105=30.(2)如图1,若PQ ∥DC ,又AD ∥BC ,则四边形PQCD 为平行四边形,从而PD =QC ,由QC =3t ,BA +AP =5t ,得50+75-5t =3t ,解得t =1258.经检验,当t =1258时,有PQ ∥DC .Q图2Q图1图3图4M图5 图1图2(3)①当点E 在CD 上运动时,如图2.分别过点A 、D 作AF ⊥BC 于点F ,DH ⊥BC 于点H ,则四边形ADHF 为矩形,且△ABF ≌△DCH ,从而FH = AD =75,于是BF =CH =30.∴DH =AF =40.又QC =3t ,从而QE =QC ·tan C =3t ·CHDH=4t .(注:用相似三角形求解亦可)∴S =S ⊿QCE =12QE ·QC =6t 2;②当点E 在DA 上运动时,如图8.过点D 作DH ⊥BC 于点H ,由①知DH =40,CH =30,又QC =3t ,从而ED =QH =QC -CH =3t -30.∴S = S 梯形QCDE =12(ED +QC )DH =120 t -600. (4)△PQE 能成为直角三角形.当△PQE 为直角三角形时,t 的取值范围是0<t ≤25且t ≠1558或t =35.(注:(4)问中没有答出t ≠1558或t =35者各扣1分,其余写法酌情给分)下面是第(4)问的解法,仅供参考:①当点P 在BA (包括点A )上,即0<t ≤10时,如图2.过点P 作PG ⊥BC 于点G ,则PG =PB ·sin B =4t ,又有QE =4t = PG ,易得四边形PGQE 为矩形,此时△PQE 总能成为直角三角形.②当点P 、E 都在AD (不包括点A 但包括点D )上,即10<t ≤25时,如图1.由QK ⊥BC 和AD ∥BC 可知,此时,△PQE 为直角三角形,但点P 、E 不能重合,即5t -50+3t -30≠75,解得t ≠1558. ③当点P 在DC 上(不包括点D 但包括点C ),即25<t ≤35时,如图3.由ED >25×3-30=45,可知,点P 在以QE =40为直径的圆的外部,故∠EPQ 不会是直角.由∠PEQ <∠DEQ ,可知∠PEQ 一定是锐角.对于∠PQE ,∠PQE ≤∠CQE ,只有当点P 与C 重合,即t =35时,如图4,∠PQE =90°,△PQE 为直角三角形.综上所述,当△PQE 为直角三角形时,t 的取值范围是0<t ≤25且t ≠1558或t =35.F (Q )图4图3。
