2020届北京是中学生标准学术能力诊断性测试诊断性测试(1月)数学(理)试题(解析版)
中学生标准学术能力诊断性测试2020年1月试题 数学(文) 含答案
中学生标准学术能力诊断性测试2020年1月测试文科数学试卷本试卷共150分，考试时间120分钟。
一、选择题：本大题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1.已知集合U ＝N ，A ＝{x|x ＝2n ，n ∈N}，B ＝{x|1<x ≤6，n ∈N}，则()U A B =I ð A. {2，3，4，5，6} B. {2，4，6} C. {1，3，5} D. {3，5}2.复数z ＝(1－mi)2(i 为虚数单位)为纯虚数，则实数m ＝ A.±1 B.－1 C.1 D.03.以双曲线2213y x -=的顶点为焦点，离心率为33的椭圆的标准方程为A.22143x y +=B.22134x y +=C.22196x y +=D.22169x y += 4.函数f(x)＝3ln xx的部分图像是5.已知α∈(0，π)，3sin 35πα⎛⎫+= ⎪⎝⎭，则cos 26πα⎛⎫+= ⎪⎝⎭ A.2425 B.－2425 C.725 D.－7256.点P ，Q 在圆x 2＋y 2＋kx －4y ＋3＝0上(k ∈R)，且点P ，Q 关于直线2x ＋y ＝0对称，则该圆的半径为3 2 C.1 27.已知函数f(x)＝x 3－x 和点P(1，－1)，则过点P 与该函数图像相切的直线条数为 A.1 B.2 C.3 D.48.某几何体的三视图如图所示(单位：cm)，则该几何体的体积是 A.372cm B.373cm C.376cm D.37cm 9.已知数列{a n }是等比数列，前n 项和为S n ，则“2a 3>a 1＋a 5”是“S 2n －1<0”的A.必要不充分条件B.充分不必要条件C.充要条件D.既不充分也不必要条件10.在△PAB 中，已知2,1OB BA ==u u u r u u u r ，∠AOB ＝45°，点P 满足OP OA OB λμ=+u u u r u u u r u u u r (λ，µ∈R)，其中2λ＋µ＝3满足，则|OP uuu r|的最小值为A.355 B.255 C.63 D.6211.边长为2的等边△ABC 和有一内角为30°的直角△ABC 1所在半平面构成60°的二面角，则下列不可能是线段CC 1的取值的是 A.30 B.10 C.10 D.10 12.已知不等式x ＋alnx ＋1x e≥x a 对x ∈(1，＋∞)恒成立，则实数a 的最小值为 A.－e B.－2eC.－eD.－2e 二、填空题：本大题共4小题，每小题5分，共20分。
中学生标准学术能力诊断性测试THUSSAT2024年1月数学试卷及答案
一、单项选择题：本题共8符合题目要求的．1． 已知R ∈m ，集合=A ，若C AB =则=mA ．−32． 已知数列a n }{满足a 1A ．+−n 21213． 复数z 满足+=z 2i )(A ．−34． 在直三棱柱−ABC A 1A ．7 5． 设x a a x +=+n1201)(A ．66． 若不等式A ．5 7． 已知==a b 2e ,ln e23A ．>>a b c8． 已知>+−x y x y ,0,33A ．15．若,αγβγ，则αβ．若,,mn m n αβ，则αβγ⊥，则⊥⊥αγβγ,，则αβx 2E F ,，5．12PE PF ⋅=−25258=12)分成长度相等的四段D ．3 则+++ααβtan 2tan )(D ．8当∈x 2,4][时，=f x )(C 上一点，线段PF 2的中垂的离心率为 ． 动直线=≠x a a 0)(与函数l 1与函数g x )(的图象+x 817)恒成立，则实数m四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．（10分）数列a n }{的前n 项和为=S a n ,11，当≥n 2时，⎝⎭ ⎪=−⎛⎫S a S nn n 212．（1）求证：数列⎩⎭⎨⎬⎧⎫S n 1是等差数列，并求S n 的表达式；（2）设+=n b n S n n212，数列b n }{的前n 项和为T n ，不等式≤−+T m m n n 32对所有的N *∈n 恒成立，求正整数m 的最小值．18．（12分）如图所示，在∆ABC 中，=AB D 1,是BC 上的点，∠=∠BAD DAC 21． （1）若∠=πBAC 2，求证：−=AD AC 21； （2）若1BD DC =4，求∆ABC 面积的最大值．19．（12分）如图所示，一只蚂蚁从正方体−ABCD A BC D 1111的顶点A 1出发沿棱爬行，记蚂蚁从一个顶点到另一个顶点为一次爬行，每次爬行的方向是随机的，蚂蚁沿正方体上、下底面上的棱爬行的概率为61，沿正方体的侧棱爬行的概率为32．（1）若蚂蚁爬行n 次，求蚂蚁在下底面顶点的概率；（2）若蚂蚁爬行5次，记它在顶点C 出现的次数为X ，求X 的分布列与数学期望．（第19题图）（第18题图）20．（12分）如图所示，已知∆ABC 是以BC 为斜边的等腰直角三角形，点M 是边AB 的中点，点N 在边BC 上，且=BNNC 3．以MN 为折痕将∆BMN 折起，使点B 到达点D 的位置，且平面⊥DMC 平面ABC ，连接DA DC ,．（1）若E 是线段DM 的中点，求证：NE 平面DAC ；（2）求二面角−−D AC B 的余弦值．21．（12分）如图所示，已知抛物线=−y x M 1,0,12)(，A ，B 是抛物线与x 轴的交点，过点M 作斜率不为零的直线l 与抛物线交于C ，D 两点，与x 轴交于点Q ，直线AC 与直线BD 交于点P ．（1）求⋅CDCM DM 的取值范围；（2）问在平面内是否存在一定点T ，使得TP TQ ⋅为定值？若存在，求出点T 的坐标；若不存在，请说明理由．22．（12分）已知函数=+−−xf x x a x1ln 2)(有两个零点<x x x x ,1212)(． （1）求实数a 的取值范围； （2）求证：<x x 112； （3）求证：−<<−x x x x 212122．（第20题图）（第21题图）中学生标准学术能力诊断性测试2024年1月测试数学参考答案一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，部分选对但不全的得2分，有错选的得0分．三、填空题：本题共4小题，每小题5分，共20分．13．4 14．135 15．216．，⎝⎦⎥ −∞⎛⎤21 四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤． 17．（10分）（1）当≥n 2时，数列a n }{的前n 项和为S n ，满足⎝⎭⎪=−⎛⎫S a S n n n 212， 即⎝⎭ ⎪=−−=−−+⎛⎫−−−S S S S S S S S S n n n n n n n n n 22211111122)(， 整理可得=−−−S S S S n n n n 211 ········································································ 1分 11S =，则=−S S S S 22112，即=−S S 2122，可得=S 312 ······························· 2分由=−S S S S 22323，即=−S S 332133，可得,,=S 513以此类推可知，对任意的N *∈>n S n ,0，在等式=−−−S S S S n n n n 211两边同时除以−S S n n 1可得−=−S S n n 2111······················· 4分所以数列⎩⎭⎨⎬⎧⎫S n 1为等差数列，且其首项为=S 111，公差为2 ································· 5分 ∴=+−=−S n n n 121211)(，因此， −=n S n 211 ············································ 6分 （2）解：()()⎝⎭⎝⎭+−+−+ ⎪ ⎪ ⎪==+=+−⎛⎫⎛⎫n n n n n b n S n n 214212148212111111112 ， ⎝⎭+ ⎪∴=+−⎛⎫n T n n 4821111 ············································································ 8分 不等式≤−+T m m n n 32对所有的N *∈n 恒成立，则−+≥m m 33022，即≥+m 69或≤m 69····································································· 9分 因此，满足条件的正整数m 的最小值为3 ······················································ 10分 18．（12分）（1）证明：由∠=∠=∠πBAC BAD DAC 22,1，知∠=∠=ππBAD DAC 63,，=+⋅⋅+⋅⋅=⋅ππ∆∆S S S AB AD AD AC AB AC ABC ABD ACD 26232,sin sin 111，即+⋅=AD AC AC 2，两边同除以⋅AD AC，得−=AD AC21······················································ 5分 （2）设∠=αBAD ，则∠=αDAC 2，∆ABD 中，由正弦定理，得∠=αBDA AB BDsin sin ①，∆ACD 中，由正弦定理，得∠=αCDA AC DCsin sin 2 ②，②÷①，结合∠=∠=BDA CDA DC BD sin sin ,4，得=αAC cos 2···················· 7分 =⋅⋅===−⋅−∆αααααααS AB AC ABCsin 33tan 4tan sin 1sin 33sin 4sin 23++=−⋅=−ααααααα1tan 1tan 3tan 4tan tan 3tan tan 2223 ···································· 9分设=∈αt tan (，即求函数+=∈−ty t t t 1,323(的最大值， ()()++'==−+−−−−++t t y t t t t t t t 113313233222222322)()()()()(，∈−t 32)(时，'>y 0，函数单调递增；∈t 3,32)(时，'<y 0，函数单调递减，当=−t 32时，函数有最大值，=y max∴∆ABC··························································· 12分 19．（12分）（1）记蚂蚁爬行n 次在底面ABCD 的概率为P n ，由题意可得，==+−+P P P P n n n 333,121211)(···················································· 3分 ⎝⎭⎩⎭ ⎪⎨⎬−=−−−⎛⎫⎧⎫+P P P n n n 2322,11111是等比数列，首项为61，公比为−31， ⎝⎭⎝⎭⎪⎪−=−=+−⎛⎫⎛⎫−−P P n n n n 263263,11111111························································ 5分（2）X =0,1,2，X =2时，蚂蚁第3次、第5次都在C 处，⎝⎭⎝⎭ ⎪ ⎪==⨯⨯⨯+⨯⨯⨯+⨯⨯⨯⨯⨯+⨯+⨯=⎛⎫⎛⎫P X 6636366363366661822221121211212211111)( ·············································································································· 7分X =1时，蚂蚁第3次在C 处或第5次在C 处， 设蚂蚁第3次在C 处的概率为P 1，⎝⎭⎝⎭ ⎪ ⎪=⨯⨯⨯+⨯⨯⨯+⨯⨯⨯⨯⨯+⨯+⨯=⎛⎫⎛⎫P 6636366366666331822211212112115152111·············································································································· 8分 设蚂蚁第5次在C 处的概率为P 2，设蚂蚁不过点C 且第3次在D 1的概率为P 3，设蚂蚁不过点C 且第3次在B 1的概率为P 4，设蚂蚁不过点C 且第3次在A 的概率为P 5，由对称性知，=P P 34，=⨯⨯⨯+⨯⨯⨯=P 6663635443111212133，=⨯⨯⨯+⨯⨯=P 636333276121222115，得=⨯⨯⨯+⨯⨯⨯=P P P 63665422212117235 ··················································· 11分 ∴==+=P X P P 271512)(， ==−=−==P X P X P X 54011241)()()(， XX 的数学期望=⨯=+⨯=+⨯==E X P X P X P X 270011228)()()()( ············ 12分20．（12分）（1）过点E 作AM 的平行线交AD 于点F ，过点N 作AB 的平行线交AC 于点G ，连接FG ．因为点E 是线段DM 的中点，=BN NC 3，∴==EF NG AM 21，且EFNG ，四边形EFGN 是平行四边形．由,NEFG NE ⊄平面DAC ，⊂FG 平面DAC ，∴NE 平面DAC ······················································································ 5分（2）解法1：以点A 为原点，AB ，AC 所在的直线为x 轴、y 轴，过点A 垂直于平面ABC 的直线为z 轴，建立空间直角坐标系····································································· 6分 设==AB AC 2，则⎝⎭⎪⎛⎫A M N 220,0,0,,1,0,0,,,013)()(，设D x y z ,,,)(，因为平面⊥DMC 平面ABC ，所以点D 在平面ABC 上的射影落在直线CM 上，∴+=x y21 ①，由题意可知，==∴−++=DM DN x y z 1,11222)( ②， ⎝⎭⎝⎭ ⎪ ⎪−+−+=⎛⎫⎛⎫x y z 222139222③，由①②③解得，⎝⎭ ⎪ ⎪==−=∴−⎛⎫x y z D 777777,,,,,8282 ·························· 8分 82211816211,,,,,AD CD ⎛⎫⎛⎫=−=− ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭777777，设平面ACD 的法向量为(,,n x y z =)，00AD n CD n ⋅=⋅=⎩⎪⎨⎪⎧，即⎩⎪−+=⎨⎪−+=⎧x y x y 48040，取===−x y z 0,4 ······················ 11分 取平面ABC 的法向量(0,0,1m =)．设二面角−−D AC B 的平面角为θ， 则43cos cos ,9m n m nm n⋅===θ， 所以，二面角−−D AC B 的余弦值为9··················································· 12分 解法2：如图，过点B 作直线 MN 的垂线交于点I ，交直线CM 于点H ．由题意知，点D 在底面ABC 上的射影在直线BI 上且在直线MC 上，所以点H 即点D 在底面上的射影，即⊥DH 平面ABC ····················································································· 6分设=AB 2，则==∠=πBM BN MBN 41,，由余弦定理，得=MN 2，∠=∠−∠=⋅+⋅=IMH IMB HMB 10510510cos cos )(，∠==IMH MH MI cos 7．过点H 作AC 的垂线交于点O ，连接DO ，由三垂线定理知，⊥DO AC ，∴∠DOH 是二面角−−D AC B 的平面角 ········································································ 9分 由=HO CH AM CM，解得===HO DH 77,8，∠==HO DOH DH 4tan，得∠=DOH 9cos ，所以，二面角−−D AC B的余弦值为9·················································· 12分 21．（12分）（1）设点C x y D x y ,,,1122)()(，设直线l 的方程为=+≠y kx k 10)(，代入抛物线=−y x 12，得−−=x kx 202（*），⎝⎭⎪ ⎪===⎛⎫CD CM DM 2,2 ·········· 4分（2）⎝⎭⎪−−−⎛⎫k C x x D x x Q ,1,,1,,01112222)()(，设T m n ,)(， 由（*）式，知+==−x x k x x ,21212 ······························································ 5分 直线AC 的方程为=−+y x x 111)()(，直线BD 的方程为=+−y x x 112)()(，解得−+−+−+===++−−−−x x x x x x x y x x x x x x x x 222,212321212112121212)()(，所以点P 的坐标为⎝⎭−+−+ ⎪+⎛⎫−−x x x x x x x x 22,2321211212)( ··············································· 7分 ()1212231,,,x x x x TP m n TQ m n −−⎛⎫+⎛⎫=−−=−−− ⎪ ⎪⎝⎭⎝⎭−+−+x x x x k 222121，TP TQ m m n n ⎛⎫⋅=−−−+−− ⎪ ⎪ ⎪⎛⎫+⎛⎫−−x x x x 1231212)()(()⎝⎭−+−+−+ ⎪=−−−+−++⎛⎫−−x x k k x x x x m m n n x x x x x x 22212321212112122212)( ⎝⎭−+−+ ⎪=−−+++−⎛⎫x x k x x m m n n k n 222121212122 21x x k −=±+82，22TP TQ m n n ∴⋅=++++±++−+−k k km n m 822212 ··············································· 10分 当m n TP TQ ==⋅20,,1为定值45， 所以存在定点T 的坐标为⎝⎭⎪⎛⎫20,1 ·································································· 12分 22．（12分）（1）()f x x '=+=−+−+x x x x x 22ln 21ln 223)( ···················································· 1分又因为函数=−+g x x x 21ln 3)()(递增，且=g 10)(，'>⇔>f x x 01)(， ∴f x )(在0,1)(递减，在+∞1,)[递增 ···························································· 2分 当=−<f a 120)(，即>a 2时，⎝⎭⎝⎭ ⎪ ⎪=+−−=+>⎛⎫⎛⎫a a a a f a a a a 1ln ln 0111122， =+−>−+>−−=>−−−−−+a a a a f a a a a a a a a a a a a 01ln 111112222)()()()(， ∴f x )(在⎝⎭⎪⎛⎫a a ,1,1,1)(上各有一个零点 ························································· 3分 当≤a 2时，f x )(的最小值为f 1)(，且=−≥f a 120)(，∴f x )(在+∞0,)(内至多只有一个零点，综上，实数a 的取值范围是>a 2 ·································································· 4分 （2）设 ⎪=−>⎛⎫F x f x f x ,11)()(，则 ⎝⎭⎪'='+'=−−+⎛⎫−−x x x x F x f x f x x x x 21ln 111212322)()()()( ⎣⎦⎢⎥⎣⎦=−−−=−−+⎡⎤⎡⎤+−x x x x x x x x x x x 12ln 221ln 2113233)()( 当>x 1时，<−x x ln 1，−−+−=+−=−++>x x x x x x x x x 22112120332)()()()(， ∴−>+−>+x x x x x x x 22111ln 3)()()(，∴F x )(在+∞1,)(上递增，当>x 1时，>=F x F 10)()(，即当>x 1时，⎝⎭⎪>⎛⎫x f x f 1)( ······································································ 6分 又因为函数f x )(有两个零点<x x x x ,1212)(，由（1）知，<<<<<x x x 01,011212， ⎝⎭⎪∴=>⎛⎫x f x f x f 1212)()(， 又()f x 在0,1)(递减，∴<x x 121， 即<x x 112 ································································································ 8分 （3）设⎝⎭⎪=−+−=−−⎛⎫x x G x f x x a x x x 1ln 12)()(， =−−==−−−+−+++'x x x G x x x x x x x x x x 211ln 21ln 121ln 2221322)()()(， ='G 101)(，当≠x 1时，⎣⎦−⎢⎥=+++⎡⎤−'x x G x x x x x 121ln 1212)()()(， 显然−+++>x x x x 1210ln 2)(∴G x 1)(在0,1)(递减，+∞1,)(递增，∴≥=G x G 1011)()(， 即>+−=xf x x a h x 11)()(，设h x 1)(的零点为<−=x x x x x x ,,343443)(， 由图象可知<<<x x x x 3124，∴−<x x 21 ·················································································· 10分 设⎝⎭⎝⎭ ⎪ ⎪−+−=−=−−⎛⎫⎛⎫−x x x x x f x x a x x 1ln 11ln 111222)(， 设=−−xG x x 1ln 12)(， 易得≤G x 02)(恒成立，即<+−=xf x x a h x 1222)()(，设h x 2)(的零点为<−=x x x x x x ,,56566522)(，由图象可知，<<<x x x x 1562，∴<<<x x x x 15622222，∴−>x x 2122∴−<<−x x x x 212122 ····································································· 12分。
中学生标准学术能力诊断性测试2020年1月数学(文)试题答案(一卷)(扫描版)
中学生标准学术能力测试诊断性测试2020年1月测试文科数学（一卷）答案一． 选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只二． 填空题：本大题共4小题，每小题5分，共20分． 13. [)(]1,00,1−14. (]}{0,2415. ()1,00,2⎛⎫−∞ ⎪⎝⎭16.14三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17~21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答． （一）必考题：60分．17． 解：记A 表示事件：考生选择生物学科B 表示事件：考生选择物理但不选择生物学科；C 表示事件：考生至少选择生物、物理两门学科中的1门学科；D 表示事件：选择生物但不选择物理E 表示事件：同时选择生物、物理两门学科 （1）()()0502P A .P B .C AB ===，，,AB =∅ ………………………………2分()()()()0.7P C P AB P A P B ==+= ………………………………5分（2）由某校高二段400名学生中，选择生物但不选择物理的人数为140，可知()350.D P = ………………………………7分 因为DE A = ………………………………9分()()()15.035.05.0=−=−=D P A P E P ………………………………12分18．解：（1）设数列{}n a 的公差为d （0d ≠），由题意得⎩⎨⎧==512211a a a a ，解得⎩⎨⎧==211d a ………………………………3分所以2,12n S n a n n =−= ………………………………6分 （2）因为()()⎪⎭⎫ ⎝⎛+−=+=−+=1114114111212n n n n n b n ………………………………9分 所以()41n nT n =+ ………………………………12分19．解（1）由已知AP ⊥面PCD ，可得AP ⊥PC ，AP ⊥ C D ，由题意得，ABCD 为直角梯形，如图所示，易得// BE CD ,所以， AP BE ⊥ ．又因为BE ⊥AC ，所以BE ⊥⊥面APC ,故BE ⊥ PO ． ………………………………3分 在直角梯形ABCD中?AC AB AP PC ==⊥，， ，所以PAC ∆为等腰直角三角形，O 为斜边AC 上的中点，所以PO AC ⊥．ABCD ,面⊂=BE O AC BE ，所以PO ⊥平面ABCD …………………………6分（2）法一：以O 为原点，分别以OB OC OP ，， 为x 轴，y 轴，z 轴的建立直角坐标系． 不妨设1BO =A(0,-1,0) , B(1,0,0), P (0,0,1), D(-2,1,0), 设(,,)n x y z =是平面PBD 的法向量．满足00n PB n BD ⎧⋅=⎪⎨⋅=⎪⎩ ,所以030x z x y −+=⎧⎨−+=⎩ ，则令1x = ，解得(1,3,1)n =…………9分 222sin cos ,11AB n AB n AB nθ⋅===⋅ ……………………………12分 法二：（等体积法求A 到平面PBD 的距离）设AB=1，点A 到平面PBD 的距离为h ，计算可得,411=ΔPBD S A PBD P ABD V V −−= …………………………9分PO S h S ΔABD ΔPBD ⋅⋅=⋅⋅3131,1,ABD S ∆=2PO =解得h =…………………………11分sin h AB θ== …………………………12分20．解（1）x xax ≥+ln 在(]1,0恒成立，得x x x a ln −≥在(]1,0恒成立。
2020年1月THUSSAT中学生标准学术能力诊断性数学测试卷
(t为参数)
，曲线
C
:
x
y
= =
2 cos a sin
( 为参数),
其中 a 0 ．若曲线 C 上所有点均在直线 l 的右上方，求 a 的取值范围．
23．[选修 4—5：不等式选讲]（10 分）
已知正数 x, y, z 满足 x + y + z = 1．
（1）求证： x2 + y2 + z2 1 ； （2）求16x +16y +16z2 的最小值． 2y + 3z 2z + 3x 2x + 3y 5
B． E E, D D
C． E E, D = D
D． E = E, D = D
AB
9．在△ABC 中，若 AB BC = BC CA = 2CA AB ，则 =
BC
A．1
B． 2 2
C． 3 2
D． 6 2
10．在矩形 ABCD 中，已知 AB = 3, AD = 4 ， E 是边 BC 上的点，
ex
A． − e
B． − e 2
C． −e
D． −2e
二、填空题：本大题共 4 小题，每小题 5 分，共 20 分．
第1页 共4页
第2页 共4页
13．如图所示的程序框图的输出值 y (0,1 ，则输入值 x
．
14．在△ABC 中， 2b sin A = a cos(B − ) , b = 2 ，若满足条件的 6
EC =1， EF / /CD ，将平面 EFDC 绕 EF 旋转 90 后记为平面
，直线 AB 绕 AE 旋转一周，则旋转过程中直线 AB 与平面 相
交形成的点的轨迹是
中学生标准学术能力诊断性测试 1月诊断性测试理科数学试卷PDF版含答案
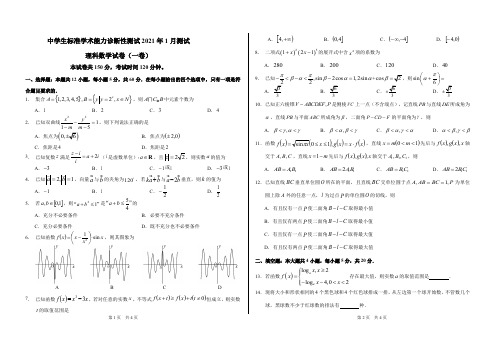
由 CD = AB = 2, ED = 2, EF = 1 ，得 CF = 5 .……8 分
'CF 与平面 ABCD 所成角的正弦值为 15 ，所以 FH = 5 × 15 = 3 .……9 分
5
5
因为 EF / /CD, EF ⊄ 平面 ABCD,CD ⊂ 平面 ABCD ，
所以 EF // 平面 ABCD ，所以 EM = FH = 3 ，
A．1
B． 2
C． 3
2．
x2 已知双曲线 1 m
y2 m5
A．焦点为 0,r 6
1 ，则下列说法正确的是
B．焦点为 r 2,0
D． 4
C．焦距是 4 3． 已知复数 z 满足 z i
i A． 3
D．焦距是 2 a 2i （ i 是虚数单位）, a R ，且 z 2 2 ，则实数 a 的值为
T2 R22
1
Tn Rn2
1
1．
第3页 共4页
20．（12
分）已知
F1
,
F2
是椭圆
C
:
x a
2 2
y2 b2
1 a ! b ! 0 的左、右焦点，弦 AB 经过点 F2 ，若
AF2
2 F2B , tanAF1B
3 4
，且
'F1F2
B
的面积为
2
．
（1）求椭圆的方程；
（2）若直线 y k x 1 1d k d 2 ，与 y 轴交于点 P ，与椭圆 C 交于 M , N 两点，线段 MN
B．1
C． 1或1
D． 3 或1
理科综合试题-A4版 - 中学生标准学术能力诊断性测试2020年1月试题(试卷 答案)
中学生标准学术能力诊断性测试2020年1月测试理科综合试卷（一卷）本试卷共300分，考试时间150分钟。
可能用到的相对原子质量：H 1 C 12 O 16 K 39 Fe 56一、选择题：本题共13小题，每小题6分，共78分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1．2019年9月11日，我国科学家发表了世界首例通过基因编辑干细胞治疗艾滋病案例的相关研究。
HIV侵染人体后与T细胞表面CD4和CCR5受体结合，破坏人体的免疫系统。
该研究采用基因编辑技术对患者的成体造血干细胞中的CCR5基因进行编辑后，将编辑细胞移植回艾滋病患者体内。
下列有关叙述正确的是A．CD4和CCR5受体的化学本质是糖蛋白，与HIV结合的过程体现了质膜具有细胞间信息交流的功能B．C D4和CCR5基因仅存在于人体的T细胞中，表达时需要RNA聚合酶参与C．被改造的造血干细胞具有全能性，可以分化为带异常CCR5受体的T细胞D．被HIV感染的T细胞的清除属于细胞凋亡，此凋亡使得人体的特异性免疫功能下降2．中科院覃重军团队用基因编辑的方法将酿酒酵母中16条天然染色体合成为1条，创建出国际首例人造单染色体真核细胞SY14，打开了“人造生命”的大门。
有关说法正确的是A．SY14的细胞壁具有支持保护作用，可被纤维素酶和果胶酶温和去除B．SY14的遗传物质是DNA，合成蛋白质时边转录边翻译C．SY14的形成发生了染色体的结构变异和数目变异D．SY14细胞膜的组成成分从外到里依次为糖类、蛋白质、磷脂分子3．生物学上的分子马达是把化学能直接转换为机械能的一类蛋白大分子的总称。
ATP合成酶—旋转分子马达之一，被称为生命能量的“印钞机”，其作用机理如图所示，下列说法错误的是A．该酶与生物膜结合后能催化合成ATP，ATP的水解通常与放能反应联系B．由于细菌细胞无其他的生物膜结构，该酶应分布于细胞膜上C．H+跨该膜的运输方式是协助扩散，因其顺浓度梯度运输且需载体协助D．该酶所催化的反应在细胞中是时刻不停发生并与ATP的水解处于动态平衡第1页共16页4．安哥拉兔体色的遗传受一对等位基因S （黑色）和s （白色）控制，某地一个随机交配的大种群中，S 和s 的基因频率各占一半，现逐代人工选择，淘汰白色兔子。
北京市2020年第一次合格性考试数学试题 含答案
12020 年北京市第一次普通高中学业水平合格性考试数学试卷1参考公式：锥体的体积公式 V = Sh ，其中 S 为锥体的底面积， h 为锥体的高 .3第一部分 选择题 (每小题 3 分，共 81 分)在每个小题给出的四个备选答案中，只有一个是符合题目要求的 .1. 已知集合 A = 1，2，3}， B = 3，4，5} ，那么集合 A B 等于A. B ． 3} C ． 1, 2 ,4 , 5} D ． 1, 2, 3,4, 5} 2. 函数 f(x) = x −1的定义域是A. (− ,1]B. [0, + )C. [1, + )D. R 3. 如果指数函数 f (x) = a x ( a > 0， 且a 1)的图象经过点(2,4) ，那么 a 的值是A. 2 B ． 2 C ． 3 D ． 4 4. 将函数 y = sin x 的图象向右平移π个单位，所得图象对应的函数表达式是3A ． y = sin(x − )3 B. y = sin(x + )3C. y = cos(x − )3D. y = cos(x + )35. 在平行四边形 ABCD 中， AB + AD 等于A ． ACB ． BDC ． BCD ． CD1. 考生要认真填写考场号和座位序号。
考 2. 本试卷共 8 页，分为两个部分，第一部分为选择题， 27 个小题(共 81 分)； 生 第二部分为解答题， 4 个小题(共 19 分) 。
须 3．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。
第一部分必 知 须用 2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。
4 ．考试结束后，考生应将试卷、答题卡放在桌面上，待监考员收回。
π π π π26. 在平面直角坐标系 xOy 中， 角a 的顶点与原点 O 重合，始边与 x 轴的非负半轴重合，终边经过点 P (3,4) ，那么 sin a 的值是3A ．53 B ．44C ．54D ．37. 已知向量 a= (1, − 1)， b =(2,m) ，且a b ，那么实数 m 的值是2A ． −11 B ． −21 C ．2D ． 18. 已知直线l 1: y = 2x ， l 2 : y = ax + 2 ，且l 1 ⊥ l 2 ，那么实数 a 的值是 1 1A. −2 B . − C. D. 22 29. 如图， 正方体ABCD − A 1B 1C 1D 1 的棱 AB ， BC ， CD ， CC 1 所在的直线中，与直线 BC 1 成异面直线的是 A. 直线 ABB. 直线 BCC. 直线 CDD. 直线CC 1110. 计算162 + log 2 4 的结果是A. 6B. 711.D. 10在学生中开展问卷调查 . 该校共有高中学生 900 人，其中高一年级学生 330 人， 高二年级学生 300 人， 高三年级学生 270 人. 现采用分层抽样的方法从高中学生 中抽取一个容量为 90 的样本，那么应抽取高一年级学生的人数为 A ． 30 B ． 31 C ． 32 D ． 33C. 81312. 计算 tan 的结果是42 2A. −1B. −C.D. 12 213. 某同学打算编织一条毛线围巾送给妈妈， 决定从妈妈喜欢的白色、 黄色和紫色中随机选择两种颜色的毛线编织， 那么这条围巾是由白色、 紫色两种颜色的毛线编织的概率是1 A.41B.3.12.3414. 计算cos69ocos24o + sin 69osin 24o 的结果是1 2 3A. B. C. D. 12 2 2 15. 经过点(1,0) ，且斜率为 2 的直线的方程是A. 2x − y + 2 = 0B. 2x − y − 2 = 0C. x − 2y +1= 0D. x − 2y −1= 016. 已知向量a ， b 满足|a |=1， | b |= 2， a 与b 夹角为30o ，那么a .b 等于A . −1 B. 2 C. 3 D. 217. 如图，在三棱柱 ABC − A 1B 1C 1 中， A 1A ⊥ 底面 ABC ， AB ⊥ A C ，A 1A = AB = AC = 2 ，那么三棱锥 A 1 − ABC 的体积是4 A.38B.3C. 4D. 818. 已知△ABC 中， 三A = 60o ， 三B = 45o ， AC = 2 ，那么 BC 等于D C 5πA. 1B. 3C. 2D. 419. 函数f (x) = log2 x − 2 的零点的个数是A. 0B. 1C. 2D. 320. 已知两条直线m， n 和平面，那么下列命题中正确的是A. 若m ⊥ ，n ⊥ ，则m n B．若m ，n ，则m nC．若m ⊥ n，n ⊥ ，则m ⊥ D．若m n，n ，则m ⊥21. 如图，给出了偶函数f(x) 的部分图象，那么f(2) 等于A. −3B. −1C. 1D. 322. 圆x2 + y2 = 1 的圆心到直线x − y + 2 = 0 的距离是2A. B. 2 C. 2 D. 2 2223. 已知直线l 经过(−1,0)，(0, 3) 两点，那么直线l 的倾斜角的大小是A. 30。
全国卷新课标2020年1月诊断性测试理科数学试卷
递增区间．
18．（12 分）如图，多面体 ABCDFE 中，四边形 ABEF 和四边形 CDFE 是
两个全等的菱形， AB = 2 , BAF = ECD = 60 ．
（1）求证： BD ⊥ DC ；
（2）如果二面角 B − EF − D 的平面角为 60 ，求直线 BD 与平面 BCE 所
B．双曲线
C．椭圆
D．抛物线
（第 10 题图）
11．已知函数 f (x) = (ln x −1)(x − 2)i − m(i = 1, 2) , e 是自然对数的底数，存在 m R
A．当 i = 1时， f (x) 零点个数可能有 3 个
B．当 i = 1时， f (x) 零点个数可能有 4 个
C．当 i = 2 时， f (x) 零点个数可能有 3 个
( ) 1,2 时，求 S△OMP 的取值范围． S△ONP
（第 20 题图）
21．（12 分）已知函数 f (x) = (x +1)(ex −1) ．
（1）求 f (x) 在点（-1, f (−1)) 处的切线方程；
（2）若方程
f
(x)
=
b
有两个实数根
x1,
x2
，且
x1
x2
，证明：
x2
−
（第 18 题图）
成角的正弦值．
19．（12 分）已知等比数列{an}的公比 q 1，且 a1 + a3 + a5 = 42, a3 + 9 是 a1 , a5 的等差中项．数列
{bn} 的通项公式 bn =
2n
,nN*．
an −1 + an+1 −1
（1）求数列{an}的通项公式；
2020届初三中考数学一诊联考试卷含答案解析 (北京)
2020届**市初三中考一诊联考试卷数 学注意事项：1.答卷前，考生务必将自己的姓名、准考证填写在答题卡上。
2.回答客观题时，选出每小题答案后，用2B 铅笔把答题卡上对应的答案标号涂黑。
如需改正，必须用橡皮擦擦涂干净，回答非客观题，将答案写在答题卡上，写在试卷上无效。
3.考试结束后，将本试卷和答题卡一并收回。
4.考试时间：120分钟。
一、单选题（共10题，每题3分，共30分，四个选项中只有一项符合题目要求）1．20192018(2)3(2)-+⨯-的值为（ ）A ．20182-B ．20182C ．20192-D ．201922．如图，在平面直角坐标系中，以O 为圆心，适当长为半径画弧，交x 轴于点M ，交y 轴于点N ，再分别以点M ，N 为圆心，大于12MN 的长为半径画弧，两条弧在第二象限交于点P ，若点P 的坐标为（a ，2b ﹣1），则a ，b 的数量关系是（ ）A ．a ＝bB ．a +2b ＝1C ．a ﹣2b ＝1D ．a +2b ＝﹣13．下列事件中必然发生的事件是（ ）A ．一个图形平移后所得的图形与原来的图形不全等B ．不等式的两边同时乘以一个数，结果仍是不等式C ．200件产品中有5件次品，从中任意抽取6件，至少有一件是正品D ．随意翻到一本书的某页，这页的页码一定是偶数4．有五张背面完全相同的卡片，正面分别写有数字1，2，3，4，5，把这些卡片背面朝上洗匀后，从中随机抽取一张，其正面的数字是偶数的概率为( )A ．45B ．35C ．25D ．155．两个袋子中分别装着写有1，2，3，4的四张卡片，卡片除数字外其余都相同，从每一个袋子中各抽取一张，则两张卡片上的数字之和不小于5的概率是（ ）A ．316B ．58C ．34D ．1316 6．如图，ABC ∆为O 的内接三角形，1tan 2ACB ∠=，且2AB =，则O 的半径为（ ）A B C ．D ．7．如图是三个反比例函数y ＝1k x ，y ＝2k x ，y ＝3k x在x 轴上方的图象，由此观察k 1、k 2、k 3得到的大小关系为（ ）A ．k 1＞k 2＞k 3B ．k 2＞k 3＞k 1C ．k 3＞k 2＞k 1D ．k 3＞k 1＞k 28．如图，一架长2.5米的梯子AB 斜靠在墙上，已知梯子底端B 到墙角C 的距离为1.5米，设梯子与地面所夹的锐角为α，则cos α的值为( )A ．35B ．45C ．34D ．439．如图，AB//CD ，∠CDE=1400，则∠A 的度数为A ．1400B ．600C ．500D ．40010．下列命题中，错误的是( )A．两条对角线互相垂直的平行四边形是菱形B．两条对角线相等的平行四边形是菱形C．一组邻边相等的平行四边形是菱形D．四边形相等的四边形是菱形二、填空题（共4题，每题4分，共16分）11．如图1，含30°和45°角的两块三角板ABC和DEF叠合在一起，边BC与EF 重合，BC＝EF＝12cm，点P为边BC（EF）的中点，现将三角板ABC绕点P按逆时针方向旋转角度α（如图2），设边AB与EF相交于点Q，则当a从0°到90°的变化过程中，点Q移动的路径长为_____（结果保留根号）12．如图所示，在平面直角坐标系中，点A0）、B（0，12），以AB为边作正方形ABCB1，延长CB1交x轴于点A1，以A1B1为边作正方形A1B1C1B2，延长C1B2交x轴于点A2，以A2B2为边作正方形A2B2C2B3，延长C2B3交x轴于点A3，以A3B3为边作正方形A3B3C3B4，…，依此规律，则△A6B7A7的周长为_____．13．如图，在Rt △ABC 中，∠ACB=90°，BC=6，CD 是斜边AB 上的中线，将△BCD 沿直线CD 翻折至△ECD 的位置，连接AE ．若DE ∥AC ，计算AE 的长度等于_____．14．如图，矩形ABCD 中，AB ＝5，BC ＝7，点E 是对角线AC 上的动点EH ⊥AD ，垂足为H ，以EH 为边作正方形EFGH ，连结AF ，则∠AFE 的正弦值为_____．三、解答题（共6题，总分54分）15．计算：（π﹣3）0﹣（13）﹣116．如图，四边形ABCO 为矩形，点A 在x 轴上，点C 在y 轴上，且点B 的坐标为（2,1），将此矩形绕点O 逆时针旋转90°得矩形DEFO ，抛物线y=-x 2+bx+c 过B 、E 两点.（1）求此抛物线的函数解析式.（2）将矩形DEFO 向右平移，当点E 的对应点E ’在抛物线上时，求线段DF 扫过的面积.（3）若将矩形ABCO 向上平移d 个单位长度后，能使此抛物线的顶点在此矩形的边上，求d的值.17．如图，AB为⊙O的直径，射线AG为⊙O的切线，点A为切点，点C为射线AG上任意一点，连接OC交⊙O于点E，过点B作BD∥OC交⊙O于点D，连接CD，DE，OD．（1）求证：△OAC≌△ODC；（2）①当∠OCA的度数为时，四边形BOED为菱形；②当∠OCA的度数为时，四边形OACD为正方形．18．如图，数轴上的点A，B，C，D表示的数分别为﹣3，﹣1，1，2，从A，B，C，D四点中任意取两点，求所取两点之间的距离为2的概率．19．如图，四边形是一张放在平面直角坐标系中的矩形纸片，点在轴上，点在轴上，将边折叠，使点落在边的点处．已知折叠，且．（1）判断与是否相似？请说明理由；。
高三中学生标准学术能力诊断性测试 2020 年 1 月测试题及答案解析
中学生标准学术能力诊断性测试 2020 年 1 月测试
文科数学试卷（一卷）
本试卷共 150 分，考试时间 120 分钟。
一、选择题：本大题共 12 小题，每小题 5 分，共 60 分．在每小题给出的四个选项中，只有一项是 符合题目要求的．
1．已知集合U = N, A = x x = 2n,n N,B = x 1 x 6,n N ，则 ( A) B = U
在直角梯形 ABCD 中，AC = 2，AB = 2AP，AP ⊥?PC ， 所以 PAC 为等腰直角三角形，O 为斜边 AC 上的中点，所以 PO ⊥ AC ． BE AC = O, BE 面ABCD ，所以 PO ⊥ 平面 ABCD …………………………6 分
（2）法一：以 O 为原点，分别以 OB，OC，OP 为 x 轴， y 轴，z 轴的建立直角坐标系． 不妨设 BO =1
6．点 P, Q 在圆 x2 + y2 + kx − 4y + 3 = 0 上 ( k R) ，且点 P, Q 关于直线 2x + y = 0 对称，则该圆
的半径为
A． 3
B． 2
C．1
D． 2 2
7．已知函数 f ( x) = x3 − x 和点 P (1，−1) ，则过点 P 与该函数图像相切的直线条数为
文科数学（一卷）答案
2020年高三生物中学生标准学术能力诊断性测试(1月)试题
2020年高三生物中学生标准学术能力诊断性测试（1月）试题本试卷共300分，考试时间150分钟。
一、选择题：本题共13小题，每小题6分，共78分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1.2019年9月11日，我国科学家发表了世界首例通过基因编辑干细胞治疗艾滋病案例的相关研究。
HIV侵染人体后与T细胞表面CD4和CCR5受体结合，破坏人体的免疫系统。
该研究采用基因编辑技术对患者的成体造血干细胞中的CCR5基因进行编辑后，将编辑细胞移植回艾滋病患者体内。
下列有关叙述正确的是A.CD4和CCR5受体的化学本质是糖蛋白，与HIV结合的过程体现了质膜具有细胞间信息交流的功能B.CD4和CCR5基因仅存在于人体的T细胞中，表达时需要RNA聚合酶参与C.被改造的造血干细胞具有全能性，可以分化为带异常CCR5受体的T细胞D.被HIV感染的T细胞的清除属于细胞凋亡，此凋亡使得人体的特异性免疫功能下降2.中科院覃重军团队用基因编辑的方法将酿酒酵母中16条天然染色体合成为1条，创建出国际首例人造单染色体真核细胞SY14，打开了“人造生命”的大门。
有关说法正确的是A.SY14的细胞壁具有支持保护作用，可被纤维素酶和果胶酶温和去除B.SY14的遗传物质是DNA，合成蛋白质时边转录边翻译C.SY14的形成发生了染色体的结构变异和数目变异D.SY14细胞膜的组成成分从外到里依次为糖类、蛋白质、磷脂分子3.生物学上的分子马达是把化学能直接转换为机械能的一类蛋白大分子的总称。
ATP合成酶－旋转分子马达之一，被称为生命能量的“印钞机”，其作用机理如图所示，下列说法错误的是A.该酶与生物膜结合后能催化合成ATP，ATP的水解通常与放能反应联系B.由于细菌细胞无其他的生物膜结构，该酶应分布于细胞膜上C.H＋跨该膜的运输方式是协助扩散，因其顺浓度梯度运输且需载体协助D.该酶所催化的反应在细胞中是时刻不停发生并与ATP的水解处于动态平衡4..安哥拉兔体色的遗传受一对等位基因S(黑色)和s(白色)控制，某地一个随机交配的大种群中，S和s的基因频率各占一半，现逐代人工选择，淘汰白色兔子。
2020年THUSSAT中学生标准学术能力诊断性测试1月诊断 理科数学答案
b1 + b2 + 那么，当 n = k +1时，
+ bk 2k+1 −1 ．
b1 + b2 +
+ bk + bk+1
2k+1 −1 +
2k +1 2k+1 −1 + 2k+2 −1
= 2k+1 −1 +
2k+1( 2k+1 −1 − 2k+2 −1)
( 2k+1 −1 + 2k+2 −1)( 2k+1 −1 − 2k+2 −1)
又 G'
( −3)
=
−
1 e3
− 3e＜0
， lim G' x→−
(x)
=
−3e ，G'
(1)
=
0 ，所以 G ( x) 在 (−,1) 上单调递
减，在 (1, +) 上单调递增． 所以 G ( x) G (1) = 0 f ( x) t ( x) = (3e −1) x − e −1 ，
当且仅当 x = −1 时取“=”
由题意得，直线 l 的斜率存在且不为 0， 可设直线 l 的方程为 x = my +1，
……………………4 分 ……………………5 分
x = my +1
联立方程组
x
2
=
4y
整理得 m2 y2 + (2m − 4) y +1 = 0, =16-16m 0, m 1.
设点 M ( x1, y1 ) , N ( x2 , y2 ) ，
(x
+1) =b
2024年1月中学生标准学术能力诊断性测试(TDA)理综试题及答案
本试卷共300可能用到的相对原子质量：H1一、选择题：本题共13题目要求的。
1的载体--SGLT1和GLUT2，A．GLUT2B．高浓度葡萄糖条件下，微绒毛主要通过主动运输加快吸收速率C．当血糖降低时，胰高血糖素可促进该过程以及肝糖原的分解等以升血糖D层生物膜2ABCD．在提取DNA3霉素合成基因GA3ox1和下列有关分析错误的是A．在红光照射下phyBBCD4林，材木不可胜用也。
C ．“水立方”采用的ETFE 膜（乙烯-四氟乙烯共聚物）是一种高分子材料，可通过加聚反应合成D ．我国率先合成的全碳纳米材料石墨炔具有重要的应用前景，石墨炔与石墨烯互为同素异形体 8．设N A 为阿伏伽德罗常数的值，下列说法中正确的是A ．12g 质量分数为25%的甲醛水溶液中含有氢原子数目为1.2N AB ．常温下1molC 5H 10分子中含有σ键的数目为14N AC ．pH=1的H 2SO 4溶液与足量的Zn 反应产生的氢气分子数目为0.05N AD ．0.1mol FeI 2与0.1molCl 2 反应时，转移电子的数目为0.3N A9．丹参素（Salvianic acid A ）是丹参水溶性成分中的主要药效成分之一，具有祛瘀、生新、活血等作用，其结构如图所示。
下列说法中错误的是A ．丹参素的分子式为C 9H 10O 5B ．丹参素与氢气加成后所得分子中有3个手性碳原子C ．1mol 该有机物最多可消耗3molNa 2CO 3D ．一定条件下丹参素可发生消去、氧化、酯化等反应10．根据操作及现象，下列结论中正确的是味气体生成。
其中Z 、W 同主族，简单离子Y 2-与Z 2+具有相同的电子结构。
下列叙述不正确的是A ．原子半径：W ＞Z ＞X ＞YB ．Z 单质可以与XY 2发生反应C ．W 与X 可形成离子化合物D ．氢化物的沸点：Y ＞X12．己知双极膜中的催化层可将水解离为H +和OH -，并实现其定向通过。
中学生标准学术能力诊断性测试2020年1月数学(理)试题(一卷)答案(扫描版)
…………………………7 分
+1)
=b
的根
x1
=
eb 1− e
−1．又 b
=
s
x1
= f ( x1 ) s ( x1 ) ，由 s ( x) 在 R 上
单调递减，所以 x1 x1．
…………………………7 分
另一方面， f ( x) 在点 (1, 2e − 2) 处的切线方程为 y = (3e −1) x − e −1．
设 t(x) = (3e −1)x − e −1
( ) 构造G( x) = f ( x) − t ( x) = ( x +1) ex −1 − (3e −1) x + e +1=(x +1)ex − 3ex + e ．
G( x) = ( x + 2) ex − 3e ， G( x) = ( x + 3) ex ． 所以 G( x) 在在 (−, −3) 上单调递减，在 (−3, +) 上单调递增． ……………………9 分
在直角坐标系下， x = cos , y = sin , = x2 + y2 .
( ) 故化成直角坐标系方程 y + x x2 + y2 = 2 x2 + y2 ，不包括点 (0, 0) ………………3 分
当 =0时 ， (0, 0) 满足原极坐标方程，
( ) 综上，所求的直角坐标方程为 y + x x2 + y2 = 2 x2 + y2
20．解：（1）由已知可得
F
0,
p 2
，
E
0，−
p 2
2020届初三中考数学一诊联考试卷含参考答案 (北京)
2020届**市初三中考一诊联考试卷数 学注意事项：1.答卷前，考生务必将自己的姓名、准考证填写在答题卡上。
2.回答客观题时，选出每小题答案后，用2B 铅笔把答题卡上对应的答案标号涂黑。
如需改正，必须用橡皮擦擦涂干净，回答非客观题，将答案写在答题卡上，写在试卷上无效。
3.考试结束后，将本试卷和答题卡一并收回。
4.考试时间：120分钟。
一、单选题（共10题，每题3分，共30分，四个选项中只有一项符合题目要求）1．20192018(2)3(2)-+⨯-的值为（ ）A ．20182-B ．20182C ．20192-D ．201922．关于分式的约分或通分，下列哪个说法正确（ ）A ．211x x +-约分的结果是1xB ．分式211x -与11x -的最简公分母是x ﹣1 C ．22x x 约分的结果是1D ．化简221x x -﹣211x -的结果是1 3．二次函数()220y ax bx a =+-≠的图象经过点（-1,0），则代数式-a b 的值为（ ）A ．0B ．-2C ．-1D ．24．下列运算正确的是（ ）A ．a 8÷a 4＝a 2B ．（a 2）3＝a 6C ．a 2•a 3＝a 6D ．（ab 2）3＝ab 65．如图是甲、乙两车在某时段速度随时间变化的图象，下列结论错误的是（ ）A ．乙前4秒行驶的路程为48米B ．在0到8秒内甲的速度每秒增加4米/秒C ．两车到第3秒时行驶的路程相等D ．在4至8秒内甲的速度都大于乙的速度6．按照如图所示的计算机程序计算，若开始输入的x 值为3，第一次得到的结果为4，第二次得到的结果为2，…第2019次得到的结果为（ ）A ．1B ．2C ．3D ．47．下图是由大小相同的5个小正方体搭成的几何体，则它的主视图是（ ）A．B．C．D．8．在平面直角坐标系xOy中，直线l经过点（0，﹣2），且直线l∥x轴．若直线l与二次函数y＝3x2+a的图象交于A，B两点，与二次函数y＝﹣2x2+b的图象交于C，D两点，其中a，b为整数．若AB＝2，CD＝4．则b﹣a的值为（）A．9B．11C．16D．249．三角形的两边长分别为3和6，第三边长是方程x2－6x+8=0的根，则这个三角形的周长是（）A．11B．13C．11或13D．11和1310．若实数m、n满足20m-=，且m、n恰好是等腰△ABC的两条边的边长，则△ABC的周长是（）A．12B．10C．8D．6二、填空题（共4题，每题4分，共16分）11．已知112a b+=，求535a ab ba ab b++=-+_____．12．如图，在△ABC中，AE⊥BC于E，点D为BC边中点，AF⊥AB交BC边于点F，∠C＝2∠B，若DE＝4，CF＝2，则CE＝_____．13．如图，在△PAB中，PA＝PB，M、N、K分别是PA，PB，AB上的点，且AM＝BK，BN＝AK．若∠MKN＝40°，则∠P的度数为___14．已知方程5x2+kx﹣6＝0有一个根是2，则另一个根是_____，k＝_____．三、解答题（共6题，总分54分）15．在某市举办的以“校园文明”为主题的中小学生手抄报比赛中，各学校认真组织初赛并按比例筛选出较好的作品参加全市决赛，所有参加市级决赛的作品均获奖，奖项分为一等奖．二等奖、三等奖和优秀奖．现从参加决赛的作品中随机抽取部分作品并将获奖结果绘制成如下两幅统计图请你根据图中所给信息解答下列问题：（1）一等奖所占的百分比是多少？三等奖的人数是多少？（2）求三等奖所对应的扇形圆心角的度数；（3）若参加决赛的作品有3000份，估计获得一等奖和二等奖的总人数有多少？16．如图，矩形ABCD中，∠ACB=30°，将一块直角三角板的直角顶点P放在两对角线AC，BD的交点处，以点P为旋转中心转动三角板，并保证三角板的两直角边分别于边AB，BC所在的直线相交，交点分别为E，F．（1）当PE⊥AB，PF⊥BC时，如图1，则PEPF的值为；（2）现将三角板绕点P逆时针旋转α（0°＜α＜60°）角，如图2，求PEPF的值；（3）在（2）的基础上继续旋转，当60°＜α＜90°，且使AP：PC=1：2时，如图3，PEPF的值是否变化？证明你的结论．17．为了丰富校园文化生活，某校计划在午间校园广播台播放“百家讲坛”的部分内容为了了解学生的喜好，抽取若干名学生进行问卷调查（每人只选一项内容），整理调查结果，绘制统计图如下：请根据统计图提供的信息回答以下问题：（1）这一调查属于_______（选填“抽样调查”或“普查”），抽取的学生数为_____名；（2）估计喜欢收听易中天《品三国》的学生约占全校学生的____%（精确到小数点后一位）；（3）已知该校女学生共有1800名，则该校喜欢收听刘心武评《红楼梦》的女学生大约有多少名？18．解古算题：“今有甲、乙二人持钱不知其数．甲得乙半而钱四十八，乙得甲太半而亦钱四十八．甲、乙持钱各几何？”.题目大意是：甲、乙两人各带了若干钱．如果甲得到乙所有钱的一半，那么甲共有钱48，如果乙得到甲所有钱的23，那么乙也共有钱48．问甲、乙两人各带了多少钱？19．如图，已知△ABC，（1）尺规作图：作AD平分∠BAC交BC于D点，再作AD的垂直平分线交AB于E点，交AC于F点（保留作图痕迹，不写作法）；（2）连接DE，DF证明：四边形AEDF是菱形；（3）若BE＝7，AF＝4，CD＝3，求BD的长．20．炎热的夏天来临之际.为了调查我校学生消防安全知识水平，学校组织了一次全校的消防安全知识培训，培训完后进行测试，在全校2400名学生中，分别抽取了男生，女生各15份成绩，整理分析过程如下，请补充完整.。
中学生标准学术能力诊断性测试2020年1月数学(理)试题(一卷)答案(扫描版)_PDF压缩
…………………………1 分
f (−1) = 1 −1， f (−1) = 0 ，
e
…………………………2 分
所以切线方程为 y = 1− e ( x +1) ．
e
…………………………3 分
（2）由（1）知 f ( x) 在点 (−1, f (−1)) 处的切线方程为 y = 1− e ( x +1) ．
( ) 方程1− e
e
(x
+1) =b
的根
x1
=
eb 1− e
−1．又 b
=
s
x1
= f ( x1 ) s ( x1 ) ，由 s ( x) 在 R 上
单调递减，所以 x1 x1．
…………………………7 分
另一方面， f ( x) 在点 (1, 2e − 2) 处的切线方程为 y = (3e −1) x − e −1．
又
F'
(−3)
=
−
1 e3
−
1 ＜0 e
， lim x→−
F'
(x)
=
−
1 e
，F
'
( −1)
=
0
，所以
F
(
x)
在 (−,
−1) 上单调
递减，在 (−1, +) 上单调递增．所以 F ( x) F (−1) = 0 f ( x) S ( x) = 1− e ( x +1)．当
e 且仅当 x = −1 时取“=”
由题意得，直线 l 的斜率存在且不为 0， 可设直线 l 的方程为 x = my +1，
……………………4 分 ……………………5 分
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2020届北京是中学生标准学术能力诊断性测试诊断性测试（1月）数学（理）试题一、单选题1．若集合{|12}A x x =-<<，{}2,0,1,2B =-，则A B =I （ ） A ．∅ B ．{0,1}C ．{0,1,2}D ．{2,0,1,2}-【答案】B【解析】根据题意，利用交集定义直接求解。
【详解】集合{|12}A x x =-<<，{}2,0,1,2B =-，所以集合{}0,1A B =I 。
【点睛】本题主要考查集合交集的运算。
2．若()25i z +=，则z 的虚部为（ ） A ．－1 B ．1C ．i -D ．i【答案】A【解析】利用复数除法运算化简z ，则虚部可求 【详解】()()()5252222i z i i i i -===-++-，故虚部为－1 故选：A 【点睛】本题考查复数的运算，意在考查计算能力，是基础题3．已知双曲线2221(0)2x y b b -=>的两条渐近线互相垂直，则e =（ ）A ．1 BC D ．2【答案】B【解析】根据题意，利用双曲线的两条渐近线垂直推出-1b b a a=-g ，可得a b =，再通过离心率的计算公式即可得出。
【详解】由题意得，-1b b a a =-g ，可得a b =，则2222222,2c a b e e a a+====。
【点睛】本题主要考查双曲线的性质中离心率的求解。
4．由两个14圆柱组合而成的几何体的三视图如图所示，则该几何体的体积为（ ）A ．π3B ．π2C ．πD ．2π【答案】C【解析】根据题意可知，圆柱的底面半径为1，高为2，利用圆柱的体积公式即可求出结果。
【详解】由三视图可知圆柱的底面半径为1，高为2， 则21122V ππ=⋅⨯=， 故答案选C 。
【点睛】本题主要考查根据几何体的三视图求体积问题，考查学生的空间想象能力。
5．函数()()22xf x x x e =-的图像大致是（ ）A ．B ．C ．D ．【答案】B【解析】求导，求出函数()y f x =的单调性，利用单调性来辨别函数()y f x =的图象，以及函数值符号来辨别函数()y f x =的图象． 【详解】()()22x f x x x e =-Q ，()()()()222222x x x f x x e x x e x e '∴=-+-=-.解不等式()0f x '<，即220x -<，得22x -<<；解不等式()0f x '>，即220x ->，得x <x >所以，函数()y f x =的单调递增区间为(,-∞和)+∞，单调递减区间为(．令()0f x >，即220x x ->，得0x <或2x >； 令()0f x <，即220x x -<，得02x <<.所以，符合条件的函数()y f x =为B 选项中的图象，故选B. 【点睛】本题考查利用函数解析式辨别函数的图象，一般从以下几个要素来进行分析：①定义域；②奇偶性；③单调性；④零点；⑤函数值符号．在考查函数的单调性时，可充分利用导数来处理，考查分析问题的能力，属于中等题．6．已知关于x 的不等式2230ax x a -+<在(]0,2上有解，则实数a 的取值范围是（ ）A ．⎛-∞ ⎝⎭B ．4,7⎛⎫-∞ ⎪⎝⎭C ．⎫∞⎪⎪⎝⎭D ．4,7⎛⎫+∞⎪⎝⎭【答案】A【解析】将不等式化为32aax x+<，讨论0a =、0a >和0a <时，分别求出不等式成立时a 的取值范围即可 【详解】(]0,2x ∈时，不等式可化为32aax x+<； 当0a =时，不等式为02<，满足题意；当0a >时，不等式化为32x x a +<，则2a >=x =所以a ，即0a <<；当0a <时，32x x a+>恒成立；综上所述，实数a 的取值范围是(,3-∞ 答案选A 【点睛】本题考查不等式与对应的函数的关系问题，含参不等式分类讨论是求解时常用方法7．已知a ，b 为实数，则01b a <<<，是log log a b b a >的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件【答案】A【解析】通过正向与反向推导来验证充分与必要条件是否成立即可 【详解】若01b a <<<，则lg lg b a <，lg lg 1,1lg lg b a a b >> ，lg lg log log lg lg a b b ab a a b>⇔>， 显然o 0l g lo 1g a b b a b a <><<⇒，充分条件成立但log log a b b a >时，比如说2,3a b ==时，却推不出01b a <<<，必要条件不成立 所以01b a <<<是log log a b b a >的充分不必要条件 【点睛】本题考查充分与必要条件的判断，推理能力与计算能力，由于参数的不确定性，故需要对参数进行讨论8．已知随机变量ξ，η的分布列如下表所示，则（ ）A ．E E ξη<，D D ξη<B ．E E ξη<，D D ξη>C ．E E ξη<，D D ξη= D ．E E ξη=，D D ξη=【答案】C【解析】由题意分别求出E ξ，D ξ，E η，D η，由此能得到E ξ＜E η，D ξ＞D η． 【详解】 由题意得： E ξ111123326=⨯+⨯+⨯=116， D ξ22211111111151(1)(2)(3)636108266=-⨯+-⨯+-⨯=． E η111131236236=⨯+⨯+⨯=，D η＝（1316-）216⨯+（2136-）212⨯+（3136-）21513108⨯=， ∴E ξ＜E η，D ξ=D η． 故选：C ． 【点睛】本题考查离散型随机变量的分布列、数学期望、方差的求法，考查运算求解能力，是中档题．9．在ABC △中，若2AB BC BC CA CA AB ⋅=⋅=⋅u u u v u u u v u u u v u u u v u u u v u u u v，则AB BC=u u u vu u u v （ ） A ．1 B．2CD．2【答案】C【解析】根据题意，由AB BC BC CA ⋅=⋅uu u v uu u v uu u v uu v可以推得AB AC =，再利用向量运算的加法法则，即可求得结果。
【详解】由题意得，AB BC BC CA ⋅=⋅uu u v uu u v uu u v uu v ，即A A =0+BC B C ⋅uu u v uu u v uuu v（），设BC 的中点为D ，则AD BC ⊥，即ABC △为等腰三角形，B=C AB AC =∠∠，又因为2BC CA CA AB ⋅=⋅uu u v uu v uu v uu u v即2222222C C cos 2C 2C cos 112C +22232C 2AB BC CA A B AB BC B A CA B CBC A BC A BC⋅=⋅-=-+-=-+⨯=uu u v uu u v uu v uu u v uuv uu u v uu u v uu u v uu v uuvuu u v uu u v uu u v uu u v uu u v （）所以3AB BC=uu u v uu u v。
【点睛】本题主要考查平面向量的线性运算。
10．在矩形ABCD 中，已知3AB =，4=AD ，E 是边BC 上的点，1EC =，EF CD ∥，将平面EFDC 绕EF 旋转90︒后记为平面α，直线AB 绕AE 旋转一周，则旋转过程中直线AB 与平面α相交形成的点的轨迹是（）A ．圆B ．双曲线C ．椭圆D ．抛物线【答案】D【解析】利用圆锥被平面截的轨迹特点求解 【详解】由题将平面EFDC 绕EF 旋转90︒后记为平面α，则平面α⊥平面ABEF ,，又直线AB 绕AE 旋转一周，则AB 直线轨迹为以AE 为轴的圆锥，且轴截面为等腰直角三角形，且面AEF 始终与面EFDC 垂直，即圆锥母线AF ⊥平面EFDC 则 则与平面α相交形成的点的轨迹是抛物线 故选：D【点睛】本题考查立体轨迹，考查圆锥的几何特征，考查空间想象能力，是难题11．已知函数()()()()ln 1212if x x x m i =---=，，e 是自然对数的底数，存在m R ∈（）A ．当1i =时，()f x 零点个数可能有3个B ．当1i =时，()f x 零点个数可能有4个C ．当2i =时，()f x 零点个数可能有3个D ．当2i =时，()f x 零点个数可能有4个 【答案】C【解析】首先将()f x 的零点转化为两个图象的交点，利用以直代曲的思想可以将(ln 1)x -等价为()x e -，根据穿针引线画出草图，即可判断.【详解】将()()()()ln 1212if x x x m i =---=，看成两个函数(),yg x y m ==的交点，利用以直代曲，可以将()g x 等价看成()()()20iy x e x x =-⋅->，利用“穿针引线”易知12i =，时图象如图，所以当1i =时最多有两个交点，当2i =时最多有三个交点.故选C .【点睛】本题考查函数的零点,函数零点个数的3种判断方法(1)直接求零点：令()0f x =，如果能求出解，则有几个解就有几个零点． (2)零点存在性定理：利用定理不仅要求函数在区间[],a b 上是连续不断的曲线，且()()0f a f b ⋅<，还必须结合函数的图象与性质(如单调性、奇偶性)才能确定函数有多少个零点．(3)利用图象交点的个数：画出两个函数的图象，看其交点的个数，其中交点的横坐标有几个不同的值，就有几个不同的零点.12．已知数列{}n a 的前n 项和为n S ，且满足()21n n n a S a -=，则下列结论中（ ）①数列{}2n S 是等差数列；②n a <11n n a a +<A ．仅有①②正确B ．仅有①③正确C ．仅有②③正确D ．①②③均正确【答案】D【解析】由条件求得2211n n S S --=，可判断①，由①得n a ，可判断②；由n a 判断③，可知①②③均正确，可选出结果． 【详解】①由条件知，对任意正整数n ，有1＝a n （2S n ﹣a n ）＝（S n ﹣S n ﹣1）（S n +S n ﹣1）221n n S S -=-，又()2111111,211,1n a S a a S =±==∴=-所以{2n S }是等差数列．②由①知n S =或显然，当1n n n n S a S S -==-≤n S =，n a =<②正确③仅需考虑a n ，a n +1同号的情况，不失一般性，可设a n ，a n +1均为正（否则将数列各项同时变为相反数，仍满足条件），由②故有n S =，1n S +=，此时n a =1n a +=从而1n n a a +＜=＜1．故选：D ． 【点睛】本题考查数列递推式，不等式的证明，属于一般综合题．二、填空题13．1742年6月7日，哥德巴赫在给大数学家欧拉的信中提出：任一大于2的偶数都可写成两个质数的和.这就是著名的“哥德巴赫猜想”，可简记为“1＋1”.1966年，我国数学家陈景润证明了“1＋2”，获得了该研究的世界最优成果.若在不超过30的所有质数中，随机选取两个不同的数，则两数之和不超过30的概率是________. 【答案】23【解析】根据题意，利用列举法求出不超过30的所有质数，再利用古典概型的概率公式进行计算即可。