《偏微分方程数值解》教学大纲
偏微分方程数值解电子教案

第一边界条件:u( 0 ,t) μ(t) 三类边值条件: 第二边界条件:ux ( 0 ,t) ν(t) 第三边界条件:u ( 0 ,t) hu( 0 ,t) θ(t) x 端点的运动规律 端点所受外力 (Tux ) 弹性体受外力 (以x 0为例,对x l也有) 若μ(t),ν(t),θ(t)为零,称为奇次边界条 件。 若ux ( 0 ,t) 0 称自由边界条件。
方程(1)在点( x0 , y0 )处是双曲型的, 如果在点( x0 , y0 ) 处 ( x0 , y0 ) 0,其中 b 2 4ac.二阶双曲型方程的 标准型是 2u 2u h( u , u , u, , ) 2 2
方程(1)在点( x0 , y0 )处是抛物型的, 如果在点( x0 , y0 ) 处 ( x0 , y0 ) 0,二阶抛物型方程的标 准型是 2u h( u , u , u, , ) 2
t 2μ
10
以线性二阶偏微分方程为例,简单回顾一 下偏微分方程的分类。考虑二阶偏微分方程 2u 2u 2u u u a 2 b c 2 d e fu g ( x , y ), (1) x xy y x y
注意
其中系数a , b, c , d , e和f设为x和y的函数,即方程(1)是线性的。 u u 如果系数 a , b和c是x , y, u, 和 的函数,称方程(1)是拟线性的 x y
u(0 , t ) 0 两端固定, u( l , t ) 0 边值条件(边界条件) 定解条件 u( x ,0 ) ( x ) 设t 0时的位置、速度为: 初值条件(初始条件) ut ( x ,0 ) ( x )
定解问题=泛定方程+定解条件 定解问题:边值问题,初值问题(Cauchy问题或无边界问题) , 混合问题。
《偏微分方程》课程大纲

《偏微分⽅程》课程⼤纲《偏微分⽅程》课程⼤纲⼀、课程简介教学⽬标:“偏微分⽅程”是重要的数学基础课程,它在数学的其它分⽀和⾃然科学与⼯程技术中的⼴泛应⽤是众所周知的。
本课程将尽可能地结合物理背景,系统地对⼏类典型⽅程数学结构、求解⽅法、解的性质以及物理意义进⾏详细阐述,为学⽣⽇后的学习和⼯作打下坚实的基础,提供强有⼒的⼯具,并为进⼀步了解和应⽤现代偏微分⽅程的有关内容提供重要帮助。
主要内容:1. 了解⼏类典型⽅程及其定解条件的物理背景2.掌握⽅程的分类及其化简⽅法3. 熟练掌握各类⽅程的求解⽅法(包括具有普适性的⽅法,如分离变量法,Fourier变换法和Green函数法等,以及针对某类⽅程的特定⽅法,如特征线法)4. 会⽤⼀些基本⽅法(如能量积分法、极值原理等)讨论解的性质并掌握解的重要性质⼆、教学内容(其中带*的部分可能随堂调整)第⼀章引论主要内容:1、偏微分⽅程简介a)偏微分⽅程的历史、现状和⽤途b)什么是偏微分⽅程?介绍有关偏微分⽅程基本概念和研究内容c)例⼦:简单⽽多样的例⼦帮助学⽣初步了解偏微分⽅程2、⼆阶线性偏微分⽅程的分类和特征理论a)两个⾃变量的⼆阶线性偏微分⽅程的分类与化简,椭圆型、双曲型和抛物型的标准形式与典型例⼦,混合型⽅程b)多个⾃变量的⼆阶线性偏微分⽅程⽅程的分类及其例⼦c)⼆阶线性⽅程的特征理论*3、四类典型⽅程的数学模型:包括波动⽅程、热传导⽅程、调和⽅程、和⼀阶⽅程4、其他预备知识:线性⽅程的叠加原理、Sturm-Liouville原理*重点与难点:通过化标准型将⼆阶⽅程进⾏分类、特征的概念(这是偏微分⽅程中最基本也是最重要的概念)、各类⽅程及其定解条件的物理意义第⼆章波动⽅程主要内容:1、弦振动⽅程Cauchy问题的存在性:D’Alembert求解公式,传播波,依赖区域、决定区域和影响区域,特征线法(⾏波法)的其他应⽤和例⼦,Duhamel齐次化原理及其物理解释2、弦振动⽅程初边值问题的存在性:分离变量法求解齐次问题及解的存在性讨论,分离变量法求解的物理意义,多种边界条件的例⼦,⾮齐次⽅程的情形,⾮齐次边界条件的情形,⾼维波动⽅程分离变量法的例⼦3、⾼维波动⽅程Cauchy问题的求解:三维波动⽅程的球平均法,⼆维波动⽅程的降维法4、波的传播与衰减:依赖区域、决定区域和影响区域,Huygens原理与波的弥散,波动⽅程解的长时间性态5、能量不等式与唯⼀性和稳定性:初边值问题解的唯⼀性和稳定性,Cauchy问题解的唯⼀性和稳定性重点与难点:针对于波动⽅程:特征线与特征锥、特征线⽅法、波的有限传播速度;适⽤于各种⽅程的普遍⽅法:能量积分⽅法、分离变量法第三章热传导⽅程主要内容:1、求解初边值问题的分离变量法:⼀维情形,⾼维的例⼦2、Cauchy问题解的存在性:Fourier变换及其基本性质,⽤Fourier变换法求解Cauchy 问题及解的存在性讨论,Fourier变换法的其他应⽤3、极值原理与唯⼀性和稳定性:有界区域的极值原理,⽆界区域的极值原理,初边值问题解的唯⼀性和稳定性,Cauchy问题解的唯⼀性和稳定性4、解的渐近性态:初边值问题解的渐近性态,Cauchy问题解的渐近性态重点与难点:Fourier变换⽅法、极值原理、关注与波动⽅程的区别第四章调和⽅程主要内容:1、调和函数的基本性质:Green公式,Neumann问题解的⾃由度与可解性条件,调和⽅程的基本解,变分原理、基本积分公式,平均值定理,极值原理、边值问题解的唯⼀性和稳定性2、Green函数:定义和性质,⽤静电源像法求⼀些特殊区域的Green函数,⼀般单连通区域的Green函数,⽤Green函数法求解调和⽅程与Poisson⽅程3、调和函数的进⼀步性质―――Harnack定理,可去奇点定律,解析性定理、强极值原理、Neumann边值问题解的唯⼀性。
2016-偏微分方程数值解法-课程大纲-谢树森

中国海洋大学本科生课程大纲课程属性:公共基础/通识教育/学科基础/专业知识/工作技能,课程性质:必修、选修一、课程介绍1.课程描述:本课程介绍数值求解偏微分方程的基本方法及相关的理论基础。
本课程针对数学类专业高年级(三年级)本科生开设。
课程基本内容包括:有限差分方法、差分格式的稳定性、收敛性分析;变分原理,Galerkin有限元方法等。
通过对模型问题的基本数值方法进行分析,阐明构造数值方法的基本思想和技巧。
通过本课程学习,使学生了解并掌握数值求解偏微分方程的基本思想、基本概念和基本理论(数值格式的相容性、稳定性、收敛性及误差估计等),能够运用算法语言对所学数值方法编制程序在计算机上运行实施并对数值结果进行分析。
培养学生理论联系实际,解决实际问题的能力和兴趣。
2.设计思路:偏微分方程是应用数学的核心内容,在其他科学、技术领域具有广泛深入的应用。
掌握偏微分方程的基础理论及求解方法是数学类专业本科生培养的基本要求。
本课程是在数学物理方程课程基础上开设的延展应用型课程,是一门数值分析理论与实践应用高度融合的专业课。
课程引导学生通过数值方法探讨和理解应用数学工具解决实际- 6 -问题的途径及理论分析框架。
学习本课程需要学生掌握了“数学分析”、“数学物理方程”、“数值分析”及“泛函分析”的核心基本内容。
课程内容安排分为有限差分方法和有限元方法两个单元模块,这是目前应用最广泛、理论发展最完善的两类数值方法,两者既有关联又有本质区别,能够体现偏微分方程数值解法的基本特征。
首先介绍有限差分方法。
有限差分方法是近似求解偏微分方程的应用最广泛的数值方法,以对连续的“导数(微分)”进行离散的“差分”近似为基本出发点,利用Fourier 分析及数值分析的基本理论,讨论椭圆、抛物、双曲等三类典型偏微分方程近似求解方法及近似方法的数学理论分析。
有限元方法是20世纪中期发展起来的基于变分原理的数值方法,具有更直接的物理背景含义,因而受到力学、工程等应用领域广泛的关注和应用。
偏微分方程数值解教学大纲
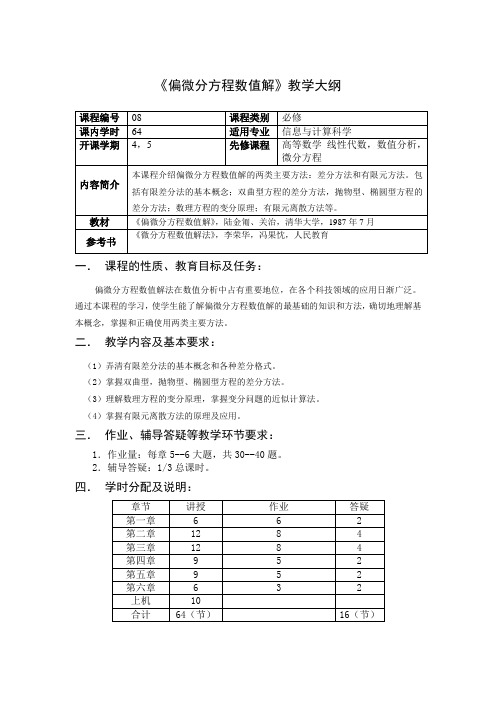
《偏微分方程数值解》教学大纲
一.课程的性质、教育目标及任务:
偏微分方程数值解法在数值分析中占有重要地位,在各个科技领域的应用日渐广泛。
通过本课程的学习,使学生能了解偏微分方程数值解的最基础的知识和方法,确切地理解基本概念,掌握和正确使用两类主要方法。
二.教学内容及基本要求:
(1)弄清有限差分法的基本概念和各种差分格式。
(2)掌握双曲型,抛物型、椭圆型方程的差分方法。
(3)理解数理方程的变分原理,掌握变分问题的近似计算法。
(4)掌握有限元离散方法的原理及应用。
三.作业、辅导答疑等教学环节要求:
1.作业量:每章5--6大题,共30--40题。
2.辅导答疑:1/3总课时。
四.学时分配及说明:。
《偏微分方程数值解》课程教学大纲

维情形的直接推广; 交替方向隐式格式; 分数步方法。第六章 变分原理 几个变分 问题;变分问题的
Euler-Lagrange方
程;一个守恒定律; 二次函数极值问题。
一维问题变分原理及 8 学时
其价性; 二维问题变 分原理及等价性;变 分问题的近似计算。 第七章 有限元离散 方法 一维问题的有 限元方法;子结构方 法。
√√ √
√√√ √
√√ √√
二、课程教学内容及学时分配(含实践、自学、作业、讨论等的内容及要求)
教学内容
学时
第一章 总论 微分方 4 学时
程数学模型及举例;
微分方程数值解的重
要意义和基本问题。
第二章 椭圆型方程
的差分方法 从一个
简单的例子谈起。
第 二 章 求 解 矩 形 域 6 学时
上 Poisson 方程的五
《偏微分方程数值解》课程教学大纲
课程名称:偏微分方程数值解 课程代码:MA309 学 分 / 学 时:4 学分 / 64 学时 适用专业:数学系和与科学计算相关的专业 先修课程:偏微分方程,科学计算(I) 后续课程:科学计算(II),科学计算选讲 开课单位:理学院数学系
一、课程性质和教学目标(需明确各教学环节对人才培养目标的贡献) 课程性质:本课程是理学院数学系的一门重要专业基础课程,其主要任务是通过理论学习和上机实算,
数值实验 4:求解稳态热传导 问题的有限元方法。
三、教学方法
以课堂教学为主,结合自学、数学实验大作业。 1. 课堂教学主要讲解偏微分方程数值解的基本概念,基本方法和基本原理,含有限差分法、变分原理和有限元方
法等,培养学生利用计算机为工具,通过数学建模、理论分析与数值求解等步骤定量化解决实际问题的能力。 2. 数值实验大作业是本课程的重要内容。共安排 4 个数值实验大作业,包括:求解五点差分格式的快速 Fourier 方
偏微分方程数值解-上海交通大学数学系
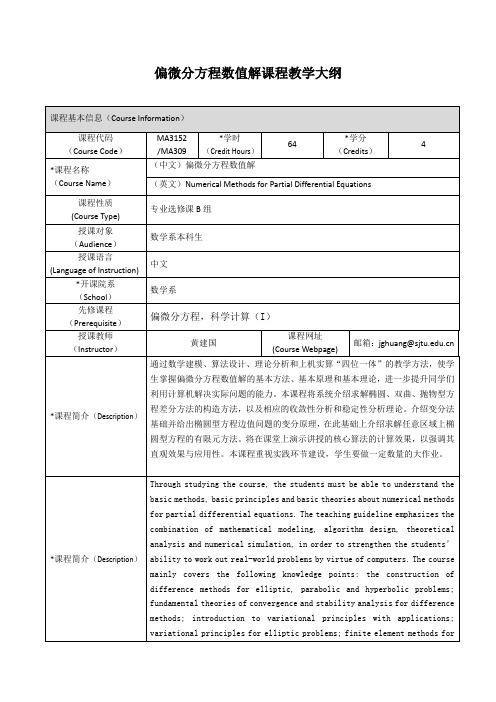
1.椭圆型方程的差分方法:从一个简单例子谈起; 求解矩形域上 Poisson 方程
的五点差分方法的构造;二维情形离散极值原理和最大模估计;五点差分方 法的收敛性分析;求解五点差分方法的迭代方法和快速方法;矩形域上 Poisson 方程九点差分格式构造方法;Matlab 介绍。 (A5,B2,B3,C4)
2.发展方程有限差分法的基本概念和理论:发展方程差分方法的构造;差分格
式的抽象描述;差分格式研究的基本概念:相容性,截断误差,收敛性和稳 定性;稳定性判别的 Fourier 方法,Von-Neumann 条件;两层和多层差分 格式的稳定性分析; 差分格式稳定性的其它研究方法和差分格式构造的其它 方法。(A5,B2,B3)
偏微分方程数值解课程教学大纲
课程基本信息(Course Information) 课程代码 (Course Code) *课程名称 (Course Name) 课程性质 (Course Type) 授课对象 (Audience) 授课语言 (Language of Instruction) *开课院系 (School) 先修课程 (Prerequisite) 授课教师 (Instructor) MA3152 /MA309 *学时 (Credit Hours) 64 *学分 (Credits) 4
6.有限元离散方法: 一维问题的有限元方法;子结构方法编程;理论分析(误
差估计与有限元线性代数方程组性质); 二维问题有限元方法简介。(A5, B2,B3,C4)
elliptic problems in arbitrary domains. The numerical performance of the core algorithms mentioned will be exhibited in class to illustrate their intuitive effect and practicability. With the practice as a highlight of the course, the students must accomplish several project reports. 课程教学大纲(course syllabus)
偏微分方程数值解讲义教学设计

偏微分方程数值解讲义教学设计1. 课程简介本课程是针对大学数学及计算机专业的高年级本科生或研究生开设的,旨在介绍偏微分方程数值解方法,包括有限差分法、有限元法和谱方法等。
本课程的学习目标是掌握偏微分方程数值解的基础理论和常用方法,以及了解数值解的数学原理和应用场景,并能够扩展应用所学知识解决相关实际问题。
2. 教学内容2.1 引言•偏微分方程的概念、分类和基本理论;•数值解的概念和分类,数值解的误差理论。
2.2 有限差分法•一维抛物方程、波动方程、椭圆方程的有限差分格式;•非线性偏微分方程的数值求解;•高维问题的数值求解。
2.3 有限元法•一维线性抛物方程、波动方程、椭圆方程的有限元求解方法;•二维和三维问题的有限元求解方法;•有限元法的加权残差方法和变分原理。
2.4 谱方法•调和方程的分离变量方法和Fourier级数解法;•Laplace方程的Fourier级数解法和离散正交函数解法;•泊松方程的Fourier级数解法和离散正交函数解法。
3. 教学手段3.1 讲课本课程采用讲课和练习相结合的方式,通过讲解理论知识和数值计算实例,并基于MATLAB或Python等数值计算软件进行演示。
3.2 练习结合课程中的实例,进行数值计算作业和课程项目的设计,以提高学生的理论知识和计算能力。
4. 教材教材推荐:•Numerical Solution of Partial Differential Equations: Finite Difference Methods by G. D. Smith •Finite Element Method: A Practical Course by C. S.Chen5. 教学评估学生的教学成绩考核由以下三部分组成:•期中考试(占成绩的30%);•期末考试(占成绩的50%);•课程设计作业(占成绩的20%)。
6. 教学进度内容讲课时间引言2课时有限差分法(一)6课时有限差分法(二)6课时有限差分法(三)4课时有限元法(一)6课时有限元法(二)6课时有限元法(三)4课时谱方法6课时课程设计作业4课时或更多7. 总结本文介绍了一个偏微分方程数值解讲义的教学设计,包括课程简介、教学内容、教学手段、教材、教学评估和教学进度等方面的内容。
偏微分方程数值解法教学大纲

《偏微分方程数值解》课程教学大纲Numerical Solution of Partial Differential Equation课程代码: 课程性质:专业基础理论课/选修适用专业:信息计算开课学期:7总学时数:48总学分数:3编写年月:2003年3月修订年月:2007年7月执笔:王琦一、课程的性质和目的《偏微分方程数值解法》是计算数学专业的一门重要专业基础课。
它不仅对学生今后从事科研具有居高临下的指导作用,而且对于学习其它后继课程和解决一些实际问题都是一门重要的工具,同时对于训练思维能力起着很大作用。
本大纲是根据教育改革发展和面向二十一世纪高等数学专业课程设置和教学内容改革的要求,针对培养目标的需要进行设计的。
二、课程教学内容及学时分配第一章常微分方程初值问题10学时第二章变分原理8学时第三章椭圆型方程----有限差分法和有限元法10学时第四章离散方程的解法8学时第五章抛物型方程和双曲型方程12学时第一章常微分方程初值问题1.1 引论1.2 Euler方法和线形多步方法1.3 稳定性,收敛性和误差估计1.4 预估—校正算法1.5 Runge—Kutta方法第二章常微分方程初值问题2.1 二次函数的极值2.2 二阶椭圆边值问题2.3 Ritz方法第三章椭圆型方程----有限差分法和有限元法3.1 差分逼近的基本概念3.2 一维差分格式,矩形网和三角网差分格式3.3 极值定理3.4 解一维问题的线形元及误差估计3.5 解二维问题的矩形元和三角形元3.6 有限元方程3.7 收敛阶的估计第四章离散方程的解法4.1 离散方程的基本特征4.2 追赶法与迭代法4.3 超松弛法4.4 共轭斜量法第五章抛物型方程和双曲型方程5.1 稳定性与收敛性5.2 分离变量法5.3 差分格式的应用5.4 交替方向隐格式5.5 线形双曲型方程的差分逼近5.6 拟线形双曲型方程组5.7 基本定解问题和特征线法5.8 特征差分格式四、本课程与其它课程的联系与分工先修课程:数学分析,高等代数,常微分方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
偏微分方程数值解
一.教学目的
大量科学技术问题的数值计算都归结为偏微分方程的数值解法,应用数学专业计算方向的学生应该掌握偏微分方程数值解的基本知识和方法,重点介绍当今流行的偏微分方程数值解的两类主要方法,即有限差分法和有限元法。
二.教学内容及学时分配
总学时为48学时
1、抛物型方程的有限差分法(9学时)
差分逼近的基本概念,抛物型方程的几种古典差分格式,差分格式的收敛性和稳定性概念, Lax等价性定理,研究稳定性的直接法和分离变量法,变系数方程与非线性方程的差分方法,多维问题交替方向法及分裂格式。
2、双曲型方程的差分方法(9学时)
一阶线性双曲型方程(组)的差分格式及稳定性分析,二阶线性双曲型方程的差分方法,拟线性双曲型方程(组)特征差分格式,守恒型方程的差分方法。
3、椭圆型方程差分方法(6学时)
二维poisson方程差分方程的建立,极坐标系下的差分格式,边界条件的处理,极值原理及先验估计,差分格式的收敛性。
4、变分原理与广义解(7学时)
引言,泛函的变分与泛函的极值,两点边值问题的变分原理,二阶椭圆边值问题的变分原理,Sobo1ev空间简介与微分方程广义解,古典Ritz—Galerkin 方法。
5、有限元离散方法(7学时)
两点边值问题的有限元法,二维边值问题的有限元法,有限元法解题的一般步骤。
6、形状函数与有限元空间(6学时)
一维高次元,二维矩形剖分的形状函数,三角形单元的形状函数,等参数单元,三维情形。
7、有限元解的收敛性与误差估计(4学时)
Sobolev空间中的插值理论,有限元方法的收敛性与误差估计。
三.教学对象及先修课程
本课程为计算数学方向本科生
先修课程:数学分析,高等代数,数理方程,数值分析,泛函分析四.教材及主要参考书
偏微分方程数值解,陆金甫,关浩,清华大学出版社,1987
微分方程数值方法,胡建伟,胡建伟,科学出版社,1999。
