大学物理电磁场与麦克斯韦方程组
大学物理第16章麦克斯韦方程组和电磁辐射
位移电流 全电流安培环路定理
稳恒磁场中，安培环路定理 H dl I j ds
l s
S1
L
-
S2
+ + + +
（以 L 为边做任意曲面 S ） H dl j ds I
L S1
I
H dl j ds 0
第16章 麦克斯韦方程组和电 磁辐射
本章主要内容
§16.1 Maxwell电磁场方程组
§16.2 电磁波和电磁辐射 §16.4 电磁波的性质 §16.5 电磁波的能量 §16.6 电磁波的动量 光压
第16章 麦克斯韦方程组和电磁辐射
电现象/磁现象
电场/磁场（稳恒态）
我国：周朝(BC8世)/战国(BC4-3世) 西方：BC6世/ AD15世末
B
2
计算得
r dQ H 2 2 π R dt
Q
0 r dQ
2 π R dt
2
代入数据计算得
Q
I d 1.1 A
B 1.1110 T
5
Ic
R
P *r
Ic
例2. 一平行板电容器的两极板都是圆形板，面积为S，其上 的电荷随时间变化，变化率为 q q sint
m
求： 1）电容器中位移电流密度的大小。
麦克斯韦18311879英国物理学家1865年麦克斯韦在总结前人工作的基础上提出完整的电磁场理论他的主要贡献是提出了有旋电场和位移电流两个假设从而预言了电磁波的存在并计算出电磁波的速度即光1888年赫兹的实验证实了他的预言麦克斯韦理论奠定了经典电动力学的基础为无线电技术和现代电子通讯技术发展开辟了广阔前景
【精品】第八讲：麦克斯韦方程组、电磁场的边界条件
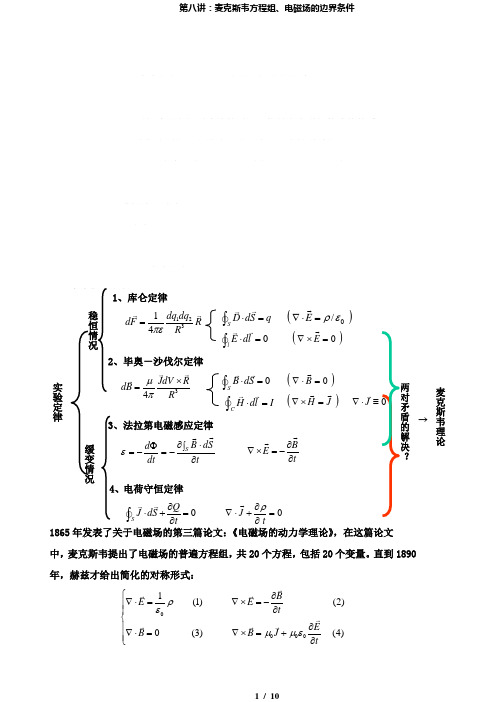
第八讲：麦克斯韦方程组、电磁场的边界条件2.6麦克斯韦方程组2.7电磁场的边值关系1、了解麦克斯韦方程组的建立过程，掌握它的基本性质；2、了解边界上场不连续的原因，能导出电磁场的边值关系；3、掌握电磁场方程微分形式和边界形式的联系与区别。
重点：1)麦克斯韦方程组的基本性质;2)电磁场的边值关系 难点：电磁场切向边值关系的推导 讲授法、讨论 2学时2.6麦克斯韦方程组（Maxwell ’sEquations ）一、麦克斯韦方程1865年发表了关于电磁场的第三篇论文：《电磁场的动力学理论》，在这篇论文中，麦克斯韦提出了电磁场的普遍方程组，共20个方程，包括20个变量。
直到1890 年，赫兹才给出简化的对称形式：00001(1)(2)0(3)(4)BE E tE B B J tρεμμε⎧∂∇⋅=∇⨯=-⎪∂⎪⎨∂⎪∇⋅=∇⨯=+⎪∂⎩实验定律3、法拉第电磁感应定律4、电荷守恒定律12314dq dq dF RR πε=S D dS q ⋅=⎰0l E dl ⋅=⎰34JdV R dB R μπ⨯=0SB dS ⋅=⎰()0=⋅∇B CH dl I ⋅=⎰()JH =⨯∇tB E ∂∂-=⨯∇ 0=∂∂+⋅∇tJ ρ 0J ∇⋅≡对矛盾的解决麦克斯韦理论稳恒况缓变情况2、毕奥－沙伐尔定律1、库仑定律()/ερ=⋅∇E()=⨯∇E t S d B dt d S ∂⎰⋅∂-=Φ-= ε0S QJ dS t ∂⋅+=∂⎰→上式即为真空中的麦克斯韦方程组，其中（2）（4）含有对时间的偏导数，对应 运动方程，（1）（3）为约束方程。
二、麦克斯韦方程组的基本性质 1、线性性麦克斯韦方程组是一组线性方程，表明场服从迭加原理。
2、自洽性方程组各个方程彼此协调，且与电荷守恒定律协调。
如（2）式和（3）式一致：由（2）式有：()0=∂⋅∂∇-=⨯∇⋅∇tBE⇒C B =⋅∇ ，考虑到静磁时0=⋅∇B,所以取0=C 。
大学物理电磁学公式总结汇总
大学物理电磁学公式总结汇总普通物理学教程大学物理电磁学公式总结，下面给大家整理了关于大学物理电磁学公式总结，方便大家学习大学物理电磁学公式总结1定律和定理1. 矢量叠加原理：任意一矢量可看成其独立的分量的和。
即：=∑ (把式中换成、、、、、就分别成了位置、速度、加速度、力、电场强度和磁感应强度的叠加原理)。
2. 牛顿定律：=m (或= );牛顿第三定律：′= ;万有引力定律：3. 动量定理：→动量守恒：条件4. 角动量定理：→角动量守恒：条件5. 动能原理：(比较势能定义式：)6. 功能原理：A外+A非保内=ΔE→机械能守恒：ΔE=0条件A 外+A非保内=07. 理想气体状态方程：或P=nkT(n=N/V，k=R/N0)8. 能量均分原理：在平衡态下，物质分子的每个自由度都具有相同的平均动能，其大小都为kT/2。
克劳修斯表述：不可能把热量从低温物体传到高温物体而不产生其它影响。
开尔文表述：不可能从单一热源吸取热量，使之完全变为有用的功而不产生其它影响。
实质：在孤立系统内部发生的过程，总是由热力学概率小的宏观状态向热力学概率大的状态进行。
亦即在孤立系统内部所发生的过程总是沿着无序性增大的方向进行。
9. 热力学第一定律：ΔE=Q+A10.热力学第二定律：孤立系统：ΔS0(熵增加原理)11. 库仑定律：(k=1/4πε0)12. 高斯定理：(静电场是有源场)→无穷大平板：E=σ/2ε013. 环路定理：(静电场无旋，因此是保守场)θ2Ir P o Rθ1I14. 毕奥—沙伐尔定律：直长载流导线：无限长载流导线：载流圆圈：，圆弧：电磁学1. 定义：= /q0 单位：N/C =V/mB=Fmax/qv;方向，小磁针指向(S→N);单位：特斯拉(T)=104高斯(G)① 和：=q( + × )洛仑兹公式②电势：电势差：电动势：( )③电通量：磁通量：磁通链：ΦB=NφB单位：韦伯(Wb)Θ ⊕-q +qS④电偶极矩：=q 磁矩：=I =IS⑤电容：C=q/U 单位：法拉(F)乘自感：L=Ψ/I 单位：亨利(H)乘互感：M=Ψ21/I1=Ψ12/I2 单位：亨利(H)⑥电流：I = ; 乘位移电流：ID =ε0 单位：安培(A)⑦乘能流密度：2. 实验定律① 库仑定律：②毕奥—沙伐尔定律：③安培定律：d =I ×④电磁感应定律：ε感= –动生电动势：感生电动势：( i为感生电场)乘⑤欧姆定律：U=IR( =ρ )其中ρ为电导率3. 乘定理(麦克斯韦方程组)电场的高斯定理：( 静是有源场)( 感是无源场)磁场的高斯定理：( 稳是无源场)( 感是无源场)电场的环路定理：(静电场无旋)(感生电场有旋;变化的磁场产生感生电场)安培环路定理：(稳恒磁场有旋)(变化的电场产生感生磁场)4. 常用公式①无限长载流导线：螺线管：B=nμ0I② 带电粒子在匀强磁场中：半径周期磁矩在匀强磁场中：受力F=0;受力矩③电容器储能：Wc= CU2 乘电场能量密度：ωe= ε0E2 电磁场能量密度：ω= ε0E2+ B2乘电感储能：WL= LI2 乘磁场能量密度：ωB= B2 电磁场能流密度：S=ωV④ 乘电磁波：C= =3.0×108m/s 在介质中V=C/n，频率f=ν=波动学大学物理电磁学公式总结2概念(2113定义和相关公式)1. 位置矢量：，其5261在直角坐标系中：; 角位置：4102θ16532. 速度：平均速度：速率：( )角速度：角速度与速度的关系：V=rω3. 加速度：或平均加速度：角加速度：在自然坐标系中其中(=rβ)，(=r2 ω)4. 力：=m (或= ) 力矩：(大小：M=rFcosθ方向：右手螺旋法则)5. 动量：，角动量：(大小：L=rmvcosθ方向：右手螺旋法则)6. 冲量：(= Δt);功：(气体对外做功：A=∫PdV)mg(重力) → mgh-kx(弹性力) → kx2/2F= (万有引力) → =Ep(静电力) →7. 动能：mV2/28. 势能：A保= –ΔEp不同相互作用力势能形式不同且零点选择不同其形式不同，在默认势能零点的情况下：机械能：E=EK+EP9. 热量：其中：摩尔热容量C与过程有关，等容热容量Cv 与等压热容量Cp之间的关系为：Cp= Cv+R10. 压强：11. 分子平均平动能：;理想气体内能：12. 麦克斯韦速率分布函数：(意义：在V附近单位速度间隔内的分子数所占比率)13. 平均速率：方均根速率：;最可几速率：14. 熵：S=KlnΩ(Ω为热力学几率，即：一种宏观态包含的微观态数)15. 电场强度：= /q0 (对点电荷：)16. 电势：(对点电荷);电势能：Wa=qUa(A= –ΔW)17. 电容：C=Q/U ;电容器储能：W=CU2/2;电场能量密度ωe=ε0E2/218. 磁感应强度：大小，B=Fmax/qv(T);方向，小磁针指向(S→N)。
大学物理电磁学
大学物理电磁学是物理学的一个重要分支，主要研究电磁现象的规律和本质。
电磁学在科学技术、工业生产和日常生活中都有着广泛的应用。
本文将从电磁学的基本概念、基本定律和电磁波的传播等方面对大学物理电磁学进行介绍。
一、基本概念1.电荷：电荷是物质的一种属性，分为正电荷和负电荷。
电荷间的相互作用规律是：同种电荷相互排斥，异种电荷相互吸引。
2.电场：电场是电荷及变化磁场周围空间里存在的一种特殊物质，它对放入其中的电荷有作用力。
电场的强度用电场强度E表示，单位是牛/库仑。
3.磁场：磁场是磁体周围空间里存在的一种特殊物质，它对放入其中的磁体有作用力。
磁场的强度用磁感应强度B表示，单位是特斯拉。
4.电磁波：电磁波是由同相振荡且互相垂直的电场与磁场在空间中以波的形式移动，其传播方向垂直于电场与磁场构成的平面，有效的传递能量。
电磁波在真空传播速度与光速一样，速度为30万千米/秒。
二、基本定律1.库仑定律：库仑定律是描述电荷之间相互作用的定律，其内容为：真空中两点电荷间的作用力与它们的电荷量的乘积成正比，与它们的距离的平方成反比，作用力在它们的连线上。
2.安培定律：安培定律是描述电流和电流激发磁场的定律，其内容为：电流I1通过一条无限长直导线时，在距离导线r处产生的磁场强度H1与I1成正比，与r成反比，即H1与I1r成反比。
磁场方向垂直于电流方向和通过点的平面。
3.法拉第电磁感应定律：法拉第电磁感应定律是描述磁场变化引起电场变化的定律，其内容为：穿过电路的磁通量发生变化时，产生感应电动势。
感应电动势的大小与磁通量变化率成正比，与电路的匝数成正比。
4.麦克斯韦方程组：麦克斯韦方程组是描述电磁场分布和电磁波传播的四个偏微分方程，包括库仑定律、法拉第电磁感应定律、安培定律和位移电流定律。
三、电磁波的传播1.电磁波的发射：电磁波的产生通常是通过振荡电路实现的。
当振荡电路中的电场和磁场相互垂直且同相振荡时，电磁波便会产生并向外传播。
大学物理课件麦克斯韦方程组
L1
L2
[C]
有一圆形平行平板电容器，R=3.0cm。现对其充电，使 电路上的传导电流 I c dQ dt 2.5 A 。现有一点P处于两 极板间，离开轴线的距离r=2.0cm，若略去边缘效应。 求: （1）两极板间的位移电流；
（2）P点处的磁感应强度 。
五、电磁波的产生与传播
0
发射
接收
如图，平板电容器（忽略边缘效应）充电时，沿环 路L1、L2磁场强度H的环流中，必有：
( A) (B) (C ) ( A)
dl H dl LH 1 L2 dl H dl LH 1 L2 dl H dl LH 1 L2 H dl 0
1 LC
L
C
L
C
辐射能与频率 的4次方成正比
＋ －
L
C
－ ＋
偶极振子的辐射 ——最重要的电磁辐射模型
2 4 p0 辐射功率：P 3 12 0c
p p0 cost
电磁波的传播机制
变化的电场 —— 磁场 变化的磁场 —— 电场 地位对称 变化率也随时间变化 变化的电场、磁场同时存在， 又以对方存在为前提
全电流总是连续的
电流的连续性问题得到解决
三、位移电流的磁场
位移电流的引入，更重要的意义是提出了位移电流 也在周围空间激发磁场！
dΦD I B d l I H d l I I c c d L L dt E LH dl I c t dS
H dl I c I d L
麦克斯韦方程组
积分形式
d m LE dl dt
大学物理电磁学公式
大学物理电磁学公式大学物理电磁学是物理学中的一个重要分支，研究电场和磁场以及它们之间的相互作用。
在学习和研究电磁学的过程中，我们经常会接触到一系列重要的公式。
以下是一些常见的大学物理电磁学公式的详细介绍。
1. 库仑定律（Coulomb's Law）：库仑定律描述了两个点电荷之间相互作用力的大小和方向。
它的数学表达式为：F = k * |q1 * q2| / r²其中，F为两个电荷所受的力，k为库仑常数，q1和q2分别为两个电荷的大小，r为两个电荷之间的距离。
2. 电场强度（Electric Field Intensity）：电场强度描述了电荷在某一点周围的电场的强弱。
对于一个点电荷，其电场强度的数学表达式为：E = k * |q| / r²其中，E为电场强度，k为库仑常数，q为电荷的大小，r为点电荷到被测点之间的距离。
3. 电势能（Electric Potential Energy）：电势能描述了电荷由于存在于电场中而具有的能量。
对于一个点电荷，其电势能的数学表达式为：U = k * |q1 * q2| / r其中，U为电势能，k为库仑常数，q1和q2分别为两个电荷的大小，r为两个电荷之间的距离。
4. 电势差（Electric Potential Difference）：电势差描述了电场中两个点之间的电势能的差异。
对于两个点电荷之间的电势差，其数学表达式为：ΔV = V2 - V1 = -∫(E · dl)其中，ΔV为电势差，V1和V2分别为两个点的电势，E为电场强度，dl为路径元素。
5. 电场线（Electric Field Lines）：电场线用于可视化电场的分布情况。
电场线从正电荷流向负电荷，并且密集的电场线表示电场强度较大，稀疏的电场线表示电场强度较小。
6. 电场的高斯定律（Gauss's Law for Electric Fields）：电场的高斯定律描述了电场通过一个闭合曲面的总通量与该闭合曲面内的电荷量之间的关系。
麦克斯韦方程组及其电磁场特性分析
工业技术科技创新导报 Science and Technology Innovation Herald96DOI：10.16660/ki.1674-098X.2006-5552-9915麦克斯韦方程组及其电磁场特性分析①郭元龙(中国石油大学（华东）理学院19级应用物理专业 山东青岛 266580)摘 要：本文在梳理麦克斯韦方程组建立相关概论知识的基础上，对麦克斯韦方程组及其电磁场特性进行探讨研究，深入分析了麦克斯韦方程组推导过程，并归纳总结了麦克斯韦方程组隐含的电磁场特性，进而对麦克斯韦方程组在无线电通信以及光的衍射、散射应用过程进行分析，旨在为不断加强麦克斯韦方程组及其电磁场特性研究的深入程度，为麦克斯韦方程组的实践应用提供更多支撑与参考。
关键词：麦克斯韦方程组 电磁场特性 应用 无线电通信中图分类号：O441 文献标识码：A 文章编号：1674-098X(2020)09(b)-0096-03Analysis of Maxwell's Equations and Electromagnetic FieldCharacteristicsGUO Yuanlong(Applied Physics, College of Science, China University of Petroleum, Qingdao,Shandong Province, 266580China)Abstract : This article in combing maxwell's equations, on the basis of introduction to establish related knowledge, further study of maxwell's equations and its electromagnetic f ield characteristics, in-depth analysis of the maxwell's equations deducing process, and summarized the electromagnetic field properties of maxwell's equations implied, then the maxwell's equations in radio communication application scattering and diffraction of light, process analysis, aimed at strengthening maxwell's equations and the in-depth research of electromagnetic field, for the practice and application of maxwell's equations to provide more support and reference.Key Words : Maxwell's equations; Electromagnetic field characteristics; Application; Radio communication①作者简介：郭元龙（2001—），男，汉族，山东临沂人，本科在读，研究方向为应用物理专业。
麦克斯韦和电磁场理论
浅析麦克斯韦和电磁场理论摘要：麦克斯韦是继法拉第之后，又一位集电磁学大成于一身的伟大科学家。
他全面地总结了电磁学研究的全部成果，并在此基础上提出了“感生电场”和“位移电流”的假说，建立了完整的电磁场理论体系，不仅科学地预言了电磁波的存在，而且揭示了光、电、磁现象的内在联系及统一性，完成了物理学的又一次大综合。
他的理论成果为现代无线电电子工业奠定了理论基础。
关键词：电磁场理论；麦克斯韦方程组；电磁感应；位移电流中图分类号：tn914 文献标识码：ａ文章编号：1005-5312（2011）麦克斯韦(james clark maxwell，1831—1879)是英国物理学家，诞生于苏格兰的古都爱丁堡。
16岁时考进了爱丁堡大学，专攻数学和物理。
19岁时又进入剑桥大学。
1854年，他在剑桥大学数学竞赛中名列第二。
1856年任苏格兰marishal学院的自然哲学讲座教授。
1860年至1868年任伦敦皇家学院和剑桥大学物理学教授。
1870年创设并主持卡文迪什物理实验室，并担任剑桥大学首任实验物理学教授。
他是英国皇家学会会员。
他的主要贡献是建立了电磁场理论和气体分子速度分布律。
一、麦克斯韦与他的《论法拉第力线》麦克斯韦于1856年发表了他的第一篇论文《论法拉弟的力线》，在这篇文章中，他试图用数学语言精确地表述法拉弟的力线概念，他采用数学推论与物理类比相结合的方法，以假想流体的力学模型去模拟电磁现象。
1846年，汤姆孙获得了剑桥大学学位后，研究了电现象和弹性现象的类似性。
他考察了处于应力状态的不可压缩弹性固体的平衡方程，指出表示弹性位移的矢量分布可与静电系统的电力分布相比拟。
而且，弹性位移还可以同样好地与一个通过b由curlα=b定义的矢量α相一致。
这里α是与纽曼，韦伯等人在电流感应论文中引用的矢势(vector potential)等价。
但汤姆孙是在不知道这一等同性时，经过不同途径，独立得到的。
二、麦克斯韦与他的《论物理力线》麦克斯韦在完成了统一已知电磁学定律的第一阶段工作后，又投入到第二阶段工作中．他于1862年发表了具有决定意义的论文《论物理学的力线》。
大学物理 麦克斯韦方程组
S
S
M dS L M dl 斯托克斯公式 S E dS L E dl S B 环路定理 d S L E dl s t B 比较上两式，可得 E t D 同理由公式 d S L H d l t s D 可得 H t
L
R Q Q P P R dydz dzdx dxdy y z z x x y S R Q Q P P R cos cos cos dS y z z x x y S N dS M dS
D H t
B E t
高斯公式
(P cos Q cos R cos )dS
S
P Q R dxdydz x y z V 设矢量 M Pi Qj Rk dS (dS cos )i (dS cos ) j (dS cos )k
S
N i j k y z z x x y
矢量乘法： A Ai x A y j Ak z
B Bi x B y j Bk z
Ax Ay Az AB Bx By Bz (Ay Bz Az By )i (Az Bx AxBz ) j (AxBy Ay Bx )k i j k
s
B dS 0
s
v
( 2) D d S L H d l t S
大学物理-13 麦克斯韦方程组(1)
H dl Id
L1
H dl Id L3
L
H
dl
S
(
j传
D t
)
dS
空间没有传导电流的情况下，有：
L
H
d
dl
S
D t
dS
比较
l
E感
dl
S
B t
dS
(Hd为Id产生的涡旋磁场)
D
B
t
t
对称美
右旋 Hd
E感 左旋
§13-2 电磁场 麦克斯韦方程组
一、电磁场
E
t
H t
James ClerkMaxwell（1831-1879）
十九世纪四十年代，关于电磁现象的三个最 基本的实验定律已经总结出来:
库仑定律（1785年） 毕奥－萨伐尔定律（1820年） 法拉第电磁感应定律（1831－1845年）
摆在物理学家面前的课题是把已发现的各个 规律囊括起来，建立电磁现象的统一理论。
“只有上帝才能创造出这样完美的诗句！”
James ClerkMaxwell （1831-1879）
麦克斯韦
是经典电磁理论的奠基 人。他在电磁理论方面的 工作可以和牛顿在力学方 面的工作相媲美。他提出 了有旋场和位移电流的概 念,建立了经典电磁场理论 的完整体系,并预言了电磁 波的存在。1873年他的«电 磁学通论»问世，这是一本 划时代的巨著。是人类探 索电磁规律的里程碑。
H
变化的电场激发磁场;
E
E
E
变化的磁场激发电场；
E
E
H
H
H
H
H
两种变化的场永远互相联系着，形成统一的电磁场
这种变化的电磁场在空间的传播就称为电磁波
大学物理第10章麦克斯韦方程组
重要性
麦克斯韦方程组统一了电场和磁场， 预言了电磁波的存在，为现代电磁学 和通信技术的发展奠定了基础。
麦克斯韦方程组的基本概念
1
麦克斯韦方程组由四个基本方程构成，包括：高 斯定理、高斯定理关于磁场的应用、法拉第电磁 感应定律和安培环路定律。
光纤通信
在光纤通信中，麦克斯韦方程组被用来 描述光波在光纤中的传播行为。通过控 制光纤的折射率，可以实现光的调制和 传播方向的控制。
VS
电磁兼容性
在电子设备和系统的设计中，麦克斯韦方 程组被用来分析电磁干扰和电磁兼容性问 题。通过合理的设计和控制，可以降低电 子设备之间的电磁干扰，提高系统的稳定 性。
02
电场和磁场具有能量、动量和力的性质，它们以波的形式传 播，其传播速度等于光速。
03
变化的电场会产生磁场，变化的磁场会产生电场，这是电磁 感应的基本原理。
麦克斯韦方程组的推导过程
麦克斯韦通过对电磁场的基本性质进行数学描述，推导出四个微分方程， 即麦克斯韦方程组的雏形。
这四个微分方程分别描述了电场和磁场在空间和时间的变化规律，以及它 们之间的相互转化关系。
应用
适用于具有周期性边界条件的问题，如电磁波在无限大均匀介质中 的传播。
有限差分法
原理
将连续的偏微分方程离散化为差 分方程，通过求解差分方程得到 原方程的近似解。
步骤
将麦克斯韦方程组中的时间和空 间坐标离散化，用差商代替导数， 将偏微分方程转化为差分方程， 通过迭代求解。
应用
适用于具有规则边界和初始条件 的问题，如电磁波在有限大小介 质中的传播。
大学物理电子教案Chp_08
εi
2011-12-1
dΨi dΦ i =− = −N m dt dt
P.12/64
电磁感应
(3) 感应电流 I
1 dΨ m I = =− R R dt
在直导体棒匀速向右运动 过程中,如果其外框是: 过程中,如果其外框是: 闭合导体回路 — 有持续电流
ε
B
本质: 本质: 磁通 量变化引起 瞬态电流, 导体不闭合 — 瞬态电流,稳定ε 了感应电场 无电流， 无导体 — 无电流，但有感应电动势
法拉第(1791--1867)， ， 法拉第 英国物理学家、 英国物理学家 、 化学 家 ， 著名的自学成才 科学家, 科学家,生于萨里郡纽 因顿一个贫苦铁匠家 庭 。 他一生献身科学 研究，成果众多， 1846年荣获伦福德奖 1846 年荣获伦福德奖 章和皇家勋章。 章和皇家勋章。
2011-12-1
N
N S
对线圈参考系： 对线圈参考系：B 变化 对磁铁参考系： 对磁铁参考系： B不变，线圈运动 不变，
不同惯性系中的变换很难概括为一个简单公式， 不同惯性系中的变换很难概括为一个简单公式，分 两种情况处理。 两种情况处理。
2011-12-1 P.16/64
电磁感应
一、动生电动势(motional electromotive force)的成因 的非静电力是什么？ 产生 ε 动 的非静电力是什么？
εi = ∫ (v×B)⋅ dl
a
∫
0
= vB 电动势指向 a→b O × × × × l × a dΦ 方法二： 方法二： ε = − i dt dΦ dx Φ = Blx εi = =B l dt dt
l × × × × ×× ×
× ×
x
大学物理静电学总结
大学物理静电学总结静电学是物理学中的一个重要分支，主要研究静止电荷之间的相互作用和电荷分布规律。
在大学物理课程中，静电学通常是一个重要的章节，涵盖了基本概念、定理、公式和应用。
本文将简要总结大学物理静电学的主要内容。
一、基本概念1、电荷：电荷是物质的基本属性，可以分为正电荷和负电荷。
电荷的量称为电荷量，用符号Q表示，单位为库仑（C）。
2、电场：电场是电荷周围存在的一种特殊物质，它可以对放入其中的电荷施加作用力。
电场强度E是描述电场性质的一个物理量，单位为牛/库仑（N/C）。
3、电势：电势是描述电场中某一点电场强度大小的物理量，用符号V表示，单位为伏特（V）。
4、电容：电容是描述电容器储存电荷能力的物理量，用符号C表示，单位为法拉（F）。
5、静电荷分布：静电荷分布是指电荷在空间中的分布情况，可以用电荷密度、电荷线密度和电荷面密度来描述。
二、基本定理和公式1、高斯定理：高斯定理表明，穿过一个封闭曲面的电场强度通量等于该曲面内电荷量的代数和除以真空介电常数。
2、静电场基本方程：静电场基本方程表明，电势V和电场强度E之间存在关系▽·E=ρ/ε0和▽×E=0，其中ρ表示电荷密度，ε0表示真空介电常数。
3、静电场中的能量：静电场中的能量可以用电势能EP和电场能量WE来表示。
其中，电势能EP=QV，电场能量WE=1/2ε0E²。
4、电容器的充电和放电：电容器的充电过程是指将电荷加到电容器两极板上，放电过程是指将电荷从电容器两极板上移走。
充电和放电过程中，电流I与电压U之间存在关系I=dQ/dt=U/R和U=dQ/dt=I×R，其中R表示电阻。
5、静电感应：当一个导体置于电场中时，由于静电感应，导体内部会产生相反的电荷分布，使得导体表面出现电荷。
静电感应的原理可以用安培环路定律和法拉第电磁感应定律来解释。
6、静电屏蔽：静电屏蔽是指将一个导体置于电场中时，由于静电感应，导体表面会产生相反的电荷分布，使得外部电场对导体内部的影响减弱。
大学物理-7麦克斯韦方程
得 I D 2.78A B 5.56106T
三、全电流定律的意义
法拉第电磁感应定律说明:变化的磁场会激发涡旋
电场；
rr
r B
r
Ñ Ei dl
L
S
t
dS
麦克斯韦全电流定律说明：变化的电场会激发涡
旋磁场。
rr
rr
r D
r
Ñ H
L
dl
J0
S
dS
S
t
dS
位移电流的引入，它给出了电场和磁场的内在联
由全电流定理
J
D
D t
dE dt
i
ID r2JD
r 2
dE dt
H r dE
2 dt
B H r dE
2 dt
H r dE B H r dE
R
2 dt
2 dt
忽略边缘效应 电容器内总位移电流
ID
dE dt
R2
作一数量级估算 若 r R R 0.1m
0 0
dE 1013(V / s) dt
t
x
t
H y Ez
x
t
第二步：由八个式子进行推论： 推论1
Ex 0 Ex 0
x
t
Ex const
H x 0 H x 0
x
t
H x const
因不变的电磁场不引起电磁波，可认为Ex和Hx为零， 所以E和H在yz平面内，电磁波沿x方向传播，电磁波 为横波。
推论2
E在yz平面，不妨若选择E沿y轴，有：
E 、H
的方向始终与传播方向垂直，且
E
H
方向
指向电磁波的传播方向;
•
E
大学物理 电磁学
大学物理：电磁学电磁学是物理学的一个分支，主要研究电磁现象、电磁辐射、电磁场以及它们与物质之间的相互作用。
在本文中，我们将探讨电磁学的基本概念、历史背景、研究领域以及在现实生活中的应用。
一、基本概念1、电荷与电荷密度电荷是物质的一种属性，它可以产生电场。
电荷分为正电荷和负电荷。
电荷的分布可以用电荷密度来描述，它表示单位体积内所包含的电荷数量。
2、电场与电场强度电场是空间中由电荷产生的力线所形成的场。
电场强度是描述电场强弱的物理量，它与电荷密度有关。
3、磁场与磁感应强度磁场是由电流或磁体产生的场。
磁感应强度是描述磁场强弱的物理量，它与电流密度和磁场中的电荷有关。
4、电磁波电磁波是由电磁场产生的波动现象，它包括无线电波、微波、红外线、可见光、紫外线、X射线和伽马射线等。
二、历史背景电磁学的研究可以追溯到17世纪和18世纪，当时科学家们开始研究静电和静磁现象。
19世纪初，英国物理学家迈克尔·法拉第发现了电磁感应定律，即变化的磁场可以产生电流。
1864年，英国物理学家詹姆斯·克拉克·麦克斯韦将法拉第的发现与自己的研究结合起来，提出了著名的麦克斯韦方程组，预言了电磁波的存在。
三、研究领域1、静电学：研究静止电荷所产生的电场、电势、电容、电导等性质。
2、静磁学：研究静止磁场以及磁体和电流所产生的磁场和磁场分布。
3、电磁感应：研究变化的磁场和电场以及它们之间的相互作用和变化规律。
4、电磁波：研究电磁波的产生、传播、散射、反射和吸收等性质以及在各种介质中的行为。
四、应用电磁学在现实生活中有着广泛的应用，如：1、电力工业：利用电磁感应原理发电、输电和用电。
2、通信工程：利用电磁波传递信息，包括无线电通信、微波通信、光纤通信等。
3、电子技术：利用电磁学原理制造电子设备，如电视机、计算机、雷达等。
4、磁悬浮技术：利用磁力使物体悬浮，减少摩擦和能耗。
5、医学成像：利用电磁波和磁场进行医学诊断和治疗。
大学物理电磁学基础知识点汇总
大学物理电磁学基础知识点汇总一、电场1、库仑定律库仑定律描述了真空中两个静止点电荷之间的相互作用力与它们电荷量的乘积成正比，与它们之间距离的平方成反比，作用力的方向沿着它们的连线。
其表达式为：＄F ＝ k\frac{q_1q_2}｛r^2}＄，其中$k$为库仑常量，＄q_1$和$q_2$为两个点电荷的电荷量，＄r$为它们之间的距离。
2、电场强度电场强度是描述电场力的性质的物理量，定义为单位正电荷在电场中所受到的力。
其表达式为：＄E ＝＼frac{F}｛q}＄。
对于点电荷产生的电场，其电场强度的表达式为：＄E ＝ k\frac{q}｛r^2}＄，方向沿径向向外（正电荷）或向内（负电荷）。
3、电场线电场线是用来形象地描述电场的一种工具。
电场线的疏密表示电场强度的大小，电场线的切线方向表示电场强度的方向。
静电场的电场线不闭合，始于正电荷或无穷远，终于负电荷或无穷远。
4、电通量电通量是通过某一面积的电场线条数。
对于匀强电场，通过平面的电通量为：＄＼Phi ＝ ES\cos\theta$，其中$E$为电场强度，＄S$为平面面积，＄＼theta$为电场强度与平面法线的夹角。
5、高斯定理高斯定理表明，通过闭合曲面的电通量等于该闭合曲面所包围的电荷量的代数和除以$＼epsilon_0$。
即：＄＼oint_S E\cdot dS ＝＼frac{1}｛＼epsilon_0}＼sum q$。
高斯定理是求解具有对称性电场分布的重要工具。
二、电势1、电势电势是描述电场能的性质的物理量，定义为把单位正电荷从电场中某点移动到参考点（通常取无穷远处）时电场力所做的功。
某点的电势等于该点到参考点的电势差。
点电荷产生的电场中某点的电势为：＄V ＝ k\frac{q}｛r}＄。
2、等势面等势面是电势相等的点构成的面。
等势面与电场线垂直，沿电场线方向电势降低。
3、电势差电场中两点之间的电势之差称为电势差，也称为电压。
其表达式为：＄U_{AB} ＝ V_A V_B$。
大学基础物理学答案(习岗) 电磁感应与电磁场
dx x O L x
I
d
a
图 7-3
99
第七章 电磁感应
于是，在 d=10cm 时，一匝线圈中产生的感生电动势为
0 2
L
2
0
ln
a
d dI d dt
N 匝线圈中产生的感生电动势为
N
由于
2
NL a d dI ln 2 d dt 500 cos100 t
dI dt
带入数据，得
4.36 10 2 cos100 t (V)
96
第七章 电磁感应
7-2 灵敏电流计的线圈处于永磁体的磁场中，通入电流线圈就会发生偏转， 切断电流后线圈在回到原来位置前总要来回摆动几次。这时，如果用导线把线圈 的两个头短路，摆动就会马上停止，这是为什么？ 答：处于永磁体磁场中的灵敏电流计的通电线圈要受到四个力矩的作用，它 们是： （1）磁场对线圈的电磁力矩 BSNIg，其中，B 为磁场的磁感应强度，S 为线 圈的截面积，N 为线圈的总匝数，Ig 为线圈中通过的电流； （2）线圈转动时张丝 扭转而产生的反抗（恢复）力矩－Dθ，其中，D 为张丝的扭转系数，θ 为线圈的 偏转角； （3）电磁阻尼力矩； （4）空气阻尼力矩。 电磁阻尼力矩产生的原因是因为线圈在磁场中运动时的电磁感应现象。根据 电磁感应定律，线圈在磁场中运动时会产生感应电动势。灵敏电流计的内阻 Rg 和外电路的电阻 R 构成一个回路，因而有感应电流 i 流过线圈，这个电流又与磁 场相互作用，产生了一个阻止线圈运动的电磁阻尼力矩 M。可以证明，M 与回路 的总电阻 Rg+R 成反比，有 d M BNSi dt 其中，
E H
电磁波的传播速度为
v 1
其中， 和 分别为介质的电容率和磁导率。在真空中 0 =8.8542× 10 － 12F/m ， 0 =4 ×10 7 H/m。由此可知，电磁波在真空中的传播速度为 C=
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
++++++++ ++++++++
维持滑杆运动必须外加一力，此过程为外力克 服安培力做功转化为焦耳热.
用 楞
B
次
定
I
律
v
判
S
断
感
应
N
电
流
方
向
B
I
N
S v
例8-1 在匀强磁场中, 置有面积为 S 的可绕 轴转动的N 匝线圈 .
若线圈以角速度
作匀速转动. 求线圈 中的感应电动势.
ω
o'
N
en
1.
定义求解：
i
b(vB )dl a
2. 法拉第电磁感应定律求解：
i
dNd
dt
dt
若回路不闭合，需增加辅助线使其闭合。计算时只 计大小，方向由楞次定律决定。
例8-3. 一矩形导体线框，宽为l，与运动导体棒构成
闭合回路。如果导体棒以速度v作匀速直线运动，求回
路内的感应电动势。
b
解：方法一
i
电磁感应现象中产生的电流称为感应电流(induction current)，相应的电动势称为感应电动势(induction emf) 。
符号法则：
1. 对回路L任取一绕行方向。
2.当回路中的磁感线方向与回路的绕行方向成右手 螺旋关系时，磁通量为正(+)，反之为负(-)。
3. 回路中的感应电动势方向凡与绕行方向一致时为 正(+)，反之为负(-) 。
N
Ψ i Φ m 1 Φ m 2 i 1Φ m iN Φ m
N称为磁通链数。
N匝线圈的总电动势为各匝产生的电动势之和：
i
dΨi dt
(dΦm1 dt
dΦm2 dt
)
d dt
(Φm1
Φm2
)
NdΦmi dt
i
dΨi NdΦmi
dt
dt
感应电流 I
B
I 1dΨm
R R dt
在直导体棒匀速向右运动 过程中,如果其外框是: 闭合导体回路 — 有持续电流
b(vB )dl a
l
vBdl
0
- v
l
vBl 电动势指向 ab O
方法二： i
1. 当载流主 线圈相对于副 线圈运动时， 线圈回路内有 电流产生。
2. 当载流主线圈相对于副线圈静止时，如果பைடு நூலகம்变 主线圈的电流，则副线圈回路中也会产生电流。
结论：当穿过闭合回路的磁通量发生变化时，不管 这种变化是由什么原因的，回路中有电流产生。这一 现象称为电磁感应现象(electromagnetic induction)。
变化、取向变化等
动生电动势
2）导体不动，磁场变化
感生电动势
一 动生电动势
动生电动势的非静电力场来源
洛伦兹力
F m( e)v B
平衡时 F m F e eE k
Ek Fm evB
+B+ +P+++
+ + Fe+ +
+ + + -+
+
+ Fm+
-
+ -
+ + + O+
+ + + + +
++
电流是时间的正弦函数.这 种电流称交流电.
o
o'
en
B
iR
例8-2. 一长直导线通以电流 i I0sint(I0为常数)。
旁边有一个边长分别为l1和l2的矩形线圈abcd与长直电 流共面，ab边距长直电流r。求线圈中的感应电动势。
解：建立坐标系Ox如图
Φ
BdS
rl1
S
r
2π0ixl2dx
0I0l2si ntlnrl1
2π
r
b l1 c
i
l2
a
d
r
i
d
dt
20π I0l2cotsl
nrl1 r
O
x dx
x
当0t π时， cost 0 当π t π时，cost 0
2
2
i 0 为逆时针转向 i 0 为顺时针转向
§ 8-2 动生电动势与感生电动势
引起磁通量变化的原因
1）稳恒磁场中的导体运动 , 或者回路面积
§8-1 电磁感应基本定律
一、法拉第电磁感应定律
实验一：
当条形磁铁插入或拔 出线圈回路时，在线圈 回路中会产生电流；而 当磁铁与线圈保持相对 静止时，回路中不存在 电流。
实验二：将闭合回路
bB
c
(abcd) 置 于 恒 定 磁 场 中 ， 当
v
导体棒在导体轨道上滑行时，
回路内出现了电流。
a
d
实验三： 以通电线圈代替条形磁铁。
任何引发电磁感应的原因
（反抗相对运动、磁场变
化或线圈变形等）.
B N
F
v
S
楞次定律 闭合的导线回路中所出现的感应电
流，总是使它自己所激发的磁场反抗任何引发电磁
感应的原因.
楞次定律是能量 守恒定律的一种表现
机械能
焦耳热
B + + + + + + + +
+ + + + + + + + v F + + m+ + + + + +
B
iR
o
已知 S, N, 求 E
解 设 t 0 时,
en与 B 同向 , 则 t
N
N NB co Sts
EdNB sSi nt
dt
ω
令 EmNBS
o
则 EEmsi nt
o'
en
B
iR
EEmsi nt
iER msi ntImsi nt
N
Im
Em R
可见,在匀强磁场中匀
ω
速转动的线圈内的感应电
+ + v+ +
++
++
Ei OPE kdlOP (v B )dl
l
设杆长为 l
Ei
vBdl
0
vBl
说明： 动生电动势存在于运动导体上；不动的导体
不产生电动势，是提供电流运行的通路。
非回路的导体在磁场中运动，有动生电动势
但没有感应(动生)电流。
导线切割磁感线时才产生动生电动势。
二、动生电动势的计算
感应电动势的方向
Ei
dΦ dt
B
d Φ Φ (t d t) Φ (t)
Φ0（ B与回路成右螺旋） N
dΦ 0 dt
Ei 0
E i 与回路取向相反
Ei
dΦ dt
B
Φ0
dΦ 0 dt
Ei 0
N
E i 与回路取向相同
当线圈有 N 匝时
Ei
N dΦ dt
对N匝线圈，其总磁通量称全磁通。
导体不闭合 — 瞬态电流,稳定
无导体 — 无电流，但有感应电动势
本质: 磁通 量变化引起 了感应电场
一定时间内通过回路截面的感应电量:
t2
1Ψ m 2
1
qt1IdtRΨ m 1 dΨ mR(Ψ m 2Ψ m 1)
Ei
dΦ dt
二 楞次定律
闭合的导线回路中所
出现的感应电流，总是使
它自己所激发的磁场反抗
Φm 0
i
L 的绕行方向
Φm 0
i
法拉第电磁感应定律: 当穿过回路所 包围面积的磁通量发生变化时，回路 中产生的感应电动势与穿过回路的磁 通量对时间变化率的负值成正比。
i
dΦm dt
反映感应电动势的 方向，楞次定律的
数学表示
法 拉 第 (1791--1867) ， 英国物理学家、化学 家，著名的自学成才 科学家,生于萨里郡纽 因顿一个贫苦铁匠家 庭。他一生献身科学 研究，成果众多， 1846 年 荣 获 伦 福 德 奖 章和皇家勋章。