静力学应用问题
流体静力学定律及其在工程中的应用实例分析

流体静力学定律及其在工程中的应用实例分析在物理学和工程学领域,流体静力学定律是一组非常重要的原理,它们对于理解和解决与静止流体相关的问题具有关键意义。
流体静力学主要研究静止流体的压力分布、浮力以及相关的力学特性。
流体静力学的基本定律之一是帕斯卡定律。
帕斯卡定律指出,施加于密闭流体上的压强能够大小不变地由流体向各个方向传递。
这一定律在许多工程应用中发挥着重要作用。
比如在液压系统中,通过一个小的活塞施加较小的力,就能在较大的活塞上产生较大的力。
这是因为施加在小活塞上的压强会通过液体均匀地传递到大活塞上,从而实现力的放大效果。
液压千斤顶就是一个典型的应用实例。
当我们使用液压千斤顶抬起一辆汽车时,通过在小活塞上施加相对较小的力,就能在大活塞上产生足够大的力来顶起汽车。
这种原理使得液压系统在需要产生大力的场合,如重型机械的操作、桥梁的建设等工程中得到广泛应用。
另一个重要的定律是阿基米德原理。
阿基米德原理表明,物体在液体中所受到的浮力等于其排开液体的重量。
这一原理在船舶设计和潜艇制造中具有至关重要的地位。
船舶能够浮在水面上,正是因为其排开的水的重量等于船舶自身的重量。
在设计船舶时,工程师需要精确计算船舶的体积和重量,以确保其能够在水中保持稳定的浮态。
潜艇则通过控制自身的排水量来实现上浮和下潜。
当潜艇需要下潜时,会吸入海水增加自身重量,使其排水量大于浮力,从而下沉;当需要上浮时,排出海水减轻重量,使浮力大于排水量。
在水利工程中,流体静力学定律也有着广泛的应用。
例如,水库大坝的设计就需要充分考虑流体静压力的影响。
大坝所承受的水压力是随着水深的增加而增大的。
因此,大坝的底部需要设计得更加厚实和坚固,以承受巨大的流体静压力。
通过对流体静力学的分析,可以计算出大坝不同位置所承受的压力大小,从而确定大坝的结构和材料强度,确保其安全性和稳定性。
在石油和天然气工业中,流体静力学定律在储油罐和管道设计中同样不可或缺。
储油罐中的油面高度不同,对罐壁产生的压力也不同。
静力学原理的工程应用

静力学原理的工程应用介绍静力学是研究物体处于静止状态下的力学学科。
它是理解和应用工程力学的基础。
本文将探讨一些静力学原理在工程应用中的重要性和应用。
1. 物体平衡物体平衡是静力学的基本概念之一。
在工程应用中,我们经常需要确定物体的平衡状态,以确保结构的稳定性和安全性。
以下是一些常见的工程应用:•建筑结构设计:在建筑结构设计中,静力学原理用于确定建筑物的稳定性和平衡。
例如,当设计一个大楼时,工程师需要考虑楼体的重力、地震力和风力,并确保结构能够平衡和抵抗这些力。
•桥梁设计:桥梁是另一个应用静力学原理的工程领域。
在桥梁设计中,工程师需要考虑桥梁的自重、荷载和风力等因素,以确保桥梁结构的平衡和稳定。
静力学原理帮助工程师计算桥梁的承载能力和抗风性能。
•建筑物基础设计:在设计建筑物的基础时,静力学原理用于计算承载力和稳定性。
工程师需要考虑地质条件、土壤类型和建筑物的重力等因素,以确定合适的基础尺寸和深度。
2. 摩擦力和静摩擦力摩擦力和静摩擦力是静力学的重要概念。
在工程中,摩擦力和静摩擦力的应用广泛,以下是一些例子:•轮胎与地面的摩擦力:在汽车工程中,摩擦力对于车辆的行驶和刹车非常重要。
工程师需要考虑轮胎和地面之间的摩擦力,以确保车辆的安全性和稳定性。
•斜面上物体的滑动:在斜面上运送重物时,静摩擦力对于物体的稳定和防止滑动很重要。
工程师需要确定斜面和物体之间的静摩擦力,以确保物体能够保持在斜面上。
•重型机械的移动和停止:在工厂和建筑工地上,需要移动和停止重型机械。
工程师需要考虑摩擦力和静摩擦力,以确保机械的平稳移动和停止。
3. 弹簧力和挠度弹簧力和挠度是静力学中经常涉及的概念。
以下是一些应用例子:•悬挂系统:在汽车和火车的悬挂系统中,弹簧力和挠度对于平稳行驶和乘坐舒适很重要。
工程师需要计算和设计合适的弹簧力和挠度,以确保良好的悬挂系统性能。
•工程结构的弹性变形:在建筑和桥梁等工程结构中,弹性变形是一个重要的考虑因素。
物体的静力学平衡与应用实验

物体的静力学平衡与应用实验静力学是物理学中的一个重要分支,主要研究物体在静止状态下力的平衡问题。
静力学平衡的应用实验广泛应用于工程学、建筑学等领域,对于保证结构的稳定性以及力学原理的实际应用具有重要意义。
一、引言静力学平衡是研究物体在静止状态下所受力之间的关系,即物体所受力的合力为零。
为了验证物体的静力学平衡,人们通过应用实验进行实际观测和测量,以验证力的平衡条件。
二、实验目的本实验的目的是通过实验验证物体的静力学平衡,并了解静力学平衡的原理和应用。
三、实验器材1. 重物挂钩:用于挂载被测物体,具有一定的承重能力。
2. 质量块组合:用于增加或减小物体所受力的大小。
3. 弹簧测力计:用于测量物体所受力的大小,精确度较高。
4. 实验台:提供稳定的工作平台,确保实验过程中的准确性和安全性。
5. 测试用物体:使用具有不同形状和重量的物体进行实验。
四、实验步骤1. 将实验台放置在水平稳定的表面上,确保其平整度。
2. 使用重物挂钩将被测物体挂载在挂钩上,并调整重物挂钩的高度,使物体悬挂且保持平衡。
3. 使用弹簧测力计逐渐将质量块组合挂在被测物体上,记录每次挂载后的测力计示数,并观察物体是否保持平衡。
4. 根据测力计示数的变化情况,计算物体所受力的大小,并记录下来。
5. 重复上述步骤,分别使用不同形状和重量的物体进行实验,以验证静力学平衡的原理。
五、实验结果1. 将实验数据整理成表格或图形的形式,以便于分析和对比。
2. 根据实验数据,可以观察到不同物质和形状的物体在静力学平衡状态下所受力的大小和方向。
六、实验分析根据实验结果进行数据分析和讨论,比较不同物体的重量、形状、自身结构等对静力学平衡的影响。
可以通过实验数据的比较和计算,验证静力学平衡的原理和公式,并探讨静力学平衡在工程学、建筑学等领域的具体应用。
七、实验结论通过本实验的观察和测量,验证了物体的静力学平衡的原理。
通过实验数据的比较和分析,可以得出结论:物体在静止状态下,所受力的合力为零。
《理论力学》第四章 静力学应用专题习题解
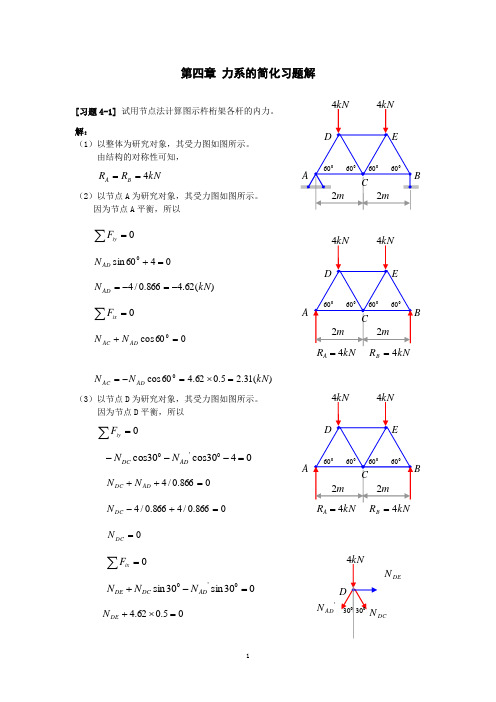
第四章 力系的简化习题解[习题4-1] 试用节点法计算图示杵桁架各杆的内力。
解:(1)以整体为研究对象,其受力图如图所示。
由结构的对称性可知, kN R R B A 4==(2)以节点A 为研究对象,其受力图如图所示。
因为节点A 平衡,所以0=∑iyF0460sin 0=+AD N)(62.4866.0/4kN N AD -=-=0=∑ixF060cos 0=+AD AC N N)(31.25.062.460cos 0kN N N AD AC =⨯=-= (3)以节点D 为研究对象,其受力图如图所示。
因为节点D 平衡,所以 0=∑iyF0430cos 30cos 0'0=---AD D C N N 0866.0/4=++AD D C N N 0866.0/4866.0/4=+-D C N0=DC N0=∑ixF030sin 30sin 0'0=-+AD D C D E N N N 05.062.4=⨯+DE NkN4)(akN4AB RkN 2AC23N A )(31.2kN N DE -=(4)根据对称性可写出其它杆件的内力如图所示。
[习题4-2] 用截面法求图示桁架指定杆件 的内力。
解:(a)(1)求支座反力以整体为研究对象,其受力图如图所示。
由对称性可知,kN R R B A 12==(2)截取左半部分为研究对象,其受力图 如图所示。
因为左半部分平衡,所以0)(=∑i CF M0612422843=⨯-⨯+⨯+⨯N 063243=⨯-++N )(123kN N =kN2AC23N A0=∑ixF0cos cos 321=++N N N αθ01252252421=+⋅+⋅N N012515221=+⋅+⋅N N0512221=++N N ……..(1) 0=∑iyF02812sin sin 21=--++αθN N025*******=+⋅+⋅N N02525121=+⋅+⋅N N052221=++N N0544221=++N N ……..(2) 05832=-N)(963.53/582kN N ==)(399.1652963.5252221kN N N -=-⨯-=--=解:(b )截取上半部分为研究对象,其受力图如图所示。
静力学原理的应用

静力学原理的应用概述静力学是力学的一个分支,它研究物体在静力平衡状态下的力学性质。
静力学原理是静力学研究中的基本原理,广泛应用于各个领域。
本文将介绍一些静力学原理的应用,并以列点的方式进行展示。
静力学原理的应用1. 建筑结构设计•静力学原理在建筑结构设计中起着重要作用。
例如,使用静力学原理可以计算建筑物的受力分布和结构的承载能力,从而确定结构的合理设计方案。
•静力学原理也可以应用于桥梁、楼房等建筑物的设计。
通过对结构的受力分析,可以确保建筑物的稳定性和安全性。
2. 机械工程•在机械工程中,静力学原理用于设计机械组件和机械系统。
通过分析力的平衡条件,可以确定各个部件之间的受力关系,从而设计出稳定和可靠的机械系统。
•静力学原理也可以应用于机械结构的优化设计。
通过对各个部件的受力分析,可以减小结构的应力集中和变形,提高机械系统的性能。
3. 土木工程•在土木工程中,静力学原理被广泛应用于土木结构的设计和施工。
通过对土地、建筑物等的受力分析,可以确保结构的稳定和安全,并提供合理的设计方案。
•静力学原理也可以应用于土木结构的强度计算和改善。
通过对结构的受力分析,可以确定合适的材料和尺寸,以提高土木结构的承载能力。
4. 航空航天工程•在航空航天工程中,静力学原理用于飞行器的设计和性能分析。
通过对飞行器的受力分析,可以确定合适的构造和材料,确保飞行器在各种条件下的稳定性和安全性。
•静力学原理也可以应用于推进系统的设计和优化。
通过对推进系统的受力分析,可以提高系统的效率和性能,从而提高飞行器的整体性能。
5. 汽车工程•在汽车工程中,静力学原理被用于汽车的设计和性能研究。
通过对汽车各个部件的受力分析,可以确定合适的材料和结构,提高汽车的稳定性和安全性。
•静力学原理还可以应用于汽车的悬挂系统和制动系统的设计,以提高汽车的操控性和舒适性。
总结静力学原理是力学研究中的重要部分,广泛应用于建筑结构设计、机械工程、土木工程、航空航天工程和汽车工程等领域。
静力学原理的现实应用

静力学原理的现实应用1. 引言静力学原理是物理学中的基础原理之一,它研究物体在静止状态下的力学特性。
静力学原理不仅在理论物理学中有重要应用,而且在现实生活中也有广泛的应用。
本文将介绍静力学原理的几个现实应用。
2. 桥梁的设计与施工•桥梁的设计:静力学原理在桥梁的设计中扮演着重要的角色。
通过静力学原理,工程师可以计算桥梁的结构强度和稳定性,确定桥梁的设计参数,例如桥梁的梁柱尺寸、支撑结构、桥墩布置等。
所以在桥梁设计中,工程师需要利用静力学原理来确保桥梁的稳定和安全。
•桥梁的施工:在桥梁的施工中,静力学原理也起到了重要的作用。
施工中的临时支撑和梁柱的调整都依赖于静力学原理的计算和分析。
此外,静力学原理还可以指导施工人员在施工过程中进行力的平衡和分配,确保施工安全。
3. 建筑物的结构分析与设计•建筑物的结构分析:在建筑物的结构设计中,静力学原理被广泛应用。
通过分析物体在静止状态下的受力情况,工程师可以确定建筑物的受力方式和结构强度。
这些分析结果对于建筑物的结构稳定性和安全性至关重要。
•建筑物的结构设计:静力学原理为建筑物的结构设计提供了重要的依据。
通过使用静力学原理,工程师可以计算建筑物所受的各种力(如重力、支撑力等),从而确定合适的结构形式和尺寸。
这些设计决策直接关系到建筑物的安全性和经济性。
4. 航天器的发射与轨道控制•航天器的发射:在航天器的发射过程中,静力学原理被广泛应用。
通过静力学原理的计算和分析,航天工程师可以确定发射台座的尺寸、材料和稳定性,确保航天器的安全发射。
•轨道控制:航天器在进入轨道后需要进行轨道控制,静力学原理是轨道控制的基础理论之一。
航天工程师利用静力学原理计算航天器所受的各种力(如引力、推力等),从而确定轨道控制的方式和参数。
静力学原理为航天器的轨道控制提供了重要的理论依据。
5. 汽车的悬挂系统设计汽车的悬挂系统是保障行车安全和舒适性的重要组成部分。
静力学原理在汽车悬挂系统的设计中起着重要的作用。
理论力学中的静力学平衡条件与应用

理论力学中的静力学平衡条件与应用在理论力学中,静力学是研究物体处于平衡状态时的力学原理和条件。
静力学平衡条件是判断物体是否处于平衡状态的基本准则。
本文将对理论力学中的静力学平衡条件进行分析,并探讨其在实际应用中的意义。
1. 刚体静力学平衡条件在理论力学中,刚体是指其形状和体积在外力作用下保持不变的物体。
刚体静力学平衡条件是判断刚体是否处于平衡状态的基本原理。
根据刚体静力学平衡条件,一个刚体处于平衡状态需要满足以下两个条件:- 力的平衡条件:合力为零。
即作用在刚体上的所有力的矢量和等于零。
- 力矩的平衡条件:合力矩为零。
即作用在刚体上的所有力矩的代数和等于零。
2. 非刚体静力学平衡条件在实际应用中,许多物体并不是刚体,而是由多个部分组成的弹性体。
对于非刚体的情况,同样存在静力学平衡条件来判断物体是否处于平衡状态。
非刚体静力学平衡条件包括以下几个方面:- 力的平衡条件:合力为零。
即作用在物体上的合外力等于零,物体保持静止。
- 力矩的平衡条件:合力矩为零。
即作用在物体上的合外力矩等于零,物体不会产生旋转。
- 形变平衡条件:物体内部各部分之间应满足力的平衡条件和形变的平衡条件,使得物体整体保持平衡。
3. 静力学平衡条件的应用静力学平衡条件在工程学、建筑学和力学等领域有着广泛的应用。
以下是一些典型的应用场景:- 结构力学:静力学平衡条件可用于判断建筑物、桥梁和机械结构等是否处于稳定的平衡状态,从而确保其安全性。
- 弹性体力学:静力学平衡条件可用于分析和设计材料的弹性性能,求解材料的应力和变形分布。
- 静力学问题求解:通过应用静力学平衡条件,可以解决一些静力学问题,如悬臂梁的荷载计算、桥梁上的力的平衡等。
4. 实例分析以建筑结构为例,应用静力学平衡条件可以分析房屋的支撑结构是否稳定。
在设计房屋的支撑结构时,需要考虑以下几个方面:- 力的平衡条件:房屋所受的重力需要通过支撑结构的柱子、墙壁等来承受,使得合力为零,保持平衡。
流体静力学原理的工业应用

流体静力学原理的工业应用1. 工业领域中的流体静力学1.1 流体静力学的概述流体静力学是研究流体在静力学平衡下的行为和性质的学科。
它主要关注流体的力学性质,如压力、密度、浮力等,并通过应用基本方程和定律来描述流体的行为。
在工业领域中,流体静力学被广泛应用于各种工艺过程和系统设计中。
1.2 工业应用中的流体静力学原理在工业应用中,流体静力学原理可以用于解决一系列问题,包括但不限于以下几个方面:•液压系统设计:流体静力学原理可以用于设计和优化液压系统,确保系统的稳定性和性能。
通过分析流体的压力传递和力平衡,在液压系统中实现力的放大、方向控制和运动控制。
•管道和管路系统:在工业领域中,流体静力学原理常被用于设计和分析管道和管路系统。
通过考虑管道内部的流体压力和速度分布,可以优化管道的尺寸、布局和材料,以满足流体输送的需求。
•流量测量和控制:流体静力学原理被广泛应用于流量测量和控制领域。
通过测量流体的压力差或速度,可以确定流体的流量,并在工业过程中进行流量的控制和调节。
•水力机械:流体静力学原理在水力机械领域中有着重要应用。
例如,通过分析流体的压力和速度分布,可以设计和优化水轮机和泵的叶轮结构,提高水力机械的效率和性能。
•气体系统设计:流体静力学原理同样适用于气体系统的设计和分析。
通过考虑气体的压力、密度和温度分布,可以设计气体系统的尺寸和参数,以满足工业过程中的需求。
2. 工业应用案例2.1 液压系统在工程机械中的应用液压系统被广泛应用于工程机械中,提供力量和控制系统的动作。
例如,挖掘机、装载机和压路机等工程机械中常使用液压系统来实现机械臂的升降、伸缩和转动等动作。
液压系统的设计中,流体静力学原理被用来确保液压系统的稳定性和安全性。
2.2 管道系统的设计与优化管道系统在化工、石油、供水等领域中起着重要作用。
通过应用流体静力学原理,可以确定管道的尺寸、布局和材料,以满足流体输送的需求。
同时,流体静力学原理可以提供管道内部流体的压力变化和速度分布信息,以帮助系统运行和维护。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
衡。
N2 Q
B
19
第一篇 静力学 第4章 摩擦
例1 (已知载荷,判断是否平衡。解析 物块重Q =80法kN和, 几水何平法力)P=20 kN, 摩擦系数f=0.3,斜面倾角α=30°。 设物块不会翻到,问物块是否滑动? 如滑动,方向分如析何:?如不滑动,摩
擦力如何? 本题第一步为已知力求状态,第二 在步已为知已载知荷状作态求用摩下擦,力物,体第平二衡步状好态 不定,且求运,动现分(析趋第势一)步方。向也不定, 故需先假设这两点,一般设物体不 求动物然体出(后呢有静即干?一摩什处种么擦于运力非动F临和趋界最势平(大衡如静)向摩,上擦可)力假;Fm设ax, 若|F|≤Fmax,则物体确实不动,且若F 其为正余,问所题假易设运动(趋势)方向正确。 解。
主具动有力最摩但─大擦与─摩系约限擦静数何束于力摩确力f 平,与擦定不面F接定?同m问a触律x。=题面fN)积,──库仑
有关吗?
通常画法
W
(并不 严
格)Pm a x
N
F
W
N
Fm ax
静滑动摩擦 最大静滑 力,简称静动摩擦力,
摩擦力 简称最大14
第一篇 静力学 第4章 摩擦
2 .
Q
摩擦角与 自W 锁
案
Nst
Pst
例
可见,Spiralock螺牙法向力提高73.2%,意味着
|
最大摩擦力提高73.2%;横向力提高200%,意味
着抗横向振动导致松动的能力提高200%。
Spiralock - nuts
静
案例分析——整体受力分析初步
力
学
案
例
|
Spiralock - nuts
标准螺母:面接触,接触刚度大,导致各牙受力不匀 Spiralock:点接触,接触刚度小,各牙受力均匀
力
学
案
例
|
Spiralock - nuts
产值:3000万元
静
Construction
力
学
案
例
|
Spiralock - nuts
静
Load Distribution
力
学
案
例
|
Spiralock - nuts
静
Photoelastic study
力
学
案
例
|
Spiralock - nuts
静
案例分析任务:
第一篇 静力学 第4章 摩擦
4.1 摩擦现象
同学举例,并说明什么
总结以下概念是(摩分擦。
类):
滑动摩擦,滑动摩擦力(摩擦力)
√
滚动摩擦,滚动摩擦阻力偶(滚动摩擦力,
滚阻力偶)
静摩 √
干摩 √
动擦摩 √
湿擦摩
擦
擦
(打√者为重点讨论)
简述:摩擦机理,摩擦利弊。——古 典摩擦理论。
13
第一篇 静力学 第4
摩擦角与自锁动画演示
17
第一篇 静力学 第4章 摩擦
3. 动滑动
动摩滑擦动摩擦力,简称动 F' f ' N ──库仑动摩擦定
方摩向擦、力作:用线如
律
何定? 4.3 考虑滑动摩擦的平衡问题
类型特点:①已知平衡,求范围;②已知载荷,
解法:平衡判方断程是+否F 补平F充m衡ax方。程fN 讨论几个问(题:①画受力图) 时,静滑动摩擦
2 F, 3
Pst
1F 3
静
案例分析——Spiralock螺母(单牙)
力
锁紧力
学 案
F
Nsp 正压力
例
60°
|
Psp 横向力
Spiralock nut thread
Spiralock - nuts
Nsp 2F, Psp 3F
静
案例分析——Spiralock螺母(单牙)
力
学
Nsp 3 1.732, Psp 3
力
学
• 建立力学简化模型
案
• 分析受力
例
• 给出结论
|
• 撰写报告
Spiralock - nuts
自愿完成,按成绩期末给以加分。
静
案例分析——标准螺母(单牙)
力
学
锁紧力
案
F
Nst 正压力
例
30°
|
Pst 横向力
Standard
nut thread
Spiralock - nuts
假设忽略横向摩擦力: Nst
静
力
Spiralock Corporation 是美国位于Detroit的一家公司。
学
案
例
|
nuts
Spiralock - nuts
产值?
静
Applications
力
学
案
例
|
Spiralock - nuts
静 力 学 案 例 |
Spiralock - nuts
静
Shanghai Detroit Precision Fastener Co., LTD
QP
R
画自行封 闭arc力tan三P 角14形0,2 先依次
画 、 , 再画 Q , 如图(d)。由图可
而则摩全擦反夹角力角与:m公法a求rc线ta得nf:16421558
(a)
(b)
20
第一篇 静力学 第4章 摩擦
解:(解析法)
设物块处于非临界平衡,并设有上滑趋势。取物块分离体, Σ X 0, F Pcos Qs画in受力0 图,如F 图P(cbos)。 Qsin 22.68 kN
Σ Y 0, N Psin Qcos 0
N Psin Qcos 79.28 kN
P
F
N
R
全反 力
摩擦 角测 定
Qm ax
m
最大 Fm a x
Qm ax
Q
Fm ax
N
m Rm ax
摩擦
全反 力
自 锁
m m N
自
Rm ax
锁
摩擦扇(锥)
tgm
角 Fmax
N
f
0 条件mm
无论主域动力多大,总平衡
无论主动力多小,总不平衡
15
自锁第举一例:篇螺钉静,力夹具学,电第工4脚章套钩摩等擦
1. 静滑动
4.2 滑动摩擦
当P 摩P力擦增W 大时,(观P设察物物体W体不受翻力倒及)P运:动状W态的 变化Pmax
F
N
N
W
Fm ax N
分析:多为分布力,一般简化
为集中力:大小、方向、作用
线──具有约束力的某些性质
P
(大小随主动力增大而增大,
作用线①由何结处构不决同定?而②不方依向赖如于
一般能判
力方向问题;
断:
18
第一篇 静力学 第4章 摩擦
有时不能判断——此时 可假设:
F
方向不 定
=
F F1 F2 N
方向不 定
+
F1
F2
N1
A
②单刚体多点摩擦 问题;
③多刚体多点摩擦
按运动(趋势)状态 判断是否同时达到最 一般不大同摩时擦达力到最大
④平衡问状题态;的选取。
摩擦力 临界平衡或非临界平
最大静摩擦 Fmax fN 0.3 79.28 23.78 kN F 力Fm:ax ,且F为 所以物块不负滑。动,且有向 下运动趋势,静摩擦力为
|F| = 22.68 kN。
(b)
21
第一篇 静力学 第4章 摩擦
另解:(几何法) 设物块处于非临界平衡。取物块分离体,
画受力图, 且以全 反力表示,如图(c)。
