平行四边形知识归纳.doc
平行四边形知识点归纳和题型归类

平行四边形知识点归纳和题型归类平行四边形知识点归纳和题型归类要点梳理】要点一、平行四边形1.定义:有两组对边分别平行的四边形叫做平行四边形。
2.性质:(1)对边相等;(2)同位角相等;(3)相邻角互补;(4)是中心对称图形。
3.面积:S = 底 ×高。
4.判定:边:(1)有两组对边分别平行的四边形是平行四边形;(2)对边相等的四边形是平行四边形;(3)对角线互相平分的四边形是平行四边形。
角:(4)有一组对边平行,且同位角相等的四边形是平行四边形。
对角线:有一组对边相等,且互相平分的四边形是平行四边形。
要点诠释:平行线的性质:(1)平行线间的距离相等;(2)等底等高的平行四边形面积相等。
要点二、矩形1.定义:有四个角都是直角的平行四边形叫做矩形。
2.性质:(1)对边相等;(2)相邻角互补;(3)对角线相等;(4)是中心对称图形,也是轴对称图形。
3.面积:S = 长 ×宽。
4.判定:有四个角都是直角的平行四边形是矩形。
要点诠释:由矩形得直角三角形的性质:(1)直角三角形斜边上的中线等于斜边的一半;(2)直角三角形中,30度角所对应的直角边等于斜边的一半。
要点三、菱形1.定义:有四个边都相等的平行四边形叫做菱形。
2.性质:(1)对边相等;(2)相邻角互补;(3)对角线相等;(4)是中心对称图形,也是轴对称图形。
3.面积:S = 对角线之积的一半。
4.判定:有一组对边平行且相等的四边形是菱形。
要点四、正方形1.定义:四条边都相等,四个角都是直角的平行四边形叫做正方形。
2.性质:(1)对边相等;(2)相邻角互补;(3)对角线相等;(4)是中心对称图形,也是轴对称图形;(5)两条对角线把正方形分成四个全等的等腰直角三角形。
3.面积:S = 边长的平方,也可以用对角线的平方的一半求解。
4.判定:(1)有一组对边平行且相等的菱形是正方形;(2)有四个角都是直角的矩形是正方形;(3)对角线互相垂直平分且相等的四边形是正方形;(4)四条边都相等,四个角都是直角的四边形是正方形。
平行四边形知识点.doc

一.平行四边形、矩形、菱形、正方形知识点梳理:一般平行四边形特殊平行四边形矩形菱形正方形图形两组对边分别平行的四边形是平行四边有一个角是直角的平行四有一组邻边相等的平行有一个角是直角,且有一组邻定形边形是矩形四边形是菱形边相等的平行四边形叫做正义方形①边:对边平行且相等除具有平行四边形的性质除具有平行四边形的性具有矩形、菱形的所有性质②角:对角相等,邻角互补外,还有质外,还有(正方形=矩形+菱形)③对角线:对角线互相平分①角:四个角都是直角①边:四条边相等①边:四条边相等性质②对角线:对角线相等, 且互相平分②对角线:对角线互相垂直平分,且每一条对角线②角:四个角是直角③对角线:对角线相等,互相平分一组对角垂直平分,每一条对角线平分一组对角;边:角:边:①对角线相等且互相垂直平①两组对边分别平行的四边形是平行四边形①有一个角是直角的平行①有一组邻边相等的平分的四边形是正方形②两组对边分别相等的四边形是平行四边形四边形是矩形行四边形是菱形②有一组邻边相等且有一个角是直③一组对边平行且相等的四边形是平行四边②有三个角是直角的四边形形是矩形定角:对角线:对角线:④对角线互相垂直的矩形是菱形②四边都相等的四边形是菱形④两组对角分别相等的四边形是平行四边形③对角线相等的平行四边③对角线互相垂直的平⑤有一个角是直角的菱形是菱形对角线:形是矩形行四边形是菱形⑥对角线相等的菱形是菱形⑤对角线互相平分的四边形是平行四边形S=ah S=ab ①S=ah①(a 为一边长,h 为这条边上的高) (a 为一边长,b 为另一边长) (a 为一边长,h 为这条边(a 为边长) ;上的高) ;面积②②(b 为对角线长)(b 、c 为两条对角线的长)对中心对称图形,对称中线是两条对角线的交点既是中心对称图形(两条对角线的交点是对称中心),又是轴对称图形有2 条对称轴,它们分别是有2 条对称轴,对称轴是有4 条对称轴,其中2 条是过称性过两组对边中点的直线两条对角线所在的直线两组对边中点的直线,另外 2条是两条对角线所在的直线平行四边形(任何四边形四边中点的连线菱形矩形正方形四边中都是一个平行四边形)线连线三角形的中位线中位线平行于第三边并且等于第三边的一半一.温故知新平行四边形的面积1)平行四边形ABCD的周长为20cm,AE⊥BC于点E,AF⊥CD于点F,AE=2cm,AF=3cm,求ABCD的面积.2)如图,四边形ABCD的对角线A C、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+C.F(1)求证:PA=PC.(2)若BD=12,AB=15,∠DBA=4°5,求四边形ABCD的面积.平行四边形与角度如图,将一平行四边形纸片ABCD沿AE,EF折叠,使点E,B′,C′在同一直线上,则∠AEF=度.平行四边形与线段1)如图,ABCD为平行四边形,AD=2,B E∥AC,DE交AC的延长线于F点,交BE 于E点.(1)求证:EF=DF;(2)若AC=2C,F∠ADC=6°0,A C⊥D C,求DE的长.2)已知,在 ?A B C 中,∠ A D C 、∠ D A 的D F 、A 段 B C 相 交于点 F 、E ,DF 与 AE 相交于点 G . (1)求证: A E ⊥D F ; (2)若 AD=10,AB=6,AE=4,求 DF 的长. 平合探究: 以 R t △A B C A B 、边向外△ ABD 和△ ACE ,F 为A B 的点,D E ,A B 相交于点 G ,若∠ B A C =3°0 ,论:① EF ⊥AC ;②四 A D 平形;③ AD=4AG ;④△ DBF ≌ △EFA .其中正确结二 1.,已知 M 、N 、P 、 为AB 、 B D 、CD 、A C 的中点形 MNPQ 是平行四边 形. 2. 已知形 A B C D 中,A B =C D ,E 、F 为B C 、A D 的中点, B A 、E F 线交于点 M ,C D、E F 线交于点 N :∠ AME=∠DNE.3. 如图,在△ABC中,P 是中线AD的中点,连接BP并延长交AC于E,F 为BE的中点,求证:AF∥DE.4. 如图,在□ABCD中,M是OB的中点,连接 A M并延长至P.使MP=AM,连接DP交AC于N.求证:(1)MN∥AD;(2)S 四边形MPNQ=S△OBC5. 如图,AD是△ABC的外角平分线, C D⊥AD于D,E是BC的中点.(AB+AC)12求证:(1)D E∥AB;(2)DE=6. 如图,在等腰梯形ABCD中,AB∥C D,AB>C D,AD=BC.对角线相交于点O,∠AOB=60°,且E、F 、M分别是O D、O A、BC的中点. 求证:△EFM是等边三角形.。
平行四边形初中知识点

平行四边形初中知识点
一、平行四边形的定义。
1. 两组对边分别平行的四边形叫做平行四边形。
- 用符号“▱”表示平行四边形,例如平行四边形ABCD记作“▱ABCD”。
二、平行四边形的性质。
1. 边的性质。
- 平行四边形的对边平行且相等。
- 即若▱ABCD,则AB = CD,AD = BC;AB∥CD,AD∥BC。
2. 角的性质。
- 平行四边形的对角相等,邻角互补。
- 在▱ABCD中,∠A = ∠C,∠B = ∠D;∠A+∠B = 180°,∠B + ∠C=180°等。
3. 对角线的性质。
- 平行四边形的对角线互相平分。
- 若▱ABCD,对角线AC、BD相交于点O,则AO = CO,BO = DO。
三、平行四边形的判定。
1. 边的判定。
- 两组对边分别平行的四边形是平行四边形(定义判定)。
- 两组对边分别相等的四边形是平行四边形。
- 一组对边平行且相等的四边形是平行四边形。
2. 角的判定。
- 两组对角分别相等的四边形是平行四边形。
3. 对角线的判定。
- 对角线互相平分的四边形是平行四边形。
四、平行四边形的面积。
1. 平行四边形的面积等于底乘以高。
- 若平行四边形的底为a,这条底边上的高为h,则面积S = ah。
- 同底(等底)等高的平行四边形面积相等。
平行四边形知识点
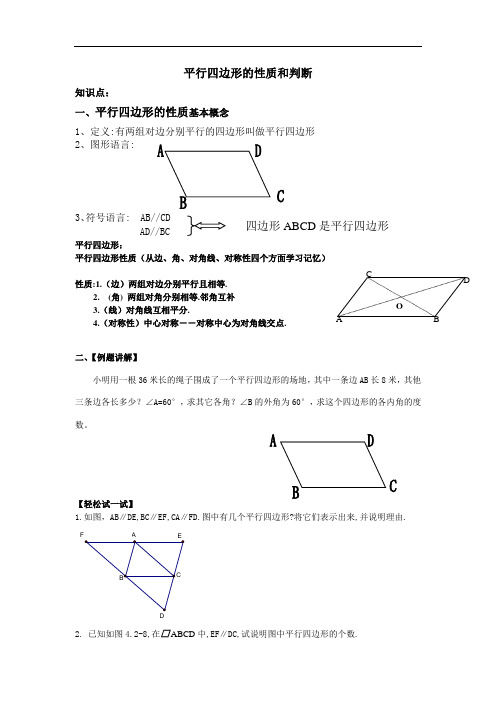
A BC DO 平行四边形的性质和判断知识点:一、平行四边形的性质基本概念1、定义:有两组对边分别平行的四边形叫做平行四边形2、图形语言:3、符号语言平行四边形:平行四边形性质(从边、角、对角线、对称性四个方面学习记忆) 性质:1.(边)两组对边分别平行且相等.2. (角) 两组对角分别相等.邻角互补3.(线)对角线互相平分.4.(对称性)中心对称--对称中心为对角线交点.二、【例题讲解】小明用一根36米长的绳子围成了一个平行四边形的场地,其中一条边AB 长8米,其他三条边各长多少?∠A=60°,求其它各角?∠B 的外角为60°,求这个四边形的各内角的度数。
【轻松试一试】1.如图,AB ∥DE,BC ∥EF,CA ∥FD.图中有几个平行四边形?将它们表示出来,并说明理由.AFD2. 已知如图4.2-8,中,EF ∥DC,试说明图中平行四边形的个数.NMH G F E D CBA图4.2-8角的计算:1、中, BC=2AB, CA ⊥AB,则∠B=______度,∠CAD=______度.DCB A2中,∠A : ∠B=3:2,则∠C=___ 度,∠D=______度.边及周长的计算1、如图,平行四边形的对角线相交于点O ,BC=7㎝,BD=10㎝,AC=6㎝。
求△AOD 的周长。
2平行四边形的周长是100cm, AB:BC=4:1,则AB 的长是_______。
3.已知平行四边形的面积是144,相邻两边上的高分别为8和9,则它的周长是______________.4.用20米长的一铁丝围成一个平行四边形,使长边与短边的比为3:2,则它的边长为________短边长为__________.平行四边形的判断平行四边形的四个(或五个)判定方法,这些判定的方法是: 从边看: ①两组对边分别平行的四边形是平行四边形; ②两组对边分别相等的四边形是平行四边形; ③一组对边平行且相等的四边形是平行四边形.从对角线看:对角线互相平分的四边形是平行四边形.(从角看:两组对角分别相等的四边形是平行四边形.)【例题讲解】已知:如图,ABCD 中,E 、F 分别是AD 、BC 的中点,求证:BE=DF .分析:证明BE=DF ,可以证明两个三角形全等,也可以证明四边形BEDF 是平行四边形,比较方法,可以看出第二种方法简单. 证明:∵ 四边形ABCD 是平行四边形, ∴ AD ∥CB ,AD=CD . ∵ E 、F 分别是AD 、BC 的中点, ∴ DE ∥BF ,且DE=21AD ,BF=21BC .∴ DE=BF .∴ 四边形BEDF 是平行四边形(一组对边平行且相等的四边形平行四边形). ∴ BE=DF .例2、已知:如图,ABCD 中,E 、F 分别是AC 上两点,且BE ⊥AC 于E ,DF ⊥AC 于F .求证:四边形BEDF 是平行四边形.分析:因为BE ⊥AC 于E ,DF ⊥AC 于F ,所以BE ∥DF .需再证明BE=DF ,这需要证明△ABE 与△CDF 全等,由角角边即可.证明:∵ 四边形ABCD 是平行四边形, ∴ AB=CD ,且AB ∥CD . ∴ ∠BAE=∠DCF .∵ BE ⊥AC 于E ,DF ⊥AC 于F ,∴ BE ∥DF ,且∠BEA=∠DFC=90°. ∴ △ABE ≌△CDF (AAS ). ∴ BE=DF .∴ 四边形BEDF 是平行四边形(一组对边平行且相等的四边形平行四边形)例3、 已知:如图3,E 、F 是平行四边形ABCD 对角线AC 上两点,且AE =CF 。
平行四边形知识归纳
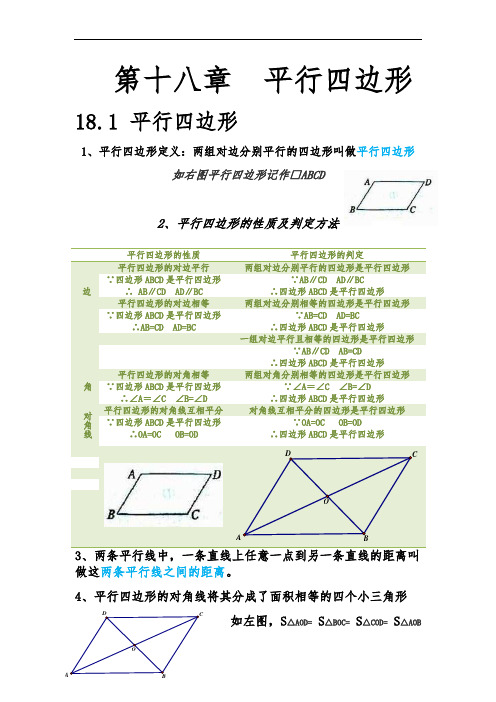
第十八章平行四边形18.1 平行四边形1、平行四边形定义:两组对边分别平行的四边形叫做平行四边形如右图平行四边形记作□ABCD平行四边形的性质平行四边形的判定2、平行四边形的性质及判定方法3、两条平行线中,一条直线上任意一点到另一条直线的距离叫做这两条平行线之间的距离。
4、平行四边形的对角线将其分成了面积相等的四个小三角形如左图,S △AOD= S △BOC= S △COD= S △AOB5、三角形的中位线连接三角形两边中点的线段叫做三角形的中位线。
三角形的中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半。
数学符号语言:如右图,∵点D 、点E 分别为AB 、AC 的中点 ∴DE 为BC 的中位线 ∴DE ∥BC DE=1/2BC18.2特殊的平行四边形矩形1、矩形的定义:有一个角是直角的平行四边形叫做矩形。
矩形是一类特殊的平行四边形。
2、矩形的性质及判定注:矩形具有平行四边形的所有性质。
(即对边相等且平行)矩形的性质 矩形的判定矩形的四个角都是直角 有一个角是直角的平行四边形是矩形。
∵四边形ABCD 是矩形 ∴∠A=∠B=∠C=∠D=90 ∵四边形ABCD 是平行四边形, ∠A=90∴四边形ABCD 是矩形 矩形的对角线相等且互相平分对角线相等的平行四边形是矩形∵四边形ABCD 是矩形∴AC=BD∴OA=OC=1/2AC OB=OD=1/2BD∵四边形ABCD 是平行四边形,AC=BD∴四边形ABCD 是矩形有三个角是直角的四边形是矩形3、如右图,可以观察出(1)S△AOD= S△BOC= S△COD= S△AOB(2)∵四边形ABCD是矩形∴AC=BD∴OA=OC=1/2AC OB=OD=1/2BD∴OA=OC=OB=OD(等量代换)(3)一共有四个等腰三角形(4)一共有八对全等三角形4、如果一个三角形是直角三角形,那么这个三角形斜边上的中线等于斜边的一半。
数学符号语言:∵在Rt△ACB中,CD为斜边AB上的中线,∠B=90∴CD=1/2AB菱形1、菱形的定义:有一组邻边相等的平行四边形叫做菱形。
平行四边形(基础)知识讲解

平行四边形(基础)【学习目标】1.理解平行四边形的概念,掌握平行四边形的性质定理和判定定理;2.能初步运用平行四边形的性质进行推理和计算,并体会如何利用所学的三角形的知识解决四边形的问题.3. 能综合运用平行四边形的判定定理和平行四边形的性质定理进行证明和计算.4. 理解三角形的中位线的概念,掌握三角形的中位线定理.【要点梳理】【高清课堂平行四边形知识要点】要点一、平行四边形的定义平行四边形的定义:两组对边分别平行的四边形叫做平行四边形. 平行四边形ABCD记作“ABCD”,读作“平行四边形ABCD”.要点诠释:平行四边形的基本元素:边、角、对角线.相邻的两边为邻边,有四对;相对的边为对边,有两对;相邻的两角为邻角,有四对;相对的角为对角,有两对;对角线有两条.要点二、平行四边形的性质1.边的性质:平行四边形两组对边平行且相等;2.角的性质:平行四边形邻角互补,对角相等;3.对角线性质:平行四边形的对角线互相平分;4.平行四边形是中心对称图形,对角线的交点为对称中心.要点诠释:(1)平行四边形的性质中边的性质可以证明两边平行或两边相等;角的性质可以证明两角相等或两角互补;对角线的性质可以证明线段的相等关系或倍半关系.(2)由于平行四边形的性质内容较多,在使用时根据需要进行选择.(3)利用对角线互相平分可解决对角线或边的取值范围的问题,在解答时应联系三角形三边的不等关系来解决.要点三、平行四边形的判定1.两组对边分别平行的四边形是平行四边形;2.两组对边分别相等的四边形是平行四边形;3.一组对边平行且相等的四边形是平行四边形;4.两组对角分别相等的四边形是平行四边形;5.对角线互相平分的四边形是平行四边形.要点诠释:(1)这些判定方法是学习本章的基础,必须牢固掌握,当几种方法都能判定同一个平行四边形时,应选择较简单的方法.(2)这些判定方法既可作为判定平行四边形的依据,也可作为“画平行四边形”的依据.要点四、三角形的中位线1.连接三角形两边中点的线段叫做三角形的中位线.2.定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.要点诠释:(1)三角形有三条中位线,每一条与第三边都有相应的位置关系与数量关系.(2)三角形的三条中位线把原三角形分成可重合的4个小三角形.因而每个小三角形的周长为原三角形周长的12,每个小三角形的面积为原三角形面积的14.(3)三角形的中位线不同于三角形的中线.要点五、平行线间的距离1.两条平行线间的距离:(1)定义:两条平行线中,一条直线上的任意一点到另一条直线的距离,叫做这两条平行线间的距离.注:距离是指垂线段的长度,是正值.(2)平行线间的距离处处相等任何两平行线间的距离都是存在的、唯一的,都是夹在这两条平行线间最短的线段的长度. 两条平行线间的任何两条平行线段都是相等的.2.平行四边形的面积:平行四边形的面积=底×高;等底等高的平行四边形面积相等.【典型例题】类型一、平行四边形的性质【高清课堂平行四边形例11】1、如图所示,已知四边形ABCD是平行四边形,若AF、BE分别为∠DAB、∠CBA的平分线.求证:DF=EC.。
第一单元《平行四边形》知识点

第一单元《平行四边形》知识点
本文档旨在介绍第一单元《平行四边形》的知识点。
1. 平行四边形的定义
平行四边形是指具有两组对边平行的四边形。
四个角均为直角的平行四边形称为矩形。
2. 平行四边形的性质
- 平行四边形的对边相等。
- 平行四边形的对角线相交于一点,并且该点到四个顶点的距离相等。
- 平行四边形的邻边互补,即相邻两边之和等于180度。
- 平行四边形的对角线等分对角线角。
3. 平行四边形的分类
根据边长和角度的不同,平行四边形可以分为以下几类:
- 矩形:具有四个内角均为直角的平行四边形。
- 正方形:具有四条边长相等且四个内角均为直角的平行四边形。
- 长方形:具有两组对边相等且四个内角均为直角的平行四边形。
- 平行四边形:为一般性的平行四边形,具有两组对边平行但
不一定角度相等或边长相等。
4. 平行四边形的应用
平行四边形的概念在几何学和实际生活中有广泛的应用。
例如,在建筑设计中,平行四边形常被用作地板砖、窗户和门的形状。
在
数学中,平行四边形的性质也与向量、矩阵和平面几何等领域密切
相关。
以上是第一单元《平行四边形》的知识点概述。
对于每个具体
的内容,我们将在课堂上进行深入讲解和练。
- 完 -。
平行四边形的相关知识点总结

平行四边形的相关知识点总结平行四边形的相关知识点总结一.正确理解定义(1)定义:两组对边分别平行的四边形是平行四边形.平行四边形的定义揭示了图形的最本质的属性,它既是平行四边形的一条性质,又是一个判定方法.(2)表示方法:用“ABCD记作,读作“平行四边形ABCD”.2.熟练掌握性质平行四边形的有关性质和判定都是从边、角、对角线三个方面的特征进行简述的.(1)角:平行四边形的邻角互补,对角相等;(2)边:平行四边形两组对边分别平行且相等;(3)对角线:平行四边形的对角线互相平分;(4)面积:①S底高=ah;②平行四边形的对角线将四边形分成4个面积相等的三角形.3.平行四边形的判别方法①定义:两组对边分别平行的四边形是平行四边形②方法1:两组对角分别相等的四边形是平行四边形③方法2:两组对边分别相等的四边形是平行四边形④方法3:对角线互相平分的四边形是平行四边形⑤方法4:一组平行且相等的四边形是平行四边形二、.几种特殊四边形的有关概念(1)矩形:有一个角是直角的平行四边形是矩形,它是研究矩形的基础,它既可以看作是矩形的性质,也可以看作是矩形的判定方法,对于这个定义,要注意把握:① 平行四边形;② 一个角是直角,两者缺一不可.(2)菱形:有一组邻边相等的平行四边形是菱形,它是研究菱形的基础,它既可以看作是菱形的性质,也可以看作是菱形的判定方法,对于这个定义,要注意把握:① 平行四边形;② 一组邻边相等,两者缺一不可.(3)正方形:有一组邻边相等且有一个直角的平行四边形叫做正方形,它是最特殊的平行四边形,它既是平行四边形,还是菱形,也是矩形,它兼有这三者的特征,是一种非常完美的图形.(4)梯形:一组对边平行而另一组对边不平行的四边形叫做梯形,对于这个定义,要注意把握:①一组对边平行;② 一组对边不平行,同时要注意和平行四边形定义的区别,还要注意腰、底、高等概念以及梯形的分类等问题.(5)等腰梯形:是一种特殊的梯形,它是两腰相等的梯形,特殊梯形还有直角梯形.2.几种特殊四边形的有关性质(1)矩形:①边:对边平行且相等;②角:对角相等、邻角互补;③对角线:对角线互相平分且相等;④对称性:轴对称图形(对边中点连线所在直线,2条).(2)菱形:①边:四条边都相等;②角:对角相等、邻角互补;③对角线:对角线互相垂直平分且每条对角线平分每组对角;④对称性:轴对称图形(对角线所在直线,2条).(3)正方形:①边:四条边都相等;②角:四角相等;③对角线:对角线互相垂直平分且相等,对角线与边的夹角为450;④对称性:轴对称图形(4条).(4)等腰梯形:①边:上下底平行但不相等,两腰相等;②角:同一底边上的两个角相等;对角互补③对角线:对角线相等;④对称性:轴对称图形(上下底中点所在直线).3.几种特殊四边形的判定方法(1)矩形的判定:满足下列条件之一的四边形是矩形①有一个角是直角的平行四边形;②对角线相等的平行四边形;③四个角都相等(2)菱形的判定:满足下列条件之一的四边形是矩形①有一组邻边相等的平行四边形;②对角线互相垂直的平行四边形;③四条边都相等.(3)正方形的判定:满足下列条件之一的四边形是正方形.① 有一组邻边相等且有一个直角的平行四边形② 有一组邻边相等的矩形;③ 对角线互相垂直的矩形.④ 有一个角是直角的菱形⑤ 对角线相等的菱形;(4)等腰梯形的判定:满足下列条件之一的梯形是等腰梯形① 同一底两个底角相等的梯形;② 对角线相等的梯形.4.几种特殊四边形的常用说理方法与解题思路分析(1)识别矩形的常用方法① 先说明四边形ABCD为平行四边形,再说明平行四边形ABCD的任意一个角为直角.② 先说明四边形ABCD为平行四边形,再说明平行四边形ABCD的对角线相等.③ 说明四边形ABCD的'三个角是直角.(2)识别菱形的常用方法① 先说明四边形ABCD为平行四边形,再说明平行四边形ABCD的任一组邻边相等.② 先说明四边形ABCD为平行四边形,再说明对角线互相垂直.③ 说明四边形ABCD的四条相等.(3)识别正方形的常用方法① 先说明四边形ABCD为平行四边形,再说明平行四边形ABCD的一个角为直角且有一组邻边相等.② 先说明四边形ABCD为平行四边形,再说明对角线互相垂直且相等.③ 先说明四边形ABCD为矩形,再说明矩形的一组邻边相等.④ 先说明四边形ABCD为菱形,再说明菱形ABCD的一个角为直角.(4)识别等腰梯形的常用方法① 先说明四边形ABCD为梯形,再说明两腰相等.② 先说明四边形ABCD为梯形,再说明同一底上的两个内角相等.③ 先说明四边形ABCD为梯形,再说明对角线相等. 5.几种特殊四边形的面积问题① 设矩形ABCD的两邻边长分别为a,b,则S矩形=ab.② 设菱形ABCD的一边长为a,高为h,则S菱形=ah;若菱形的两对角线的长分别为a,b,则S菱形=③ 设正方形ABCD的一边长为a,则S正方形=a;若正方形的对角线的长为a,则S正方形=④ 设梯形ABCD的上底为a,下底为b,高为h,则S梯形=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行四边形的性质及判定一、平行四边形的性质【知识要点及基础例题】1、定义:有两组对边分别平行的四边形叫做平行四边形。
2、平行四边形的中心对称性及性质定理1:平行四边形的对边相等。
例1、如图所示,已知四边形ABDE 是平行四边形,C 为边BD 延长线上一点,连结AC 、CE ,有AC=DE 。
求证:AD=CE练习:如图,在△ABC 中,AB=AC ,D 为BC 上一点,以AB 、BD 为邻边作平行四边形ABDE ,连结AD 、EC 。
求证:△ADC ≌△ECD3、平行四边形性质定理2:平行四边形的对角相等。
例2、如图,在平行四边形ABCD 中,︒=∠-∠40B A ,求平行四边形ABCD 各个内角的度数。
4、平行四边形性质定理3:平行四边形的对角线互相平分。
例3、如图,在平行四边形ABCD 中,AC 与BD 相交于点O ,AB=4,AC=6,并且AB ⊥CA ,求对角线BD 的长。
练习:如图所示,在平行四边形ABCD 中,对角线AC 、BD 相交于点O 。
若AC=14,BD=8,AB=10,则△OAB 的周长为( )5、平行四边形是中心对称图形,两条对角线的交点是它的对称中心。
6、平行线间的距离①两条直线平行,其中一条直线上的任一点到另一条直线的距离,叫做这两条平行线之间的距离。
②平行线的性质:平行线之间的距离处处相等。
例4、如图,直线21l l ∥,点P 在直线1l 上,点A 、B 在直线2l 上,设△PAB 面积为S 。
当点P 运动到1P 位置时,△PAB 与△AB P 1的面积相等吗?为什么?练习:如图所示,直线121,l l l ∥和AB 的夹角︒=∠135DAB ,且AB=50mm,求两平行线21l l 和之间的距离。
【思维拓展】一、利用平行四边形的性质进行计算例1、若平行四边形ABCD 的对角线相交与O 点,且AB ≠BC ,过O 点作OE ⊥AC ,交BC 于E 。
如果三角形ABE 的周长为b 。
则平行四边形ABCD 的周长是( )(例1图)例2、如图,在平行四边形ABCD 中,点E 为AD 的中点,CE 交BA 的延长线于点F 。
若BC=2AB ,,︒=∠70FBC 求EBC ∠的度数。
练习:1、如图,在平行四边形ABCD 中,点E 在边AD 上,以BE 为折痕,将△ABE 向上翻折,点A 正好落在CD 上的点F ,若△FDE 的周长为8,△FCB 的周长为12,则FC 的长为( )2、如图,在平行四边形ABCD 中,︒=∠70A ,将平行四边形ABCD 折叠,使点D 、C 分别落在点F 、E 处(点F 、E 都在AB 所在的直线上),折痕为MN ,则AMF ∠等于( )二、利用平行四边形的性质进行证明例3、如图甲所示,在平行四边形ABCD 中,AE 、BF 分别平分ABC DAB ∠∠和,并分别交CD 于点E 、F,AE 、BF 相交于点M 。
(1)求证:AE ⊥BF ;(2)判断线段DF 与CE 的大小关系,并予以证明。
(两种解法)练习:如图,四边形ABCD 是平行四边形,O 是对角线AC 的中点,过点O 的直线EF 分别交AB 、DC 于点E 、F ,与CB 、AD 的延长线分别交于点G 、H 。
除AB=CD ,AD=BC ,OA=OC 这三对相等的线段外,图中还有多对相等的线段,请选出其中一对加以证明.三、与平行四边形面积有关的计算例4、如图,点E是平行四边形ABCD内任意一点,平行四边形ABCD的面积是6,连结点E与平行四边形的四个顶点,求图中阴影部分的面积。
练习:如图所示,在平行四边形ABCD中,点E为AC上一点,AE=2EC,点F为AB上一点,BF=2AF,△BEF的面积为2平方厘米,求平行四边形ABCD的面积。
四、利用平行四边形的性质进行方案设计例5、如图是一块平行四边形贴片ABCD,且AB=2AD。
现在想用这块贴片截出一个直角三角形,并要求斜边与AB重合,且面积最大,能否截出符合条件的三角形?如果能截出,画出截线;如果不能截出,请说明理由。
练习:张大伯承包了一个呈四边形的池塘:如图所示,它的四个角A,B,C,D处均有一棵核桃树,张大伯今年养鱼喜获丰收,明年准备把池塘面积扩大一倍,但又不想毁掉这四棵大树,并且扩建后的池塘呈平行四边形形状.张大伯这一设想是否能实现?请你帮助他解决一下,并画出草图.二、平行四边形的判定【知识要点及基础例题】平行四边形的判定方法1:定义:两组对边分别平行的四边形是平行四边形。
例1、如图所示,已知四边形ABCD中,AB∥CD,AD∥BC,P、Q分别是AB、CD上的点,且AP=CQ,求证:四边形PDQB 为平行四边形。
平行四边形判定方法2:两组对边分别相等的四边形是平行四边形。
例2、如图所示,在平行四边形ABCD 中,M 、N 分别是CD 、AB 上的点,CM=AN ,E 、F 是AC 上的点,且AE=CF.求证:四边形MENF 是平行四边形。
平行四边形判定3:一组对边平行且相等的四边形是平行四边形。
例3、如图所示,在平行四边形ABCD 中,点E 是AD 的中点,BE 的延长线与CD 的延长线交于点F 。
(1)△ABE ≌△DFE (2)试连结BD 、AF ,判断四边形ABDF 的形状。
平行四边形判定4:对角线互相平分的四边形是平行四边形。
例4、如图所示,在平行四边形ABCD 中,E 、F 分别是对角线A 、C 的三等分点,求证:四边形BFDE 是平行四边形。
平行四边形判定5:两组对角分别相等的四边形是平行四边形。
例5、如图所示,AE 、CF 分别是平行四边形ABCD 的内角BCD DAB ∠∠、的平分线。
求证:四边形AECF 是平行四边形。
★★平行四边形判定方法的选择平行四边形的五种判定方法:①定义法:两组对边分别平行的四边形是平行四边形;②两组对边分别相等的四边形是平行四边形;③一组对边平行且相等的四边形是平行四边形;④对角线互相平分的四边形是平行四边形;⑤两组对角分别相等的四边形是平行四边形。
这五种判定方法分别是从四边形的边、角、对角线三个方面来判定,我们应仔细观察题目中所给出的条件,仔细选择适合题目的判定方法进行解答。
在这五种方法中,有一种与对角线有关,一种与对角有关,其他三种与边有关,这五种判定方法还与平行四边形的性质相呼应,注意区别与联系。
已知条件选择的判定方法边一组对边相等方法2,方法3一组对边平行定义(方法1),方法3角一组对角相等方法5对角线方法4例6、如图所示,在平行四边形ABCD中,点E、F在AC上且AF=CE,点G、H分别在AB、CD上且AG=CH,AC与GH 相交于点O。
(1)求证:EG∥FH(2)GH、EF互相平分。
【拓展提高】例1、如图所示,在平行四边形ABCD中,以对角线AC为边长在其两侧各作一个正△ACP和正△ACQ,求证:四边形BPDQ 是平行四边形。
例2、如图所示,在平行四边形ABCD中,点E、F在对角线AC上,且AF=CE.求证:四边形BEDF是平行四边形。
(多种方法证明)例3、如图所示,已知现有六边形的铁板ABCDEF,其中∠A=∠B=∠C=∠D=∠E=∠F=120°,AB=10cm,BC=70cm,CD=20cm,DE=40cm,求AF和EF的长.(两种思路)例4、加倍中线构造平行四边形解题如图所示,已知AD为△ABC的中线,E为AC上一点,连结BE交AD于点F且AE=FE。
求证:AC=BF例5、与平行四边形相关的动点问题如图,在四边形ABCD中,AD∥BC,且AD>BC,BC=6cm,点P、Q分别从点A、C同时出发,点P以1cm/s的速度由A 向D运动,Q以2cm/s的速度由C出发向B运动,几秒后,四边形ABQP是平行四边形?【规律总结】1、证明两条线段相等的常用方法:①等角对等边;②“三线合一”的性质;③证明两线段所在三角形全等;④平行四边形对边相等或对角线互相平分。
2、当题中有三角形中线时,常加倍中线构造平行四边形,然后利用平行四边形的性质推出线段相等、平行或角相等。
例5、如图所示,在平行四边形ABCD中,E、F分别是边AD、BC上的点,请你自行规定E、F在边AD、BC上的位置,然后补充题设,提出结论并证明(要求至少编制两个正确命题,且补充题设不能相同)例6、如图所示,某城市部分街道示意图,其中CD垂直平分AF,AB∥CD,BC∥DF。
从B站乘车到E站只有两条路线有直接到达的公交车,路线1是B⇒D⇒A⇒E,路线2是B⇒C⇒F⇒E,请比较两条路线路程的长短,并给出证明.【中考对接】1、(厦门)如图所示,已知△ABC是等边三角形,点D、F分别在线段BC、AB上,,∠E F B=60°,D C=E F.(1)求证四边形EFCD是平行四边形。
(2)若BF=EF,求证:AE=AD2、(2010江苏)如图所示,在平行四边形ABCD 中,点E 、F 是对角线AC 上两点,且AE=CF 。
求证:FDE EBF ∠=∠【强化练习】1、(天津)如图所示,点D 、E 、F 分别是△ABC 的边AB 、BC 、CA 的中点,连结DE 、EF 、FD,则图中平行四边形的个数为( )个2、如图所示,D 、E 、F 分别在△ABC 的各边上且DE ∥AF,DE=AF,延长FD 至G ,使FG=2DF 。
求证:ED 与AG 互相平分。
-3、(四川)有一块形状如图所示的玻璃,不小心把DEF 部分打碎,现在只测得AB=60cm,BC=80cm ,∠B=60°,∠A=120°,∠C=120°.你能根据测得的数据计算AD 的长吗?4、如图所示,E 、F 分别是平行四边形ABCD 的AD 、BC 边上的点,且AE=CF 。
(1)求证:△ABE ≌△CDF(2)若M 、N 分别是BE 、DF 的中点,连结MF 、EN 。
试判断四边形MFNE 的形状,并证明你的结论。
