数模201001A卷
广东工业大学数学建模试卷和答案—2010A
广东工业大学试卷用纸,共 页,第 页
广东工业大学试卷参考答案及评分标准 (A)
课程名称:
பைடு நூலகம்
数学建模
试卷满分 100 分
考试时间: 2010 年 6 月 28 日 (第 18 周 星期一)
一.(本小题 15 分) 1、1.数学建模的基本步骤主要是:
1)模型准备。了解问题的实际背景,明确建模的目的,搜集必要的信息如现象,数据等,尽量弄清楚 对象的特征,由此初步确定用那一类模型。(2 分); 2)模型假设。根据对象的特征和建模目的,抓住问题的本质,忽略次要因素,做出必要的合理的假设。 (3 分); 3)模型构成。根据所做的假设,用数学语言,符号描述对象的内在规律,建立包含常量,变量等的数 学模型。(4 分); 4)模型求解。可以采用解方程,画图形,优化方法,数值方法,统计分析等各种数学方法,特别是数 学软件和计算机技术。(6 分)。 5)模型分析。对求解结果进行数学上的分析。(8 分) 6)模型检验。把求解和分析结果翻译到实际问题,与实际的现象,数据比较,检验模型的合理性和适 用性。(9 分) 7)模型应用。 (10 分)
型,确定应该如何投资?(只需建模,不用求解)
债券名称
债券种类
信用等级
到期年限
到期税前收益
率(%)
A
国债
1
9
4.3
B
企业债
3
10
5.4
C
地方政府债
2
4
5.0
D
地方政府债
2
3
4.4
E
国债
1
5
4.5
2.某广告公司想在电视、广播上做广告,其目的是尽可能多的招揽顾客。下面是市
场调查结果:
201001试卷答案B

共5页 第1页东 南 大 学 考 试 卷(A 卷)课程名称 数学模型与数学实验 考试学期 04-05-3得分适用专业 数学各专业 考试形式开卷考试时间长度 120分钟一. (20`)在计时工资制体系下,雇主的付薪方式是按计时工资率(元/小时)付薪(kt w =)。
如果雇员的满意度曲线为2/1).(3=+-c t w (c 为参数) (1) 如果协议为每天工作6小时,给出雇员的满意度曲线。
(2) 求雇员与雇主的协议曲线。
解 (1)协议时间为=t 6,对应雇员的满意度曲线上点(2/)(,3c t t +),过此点的切线方程为 2/)()(32/)(23t T c t c t W -+=+-, 4` 它应与雇主的付薪曲线()232W kT t c T ==+一致。
由此得到t c 2=。
4` 因为12,6==c t ,所以 2/)12(3+=t w 4`(2)所求的切点为(2/27,3t t ), 4` 协议曲线为 2/273t w =。
4`共5页 第2页二. (20`) 在层次分析法建模中,我们用到了一致矩阵的概念,即如果矩阵[]nn ija A ⨯=是成对比较矩阵,且k j i a a a jk ij ik ,,.∀=,。
证明(1)A 的转置也是一致矩阵。
(2)A 的秩为1,且A 的非零特征值位n ; 证明(1)只需验证一致矩阵的几个条件成立即可。
令 )(ij Tb A =ij ji ji ij b b a b /1,0=>= 1` jk ij ik b b b = 4` (2)只需证明对应行的元素呈比例jijkkj lj il ik lj il kj ik ij a a a a a a a a a a a ====, 3`上式表明j i ,列元素呈比例,令1=i 得所有列均与第一列呈比例,所以A 的秩为1。
2`令],,,[],,,,[][21321n Tn ij b b b a a a a a A == 3` 由 1=ii a ,得 i i a b /1= 3` Tn Tn a a a n a a a A ],,,[],,,[2121 = 2` 得非零特征值为 n. 2`共5页 第3页三. (20`)如果雨滴的下落速度v 仅与雨滴的半径r 、重力加速度g 和粘性系数μ(压强xvP ∂∂=μ)有关,利用量纲分析法給出速度v 与其它变量的关系。
数学与统计学学院2010年数学建模竞赛试题

数学与统计学学院2010年数学建模竞赛试题(请先仔细阅读竞赛要求)A题、武汉房地产价格问题房地产价格是一个备受关注的问题。
现在请你就以下几个方面的问题进行讨论1.给出你的房地产价格指标的定义(考虑房子所处的位置(交通,学校,医院,商场…),房子的户型,房子的楼层,房子的朝向,小区的内环境(绿化,容积率…等等),房子的开发商,物业,房子的质量,小区的大小,噪音大小,空气等等…);2.请搜集武汉近两年来的房子日销售情况表(至少搜集10天的武汉的房子日销售情况表);对你的上述房地产价格指标的定义做简化,给出一个简化的武汉的房地产价格指标的定义;并且假设:以你搜集到的10天的武汉的房子日销售情况表中时间最早的那一天武汉的房地产价格指标为100,利用你的简化的武汉的房地产价格指标的定义,计算其他天的武汉的房地产价格指标;3.请搜集相应10天的武汉(或者全国)的物价指标,请你建立武汉的房地产价格指标与武汉(或者全国)的物价指标的关系模型,并假设有一天武汉(或者全国)的物价指标,是你搜集到的10天的武汉的房子日销售情况表中时间最早的那一天的武汉(或者全国)的物价指标的100倍,请你预测那一天的武汉的房地产价格指标;4.如果某人准备在武汉买房,请你给他买房的时机的建议。
中南民族大学数学与统计学学院2010年首届数学建模竞赛要求1、参赛者为中南民族大学任意在校本科生, 以队为单位参赛。
学生自愿组队,每队有且仅有三人,鼓励学生跨院系组队。
比赛开始后不允许更换队员。
2、竞赛时间为:2010年4月9日16时至4月14日16时。
3、竞赛按照甲、乙组分别命题,甲组(参加对象为2007,2008级学生)分为A,B两题,乙组(2009级学生)分为C,D两题,每个参赛队可任选一题,4月9日16时起可在院网页上下载试题。
4、竞赛采取开放的竞赛方式,竞赛期间参赛队员可以使用各种图书资料、计算机和软件,在国际互联网上浏览,但不得与队外任何人(包括在网上)讨论。
2010年全国高中数学联合竞赛一试试题(A卷)解析

.
解答
若 a > 1 时,f (x) = a2x + 3ax − 2 在区间 x ∈ [−1, 1] 上单调递增,
则 f (1) = a2 + 3a − 2 = 8 ⇒ a2 + 3a − 10 = (a − 2)(a + 5) = 0 ⇒ a = 2;
若 0 < a < 1 时,f (x) = a2x + 3ax − 2 在区间 x ∈ [−1, 1] 上单调递减,
求 a 的最大值.
解答
f ′(0) = c,
f
′(x)
=
3ax2
+
2bx
+
c
⇒
ff
′(1) ′1
= 3a + 3
=a
2b + c, +b+c
24
2 ⇒a=
f ′(0) + f ′(1) − 2f ′
1
3
2
f ′(0) = c = 1,
⩽ 2 |f ′(0)| + |f ′(1)| + 2 f ′ 1
······ x = 99 时,y = −98, −97, · · · , 97, 98 共 197 个整点. 所以区域内部整点的个数是 98(3 + 197) = 9800.
2 4. 已知 {an} 是公差不为 0 的等差数列,{bn} 是等比数列,其中 a1 = 3, b1 = 1, a2 =
b2, 3a5 = b3,且存在常数 α, β 使得对每一个正整数 n 都有 an = logα bn + β,则
+ 5r
−
2
=
0.
2010年数学建模A题论文

储油罐的变位识别与罐容表标定摘要本文主要运用了积分知识和几何知识分析解决储油罐的变位识别和罐容表标定问题。
模型一的对象是小椭圆形储油罐(两端平头的椭圆柱体)。
我们首先运用几何知识对变位罐体进行分析,得到垂直于罐体的液高1h 和储油罐水平状态下的液高2h 之间的关系,2h =1h +1L ×tan()α(倾斜角α,1L =0.4m ,为罐体长的一部分)。
然后以椭圆中心为中心,以椭圆的长轴和短轴分别为x 轴y 轴,建立空间直角坐标系,再对x 求定积分可得椭圆面上的储油面积为S =(2)f h dx ⎰,继而求得储油的体积V =S ×L (L 为罐体的水平总长度)。
并且在不同的情况下,运用分段函数的思想将罐容分为四段,解得各部分罐容表达式。
并且,以附件一中给出的油位高度为自变量,运用matlab 求得对应的罐容。
将求的的罐容与附件一中加上初始油量后的罐容相比较,分析数据得到其平均误差率为0.038371<0.05,较为合理。
因此,便可根据上述函数关系编定小椭圆罐体罐体变位后的油位高度1h 间隔为1cm 的罐容表标定。
模型二对于图4所示的实际储油罐,可由题中所给数据算出球冠形封头的半径为1.625m,所对应的圆心角为134.76度,弧长为 3.822m考虑到所对圆心角较大及弧长相对于油罐的高度D = 3m 相差不是很大,利用问题一中的模型可近似的认为 当液面由倾斜状态转化为水平状态时,两球冠形内的液面高度与卧式圆柱体内的液面高度近似相等,都等于圆柱体内的油在水平状态下的高度2h ,此时罐内液体的体积为两球冠形封头内液体的体积与圆柱体内液体的体积之和。
当油罐同时在倾斜和偏转的状态下时,利用油浮子测得的液面高度为3h ,3h 可化为仅在倾斜状态下的液面高度1h ,进而转化为水平状态下的液面高度2h ,从而h2可油位高度及纵向倾斜角α和横向偏转角β 表示出来,即()()()()()()13cos ,212tan 3cos tan h R h R h h R h R βαβα=+-=+=+-+cos(β)在已建立的较合理的模型一的基础上建立问题二的模型,将h2带入即可求得罐体变位后储油量与油位高度和变位参数α,β的关系。
2010数学建模a题广东省成绩
2 2 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
GDA0905 GDA0215 GDA3106 GDA1204 GDA2005 GDA1703 GDA2803 GDA1405 GDA1010 GDA0108 GDA2002 GDA0122 GDA0407 GDA1604 GDA2704 GDA0503 GDA6301 GDA2507 GDA1701 GDA2401 GDA3001 GDA0802 GDA2802 GDA1410 GDA1502 GDA0301 GDA2603 GDA1006 GDA0404 GDA2109 GDA1301 GDA6704 GDA0116 GDA2601 GDA6801
3915 3819 4191 4127 3865 4144 4049 3790 4208 3177 3862 3193 4160 3718 4041 3885 3230 4027 4142 3983 4066 3837 4048 3797 3730 4092 3705 4201 4153 3954 3103 4283 3186 3701 4286
省队号 GDA2403 GDA0601 GDA0131 GDA6305 GDA2003 GDA0115 GDA0106 GDA6813 GDA3603 GDA0302 GDA0214 GDA2402 GDA1201 GDA1501 GDA1412 GDA0208 GDA1704 GDA2404 GDA0504 GDA0128 GDA1506 GDA2911 GDA0309 GDA3105 GDA1202 GDA6803 GDA1806 GDA0225 GDA1313 GDA6401 GDA0305 GDA1504 GDA0406
2010全国大学生数学建模竞赛A题

2010全国大学生数学建模竞赛A题合作人:何争流,史剑作者:学院:计算机科学与技术;学号:文摘:加油站、燃油生产厂一般都用储油罐来储存燃油,并通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
但许多储油罐在使用一段时间后,罐体位置会因地基变形等原因发生变化,从而导致罐容表发生改变,故需定期对罐容表进行重新标定。
关键词:储油罐,变位,重新标定,几何法,拟合--插值法。
正文:储油罐可能发生纵向倾斜和横向偏转,故需从这两方面研究罐体变位后的标定问题,即罐内储油量与油位高度及变位参数(纵向倾斜角度和横向偏转角度)之间的一般关系,进而对罐容表进行重新标定。
两端平头的小椭圆形储油罐情形拟合—插植法首先我们根据所给的数据,求出拟合函数:设x为测得油位高度,y为罐内油量。
(1)进油情形:1、无变位进油,初值为262L。
设v为测量体积,h为测量高度,对表中数据进行拟合。
2、斜变位进油(θ=4.1),初始值为215L。
设v2为测量体积,h2为测量高度,则由表中数据进行拟合。
对无变位(θ=0)和斜变位(θ=4.1)进油时的数据作图、拟合得到油位高度与罐内储油量的函数关系。
函数的差别为系数不同,而系数不同是由角度不同引起的,所以我们想到对系数关于θ插值,得出θ为变位角,转化为弧度表示则a7 = -2.7165e-005*g-5.5000e-008a6=0.0134*g+2.4000e-005a5= -2.7332*g+0.0043a4=315.3631*g+0.42a3= -2.0587e+004*g-26a2=8.0726e+005*g+1200a1= -1.6824e+007*g+4600a0=1.5337e+008*g+19000当θ=1.8时,g=0.0314,带入上面的式子得到:y=-9.0841e-007*x^7+4.4497e-004*x^6-0.0816*x^5+10.3274*x^4-672.7597*x^3+2.6561e+004*x^2-5.2394e+005*x+4.8373e+006根据这个方程,计算得出罐体变位后油位高度间隔为1cm的实际罐容量。
2010年研究生数学建模A题
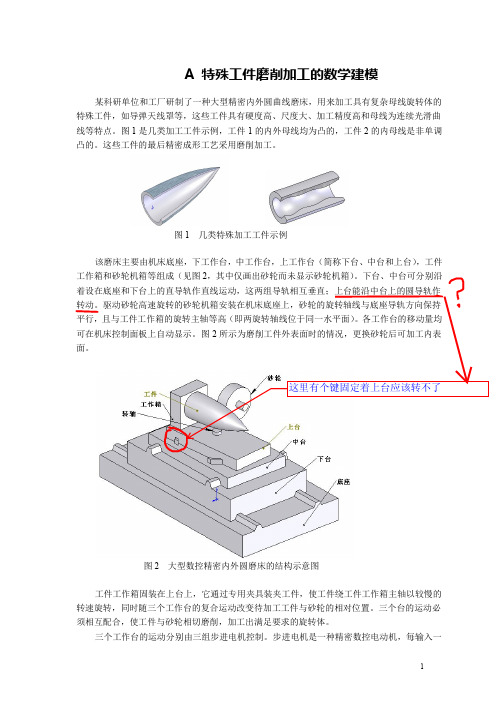
这里有个键固定着丆上台应该转不了
图 2 大型数控精密内外圆磨床的结构示意图 工件工作箱固装在上台上,它通过专用夹具装夹工件,使工件绕工件工作箱主轴以较慢的 转速旋转,同时随三个工作台的复合运动改变待加工工件与砂轮的相对位置。三个台的运动必 须相互配合,使工件与砂轮相切磨削,加工出满足要求的旋转体。 三个工作台的运动分别由三组步进电机控制。步进电机是一种精密数控电动机,每输入一
A 特殊工件磨削加工的数学建模
某科研单位和工厂研制了一种大型精密内外圆曲线磨床,用来加工具有复杂母线旋转体的 特殊工件,如导弹天线罩等,这些工件具有硬度高、尺度大、加工精度高和母线为连续光滑曲 线等特点。图 1 是几类加工工件示例,工件 1 的内外母线均为凸的,工件 2 的内母线是非单调 凸的。这些工件的最后精密成形工艺采用磨削加工。
中台转轴 工件工作箱 夹具基准面
`
中台两对称轴
b
中台 夹具基体 上台
R
螺母 丝杠
传动系统
步进电机
图 4 上台相对中台的转动示意关系 磨床的磨削工具是能磨削高硬度材质的金刚砂轮(指磨削表面含有超高硬度的金刚砂
2
粒) ,磨外圆时根据工件母线的形状,砂轮可采用圆柱体式或轮式,作内圆磨削的砂轮为轮式。 圆柱型砂轮的主要几何参数是砂轮直径 和砂轮厚度 a 。轮式砂轮的主要几何参数有砂轮最大 纵截面(垂直于砂轮转轴的最大截面)的直径 和砂轮厚度 a ,以及其横截面(通过砂轮转轴 的截面)的外端轮廓线参数(理论上它可以是任一凸光滑曲线,但工程上常选用半径为 r 、张 角 不大于 180 的圆弧) ,合理的砂轮几何参数是加工能否实现的关键因素之一(见图 5) 。 在 整个加工过程中工件与砂轮不应脱离接触。
3
3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.(20分)某企业根据去年(t=0)的统计得知,共有技术人员300 名,其中技术员职称(初级职称)的有140名,助理工程师(中级职 称)100名,工程师(包括高级工程师,高级职称)60名。现规定技 术员每年可以有30%晋升为助理工程师,又有10%的技术员因各种原 因调离该企业,余下60%留任原岗位,助理工程师每年要有40%留 任,30%晋升工程师,30%调离,工程师则每年有60%留任,40%调离 或退休。同时,该企业计划每年向社会招聘80名大学生一补充技术 员队伍。现要求 (1)建立合适的数学模型,以便可以预测今后若干年内该企业中的 各类技术人员的人数分布情况;(只要求建立数学模型,不要求具 体结果) (2)在(1)的基础上,建立合适的数学模型,以便可以预测今后 若干年内该企业中的技术人员总量情况。(只要求建立数学模型, 不要求具体结果)
()
A. B. C. D.
3. 模28倒数表中可能出现的数是
()
A. 12
B.5
C.14
D.7
4. 线性最小二乘法得到的函数不可能为
()
A.线性函数 B. 对数函数 C. 样条函数 D. 指数函数
5. 关于泛函极值问题,下面的描述正确的有
()
A.泛函在处取极值的充要条件是泛函变分;
B. 泛函在处取极值的充分条件是泛函变分;
试确定x与y的最佳拟合多项式的阶数,确定该拟合函数表达式,并估
计加热1小时时的温度。
4.(20分)如果在用层次分析法建模时构造了某个判断矩阵, (1) 计算矩阵A的最大特征值(保留到小数点后2位,采用其它方法
计算不给分); (2) 判断该矩阵能否通过一致性检验?
附表 随机一致性指标值
n 1 2 3 4 5 6 7 8 9 10 11 0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49 1.51
()
5.一阶线性齐次差分方程平衡点的稳定性由系数矩阵谱半径决定。
()
四.应用题(共70分)
1.(5分)某外贸进出口公司拟用集装箱托运甲乙两种货物,每包体
积、重量、可获利润及集装箱数目所受限制见下表:
货物 体积(立方米) 重量(千克) 利润(千元)
(包)
甲
5
2
20
乙
4
5
10
集装箱限
24
13
制
问每个集装箱中两种货物各装多少包,可以使所获利润最大?试对该
问题建立合适的数学模型,不需要求出具体结果。
2(10分)深水中的波速与波长、水深、水的密度和重力加速度有关。 用量纲分析法确定与其余变量之间的关系。
3.(15分)某种电热水器加热时间x与水温y之间有如下的实验数
据:
x( 分钟) 15 20 25 30 35
y(℃)
12.16 13.97 14.96 15.49 16.8
C. 泛函在处取极值的必要条件是泛函变分;
D. A,B,C均正确
三.判断题(每题2分,共10分)
1. Hill密码体系中,任意一个可逆矩阵都可以作为加密矩阵。
(
)
2. 拟合函数不要求通过样本数据点。
()
3. Matlab软件内置命令程序可以直接求解一般的整数线性规划问题。
()
4. Volterra模型得到的周期解里,食饵与捕食者可以同时达到峰值。
。
4. 根据Malthus模型,如果自然增长率为2%,则人口数量增长为初
值3倍所需时间为(假设初值为正)
。
5. 请补充判断矩阵缺失的元素。
二.选择题:(每题2分,共10分)
1. 在下列Leslie矩阵中,不能保证模最大特征值唯一的是
(
)
A. ; B. ; C. ; D.以上都不对
2. 判断矩阵能通过一致性检验的标准是
东 南 大 学 考 试 卷(A卷)
姓名
学号
班级
课程名 数学建模与实 称验
考试学 期 09-10-2
得分
适用专 各专业 业
考试 形式 闭卷
考试时 120分
间长度
钟
学号
姓名
一.填空题:(每题2分,共10分)
1. 阻滞增长模型的解为
。
2. 用Matlab做常微分方程数学实验,常用的命令有
。
3. 整数m关于模12可逆的充要条件是:
