二元一次方程组的定义解析
二元一次方程组格式_概述说明以及解释

二元一次方程组格式概述说明以及解释1. 引言1.1 概述二元一次方程组是数学中常见的基本代数方程组之一。
它由两个未知数和两个等式组成,其中每个等式都是未知数的一次项与常数项的和。
解决二元一次方程组可以帮助我们在现实生活、商业领域以及工程问题中找到解决方案。
1.2 二元一次方程组定义二元一次方程组通常表示为:```ax + by = cdx + ey = f```其中a、b、c、d、e和f分别代表系数,x和y代表未知数。
此类方程组有两个未知数x和y,并且每个方程的最高次幂为1,因此称为一次方程组。
1.3 解法方法介绍解决二元一次方程组可以使用多种解法方法,例如消元法、代入法和矩阵法等。
消元法通过逐步变换原方程组,将其转化为更简单的形式来求解。
代入法则先求得一个未知数的值,再将其代入另一个方程中求得第二个未知数的值。
矩阵法则通过矩阵运算来求得未知数的值。
在接下来的文章中,我们将详细介绍二元一次方程组的格式说明、解题步骤以及在实际问题中的应用场景分析。
同时,我们也会总结要点回顾,并探讨学习启示、拓展延伸思考以及未来发展趋势的展望。
通过本文的阅读,相信您将对二元一次方程组有更加深入的理解,并能够灵活运用于各种问题的求解中。
2. 二元一次方程组格式说明2.1 标准形式与一般形式对比二元一次方程组可以有不同的表示形式,其中最常见的是标准形式和一般形式。
标准形式的方程组可以写为:```ax + by = cdx + ey = f```其中,a、b、c、d、e、f是已知的实数系数,x和y是未知数。
一般形式的方程组可以写为:```Ax + By + C = 0Dx + Ey + F = 0其中,A、B、C、D、E、F是已知的实数系数。
标准形式和一般形式之间存在着对应关系。
通过对标准形式适当变换,我们可以得到等价的一般形式方程组,反之亦然。
2.2 系数与未知数的关系解析二元一次方程组中的未知数通常用x和y表示。
在标准形式中,每个未知数都会带上一个系数。
(word完整版)二元一次方程组的概念和解法-教师版

(word 完整版)二元一次方程组的概念和解法-教师版二元一次方程的基本概念1。
含有两个未知数,并且含未知数项的最高次数是1的方程叫二元一次方程。
判定一个方程是二元一次方程必须同时满足三个条件: ①方程两边的代数式都是整式——整式方程; ②含有两个未知数——“二元”;③含有未知数的项的次数为1——“一次”。
2。
二元一次方程的一般形式:0ax by c ++=(0a ≠,0b ≠)3。
二元一次方程的解:使二元一次方程左、右两边的值相等的两个未知数的值,叫做二元一次方程的解。
一般情况下,一个二元一次方程有无数个解。
【例1】 下列各式是二元一次方程的是( )A 。
30x y z -+=B 。
30xy y x -+=C 。
12023x y -= D 。
210y x+-=【解析】根据二元一次方程的定义,从二元一次方程的未知数的个数和次数方面辨别. 【答案】故本题选C .【巩固】下列方程是二元一次方程的是( )A.31x xy -= B 。
2430x x += C.23y += D.3x y =【答案】D .【例2】 若32125m n x y ---=是二元一次方程,则求m 、n 的值.【答案】由定义知:321m -=,11n -=,所以:1m =,2n =.【巩固】已知方程11(2)2m n m x y m ---+=是关于x 、y 的二元一次方程,求m 、n 的值。
【答案】根据题意可得:20m -≠,11n -=,11m -=,所以2n =,0m =.二元一次方程组的概念和解法同步练习知识讲解(word 完整版)二元一次方程组的概念和解法-教师版【例3】 若32125m n x y ---=是二元一次方程,则求m 、n 的值。
【答案】由定义知:321m -=,11n -=,所以:1m =,2n =。
【巩固】已知方程11(2)2m n m x y m ---+=是关于x 、y 的二元一次方程,求m 、n 的值。
七年级数学上册-8.1二元一次方程组 解析版

8.1二元一次方程组【考点梳理】考点一:二元一次方程的概念理解考点二:二元一次方程的解考点三:二元一次方程组的概念考点四:判断是否是二元一次方程组的解考点五:二元一次方程组的解求参数知识点一:二元一次方程的概念含有两个未知数,并且未知数的指数都是1的方程叫做二元一次方程。
知识点二:二元一次方程的解使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解。
二元一次方程的解有无数个,可以理解为在一条直线上的点的坐标。
知识点三:二元一次方程组把含有两个未知数的两个一次方程合在一起,就组成一个二元一次方程组。
即两个二元一次方程组成的方程组称二元一次方程组。
(两个方程中的未知数相同)技巧归纳:二元一次方程组的特点:1.有两个未知数.(二元)2.含未知数的指数都为1.(一次)3.两个一次方程组成.(方程组)知识点四:二元一次方程组的解二元一次方程组的两个方程的公共解,叫做二元一次方程组的解。
二元一次方程组的解只有一个,可以理解为两条直线相交点的坐标。
题型一:二元一次方程的概念理解1.(23-24七年级下·浙江·期中)下列各式是二元一次方程的是()A .223x y -=B .23x y-=C .3x y +=D .23x y z+=【答案】C【分析】本题考查了二元一次方程的定义,注意二元一次方程必须符合以下三个条件:(1)方程中只含有2个未知数;(2)含未知数项的最高次数为一次;(3)方程是整式方程.根据二元一次方程的定义,依次分析各个选项,选出是二元一次方程的选项即可.【详解】解:A .该方程含未知数项的最高次数为二次,不符合二元一次方程的定义,不是二元一次方程,即A 选项不合题意;B .是分式方程,不符合二元一次方程的定义,不是二元一次方程,即B 选项不合题意;C .符合二元一次方程的定义,是二元一次方程,即C 选项符合题意;D.是三元一次方程,不符合二元一次方程的定义,不是二元一次方程,即D 选项不合题意.故选:C .2.(23-24七年级下·重庆·期中)若关于x y 、的方程1325m n x y -+-=是二元一次方程,则m n +=()A .0B .1C .2D .3【答案】A【分析】本题考查了二元一次方程的定义,二元一次方程必须符合以下三个条件:(1)方程中只含有2个未知数;(2)含未知数项的最高次数为一次;(3)方程是整式方程.利用二元一次方程的定义判断即可.【详解】解:∵关于x 、y 的方程程1325m n x y -+-=是二元一次方程,∴11,31m n -=+=,解得:22m n ==-,,∴()220m n +=+-=,故选:A .3.(23-24七年级下·湖南衡阳·阶段练习)下列方程中,是二元一次方程的有()①25x y -=,②41x -=,③23xy =,④27x y z ++=,⑤152x y +=,⑥782x y +=A .1个B .2个C .4个D .6个【答案】B【分析】本题考查了二元一次方程的定义,牢记“只含有二个未知数(元),且未知数的次数是1,这样的整式方程叫二元一次方程”是解题的关键.利用二元一次方程的定义,逐一分析各方程,即可得出结论.【详解】解:①25x y -=是二元一次方程,符合题意;②41x -=是一元一次方程,不符合题意;③23xy =含有两个未知数,最高次数是2,不是二元一次方程,不符合题意;④27x y z ++=含三个未知数,不是二元一次方程,不符合题意;⑤152x y+=不是二元一次方程,不符合题意;⑥782x y +=是二元一次方程,符合题意;综上,是一元一次方程的有①⑥,共2个,故选:B .题型二:二元一次方程的解4.(23-24七年级下·河南周口·阶段练习)已知21x y =⎧⎨=-⎩是二元一次方程29ax y -=的解,则a 的值为()A .2-B .2C .12D .12-【答案】B【分析】本题考查二元一次方程解的定义、解一元一次方程等知识,将21x y =⎧⎨=-⎩代入29ax y -=,解一元一次方程即可得到答案,熟练掌握二元一次方程的解是解决问题的关键.【详解】解: 21x y =⎧⎨=-⎩是二元一次方程29ax y -=的解,()419a ∴--=,解得2a =,故选:B .5.(23-24七年级下·河南周口·阶段练习)下列哪组x ,y 的值是二元一次方程25x y +=的解()A .22x y =-⎧⎨=-⎩B .02x y =⎧⎨=⎩C .22x y =⎧⎨=⎩D .31x y =⎧⎨=⎩【答案】D【分析】本题主要考查了二元一次方程的解,二元一次方程的解是使方程左右两边相等的未知数的值,据此把四个选项中的x ,y 的值代入原方程,看方程左右两边是否相等即可得到答案.【详解】解:A 、把22x y =-⎧⎨=-代入方程25x y +=中得,左边()2226=-+⨯-=-,方程左右两边不相等,则22x y =-⎧⎨=-不是方程25x y +=的解,不符合题意;B 、把02x y =⎧⎨=⎩代入方程25x y +=中得,左边0224=+⨯=,方程左右两边不相等,则02x y =⎧⎨=⎩不是方程25x y +=的解,不符合题意;C 、把22x y =⎧⎨=⎩代入方程25x y +=中得,左边2226=+⨯=,方程左右两边不相等,则22x y =⎧⎨=⎩不是方程25x y +=的解,不符合题意;D 、把31x y =⎧⎨=⎩代入方程25x y +=中得,左边3215=+⨯=,方程左右两边相等,则31x y =⎧⎨=⎩是方程25x y +=的解,符合题意;故选:D .6.(23-24八年级上·安徽宿州·期末)方程组2?3x y x y +=⎧⎨+=⎩的解为2?x y =⎧⎨=⎩,则被遮盖的两个数分别为()A .1,2B .1,3C .5,1D .2,4【答案】C【分析】本题主要考查二元一次方程组的解,根据题意,把2x =代入方程3x y +=中可求出y 的值,由此即可求解,掌握解二元一次方程组的方法是解题的关键.【详解】解:根据题意,把2x =代入方程3x y +=得,1y =,把21x y ==,代入方程2?x y +=得,2215⨯+=,∴被遮盖的两个数分别是51,,故选:C .题型三:二元一次方程组的概念7.(2024七年级下·全国·专题练习)下列方程组中,是二元一次方程组的是()A .34m n mn +=⎧⎨=⎩B .23324x yx ⎧-=-⎪⎨⎪=⎩C .2125s t t s=+⎧⎨=⎩D .7116x y x y -=⎧⎪⎨+=⎪⎩【答案】C【分析】本题考查了二元一次方程组的定义,熟练掌握二元一次方程组的定义是解答本题的关键.根据二元一次方程组的定义判断逐项分析即可,方程的两边都是整式,含有两个未知数,并且未知数的项的次数都是1次的方程叫做二元一次方程.【详解】解:A .34m n mn +=⎧⎨=⎩的最高项的次数是2,故不是二元一次方程组;B .23324x yx ⎧-=-⎪⎨⎪=⎩的最高项的次数是2,故不是二元一次方程组;C .2125s t t s=+⎧⎨=⎩是二元一次方程组;D .7116x y x y -=⎧⎪⎨+=⎪⎩的分母含未知数,故不是二元一次方程组;故选C .8.(23-24七年级下·浙江杭州·阶段练习)下列是二元一次方程组的是()A .141y xx y ⎧+=⎪⎨⎪-=⎩B .12x y =⎧⎨=⎩C .2132x y y z -=⎧⎨+=⎩D .521x y xy +=⎧⎨=⎩【答案】B【分析】本题考查了二元一次方程组的定义,熟练掌握定义是解题的关键.由两个一次方程组成,并含有两个未知数的方程组叫做二元一次方程组,据此判断即可.【详解】A.141y x x y ⎧+=⎪⎨⎪-=⎩,不是二元一次方程组,不符合题意;B.12x y =⎧⎨=⎩,是二元一次方程组,符合题意;C.2132x y y z -=⎧⎨+=⎩,不是二元一次方程组,不符合题意;D.521x y xy +=⎧⎨=⎩,不是二元一次方程组,不符合题意;故选:B .9.(23-24八年级上·河南平顶山·阶段练习)下列方程组,属于二元一次方程组的是().A .52x y y +=⎧⎨=⎩B .28x y y z +=⎧⎨-=⎩C .41y xy ⎧=⎪⎨⎪=⎩D .2103x x y ⎧-=⎨+=⎩【分析】本题主要考查二元一次方程组的概念,组成二元一次方程组的两个方程应共含有两个未知数,且含未知数的项最高次数都是一次,方程的两边都是整式,那么这样的方程组叫做二元一次方程组.根据二元一次方程组的定义逐项分析即可解答.【详解】解:A .52x y y +=⎧⎨=⎩是二元一次方程组,符合题意;B .28x y y z +=⎧⎨-=⎩含有3个未知数,不是二元一次方程组,不符合题意;C .4yx=不是整式方程,不符合题意;D .2103x x y ⎧-=⎨+=⎩含有2次项,不是二元一次方程组,不符合题意.故选A .题型四:判断是否是二元一次方程组的解10.(23-24八年级上·河南驻马店·期末)下列方程组中,解为82x y =⎧⎨=⎩的方程组是()A .104x y x y +=⎧⎨-=⎩B .1024x y x y +=⎧⎨-=⎩C .2113218x y x y +=⎧⎨-=⎩D .253220x y x y -=⎧⎨-=⎩【答案】B【分析】本题主要考查了二元一次方程组的解的定义,正确理解定义是关键.根据方程组的解的定义,只要检验12x y =⎧⎨=⎩是否是选项中方程的解即可.【详解】解:A 、把82x y =⎧⎨=⎩代入方程4x y -=,左边64=≠,故不是方程组的解,故选项错误;B 、把82x y =⎧⎨=⎩满足1024x y x y +=⎧⎨-=⎩中的两个方程,故是方程组的解,故选项正确;C 、把82x y =⎧⎨=⎩代入方程211x y +=,左边1211=≠,故不是方程组的解,故选项错误;D 、把82x y =⎧⎨=代入方程25x y -=,左边45=≠,故不是方程组的解,故选项错误.11.(22-23七年级下·湖北随州·期中)若方程组231328a b a b -=⎧⎨+=⎩的解是21a b =⎧⎨=⎩,则方程组()()()()2132131228x y x y ⎧+--=⎪⎨++-=⎪⎩的解为()A .31x y =⎧⎨=-⎩B .13x y =⎧⎨=⎩C .11x y =-⎧⎨=-⎩D .21x y =⎧⎨=⎩【答案】B【分析】设1,2x m y n +=-=,则原方程组即为231328m n m n -=⎧⎨+=⎩,根据题意可得方程组231328m n m n -=⎧⎨+=⎩的解是21m n =⎧⎨=⎩,可得12,21x y +=-=,即可求解.【详解】解:设1,2x m y n +=-=,则方程组()()()()2132131228x y x y ⎧+--=⎪⎨++-=⎪⎩即为231328m n m n -=⎧⎨+=⎩,因为方程组231328a b a b -=⎧⎨+=⎩的解是21a b =⎧⎨=⎩,所以方程组231328m n m n -=⎧⎨+=⎩的解是21m n =⎧⎨=⎩,所以12,21x y +=-=,解得:13x y =⎧⎨=⎩;故选:B.【点睛】本题考查了二元一次方程组的解,正确理解二元一次方程组的解的含义是解题的关键.12.(22-23七年级下·河北廊坊·期中)若二元一次方程组4313x y -=⎧⎨⊗⎩的解为13x y =⎧⎨=-⎩,则⊗表示的方程可以是()A .4x y +=B .14y x-=C .3xy =-D .=3y -【答案】D【分析】将方程组的解代入每个选项分别计算即可判断.【详解】解:A 、将13x y =⎧⎨=-⎩代入4x y +=,左边≠右边,故不符合题意;B 、将13x y =⎧⎨=-⎩代入14y x -=,左边=右边,但不是整式方程,故不符合题意;C 、将13x y =⎧⎨=-⎩代入3xy =-,左边=右边,但不是二元一次方程,故不符合题意;D 、将13x y =⎧⎨=-⎩代入=3y -,故符合题意;故选:D .【点睛】此题考查了二元一次方程组的解,正确理解二元一次方程组的定义及正确代入计算是解题的关键.题型五:二元一次方程组的解求参数13.(23-24七年级下·河南周口)若关于x ,y 的二元一次方程组42x y +=⎧⎨=⎩ 的解为13x y =⎧⎨=⎩,则“W ”可以表示为()A .xB .23x y-C .y x-D .x y-【答案】C【分析】本题主要考查了二元一次方程组的解和二元一次方程组的定义,分别把13x y =⎧⎨=⎩代入四个选项中的式子中看计算的结果是否为2,以及根据二元一次方程组的定义进行求解即可.【详解】解:A 、∵12x =≠,∴“W ”不可以表示为x ,故此选项不符合题意;B 、232x y -=不是二元一次方程,故此选项不符合题意;C 、当13x y =⎧⎨=⎩时,312y x -=-=,则“W ”可以表示为y x -,故此选项符合题意;D 、当13x y =⎧⎨=⎩时,1322x y =-=-≠-,则“W ”不可以表示为x y -,故此选项不符合题意;故选:C .14.(23-24七年级下·湖南衡阳·阶段练习)已知关于x 、y 的二元一次方程组79ax by bx ay +=⎧⎨+=⎩的解为23x y =⎧⎨=⎩,那么关于m 、n 的二元一次方程组(1)(2)7(1)(2)9a m b n b m a n ++-=⎧⎨++-=⎩的解为()A .23m n =⎧⎨=⎩B .12m n =⎧⎨=⎩C .34m n =⎧⎨=⎩D .15m n =⎧⎨=⎩【答案】D【分析】本题主要考查了二元一次方程组的解,解题的关键是掌握整体代值的数学思想.首先利用整体代值的数学思想可以得到1m +与2n -的值,然后解关于m 、n 的方程组即可求解.【详解】解:∵二元一次方程组79ax by bx ay +=⎧⎨+=⎩的解为23x y =⎧⎨=⎩,∴关于m 、n 的二元一次方程组()()()()127129a m b n b m a n ⎧++-=⎪⎨++-=⎪⎩中1223m n +=⎧⎨-=⎩,解得:15m n =⎧⎨=⎩,故选D .15.(23-24八年级上·陕西西安·期末)若关于x ,y 的方程组32mx y n x ny m -=⎧⎨+=⎩的解为11x y =⎧⎨=⎩则2()m n -等于()A .1B .4C .9D .25【答案】B【分析】此题考查了二元一次方程组的解和解二元一次方程组,代数式求值.解决本题的关键是理解二元一次方程组的解.将x 、y 的值代入,可得关于m 、n 的二元一次方程组,解出m 、n 的值,代入代数式即可.【详解】解:把11x y =⎧⎨=⎩代入方程组32mx y nx ny m -=⎧⎨+=⎩得312m n n m-=⎧⎨+=⎩,解得:1252m n ⎧=-⎪⎪⎨⎪=-⎪⎩∴2215()()422m n -=-+=.故选:B .一、单选题16.(23-24七年级下·山东潍坊)下列方程组中,是二元一次方程组的是()A .23124x y x y ⎧+=⎨-=⎩B .24124x y xy +=⎧⎨=⎩C .2363x y y +=⎧⎨=⎩D .3113y x y =⎧⎪⎨-=⎪⎩【答案】C【分析】本题考查二元一次方程组的定义,根据二元一次方程组的基本形式及特点,①方程组中的两个方程都是整式方程;②方程共含有两个未知数;③每个方程都是一次方程.【详解】解:A .23124x y x y ⎧+=⎨-=⎩,第一个方程是二次方程,方程组不是二元一次方程组,故该选项不符合题意;B .24124x y xy +=⎧⎨=⎩,第二个方程是二次方程,方程组不是二元一次方程组,故该选项不符合题意;C .2363x y y +=⎧⎨=⎩符合二元一次方程组的定义,故该选项符合题意;D .3113y x y =⎧⎪⎨-=⎪⎩,第二个方程是分式方程,方程组不是二元一次方程组,故该选项不符合题意;故选:C .17.(23-24七年级下·浙江金华·阶段练习)二元一次方程21x y -=有无数多个解,下列四组值中不是该方程的解的是()A .11x y =-⎧⎨=-⎩B .11x y =⎧⎨=⎩C .10x y =⎧⎨=⎩D .012x y =⎧⎪⎨=-⎪⎩【答案】B【分析】此题主要考查了二元一次方程的解,关键是把结果代入原方程,看方程两边是否相等.【详解】解:A、把=1x -代入方程21x y -=可得1y =-,故该选项是方程的解;B、把1x =代入21x y -=可得0y =,故该选项不是方程的解;C、把1x =代入方程21x y -=可得0y =,故该选项是方程的解;D、把0x =代入21x y -=可得12y =-,故该选项是方程的解.故选:B .18.(23-24七年级下·湖北·周测)已知11x y =-⎧⎨=⎩是方程3mx y +=的解,m 的值是()A .2-B .2C .1-D .1【答案】A【分析】此题考查了二元一次方程解的定义和一元一次方程的解法,熟练掌握二元一次方程解的定义是解题的关键.根据方程解的定义代入方程进行求解即可.【详解】解:∵11x y =-⎧⎨=⎩是方程3mx y +=的解,∴13m -+=,解得2m =-,故选:A .19.(2024七年级下·全国·专题练习)若458kx y x -=+是关于x 、y 的二元一次方程,则k 的取值范围是()A .0k ≠B .5k ≠C .3k ≠D .1k ≠-【答案】B【分析】本题考查了二元一次方程的定义,熟练掌握二元一次方程组的定义是解答本题的关键.方程的两边都是整式,含有两个未知数,并且未知数的项的次数都是1次的方程叫做二元一次方程.先移项并合并关于x 同类项,然后令未知数的系数不等于零列式求解即可.【详解】解:∵458kx y x -=+,∴5480kx x y ---=,∴()5480k x y ---=,∵458kx y x -=+是关于x 、y 的二元一次方程,∴50k -≠,∴5k ≠.故选B .20.(23-24七年级下·河南周口·阶段练习)已知34x y =⎧⎨=⎩是二元一次方程31x my -=的一个解,则m 的值是()A .2-B .1-C .1D .2【答案】D【分析】本题考查了二元一次方程的解以及解一元一次方程,将34x y =⎧⎨=⎩代入二元一次方程,得到关于m 的一元一次方程,求解即可.【详解】解:34x y =⎧⎨=⎩是二元一次方程31x my -=的一个解,3341m ∴⨯-=,2m ∴=,故选:D .21.(23-24七年级下·湖南长沙·阶段练习)解方程组274ax y cx dy +=⎧⎨-=⎩时,一学生把a 看错后得到51x y =⎧⎨=⎩,而正确的解为31x y =⎧⎨=-⎩,(1)求a ,b ,c 的值;(2)求2a c d ++的立方根.【答案】(1)3a =,1c =,1d =(2)2【分析】本题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程成立的未知数的值.(1)将51x y =⎧⎨=⎩代入第二个方程,将31x y =⎧⎨=-⎩代入第二个方程,组成方程组求出c 与d 的值,将正确解代入第一个方程求出a 即可;(2)由(1)知a ,b ,c 的值,代入2a c d ++即可求解.【详解】(1)解:将51x y =⎧⎨=⎩;31x y =⎧⎨=-⎩分别代入4cx dy -=得:5434c d c d -=⎧⎨+=⎩,解得:11c d =⎧⎨=⎩,将31x y =⎧⎨=-⎩代入27ax y +=中得:327a -=,解得:3a =,则3a =,1c =,1d =;(2)解:把3a =,1c =,1d =代入2a c d ++得223118a c d ++=⨯++=,8的立方根是2,2a c d ∴++的立方根为2.22.(23-24七年级下·湖南衡阳·阶段练习)两个同学对问题“若方程组111222a x b y c a x b y c +=⎧⎨+=⎩的解是34x y =⎧⎨=⎩,求方程组111222325325a x b y c a x b y c +=⎧⎨+=⎩的解”.提出了各自的想法,甲说:“这个题目好像条件不够,不能求解.”乙说:“它们的系数有一定规律,可以试试.”请你参考他们的讨论,求出这个题目的正确答案.【答案】510x y =⎧⎨=⎩【分析】本题考查了二元一次方程组的解,熟练掌握二元一次方程组的解的含义是解题的关键.先把所求方程组变形后,根据已知方程组的解求出解即可.【详解】解:将方程组111222325325a x b y c a x b y c +=⎧⎨+=⎩化简得11122232553255a x b y c a x b y c ⎧⋅+⋅=⎪⎪⎨⎪⋅+⋅=⎪⎩,335245x y ⎧=⎪⎪∴⎨⎪=⎪⎩,解得510x y =⎧⎨=⎩.一、单选题23.(23-24七年级下·江苏南通·阶段练习)已知关于x ,y 的方程组()21223ax a y a x y ⎧+-=⎨+=⎩有下列几种说法:①一定有唯一解;②可能有无数多解;③当2a =时方程组无解;④若方程组的一个解中y 的值为0,则0a =.其中正确的说法有()A .0种B .1种C .2种D .3种【答案】C【分析】本题考查了解二元一次方程组.方程组整理得()122a y a -=-,针对四种说法逐一分析即可判断.【详解】解:()21223ax a y a x y ⎧+-=⎨+=⎩①②,由②得322y x -=,把322y x -=代入①得()32221a a y a y ⎛⎫+- ⎪⎝-=⎭,整理得()122a y a -=-,当2a =时,方程组无解;当2a ≠时,方程组有唯一解;如果0y =,则()1202a a -⨯=-,解得0a =,观察四种说法,①②错误,③④正确,故选:C .24.(23-24七年级下·河北沧州·阶段练习)方程组23x y x y +=⎧⎨-=⎩ 的解为1x y =⎧⎨=◊⎩,则“ ”“◊”代表的两个数分别为()A .4,2B .1,3C .0,2-D .2,3【答案】C 【分析】本题主要考查了二元一次方程组的解的定义,根据二元一次方程组的解是使方程组两个方程都成立的未知数的值,把1x =代入方程3x y -=中求出y 的值,进而求出2x y +的值即可得到答案.【详解】解:∵方程组23x y x y +=⎧⎨-=⎩ 的解为1x y =⎧⎨=◊⎩,∴13y -=,∴=2y -,∴2220x y +=-=,∴“ ”“◊”代表的两个数分别为0,2-,故选:C .25.(23-24七年级下·浙江金华·阶段练习)已知二元一次方程组1*x y +=⎧⎨⎩的解是1x y a =-⎧⎨=⎩,则*表示的方程可能是()A .3x y -=-B .4x y +=C .23x y -=-D .234x y +=-【答案】A 【分析】本题考查二元一次方程组的解,根据方程组的解使方程组中的每一个方程都成立,求出a 的值,再将方程组的解分别代入各个选项中,进行判断即可.【详解】解:∵二元一次方程组1*x y +=⎧⎨⎩的解是1x y a =-⎧⎨=⎩,∴11a -+=,∴2a =,∴12x y =-⎧⎨=⎩,∴123x y -=--=-,1x y +=,24x y -=-,234x y +=;故*表示的方程可能是3x y -=-;故选A .26.(2024七年级下·全国·专题练习)若()()217a x b y ++-=是关于x y 、的二元一次方程,则()A .2,1a b ≠-=B .2a ≠-且1b ≠C .2a ≠且1b ≠D .2a ≠-【答案】B 【分析】本题考查了二元一次方程的概念;根据方程中只含有2个未知数;含未知数的项的最高次数为一次的整式方程是二元一次方程可得20,10a b +≠-≠,据此求解即可.【详解】解:∵()()217a x b y ++-=是关于x y 、的二元一次方程,∴20,a +≠且10b -≠,∴2a ≠-且1b ≠,故选:B .27.(2024七年级下·全国·专题练习)如果12x y =⎧⎨=⎩是二元一次方程组12ax by bx ay +=⎧⎨+=⎩的解,那么a ,b 是()A .10a b =-=,B .10a b ==,C .01a b ==,D .01a b ==-,【答案】B【分析】此题考查了二元一次方程组的解的定义和解二元一次方程组的方法,把方程组的解代入方程组,解关于a b ,的方程组,即可求出 a b ,的值.【详解】解:根据题意可得2122a b b a +=⎧⎨+=⎩,即24222a b a b +=⎧⎨+=⎩,两个方程相减得到0b =,把0b =代入可得1a =,故选:B .二、填空题28.(23-24七年级下·江苏南通·阶段练习)若12323m m x y --+=是关于,x y 的二元一次方程,则m =.【答案】0【分析】本题主要考查了二元一次方程的定义,只含有两个未知数,且含未知数的项的次数为1的整式方程叫做二元一次方程,据此得到2011m m -≠-=,,解之即可得到答案.【详解】解:∵12323m m x y --+=是关于,x y 的二元一次方程,∴2011m m -≠-=,,解得0m =,故答案为:0.29.(23-24九年级下·江苏无锡·阶段练习)请写出一个二元一次方程,使得它的一个解为12x y =⎧⎨=⎩.【答案】3x y +=(答案不唯一)【分析】本题考查了二元一次方程的解以及解二元一次方程,根据二元一次方程的解使方程左右两边值相等进行列式,即可作答.【详解】解:依题意,3x y +=是二元一次方程,且满足它的一个解为12x y =⎧⎨=⎩故答案为:3x y +=(答案不唯一)30.(23-24七年级下·江西赣州·期中)若21x y =⎧⎨=-⎩是方程2ax by -=-的一个解,则1065a b +-的值是.【答案】16【分析】本题考查了二元一次方程的解,能使二元一次方程左右两边相等的未知数的值叫做二元一次方程的解.把21x y =⎧⎨=-⎩代入2ax by -=-求出22a b -=,然后用整体代入法求解即可.【详解】把21x y =⎧⎨=-⎩代入2ax by -=-,得22a b -=,∴22a b -=,∴1065a b+-()526a b =-+52616=⨯+=.故答案为:16.31.(2024·河南郑州·模拟预测)已知21x y =⎧⎨=⎩是方程123ax by bx ay +=⎧⎨+=⎩的解,则(())a b a b +-的值为.【答案】45【分析】本题主要考查二元一次方程的解,把x ,y 的值代入方程组,求出a b +和a b -的值代入计算即可.【详解】解:把21x y =⎧⎨=⎩代入方程组123ax by bx ay +=⎧⎨+=⎩①②中,-①②得,9a b -=,+①②得,5a b +=,则()()5945a b a b +-=⨯=,故答案为:45.32.(23-24七年级下·浙江嘉兴·阶段练习)三个同学对问题“若方程组111222a x b y c a x b y c +=⎧⎨+=⎩的解是56x y =⎧⎨=⎩,求方程组111222534534a x b y c a x b y c +=⎧⎨+=⎩的解”提出各自的想法.甲说:“这个题目好像条件不够,不能求解”;乙说:“它们的系数有一定的规律,这可以试试”;丙说:“能不能通过换元替代的方法来解决”,参照他们的讨论,你认为这个题目的解应该是.【答案】48x y =⎧⎨=⎩【分析】本题考查了二元一次方程的解,所求方程组变形后,根据已知方程组的解求出解即可.【详解】111222534534a x b y c a x b y c +=⎧⎨+=⎩,方程组中两个方程的两边都除以4,得11122253445344a x b y c a x b y c ⎧+=⎪⎪⎨⎪+=⎪⎩,∵方程组111222a x b y c a x b y c +=⎧⎨+=⎩的解是56x y =⎧⎨=⎩,∴55 436 4xy⎧=⎪⎪⎨⎪=⎪⎩,∴48 xy=⎧⎨=⎩,故答案为48 xy=⎧⎨=⎩.三、解答题33.(23-24七年级下·山西长治·阶段练习)解方程组2718ax bycx y+=⎧⎨-=⎩时,小明本应该解出32xy=⎧⎨=-⎩,由于看错了系数c,从而得到解22xy=-⎧⎨=⎩,试求出a b c-+的值【答案】1 3【分析】此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程成立的未知数的值.将第一对x与y的值代入方程组第二个方程求出c的值,将两对x与y的值代入方程组中第一个方程,求出a,b 的值即可.【详解】解:把32xy=⎧⎨=-⎩代入718cx y-=,得31418c+=,解得43c=,把32xy=⎧⎨=-⎩代入2ax by+=,得322a b-=①,把22xy=-⎧⎨=⎩代入2ax by+=,得222a b-+=②,①,②联立方程组,得322 222 a ba b-=⎧⎨-+=⎩解得45 ab=⎧⎨=⎩,∴414533 a b c-+=-+=.34.(22-23七年级下·重庆开州·期中)对于任意一个三位数m,将个位数字和百位数字对调后得到新的三位数n,记22m nP -=,若P 为整数,则称m 为“有趣数”,此时的P 值称为m 的“有趣值”.例如:432对调后的三位数为234,则432234922P -==,∵9为整数,∴432为“有趣数”.(1)试判断826,326是否为“有趣数”.(2)若f 和s 都是“有趣数”,且满足10042f x =+,120s y =+(19x ≤≤,19y ≤≤,且x ,y 均为整数),把f 和s 的“有趣值”分别记1P 和2P ,满足12236P P -=,求出满足条件的三位数f 和s .【答案】(1)826是有趣数;326不是有趣数(2)642123f s =⎧⎨=⎩或242125f s =⎧⎨=⎩【分析】(1)根据“有趣数”的定义进行验证即可;(2)根据“有趣数”的定义表示出1P 和2P ,结合12236P P -=可得212x y +=,找到满足条件的x 和y 值,分别根据定义验证是否满足题意即可.【详解】(1)解:826628922P -==,∵9为整数,∴826为“有趣数”,32662313.522P -==-,∵13.5-不是整数,∴13.5-不是“有趣数”,(2)解:∵10042f x =+,120s y =+,f 和s 的“有趣值”分别记1P 和2P ,∴()()110042240929919822222P x x x x +-+--===,()29112010021999922222P y y y y -+---===,∵12236P P -=,∴()()929123622x y ---⨯=,整理可得212x y +=,∵19x ≤≤,19y ≤≤,且x ,y 均为整数,∴25x y =⎧⎨=⎩,44x y =⎧⎨=⎩,63x y =⎧⎨=⎩或82x y =⎧⎨=⎩,将25x y =⎧⎨=⎩代入,可得()192202P ⨯-==,()2915182P ⨯-==-,符合题意,∴242125f s =⎧⎨=⎩将44x y =⎧⎨=⎩代入,可得()194292P ⨯-==,()291413.52P ⨯-==-,13.5-不是整数,不符合题意;将63x y =⎧⎨=⎩代入,可得()1962182P ⨯-==,()291392P ⨯-==-,符合题意,∴642123f s =⎧⎨=⎩将82x y =⎧⎨=⎩代入,可得()1982272P ⨯-==,()2912 4.52P ⨯-==-,4.5-不是整数,不符合题意,∴满足条件的三位数f 和s 分别为642123f s =⎧⎨=⎩或242125f s =⎧⎨=⎩.【点睛】本题考查新定义的运算,掌握二元一次方程的解法,新定义的运算是解题的关键.35.(22-23七年级下·河北沧州·期中)按一定规律排列方程组和它的解的对应关系如下:111__________,,,12439__________x y x y x y x y x y x y ⎧⎧⎧+=+=+=⎧⎪⎪⎨⎨⎨⎨-=-=-=⎩⎪⎩⎪⎩⎩.……123______,,,012______x x x x y y y y ⎧⎧⎧====⎧⎪⎪⎨⎨⎨⎨==-=-=⎩⎪⎩⎪⎩⎩.……(1)依据方程组和它的解的变化规律,将第4个方程组和它的解直接填入横线处.(2)猜想第n 个方程组和它的解并验证.(3)若方程组116x y x my +=⎧⎨-=⎩的解是54x y =⎧⎨=-⎩,求m 的值,并判断该方程组是否符合(1)中的规律.【答案】(1)43x y =⎧⎨=-⎩(2)见解析(3)114m =,它不符合(1)中的规律21【分析】(1)根据已知的方程组,观察方程未知数系数,常数与解的关系,确定第4个方程组;(2)通过观察,知第n 个方程组为21x y x ny n +=⎧⎨-=⎩解为1x n y n =⎧⎨=-⎩,将解代入方程组验证;(3)将解代入方程求得参数值,故可知本方程组不符合规律.【详解】(1)解:1,4,4163x y x x y y ⎧+==⎧⎨⎨-==-⎩⎩(2)21,,1x y x n x ny n y n ⎧+==⎧⎨⎨-==-⎩⎩把1x n y n=⎧⎨=-⎩代入21,x y x ny n +=⎧⎨-=⎩得()()211,1n n n n n n +-=--=,所以成立.(3)将54x y =⎧⎨=-⎩代入16x my -=,解得114m =,即方程组为111164x y x y +=⎧⎪⎨-=⎪⎩,所以它不符合(1)中的规律.【点睛】本题考查规律探索,观察方程组,探索出方程未知数系数,常数与解的关系是解题的关键.。
二元一次方程的定义 解二元一次方程组

3.把这个未知数的值代入上面的式子,求得另一个未知数的值, 即“求”.
4.写出方程的解,即“写”. 注意:用带入消元法解二元一次方程组时,尽量选取一个未知数的 系数是1或-1的方程进行变形.
二、加减消元法 定义:通过两式相加或相减消去其中一个未知数,这种解二元一次 方程的方法叫做加减消元法. 步骤:1、方程组的两个方程中,如果同一个未知数的系数既不相 等也不互为相反数,就要用适当的数去乘方程的两边,使某一个未 知数的系数相等或互为相反数.“乘” 2、当同一个未知数的系数互为相反数时,用加法消去这个未知数, 得到关于另一个未知数的一元一次方程;当同一个未知数的系数相 等时,用减法消去这个未知数,得到.关于另一个未知数的一元一次 方程.“加减” 3、解这个一元一次方程,求得一个未知数的值,即“解” 4、将这个求得的未知数的值代入原方程组中任意一个方程中,求 出另一个未知数的值即“回代”. 5、把求得的两个未知数的值用{联立起来,即“联”.
(2) (4)
解:
解:方程组整得:
②①解把则×得方﹣ y=:程4③得﹣组得y=1:的:代4﹣解1x入11-为y, ②8=y得=﹣1:61x1=,③2,①②③把则-y××方④=23程得得得﹣组:::2的466﹣代解xxyy入++为=89=②yy2﹣==4得11264:484,x=③ ④60,
方程组可化为
在代数ax2+bx中,当x=1时,其值为13;
当x=2时,其值为18,求当x=−2时,这个
代数式的值为多少?
解答: 由题意可得方程组{a+b=13
4a+2b=18, 解得{a=−4
b=17. 原式=ax2+bx=−4x2+17x, 把x=−2代入,得−4×(−2)2+17×(−2)
七年级下-二元一次方程组的定义及解法
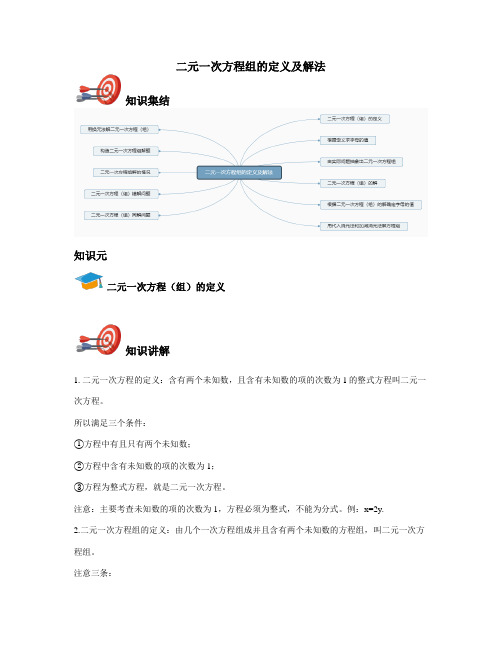
二元一次方程组的定义及解法知识集结知识元二元一次方程(组)的定义知识讲解1. 二元一次方程的定义:含有两个未知数,且含有未知数的项的次数为1的整式方程叫二元一次方程。
所以满足三个条件:①方程中有且只有两个未知数;②方程中含有未知数的项的次数为1;③方程为整式方程,就是二元一次方程。
注意:主要考查未知数的项的次数为1,方程必须为整式,不能为分式。
例:x=2y.2.二元一次方程组的定义:由几个一次方程组成并且含有两个未知数的方程组,叫二元一次方程组。
注意三条:①方程组中有且只有两个未知数。
②方程组中含有未知数的项的次数为1。
③方程组中每个方程均为整式方程。
注意:二元一次方程组不一定由两个二元一次方程合在一起:①方程可以超过两个;②有的方程可以只有一元。
例题精讲二元一次方程(组)的定义例1.下列方程中,是二元一次方程的是().A.8x2+1=y B.y=8x+1C.y=D.xy=1例2.下列方程组中,是二元一次方程组的是().C.D.A.B.例3.有下列方程组:(1)(2)(3)(4),其中说法正确的是().A.只有(1)、(3)是二元一次方程组B.只有(3)、(4)是二元一次方程组C.只有(4)是二元一次方程组D.只有(2)不是二元一次方程组根据定义求字母的值知识讲解含有参数的二元一次方程组,根据二元一次方程的定义:1.二元的系数不为零。
2.未知数的次数为1。
注意:出现在选择填空题时,可以不用解出方程,可以直接将m,n的值代入验证即可。
例题精讲根据定义求字母的值例1.已知3 =y是二元一次方程,那么k的值是().A.2B.3C.1D.0例2.若﹣8 =10是关于x,y的二元一次方程,则m+n=.例3.'若(a-3)x+=9是关于x,y的二元一次方程,求a的值。
'由实际问题抽象出二元一次方程组知识讲解分析实际问题,找出等量关系,列出实际问题.例题精讲由实际问题抽象出二元一次方程组例1.4辆板车和5辆卡车一次能运27吨货,10辆板车和3车卡车一次能运货20吨,设每辆板车每次可运x吨货,每辆卡车每次能运y吨货,则可列方程组().A.B.C.D.例2.元旦期间,某服装商场按标价打折销售,小王去该商场买了两件衣服,第一件打6折,第二件打5折,共记230元,付款后,收银员发现两件衣服的标价牌换错了,又找给小王20元,请问两件衣服的原标价各是多少?解:设第一件衣服的原标价为x元,第二件衣服的原标价为y元;由题意可得方程组__________。
二元一次方程组知识点归纳及解题技巧

二元一次方程组知识点归纳及解题技巧一,基本定义:二元一次方程定义:一个含有两个未知数,并且未知数的都指数是1的整式方程,叫二元一次方程。
二元一次方程组定义:两个结合在一起的共含有两个未知数的一次方程,叫二元一次方程组。
二元一次方程的解:使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解。
二元一次方程组的解:二元一次方程组的两个公共解,叫做二元一次方程组的解。
二,解的状况:二元一次方程组的解有三种状况:1.有一组解如方程组x+y=5①6x+13y=89②x=-24∕7y=59∕7为方程组的解2.有多数组解如方程组x+y=6①2x+2y=12②因为这两个方程事实上是一个方程(亦称作“方程有两个相等的实数根”),所以此类方程组有多数组解。
3.无解如方程组x+y=4①2x+2y=10②,因为方程②化简后为x+y=5 这与方程①相冲突,所以此类方程组无解。
三,二元一次方程的解法:1,一般解法,消元:将方程组中的未知数个数由多化少,逐一解决。
消元的方法有两种:1,代入消元法2,加减消元法3,教科书中没有的几种解法(一)加减•■代入混合运用的方法.例:i3x+14y=41(1)^14x+13y=40(2)解:(2)-⑴得x-y=-1x=y-1(3)把(3)代入⑴得13(y-1)+14y=41y=2把y=2代入⑶得x=1所以:x=1,y=2特点:两方程相加减,单个X或单个y,这样就适用接下来的代入消元.(二)换元法例3:rx:y=1:4>5x+6y=29令X=1y=41 则方程2可写为:5t+6×4(=2929t=29t=1所以x=1,y=4四,列方程(组)解应用题(一),其详细步骤是:⑴审题。
理解题意。
弄清问题中已知量是什么,未知量是什么,问题给出和涉及的相等关系是什么。
⑵设元(未知数)。
①直接未知数②间接未知数(往往二者兼用)。
一般来说,未知数越多,方程越易列,但越难解。
⑶用含未知数的代数式表示相关的量。
(完整)二元一次方程组的定义解析

考点名称:二元一次方程组的定义•(一)二元一次方程组:含有两个未知数,并且所含未知数的项的次数都是1的方程叫做二元一次方程。
把两个含有相同未知数的一次方程联合在一起,那么这两个方程就组成了一个二元一次方程组。
二元一次方程组的解:一般的,二元一次方程组的两个二元一次方程的公共解,叫做二元一次方程组的解.一般形式为:(其中a1,a2,b1,b2不同时为零).••(二)二元一次方程组的特点:1.组成二元一次方程组的两个一次方程不一定都是二元一次方程,但这两个方程必须一共含有两个未知数,如也是二元一次方程组。
2。
在方程组的每个方程中,相同字母必须代表同一未知量,否则不能将两个方程合在一起。
3。
二元一次方程组中的各个方程应是整式方程。
4。
二元一次方程组有时也由两个以上的方程组成。
••(三)二元一次方程与二元一次方程组的区别:•二元一次方程二元一次方程组条件①含有两个未知数;②含未知数的项的次数都是1;③整式方程。
①含有两个未知数;②含未知数的项的次数都是1;③整式方程组(可任意话说你有两个以上的方程)一般形式ax+by=c(a、b、c都是常数,且a≠0,b≠0)(a1,a2,b1,b2不同时为零).解的情况无数组解或无数组解或有唯一解或无解解的定义适合二元一次方程的每一对未知数的值,叫做这个二元一次方程的一组解二元一次方程组中各个方程的公共解叫做这个二元一次方程组的解••(四)二元一次方程组的判定:①方程组各方程中,相同的字母必须代表同一数量,否则不能将两个方程合在一起.②怎样检验一组数值是不是某个二元一次方程组的解,常用的方法如下:将这组数值分别代入方程组中的每个方程,只有当这组数值满足其中的所有方程时,才能说这组数值是此方程组的解,否则,如果这组数值不满足其中任一个方程,那么它就不是此方程组的解.••(五)二元一次方程:如果一个方程含有两个未知数,并且所含未知项都为1次方,那么这个整式方程就叫做二元一次方程,有无穷个解,若加条件限定有有限个解。
《二元一次方程组》知识讲解及例题解析

《二元一次方程组》知识讲解及例题解析◆知识讲解1.二元一次方程组的有关概念二元一次方程:含有两个未知数,并且含有未知数的项的次数都是1•的整式方程叫做二元一次方程.二元一次方程的解集:适合一个二元一次方程的每一对未知数的值,叫做这个二元一次方程的一个解.对于任何一个二元一次方程,令其中一个未知数取任意一个值,都能求出与它对应的另一个未知数的值.因此,任何一个二元一次方程都有无数多个解.由这些解组成的集合,叫做这个二元一次方程的解集.二元一次方程组及其解:两个二元一次方程合在一起就组成了一个二元一次方程组.一般地,能使二元一次方程组的两个方程左右两边的值都相等的两个未知数的值,叫做二元一次方程组的解.2.二元一次方程组的解法代入消元法:在二元一次方程组中选取一个适当的方程,将一个未知数用含另一个未知数的式子表示出来,再代入另一个方程,消去一个未知数得到一元一次方程,求出这个未知数的值,进而求得这个二元一次方程组的解,这种方法叫做代入消元法.加减消元法:两个二元一次方程中同一未知数的系数相反或相等时,将两个方程的两边分别相加或相差,从而消去这个未知数,得到一个一元一次方程,这种求二元一次方程组的解的方法叫做加减消元法,简称加减法.3.二元一次方程组的应用对于含有多个未知数的问题,利用列方程组来解,一般比列一元一次方程解题容易得多.列方程组解应用问题有以下几个步骤:(1)选定几个未知数;(2)依据已知条件列出与未知数的个数相等的独立方程,组成方程组;(3)解方程组,得到方程组的解;(4)检验求得未知数的值是否符合题意,符合题意即为应用题的解.◆例题解析例1 已知21xy=⎧⎨=⎩是方程组2(1)21x m ynx y+-=⎧⎨+=⎩的解,求(m+n)的值.【分析】由方程组的解的定义可知21xy=⎧⎨=⎩,同时满足方程组中的两个方程,将21xy=⎧⎨=⎩代入两个方程,分别解二元一次方程,即得m 和n 的值,从而求出代数式的值.【解答】把x=2,y=1代入方程组2(1)21x m y nx y +-=⎧⎨+=⎩中,得22(1)12211m n ⨯+-⨯=⎧⎨+=⎩ 由①得m=-1,由②得n=0.所以当m=-1,n=0时,(m+n )=(-1+0)=-1.【点评】如果是方程组的解,那么它们就能满足这个方程组中的每一个方程. 例2 “5.12”汶川大地震后,灾区急需大量帐篷.•某服装厂原有4条成衣生产线和5条童装生产,工厂决定转产,计划用3天时间赶制1000•顶帐篷支援灾区.若启用1条成衣生产线和2条童装生产线,一天可以生产帐篷105顶;•若启用2条成衣生产线和3条童装生产线,一天可以生产帐篷178顶.(1)每条成衣生产线和童装生产线平均每天生产帐篷各多少顶?(2)工厂满负荷全面转产,是否可以如期完成任务?如果你是厂长,你会怎样体现你的社会责任感?【解答】(1)设每条成衣生产线和童装生产线平均每天生产帐篷各x ,y 顶,则210523178x y x y +=⎧⎨+=⎩ 解得:x=41;y=32答:每条成衣生产线平均每天生产帐篷41顶,每条童装生产线平均每天生产帐篷32顶.(2)由3×(4×41+5×32)=972<1000知,即使工厂满负荷全面转产,也不能如期完成任务.可以从加班生产,改进技术等方面进一步挖掘生产潜力,或者动员其他厂家支援等,想法尽早完成生产任务,为灾区人民多做贡献.例3 某商场正在热销2008年北京奥运会吉祥物“福娃”和徽章两种奥运商品,根据下图提供的信息,•求一盒“福娃”玩具和一枚徽章的价格各是多少元?【分析】本题以图文形式提供了部分信息,主要考查学生运用二元一次方程组解决实际问题的能力.【解答】设一盒“福娃”玩具和一枚徽章的价格分别为x 元和y 元.依题意,得214523280x y x y +=⎧⎨+=⎩解这个方程组,得12510x y =⎧⎨=⎩ 故一盒“福娃”玩具的价格为125元,一枚徽章的价格为10元.例4 为满足用水量不断增长的需求,昆明市最近新建甲,乙,•丙三个水厂,这三个水厂的日供水量共计11.8万m 3,•其中乙水厂的日供水量是甲水厂日供水量的3倍,丙水厂的日供水量比甲水厂日供水量的一半还多1万m 3.(1)求这三个水厂的日供水量各是多少万立方米?(2)在修建甲水厂的输水管道的工程中要运走600t 土石,运输公司派出A 型,B •型两种载重汽车,A 型汽车6辆,B 型汽车4辆,分别运5次,可把土石运完;或者A 型汽车3辆,B 型汽车6辆,分别运5次,也可把土石运完,那么每辆A 型汽车,每辆B 型汽车每次运土石各多少吨?(每辆汽车运土石都以准载重量满载)【分析】(1)可设甲水厂的日供水量是x 万m 3,则乙水厂的日供水量是3x 万m 3,丙水厂的日供水量是(12x+1)万m 3,由三个水厂的日供水量总和为11.8万m 3,可列方程x+3x+12x+1=11.8; (2)设每辆A 型汽车每次运土石xt ,B 型车每辆每次运土石yt ,•依题意可列方程组30206001530600x y x y +=⎧⎨+=⎩解方程后可求解.【解答】(1)设甲水厂的供水量是x 万m 3,则乙水厂的日供水量是3x 万m 3,丙水厂的日供水量是(12x+1)万m 3. 由题意得:x+3x+12x+1=11.8,解得x=2.4. 则3x=7.2,x+1=2.2.答:甲水厂日供水量是2.4万m 3,乙水厂日供水量是7.2万m 3,•丙水厂日供水量是2.2万m 3.(2)设每辆A 型汽车每次运土石xt ,每辆B 型汽车每次运土石yt ,由题意得: 30206001530600x y x y +=⎧⎨+=⎩ ∴1015x y =⎧⎨=⎩答:每辆A型汽车每次运土石10t,每辆B型汽车每次运土石15t.【点评】本例系统地考查了一元一次方程和二元一次方程组这两个重要内容,在同一背景下提供不同的动作方案是近年中考应用题的发展方法.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考点名称:二元一次方程组的定义
•
(一)二元一次方程组:
含有两个未知数,并且所含未知数的项的次数都是1的方程叫做二元一次方程。
把两个含有相同未知数的一次方程联合在一起,那么这两个方程就组成了一个二元一次方程组。
二元一次方程组的解:一般的,二元一次方程组的两个二元一次方程的公共解,叫做二元一次方程组的解。
一般形式为:(其中a1,a2,b1,b2不同时为零).
•
•
(二)二元一次方程组的特点:
1.组成二元一次方程组的两个一次方程不一定都是二元一次方程,但这两个方程必须一共含
有两个未知数,如也是二元一次方程组。
2.在方程组的每个方程中,相同字母必须代表同一未知量,否则不能将两个方程合在一起。
3.二元一次方程组中的各个方程应是整式方程。
4.二元一次方程组有时也由两个以上的方程组成。
•
•
(三)二元一次方程与二元一次方程组的区别:
•
二元一次方程二元一次方程组
条件①含有两个未知数;
②含未知数的项的次数都是1;
③整式方程。
①含有两个未知数;
②含未知数的项的次数都是1;
③整式方程组(可任意话说你有两个以上的方
程)
一般
形式
ax+by=c(a、b、c都是常数,且a≠0,b≠0)
(a1,a2,b1,b2不同时为零).解的
情况
无数组解或无数组解或有唯一解或无解
解的定义适合二元一次方程的每一对未知数的值,叫
做这个二元一次方程的一组解
二元一次方程组中各个方程的公共解叫做这个
二元一次方程组的解
•
•
(四)二元一次方程组的判定:
①方程组各方程中,相同的字母必须代表同一数量,否则不能将两个方程合在一起.
②怎样检验一组数值是不是某个二元一次方程组的解,常用的方法如下:将这组数值分别代
入方程组中的每个方程,只有当这组数值满足其中的所有方程时,才能说这组数值是此方程组的解,否则,如果这组数值不满足其中任一个方程,那么它就不是此方程组的解.
•
•
(五)二元一次方程:
如果一个方程含有两个未知数,并且所含未知项都为1次方,那么这个整式方程就叫做二元一次方程,有无穷个解,若加条件限定有有限个解。
二元一次方程组,则一般有一个解,有时没有解,有时有无数个解。
二元一次方程的一般形式:ax+by+c=0其中a、b不为零。
二元一次方程的解:使二元一次方程左、右两边的值相等的一对未知数的值,叫做二元一次方程的一个解。
•
•
(六)二元一次方程的特点:
1.在方程中“元”是指未知数,“二元”是指方程中有且只
有两个未知数。
2.未知数的项的次数是1,指的是含有未知数的项(单项式)
的次数是1,如3xy的次数是2,所以方程3xy-2=0不是二元一次方程。
3.二元一次方程的左边和右边都必须是整式,例如方程
1/x-y=1的左边不是整式,所以她不是二元一次方程。
(七)二元一次方程的解的特点:
1.二元一次方程的每个解都包括两个未知数的值,是一对数
值,而不是一个数值,如x=7不是方程x+y=18的一个解,
而才是方程x+y=18的一个解。
2.二元一次方程的解是具有相关性的一对未知数的值,二者
相互制约,相互对应,不独立存在,当其中一个未知数的值确定以后,另一个未知数的值也确定了。
3.一般情况下,一个二元一次方程有无数个解,如方程
x+y=18的解还可以是
等等。
•
(八)二元一次方程的判定标准:
1.二元:有两个未知数
2.一次:未知数的系数为1
3.整式方程:分母不含未知数
•。
