三元相图练习题
三元相图练习题

三元相图练习题1一、在如图所示的相图中完成下面各个问题。
(25分)1. 直接在给定图中划分副三角形;2. 直接在给定图中用箭头标出界线上温度下降的方向及界线的性质;3. 判断化合物D 和M 的性质;4. 写出各无变量点的性质及反应式;5. G 点的析晶路程;6. 组成为H 的液相在完全平衡条件下进行冷却,写出结晶结束时各物质的百分含量(用线段比表示)。
解:1、 见图;2、 见图;3、 D ,一致熔融二元化合物,高温稳定、低温分解;M ,不一致熔融三元化合物;4、 E1,单转熔点,M C A L +↔+E2,低共熔点,M B C L ++↔E3,单转熔点,M B A L +↔+E4,过渡点,B A D L +−→←5、6、过H 点做副三角形BCM 的两条边CM 、BM 的平行线HH 1、HH 2,C%=BH 2/BC ×100%,B%=CH 1/BC ×100%,C%=H 1H 2/BC ×100%1 没有心脏我还可以思念你没有下体我还可以燃烧你 ■■■■■■■■■■■■■张为政整理■■■■■■■■■■■■■勿删■■■■■■■■■■■■■■ L ⇔ A f=2 熔体G L f=3 G[B ,(B)] 1[B,B+(A)] L ⇔A +B f=1 E 3[2,A+B+(M)] L +A ⇔B +M f=0 E 3[3,A 消失+B +M] L ⇔ B +M f=2 E 2[4, B +M +(C)] L ⇔M +C +B f=0E 2(L 消失)[G,M+B+C]二(20分)下图为CaO-A12O3-SiO2系统的富钙部分相图,对于硅酸盐水泥的生产有一定的参考价值。
试:1、画出有意义的付三角形;2、用单、双箭头表示界线的性质;3、说明F、H、K三个化合物的性质和写出各点的相平衡式;4、写出M熔体的冷却平衡结晶过程;5、为何在缓慢冷却到无变量点K(1455℃)时再要急剧冷却到室温?解:二1、画出有意义的付三角形;(如图所示); (4分)2、用单、双箭头表示界线的性质;(如图所示); (4分)3、说明F 、H 、K 三个化合物的性质和写出各点的相平衡式; (4分) F 点低共熔点,LF →C 3A+C 12A 7+C 2SH 点单转熔点,LH+CaO →C 3A+C 3SK 点单转熔点,LK+C 3S →C 3A+C 2S4、分析M #熔体的冷却平衡结晶过程并写出相变式; (4分) M 点:5、为何在缓慢冷却到无变量点K (1455℃)时再要急剧冷却到室温? (4分) 因为缓慢冷却到K 点,可以通过转熔反应L+C2S →C3S 得到尽可能多的C3S 。
三元相图五套题

试题一一. 图1是Na2O的理想晶胞结构示用意,试回答:1.晶胞分子数是多少;2.结构中何种离子做何种密堆积;何种离子填充何种空隙,所占比例是多少;3.结构中各离子的配位数为多少,写出其配位多面体;4.计算说明O2-的电价是不是饱和;5.画出Na2O结构在(001)面上的投影图。
二. 图2是高岭石(Al2O3·2SiO2·2H2O)结构示用意,试回答:1.请以结构式写法写出高岭石的化学式;2.高岭石属于哪种硅酸盐结构类型;3.分析层的构成和层的堆积方向;4.分析结构中的作用力;5.根据其结构特点推测高岭石具有什么性质。
三. 简答题:1.晶体中的结构缺陷按几何尺寸可分为哪几类?2.什么是负扩散?3.烧结初期的特征是什么?4.硅酸盐晶体的分类原则是什么?5.烧结推动力是什么?它可凭哪些方式推动物质的迁移?6.相变的含义是什么?从热力学角度来划分,相变可以分为哪几类?四. 出下列缺陷反应式:形成肖特基缺陷;形成弗仑克尔缺陷(Ag+进入间隙);掺入到Nb2O3中,请写出二个合理的方程,并判定可能成立的方程是哪一种?再写出每一个方程的固溶体的化学式。
溶入CaCl2中形成空位型固溶体五. 表面力的存在使固体表面处于高能量状态,然而,能量愈高系统愈不稳定,那么固体是通过何种方式降低其过剩的表面能以达到热力学稳定状态的。
六.粒径为1μ的球状Al2O3由过量的MgO微粒包围,观看尖晶石的形成,在恒定温度下,第一个小时有20%的Al2O3起了反映,计算完全反映的时刻:⑴用杨德方程计算;⑵用金斯特林格方程计算。
七.请分析熔体结构中负离子团的堆积方式、聚合度及对称性等与玻璃形成之关系。
八.试从结构和能量的观点解释为什么D晶界>D晶内?九.试分析二次再结晶过程对材料性能有何影响?工艺上如何防止或延缓二次再结晶的发生?十.图3是A-B-C三元系统相图,根据相图回答下列问题:1.写出点P,R,S的成分;2.设有2kgP,问需要多少何种成分的合金Z才可混熔成6kg成分为R的合金。
元相图-题库

1.匀晶转变2.包晶转变3.平衡凝固4.伪共晶:5.非平衡共晶:6.共晶转变7.偏晶转变8.共析反应9.包析转变10.熔晶转变11.合晶转变12.一次相或初生相;13.二次相或次生相14.扩散退火15.离异共晶16.钢17.铸铁18.奥氏体:19.莱氏体:20.珠光体:21.三次渗碳体22.调幅分解23.成分过冷24.枝晶偏析25.正偏析26.宏观偏析概念辨析题1、共晶转变与共析转变2、奥氏体与铁素体的异同点:3、二次渗碳体与共析渗碳体的异同点4、稳定化合物与不稳定化合物5、均匀形核与非均匀形核6、平衡凝固与非平衡凝固7、光滑界面与粗糙界面8、钢与铸铁9、热过冷与成分过冷10、一次相与二次相11、伪共晶与离异共晶12、正偏析与反偏析相图题一、相图题(20 分)1 •画岀Fe-Fe3C相图,填岀各区的组织组成物。
(6分)2.分析含碳%的铁碳合金的平衡结晶过程,画出其冷却曲线和室温时的显微组织示意图。
(8分)3 •用杠杆定律计算该合金在室温时的组织组成物和相组成物的量。
(6分)Fe-Fe3C 相图为二、相图题(22 分)1_画出F e-Fe3C相图,填出各区域的组织组成物。
(6分)2 .分析含碳%的铁碳合金的平衡结晶过程,画岀其冷却曲线和室温时的显微组织示意图。
(8 分)3.用杠杆定律计算该合金在室温时的组织组成物和相组成物的量。
(8分)三、 相图题(25分)1. 画岀Fe-F^C 相图,标岀重要点的温度与含碳量,填岀各区域的组织组成物。
2•分析含碳%的铁碳合金的平衡凝固过程,画岀其冷却曲线和室温时的显微组织示意图。
分)3 .用杠杆定律计算该合金在室温时的组织组成物和相组成物的量。
(8分)四、 相图题1、Fe — Fe s C 相图,结晶过程分析及计算3) 分析含碳〜%的铁碳合金的结晶过程。
4) 计算室温下过共析钢(含碳量为 X )的组织组成物的相对量。
5) 分析共析钢的结晶过程,并画出结晶示意图。
三组分相图练习及答案

一、选择题1、某一水溶液中有 n 种溶质,其摩尔分数分别是 x 1,x 2,...,x n ,若使用只允许水出入的半透膜将此溶液与纯水分开,当达到渗透平衡时水面上的外压为 p w ,溶液面上外压为 p s ,则该体系的自由度数为: ( C ) (A) f =n (B) f =n +1 (C) f =n +2 (D) f =n +3S = n + 1 , R = 0 , R ' = 0 又C = n + 1,Φ = 2 f = C + 3 -Φ = n + 1 + 3 - 2 = n + 22、 一体系如下图所示,其中半透膜 aa '只允许 O 2(g ) 通过,请选择正确的答案。
(1) 体系的组分数为: ( B )(A) 2 (B) 3 (C) 4 (D) 1(2) 体系的相数为: ( B )(A) 3相 (B) 4相 (C) 5相(3) 体系的自由度数为: ( B )(A) 1 (B) 2 (C) 3 (D) 4f = C + 3 - Φ = 3 + 3 - 4 = 23、对于渗透平衡体系,相律的形式为: ( A )(A)f C =-+Φ3 (B)f C =-+Φ2(C)f C =-+Φ1 (D)f C =-+Φ0因为有两个平衡压力:p (纯溶剂)和p (溶液),再加上T ,所以最后应加3。
4、 当用三角形坐标来表示三组分物系时,若某物系其组成在平行于底边BC 的直线上变动时,则该物系的特点是: ( B )(A) B 的百分含量不变 (B) A 的百分含量不变(C) C 的百分含量不变 (D) B 和C 的百分含量之比不变5、 如图所示,当物系点在通过A 点的一条直线上变动时,则此物系的特点是: ( A )(A) B 和C 的百分含量之比不变 (B) A 的百分含量不变(C) B 的百分含量不变 (D) C 的百分含量不变6、H 2O -NaCl -Na 2SO 4的三元系中,Na 2SO 4和H 2O 能形成水合物Na 2SO 4·10H 2O (D),在DBC 区中存在的是: ( B )(A) 水合物D 和溶液(B) 水合物D 和纯Na 2SO 4及纯NaCl 三相共存(C) 水合物D ,NaCl 和组成为F 的溶液(D) 纯NaCl ,纯Na 2SO 4和水溶液7、H 2O -KNO 3-NaNO 3的相图如下,则BEC 相区内是: ( D )(A) 纯NaNO 3和其饱和溶液(B) 纯KNO 3和其饱和溶液(C) 含有NaNO 3和KNO 3的不饱和溶液和溶液的单相区(D) KNO 3,NaNO 3和组成为E 的饱和溶液三相共存液氦(Ⅰ)、液氦(Ⅱ)是属于二级相变,对这类相变特征的描述, ( D )错误(A) 无相变热 (B) 相变时无熵变化(C) 相变时两相的密度相同 (D) 相变时两相的热容相同8、二级相变符合的爱伦菲斯方程式是: ( B )(A ))/(d /d α∆∆=TV C T p V (B ))/(d /d α∆∆=TV C T p p(C )p p /ln(d )/(d /)α∆∆=TV C T V (D )p p /ln(d )/(d /)α∆∆=TV C T p9、二级相变服从的基本方程为: ( C )(A )克拉贝龙方程 (B )克拉贝龙—克劳修斯方程(C )爱伦菲斯方程 (D )以上均可10、对二级相变而言,则 ( D )(A )∆相变H =0,∆相变V <0 (B )∆相变H <0,∆相变V =0(C )∆相变H <0,∆相变V <0 (D )∆相变H =0,∆相变V =0二、填空题1、对三组分体系来说,体系最多可能有 4 个自由度,它们是:温度、压力和两个浓度项2、 二级相变符合爱伦菲斯方程:d p /d T =ΔC p /(TV Δα) [α=(1/V )(∂V/∂T ), x =-(1/V )(∂V /∂p )T ]3、二级相变的特点是: , , ,和 。
材料科学基础下学期选择与判断(带答案)

第七章三元相图一、判断题1.在热力学平衡条件下,三元系统最多4相平衡共存。
√2.三元相图的垂直截面的两相区内杠杆定律不适用。
√3.三元相图的垂直截面可确定合金相成分和量的变化。
×4.在三元相图的三相共存区,系统的自由度数为0。
×5.在三元相图的四相共存区,系统的自由度数为0。
√6.三元相图的垂直截面可应用杠杆定律确定平衡相的成分和相对量。
×7.三元相图的水平截面虽然可以确定合金的相组成,但不能确定平衡相的成分和相对量。
×8.三元相图的投影图可分析合金的结晶过程,并确定合金相与组织的相对量。
√二、选择题1.在三元系相图中,三相区的等温截面都是一个连接的三角形,其顶点触及_A__。
A 单相区B两相区C三相区D四相区2.根据三元相图的垂直截面图。
可以_B_ __。
A分析相成分的变化规律B分析合金的凝固过程C用杠杆法则计算各相的相对量D用重心法则计算各相的相对量。
3.在三元相图的两相共存区,系统的自由度数为__B_。
A 1B 2C 0D 34.在三元相图的三相共存区,系统的自由度数为_A_。
A 1B 2C 0D 35.三元系最多存在___C___相平衡。
A. 2B. 3C. 4D. 5第八章铁碳合金与铁碳合金相图一、判断题1.在Fe-Fe3C系合金中,只有过共析钢的平衡结晶组织中才有二次渗碳体存在。
×2.凡是碳钢的平衡结晶过程都具有共析转变,而没有共晶转变;相反,对于铸铁则只有共晶转变而没有共析转变。
×3.无论何种成分的碳钢,随着碳含量的增加,组织中铁素体相对量减少,而珠光体相对量增加。
×4.在退火状态下,随含碳量增加,钢的强度总是提高的。
×5.在退火状态下,随含碳量增加,钢的硬度总是提高的。
√6.在优质钢中,S、P元素总是有害元素。
(√)7.亚共析钢和过共析钢室温相组成物都是α和Fe3C。
√8.P元素将造成材料冷脆,S元素将导致热脆。
材料科学基础相图分析题

相图分析(26分)1、判读如下A-B-C三元相图(1)指出如下三元体系中化合物D和F的性质。
(2分)(2)划分副三角形并判定各界线上的温降方向(4分)(3)判定各界线的性质。
(3分)(4)判定无变量点性质,并写出液相组成在无变点处的反应式。
(4分)(5)分析M点熔体的析晶过程,并计算液相组成刚到析晶结束点的固液相的比例及固相中各物质的比例。
(7分)(6)指出N点组成的A、B、C混合物在平衡加热时最先在哪一点的温度出现液相?(2分)(7) 画出A-B二元系统示意相图,并标出各区域的平衡相组成。
(4分)2、判读如下三元相图(共26分)(1)指出如下三元体系中化合物D1、D2和D3的性质。
(3分)(2)划分副三角形。
(2分)(3)判定各界线上的温降方向及界线的性质(转熔线上用双箭头表示)。
(4分)(4)判定无变量点性质,并写出冷却时无变点处的平衡反应式。
(5分)(5)分析M点熔体的析晶过程,并计算液相组成刚到析晶结束点的固液相的比例,固相中各固相的比例。
(6分)(6)说明组成为N点A-B-C混合物在平衡加热时最先在哪一点的温度出现液相?(1分)(7) 画出A-B二元系统示意相图,并标出各区域的平衡相组成。
(3分)3、判读如下三元相图(24分)(1)指出如下三元体系中化合物D的性质。
(2分)(2)划分副三角形及判定各界线上的温降方向。
(4分)(3) 判定各界线的性质。
(2分)(4) 判定无变量点性质,并写出液相组成在无变点处的反应式。
(3分)(5) 分析M点熔体的析晶过程,并计算液相组成刚到析晶结束点的固液相的比例,固相中各固相的比例。
(6分)(6) 说明组成为N点A-B-C混合物在平衡加热时最先在哪一点的温度出现液相?(2分)(7) 画出A-B二元系统示意相图,并标出各区域的平衡相组成。
(5分)4、下图是A-B-C三元系统相图,根据相图回答下列问题:(24分)(1)指出如下三元体系中化合物S的性质。
(2分)(2)划分副三角形及判定各界线上的温降方向。
练习题(三元相图)
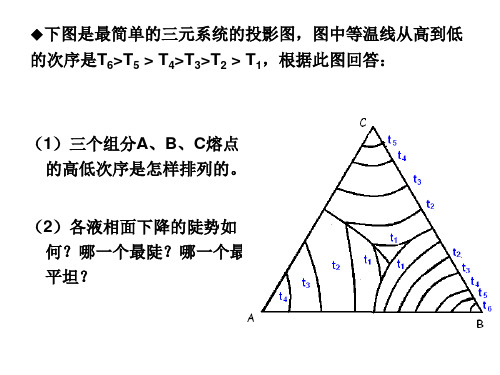
(4) 写出组成点G在完全 平衡条件下的冷却结晶过程。
(5) 画出AB边上的二元系统 相图。
(1)在图上划分副三角形,用箭头表示各条界线上温度下 降方向及界线的性质; (2) 判断化合物D、M的性质;
(3) 写出各三元无变 量点的性质及其对应的 平衡关系式; (4) 写出组成点G在完 全平衡条件下的冷却结 晶过程。
(2)组成点为1、2、3及 4各熔体的冷却结晶过程;
(3)分别将组成为5和组 成为6 的物系,在平衡 的条件下加热到完全熔 融,说明其固液相组成 的变化途径。
◆根据下图回答下列问题:
(1)说明化合物S1、S2的性质; (2)在图中划分分三元系统及用箭头指示出各界线的温度 下降方向及性质。
(3)指出各无变量点的 性质并写出各点的平衡 关系。
(1) 判断化合物N(AmBn) 的性质;
(2) 标出边界曲线的温降 方向及性质; (3) 指出无变量点的性质, 并说明在无变量点温度下
系统所发生的相变化
(4) 分析点1,2的结晶路 程。
◆如图是A-B-C三元系统相图,根据相图回答下列问题:
(1)在图上划分副三角形,用箭头表示各条界线上温度 下降方向及界线的性质;
降方向;
(3)可划分出几个副三角形? 请画出来;
(4)判断各无变量点的性质, 并写出平衡关系式。
◆指出如下相图中的错误,并说明理由。
◆ A-B-C三元相图如图所示。
(1) 判断化合物N(AmBn) 的性质;
(2) 标出边界曲线的温降 方向及性质; (3) 指出无变量点的性质, 并说明在无变量点温度下 系统所发生的相变化 (4) 分析点1,2的结晶路 程。
第二章 相图练习题

第二章 相图一、名词解释:三元系相图中的液相面,三元系相图中的等温线,相图中的无变量点,三元系相图中的初晶面二、其它1、相律是指______________________。
冶金炉渣三元系的相律表达式为______________________。
2、表示三元系的组成用浓度三角形,浓度三角形内的等含量规则是指_____________________________。
3、三元系的组成用浓度三角形来表示,浓度三角形中的等比规则是指______________________________。
在冶金渣三元系中,若自由度为零,则一定是_____相共存。
4.三元系相图中的等温线表示______________________________,相图中等温线之间相距越近的区域,则说明该区间炉渣组成的改变对_______影响大。
5.三元相图中三元共晶点有________相平衡共存,自由度为___ 。
6.在冶金三元系渣相图中,自由度为零时,相数为_____;四相平衡的三元共晶点处的自由度为_____,其析晶反应可以表示为_________。
7.通常对冶金炉渣,相律的表达式为_________,由此推导出三元冶金炉渣系中最多可能存在的相数为_________,此时的自由度为___。
8、如图,回答下列问题:(1)写出P 点的结晶反应式。
(2)指出自由度为零的点。
(3)写出E e 3线上发生的结晶反应式。
8、如图1所示,回答下列问题:(1)指出化合物D 的稳定性。
(2)相图中三角形ADB 区(即分三角形ADB )可以似为哪一类基本相图?(3)写出1E 点、23e E 线、51e E 线的析晶反应式,并指出其中自由度为零的点或线9.如下所示的相图。
回答下列问题:(1)物系点a,从液体降温过程中首先析出的物质是什么?(2)写出P点的相平衡关系。
(3)P点和E点比较,哪一点的熔点低?(4)绘出b点的步冷曲线。
10.对冶金熔体三元系相图,回答下列问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三元相图练习题1
一、
在如图所示的相图中完成下面各个问题。
(25分)
1. 直接在给定图中划分副三角形;
2. 直接在给定图中用箭头标出界线上温
度下降的方向及界线的性质;
3. 判断化合物D 和M 的性质;
4. 写出各无变量点的性质及反应式;
5. G 点的析晶路程;
6. 组成为H 的液相在完全平衡条件下进
行冷却,写出结晶结束时各物质的百
分含量(用线段比表示)。
解:
1、 见图;
2、 见图;
3、 D ,一致熔融二元化合物,高温稳定、低温分解;
M ,不一致熔融三元化合物;
4、 E1,单转熔点,M C A L +↔+
E2,低共熔点,M B C L ++↔
E3,单转熔点,M B A L +↔+
E4,过渡点,B A D L +−→←
5、
6、过H 点做副三角形BCM 的两条边CM 、BM 的平行线HH 1、HH 2,C%=BH 2/BC ×100%,B%=CH 1/BC ×100%,C%=H 1H 2/BC ×100%
1 没有心脏我还可以思念你没有下体我还可以燃烧你 ■■■■■■■■■■■■■张为政整理■■■■■■■■■■■■■勿删■■■■■■■■■■■■■■ L ⇔ A f=
2 熔体G L f=
3 G[B ,(B)] 1[B,B+(A)] L ⇔A +B f=1 E 3[2,A+B+(M)] L +A ⇔B +M f=0 E 3[3,A 消失+B +M] L ⇔ B +M f=2 E 2[4, B +M +(C)] L ⇔M +C +B f=0
E 2(L 消失)[G,M+B+C]
二(20分)下图为CaO-A12O3-SiO2系统的富钙部分相图,对于硅酸盐水泥的生产有一定的参考价值。
试:
1、画出有意义的付三角形;
2、用单、双箭头表示界线的性质;
3、说明F、H、K三个化合物的性质和写出各点的相平衡式;
4、写出M熔体的冷却平衡结晶过程;
5、为何在缓慢冷却到无变量点K(1455℃)时再要急剧冷却到室温?
解:
二
1、画出有意义的付三角形;(如图所示); (4分)
2、用单、双箭头表示界线的性质;(如图所示); (4分)
3、说明F 、H 、K 三个化合物的性质和写出各点的相平衡式; (4分) F 点低共熔点,LF →C 3A+C 12A 7+C 2S
H 点单转熔点,LH+CaO →C 3A+C 3S
K 点单转熔点,LK+C 3S →C 3A+C 2S
4、分析M #熔体的冷却平衡结晶过程并写出相变式; (4分) M 点:
5、为何在缓慢冷却到无变量点K (1455℃)时再要急剧冷却到室温? (4分) 因为缓慢冷却到K 点,可以通过转熔反应L+C2S →C3S 得到尽可能多的C3S 。
到达K 点后,急剧冷却到室温,可以(1)防止C3S 含量降低,因为K 点的转熔反应LK+C3S →C2S+C3A ;(2)使C2S 生成水硬性的β-C2S ,而不是非水硬性的γ-C2S ;(3)液相成为玻璃相,可以提高熟料的易磨性。
L ⇔ C 2S p=2 f=2 熔体M L p=1 f=3 M[D ,(C 2S)] a[b,C 2S +(C 3S)] J[b /, C 2S +C 3S] k[d, C 2S+C 3S +(C 3A)] L +C 3S ⇔C 2S+C 3A p=4 f=0 K(液相消失)[M, C 3S +C 2S+C 3A]
L ⇔ C 2S +C 3S p=3 f=1 L +C 2S ⇔C 3S
p=3 f=1
三、图6-11是三元相图A-B-C 的A-B-S 初晶区部分,试分析M 点析晶路程,并画出该相图内可能发出穿越相区的组成点范围(用阴影线表示。
)
解:M 点落在△SCB 析晶应在△SCB 的无变量点E 1点结束。
晶体析晶路程如下: 液相:
)(211A C B S L E R R m M C S L S
L S A L S B A L B A L L ++→−−−−→−−−−→−−−−−→−−−−−−→−−−−−→−−−−→−+→→→+→+++→→
固相:M n s i h A −−−→−−−→−−−→−→−−→−+++++B C S C S S
A B A M 点的析晶达到R 点后,析晶达到由PE 1和PE 2两个温度下降界线交汇点。
在这个析晶三叉路上,按习惯析晶在E 1点结束,此时析晶向RW 1界线移动应该是合理的。
但在这交叉路口上,准确判断析晶趋向应该由固相内二个晶相的相对比例而定。
如析晶达R 点发生相变过程是L+A+B →S (F =0)四相共存。
析晶要继续进行必须消失一相。
固相中A/B 的相对比例为Bh/Ah =A/B ,由于Bh>Ah ,因此晶相相量是A>B 。
必然是B 晶相首先回吸完。
所以析晶是沿RE 2线继续下去,而不走RE 1线。
从图中也可看到,刚达R 点时,固相组成在h 点,根据液相组成(原始组成)固相组成永远为一条围绕原始组成点M 为支点的杠杆这一个规律,当液相达到R 点,RMh 这条界线交于△ASB 的SA 边上的i 点,这也证明此时液相中B 已回吸完,而晶相A 还有多余,而液相组成中对A 饱和。
因此析晶沿RE 2继续 下去。
图6-11 例6-14附图
图6-11中∆SRN 为该相图可能发生穿越相区的组成点范围。
四、(20分)分析下列相图
1、划分副三角形;
2、用箭头标出界线上温度下降的方向及界线的性质;
3、判断化合物S 的性质;
4、写出各无变量点的性质及反应式;
5、分析点1、2熔体的析晶路程。
( 注:S 、1、E 3在一条直线上)
解: 1、如图所示;
2、温度下降方向如图所示;界线性质:单箭头所示为共熔线,双箭头所示为转熔线。
3、不一致熔融三元化合物;
4、E1:三元低共熔点,L →A+S+C ;
E2:三元低共熔点,L →C+S+B ;
E3:双转熔点,L+A+B →S ;
5、
d L ⇔ A f=2
熔体1 L f=3 1[A ,(A)] C[A,A+(B)] L ⇔A +B f=1 E 3[a,A+B+(S)] L +A +B ⇔S f=0 E 3[s,(A+B)消失+S] L ⇔ S f=2 d[S,S+(B)] L ⇔S +B f=1 E 2[e,S+B+(C)] L ⇔S +C +B f=0
E 2(L 消失)[1,S+B+C] a b g L ⇔ B f=2 熔体2 L f=3 2[B ,(B)] f[B,B+(A)] L ⇔A +B f=1 E 3[g,A+B+(S)] L +A +B ⇔S f=0 E 3[h,(A 消失)+B +S]
L+B ⇔ S f=2 i[I,S+B] L ⇔S +B f=1 E 2[k,S+B+(C)] L ⇔S +A +B f=0 E 2(L 消失)[2,S+B+C]。
