母子型相似三角形模型典型
母子型相似三角形模型 典型

母子型相似三角形【知识要点】一、直角三角形相似1、直角三角形被斜边上的高分成两个直角三角形和原三角形相似。
2、如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。
基本图形(母子三角形)举例:1、条件:如图,已知△ABC 是直角三角形,CD 为斜边AB 上的高. 结论:(1)△ACD ∽△CBD ,△BDC ∽△BCA ,△CDA ∽△BCA(2)△ACD ∽△CBD 中,2CD AD BD = △BDC ∽△BCA 中,2BC BD AB =△CDA ∽△BCA 中,2AC AD AB =2、条件:如图,已知∠ACD=∠ABC结论:△ACD ∽△ABC 中,2AC AD AB =【例题解析】类型一:三角形中的母子型【例1】1.如图,ΔABC 中,∠A=∠DBC,BC=,S ΔBCD ∶S ΔABC=2∶3,则CD=______.【练】如图,D 是 △ABC 的边AB 上一点,连结CD.若AD= 2,BD = 4, ∠ACD =∠B 求AC 的长.【例2】如图,在△ABC 中,AD 为∠A 的平分线,AD 的垂直平分线交AD 于E ,交BC 的延长线于F ,求证:FC FB FD ⋅=2DCBA【练】已知CD 是ABC ∆的高,,DE CA DF CB ⊥⊥,如图3-1,求证:CEF CBA ∆∆∽类型二:直角三角形中的母子型【例1】.如图,在△ABC 中,AD 、BE 分别为BC 、AC 边上的高,过D 作AB 的垂线交AB 于F ,交BE 于G ,交AC 的延长于H ,求证:2DF FG FH =∙【练】如图5,Rt ΔABC 中,∠ACB=90°,CD ⊥AB,AC=8,BC=6,则AD=____,CD=_______.【例2】如图1,∠ADC=∠ACB=90°,∠1=∠B,AC=5,AB=6,则AD=______.【练】如图,CD 是 Rt △ABC 斜边上的高.若AD= 2,BD = 4, 求CD 的长.类型三:四边形中的母子型【例1】1.如图,矩形ABCD 中,BH ⊥AC 于H ,交CD 于G ,求证:2BC CG CD =∙。
相似三角形的常见模型(地总结)
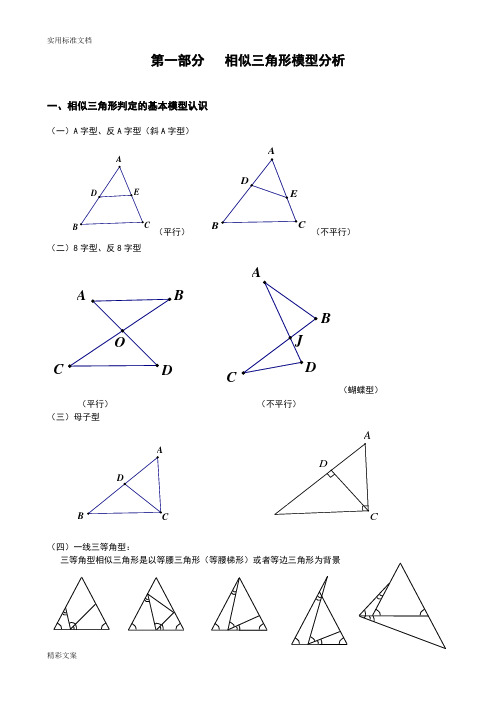
第一部分 相似三角形模型分析一、相似三角形判定的基本模型认识(一)A 字型、反A 字型(斜A 字型)ABCDE(平行)CBA DE(不平行)(二)8字型、反8字型J OADBCAB CD(蝴蝶型)(平行) (不平行) (三)母子型ABCDCAD(四)一线三等角型:三等角型相似三角形是以等腰三角形(等腰梯形)或者等边三角形为背景(五)一线三直角型:(六)双垂型:CAD二、相似三角形判定的变化模型旋转型:由A 字型旋转得到。
8字型拓展CB EDA共享性GABCEF一线三等角的变形一线三直角的变形第二部分 相似三角形典型例题讲解母子型相似三角形例1:如图,梯形ABCD 中,AD ∥BC ,对角线AC 、BD 交于点O ,BE ∥CD 交CA 延长线于E . 求证:OE OA OC ⋅=2.例2:已知:如图,△ABC 中,点E 在中线AD 上, ABC DEB ∠=∠.求证:(1)DA DE DB ⋅=2; (2)DAC DCE ∠=∠.例3:已知:如图,等腰△ABC 中,AB =AC ,AD ⊥BC 于D ,CG ∥AB ,BG 分别交AD 、AC 于E 、F . 求证:EG EF BE ⋅=2.相关练习:1、如图,已知AD 为△ABC 的角平分线,EF 为AD 的垂直平分线.求证:FC FB FD ⋅=2.AC D E B2、已知:AD 是Rt △ABC 中∠A 的平分线,∠C=90°,EF 是AD 的垂直平分线交AD 于M ,EF 、BC 的延长线交于一点N 。
求证:(1)△AME ∽△NMD; (2)ND 2=NC ·NB3、已知:如图,在△ABC 中,∠ACB=90°,CD ⊥AB 于D ,E 是AC 上一点,CF ⊥BE 于F 。
求证:EB ·DF=AE ·DB4.在∆ABC 中,AB=AC ,高AD 与BE 交于H ,EF BC ⊥,垂足为F ,延长AD 到G ,使DG=EF ,M 是AH 的中点。
2023年中考数学常见几何模型(全国通用版):相似模型(解析版)

专题06相似模型-母子型(共角共边模型)和A (X )字型相似三角形是初中几何中的重要的内容,常常与其它知识点结合以综合题的形式呈现,其变化很多,是中考的常考题型。
如果大家平时注重解题方法,熟练掌握基本解题模型,再遇到相似三角形的问题就信心更足了.本专题重点讲解相似三角形的六大基本模型.模型1.“母子”模型(共边角模型)【模型解读与图示】“母子”模型的图形(通常有一个公共顶点和另外一个不是公共的顶点,由于小三角形寓于大三角形中,恰似子依母怀),也是有一个“公共角”,再有一个角相等或夹这个公共角的两边对应成比例就可以判定这两个三角形相似.“双垂线”型是其特例。
“母子”模型(斜射影)双垂直(射影定理)“母子型”的变形斜射影结论:△ABD ∽△ACB ,AB 2=AD ·AC .双垂直结论:①△ABD ∽△ACB ,AB 2=AD ·AC ;②△ADC ∽△ACB ,AC 2=AD ·AB ;③△CDB ∽△ACB ,CB 2=BD ·BA .1.(2022·贵州贵阳·中考真题)如图,在ABC 中,D 是AB 边上的点,B ACD ,:1:2AC AB ,则ADC 与ACB △的周长比是()A .B .1:2C .1:3D .1:4【答案】B 【分析】先证明△ACD ∽△ABC ,即有12AC AD CD AB AC BC ,则可得12AC AD CD AB AC BC ,问题得解.【详解】∵∠B =∠ACD ,∠A =∠A ,∴△ACD ∽△ABC ,∴AC AD CD AB AC BC,∵12AC AB ,∴12AC AD CD AB AC BC ,∴12AC AD CD AC AD CD AB AC BC AB AC BC ,∴△ADC 与△ACB 的周长比1:2,故选:B .【点睛】本题主要考查了相似三角形的判定与性质,证明△ACD ∽△ABC 是解答本题的关键.2.(2022·陕西汉中·九年级期末)如图,CD 是等腰直角ABC 斜边AB 的中线,以点D 为顶点的EDF 绕点D 旋转,角的两边分别与AC 、BC 的延长线相交,交点分别为点E 、F ,DF 与AE 交于点M ,DE 与BC 交于点N ,且45EDF .(1)如图1,若CE CF ,求证:DE DF ;(2)如图2,若CE CF ,求证:2CD CE CF ;(3)如图2,过D 作DG BC 于点G ,若2CD,CF DN的长.∵DG ⊥BC ,∠ACB =90°,∴∠DGN =∠ECN =90°,∠当CD =2,CF =2时,由CD 在Rt △DCG 中,CG DG ∵∠ECN =∠DGN ,∠ENC 3.(2022·浙江绍兴·九年级期末)如果两个相似三角形的对应边存在2倍关系,则称这两个相似三角形互为母子三角形.(1)如果DEF 与ABC 互为母子三角形,则DE AB 的值可能为()A .2B .12C .2或12(2)已知:如图1,ABC 中,AD 是BAC 的角平分线,2,AB AD ADE B .求证:ABD △与ADE 互为母子三角形.(3)如图2,ABC 中,AD 是中线,过射线CA 上点E 作//EG BC ,交射线DA 于点G ,连结BE ,射线BE 与射线DA 交于点F ,若AGE 与ADC 互为母子三角形.求AG GF 的值.AG DG ,4.(2022.浙江中考模拟)如图,在 ABC中,∠ACB=90°,CD⊥AB.(1)图1中共有对相似三角形,写出来分别为(不需证明):(2)已知AB=5,AC=4,请你求出CD的长:(3)在(2)的情况下,如果以AB为x轴,CD为y轴,点D为坐标原点O,建立直角坐标系(如图2),若点P从C点出发,以每秒1个单位的速度沿线段CB运动,点Q出B点出发,以每秒1个单位的速度沿线段BA运动,其中一点最先到达线段的端点时,两点即刻同时停止运动;设运动时间为t秒是否存在点P,使以点B、P、Q为顶点的三角形与△ABC相似?若存在,请求出点P的坐标;若不存在,请说明理由.【答案】(1)3, ABC∽ ACD, ABC∽ CBD, ACD∽ CBD;(2)125;(3)存在,(2740,32),(98,910)【分析】(1)根据两角对应相等的两三角形相似即可得到3对相似三角形,分别为:△ABC∽△ACD,△ABC∽△CBD,△ACD∽△CBD.(2)先在△ABC中由勾股定理求出BC的长,再根据△ABC的面积不变得到12AB•CD=12AC•BC,即可求出CD的长.(3)由于∠B公共,所以以点B、P、Q为顶点的三角形与△ABC相似时,分两种情况进行讨论:①△PQB∽△ACB;②△QPB∽△ACB.【详解】解:(1)图1中共有3对相似三角形,分别为:△ABC∽△ACD,△ABC∽△CBD,△ACD∽△CBD.证明:∵CD⊥AB,∴∠ADC=∠ACB=90°,又∵∠A=∠A,∴△ADC∽△ACB同理可证:△ABC∽△CBD,△ACD∽△CBD.故答案为:3;△ABC∽△ACD,△ABC∽△CBD,△ACD∽△CBD.(2)如图2中,在△ABC中,∵∠ACB=90°,AB=5,AC=4,∴BC=3.∵△ABC 的面积=12AB•CD =12AC•BC ,∴CD =AC BC AB =125.(3)存在点P ,使以点B 、P 、Q 为顶点的三角形与△ABC 相似,理由如下:在△BOC 中,∵∠COB =90°,BC =3,OC =125,∴OB =95.分两种情况:①当∠BQP =90°时,如图2①,此时△PQB ∽△ACB,∴BP AB =BQ BC ,∴353t t ,解得t =98,即98BQ CP ,∴915388BP BC CP .在△BPQ中,由勾股定理,得32PQ ,∴点P 的坐标为273(,)402;②当∠BPQ =90°时,如图2②,此时△QPB ∽△ACB ,∴BP BQ BC AB ,∴335t t ,解得t =158,即15159,3888BQ cP BP BC CP ,过点P 作PE ⊥x 轴于点E .∵△QPB ∽△ACB ,∴PE BQ CO AB ,即1581255PE ,∴PE =910.在△BPE中,2740BE ,∴92795408OE OB BE ,∴点P 的坐标为99(,810,综上可得,点P 的坐标为(2740,32);(98,910).【点睛】本题属于相似形综合题,考查了相似三角形的判定与性质,勾股定理等知识,解题的关键是学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题,属于中考常考题型.模型2.“A ”字模型【模型解读与图示】“A ”字模型图形(通常只有一个公共顶点)的两个三角形有一个“公共角”(是对应角),再有一个角相等或夹这个公共角的两边对应成比例,就可以判定这两个三角形相似.1.(2022·湖南怀化·中考真题)如图,△ABC 中,点D 、E 分别是AB 、AC 的中点,若S △ADE =2,则S △ABC =_____.【答案】8【分析】根据三角形中位线定理求得DE ∥BC ,12DE BC ,从而求得△ADE ∽△ABC ,然后利用相似三角形的性质求解.【详解】解:∵D 、E 分别是AB 、AC 的中点,则DE 为中位线,所以DE ∥BC ,12DE BC 所以△ADE ∽△ABC ∴21()4ADE ABCS DE S BC ∵S △ADE =2,∴S △ABC =8故答案为:8.【点睛】本题考查中位线及平行线性质,本题难度较低,主要考查学生对三角形中位线及平行线性质等知识点的掌握.2.(2022·浙江杭州·中考真题)如图,在 ABC 中,点D ,E ,F 分别在边AB ,AC ,BC 上,连接DE ,EF ,已知四边形BFED 是平行四边形,DE 1BC 4.(1)若8AB ,求线段AD 的长.(2)若ADE 的面积为1,求平行四边形BFED的面积.【答案】(1)2(2)6【分析】(1)利用平行四边形对边平行证明ADE ABC △△∽,得到DE AD BC AB即可求出;(2)利用平行条件证明ADE EFC ∽ ,分别求出ADE EFC 与、ADE ABC 与的相似比,通过相似三角形的面积比等于相似比的平方分别求出EFC S V 、ABC S ,最后通过BFED ABC EFC ADE S S S S 求出.(1)∵四边形BFED 是平行四边形,∴∥DE BC ,∴ADE ABC △△∽,∴DE AD BC AB ,∵DE 1BC 4 ,∴AD 1AB 4,∴118244AD AB ;(2)∵四边形BFED 是平行四边形,∴∥DE BC ,EF AB ,DE =BF ,∴,AED ECF EAD CEF ,∴ADE EFC ∽ ∴2ADE EFC S DE S FC,∵DE 1BC 4,DE =BF ,∴43FC BC DE DE DE DE ,∴133DE DE FC DE ,∴221139ADE EFC S DE S FC ,∵ADE ABC △△∽,DE 1BC 4 ,∴2211416ADE ABC S DE S BC ,∵1ADE S △,∴9,16EFC ABC S S ,∴16916BFED ABC EFC ADE S S S S .【点睛】本题考查了相似三角形,熟练掌握相似三角形的面积比等于相似比的平方、灵活运用平行条件证明三角形相似并求出相似比是解题关键.3.(2022·浙江宁波·中考真题)(1)如图1,在ABC 中,D ,E ,F 分别为,,AB AC BC 上的点,,,DE BC BF CF AF ∥交DE 于点G ,求证:DG EG .(2)如图2,在(1)的条件下,连接,CD CG .若,6,3 CG DE CD AE ,求DE BC的值.(3)如图3,在ABCD 中,45, ADC AC 与BD 交于点O ,E 为AO 上一点,EG BD ∥交AD 于点G , EF EG 交BC 于点F .若40, EGF FG 平分,10 EFC FG ,求BF 的长.【答案】(1)证明见详解(2)13(3)5【分析】(1)利用∥DE BC ,证明,ADG ABF AEG ACF △△△△ ,利用相似比即可证明此问;(2)由(1)得DG EG ,CG DE ,得出DCE 是等腰三角形,利用三角形相似即可求出DE BC 的值;(3)遵循第(1)、(2)小问的思路,延长GE 交AB 于点M ,连接FM ,作MN BC ,垂足为N .构造出等腰三角形、含30°、45°角的特殊直角三角形,求出BN 、FN 的值,即可得出BF 的长.(1)解:∵DE BC ∥,∴,ADG ABF AEG ACF △△△△ ,∴, DG AG EG AG BF AF CF AF ,∴DG EG BF CF.∵BF CF ,∴DG EG .(2)解:由(1)得DG EG ,∵CG DE ,∴6CE CD .∵3AE ,∴9AC AE CE .∵DE BC ∥,∴ADE ABC .∴13DE AE BC AC .(3)解:如图,延长GE 交AB 于点M ,连接FM ,作MN BC ,垂足为N .在ABCD 中,,45 BO DO ABC ADC .∵EG BD ∥,∴由(1)得 ME GE ,∵ EF EG ,∴10 FM FG ,∴ EFM EFG .∵40 EGF ,∴40EMF ,∴50EFG .∵FG 平分EFC ,∴50 EFG CFG ,∴18030 BFM EFM EFG CFG .∴.在Rt FMN 中,sin 305,cos30 MN FM FN FM ∵45, MBN MN BN ,∴5 BN MN ,∴5 BF BN FN 【点睛】本题考查了相似三角形的性质及判定、等腰三角形的性质及判定、解特殊的直角三角形等知识,遵循构第(1)、(2)小问的思路,构造出等腰三角形和特殊的直角三角形是解决本题的关键.4.(2022·辽宁·中考真题)如图,在ABC 中,4AB AC BC ,D ,E ,F 分别为,,AC AB BC 的中点,连接,DE DF .(1)如图1,求证:52DF DE ;(2)如图2,将EDF 绕点D 顺时针旋转一定角度,得到PDQ ,当射线DP 交AB 于点G ,射线DQ 交BC 于点N 时,连接FE 并延长交射线DP 于点M ,判断FN 与EM 的数量关系,并说明理由;(3)如图3,在(2)的条件下,当DP AB 时,求DN 的长.【答案】(1)见解析(2)2FN ,理由见解析(3)103【分析】(1)连接AF ,可得AF BC ,根据直角三角形斜边上的中线等于斜边的一半可得12DF AC根据中位线定理可得122DE BC ,即可得证;(2)证明DNF DME ∽,根据(1)的结论即可得FN;(3)连接AF ,过点C 作CH AB 于H ,证明AGD AHC ∽,可得125GD HC ,勾股定理求得,GE AG ,根据3tan 4AG ADG GD ,EMG ADG ,可得3tan 4EG EMG MG ,进而求得MG ,根据MD MG GD求得MD ,根据(2)的结论2DN DM,即可求解.(1)证明:如图,连接AF ,∵4AB AC BC ,D ,E ,F 分别为,,AC AB BC 的中点,122DE BC ,AF BC , 12DF AC , DF ,(2)2FN,理由如下,连接AF ,如图,∵4AB AC BC ,D ,E ,F 分别为,,AC AB BC 的中点,1,2EF AC CD EF DC∥, 四边形CDEF 是平行四边形,DEF C ,∵12DF AC DC ,DFC C ,DEF DFC ,180180DEF DFC , DEM DFN ,∵将EDF 绕点D 顺时针旋转一定角度,得到PDQ , EDF PDQ ,FDN NDE EDM NDE ∵,FDN EDM ,DNF DME ∽,NF DF EM DE,FN ,(3)如图,连接AF ,过点C 作CH AB 于H ,Rt AFC △中,122FC BC ,4AF ,1122ABC S BC AF AB CH∵,5BC AF HC AB ,∵DP AB ,AGD AHC ∽,12GD AD HC AC,12GD HC Rt GED中,255GE Rt AGD中,355AG,3535tan 44AG ADG GD ,EF AD ∥∵,EMG ADG ,3tan 4EG EMGMG,4433515MG GE,1553MD MG GD,∵DNF DME ∽,DN DF DMDE103DN DM .【点睛】本题考查了勾股定理,直角三角形斜边上的中线等于斜边的一半,中位线的性质定理,相似三角形的性质与判定,求角的正确,掌握相似三角形的性质与判定是解题的关键.模型3.“X ”字模型(“8”模型)【模型解读与图示】“X ”字模型图形的两个三角形有“对顶角”,再有一个角相等或夹对顶角的两边对应成比例就可以判定这两个三角形相似.1.(2022·河北·中考真题)如图是钉板示意图,每相邻4个钉点是边长为1个单位长的小正方形顶点,钉点A ,B 的连线与钉点C ,D 的连线交于点E ,则(1)AB 与CD 是否垂直?______(填“是”或“否”);(2)AE =______.【答案】是5【分析】(1)证明△ACG ≌△CFD ,推出∠CAG =∠FCD ,证明∠CEA =90°,即可得到结论;(2)利用勾股定理求得AB 的长,证明△AEC ∽△BED ,利用相似三角形的性质列式计算即可求解.【详解】解:(1)如图:AC =CF =2,CG =DF =1,∠ACG =∠CFD =90°,∴△ACG ≌△CFD ,∴∠CAG =∠FCD ,∵∠ACE +∠FCD =90°,∴∠ACE +∠CAG =90°,∴∠CEA =90°,∴AB 与CD 是垂直的,故答案为:是;(2)AB ∵AC ∥BD ,∴△AEC ∽△BED ,∴AC AE BD BE ,即23AE BE ,∴25AE BE ,∴AE =25BE【点睛】本题考查了相似三角形的判定和性质,全等三角形的判定和性质,解答本题的关键是明确题意,找出所求问题需要的条件.2.(2022·四川内江·中考真题)如图,在矩形ABCD 中,AB =6,BC =4,点M 、N 分别在AB 、AD 上,且MN ⊥MC ,点E 为CD 的中点,连接BE 交MC 于点F.(1)当F 为BE 的中点时,求证:AM =CE ;(2)若EF BF=2,求AN ND 的值;(3)若MN ∥BE ,求ANND 的值.【答案】(1)见解析(2)2737(3)27【分析】(1)根据矩形的性质,证明△BMF ≌△ECF ,得BM =CE ,再利用点E 为CD 的中点,即可证明结论;(2)利用△BMF ∽△ECF ,得12BM B EF CE F ,从而求出BM 的长,再利用△ANM ∽△BMC ,得AN AMBM BC,求出AN 的长,可得答案;(3)首先利用同角的余角相等得∠CBF =∠CMB ,则tan ∠CBF =tan ∠CMB ,得CE BCBC BM,可得BM 的长,由(2)同理可得答案.(1)证明:∵F 为BE 的中点,∴BF =EF ,∵四边形ABCD 是矩形,∴AB ∥CD ,AB =CD ∴∠BMF =∠ECF ,∵∠BFM =∠EFC ,∴△BMF ≌△ECF (AAS ),∴BM =CE ,∵点E 为CD 的中点,∴CE =12CD ,∵AB =CD ,∴12BM CE AB ,∴AM BM ,∴AM =CE ;(2)∵∠BMF =∠ECF ,∠BFM =∠EFC ,∴△BMF ∽△ECF ,∴12BM B EF CE F ,∵CE =3,∴BM =32,∴AM =92,∵CM ⊥MN ,∴∠CMN =90°,∴∠AMN +∠BMC =90°,∵∠AMN +∠ANM =90°,∴∠ANM =∠BMC ,∵∠A =∠MBC ,∴△ANM ∽△BMC ,∴AN AM BM BC,∴92342AN ,∴7162AN ,∴DN =AD ﹣AN =4﹣2716=3716,∴272716373716AN DN ;(3)∵MN ∥BE ,∴∠BFC =∠CMN ,∴∠FBC +∠BCM =90°,∵∠BCM +∠BMC =90°,∴∠CBF =∠CMB ,∴tan ∠CBF =tan ∠CMB ,∴CE BC BC BM ,∴344BM ,∴163BM ,∴162633AM AB BM ,由(2)同理得,AN AMBM BC,∴231643AN ,解得:AN =89,∴DN =AD ﹣AN =4﹣89=289,∴8292879AN ND .【点睛】本题是相似形综合题,主要考查了矩形的性质,全等三角形的判定与性质,相似三角形的判定与性质,三角函数等知识,求出BM 的长是解决(2)和(3)的关键.3.(2022·广西贵港·中考真题)已知:点C ,D 均在直线l 的上方,AC 与BD 都是直线l 的垂线段,且BD 在AC 的右侧,2BD AC ,AD 与BC 相交于点O .(1)如图1,若连接CD ,则BCD △的形状为______,AOAD的值为______;(2)若将BD 沿直线l 平移,并以AD 为一边在直线l 的上方作等边ADE .①如图2,当AE 与AC 重合时,连接OE ,若32AC,求OE 的长;②如图3,当60ACB 时,连接EC 并延长交直线l 于点F ,连接OF .求证:OF AB.【答案】(1)等腰三角形,13(2)①OE ②见解析【分析】(1)过点C 作CH ⊥BD 于H ,可得四边形ABHC 是矩形,即可求得AC =BH ,进而可判断△BCD 的形状,AC 、BD 都垂直于l ,可得△AOC ∽△BOD ,根据三角形相似的性质即可求解.(2)①过点E 作EF AD 于点H ,AC ,BD 均是直线l 的垂线段,可得//AC BD ,根据等边三角形的性质可得30BAD ,再利用勾股定理即可求解.②连接CD ,根据//AC BD ,得60CBD ACB ,即BCD △是等边三角形,把ABD △旋转得90ECD ABD ,根据30°角所对的直角边等于斜边的一般得到13AF AO AB AD ,则可得AOF ADB △∽△,根据三角形相似的性质即可求证结论.(1)解:过点C 作CH ⊥BD 于H ,如图所示:∵AC ⊥l ,DB ⊥l ,CH ⊥BD ,∴∠CAB =∠ABD =∠CHB =90°,∴四边形ABHC 是矩形,∴AC =BH ,又∵BD =2AC ,∴AC=BH=DH ,且CH ⊥BD ,∴BCD △的形状为等腰三角形,∵AC 、BD 都垂直于l ,∴△AOC ∽△BOD ,122AO AC AC DO DB AC ,即2DO AO ,133AO AO AD AO DO A AO O,故答案为:等腰三角形,13.(2)①过点E 作EF AD 于点H ,如图所示:∵AC ,BD 均是直线l 的垂线段,∴//AC BD ,∵ADE 是等边三角形,且AE 与AC 重合,∴∠EAD =60°,∴60ADB EAD ,∴30BAD ,∴在Rt ADB 中,2AD BD , AB ,又∵2BD AC ,32AC,∴6,AD AB ∴132AH DH AD ,又Rt ADB ,∴EH又由(1)知13AO AD =,∴123AO AD ,则1OH ,∴在Rt EOH △中,由勾股定理得:OE ②连接CD ,如图3所示:∵//AC BD ,∴60CBD ACB ,∵BCD △是等腰三角形,∴BCD △是等边三角形,又∵ADE 是等边三角形,∴ABD △绕点D 顺时针旋转60 后与ECD 重合,∴90ECD ABD ,又∵60BCD ACB ,∴30ACF FCB FBC ,∴2FC FB AF ,∴13AF AO AB AD ,又OAF DAB ,∴AOF ADB △∽△,∴90AFO ABD ,∴OF AB .【点睛】本题考查了矩形的判定及性质、三角形相似的判定及性质、等边三角形的判定及性质、勾股定理的应用,熟练掌握三角形相似的判定及性质和勾股定理的应用,巧妙借助辅助线是解题的关键.4.(2022·江苏镇江·九年级期末)梅涅劳斯(Menelaus )是古希腊数学家,他首先证明了梅涅劳斯定理,定理的内容是:如图(1),如果一条直线与△ABC 的三边AB ,BC ,CA 或它们的延长线交于F 、D 、E 三点,那么一定有••1AF BD CEFB DC EA.下面是利用相似三角形的有关知识证明该定理的部分过程:证明:如图(2),过点A 作AG BC ∥,交DF 的延长线于点G ,则有AF AG FB BD ,CE CDEA AG ,∴1AF BD CE AG BD CD FB DC EA BD DC AG.请用上述定理的证明方法解决以下问题:(1)如图(3),△ABC 三边CB ,AB ,AC 的延长线分别交直线l 于X ,Y ,Z 三点,证明:1BX CZ AYXC ZA YB.(2)如图(4),等边△ABC 的边长为2,点D 为BC 的中点,点F 在AB 上,且2BF AF ,CF 与AD 交于点E ,则AE 的长为________.(3)如图(5),△ABC 的面积为2,F 为AB 中点,延长BC 至D ,使CD BC ,连接FD 交AC 于E ,则四边形BCEF 的面积为________.代入∴YBX YAE YXB E ZCX ,;故可知△YBX ∽△YAE ,△ZCX ∽△课后专项训练:1.(2022•江苏中考模拟)对于两个相似三角形,如果沿周界按对应点顺序环绕的方向相同,那么称这两个三角形互为顺相似;如果沿周界按对应点顺序环绕的方向相反,那么称这两个三角形互为逆相似.例如,如图(1),△CDE∽△CAB,且沿周界CDEC与CABC环绕的方向(同为逆时针方向)相同,因此△CDE 和△CAB互为顺相似;如图(2),△CDE∽△CBA,且沿周界CDEC与CBAC环绕的方向相反,因此△CDE 和△CBA互为逆相似.(1)根据以上材料填空:①如图(3),AB∥CD,则△AOB∽△COD,它们互为相似(填“顺”或“逆”,下同);②如图(4),Rt△ABC中,∠ACB=90°,CD⊥AB于点D,则△ABC∽,它们互为相似;③如图(5),若∠DAB=∠EBC=90°,并且BD⊥CE于点F,则△ABD∽,它们互为相似;(2)如图(6),若△AOB∽△COD,指出图中另外的一对相似三角形并说明理由,同时指出它们互为顺相似还是互为逆相似;(3)如图(7),在Rt△ABC中,∠C=90°,AC=20,BC=15,点P在△ABC的斜边上,且AP=16,过点P画直线截△ABC,使截得的一个三角形与△ABC相似,则满足的截线共有条.【答案】(1)①逆;②△ACD或△CBD,逆;③△BCE,顺;(答案不唯一);(2)△AOC∽△BOD,理由见解析;△AOC和△BOD互为顺相似;(3)3.【分析】(1)①根据新定义直接判断,即可得出结论;②先判断出∠ADC=∠BDC=90°=∠ACB,进而分两种情况,判断出两三角形相似,最后根据新定义判断,即可得出结论;③先判断出∠ABD=∠C,进而得出△ABD∽△BCE,最后用新定义判断,即可得出结论;(2)先由△AOB∽△COD,判断出AO OBCO OD,∠AOB=∠COD,进而得出∠AOC=∠BOD,即可得出结论;(3)先求出BP=9,分三种情况,过点P作AB,AC,BC的垂线,利用相似三角形得出比例式,建立方程求解,即可得出结论.【详解】(1)①∵AB∥CD,∴△AOB∽△COD,∴△AOB和△COD互为逆相似,故答案为:逆;②∵CD⊥AB,∴∠ADC=∠BDC=90°=∠ACB,Ⅰ、∵∠A=∠A,∴△ABC∽△ACD,∴△ABC和△ACD互为逆相似;Ⅱ、∠B=∠B,∴△ABC∽△CBD,∴△ABC和△CBD互为逆相似;故答案为:△ACD或△CBD,逆;③∵BD⊥CE,∴∠BFC=90°,∴∠CBD+∠C=90°,∵∠EBC=90°,∴∠CBD+∠ABD=90°,∴∠ABD=∠C,∴△ABD∽△BCE,∴△ABD和△BCE互为顺相似;故答案为:△BCE,顺;(2)△AOC∽△BOD,△AOC和△BOD互为顺相似;理由:∵△AOB∽△COD,∴AOCO=OBOD,∠AOB=∠COD,∴∠AOB﹣∠BOC=∠COD﹣∠BOC,∴∠AOC=∠BOD,∵AO CO=OB OD,∴OA OB=OC OD,∴△AOC∽△BOD,∴△AOC和△BOD互为顺相似;(3)在Rt△ABC中,AC=20,BC=15,根据勾股定理得,AB25,∵AP=16,∴BP=AB﹣AP=9,如图1,①过点P 作PG ⊥BC 于G ,∴∠BGP =90°=∠ACB ,∵∠B =∠B ,∴△ABC ∽△PBG ,∴AB BC BP BG ,∴25159BG,∴BG =15925=275<BC ,∴点G 在线段BC (不包括端点)上,②过点P 作PG ''⊥AC 于G '',∴∠AG ''P =∠ACB ,∵∠A =∠A ,∴△ABC ∽△APG '',∴AB AC AP AG ,∴252016AG,∴AG ''=201625 =645<AC ,∴点G ''在线段AC (不包括端点)上,③过点P 作PG '⊥AB ,交直线BC 与G ',交直线AC 于H ,∵∠APG '=∠APH =90°=∠ACB ,∵∠A =∠A ,∴△ABC ∽△G 'BP ,∴AB BC BG BP ,∴25159BG ,∴BG '=25915=15=BC ,∴点G '和点H 都和点C 重合(注:为了说明问题,有意将点G '和点H 没画在点C 处),故答案为:3.【点睛】此题是相似形综合题,主要考查了相似三角形的判定和性质,新定义的理解和应用,理解新定义、熟练掌握相似三角形的判定和性质是解本题的关键.2.(2022·吉林·中考真题)下面是王倩同学的作业及自主探究笔记,请认真阅读并补充完整.【作业】如图①,直线12l l ∥,ABC 与DBC △的面积相等吗?为什么?解:相等.理由如下:设1l 与2l 之间的距离为h ,则12ABC S BC hV ,12DBC S BC h △.∴ABC DBC S S .【探究】(1)如图②,当点D 在1l ,2l 之间时,设点A ,D 到直线2l 的距离分别为h ,h ,则ABC DBC S hS h△△.证明:∵ABCS (2)如图③,当点D 在1l ,2l 之间时,连接AD 并延长交2l 于点M ,则ABC DBC S AM S DM△△.证明:过点A 作AE BM ,垂足为E ,过点D 作DF BM ,垂足为F ,则90AEM DFM ,∴AE ∥.∴AEM △∽.∴AE AM DF DM.由【探究】(1)可知ABC DBC S S △△,∴ABC DBC S AM S DM△△.(3)如图④,当点D 在2l 下方时,连接AD 交2l 于点E .若点A ,E ,D 所对应的刻度值分别为5,1.5,0,ABC DBCS S △△的值为.【答案】(1)证明见解析(2)证明见解析(3)73【分析】(1)根据三角形的面积公式可得11,22ABC DBC S S BC h BC h ,由此即可得证;(2)过点A 作AE BM ,垂足为E ,过点D 作DF BM ,垂足为F ,先根据平行线的判定可得AE DF ,再根据相似三角形的判定可证AEM DFM ,根据相似三角形的性质可得AE AM DF DM,然后结合【探究】(1)的结论即可得证;(3)过点A 作AM BC 于点M ,过点D 作DN BC 于点N ,先根据相似三角形的判定证出AME DNE V V ,再根据相似三角形的性质可得73AM AE DN DE ,然后根据三角形的面积公式可得12ABC S BC AM ,12DBC S BC DN ,由此即可得出答案.(1)证明:12ABC S BC h ∵,12DBC BC h S ,ABC DBC S h S h .(2)证明:过点A 作AE BM ,垂足为E ,过点D 作DF BM ,垂足为F ,则90AEM DFM,AE DF ∥.AEM DFM .AE AM DF DM.由【探究】(1)可知ABC DBC S AE S DF V V ,ABC DBC S AM S DMV V .(3)解:过点A 作AM BC 于点M ,过点D 作DN BC 于点N ,则90AME DNE,AM DN P ,AME DNE V V ,AM AE DN DE,∵点,,A E D 所对应的刻度值分别为5,1.5,0,5 1.5 3.5AE , 1.5DE , 3.571.53AM DN ,又12ABC S BC AM ∵,12DBC S BC DN ,73ABC DBC S AM S DN V V ,故答案为:73.【点睛】本题考查了相似三角形的判定与性质、平行线的判定、三角形的面积等知识点,熟练掌握相似三角形的判定与性质是解题关键.3.(2022·上海·九年级专题练习)如图,在Rt ABC 中,90ACB ,60BAC ,6AC ,AD 平分BAC ,交边BC 于点D ,过点D 作CA 的平行线,交边AB 于点E.(1)求线段DE 的长;(2)取线段AD 的中点M ,联结BM ,交线段DE 于点F ,延长线段BM 交边AC 于点G ,求EF DF的值.【答案】(1)4;(2)23【分析】(1)分别求出CD ,BC ,BD ,证明BDE BCA ∽,根据相似性质即可求解;(2)先证明DF AG ,再证明BEF BAG △∽△,根据相似三角形性质求解即可.【详解】解:(1)∵AD 平分BAC ,60BAC ,∴30DAC .在Rt ACD 中,90ACD ,30DAC ,6AC ,∴CD 在Rt ACB 中,90ACB ,60BAC ,6AC ,∴BC∴BD BC CD .∵//DE CA ,∴BDE BCA ∽∴23DE BD CA BC .∴4DE.(2)∵点M 是线段AD 的中点,∴DM AM .∵//DE CA ,∴DFM AGM △∽△∴DF DM AG AM .∴DF AG .∵//DE CA ,∴BEF BAG △∽△∴23EF BE BD AG BA BC ∴23EF DF .【点睛】本题考查了含30°角的直角三角形性质,相似的判定与性质,解题的关键是能根据题意确定相似三角形,并根据相似性质解题.4.(2022·上海市奉贤区古华中学九年级期中)已知:如图,四边形ABCD是平行四边形,在边AB的延长线上截取BE=AB,点F在AE的延长线上,CE和DF交于点M,BC和DF交于点N,联结BD.(1)求证:△BND∽△CNM;(2)如果AD2=AB•AF,求证:CM•AB=DM•CN.【分析】(1)利用平行四边形的性质得AB=CD,AB∥CD,再证明四边形BECD为平行四边形得到BD∥CE,根据相似三角形的判定方法,由CM∥DB可判断△BND∽△CNM;(2)先利用AD2=AB•AF可证明△ADB∽△AFD,则∠1=∠F,再根据平行线的性质得∠F=∠4,∠2=∠3,所以∠3=∠4,加上∠NMC=∠CMD,于是可判断△MNC∽△MCD,所以MC:MD=CN:CD,然后利用CD=AB 和比例的性质即可得到结论.【详解】证明:(1)∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,而BE=AB,∴BE=CD,而BE∥CD,∴四边形BECD为平行四边形,∴BD∥CE,∵CM∥DB,∴△BND∽△CNM;(2)∵AD2=AB•AF,∴AD:AB=AF:AD,而∠DAB=∠FAD,∴△ADB∽△AFD,∴∠1=∠F,∵CD∥AF,BD∥CE,∴∠F=∠4,∠2=∠3,∴∠3=∠4,而∠NMC=∠CMD,∴△MNC∽△MCD,∴MC:MD=CN:CD,∴MC•CD=MD•CN,而CD=AB,∴CM•AB=DM•CN.【点睛】本题考查了三角形相似的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.在运用相似三角形的性质时主要利用相似比计算线段的长.也考查了平行四边形的判定与性质.5.(2022•安庆模拟)在四边形ABCD中,对角线AC、BD相交于点O.(1)如图①,若四边形ABCD为矩形,过点O作OE⊥BC,求证:OE=CD.(2)如图②,若AB∥CD,过点O作EF∥AB分别交BC、AD于点E、F.求证:=2.(3)如图③,若OC平分∠AOB,D、E分别为OA、OB上的点,DE交OC于点M,作MN∥OB交OA于一点N,若OD=8,OE=6,直接写出线段MN长度.【分析】(1)由OE⊥BC,DC⊥BC,可知EO∥CD,且OB=OD,可得结论;(2)由△DFO∽△DAB,得,同理,,,利用等式的性质将比例式相加,从而得出结论;(3)作DF∥OB交OC于点F,连接EF,可知△ODF是等腰三角形,得DO=DF=8,由△DMF∽△EMO,可得EM=,由△DMN∽△DOE,得,从而得出答案.【解答】(1)证明:∵四边形ABCD是矩形,∴O是AC中点,AB⊥BC,∵OE⊥BC,∴OE∥AB,∴E是BC中点,∴OE=;(2)证明:∵EF∥AB,∴△DFO∽△DAB,∴,同理,,,∴=,∴,即;(3)解:作DF∥OB交OC于点F,连接EF,∵OC平分∠AOB,∴∠AOC=∠BOC,∵DF∥OB,∴∠DFO=∠BOC=∠AOC,∴△ODF是等腰三角形,∴DO=DF=8,∵DF∥OE,∴△DMF∽△EMO,∴,∴EM=,∴,∵MN ∥OE ,∴△DMN ∽△DOE ,∴,∴,∴MN =.【点评】本题是相似形综合题,主要考查了矩形的性质,相似三角形的判定与性质,等腰三角形的性质,对比例式进行恒等变形是解题的关键.6.(2022•重庆中考模拟)问题提出:如图1,D 、E 分别在△ABC 的边AB 、AC 上,连接DE ,已知线段AD =a ,DB =b ,AE =c ,EC =d ,则S △ADE ,S △ABC 和a ,b ,c ,d之间会有怎样的数量关系呢?问题解决:探究一:(1)看到这个问题后,我们可以考虑先从特例入手,找出其中的规律.如图2,若DE ∥BC ,则∠ADE =∠B ,且∠A =∠A ,所以△ADE ∽△ABC ,可得比例式:a c a b c d而根据相似三角形面积之比等于相似比的平方.可得 22ADE ABC S a S a b .根据上述这两个式子,可以推出:22ADE ABC S a a a a c ac S a b a b a b c d a b c d a b .(2)如图3,若∠ADE =∠C ,上述结论还成立吗?若成立,请写出证明过程;着不成立,请说明理由.探究二:回到最初的问题,若图1中没有相似的条件,是否仍存在结论:ADE ABC S ac S a b c d ?方法回顾:两个三角形面积之比,不仅可以在相似的条件下求得,当两个三角形的底成高具有一定的关系时,也可以解决.如图4,D 在△ABC 的边上,做AH ⊥BC 于H ,可得:1212ABD ADC BD AH S BD S DC DC AH .借用这个结论,请你解决最初的问题.延伸探究:(1)如图5,D 、E 分别在△ABC 的边AB 、AC 反向延长线上,连接DE ,已知线段AD =a ,AB =b ,AE =c ,AC =d ,则ADE ABC S S .(2)如图6,E 在△ABC 的边AC 上,D 在AB 反向延长线上,连接DE ,已知线段AD =a ,AB =b ,AE =c ,AC =d ,ADE ABC S S .结论应用:如图7,在平行四边形ABCD 中,G 是BC 边上的中点,延长GA 到E ,连接DE 交BA 的延长线于F ,若AB =5,AG =4,AE =2,▱ABCD 的面积为30,则△AEF 的面积是.【答案】探究一:(2)见解析;延伸探究:(1)ac bd ;(2)ac bd ;结论应用:32【分析】问题解决:探究一(2):参照(1)中证明方法解答即可;探究二,过D 、B 点分别作,DM AC BN AC ,垂足分别为M 、N ,然后按照探究一中方法证明即可;延伸探究:(1)过D 、B 点分别作,DM AC BN AC ,垂足分别为M 、N ,然后按照探究一中方法证明即可;(2)过D 、B 点分别作,DM AC BN AC ,垂足分别为M 、N ,然后按照探究一中方法证明即可;结论应用:取AD 的中点M ,连接GM 并延长交DE 于点N ,连接DG ,可得15ADG S ,根据题意,进而得出152ADE S ,根据AM =DM ,MN AF ∥,可得FN =DN ,根据AE =2,AG =4,GN AF ∥,可得FN =2EF ,进而可得ED =5EF ,即可得出1352AEF ADE S S.【详解】解:问题解决:探究一:(2)成立,理由如下:∵∠ADE =∠C ,∠A =∠A ,∴ADE ACB ∽,∴a c c d a b,∴ 22()()ADE ABC S b a S c a c ac c d a b c d a d ;探究二:过D 、B 点分别作,DM AC BN AC ,垂足分别为M 、N ,∵,DM AC BN AC ,∴//DM BN ,∴AD DM a AB BN a b,121()()2ADE ABC AE DM S AE DM c a ac S AC BN c d a b a b c d AC BN;延伸探究:(1)过D 、B 点分别作,DM AC BN AC ,垂足分别为M 、N ,∵,DM AC BN AC ,∴//DM BN ,∴AD DM a AB BN b ,1212ADE ABC AE DM S AE DM c a ac S AC BN d b bd AC BN ;(2)过D 、B 点分别作,DM AC BN AC ,垂足分别为M 、N,∵,DM AC BN AC ,∴//DM BN ,∴AD DM a AB BN b ,1212ADE ABC AE DM S AE DM c a ac S AC BN d b bd AC BN ;结论应用:取AD 的中点M ,连接GM 并延长交DE 于点N ,连接DG ,∴AM =DM ,1152ADG ABCD S S 平行四边形,∵AE =2,AG =4,∴11522ADE ADG S S ,∵AM =DM ,MN AF ,∴FN =DN ,∵AE =2,AG =4,GN AF ∥,∴12EF AE FN AG ,即:FN =2EF ,∴ED =5EF ,∴1352AEF ADE S S .【点睛】本题考查了相似三角形的判定与性质,平行线分线段成比例等知识点,熟练运用相似三角形的性质是解题的关键.7.(2022·贵州铜仁·中考真题)如图,在四边形ABCD 中,对角线AC 与BD 相交于点O ,记COD △的面积为1S ,AOB 的面积为2S .(1)问题解决:如图①,若AB //CD ,求证:12 S OC OD S OA OB(2)探索推广:如图②,若AB 与CD 不平行,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由.(3)拓展应用:如图③,在OA 上取一点E ,使OE OC ,过点E 作EF CD ∥交OD 于点F ,点H 为AB 的中点,OH 交EF 于点G ,且2 OG GH ,若56OE OA ,求12S S值.【答案】(1)见解析;(2)(1)中的结论成立,理由见解析:(3)2554【分析】(1)如图所示,过点D 作AE ⊥AC 于E ,过点B 作BF ⊥AC 于F ,求出sin sin DE OD DOE BF OB BOF ∠,∠,然后根据三角形面积公式求解即可;(2)同(1)求解即可;(3)如图所示,过点A 作AM EF ∥交OB 于M ,取BM 中点N ,连接HN ,先证明△OEF ≌△OCD ,得到OD =OF ,证明△OEF ∽△OAM ,得到5==6OF OE OM OA ,设55OE OC m OF OD n ,,则66OA m OM n ,,证明△OGF ∽△OHN ,推出31522n ON OF ,32n BN MN ON OM ,则9OB ON BN n ,由(2)结论求解即可.【详解】解:(1)如图所示,过点D 作AE ⊥AC 于E ,过点B 作BF ⊥AC 于F ,∴sin sin DE OD DOE BF OB BOF ∠,∠,∴111===sin 22OCD S S OC DE OC OD DOE △∠,211==sin 22AOB S S OA BF OA OB BOF △∠,∵∠DOE =∠BOF ,∴sin sin DOE BOF ;∴121sin 2==1sin 2OC OD DOE S OC OD S OA OB OA OB BOF ∠∠;。
20 相似三角形重要模型之母子型(共边共角模型)(学生版)-2024年中考数学几何模型归纳讲练

专题20. 相似三角形重要模型--母子型(共边共角模型)相似三角形是初中几何中的重要的内容,常常与其它知识点结合以综合题的形式呈现,其变化很多,是中考的常考题型。
在相似三角形中存在众多的相似模型,其中“母子型”相似模型应用较为广泛,深入理解模型内涵,灵活运用相关结论可以显著提高解题效率,本专题重点讲解相似三角形的“母子”模型。
母子相似证明题一般思路方法:①由线段乘积相等转化成线段比例式相等;②分子和分子组成一个三角形、分母和分母组成一个三角形;③第②步成立,直接从证这两个三角形相似,逆向证明到线段乘积相等;④第②步不成立,则选择替换掉线段比例式中的个别线段,之后再重复第③步。
模型1.“母子”模型(共边角模型)【模型解读与图示】“母子”模型的图形(通常有一个公共顶点和另外一个不是公共的顶点,由于小三角形寓于大三角形中,恰似子依母怀),也是有一个“公共角”,再有一个角相等或夹这个公共角的两边对应成比例就可以判定这两个三角形相似.图1 图2 图3 图41)“母子”模型(斜射影模型)条件:如图1,∠C=∠ABD ; 结论:△ABD ∽△ACB ,AB 2=AD ·AC .2)双垂直模型(射影模型)条件:如图2,∠ACB=90o ,CD ⊥AB ;结论:△ACD ∽△ABC ∽△CBD ;CA 2=AD ·AB ,BC 2=BD ·BA ,CD 2=DA ·DB .3)“母子”模型(变形)条件:如图3,∠D=∠CAE ,AB=AC ; 结论:△ABD ∽△ECA ;4)共边模型条件:如图1,在四边形ABCD 中,对角线BD 平分ABC ∠,ADB DCB ∠=∠,结论:2BD BA BC =⋅;例1.(2022·贵州贵阳·中考真题)如图,在ABC V 中,D 是AB 边上的点,B ACD ∠=∠,:1:2AC AB =,则ADC V 与ACB △的周长比是( )A.B .1:2C .1:3D .1:4例3.(2022.山西九年级期中)如图,点C ,D 在线段AB 上,△PCD 是等边三角形,且∠APB =120°,求证:(1)△ACP ∽△PDB ,(2)CD 2=AC •BD .例4.(2023·湖南·统考中考真题)在Rt ABC △中,90BAC AD ∠=︒,是斜边BC 上的高.(1)证明:C ABD BA ∽△△;(2)若610AB BC ==,,求BD 的长.例5.(2023.浙江中考模拟)如图,在V ABC 中,∠ACB =90°,CD ⊥AB .(1)图1中共有 对相似三角形,写出来分别为 (不需证明):(2)已知AB =5,AC =4,请你求出CD 的长:(3)在(2)的情况下,如果以AB 为x 轴,CD 为y 轴,点D 为坐标原点O ,建立直角坐标系(如图2),若点P 从C 点出发,以每秒1个单位的速度沿线段CB 运动,点Q 出B 点出发,以每秒1个单位的速度沿线段BA 运动,其中一点最先到达线段的端点时,两点即刻同时停止运动;设运动时间为t 秒是否存在点P ,使以点B 、P 、Q 为顶点的三角形与△ABC 相似?若存在,请求出点P 的坐标;若不存在,请说明理由.例6.(2022·陕西汉中·九年级期末)如图,CD 是等腰直角ABC V 斜边AB 的中线,以点D 为顶点的EDF ∠绕点D 旋转,角的两边分别与AC 、BC 的延长线相交,交点分别为点E 、F ,DF 与AE 交于点M ,DE 与BC 交于点N ,且45EDF ∠=︒.(1)如图1,若CE CF =,求证:DE DF =;(2)如图2,若CE CF ≠,求证:2CD CE CF =⋅;(3)如图2,过D 作DG BC ⊥于点G ,若2CD =,CF =DN 的长.例7.(2023·浙江·九年级期末)(1)如图1,在ABC V 中,D 为AB 上一点,2AC AD AB =⋅.求证:ACD B ∠=∠.(2)如图2,在ABCD Y 中,E 是AB 上一点,连接AC ,EC .已知4AE =,6AC =,9CD =.求证:23AD EC =.(3)如图3,四边形ABCD 内接于O ,AC 、BD 相交于点E .已知O 的半径为2,AE CE =,AB =,BD =ABCD 的面积.【拓展提高】(3)如图ABC V 中,D 是BC 上一点,连结AD ,点E ,F 分别在BE ,CE ,EF ,若DE ,BEC AEF ∠=∠,16BE =,7=,34CE BC =,求课后专项训练1.(2023成都市九年级期中)如图,矩形ABCD 中,F 是DC 上一点,BF ⊥AC ,垂足为E ,AD AB =12,△CEF 的面积为S 1,△AEB 的面积为S 2,则S 1S 2的值等于( )A .1B .1C .1D .1A .AG CG = B .2B HAB ∠=∠3.(2023·湖北恩施·校考模拟预测)如图,在正确的是( )A .2BC BD AB =⋅ B .CD 4.(2023·山东济南·统考中考真题)如图,在半径作弧交AC 于点D ,再分别以A.36∠=︒BCE5.(2023·云南临沧△V与BCDACDA.1:2B.6.(2023·山东东营·统考中考真题)于点D,E;分别以点D7.(2020·山西·统考中考真题)如图,在Rt∆D,E为BC的中点,AE与CD交于点F,则8.(2022·河北邢台·校考二模)如图1,在ABC V 中,AB AC =,24BC =,5tan 12C =,点P 为BC 边上一点,则点P 与点A 的最短距离为______.如图2,连接AP ,作APQ ∠,使得APQ B ∠=∠,PQ 交AC 于Q ,则当11BP =时,AQ 的长为______.10.(2020·广东广州·AC '分别交对角线BD 11.(2021·四川南充·中考真题)如图,在ABC V 中,D 为BC 上一点,3BC BD ==,则:AD AC 的值为________.12.(2022·四川宜宾·九年级期末)如图,在△ABC 中,点D 在BC 边上,点E 在AC 边上,且AD =AB ,∠DEC =∠B .(1)求证:△AED ∽△ADC ;(2)若AE =1,EC =3,求AB 的长.13.(2022·江苏盐城·中考真题)如图,在ABC V 与A B C '''V 中,点D 、D ¢分别在边BC 、B C ''上,且ACD A C D '''∽△△,若___________,则ABD A B D '''△∽△.请从①BD B D CD C D ''='';②AB A B CD C D ''='';③BAD B A D '''∠=∠这三个选项中选择一个作为条件(写序号),并加以证明.14.(2023·湖南·统考中考真题)在Rt ABC △中,90BAC AD ∠=︒,是斜边BC 上的高.(1)证明:C ABD BA ∽△△;(2)若610AB BC ==,,求BD 的长.探究发现:如图1,在ABC V 中,36A ∠=︒,AB AC =.(1)操作发现:将ABC V 折叠,使边BC 落在边BA 上,点C 的对应点是点E ,折痕交AC DE ,DB ,则BDE ∠=_______︒,设1AC =,BC =,那么AE =______(用含x 的式子表示)(2)进一步探究发现:512-=底腰,这个比值被称为黄金比.在(1)的条件下试证明:51BC -底当等腰三角形的底与腰的比等于黄金比时,这个三角形叫黄金三角形.例如,图(1)如图2,在ABC V 中,2BC AB =,求证:ABC V 为关于边BC 的“华益美三角”;(2)如图3,已知ABC V 为关于边BC 的“华益美三角”,点D 是ABC V 边BC 的中点,以BD 为直径的经过点A .①求证:直线CA 与O e 相切;②若O e 的直径为26,求线段AB 的长;(3)已知ABC V 为关于边BC 的“华益美三角”,4BC =,30B ∠=︒,求ABC V 的面积.20.(2022·浙江台州·统考一模)已知在▱ABCD ,AB =BC =10,∠B =60°,E 是边BC 上的动点,以AE 为一边作▱AEFG ,且使得直线FG 经过点D .(1)如图1,EF 与AD 相交于H ,若H 是EF 的中点.①求证:GF =DF ;②若GF ⊥CD ,求GD 的长;(2)如图2,设AE =x ,AG =y ,当点E 在边BC 上移动时,始终保持∠AEF =45°,①求y 关于x 的函数关系式,并求函数y 的取值范围;②连接ED ,当△AED 是直角三角形时,求DF 的值.2BAC B BAD ∠∠∠=∴= ,设DC x =,则AD BD a ==-22b ax a ax bc ∴=-=, 2a ∴证法2:如图2,延长CA 到点任务:(1)上述材料中的证法似”).(2)请补全证法2剩余的部分.22.(2022·安徽·校联考三模)在ABC V 中,2ABC ACB ∠=∠,BD 平分ABC ∠.(1)如图1,若3AB =,5AC =,求AD 的长.(2)如图2,过A 分别作AE AC ⊥交BC 于E ,AF BD ⊥于F .①求证:ABC EAF ∠=∠;②求BF AC的值.∠,交AB于CD平分ACB是否为定值.如果是,请求出这个定值;如果不∠∠,CD平分BCF2CBG。
相似三角形常见模型(总结)

相似三角形常见模型(总结)第一部分相似三角形模型分析一、相似三角形判定的基本模型认识(一)A字型、反A字型(斜A字型)B(平行)B(不平行)(二)8字型、反8字型BCBC(蝴蝶型)(平行)(不平行)(三)母子型B(四)一线三等角型:三等角型相似三角形是以等腰三角形(等腰梯形)或者等边三角形为背景(五)一线三直角型:(六)双垂型:C D二、相似三角形判定的变化模型旋转型:由A 字型旋转得到。
8字型拓展C B ED A 共享性G B EF一线三等角的变形一线三直角的变形第二部分相似三角形典型例题讲解母子型相似三角形例1:如图,梯形ABCD 中,AD ∥BC ,对角线AC 、BD 交于点O ,BE ∥CD 交CA 延长线于E .求证:OE OA OC ?=2 .例2:已知:如图,△ABC 中,点E 在中线AD 上, ABC DEB ∠=∠.求证:(1)DA DE DB ?=2;(2)DAC DCE ∠=∠.A C D E B例3:已知:如图,等腰△ABC 中,AB =AC ,AD ⊥BC 于D ,CG ∥AB ,BG 分别交AD 、AC 于E 、F .求证:EG EF BE ?=2.相关练习:1、如图,已知AD 为△ABC 的角平分线,EF 为AD 的垂直平分线.求证:FC FB FD ?=2.2、已知:AD 是Rt △ABC 中∠A 的平分线,∠C=90°,EF 是AD 的垂直平分线交AD 于M ,EF 、BC 的延长线交于一点N 。
求证:(1)△AME ∽△NMD; (2)ND 2=NC NB3、已知:如图,在△ABC中,∠ACB=90°,CD⊥AB于D,E是AC上一点,CF⊥BE于F。
求证:EBDF=AEDB4.在?ABC中,AB=AC,高AD与BE交于H,EF BC⊥,垂足为F,延长AD到G,使DG=EF,M是AH的中点。
求证:∠=?GBM905.(本题满分14分,第(1)小题满分4分,第(2)、(3)小题满分各5分)已知:如图,在Rt△ABC中,∠C=90°,BC=2,AC=4,P是斜边AB上的一个动点,PD⊥AB,交边AC于点D(点D与点A、C都不重合),E是射线DC上一点,且∠EPD=∠A.设A、P两点的距离为x,△B EP的面积为y.AB PD E(第25题图)GMFEHDCBA(1)求证:AE=2PE;(2)求y关于x的函数解析式,并写出它的定义域;(3)当△BEP与△ABC相似时,求△BEP的面积.双垂型1、如图,在△ABC中,∠A=60°,BD、CE分别是AC、AB 上的高2、如图,已知锐角△ABC,AD、CE分别是BC、AB边上的高,△ABC和△BDE的面积分别是27和3,DE=62,求:点B到直线AC的距离。
九年级数学相似三角形--母子型

相似三角形之母子三角形【知识要点】一、直角三角形相似1、直角三角形被斜边上的高分成两个直角三角形和原三角形相似。
2、如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。
基本图形(母子三角形)举例:1、条件:如图,已知△ABC 是直角三角形,CD 为斜边AB 上的高.(射影定理) 结论:(1)△ACD ∽△CBD ,△BDC ∽△BCA ,△CDA ∽△BCA(2)△ACD ∽△CBD 中,2CD AD BD =△BDC ∽△BCA 中,2BC BD AB =}△CDA ∽△BCA 中,2AC AD AB =2、条件:如图,已知∠ACD=∠ABC (母子)结论:△ACD ∽△ABC 中,2AC AD AB =【例题解析】类型一:三角形中的母子型 【例1】1.如图,ΔABC 中,∠A=∠DBC,BC=,S ΔBCD ∶S ΔABC=2∶3,则CD=______.【练】如图,D 是 △ABC 的边AB 上一点,连结CD.若AD= 2,BD = 4, ∠ACD =∠B 求AC 的长.CBA@【例2】如图,在△ABC 中,AD 为∠A 的平分线,AD 的垂直平分线交AD 于E ,交BC 的延长线于F ,求证:FC FB FD ⋅=2 A D C B A D CB【练】已知CD 是ABC ∆的高,,DE CA DF CB ⊥⊥,如图3-1,求证:CEF CBA ∆∆∽类型二:直角三角形中的母子型【例1】.如图,在△ABC 中,AD 、BE 分别为BC 、AC 边上的高,过D 作AB 的垂线交AB 于F ,交BE 于G ,交AC 的延长于H ,求证:2DF FG FH =•H G FED C B A【练】如图5,RtΔABC 中,∠ACB=90°,CD ⊥AB,AC=8,BC=6,则AD=____,CD=_______.】【例2】如图1,∠ADC=∠ACB=90°,∠1=∠B,AC=5,AB=6,则AD=______.【练】如图,CD 是Rt△ABC 斜边上的高.若AD= 2,BD = 4, 求CD的长.BA类型三:四边形中的母子型【例1】1.如图,矩形ABCD中,BH⊥AC于H,交CD于G,求证:2BC CG CD=•。
相似三角形模型分析之母子型

相似三角形模型分析之母子型第五讲:相似三角形模型分析大全一、相似三角形判定的基本模型认识(一)A字型、反A字型(斜A字型)(平行)B(不平行)(二)8字型、反8字型BCBC(平行)(不平行)(三)母子型B(四)一线三等角型:三等角型相似三角形是以等腰三角形(等腰梯形)或者等边三角形为背景(五)一线三直角型:(六)双垂型:ADC 二、相似三角形判定的变化模型旋转型:由A字型旋转得到。
8字型拓展CBEDA共享性GABE F一线三等角的变形一线三直角的变形母子型相似三角形例1:如图,梯形ABCD中,AD∥BC,对角线AC、BD交于点O,BE∥CD交CA延长线于E.求证:OEOAOC?=2.例2:已知:如图,△ABC 中,点E 在中线AD 上, ABC DEB ∠=∠.求证:(1)DA DE DB ?=2;(2)DAC DCE ∠=∠.DEB例3:已知:如图,等腰△ABC 中,AB =AC ,AD ⊥BC 于D ,CG ∥AB ,BG 分别交AD 、AC 于E 、F .求证:EG EF BE ?=2.相关练习:1、如图,已知AD 为△ABC 的角平分线,EF 为AD 的垂直平分线.求证:FC FB FD ?=2.2、已知:AD是Rt△ABC中∠A的平分线,∠C=90°,EF是AD的垂直平分线交AD于M,EF、BC的延长线交于一点N。
求证:(1)△AME∽△NMD; (2)ND2=NC·NB3、已知:如图,在△ABC中,∠ACB=90°,CD⊥AB于D,E是AC上一点,CF⊥BE于F。
求证:EB·DF=AE·DB⊥,垂足为F,延长AD到G,使DG=EF,M是4.在?ABC中,AB=AC,高AD与BE交于H,EF BCAH的中点。
GBM90求证:∠=?5.(本题满分14分,第(1)小题满分4分,第(2)、(3)小题满分各5分)已知:如图,在Rt△ABC中,∠C=90°,BC=2,AC=4,P是斜边AB上的一个动点,PD ⊥AB,交边AC于点D(点D与点A、C都不重合),E是射线DC上一点,且(1)求证:AE=2PE;(2)求y关于x的函数解析式,并写出它的定义域;(3)当△BEP与△ABC相似时,求△BEP的面积.。
2023年中考数学常见几何模型之相似模型中的母子型与A(X)字型

专题06 相似模型-母子型(共角共边模型)和A (X )字型 相似三角形是初中几何中的重要的内容,常常与其它知识点结合以综合题的形式呈现,其变化很多,是中考的常考题型。
如果大家平时注重解题方法,熟练掌握基本解题模型,再遇到相似三角形的问题就信心更足了.本专题重点讲解相似三角形的六大基本模型. 模型1.“母子”模型(共边角模型)【模型解读与图示】“母子”模型的图形(通常有一个公共顶点和另外一个不是公共的顶点,由于小三角形寓于大三角形中,恰似子依母怀),也是有一个“公共角”,再有一个角相等或夹这个公共角的两边对应成比例就可以判定这两个三角形相似.“双垂线”型是其特例。
“ 母子”模型(斜射影) 双垂直(射影定理) “母子型”的变形 斜射影结论:△ABD ∽△ACB ,AB 2=AD ·AC .双垂直结论:①△ABD ∽△ACB ,AB 2=AD ·AC ;②△ADC ∽△ACB ,AC 2=AD ·AB ;③△CDB ∽△ACB ,CB 2=BD ·BA .1.(2022·贵州贵阳·中考真题)如图,在ABC V 中,D 是AB 边上的点,B ACD ∠=∠,:1:2AC AB =,则ADC V 与ACB △的周长比是( )A .B .1:2C .1:3D .1:4 【答案】B【分析】先证明△ACD ∽△ABC ,即有12AC AD CD AB AC BC ===,则可得12AC AD CD AB AC BC ++=++,问题得解.【详解】∵∠B =∠ACD ,∠A =∠A ,∴△ACD ∽△ABC ,∴AC AD CD AB AC BC ==, ∵12AC AB =,∴12AC AD CD AB AC BC ===, ∴12AC AD CD AC AD CD AB AC BC AB AC BC ++====++, ∴△ADC 与△ACB 的周长比1:2,故选:B .【点睛】本题主要考查了相似三角形的判定与性质,证明△ACD ∽△ABC 是解答本题的关键.2.(2022·陕西汉中·九年级期末)如图,CD 是等腰直角ABC V 斜边AB 的中线,以点D 为顶点的EDF ∠绕点D 旋转,角的两边分别与AC 、BC 的延长线相交,交点分别为点E 、F ,DF 与AE 交于点M ,DE 与BC 交于点N ,且45EDF ∠=︒.(1)如图1,若CE CF =,求证:DE DF =;(2)如图2,若CE CF ≠,求证:2CD CE CF =⋅;(3)如图2,过D 作DG BC ⊥于点G ,若2CD =,CF DN 的长.∵DG⊥BC,∠ACB=90°,∠∴∠DGN=∠ECN=90°,∠当CD=2,CF=2时,由CD在Rt△DCG中,CG DG=3.(2022·浙江绍兴·九年级期末)如果两个相似三角形的对应边存在2倍关系,则称这两个相似三角形互为母子三角形.(1)如果DEF V 与ABC V 互为母子三角形,则DE AB 的值可能为( ) A .2 B .12 C .2或12(2)已知:如图1,ABC V 中,AD 是BAC ∠的角平分线,2,AB AD ADE B =∠=∠. 求证:ABD △与ADE V 互为母子三角形.(3)如图2,ABC V 中,AD 是中线,过射线CA 上点E 作//EG BC ,交射线DA 于点G ,连结BE ,射线BE 与射线DA 交于点F ,若AGE V 与ADC V 互为母子三角形.求AG GF 的值.V互为母子三角形,∴QV与ADCAGE4.(2022.浙江中考模拟)如图,在V ABC中,∠ACB=90°,CD⊥AB.(1)图1中共有对相似三角形,写出来分别为(不需证明):(2)已知AB=5,AC=4,请你求出CD的长:(3)在(2)的情况下,如果以AB为x轴,CD为y轴,点D为坐标原点O,建立直角坐标系(如图2),若点P从C点出发,以每秒1个单位的速度沿线段CB运动,点Q出B点出发,以每秒1个单位的速度沿线段BA运动,其中一点最先到达线段的端点时,两点即刻同时停止运动;设运动时间为t秒是否存在点P,使以点B、P、Q为顶点的三角形与△ABC相似?若存在,请求出点P的坐标;若不存在,请说明理由.【答案】(1)3,V ABC∽V ACD,V ABC∽V CBD,V ACD∽V CBD;(2)125;(3)存在,(2740,32),(98,910)【分析】(1)根据两角对应相等的两三角形相似即可得到3对相似三角形,分别为:△ABC∽△ACD,△ABC∽△CBD,△ACD∽△CBD.(2)先在△ABC中由勾股定理求出BC的长,再根据△ABC的面积不变得到12AB•CD=12AC•BC,即可求出CD的长.(3)由于∠B公共,所以以点B、P、Q为顶点的三角形与△ABC相似时,分两种情况进行讨论:①△PQB∽△ACB;②△QPB∽△ACB.【详解】解:(1)图1中共有3对相似三角形,分别为:△ABC∽△ACD,△ABC∽△CBD,△ACD∽△CBD.证明:∵CD⊥AB,∴∠ADC=∠ACB=90°,又∵∠A=∠A,∴△ADC∽△ACB同理可证:△ABC∽△CBD,△ACD∽△CBD.故答案为:3;△ABC∽△ACD,△ABC∽△CBD,△ACD∽△CBD.(2)如图2中,在△ABC中,∵∠ACB=90°,AB=5,AC=4,∴BC3.∵△ABC的面积=12AB•CD=12AC•BC,∴CD=AC BCAB⋅=125.(3)存在点P,使以点B、P、Q为顶点的三角形与△ABC相似,理由如下:在△BOC中,∵∠COB=90°,BC=3,OC=125,∴OB=95.分两种情况:①当∠BQP=90°时,如图2①,此时△PQB∽△ACB,∴BP AB =BQ BC ,∴353t t −=,解得t =98,即98BQ CP ==,∴915388BP BC CP =−=−=. 在△BPQ中,由勾股定理,得32PQ ===,∴点P 的坐标为273(,)402; ②当∠BPQ =90°时,如图2②,此时△QPB ∽△ACB ,∴BP BQ BC AB =,∴335t t −=, 解得t =158,即15159,3888BQ cP BP BC CP ===−=−=, 过点P 作PE ⊥x 轴于点E .∵△QPB ∽△ACB ,∴PE BQ CO AB ⋅=,即1581255PE =,∴PE =910. 在△BPE中,2740BE ==, ∴92795408OE OB BE =−=−=,∴点P 的坐标为99(,)810, 综上可得,点P 的坐标为(2740,32);(98,910). 【点睛】本题属于相似形综合题,考查了相似三角形的判定与性质,勾股定理等知识,解题的关键是学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题,属于中考常考题型.模型2. “A ”字模型【模型解读与图示】“A ”字模型图形(通常只有一个公共顶点)的两个三角形有一个“公共角”(是对应角),再有一个角相等或夹这个公共角的两边对应成比例,就可以判定这两个三角形相似.1.(2022·湖南怀化·中考真题)如图,△ABC 中,点D 、E 分别是AB 、AC 的中点,若S △ADE =2,则S △ABC =_____.【答案】8【分析】根据三角形中位线定理求得DE ∥BC ,12DE BC =,从而求得△ADE ∽△ABC ,然后利用相似三角形的性质求解.【详解】解:∵D 、E 分别是AB 、AC 的中点,则DE 为中位线,所以DE ∥BC ,12DE BC =所以△ADE ∽△ABC ∴21()4ADE ABC S DE S BC ==V V ∵S △ADE =2,∴S △ABC =8故答案为:8.【点睛】本题考查中位线及平行线性质,本题难度较低,主要考查学生对三角形中位线及平行线性质等知识点的掌握.2.(2022·浙江杭州·中考真题)如图,在V ABC 中,点D ,E ,F 分别在边AB ,AC ,BC 上,连接DE ,EF ,已知四边形BFED 是平行四边形,DE 1BC 4=.(1)若8AB =,求线段AD 的长.(2)若ADE V 的面积为1,求平行四边形BFED 的面积.【答案】(1)2(2)6【分析】(1)利用平行四边形对边平行证明ADE ABC △△∽,得到DE AD BC AB=即可求出; (2)利用平行条件证明ADE EFC ∽V V ,分别求出ADE EFC V V 与、ADE ABC V V 与的相似比,通过相似三角形的面积比等于相似比的平方分别求出EFC S、ABC S V ,最后通过BFED ABC EFC ADE S S S S =−−Y V V V 求出. (1)∵四边形BFED 是平行四边形,∴∥DE BC ,∴ADE ABC △△∽,∴DE AD BC AB =, ∵DE 1BC 4=,∴AD 1AB 4=,∴118244AD AB ==⨯=; (2)∵四边形BFED 是平行四边形,∴∥DE BC ,EF AB ∥,DE =BF ,∴,AED ECF EAD CEF ∠=∠∠=∠,∴ADE EFC ∽V V ∴2ADE EFC S DE S FC ⎛⎫= ⎪⎝⎭V V , ∵DE 1BC 4=,DE =BF ,∴43FC BC DE DE DE DE =−=−=, ∴133DE DE FC DE ==,∴221139ADE EFC S DE S FC ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭V V , ∵ADE ABC △△∽,DE 1BC 4=,∴2211416ADE ABC S DE S BC ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭V V , ∵1ADE S =△,∴9,16EFC ABC S S ==V V ,∴16916BFED ABC EFC ADE S S S S =−−=−−=Y V V V .【点睛】本题考查了相似三角形,熟练掌握相似三角形的面积比等于相似比的平方、灵活运用平行条件证明三角形相似并求出相似比是解题关键.3.(2022·浙江宁波·中考真题)(1)如图1,在ABC V 中,D ,E ,F 分别为,,AB AC BC 上的点,,,DE BC BF CF AF =∥交DE 于点G ,求证:DG EG =.(2)如图2,在(1)的条件下,连接,CD CG .若,6,3⊥==CG DE CD AE ,求DE BC的值. (3)如图3,在ABCD Y 中,45,︒∠=ADC AC 与BD 交于点O ,E 为AO 上一点,EG BD ∥交AD 于点G ,⊥EF EG 交BC 于点F .若40,︒∠=EGF FG 平分,10∠=EFC FG ,求BF 的长.【答案】(1)证明见详解(2)13(3)5+【分析】(1)利用∥DE BC ,证明,ADG ABF AEG ACF △△△△::,利用相似比即可证明此问;(2)由(1)得DG EG =,CG DE ⊥,得出DCE V 是等腰三角形,利用三角形相似即可求出 DE BC的值; (3)遵循第(1)、(2)小问的思路,延长GE 交AB 于点M ,连接FM ,作MN BC ⊥,垂足为N .构造出等腰三角形、含30°、45°角的特殊直角三角形,求出BN 、FN 的值,即可得出BF 的长.(1)解:∵DE BC ∥,∴,ADG ABF AEG ACF △△△△::, ∴,==DG AG EG AG BF AF CF AF ,∴DG EG BF CF=. ∵BF CF =,∴DG EG =.(2)解:由(1)得DG EG =,∵CG DE ⊥,∴6CE CD ==.∵3AE =,∴9AC AE CE =+=.∵DE BC ∥,∴ADE ABC V :V . ∴13DE AE BC AC ==. (3)解:如图,延长GE 交AB 于点M ,连接FM ,作MN BC ⊥,垂足为N .在ABCD Y 中,,45=∠=∠=︒BO DO ABC ADC .∵EG BD ∥,∴由(1)得=ME GE ,∵⊥EF EG ,∴10==FM FG ,∴∠=∠EFM EFG .∵40∠︒=EGF ,∴40EMF ∠=︒,∴50EFG ∠=︒.∵FG 平分EFC ∠,∴50∠=∠=︒EFG CFG ,∴18030∠=︒−∠−∠−∠=︒BFM EFM EFG CFG .∴.在Rt FMN V 中,sin 305,cos30=︒==︒=MN FM FN FM∵45,∠=︒⊥MBN MN BN ,∴5==BN MN ,∴5=+=+BF BN FN【点睛】本题考查了相似三角形的性质及判定、等腰三角形的性质及判定、解特殊的直角三角形等知识,遵循构第(1)、(2)小问的思路,构造出等腰三角形和特殊的直角三角形是解决本题的关键.4.(2022·辽宁·中考真题)如图,在ABC V 中,4AB AC BC ===,D ,E ,F 分别为,,AC AB BC 的中点,连接,DE DF .(1)如图1,求证:2DF DE =;(2)如图2,将EDF ∠绕点D 顺时针旋转一定角度,得到PDQ ∠,当射线DP 交AB 于点G ,射线DQ 交BC 于点N 时,连接FE 并延长交射线DP 于点M ,判断FN 与EM 的数量关系,并说明理由;(3)如图3,在(2)的条件下,当DP AB ⊥时,求DN 的长.【答案】(1)见解析(2)FN EM =,理由见解析(3)103 【分析】(1)连接AF ,可得AF BC ⊥,根据直角三角形斜边上的中线等于斜边的一半可得12DF AC ==122DE BC ==,即可得证;(2)证明DNF DME V V ∽,根据(1)的结论即可得FN ;(3)连接AF ,过点C 作CH AB ⊥于H ,证明AGD AHC V V ∽,可得12GD HC ==,勾股定理求得,GE AG ,根据3tan 4AG ADG GD ∠==,EMG ADG ∠=∠,可得3tan 4EG EMG MG ∠==,进而求得MG ,根据MD MG GD =+求得MD ,根据(2)的结论2DN DM =,即可求解. (1)证明:如图,连接AF ,Q 4AB AC BC ===,D ,E ,F 分别为,,AC AB BC 的中点,122DE BC ∴==,AF BC ⊥,∴12DF AC ==∴2DF DE =,(2)FN =,理由如下,连接AF ,如图,Q 4AB AC BC ===,D ,E ,F 分别为,,AC AB BC 的中点,1,2EF AC CD EF DC ∴==∥,∴四边形CDEF 是平行四边形,DEF C ∴∠=∠, Q 12DF AC DC ==,DFC C ∴∠=∠,DEF DFC ∴∠=∠, 180180DEF DFC ∴︒−∠=︒−∠,∴DEM DFN ∠=∠,Q 将EDF ∠绕点D 顺时针旋转一定角度,得到PDQ ∠,∴EDF ∠=PDQ ∠,FDN NDE EDM NDE ∠+∠=∠+∠Q ,FDN EDM ∴∠=∠,DNF DME ∴V V ∽,NF DF EM DE ∴==,∴FN =, (3)如图,连接AF ,过点C 作CH AB ⊥于H ,Rt AFC △中,122FC BC ==,∴4AF ==, 1122ABC S BC AF AB CH =⋅=⋅V Q,BC AF HC AB ⋅∴== Q DP AB ⊥,AGD AHC ∴V V ∽,12GD AD HC AC ∴==,12GD HC ∴== Rt GED V中,5GE ===, Rt AGD V中,5AG ==,35tan 44AG ADG GD ∴∠===,EF AD ∥Q ,EMG ADG ∴∠=∠,3tan 4EG EMG MG ∴∠==,4433515MG GE ∴==⨯=,1553MD MG GD ∴=+=+=,Q DNF DME V V ∽,DN DF DM DE ∴==,103DN ∴==. 【点睛】本题考查了勾股定理,直角三角形斜边上的中线等于斜边的一半,中位线的性质定理,相似三角形的性质与判定,求角的正确,掌握相似三角形的性质与判定是解题的关键.模型3. “X ”字模型(“8”模型)【模型解读与图示】“X ”字模型图形的两个三角形有“对顶角”,再有一个角相等或夹对顶角的两边对应成比例就可以判定这两个三角形相似.1.(2022·河北·中考真题)如图是钉板示意图,每相邻4个钉点是边长为1个单位长的小正方形顶点,钉点A ,B 的连线与钉点C ,D 的连线交于点E ,则(1)AB 与CD 是否垂直?______(填“是”或“否”);(2)AE =______.【答案】 是 【分析】(1)证明△ACG ≌△CFD ,推出∠CAG =∠FCD ,证明∠CEA =90°,即可得到结论;(2)利用勾股定理求得AB 的长,证明△AEC ∽△BED ,利用相似三角形的性质列式计算即可求解.【详解】解:(1)如图:AC =CF =2,CG =DF =1,∠ACG =∠CFD =90°,∴△ACG ≌△CFD , ∴∠CAG =∠FCD ,∵∠ACE +∠FCD =90°,∴∠ACE +∠CAG =90°,∴∠CEA =90°,∴AB 与CD 是垂直的,故答案为:是;(2)AB =AC ∥BD ,∴△AEC ∽△BED ,∴AC AE BD BE =,即23AE BE =,∴25AE BE =,∴AE =25BE【点睛】本题考查了相似三角形的判定和性质,全等三角形的判定和性质,解答本题的关键是明确题意,找出所求问题需要的条件.2.(2022·四川内江·中考真题)如图,在矩形ABCD 中,AB =6,BC =4,点M 、N 分别在AB 、AD 上,且MN ⊥MC ,点E 为CD 的中点,连接BE 交MC 于点F .(1)当F 为BE 的中点时,求证:AM =CE ;(2)若EF BF=2,求AN ND 的值;(3)若MN ∥BE ,求AN ND 的值. 【答案】(1)见解析(2)2737(3)27 【分析】(1)根据矩形的性质,证明△BMF ≌ △ECF ,得BM =CE ,再利用点E 为CD 的 中点,即可证明结论; (2)利用△BMF ∽△ECF ,得12BM B EF CE F ==,从而求出BM 的长,再利用△ANM ∽△BMC ,得AN AM BM BC= ,求出AN 的长,可得答案; (3)首先利用同角的余角相等得 ∠CBF = ∠CMB ,则tan ∠CBF =tan ∠CMB ,得CE BC BC BM= ,可得BM 的长,由(2)同理可得答案. (1)证明:∵F 为BE 的中点,∴BF =EF ,∵四边形ABCD 是矩形,∴AB ∥CD ,AB =CD ∴∠BMF =∠ECF ,∵∠BFM =∠EFC ,∴△BMF ≌△ECF (AAS ),∴BM =CE , ∵点E 为CD 的中点,∴CE =12CD ,∵AB =CD ,∴12BM CE AB ==, ∴AM BM =,∴AM =CE ;(2)∵∠BMF =∠ECF ,∠BFM =∠EFC ,∴△BMF ∽△ECF ,∴12BM B EF CE F ==, ∵CE =3,∴BM =32,∴AM =92,∵CM ⊥MN ,∴∠CMN =90°,∴∠AMN +∠BMC =90°,∵∠AMN +∠ANM =90°,∴∠ANM =∠BMC ,∵∠A =∠MBC ,∴△ANM ∽△BMC ,∴AN AM BM BC =,∴92342AN =,∴7162AN =, ∴DN =AD ﹣AN =4﹣2716=3716,∴272716373716AN DN ==; (3)∵MN ∥BE ,∴∠BFC =∠CMN ,∴∠FBC +∠BCM =90°,∵∠BCM +∠BMC =90°,∴∠CBF =∠CMB ,∴tan ∠CBF =tan ∠CMB , ∴CE BC BC BM =,∴344BM =,∴163BM =,∴162633AM AB BM =−=−=, 由(2)同理得,AN AM BM BC=,∴231643AN =,解得:AN =89, ∴DN =AD ﹣AN =4﹣89=289,∴8292879AN ND ==. 【点睛】本题是相似形综合题,主要考查了矩形的性质,全等三角形的判定与性质,相似三角形的判定与性质,三角函数等知识,求出BM 的长是解决(2)和(3)的关键. 3.(2022·广西贵港·中考真题)已知:点C ,D 均在直线l 的上方,AC 与BD 都是直线l 的垂线段,且BD 在AC 的右侧,2BD AC =,AD 与BC 相交于点O .(1)如图1,若连接CD ,则BCD △的形状为______,AO AD的值为______; (2)若将BD 沿直线l 平移,并以AD 为一边在直线l 的上方作等边ADE V .①如图2,当AE 与AC 重合时,连接OE ,若32AC =,求OE 的长; ②如图3,当60ACB ∠=︒时,连接EC 并延长交直线l 于点F ,连接OF .求证:OF AB ⊥.【答案】(1)等腰三角形,13(2)①OE =②见解析 【分析】(1)过点C 作CH ⊥BD 于H ,可得四边形ABHC 是矩形,即可求得AC =BH ,进而可判断△BCD 的形状,AC 、BD 都垂直于l ,可得△AOC ∽△BOD ,根据三角形相似的性质即可求解.(2)①过点E 作EF AD ⊥于点H ,AC ,BD 均是直线l 的垂线段,可得//AC BD ,根据等边三角形的性质可得30BAD ∠=︒,再利用勾股定理即可求解.②连接CD ,根据//AC BD ,得60CBD ACB ∠=∠=︒,即BCD △是等边三角形,把ABD △旋转得90ECD ABD ∠=∠=︒,根据30°角所对的直角边等于斜边的一般得到13AF AO AB AD ==,则可得AOF ADB △∽△,根据三角形相似的性质即可求证结论. (1)解:过点C 作CH ⊥BD 于H ,如图所示:∵AC ⊥l ,DB ⊥l ,CH ⊥BD ,∴∠CAB =∠ABD =∠CHB =90°,∴四边形ABHC 是矩形,∴AC =BH ,又∵BD =2AC ,∴AC=BH=DH ,且CH ⊥BD ,∴BCD △的形状为等腰三角形,∵AC 、BD 都垂直于l ,∴△AOC ∽△BOD ,122AO AC AC DO DB AC ∴===,即2DO AO =, 133AO AO AD AO DO A AO O ∴===+,故答案为:等腰三角形,13. (2)①过点E 作EF AD ⊥于点H ,如图所示:∵AC ,BD 均是直线l 的垂线段,∴//AC BD ,∵ADE V 是等边三角形,且AE 与AC 重合,∴∠EAD =60°,∴60ADB EAD ∠=∠=︒,∴30BAD ∠=︒,∴在Rt ADB V 中,2AD BD =,AB ,又∵2BD AC =,32AC =,∴6,AD AB ==132AH DH AD ===,又Rt ADB V ,∴EH ==又由(1)知13AO AD ,∴123AO AD ==,则1OH =,∴在Rt EOH △中,由勾股定理得:OE =②连接CD ,如图3所示:∵//AC BD ,∴60CBD ACB ∠=∠=︒,∵BCD △是等腰三角形,∴BCD △是等边三角形,又∵ADE V 是等边三角形, ∴ABD △绕点D 顺时针旋转60︒后与ECD V 重合,∴90ECD ABD ∠=∠=︒,又∵60BCD ACB ∠=∠=︒,∴30ACF FCB FBC ∠=∠=∠=︒,∴2FC FB AF ==,∴13AF AO AB AD ==,又OAF DAB ∠=∠,∴AOF ADB △∽△, ∴90AFO ABD ∠=∠=︒,∴OF AB ⊥.【点睛】本题考查了矩形的判定及性质、三角形相似的判定及性质、等边三角形的判定及性质、勾股定理的应用,熟练掌握三角形相似的判定及性质和勾股定理的应用,巧妙借助辅助线是解题的关键.4.(2022·江苏镇江·九年级期末)梅涅劳斯(Menelaus )是古希腊数学家,他首先证明了梅涅劳斯定理,定理的内容是:如图(1),如果一条直线与△ABC 的三边AB ,BC ,CA 或它们的延长线交于F 、D 、E 三点,那么一定有••1AF BD CE FB DC EA=.下面是利用相似三角形的有关知识证明该定理的部分过程:证明:如图(2),过点A 作AG BC ∥,交DF 的延长线于点G , 则有AF AG FB BD =,CE CD EA AG =,∴1AF BD CE AG BD CD FB DC EA BD DC AG••=••=. 请用上述定理的证明方法解决以下问题:(1)如图(3),△ABC 三边CB ,AB ,AC 的延长线分别交直线l 于X ,Y ,Z 三点,证明:1BX CZ AY XC ZA YB⋅⋅=. (2)如图(4),等边△ABC 的边长为2,点D 为BC 的中点,点F 在AB 上,且2BF AF =,CF 与AD 交于点E ,则AE 的长为________.(3)如图(5),△ABC 的面积为2,F 为AB 中点,延长BC 至D ,使CD BC =,连接FD 交AC 于E ,则四边形BCEF 的面积为________.课后专项训练:1.(2022•江苏中考模拟)对于两个相似三角形,如果沿周界按对应点顺序环绕的方向相同,那么称这两个三角形互为顺相似;如果沿周界按对应点顺序环绕的方向相反,那么称这两个三角形互为逆相似.例如,如图(1),△CDE∽△CAB,且沿周界CDEC与CABC环绕的方向(同为逆时针方向)相同,因此△CDE和△CAB互为顺相似;如图(2),△CDE∽△CBA,且沿周界CDEC与CBAC环绕的方向相反,因此△CDE和△CBA互为逆相似.(1)根据以上材料填空:①如图(3),AB∥CD,则△AOB∽△COD,它们互为相似(填“顺”或“逆”,下同);②如图(4),Rt△ABC中,∠ACB=90°,CD⊥AB于点D,则△ABC∽,它们互为相似;③如图(5),若∠DAB=∠EBC=90°,并且BD⊥CE于点F,则△ABD∽,它们互为相似;(2)如图(6),若△AOB∽△COD,指出图中另外的一对相似三角形并说明理由,同时指出它们互为顺相似还是互为逆相似;(3)如图(7),在Rt△ABC中,∠C=90°,AC=20,BC=15,点P在△ABC的斜边上,且AP=16,过点P画直线截△ABC,使截得的一个三角形与△ABC相似,则满足的截线共有条.【答案】(1)①逆;②△ACD或△CBD,逆;③△BCE,顺;(答案不唯一);(2)△AOC∽△BOD,理由见解析;△AOC和△BOD互为顺相似;(3)3.【分析】(1)①根据新定义直接判断,即可得出结论;②先判断出∠ADC=∠BDC=90°=∠ACB,进而分两种情况,判断出两三角形相似,最后根据新定义判断,即可得出结论;③先判断出∠ABD=∠C,进而得出△ABD∽△BCE,最后用新定义判断,即可得出结论;(2)先由△AOB∽△COD,判断出AO OBCO OD=,∠AOB=∠COD,进而得出∠AOC=∠BOD,即可得出结论;(3)先求出BP=9,分三种情况,过点P作AB,AC,BC的垂线,利用相似三角形得出比例式,建立方程求解,即可得出结论.【详解】(1)①∵AB∥CD,∴△AOB∽△COD,∴△AOB和△COD互为逆相似,故答案为:逆;②∵CD⊥AB,∴∠ADC=∠BDC=90°=∠ACB,Ⅰ、∵∠A=∠A,∴△ABC∽△ACD,∴△ABC和△ACD互为逆相似;Ⅱ、∠B=∠B,∴△ABC∽△CBD,∴△ABC和△CBD互为逆相似;故答案为:△ACD或△CBD,逆;③∵BD⊥CE,∴∠BFC=90°,∴∠CBD+∠C=90°,∵∠EBC=90°,∴∠CBD+∠ABD=90°,∴∠ABD=∠C,∴△ABD∽△BCE,∴△ABD和△BCE互为顺相似;故答案为:△BCE,顺;(2)△AOC∽△BOD,△AOC和△BOD互为顺相似;理由:∵△AOB∽△COD,∴AOCO=OBOD,∠AOB=∠COD,∴∠AOB﹣∠BOC=∠COD﹣∠BOC,∴∠AOC=∠BOD,∵AOCO=OBOD,∴OAOB=OCOD,∴△AOC∽△BOD,∴△AOC和△BOD互为顺相似;(3)在Rt△ABC中,AC=20,BC=15,根据勾股定理得,AB =25,∵AP=16,∴BP=AB﹣AP=9,如图1,①过点P 作PG ⊥BC 于G ,∴∠BGP =90°=∠ACB ,∵∠B =∠B ,∴△ABC ∽△PBG ,∴AB BC BP BG =,∴25159BG =, ∴BG =15925⨯=275<BC ,∴点G 在线段BC (不包括端点)上, ②过点P 作PG ''⊥AC 于G '',∴∠AG ''P =∠ACB ,∵∠A =∠A ,∴△ABC ∽△APG '',∴AB AC AP AG ='',∴252016AG ='', ∴AG ''=201625⨯=645<AC ,∴点G ''在线段AC (不包括端点)上, ③过点P 作PG '⊥AB ,交直线BC 与G ',交直线AC 于H ,∵∠APG '=∠APH =90°=∠ACB ,∵∠A =∠A ,∴△ABC ∽△G 'BP ,∴AB BC BG BP =',∴25159BG =',∴BG '=25915⨯=15=BC , ∴点G '和点H 都和点C 重合(注:为了说明问题,有意将点G '和点H 没画在点C 处),故答案为:3.【点睛】此题是相似形综合题,主要考查了相似三角形的判定和性质,新定义的理解和应用,理解新定义、熟练掌握相似三角形的判定和性质是解本题的关键.2.(2022·吉林·中考真题)下面是王倩同学的作业及自主探究笔记,请认真阅读并补充完整.【作业】如图①,直线12l l ∥,ABC V 与DBC △的面积相等吗?为什么?解:相等.理由如下:设1l 与2l 之间的距离为h ,则12ABC S BC h =⋅,12DBC S BC h =⋅△.∴ABC DBC S S =V V .【探究】(1)如图②,当点D 在1l ,2l 之间时,设点A ,D 到直线2l 的距离分别为h ,h ',则ABC DBC S h S h ='△△.证明:∵ABC S V(2)如图③,当点D 在1l ,2l 之间时,连接AD 并延长交2l 于点M ,则ABC DBC S AM S DM=△△.证明:过点A 作AE BM ⊥,垂足为E ,过点D 作DF BM ⊥,垂足为F ,则90AEM DFM ∠=∠=︒,∴AE ∥ .∴AEM △∽ . ∴AE AM DF DM=. 由【探究】(1)可知ABC DBC S S =△△ ,∴ABC DBC S AM S DM =△△. (3)如图④,当点D 在2l 下方时,连接AD 交2l 于点E .若点A ,E ,D 所对应的刻度值分别为5,1.5,0,ABC DBCS S △△的值为 .【答案】(1)证明见解析(2)证明见解析(3)73【分析】(1)根据三角形的面积公式可得11,22ABC DBC S S BC h BC h '=⋅=⋅V V ,由此即可得证; (2)过点A 作AE BM ⊥,垂足为E ,过点D 作DF BM ⊥,垂足为F ,先根据平行线的判定可得AE DF P,再根据相似三角形的判定可证AEM DFM ~V V ,根据相似三角形的性质可得AE AM DF DM=,然后结合【探究】(1)的结论即可得证; (3)过点A 作AM BC ⊥于点M ,过点D 作DN BC ⊥于点N ,先根据相似三角形的判定证出AME DNE ~,再根据相似三角形的性质可得73AM AE DN DE ==,然后根据三角形的面积公式可得12ABC S BC AM =⋅V ,12DBC S BC DN =⋅V ,由此即可得出答案. (1)证明:12ABC S BC h =⋅V Q ,12DBC BC h S '=⋅V ,ABC DBC S h S h ∴='V V . (2)证明:过点A 作AE BM ⊥,垂足为E ,过点D 作DF BM ⊥,垂足为F ,则90AEM DFM ∠=∠=︒,AE DF ∴∥.AEM DFM ~∴V V .AE AM DF DM ∴=. 由【探究】(1)可知ABC DBC SAE S DF=,ABC DBC S AM S DM ∴=. (3)解:过点A 作AM BC ⊥于点M ,过点D 作DN BC ⊥于点N ,则90AMEDNE ∠=∠=︒,AM DN ∴,AME DNE ∴~,AM AE DN DE∴=, Q 点,,A E D 所对应的刻度值分别为5,1.5,0,5 1.5 3.5AE ∴=−=, 1.5DE =, 3.571.53AM DN ∴==, 又12ABC S BC AM =⋅V Q ,12DBC S BC DN =⋅V , 73ABC DBC SAM S DN =∴=,故答案为:73. 【点睛】本题考查了相似三角形的判定与性质、平行线的判定、三角形的面积等知识点,熟练掌握相似三角形的判定与性质是解题关键.3.(2022·上海·九年级专题练习)如图,在Rt ABC ∆中,90ACB ∠=︒,60BAC ∠=︒,6AC =,AD 平分BAC ∠,交边BC 于点D ,过点D 作CA 的平行线,交边AB 于点E .(1)求线段DE 的长;(2)取线段AD 的中点M ,联结BM ,交线段DE 于点F ,延长线段BM 交边AC 于点G ,求EF DF的值. 【答案】(1)4;(2)23【分析】(1)分别求出CD ,BC ,BD ,证明BDE BCA V V ∽,根据相似性质即可求解; (2)先证明DF AG =,再证明BEF BAG △∽△,根据相似三角形性质求解即可.【详解】解:(1)∵AD 平分BAC ∠,60BAC ∠=︒,∴30DAC ∠=︒.在Rt ACD ∆中,90ACD ∠=︒,30DAC ∠=︒,6AC =,∴CD =在Rt ACB ∆中,90ACB ∠=︒,60BAC ∠=︒,6AC =,∴BC =∴BD BC CD =−=//DE CA ,∴BDE BCA V V ∽∴23DE BD CA BC ==.∴4DE =.(2)∵点M 是线段AD 的中点,∴DM AM =.∵//DE CA ,∴DFM AGM △∽△∴DF DM AG AM =.∴DF AG =. ∵//DE CA ,∴BEF BAG △∽△∴23EF BE BD AG BA BC ===∴23EF DF =. 【点睛】本题考查了含30°角的直角三角形性质,相似的判定与性质,解题的关键是能根据题意确定相似三角形,并根据相似性质解题.4.(2022·上海市奉贤区古华中学九年级期中)已知:如图,四边形ABCD 是平行四边形,在边AB 的延长线上截取BE =AB ,点F 在AE 的延长线上,CE 和DF 交于点M ,BC 和DF 交于点N ,联结BD .(1)求证:△BND ∽△CNM ;(2)如果AD 2=AB •AF ,求证:CM •AB =DM •CN .【分析】(1)利用平行四边形的性质得AB =CD ,AB ∥CD ,再证明四边形BECD 为平行四边形得到BD ∥CE ,根据相似三角形的判定方法,由CM ∥DB 可判断△BND ∽△CNM ; (2)先利用AD 2=AB •AF 可证明△ADB ∽△AFD ,则∠1=∠F ,再根据平行线的性质得∠F =∠4,∠2=∠3,所以∠3=∠4,加上∠NMC =∠CMD ,于是可判断△MNC ∽△MCD ,所以MC :MD =CN :CD ,然后利用CD =AB 和比例的性质即可得到结论.【详解】证明:(1)∵四边形ABCD 是平行四边形,∴AB =CD ,AB ∥CD ,而BE =AB , ∴BE =CD ,而BE∥CD,∴四边形BECD为平行四边形,∴BD∥CE,∵CM∥DB,∴△BND∽△CNM;(2)∵AD2=AB•AF,∴AD:AB=AF:AD,而∠DAB=∠F AD,∴△ADB∽△AFD,∴∠1=∠F,∵CD∥AF,BD∥CE,∴∠F=∠4,∠2=∠3,∴∠3=∠4,而∠NMC=∠CMD,∴△MNC∽△MCD,∴MC:MD=CN:CD,∴MC•CD=MD•CN,而CD=AB,∴CM•AB=DM•CN.【点睛】本题考查了三角形相似的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.在运用相似三角形的性质时主要利用相似比计算线段的长.也考查了平行四边形的判定与性质.5.(2022•安庆模拟)在四边形ABCD中,对角线AC、BD相交于点O.(1)如图①,若四边形ABCD为矩形,过点O作OE⊥BC,求证:OE=CD.(2)如图②,若AB∥CD,过点O作EF∥AB分别交BC、AD于点E、F.求证:=2.(3)如图③,若OC平分∠AOB,D、E分别为OA、OB上的点,DE交OC于点M,作MN ∥OB交OA于一点N,若OD=8,OE=6,直接写出线段MN长度.【分析】(1)由OE⊥BC,DC⊥BC,可知EO∥CD,且OB=OD,可得结论;(2)由△DFO∽△DAB,得,同理,,,利用等式的性质将比例式相加,从而得出结论;(3)作DF∥OB交OC于点F,连接EF,可知△ODF是等腰三角形,得DO=DF=8,由△DMF∽△EMO,可得EM=,由△DMN∽△DOE,得,从而得出答案.【解答】(1)证明:∵四边形ABCD是矩形,∴O是AC中点,AB⊥BC,∵OE⊥BC,∴OE∥AB,∴E是BC中点,∴OE=;(2)证明:∵EF∥AB,∴△DFO∽△DAB,∴,同理,,,∴=,∴,即;(3)解:作DF∥OB交OC于点F,连接EF,∵OC平分∠AOB,∴∠AOC=∠BOC,∵DF∥OB,∴∠DFO=∠BOC=∠AOC,∴△ODF是等腰三角形,∴DO=DF=8,∵DF∥OE,∴△DMF∽△EMO,∴,∴EM=,∴,∵MN∥OE,∴△DMN∽△DOE,∴,∴,∴MN=.【点评】本题是相似形综合题,主要考查了矩形的性质,相似三角形的判定与性质,等腰三角形的性质,对比例式进行恒等变形是解题的关键.6.(2022•重庆中考模拟)问题提出:如图1,D、E分别在△ABC的边AB、AC上,连接DE,已知线段AD=a,DB=b,AE=c,EC=d,则S△ADE,S△ABC和a,b,c,d之间会有怎样的数量关系呢?问题解决:探究一:(1)看到这个问题后,我们可以考虑先从特例入手,找出其中的规律.如图2,若DE ∥BC ,则∠ADE =∠B ,且∠A =∠A ,所以△ADE ∽△ABC ,可得比例式:a c a b c d =++而根据相似三角形面积之比等于相似比的平方.可得()22ADE ABC S a S a b =+V V .根据上述这两个式子,可以推出:()()()22ADE ABC S a a a a c ac S a b a b a b c d a b c d a b ==⋅=⋅=+++++++V V . (2)如图3,若∠ADE =∠C ,上述结论还成立吗?若成立,请写出证明过程;着不成立,请说明理由.探究二:回到最初的问题,若图1中没有相似的条件,是否仍存在结论:()()ADE ABC S ac S a b c d =++V V 方法回顾:两个三角形面积之比,不仅可以在相似的条件下求得,当两个三角形的底成高具有一定的关系时,也可以解决.如图4,D 在△ABC的边上,做AH ⊥BC 于H ,可得:1212ABDADC BD AH S BD S DC DC AH ⋅==⋅V V .借用这个结论,请你解决最初的问题. 延伸探究:(1)如图5,D 、E 分别在△ABC 的边AB 、AC 反向延长线上,连接DE ,已知线段AD =a ,AB =b ,AE =c ,AC =d ,则ADE ABCS S =V V .(2)如图6,E 在△ABC 的边AC 上,D 在AB 反向延长线上,连接DE ,已知线段AD =a ,AB =b ,AE =c ,AC =d ,ADE ABCS S =V V . 结论应用:如图7,在平行四边形ABCD 中,G 是BC 边上的中点,延长GA 到E ,连接DE 交BA 的延长线于F ,若AB =5,AG =4,AE =2,▱ABCD 的面积为30,则△AEF 的面积是 .【答案】探究一:(2)见解析;延伸探究:(1)ac bd ;(2)ac bd ;结论应用: 32【分析】问题解决:探究一(2):参照(1)中证明方法解答即可;探究二,过D 、B 点分别作,DM AC BN AC ⊥⊥,垂足分别为M 、N ,然后按照探究一中方法证明即可;延伸探究:(1)过D 、B 点分别作,DM AC BN AC ⊥⊥,垂足分别为M 、N ,然后按照探究一中方法证明即可;(2)过D 、B 点分别作,DM AC BN AC ⊥⊥,垂足分别为M 、N ,然后按照探究一中方法证明即可;结论应用:取AD 的中点M ,连接GM 并延长交DE 于点N ,连接DG ,可得15ADG S =V ,根据题意,进而得出152ADE S =V ,根据AM =DM ,MN AF ∥,可得FN =DN ,根据AE =2,AG =4,GN AF ∥,可得FN =2EF ,进而可得ED =5EF ,即可得出1352AEF ADE S S ==V V . 【详解】解:问题解决:探究一:(2)成立,理由如下:∵∠ADE =∠C ,∠A =∠A ,∴ADE ACB V V ∽,∴a c c d a b =++, ∴()22()()ADE ABC S b a S c a c ac c d a b c d a d =+=++++=V V g ; 探究二:过D 、B 点分别作,DM AC BN AC ⊥⊥,垂足分别为M 、N ,∵,DM AC BN AC ⊥⊥,∴//DM BN ,∴AD DM a AB BN a b==+,121()()2ADEABC AE DM S AE DM c a ac S AC BN c d a b a b c d AC BN ⨯==⨯=⨯=++++⨯V V ;延伸探究:(1)过D 、B 点分别作,DM AC BN AC ⊥⊥,垂足分别为M 、N ,∵,DM AC BN AC ⊥⊥,∴//DM BN ,∴AD DM a AB BN b==,1212ADEABC AE DM S AE DM c a ac S AC BN d b bd AC BN ⨯==⨯=⨯=⨯V V ; (2)过D 、B 点分别作,DM AC BN AC ⊥⊥,垂足分别为M 、N ,∵,DM AC BN AC ⊥⊥,∴//DM BN ,∴AD DM a AB BN b==,1212ADEABC AE DM S AE DM c a ac S AC BN d b bd AC BN ⨯==⨯=⨯=⨯V V ; 结论应用:取AD 的中点M ,连接GM 并延长交DE 于点N ,连接DG ,∴AM =DM ,1152ADG ABCD S S ==V 平行四边形,∵AE =2,AG =4,∴11522ADE ADG S S ==V V , ∵AM =DM ,MN AF P ,∴FN =DN ,∵AE =2,AG =4,GN AF ∥,∴12EF AE FN AG ==,即:FN =2EF ,∴ED =5EF ,∴1352AEF ADE S S ==V V . 【点睛】本题考查了相似三角形的判定与性质,平行线分线段成比例等知识点,熟练运用相似三角形的性质是解题的关键.7.(2022·贵州铜仁·中考真题)如图,在四边形ABCD 中,对角线AC 与BD 相交于点O ,记COD △的面积为1S ,AOB V 的面积为2S .(1)问题解决:如图①,若AB //CD ,求证:12⋅=⋅S OC OD S OA OB(2)探索推广:如图②,若AB 与CD 不平行,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由.(3)拓展应用:如图③,在OA 上取一点E ,使OE OC =,过点E 作EF CD ∥交OD 于点F ,点H 为AB 的中点,OH 交EF 于点G ,且2=OG GH ,若56=OE OA ,求12S S 值.【答案】(1)见解析;(2)(1)中的结论成立,理由见解析:(3)2554【分析】(1)如图所示,过点D 作AE ⊥AC 于E ,过点B 作BF ⊥AC 于F ,求出sin sin DE OD DOE BF OB BOF =⋅=⋅∠,∠,然后根据三角形面积公式求解即可; (2)同(1)求解即可;(3)如图所示,过点A 作AM EF ∥交OB 于M ,取BM 中点N ,连接HN ,先证明△OEF ≌△OCD ,得到OD =OF ,证明△OEF ∽△OAM ,得到5==6OF OE OM OA ,设55OE OC m OF OD n ====,,则66OA m OM n ==,,证明△OGF ∽△OHN ,推出31522n ON OF ==,32n BN MN ON OM ==−=,则9OB ON BN n =+=,由(2)结论求解即可.【详解】解:(1)如图所示,过点D 作AE ⊥AC 于E ,过点B 作BF ⊥AC 于F , ∴sin sin DE OD DOE BF OB BOF =⋅=⋅∠,∠,∴111===sin 22OCD S S OC DE OC OD DOE ⋅⋅⋅△∠, 211==sin 22AOB S S OA BF OA OB BOF ⋅=⋅⋅△∠, ∵∠DOE =∠BOF ,∴sin sin DOE BOF ∠=∠; ∴121sin 2==1sin 2OC OD DOE S OC OD S OA OBOA OB BOF ⋅⋅⋅⋅⋅⋅∠∠;(2)(1)中的结论成立,理由如下:如图所示,过点D 作AE ⊥AC 于E ,过点B 作BF ⊥AC 于F ,∴sin sin DE OD DOE BF OB BOF =⋅=⋅∠,∠, ∴111===sin 22OCD S S OC DE OC OD DOE ⋅⋅⋅△∠, 211==sin 22AOB S S OA BF OA OB BOF ⋅=⋅⋅△∠, ∵∠DOE =∠BOF ,∴sin sin DOE BOF ∠=∠; ∴121sin 2==1sin 2OC OD DOE S OC OD S OA OBOA OB BOF ⋅⋅⋅⋅⋅⋅∠∠; (3)如图所示,过点A 作AM EF ∥交OB 于M ,取BM 中点N ,连接HN ,∵EF CD ∥,∴∠ODC =∠OFE ,∠OCD =∠OEF ,又∵OE =OC ,∴△OEF ≌△OCD (AAS ),∴OD =OF ,∵EF AM ∥,∴△OEF ∽△OAM ,∴5==6OF OE OM OA , 设55OE OC m OF OD n ====,,则66OA m OM n ==,,∵H 是AB 的中点,N 是BM 的中点,∴HN 是△ABM 的中位线,∴HN AM EF ∥∥,∴△OGF ∽△OHN ,∴OG OF OH ON=,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
母子型相似三角形
【知识要点】
一、直角三角形相似
1、直角三角形被斜边上的高分成两个直角三角形和原三角形相似。
2、如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。
基本图形(母子三角形)举例:
1、条件:如图,已知△ABC 是直角三角形,CD 为斜边AB 上的高. 结论:(1)△ACD ∽△CBD ,△BDC ∽△BCA ,△CDA ∽△BCA
(2)△ACD ∽△CBD 中,2
CD AD BD = △BDC ∽△BCA 中,2
BC BD AB = △CDA ∽△BCA 中,2
AC AD AB =
2、条件:如图,已知∠ACD=∠ABC
结论:△ACD ∽△ABC 中,2
AC AD AB =
【例题解析】
类型一:三角形中的母子型
【例1】1.如图,ΔABC 中,∠A=∠DBC,BC=,SΔBCD ∶SΔABC=2∶3,则CD=______.
【练】如图,D 是 △ABC 的边AB 上一点,连结CD.若AD= 2,BD = 4, ∠ACD =∠B 求AC 的长.
【例2】如图,在△ABC 中,AD 为∠A 的平分线,AD 的垂直平分线交AD 于E ,交BC 的延长线于F ,
求证:FC FB FD ⋅=2
【练】已知CD 是ABC ∆的高,,DE CA DF CB ⊥⊥,如图3-1,求证:CEF CBA ∆∆∽
类型二:直角三角形中的母子型
【例1】.如图,在△ABC 中,AD 、BE 分别为BC 、AC 边上的高,过D 作AB 的垂线交AB 于F ,交BE
于G ,交AC 的延长于H ,求证:
2DF FG FH =∙ 【练】如图5,RtΔABC 中,∠ACB=90°,CD ⊥AB,AC=8,BC=6,则AD=____,CD=_______.
【例2】如图1,∠ADC=∠ACB=90°,∠1=∠B,AC=5,AB=6,则AD=______. 【练】如图,CD 是 Rt △ABC 斜边上的高.若AD= 2,BD = 4, 求CD 的长. 类型三:四边形中的母子型
【例1】1.如图,矩形ABCD 中,BH ⊥AC 于H ,交CD 于G ,求证:2
BC CG CD =∙。
2.如图,菱形ABCD 中,AF ⊥BC 于F ,AF 交BD 于E ,求证:
21
2AD DE DB =
∙。
类型四:圆中的母子型
【例1】1.如图,△ABC 内接于⊙O ,∠BAC 的平分线交BC 于D ,交⊙O 于E , 求证:2
EB DE AE =∙。
2.如图,PA 切⊙O 于A ,AB 为⊙O 的直径,M 为PA 的中点,连BM 交⊙O 于C ,
求证:(1)2
AM MC MB =∙ (2)∠MPC=∠MBP 。
“K 字型”相似专题复习
【活动一】
K 字型相似基本图形1:
条件:B ,C ,E 三点共线,∠B=∠ACD=∠E=90° 结论:△ABC ∽△CED 【应用】
1.如图,已知点A (0,4)、B (4,1),BC ⊥x 轴于点C ,点P 为线段OC 上一点,且PA ⊥PB .则点P 的坐标为
2.如图,在梯形ABCD 中,已知AD ∥BC ,∠B=90°,AB=7,AD=9,BC=12,在线段BC 上任取一点E ,连接DE ,作EF ⊥DE ,
交直线AB 于点F .
(1)若点F 与B 重合,求CE 的长;
(2)若点F 在线段AB 上,且AF=CE ,求CE 的长.
3.(1)如图②,已知点A (-2,1),点B 在直线y=-2x+3上运动,若∠AOB=90°,求此时点B 的坐标;
(2)如图③,过点A (-2,1)作x 轴与y 轴的平行线,交直线y=-2x+3于点C 、D ,求点A 关于直线CD 的对称点E 的坐标.
A B
C
D
E
【活动二】
K 字型相似基本图形2:
条件:B ,D ,C 三点共线,∠B=∠EDF=∠C= α 结论:△BDE ∽△CFD 证明: 【应用】
1.如图,在平面直角坐标中,四边形OABC 是等腰梯形,CB ∥OA ,OA=7,BC=1,AB=5,点P 为x 轴上的一个动点,点P 不与点0、点A 重合.连接CP ,过点P 作
PD
交AB 于点D .
(1)直接写出点B 的坐标 .
(2)当点P 在线段OA 上运动时,使得∠CPD=∠OAB ,且BD: AD=3:2
,求点P 的坐标.
B。
