万有引力:模型分类(含答案)
万有引力中常考的物理模型

万有引力中必考的几个模型一. 地球表面上的物体的重力与万有引力的关系在地球表面上的物体随地球的自转而做匀速圆周运动,物体受到指向圆周圆心的向心力作用,其方向垂直指向转轴(地轴),圆心在地轴上。
此向心力由地球对物体的万有引力的分力提供,而万有引力的另一个分力,即物体所受的重力G =mg ,如图所示。
1.在赤道,万有引力方向指向_____,向心力大小最___,方向指向______,重力大小最_____,方向指向________; 2.在两极,万有引力方向指向_____,向心力大小最___,方向指向______,重力大小最_____,方向指向________。
3.只有物体在______时,物体所受的万有引力才等于重力。
总之,无论如何,都不能说重力就是万有引力。
注意:“当地球自转影响可以忽略不计时,可以认为物体的重力近似等于物体所受万有引力”二、星球表面的和某一高度处的重力加速度当物体在距地面一定高度绕地心做匀速圆周运动时,物体仅受地球的引力,且此时地球对物体的万有引力就等于物体重力,引力提供物体做圆周运动的向心力,所以三者相等,但要明白,向心力只是从效果上的命名。
由2)(h R Mm Gg m +='得,离地面高h 处重力加速度2)(h R M Gg +=',这里M 、R 分别为地球的质量和半径,将h 取作0,即得地球表面的重力加速度为2RM Gg =利用黄金代换2gR GM =得:22/)(h R gRg +=注意:重力加速度随高度的增加而减小三、卫星运行速度v 、角速度ω、周期T 与轨道半径R 的关系:(天上模型,我们可以理解为离中心天体远,运动的慢,离得近,运动的快。
)①由2RGmM=R mv2有v='R GM 即v ∝R 1,故R 越大,运行速度v 越小; ②由2RGmM=m ω2R 有ω=3RGM,即v ∝31R,故R 越大,角速度ω越小;③由2R GmM=m(T π2)2R 有T=GM R324π,即T ∝3R ,故R 越大,周期T 越大.四、求中心天体的质量的方法1.根据天体表面上物体的重力近似等于物体所受的万有引力,由天体表面上的重力加速度和天体的半径求天体的质量 由mg=G2RMm 得 Gg R M 2=.2.根据绕中心天体运动的卫星的运行周期和轨道半径,求中心天体的质量卫星绕中心天体运动的向心力由中心天体对卫星的万有引力提供,利用牛顿第二定律得 222224Tmrmr rvmrMm G πω===若已知卫星的轨道半径r 和卫星的运行周期T 、角速度ω或线速度v ,可求得中心天体的质量为Gr GTr Grv M 3223224ωπ===注意:除了知道G ,r 之外还要知道v ,T 、ω、f ,a 中的一个就可以求出中心天体的质量。
专题04 万有引力与航天方法模型(原卷版)

专题04 万有引力与航天方法模型一、天体质量和密度的估算1.如图所示是嫦娥探测器的变轨示意图,已知探测器在变入低轨后的绕月圆轨道上运动的周期为T ,轨道半径为r ,月球表面重力加速度为0g ,则( ) A .探测器在变轨以后机械能比变轨前大B .探测器在圆轨道上运动时处于平衡状态,飞船内的物体所受合力为零C 02rrTg π D .月球的平均密度为3023()8g rπ 2.中国空间站天和核心舱绕地球的运行可视为匀速圆周运动,已知其轨道距地面的高度为h ,运行周期为T ,地球半径为R ,万有引力常量为G ,由此可得到地球的平均密度为( ) A .23GT πB .24GT πC .3233()R h GT R π+D .23233()R h GT R π-3.北斗卫星导航系统[BeiDou (COMPASS )NavigationSatelliteSystem]是我国自主发展、独立运行的全球卫星导航系统。
如图,I 为地球近地卫星,II 为北斗卫星导航系统中的一颗静止轨道卫星,其对地张角为2θ。
已知地球自转周期为0T ,万有引力常量为G 。
下列说法正确的是( )A .地球的平均密度为2303sin GT πθ B .卫星I 和卫星II 的加速度之比为31sin θC .卫星I 的周期为3sin 2T θD .卫星II 的发射速度大于11.2km/s4.2022年11月1日,梦天实验舱与“天宫”空间站在轨完成交会对接,目前已与天和核心舱、问天实验舱形成新的空间站“T”字基本构型组合体。
已知组合体的运行轨道距地面高度为h (约为400km ),地球视为理想球体质量为M ,半径为R ,地球表面的重力加速度为g ,引力常量为G ,下列说法正确的是( ) A .航天员漂浮在组合体中,处于平衡状态 B .地球的平均密度可表示为34gGRρπ= C .组合体轨道处的重力加速度为22()gR R h + D .组合体的运行速度为GMR h+ 【模型方法总结】1.“自力更生”法(g -R ):利用天体表面的重力加速度g 和天体半径R 。
万有引力定律在天体运动问题中的应用模型 (含答案)(5)

万有引力定律在天体运动问题中的应用模型大连市物理名师工作室 门贵宝1、一个简化模型: 一颗 环绕天体 绕一颗 中心天体 做近似的匀速圆周运动。
如图所示:中心天体的质量为M ,半径为R ,表面重力加速度为g ;环绕天体的质量为m ,环绕速度(线速度)为v ,角速度为ω,环绕周期为T ,轨道半径为r ,环绕天体可看成质点。
2、一个核心方程:环绕天体做匀速圆周运动所需的向心力由中心天体对它的万有引力提供。
r v mrMm G 22= 或 22ωmr rMm G = 3、两组常用推论:第一组:环绕速度与轨道半径的关系rGMv = 3r GM =ω第二组:轨道半径和环绕周期的关系2234πGM T r =2324GT r M π=4、两个常用近似:当研究中心天体表面问题或近天体表面环绕问题时,有以下两个近似关系:r R =mg R MmG =2mRT )M ( g )5、综合“金三角”关系圈:6、“人造地球同步卫星”问题:地球同步卫星的特点是它绕地轴运转的角速度与地球自转的角速度相同,同步卫星轨道是 (“椭圆”、“圆 ” ),为 (赤道轨道、极地轨道、顺行轨道、逆行轨道 );其高度一定,约为36000Km ,环绕速度一定,约为 3100m ∕s 。
同步卫星的发射,通常都采用变轨发射的方法。
要实现全球通信,至少需发射三颗地球同步卫星且对称分布在同一轨道上。
7、 “嫦娥1号”奔月问题:一般环绕问题天体表面问题近天体表面环绕问题rGM v =2234πGM T r =2RGM g =mggRv =)(22ωmr rv m 2rMmG8、“神舟八号”与“天宫一号”的对接问题: 9、“双星”问题: 针对训练1.人造地球卫星的轨道半径越大,则( B ) A .速度越小,周期越小 B .速度越小,周期越大 C .速度越大,周期越小 D .速度越大,周期越大2.两颗人造地球卫星,都在圆形轨道上运行,它们的质量相等,轨道半径之比r 1/r 2=2,则它们动能之比E 1/E 2等于( C ) A . 2 B .1 C . 1/2 D . 43.已知引力常量G 、月球中心到地球中心的距离R 和月球绕地球运行的周期T 。
2020年高考物理《解题模型》之力学篇-专题04 曲线运动与万有引力定律(含答案解析)
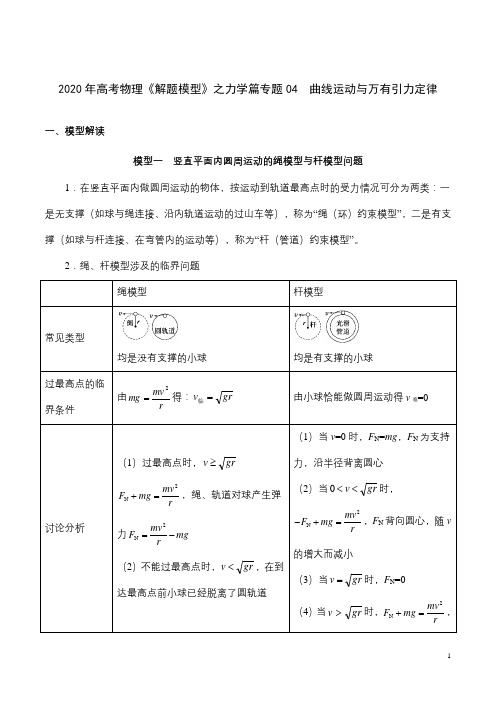
2020年高考物理《解题模型》之力学篇专题04 曲线运动与万有引力定律一、模型解读模型一竖直平面内圆周运动的绳模型与杆模型问题1.在竖直平面内做圆周运动的物体,按运动到轨道最高点时的受力情况可分为两类:一是无支撑(如球与绳连接、沿内轨道运动的过山车等),称为“绳(环)约束模型”,二是有支撑(如球与杆连接、在弯管内的运动等),称为“杆(管道)约束模型”。
2.绳、杆模型涉及的临界问题绳模型杆模型常见类型均是没有支撑的小球均是有支撑的小球过最高点的临界条件由rmvmg2=得:grv=临由小球恰能做圆周运动得v临=0讨论分析(1)过最高点时,grv≥2NmvF mgr+=,绳、轨道对球产生弹力2NmvF mgr=-(2)不能过最高点时,grv<,在到达最高点前小球已经脱离了圆轨道(1)当v=0时,F N=mg,F N为支持力,沿半径背离圆心(2)当grv<<0时,2NmvF mgr-+=,F N背向圆心,随v的增大而减小(3)当grv=时,F N=0(4)当grv>时,2NmvF mgr+=,F N指向圆心并随v的增大而增大3.竖直面内圆周运动的求解思路(1)定模型:首先判断是轻绳模型还是轻杆模型,两种模型过最高点的临界条件不同.(2)确定临界点:gr,对轻绳模型来说是能否通过最高点的临界点,而对轻杆模v临型来说是F N表现为支持力还是拉力的临界点.(3)研究状态:通常情况下竖直平面内的圆周运动只涉及最高点和最低点的运动情况.(4)受力分析:对物体在最高点或最低点时进行受力分析,根据牛顿第二定律列出方程,F合=F向.(5)过程分析:应用动能定理或机械能守恒定律将初、末两个状态联系起来列方程.模型二双星系统模型1.模型特点(1)“向心力等大反向”——两颗星做匀速圆周运动的向心力由它们之间的万有引力提供,故F1=F2,且方向相反,分别作用在两颗行星上,是一对作用力和反作用力。
(2)“周期、角速度相同”——两颗行星做匀速圆周运动的周期、角速度相等。
7-2 万有引力定律 -高一物理(2019人教版必修第二册)(解析版)

万有引力定律知识导航知识精讲考点1:太阳与行星间引力的理解1.两个理想化模型(1)匀速圆周运动模型:由于太阳系中行星绕太阳做椭圆运动的轨迹的两个焦点靠得很近,行星的运动轨迹非常接近圆,所以将行星的运动看成匀速圆周运动。
(1)质点模型:由于天体间的距离很远,研究天体间的引力时将天体看成质点,即天体的质量集中在球心上。
2.推导过程(1)太阳对行星的引力(2)太阳与行星间的引力【例1】(多选)关于太阳与行星间的引力,下列说法中正确的是()A.由于地球比木星离太阳近,所以太阳对地球的引力一定比对木星的引力大B.行星绕太阳沿椭圆轨道运动时,在从近日点向远日点运动时所受引力变小C .由F =GMm r 2可知G =Fr 2Mm ,由此可见G 与F 和r 2的乘积成正比,与M 和m 的乘积成反比D .行星绕太阳的椭圆轨道可近似看成圆形轨道,其向心力来源于太阳对行星的引力【解析】BD 由F =GMmr 2,太阳对行星的引力大小与m 、r 有关,对同一行星,r 越大,F 越小,选项B 正确;对不同行星,r 越小,F 不一定越大,还要由行星的质量决定,选项A 错误;公式中G 为比例系数,是一常量,与F 、r 、M 、m 均无关,选项C 错误;通常的研究中,行星绕太阳的椭圆轨道可近似看成圆形轨道,向心力由太阳对行星的引力提供,选项D 正确。
太阳与行星间的引力特点(1)太阳与行星间的引力大小与三个因素有关:太阳质量、行星质量、太阳与行星间的距离。
太阳与行星间引力的方向沿着二者的连线方向。
(2)太阳与行星间的引力是相互的,遵守牛顿第三定律。
1.(多选)下列叙述正确的是 ( )A .在探究太阳对行星的引力规律时,我们引用了公式F =m v 2r ,这个关系式实际上是牛顿第二定律,是可以在实验室中得到验证的B .在探究太阳对行星的引力规律时,我们引用了公式v =2πrT ,这个关系式实际上是匀速圆周运动的一个公式,它是由线速度的定义式得来的C .在探究太阳对行星的引力规律时,我们引用了公式r 3T 2=k ,这个关系式是开普勒第三定律,是可以在实验室中得到验证的D .在探究太阳对行星的引力规律时,使用以上三个公式,都是可以在实验室中得到验证的【解析】AB 公式F =m v 2r 中,v 2r 是行星做圆周运动的加速度,故这个关系式实际上是牛顿第二定律,也是向心力公式,所以能通过实验验证,故A 正确;v =2πrT 是在匀速圆周运动中,周长、时间与线速度的关系式,故B 正确;开普勒第三定律r 3T 2=k 是无法在实验室中得到验证的,是开普勒在研究天文学家第谷的行星观测记录时发现的,故C 、D 错误。
万有引力与航天专题:双星模型、变轨问题和地球表面物体的运动

二、变轨问题
卫 星 的 发 射 过 程 动 画
二、卫星的变轨问题
1.变轨原理及过程 人造卫星的发射过程要经过多
次变轨方可到达预定轨道,如图所示。
(1)为了节省能量 ,在赤道上顺着地球自转方向发射卫星到圆 轨道Ⅰ上。 (2)在A点点火加速,由于速度变大,进入椭圆轨道Ⅱ。 (3)在B点(远地点)再次点火加速进入圆形轨道Ⅲ。
期相等,角速度也相等。由 v=rω 得线速度与 两子星圆周运动的半径是成正比的。因为两子 星圆周运动的向心力由两子星间的万有引力提 供,向心力大小相等,
由G
M1M 2 L2
M1r12 , G
M1M 2 L2
M 2r22
可知: M1r1 2 M 2r2 2 ,所以它们的轨道半径
与它们的质量是成反比的。而线速度又与轨 道半径成正比,所以线速度与它们的质量也 是成反比的。正确答案为:BD。
【解析】这两颗星必须各自以一定的速度绕某一中心转 动才不至于因万有引力作用而吸引在一起,从而保持两 星间距离L不变,且两者做匀速圆周运动的角速度ω必 须相同。如图所示,两者轨迹圆的圆心为O,圆半径分 别为R1和R2。由万有引力提供向心力,有
处理方法:
对m1来说:
G
m1m2 L2
=m1ω2R1
对m2来说:
A.飞船在轨道Ⅱ上经过P的速度小于经过Q的速度 B.飞船在轨道Ⅱ上经过P的速度小于在轨道Ⅰ上经 过M的速度 C.飞船在轨道Ⅱ上运动的周期大于在轨道Ⅰ上运 动的周期 D.飞船在轨道Ⅱ上经过P的加速度小于在轨道Ⅰ上 经过M的加速度
反思总结 1.变轨的两种情况
2.相关物理量的比较
(1)两个不同轨道的“切点”处线速度v不相等,图中vⅢ>vⅡB,vⅡA>vⅠ。 (2)同一个椭圆轨道上近地点和远地点线速度大小不相等,vⅡA>vⅡB, (3)两个不同圆轨道上的线速度v不相等,轨道半径越大,v越小,图中vⅠ>vⅢ。 (4)卫星在同一点的不管是椭圆还是圆,加速度一定相等。
万有引力 星表模型、环绕模型 高三物理二轮复习新高考版(含解析)

万有引力星表模型、环绕模型-名校高中物理精品1.下列说法符合物理学史的是()。
A.英国物理学家笛卡儿在实验室测出了引力常量G的数值,被称为“称量地球重量”的人B.牛顿对引力常量G进行准确测定,并于1687年发表在其传世之作《自然哲学的数学原理》中C.牛顿做过著名的“月—地”检验来证明重力和星体间的引力是同一性质的力D.开普勒行星运动定律是开普勒在自己观测记录的基础上整理和研究出来的2.2020年3月9日19时55分,我国在西昌卫星发射中心成功发射北斗系统第五十四颗导航卫星——北斗三号GEO-2,该卫星是一颗地球同步轨道卫星。
关于这颗卫星的判断,下列说法正确的是()。
A.地球同步轨道卫星的轨道平面可以与赤道平面垂直B.地球同步轨道卫星绕地运行时所受引力保持不变C.地球同步轨道卫星绕地运行时处于平衡状态D.地球同步轨道卫星的在轨运行速度小于第一宇宙速度3.已知某行星的密度为地球密度的两倍,地球近地卫星的周期约为84 min,则该行星的近地卫星周期大约为()。
A.40 minB.60 minC.120 minD.170 min4.“天琴一号”卫星于2019年12月20日11时22分在山西太原升空,并于2020年1月18日成功完成了无拖曳控制技术的在轨验证。
它是我国“天琴”计划的首颗技术验证卫星。
已知“天琴一号”卫星和地球同步卫星的周期之比约为1∶6√6。
则可以判断()。
A.“天琴一号”卫星的角速度和同步卫星的角速度之比约为1∶6√6B.“天琴一号”卫星的线速度和同步卫星的线速度之比约为6√6∶1C.“天琴一号”卫星的轨道半径和同步卫星的轨道半径之比约为1∶6D.“天琴一号”卫星的向心加速度和同步卫星的向心加速度之比约为6√6∶15.北京时间2019年12月27日20时45分10秒,“长征五号”遥三运载火箭自中国文昌航天发射场点火升空,将“实践二十号”卫星准确送入预定轨道。
未来,“长征五号”将运送宇航员登上月球,探索月球的奥秘。
《万有引力与天体运动》习题及答案

地球abc 万有引力航天一、“中心天体-圆轨道”模型【应用知识】由万有引力提供环绕天体做圆周运动的向心力,据牛顿第二定律列出圆周运动的动力学方程。
1、对中心天体可求质量和密度2、对环绕天体可求线速度、角速度、周期、向心加速度、向心力、轨道所在处的重力加速度3、可求第一宇宙速度例1.如图所示,a 、b 、c 是环绕地球在圆形轨道上运行的3颗人造卫星,它们质量关系是m a =m b <m c ,则: A .b 、c 的线速度大小相等,且大于a 的线速度 B .b 、c 的周期相等,且小于a 的周期C .b 、c 的向心加速度大小于相等,且大于a 的向心加速度D .b 所需向心力最小例2、我国将要发射一颗绕月运行的探月卫星“嫦娥1号”。
设该卫星的轨道是圆形的,且贴近月球表面。
已知月球的质量约为地球质量的181 ,月球的半径约为地球半径的14,地球上的第一宇宙速度约为7.9km/s ,则该探月卫星绕月运行的速率约为( D )A .0.4km/sB .1.8km/sC .11km/sD .36km/s二、“同步卫星”模型同步卫星具有四个一定1、 定轨道平面2、 定运行周期:T =24h3、 定运动高度:km R GMT h 4322106.34⨯=-=π4、 定运行速率:s km /0.3=υ例3.某颗地球同步卫星正下方的地球表面上有一观察者,他用天文望远镜观察被太阳照射的此卫星,试问,春分那天(太阳光直射赤道)在日落12h 内有多长时间该观察者看不见此卫星?已知地球半径为R ,地球表面处的重力加速度为g ,地球的自转周期为T ,不考虑大气对光的折射。
例4.地球赤道上有一物体随地球的自转而做圆周运动,所受的向心力为F 1,向心加速度为a 1,线速度为v 1,角速度为ω1;绕地球表面附近做圆周运动的人造卫星受的向心力为F 2,向心加速度为a 2,线速度为v 2,角速度为ω2;地球同步卫星所受的向心力为F 3,向心加速度为a 3,线速度为v 3,角速度为ω3.地球表面重力加速度为g ,第一宇宙速度为v ,假设三者质量相等.则( )A.F 1=F 2>F 3B.a 1=a 2=g >a 3 3122)4arcsin(gT R T t ππ=C.v 1=v 2=v >v 3D.ω1=ω3<ω2三、“天体相遇”模型 两天体相遇,实际上是指两天体相距最近,条件是)3,2,1(221 ==-n n t t πωω 两天体相距最远,条件是)3,2,1()12(21 =-=-n n t t πωω例5.A 是地球的同步卫星,另一卫星B 的圆形轨道位于赤道平面内,离地面高度为h ,已知地球半径为R ,地球自转角速度ω0,地球表面的重力加速度为g ,O 为地球中心。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1(2018广州一模)如图,已知现在地球的一颗同步通讯卫星信号最多覆盖地球赤道上的经度范围为。
假设地球的自转周期变大,周期变大后的一颗地球同步通讯卫星信号最多覆盖的赤道经度范围为,则前后两次同步卫星的运行周期之比为A.B.C.D.2.(2016·河北石家庄二中一模)有a 、b 、c 、d 四颗地球卫星,a 还未发射,在赤道表面上随地球一起转动,b 是近地轨道卫星,c 是地球同步卫星,d 是高空探测卫星,它们均做匀速圆周运动,各卫星排列位置如图所示,则( )A .a 的向心加速度等于重力加速度gB .在相同时间内b 转过的弧长最长2α2βC .c 在4小时内转过的圆心角是π6D .d 的运动周期有可能是20小时3(9分)(2016北京东城期末)我国自1970年4月24日发射第一颗人造地球卫星----“东方红”1号以来,为了满足通讯、导航、气象预报和其它领域科学研究的不同需要,又发射了许多距离地面不同高度的人造地球卫星。
卫星A 为近地卫星,卫星B 为地球同步卫星,它们都绕地球做匀速圆周运动。
已知地球半径为R ,卫星A 距地面高度可忽略不计,卫星B 距地面高度为h ,不计卫星间的相互作用力。
求: ⑴卫星A 与卫星B 运行速度大小之比; ⑵卫星A 与卫星B 运行周期之比; ⑶卫星A 与卫星B 运行的加速度大小之比。
4(2014·全国大纲卷)已知地球的自转周期和半径分别为T 和R 。
地球同步卫星A 的圆轨道半径为h ,卫星B 沿半径为r (r<h )的圆轨道在地球赤道的正上方运行,其运行方向与地球自转方向相同。
求:(1)卫星B 做圆周运动的周期;(2)卫星A 和B 连续地不能直接通讯的最长时间间隔(信号传输时间可忽略)。
5. (2004·广东)某颗地球同步卫星正下方的地球表面上有一观察者,他用天文望远镜观察被太阳光照射的此卫星,试问,春分那天(太阳光直射赤道)在日落12小时内有多长时间该观察者看不见此卫星?已知地球半径为R ,地球表面处的重力加速度为g,地球自转周期为T ,不考虑大气对光的折射。
1.(2018河南八市学评测试)地球赤道上一位观察者a ,赤道平面内有一颗自西向东运行的近地卫星b ,a 观测发现,其正上方有一颗静止不动的卫星c ,每隔时间T 卫星b 就会从其正上方飞过。
已知地球半径为R ,地球表面的重力加速度为g ,万有引力常量为G ,下列说法正确的是A .c 的加速度大于b 的加速度B .a 的线速度大于c 的线速度C .地球的质量为D .c2324R GT π2、(2016·赣州高三第一次联考)太阳系中某行星运行的轨道半径为R 0,周期为T 0,但天文学家在长期观测中发现,其实际运行的轨道总是存在一些偏离,且周期性地每隔t 0时间发生一次最大的偏离(行星仍然近似做匀速圆周运动)。
天文学家认为形成这种现象的原因可能是该行星外侧还存在着一颗未知行星。
假设两行星的运行轨道在同一平面内,且绕行方向相同,则这颗未知行星运行轨道的半径R 和周期T 是(认为未知行星近似做匀速圆周运动)( ) A .T =t 20t 0-T 0B .T =t 0t 0-T 0T 0C .R =R 03(t 0t 0-T 0)2D .R =R 03(t 0-T 0t 0)23.(2016·江苏南通如东一检)某行星和地球绕太阳公转的轨道均可视为圆。
每过N 年,行星会运行到日地连线的延长线上(相距最近),如图所示。
设该行星与地球的公转周期之比为k 1,公转半径之比为k 2,则( )A .k 1=N +1NB .k 1=NN -1C .k 2=⎝⎛⎭⎪⎫N +1N 2/3 D .k 2=⎝ ⎛⎭⎪⎫N N -12/34.(2016·云南昆明高三月考)太阳系各行星可近似看成在同一平面内沿同一方向绕太阳做匀速圆周运动。
设天王星公转周期为T 1,公转半径为R 1;地球公转周期为T 2,公转半径为R 2。
当地球和天王星运行到太阳两侧,且三者排成一条直线时,(忽略两者之间的引力作用,万有引力常量为G )下列说法正确的是( ) A .天王星公转速度大于地球公转速度B .地球与天王星相距最近至少需经历T 1T 22(T 1-T 2)C .太阳的质量为4π2R 31GT 22D .天王星公转的向心加速度与地球公转的向心加速度之比为R 21R 225.设金星和地球绕太阳中心的运动是公转方向相同且轨道共面的匀速圆周运动,金星在地球轨道的内侧(称为地内行星)。
在某些特殊时刻,地球、金星和太阳会出现在一条直线上,这时候从地球上观测,金星像镶嵌在太阳脸上的小黑痣缓慢走过太阳表面。
天文学称这种现象为“金星凌日”。
如图所示,2012年6月6日天空上演的“金星凌日”吸引了全世界数百万天文爱好者。
假设地球公转轨道半径为R,“金星凌日”每隔t0年出现一次,则金星的公转轨道半径为( )A.t01+t0R B.R3(t01+t0)2C.R 3(1+t0t0)2 D.R(t01+t0)36.(2016·河北石家庄质检)太阳系中某行星A运行的轨道半径为R,周期为T,但科学家在观测中发现,其实际运行的轨道与圆轨道存在一些偏离,且每隔时间t发生一次最大的偏离。
天文学家认为形成这种现象的原因可能是A外侧还存在着一颗未知星B,它对A的万有引力引起A行星轨道的偏离,假设其运行轨道与A在同一平面内,且与A的绕行方向相同,由此可推测未知行星B绕太阳运行的圆轨道半径为( )A.R 3⎝⎛⎭⎪⎫tt-T2B.tt-TRC.R 3⎝⎛⎭⎪⎫t-Tt2D.R3t2t-T1.(2017·全国卷Ⅲ,14)2017年4月,我国成功发射的天舟一号货运飞船与天宫二号空间实验室完成了首次交会对接,对接形成的组合体仍沿天宫二号原来的轨道(可视为圆轨道)运行。
与天宫二号单独运行时相比,组合体运行的( )A.周期变大B.速率变大C.动能变大D.向心加速度变大2.(2018江苏淮安宿迁质检)2017年4月,我国第一艘货运飞船天舟一号顺利升空,随后与天宫二号交会对接.假设天舟一号从B点发射经过椭圆轨道运动到天宫二号的圆轨道上完成交会,如图所示.已知天宫二号的轨道半径为r,天舟一号沿椭圆轨道运动的周期为T,A、B 两点分别为椭圆轨道的远地点和近地点,地球半径为R,引力常量为G.则A.天宫二号的运行速度小于7.9km/sB.天舟一号的发射速度大于11.2km/sC.根据题中信息可以求出地球的质量D.天舟一号在A点的速度大于天宫二号的运行速度3、(2016·天津)我国即将发射“天宫二号”空间实验室,之后发射“神舟十一号”飞船与“天宫二号”对接。
假设“天宫二号”与“神舟十一号”都围绕地球做匀速圆周运动,为了实现飞船与空间实验室的对接,下列措施可行的是A.使飞船与空间实验室在同一轨道上运行,然后飞船加速追上空间实验室实现对接B.使飞船与空间实验室在同一轨道上运行,然后空间实验室减速等待飞船实现对接C.飞船先在比空间实验室半径小的轨道上加速,加速后飞船逐渐靠近空间实验室,两者速度接近时实现对接D.飞船先在比空间实验室半径小的轨道上减速,减速后飞船逐渐靠近空间实验室,两者速度接近时实现对接4.(2016·北京)如图所示,一颗人造卫星原来在椭圆轨道1绕地球E运行,在P点变轨后进入轨道2做匀速圆周运动,下列说法正确的是A.不论在轨道1还是在轨道2运行,卫星在P点的速度都相同B.不论在轨道1还是在轨道2运行,卫星在P点的加速度都相同C.卫星在轨道1的任何位置都具有相同加速度D.卫星在轨道2的任何位置都具有相同动量5.中国国家航天局目前计划于2020年发射嫦娥工程第二阶段的月球车“嫦娥四号”。
中国探月计划总工程师吴伟仁近期透露,此台月球车很可能在离地球较远的月球背面着陆,假设运载火箭先将“嫦娥四号”月球探测器成功送入太空,由地月转移轨道进入100千米环月轨道后成功变轨到近月点为15千米的椭圆轨道,在从15千米高度降至月球表面成功实现登月。
则关于“嫦娥四号”登月过程的说法正确的是( )A.“嫦娥四号”由地月转移轨道需要减速才能进入100千米环月轨道B.“嫦娥四号”在近月点为15千米的椭圆轨道上各点的速度都大于其在100千米圆轨道上的速度C.“嫦娥四号”在100千米圆轨道上运动的周期小于其在近月点为15千米的椭圆轨道上运动的周期D .从15千米高度降至月球表面过程中,“嫦娥四号”处于失重状态 多星系统1(2017·广州执信中学检测)(多选)太空中存在一些离其他恒星较远的、由质量相等的三颗星组成的三星系统,通常可忽略其他星体对它们的引力作用。
已观测到稳定的三星系统存在两种基本的构成形式(如图9):一种是三颗星位于同一直线上,两颗星围绕中央星在同一半径为R 的圆轨道上运行;另一种形式是三颗星位于等边三角形的三个顶点上,并沿外接于等边三角形的圆形轨道运行。
设这三颗星的质量均为M ,并设两种系统的运动周期相同,则( )图9A.直线三星系统中甲星和丙星的线速度相同B.直线三星系统的运动周期T =4πRR 5GMC.三角形三星系统中星体间的距离L =3125RD.三角形三星系统的线速度大小为125GMR2(2015·安徽)由三颗星体构成的系统,忽略其它星体对它们的作用,存在着一种运动形式:三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O 在三角形所在的平面内做相同角速度的圆周运动(图6示为A 、B 、C 三颗星体质量不相同时的一般情况)。
若A 星体质量为2m ,B 、C 两星体的质量均为m ,三角形的边长为a ,求: (1)A 星体所受合力大小F A ; (2)B 星体所受合力大小F B ; (3)C 星体的轨道半径R C ;(4)三星体做圆周运动的周期T。
3.宇宙中存在由质量相等的四颗星组成的四星系统,四星系统离其他恒星较远,通常可忽略其他星体对四星系统的引力作用.已观测到稳定的四星系统存在两种基本的构成形式:一种是四颗星稳定地分布在边长为L的正方形的四个顶点上,均围绕正方形对角线的交点做匀速圆周运动,其运动周期为T1;另一种形式是有三颗星位于边长为L的等边三角形的三个项点上,并沿外接于等边三角形的圆形轨道运行,其运动周期为T2,而第四颗星刚好位于三角形的中心不动.试求两种形式下,星体运动的周期之比T1/ T2.1【参考答案】A【命题意图】本题考查万有引力定律、同步卫星的运动及其相关的知识点。
2【参考答案】B3【名师解析】.(9分):⑴卫星绕地球做匀速圆周运动,设地球质量为M ,卫星质量为m ,轨道半径为r ,运行速度大小为v由万有引力定律和牛顿运动定律 rv m r Mm G 22= ①解得 rGMv =卫星A 与卫星B 运行速度大小之比RhR v v BA+= ⑵由万有引力定律和牛顿运动定律r Tm r Mm G 2224π= ② 可知卫星运行周期GMr T 324π=卫星A 与卫星B 运行周期之比33)(h R R T T B A += ⑶由万有引力定律和牛顿运动定律 卫星运行的加速度大小2rGMm F a ==合 ③ 卫星A 与卫星B 运行的加速度大小之比22)(Rh R a a B A += 说明:其他方法正确同样给分。
