第三章偏好与效用
第三章效用论

与边际 效用递 减规律 相似
原因: 对某一商品拥有量较少时,对其偏爱程度高;而拥有
量较多时,偏爱程度较低。 随着消费量的增加,想要获得更多这种商品的愿望就 会减少,所愿意放弃的另一种商品量就会越来越少。
边际替代率递减,意味着无差异曲线的斜率的绝对值
越来越小,因此该曲线必定凸向圆点。
衣服
U(b)=U(c)
U(a)=U(b)
3.3.2边际替代率 MRS
商品的边际替代率:在维持效用水平不变的前提下,消费
者增加一单位某种商品的消费量所需要放弃的另一种商品 的消费量,被称为商品的边际替代率。
商品边替代率的推算
商品边际替代率递减规律
• 边际替代率递减规律:随着某种商品和服务的消费 量增加,为了保持总效用不变,消费者愿意放弃的 其他商品和服务的数量越来越小,也即这种商品能 够替代的其他商品的数量越来越小。
萝卜最好吃。萝卜又甜又脆又解渴,我一想起萝卜就要流口 水。”
猫不同意,说,“世界上最好吃的东西是老鼠。老鼠的肉非
常嫩,嚼起来又酥又松,味道美极了!”
免子和猫争论不休、相持不下,跑去请猴子评理。
猴子听了,不由得大笑起来:“瞧你们这两个傻瓜蛋,连这点儿
常识都不懂!世界上最好吃的东西是什么?是桃子!桃子不但美 味可口,而且长得漂亮。我每天做梦都梦见吃桃子。”
消费者剩余概念用如下图表来说明
P
26 8 7 6 消费者剩余 5 26-20=6 S
E
D
O 1 2 20 3 4 Q
第三节 序数效用与消费者均衡
1.消费者偏好 序数效用理论认为,效用只能根据偏好程度排列出顺序
,即偏好。 即消费者能对可能消费的商品进行先后排列。 理性 消费 者的 三大 基本 偏好
尼科尔森微观经济理论_基本原理与扩展(第9版)课后习题详解(第3章 偏好与效用)
尼科尔森《微观经济理论-基本原理与扩展》(第9版)第2篇 选择与需求 第3章 偏好与效用课后习题详解跨考网独家整理最全经济学考研真题,经济学考研课后习题解析资料库,您可以在这里查阅历年经济学考研真题,经济学考研课后习题,经济学考研参考书等容,更有跨考考研历年辅导的经济学学哥学姐的经济学考研经验,从前辈中获得的经验对初学者来说是宝贵的财富,这或许能帮你少走弯路,躲开一些陷阱。
以下容为跨考网独家整理,如您还需更多考研资料,可选择经济学一对一在线咨询进行咨询。
1.画出下列效用函数的无差异曲线,并判断它们是否是凸状的(即边际替代率MRS 是否随着x 的增加而递减)。
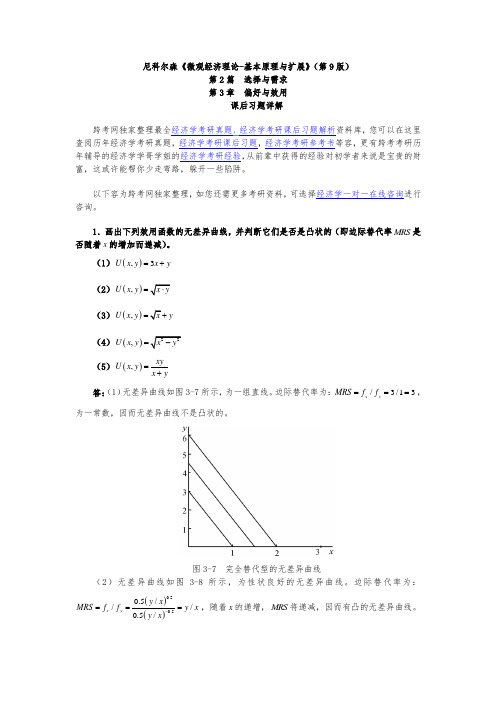
(1)(),3U x y x y =+ (2)(),U x y x y =⋅ (3)(),U x y x y =+ (4)()22,U x y x y =- (5)(),xyU x y x y=+ 答:(1)无差异曲线如图3-7所示,为一组直线。
边际替代率为:/3/13x y MRS f f ===,为一常数,因而无差异曲线不是凸状的。
图3-7 完全替代型的无差异曲线(2)无差异曲线如图3-8所示,为性状良好的无差异曲线。
边际替代率为:()()0.50.50.5///0.5/x y y x MRS f f y x y x -===,随着x 的递增,MRS 将递减,因而有凸的无差异曲线。
图3-8 凸状的无差异曲线(3)无差异曲线如图3-9所示。
边际替代率为:0.5/0.5x y MRS f f x -==,因而边际替代率递减,无差异曲线是凸状的,此为拟线性偏好的效用函数。
图3-9 拟线性型的无差异曲线(4)无差异曲线如图3-10所示。
边际替代率为:()0.522220.5/0.52/0.5()2/x y MRS f f x y x x y y x y --==-⋅-⋅=,因而边际替代率递增,无差异曲线不是凸状的。
图3-10 凹状的无差异曲线(5)无差异曲线如图3-11所示。
微观经济学第三章

微观经济学第三章第三章消费者行为理论第一节基数效用论一、效用与选择1.消费者是如何选择他们最喜欢的商品组合?怎样解释我们所观察到的需求行为?2.案例:牛奶消费与白酒相比较3.人们消费的基本原则–人们总是倾向于选择他们最偏好(评价最高)的产品与服务。
二、效用(Utility)1.效用:消费者消费物品或劳务所获得的满足程度(satisfaction) 。
注(1)这种满足程度纯粹是一种消费者主观心理感觉。
效用本身不包含有关是非的价值判断。
效用因人、因时、因地而不同。
(2)效用绝不是可以观察与度量的心理函数。
它仅仅是经济学家用来理解个人选择行为一种科学工具。
2.基数效用(Cardinal Utility)把消费者消费物品或劳务所获得的满足程度用具体的数字来衡量所表达出来的效用。
3.效用的解释——主观心理感觉例子一:《最好吃的东西》免子和猫争论,世界上什么东西最好吃。
免子说,“世界上萝卜最好吃。
萝卜又甜又脆又解渴,我一想起萝卜就要流口水。
”猫不同意,说,“世界上最好吃的东西是老鼠。
老鼠的肉非常嫩,嚼起来又酥又松,味道美极了!”免子和猫争论不休、相持不下,跑去请猴子评理。
猴子听了,不由得大笑起来:“瞧你们这两个傻瓜蛋,连这点儿常识都不懂!世界上最好吃的东西是什么?是桃子!桃子不但美味可口,而且长得漂亮。
我每天做梦都梦见吃桃子。
”免子和猫听了,全都直摇头。
那么,世界上到底什么东西最好吃?说明了效用完全是个人的心理感觉。
不同的偏好决定了人们对同一种商品效用大小的不同评价。
例子二:《钻石和木碗》一个穷人家徒四壁,只得头顶着一只旧木碗四处流浪。
一天,穷人上一只渔船去帮工。
不幸的是,渔船在航行中遇到了特大风浪,被大海吞没了。
船上的人几乎都淹死了,穷人抱着一根大木头,才得幸免遇难。
穷人被海水冲到一个小岛上,岛上的酋长看见穷人头顶的木碗,感到非常新奇,便用一大口袋最好的珍珠宝石换走了木碗,还派人把穷人送回了家。
一个富翁听到了穷人的奇遇,心中暗想,一只木碗都能换回这么多宝贝,如果我送去很多可口的食物,该换回多少宝贝!”于是,富翁装了满满一船山珍海味和美酒,找到了穷人去过的小岛。
《微观经济学》第三章 效用理论

思考
• 是基数效用论合理一些,还是序数效 用论更合理一些,为什么?
第二节 无差异曲线(等效用曲线)
• 定义:给消费者相同效用满足的所有商 品组合所连接成的曲线或多维曲面
y
• 无差异曲线图
I3
I2
I1
x
无差异曲线的性质
y
• 无数条 • 无差异曲线不能相交
I3
I2
I1
x
• 无差异曲线凸性(凸向原点)
PX
PY
均衡的形成——切点定律
Y
Y0
• 切点定律:
0
无差异曲线与预算线切点的组
X0
合,为效用最大组合。
预算线的斜率 = 边际替代率
无差异曲线 X
货币的边际效用
• 严格地,货币的边际效用也递减。
MU X MU Y
PX
PY
• 为了分析上的便利,总收入量相对很大情 况下,可假定货币的边际效用不变。
未来科学的发展,“效用”(身心满足程 度、幸福快乐和痛苦程度),能否可以量度?
• 在19世纪,一些哲学家相信,消费物品和劳务 所获得的福利或效用确确实实是可以衡量的。 他们的想法是,创造一种机器。☆
偏好与效用满足
• 偏好的基本假设 完全性( X1 X 2, X1 X 2, X1 X 2 必居其一) 传递性 X1 X 2 , X 2 X3 X1 X 3 所有商品都是“好”的,“负商品”的比较罕 见
边际效用的表达式
MU lim TU (Q) Q0 Q
总效用与边际效用关系(微分-积分关系)
《炸鸡翅膀》的故事:
炸鸡翅膀(块) 0 1 2 3 4 5 6 7 8
总效用 0 6 11 15 18 20 21 21 20
微观经济学第三章效用论

10
50
40
20
30
40
10
20
10
40
消费者偏好
二、无差异曲线及其特点
无差异曲线 表示消费者偏好相同的商品组合 通常以两种商品为例
无差异曲线
无差异曲线
效用函数和无差异曲线
效用函数和无差异曲线
效用函数和无差异曲线
无差异曲线及其特点 效用函数 某一商品组合给消费者带来的效用水平 效用水平是对消费者在消费商品组合过 程中获得满足程度的度量。
替代效应和收入效应
替代效应和收入效应的含义 替代效应 当商品变得相对更便宜时,消费者倾向于 增加购买量;当商品变得相对更昂贵时, 则减少购买量。
替代效应和收入效应
替代效应和收入效应的含义 比较 收入效应反映了在保持商品价格不变的条 件下,实际购买力变化所引起的对该商品 购买量的变化。
替代效应和收入效应
第三节 预算线
无差异曲线描述了消费者对不同的商品组合的偏 好,但这并不能说明消费者选择行为的所有方 面。
消费者在购买商品时,必然会受到自己的收入水 平和市场上商品价格的限制,这就是预算约束。
一、预算线的含义
预算线表示在消费者的收入和商品的价格给定的 条件下,消费者的全部收入所能购买到的两种 商品的各种组合。 预算约束线、消费可能线、价格线
40
120
30
120
20
120
10
120
0
120
P2 = 3
I=120
该公式可以必写成:X2=-(P1/P2)X1+I/P2。这一公
式的预算线方程告诉我们,预算线的斜率为-P1/P2,纵 截距为I/P2
二、预算线的变动
收入变化 在两种商品的价格不变的条件下 收入增加将导致预算线向外平移 收入减少将导致预算线向内平移
尼科尔森《微观经济理论-基本原理与扩展》(第9版)课后习题详解(第3章--偏好与效用)
尼科尔森《微观经济理论-基本原理与扩展》(第9版)第2篇选择与需求 第3章偏好与效用课后习题详解跨考网独家整理最全经济学考研真题,经济学考研课后习题解析资料库,您可以在这里查阅历年经济学考研真题,经济学考研课后习题,经济学考研参考书等内容,更有跨考考研历年辅导的经济学学哥学姐的经济学考研经验,从前辈中获得的经验对初学者来说是宝贵的财富,这或许能帮你少走弯路,躲开一些陷阱。
以下内容为跨考网独家整理,如您还需更多考研资料,可选择经济学一对一在线咨询进行咨询。
1.画出下列效用函数的无差异曲线,并判断它们是否是凸状的(即边际替代率MRS 是否随着x 的增加而递减)。
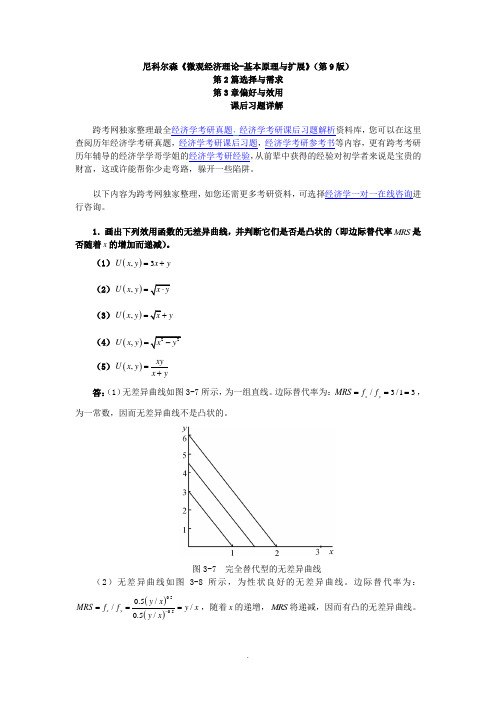
(1)(),3U x y x y =+ (2)(),U x y x y =⋅ (3)(),U x y x y =+ (4)()22,U x y x y =- (5)(),xyU x y x y=+ 答:(1)无差异曲线如图3-7所示,为一组直线。
边际替代率为:/3/13x y MRS f f ===,为一常数,因而无差异曲线不是凸状的。
图3-7 完全替代型的无差异曲线(2)无差异曲线如图3-8所示,为性状良好的无差异曲线。
边际替代率为:()()0.50.50.5///0.5/x y y x MRS f f y x y x -===,随着x 的递增,MRS 将递减,因而有凸的无差异曲线。
图3-8 凸状的无差异曲线(3)无差异曲线如图3-9所示。
边际替代率为:0.5/0.5x y MRS f f x -==,因而边际替代率递减,无差异曲线是凸状的,此为拟线性偏好的效用函数。
图3-9 拟线性型的无差异曲线(4)无差异曲线如图3-10所示。
边际替代率为:()0.522220.5/0.52/0.5()2/x y MRS f f x y x x y y x y --==-⋅-⋅=,因而边际替代率递增,无差异曲线不是凸状的。
图3-10 凹状的无差异曲线(5)无差异曲线如图3-11所示。
第三章 效用论

牛奶
U1 U2
U3
(2)完全互补:两种商品必须按固定不变的比例配合同时 )完全互补: 被使用。 被使用。 眼镜架 无差异曲线为直角形状。 无差异曲线为直角形状。 2 1 U(x1,x2)=min(ax1,bx2) 0 1 2 3 U1 U2 4 眼镜片
完全互补品
26
预算线
27
预算线
收入与商品价格既定, 收入与商品价格既定,消费 者所能购买到的两种商品最 大数量的组合线。 大数量的组合线。 X2(衣服) 衣服) B
2
第一节 效用论概述
3
效用
消费者从商品消费中得到的满足程度。 消费者从商品消费中得到的满足程度。
满足程度高,效用大; 满足程度高,效用大; 满足程度低,效用小。 满足程度低,效用小。
效用 萨缪尔森提出:幸福= 萨缪尔森提出:幸福 ——— 欲望
4
两种效用理论
基数效用论: 基数效用论: 效用的大小可以用基数( , , , 效用的大小可以用基数(1,2,3,……)来表示,可以 )来表示, 计量并加总求和。 计量并加总求和。 基数效用论采用的是边际效用分析法 边际效用分析法。 基数效用论采用的是边际效用分析法。 序数效用论 序数效用论: 效用作为一种心理现象无法计量,也不能加总求和, *效用作为一种心理现象无法计量,也不能加总求和,只能 表示出满足程度的高低与顺序,效用只能用序数(第一, 表示出满足程度的高低与顺序,效用只能用序数(第一,第 第三, 二,第三,……)来表示。 )来表示。 序数效用论采用的是无差异曲线分析法 无差异曲线分析法。 *序数效用论采用的是无差异曲线分析法。
第三章
第一节 第二节 第三节 第四节 第五节
效用论
效用论概述 基数效用论 序数效用论 价格和收入变化对消费者均衡的影响 替代效应与收入效应
微观经济学第三章效用论

解:1、 由均衡条件求解
∂U MU X = = 2 +Y ∂X ∂U MU Y = = 2+ X ∂Y
代入均衡条件 (2+Y)/5 = (2+X)/10 5X+10Y=50 得: X=6 ,Y=2
2、 Mum=Muy/Py=0.8 3、 U=36
例2: 期末考试前只剩6小时的复习时间, 现在知道如下关系: 0
Y U2 U3 U1
X
三、消费者的预算线
预算线的含义 • 在消费者的收入与商品价格既定的条件 下,消费者的全部收入所能购买到的两 种商品的各种数量组合。 • 预算线的方程: I=PxX+PyY
I PX y = − Py PY
x
M=100, Px=4, Py=5
商品Y 20
100 = 4 x + 5 y
二、效用的特征
效用是一种心理感受,是主观的; 同一种商品的效用在不同的消费者之间不能进行 比较; 同一种商品对同一各消费者也是不同的,会随着 消费条件的改变而发生变化; 不同的商品效用对同一消费者可以进行比较。
三、效用的衡量——序数效用与基数效用 效用的衡量 序数效用与基数效用
对于效用的衡量,基数论者认为,效用 可以象长度,温度一样加以具体的衡量并可 加总求和。 序数论者认为,效用的大小无法具体衡 量,人们只能区分不同商品的效用等级。
1 完备性:对于任意两个商品组合,消费者 能作出偏好的准确判断 2 传递性:任意三个商品组合,偏好具有传 递性 3不满足性:较多数量组合的偏好大于较少 数量的组合偏好
二、无差异曲线及特点
1、无差异曲线 两种商品不同数量的组合能带给消费 者相同效用的那些组合点的轨迹。 与无差异曲线对应的效用函数: U=f(X1 , X2)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
偏好可以说是每个人对各种物品的喜好程度。在经济学中,我们假设偏好有下面 的几个性质。举例, “苹果和梨、橘子” 1 理性选择定理 偏好(preference)的三个基本性质: 1) 完全性(completeness) :如果 A 与 B 是任何两种情况,个人总是准确地 指定下列三种可能性中的一种: a) “A 优于 B” b) “B 优于 A”或者 c) “A 与 B 的吸引力相等” 2) 传递性(transitivity) :如果一个人认为“A 优于 B” ,同时又认为“B 优 于 C” ,那么一定意味着它也认为“A 优于 C” 3) 连续性(continuity) :如果一个人认为“A 优于 B” ,那么“接近”A 的 情况也一定优于 B 当我们针对个人行为对收入或价格一个相对很小的变化的反应进行分析 时,这一技术性的假定是必要的。 2 效用 当给定完全性、 传递性和连续性的假设之下, 就可以规范的表达偏好的次序, 从最合心意的到最不合心意的。19 世纪的政治理论家 Jeremy Bentham 引入了经 济学家称之为效用序列的术语。如果一个人认为情形 A 优于情形 B,我们就说 选择 A (用 U(A)来表示)的效用超过了选择 B(用 U(B)来表示)的效用。 1) 效用测度的非唯一性(Non-Uniqueness of Utility Measures) 。我们可以用 数字来表示效用,但这些数字不是唯一的。任意指定的可以准确反映最 初偏次序的任何一组数字,都意味同样的选择。 2) 其他情况不变的假设(the Ceteris Paribus Assumption) :由于效用涉及人 们的总体满足程度。因此对效用的测度会受到多种因素的影响(个人经 历、文化环境) 。通常在经济分析中,假定其他影响因素不变,集中精力 值分析可计量、可挑选的物品之间的选择,从而确保分析形式简单。 3) 效用定义:假定以下效用函数形式代表了个人的偏好。 U ( x1 , x2 ,..., xn ) , 这里 x1 , x2 ,..., xn 分别代表了一个时期消费的每一种商品的数量。仅在消 费者保持的偏好序发生变化之前,这个函数是唯一的。同时这个函数的 任意单调正转换都代表了同样的偏好。 4) goods(经济品) :无论它们所表示的数量是多少,我们都假定在一个时 期,任何较多的特定的 xi 都优于较少的 xi 。
MRS
Y
dY dX
,这个概念指出沿着无差异曲线 U1 来计算斜率。
U U1
Y1 Y2
U1 X
X1
X2
根据图形解释无差异曲线斜率为负,且边际替代率递减的原因。 2) 无差异曲线图 在 X-Y 平面上的每一点都有一条无差异曲线通过。 每一条无差异曲线及 记录了 X 与 Y 商品的一种组合,这种组合给个人带来某已确定水平的 满足。曲线移向东北,表示更高满足程度。
Y
U1 X
画图 举例说明:假设一个人对汉堡包(Y)和饮料(X)的偏好可以用下列效用 函数来表达: 效用= XY ,我们随意假设改组合集的效用是 10,则无差异曲线 可以表示为:100 XY ,边际替代率为: MRS dY dX 100 / X 2 ,这显示在 无差异曲线的 A 点上有许多汉堡包(比如,X=5,Y=20)时,边际替代率为 4, 消费者愿意放弃 4 个汉堡包去换取 1 瓶饮料。而在 B 点,他只有很少的汉堡包 (X=20,Y=5) ,边际替代率为 1/4,他只愿意为换取一瓶饮料放弃 1/4 个汉堡包。 在 C 点,即 A 和 B 两点的中点,他有 12.5 个汉堡包和 12.5 瓶饮料,这时他的效 用为 12.5,超过了 A 和 B 点的效用。
, ) U( X , Y ) m i n (X ,Y , 是正的常数。无差异曲线中的直线表示这
些对商品将以固定的比率来使用。多增加某一种商品是没有效用的。比如 100 克牛奶要配合 2 克糖。只增加牛奶,或只增加糖是没有效用的。
Y
X
4) CES 效用(constant elasticity of substitution function)
f 22 f11 2 f1 f 2 f12 f12 f 22 0 。
因此边际效用递减 f11 0, f 22 0 , 不能保证不等式成立, 必须关注 f12 项。 即了解 y 的减少对 x 边际效用影响。通常对这项的预测是不可能的。 举例说明:假设一个人对汉堡包(Y)和饮料(X)的偏好可以用下列效用 函数来表达:效用= XY X 0.5Y 0.5 , 边际效用为:MU X U X 0.5 X 0.5Y 0.5 ,
X
2) 完全替代效用(Perfect Substitution) :UXY ( ,)
X Y , , 是正的
常数。这一函数的无差异曲线是一条直线。边际替代率沿整个无差异曲 线是不变的。这种情形可能是描绘基本相同产品的不同品牌之间的关 系。
Y
X
3) 完全互补效用(Perfect complement) :
dU 0
U U dx dy MU x dx MU y dy x y
MU x u x dy dx U cons tan t MU y u y
虽然边际效用不独立于效用的测度单位,但边际替代率独立于效用的测 度单位。 3) 边际效用递减与边际替代率(MRS)递减
Y
U3 U1 U2 X
一个人的任意两条无差异曲线不会相交。 (画图证明)
我们分析一下 A、B、C、D 点所代表的商品组合,应该说“A 优于 B” , “C 优于 D” ,但是 B 和 C 在同一条无差异曲线上,则“B 和 C 相同” ,根据传递性 定理, “A 优于 D” ,这与 A 和 D 在同一条无差异曲线上相矛盾。
3) 无差异曲线的凸性 凸集: 如果集内任何两点可以用直线相连, 直线完全在集内。 就可以说, 这个点集是凸的。边际替代率递减的假定相等于这样一个假定:优于或 无差异于特定的( X * , Y * )组合的所有的 XY 的组合形成一个凸集。 如果无差异曲线是凸的(即服从边际替代率递减的假定) ,曲线上任两 点的连线上的点所表示的组合都优于初始组合,直观地看,平衡组合优 于不平衡组合。
合并同类项,已知 f12 f 21 ,可知上式
f 2 f11 2 f1 f12 ( f 22 f1 ) 2 / f 2 f 22 f 22 f11 2 f1 f 2 f12 f12 f 22 f 23
假 设 ( f 2 >0 , 边 际 效 用 为 正 ) ,那么边际替代率递减,有
Y ? 比 A 偏好
比A糟
? X
3 交易与替代 大多数的经济活动都涉及个人之间的自愿交易。为了考察这种自愿交易,需要 在效用函数范围内提出一种规范的表达方式。 1) 无差异曲线和边际替代率 无差异曲线(indifference curve) :一条无差异曲线(或在多维时的无差 异表面)显示了个人无差别的消费组合集。也就是说,所有的组合提供 了相同程度的效用水平。 配图说明,假设只考虑两种消费品 X 和 Y 的情况, 边际替代率(marginal rate of substitution MRS) :无差异曲线(U)某些 点上的斜率为负的术语是这些点的边际替代率。
U f ( x, y)
MRS
fx f dy 1 f y f2 dx
边际替代率递减意味着:
dMRS 0 dx
dMRS f 2 ( f11 f12 dy dx) f1[ f 21 f 22 dy dx ] dx f 22 f 2 [ f11 f12 ( f1 f 2 )] f1[ f 21 f 22 ( f1 f 2 )] f 22
Y 20 12.5 5 5 12.5 A B C
U=10
20
X
4 边际效用 1) 定义:效用 U ( x1 , x2 ,..., xn ) , x1 , x2 ,..., xn 是消费的 N 种商品(X)中每一 种的数量。商品 x1 的边际效用可以表达为:
x1的边际效用=MU x1
U ,边际效用的值取决于个人消费 x1 , x2 ,..., xn 的 x1
MUY U Y 0.5 X 0.5Y 0.5 , MRS
dY dX
U cons tan t
MU X Y MUY X
5 效用函数举例 1) 柯布-道格拉斯效用(Cobb-Douglas Utility) :
,其中, , 是常数,且 1 。 U ( x, y) x y Y
数量,也取决于测量效用所用的特定的标度。
dU
U U U dx1 dx2 ... dxn x1 x2 xn
MU x1 dx1 MU x2 dx2 ... MU xn dxn
2) 边际替代律的推导:考虑只有两种商品 X 与 Y 的情况,保持个人效用
