初中常见轨迹问题解题策略
九年级专题突破:轨迹问题

九年级专题突破:轨迹问题考点梳理(1)旋转型轨迹问题这一类动点问题的特点是:所求的点是从动点,是先有其他点在动,然后所求动点才动,而且主动点和从动点会有一个定点作为“旋转中心”,旋转的情形满足下列两种之一:第一种是主动点、从动点和旋转中心三点共线;(运动路径是线段)第二种是主动点与旋转中心的连线和从动点与旋转中心的连线夹角固定,而且两条线段之间的比例不变。
这时,要求从动点的轨迹,只需要求出主动点的轨迹就可以确定运动路径是圆。
因为根据几何画板,他们的轨迹形状相同,长度成比例。
(2)定角对定长这一类动点问题的特点是:以该动点为顶点的某个角度大小是固定不变的,而且该固定角度所对的某一条边是固定的。
由圆周角的特点可知,这个动点的轨迹就是一个圆周或者一段弧。
而且这个固定角度就是圆周角,这个固定边就是弦。
如果需要求轨迹长的话,再把圆心角和半径算出来就行了。
不过有一点需要注意,这时需要把起始点和终点找到才能准确求出圆心角。
对于这种题型,找圆心可以用三角形外心的结论:锐角三角形的外心在三角形内部,直角三角形的外心在斜边中点,钝角三角形的外心在三角形外部。
所以,当这个固定角度是锐角时,圆心和动点位于固定边的同侧;当这个固定角度是直角时,圆心就在固定边的中点;当这个固定角度是钝角时,圆心和动点位于固定边的两侧。
题型分类题型一 运动路径是线段(动点与某条直线的距离始终保持不变) 例1 如图:已知AB =10,点C 、D 在线段AB 上且AC =DB =2;P 是线段CD 上的动点,分别以AP 、PB 为边在线段AB 的同侧作正方形APEF 和正方形PBGH ,点O 1和O 2是 两个正方形的中心,连接O 1O 2,设O 1O 2的中点为Q ; 当这点P 从点C 运动到点D 时,则点Q 移动路径的长 是___________.例2 如图,已知线段AB =6,C 、D 是AB 上两点,且AC =DB =1,P 是线段CD 上一动点,在AB 同侧分别作等边三角形APE 和等边三角形PBF ,G 为线段EF 的中点,点P 由点C 移动到点D 时,G 点移动的路径长度为_______.PC变式 如图,正方形ABCD 的边长为2,CD 边上一动点P ,连接BP ,过点P 作PQ ⊥BP ,截取PQ=BP ,当点P 从点C 运动到点D 时,求Q 的轨迹长QDCA BP题型二 运动路径是圆弧(动点到定点的距离等于定长)要点:这一类动点问题的特点是:所求的动点到某一个定点的距离是不变的。
中考热点题型:最常见轨迹问题解题策略靠套路就能拿高分!

中考热点题型:最常见轨迹问题解题策略靠套路就能拿高分!对于初中数学中动点轨迹的问题,一般有两种情况:线段或圆弧。
在研究动点问题时,可以在运动中寻找不变的量,即不变的数量关系或位置关系:如果动点的轨迹是一条线段,那么其中不变的量便是该动点到某条直线的距离始终保持不变;如果动点的轨迹是一段圆弧,那么其中不变的量便是该动点到某个定点的距离始终保持不变。
因此,解决此类动点轨迹问题便可转化为寻找定直线或定点。
轨迹问题三部曲:猜测轨迹形状——证明轨迹形状——代入图形应用其中第二步很重要,初中证明轨迹有两种证明方法:几何法和解析法。
所谓几何法就是通过纯几何证明,抓紧不变量,得出轨迹形状,一般是圆或直线(线段)证明方法:01圆弧——圆周角法已知Rt△ABC,AB=6cm,BC=8cm,AC=10cm,∠ABC=90°。
半径为1cm的圆,若将圆心由点A沿ABCA的方向运动回到点A,求圆扫过的区域面积为。
02圆弧——定义法如图,已知正方形OABC的边长为2,顶点A、C分别在x、y轴的正半轴上,M是BC的中点.P(0,m)是线段OC上一动点(C点除外),直线PM交AB的延长线于点D.(1)求点D的坐标(用含m的代数式表示);(2)当△APD是等腰三角形时,求m的值;(3)设过P、M、B三点的抛物线与x轴正半轴交予点E,过点O作直线ME的垂线,垂足为H(如图7).当点P从点O向点C运动时,点H也随之运动,请直接写出点H所经过的路径长.(不必写解答过程)解析此题中主动点是P,动点H是因点P的变化而变化.动点P在运动过程中始终保持不变的量是OH始终垂直ME,即日始终为垂足.而求动点H的运动轨迹,则需考虑点H是到某条直线的距离始终不变,还是到某个定点的距离始终保持不变.由于OH⊥ME,连结OM后,△AMH始终为直角三角形,而斜边OM不变,因此根据直角三角形的性质容易得到动点日到DM的中点的距离始终不变,从而可得到点H 的运动轨迹是一段圆弧。
轨迹问题的解法大全

轨迹问题的求法
一、直接法
当所求动点的要满足的条件简单明确时,直接按“建系设点、列出条件、代入坐标、整理化简、限制说明”五个基本步骤求轨迹方程,称之直接法.
定义法是指先分析、说明动点的轨迹满足某种特殊曲线(如圆、椭圆、双曲线、抛物线等)的定义或特征,再求出该曲线的相关参量,从而得到轨迹方程.
将直线与圆锥曲线的交点代入圆锥曲线的方程并对所得两式作差,得到一个与弦的中点和斜率有关的式子,可以大大减少运算量.我们称这种代点作差的方法为"点差法"。
四、几何法
几何法是指利用平面几何或解析几何知识分析图形性质,发现动点的运动规律和要满足的条件,从而得到动点的轨迹方程.
五、参数法
参数法是指先引入一个中间变量(参数),使所求动点的横、纵坐标间建立起联系,然后再从所求式子中消去参数,得到间的直接关系式,即得到所求轨迹方程
例3.【2017年全国二卷文科】
六、交轨法
求两曲线的交点轨迹时,可由方程直接消去参数,或者先引入参数来建立这些动曲线的联系,然后消去参数来得到轨迹方程,称之交轨法.
七、代入法
当题目中有多个动点时,将其他动点的坐标用所求动点的坐标来表示,再代入到其他动点要满足的条件或轨迹方程中,整理即得到动点的轨迹方程,称之代入法,也称相关点法、转移法
.。
初中常见轨迹问题解题策略
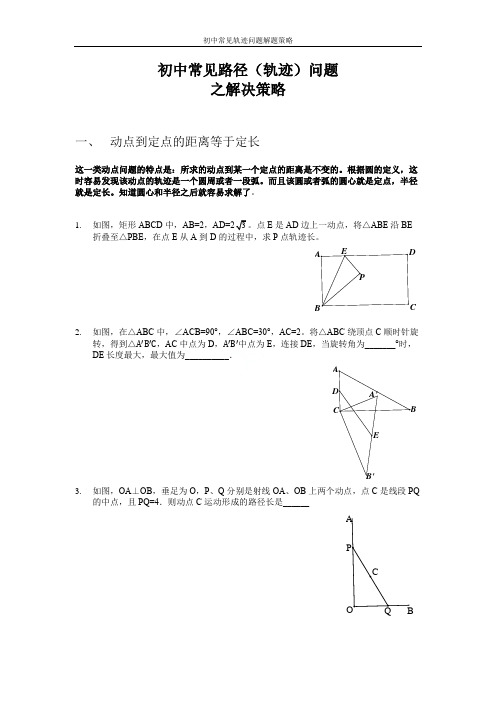
初中常见路径(轨迹)问题之解决策略一、 动点到定点的距离等于定长这一类动点问题的特点是:所求的动点到某一个定点的距离是不变的。
根据圆的定义,这时容易发现该动点的轨迹是一个圆周或者一段弧。
而且该圆或者弧的圆心就是定点,半径就是定长。
知道圆心和半径之后就容易求解了。
1. 如图,矩形ABCD 中,AB=2,E 是AD 边上一动点,将△ABE 沿BE折叠至△PBE ,在点E 从A 到D 的过程中,求P 点轨迹长。
2. 如图,在△ABC 中,∠ACB=90°,∠ABC=30°,AC=2。
将△ABC 绕顶点C 顺时针旋转,得到△A′B′C ,AC 中点为D ,A′B′中点为E ,连接DE ,当旋转角为_______°时,DE 长度最大,最大值为__________.3. 如图,OA ⊥OB ,垂足为O ,P 、Q 分别是射线OA 、OB 上两个动点,点C 是线段PQ的中点,且PQ=4.则动点C 运动形成的路径长是______二、定角对定长这一类动点问题的特点是:以该动点为顶点的某个角度大小是固定不变的,而且该固定角度所对的某一条边是固定的。
由圆周角的特点可知,这个动点的轨迹就是一个圆周或者一段弧。
而且这个固定角度就是圆周角,这个固定边就是弦。
如果需要求轨迹长的话,再把圆心角和半径算出来就行了。
不过有一点需要注意,这时需要把起始点和终点找到才能准确求出圆心角。
对于这种题型,找圆心可以用三角形外心的结论:锐角三角形的外心在三角形内部,直角三角形的外心在斜边中点,钝角三角形的外心在三角形外部。
所以,当这个固定角度是锐角时,圆心和动点位于固定边的同侧;当这个固定角度是直角时,圆心就在固定边的中点;当这个固定角度是钝角时,圆心和动点位于固定边的两侧。
4.如图,点E,F是正方形ABCD的边AD上两个动点,满足AE=DF。
连接CF交BD于点G,连接BE交AG于点H。
若正方形的边长为2,则线段DH的最小值是___.5.等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连结AF,BE相交于点P.若BF=CE,当点E从点A运动到点C时,试求点P经过的路径长.6.如图,正方形ODEF的边长为2,以O为圆心,AB为直径的半圆经过点D,连接AF,BD相交于点P,将正方形ODEF从OD与OA重合的位置开始,绕着点O逆时针旋转90°,求交点P运动的路径长.7.如图,圆O的直径AB=4,C为圆周上一点,AC=2。
初中常见的动点轨迹问题归纳与突破策略

②“定边对定
角”的动点轨迹为在以定边为弦且经过定点的圆弧
上 . 直线型中常见的有四种 :①动点到定直线的距离
相等 ,那么该动点的轨迹为平行与该直线的直线 ;
②
一、动点的运动轨迹为圆弧型
同弧所对的圆周角相等 ,反之 ,如图 1,如果一个
动点 M ,
以 M 为顶点的角 ∠AMB 始终不变 ,
动点轨迹;圆弧型;直线型;定边对定角;夹角定位法
初中数学动点轨迹问题是一个比较抽象的问题,
动点轨迹问题在初中数学的学习中,
以及以后高中数
学的学习中都是非常重要的 . 动点轨迹问题的解决策
略是化动为静,
寻找运动过程中的不变量 .
初中阶段常见的动点轨迹有圆弧型与直线型 . 圆
弧型中又分为两种 :①动点到定点的距离等于定长 ,
且这个定角的对边是定边 .
动点到线段两个端点的距离相等,
该动点的轨迹为该
线段的垂直平分线(线段垂直平分线的判定定理);
③
动点到角两边距离相等,
该动点的轨迹为这个角的角
平分线(角平分线的判定定理);
④动点与定点的连线
与定直线的夹角为定角,
那么该动点的轨迹为这个夹
角的另一边 .
图1
图2
由于“圆弧型中动点到定点的距离等于定长 ,那
角的动点轨迹)进行分析讲解:题目中如能找到定边对定角,则该动点的运动轨迹为在以定边为弦且经过定点的圆弧上,
这一类型关键的突破口是求出定边对面角的具体度数,为定值 . 而题目中如出现动点与定点的连线与定直线的夹角为定
关键词
角时,则该动点的轨迹为直线型(这个夹角的另一边),解决这一类型的方法为夹角定位法 .
求轨迹方程的思路,方法和对应的题型

求轨迹方程的思路,方法和对应的题型全文共四篇示例,供读者参考第一篇示例:求轨迹方程是解析几何中的一个重要内容,它是描述一个物体在运动过程中的路径的数学方法。
在数学中,求轨迹方程的过程通常需要经过一系列的思路和方法,且会涉及到不同类型的题目。
本文将介绍求轨迹方程的思路、方法以及对应的题型,希望对读者有所帮助。
一、思路在求解轨迹方程时,我们首先需要明确物体的运动规律和路径,然后通过数学方法来描述它的运动状态。
通常来说,我们可以采用以下思路来求解轨迹方程:1. 分析运动规律:首先我们需要分析物体的运动规律,包括其运动方向、速度和加速度等。
了解物体的运动规律有助于我们更好地建立数学模型。
2. 建立数学模型:根据物体的运动规律,我们可以建立数学模型,一般是通过对其位置、速度和加速度等数据进行分析得到。
建立好数学模型后,我们就可以利用数学方法来求解轨迹方程。
3. 求解轨迹方程:根据建立的数学模型,我们可以利用数学方法如微积分、几何等来求解轨迹方程。
最终得到的轨迹方程可以描述物体在运动过程中的路径。
4. 验证结果:最后我们还需要验证求解得到的轨迹方程是否准确,通常可以通过数学推导和实际运动情况进行验证。
三、对应的题型在求解轨迹方程的过程中,我们会遇到不同类型的题目,包括但不限于以下几种:1. 直线运动问题:给定物体在直线运动过程中的速度和加速度,求解其轨迹方程。
2. 圆周运动问题:给定物体在圆周运动过程中的角速度和半径,求解其轨迹方程。
3. 曲线运动问题:给定物体在曲线运动过程中的运动规律,求解其轨迹方程。
4. 三维空间运动问题:给定物体在三维空间中的运动规律,求解其轨迹方程。
第二篇示例:求轨迹方程是数学中一个常见的问题,涉及到函数、几何和代数等多个方面的知识。
在解决这类问题时,我们需要掌握一定的思路和方法,同时要能灵活应用这些知识来解决具体的题目。
本文将介绍求轨迹方程的思路、方法以及几种常见的题型,并给出相应的解题思路和步骤。
求轨迹方程问题—6大常用方法

求轨迹方程问题—6大常用方法知识梳理:(一)求轨迹方程的一般方法:1. 待定系数法:如果动点P的运动规律合乎我们已知的某种曲线(如圆、椭圆、双曲线、抛物线)的定义,则可先设出轨迹方程,再根据已知条件,待定方程中的常数,即可得到轨迹方程,也有人将此方法称为定义法。
2. 直译法:如果动点P的运动规律是否合乎我们熟知的某些曲线的定义难以判断,但点P满足的等量关系易于建立,则可以先表示出点P所满足的几何上的等量关系,再用点P的坐标(x,y)表示该等量关系式,即可得到轨迹方程。
3. 参数法:如果采用直译法求轨迹方程难以奏效,则可寻求引发动点P运动的某个几何量t,以此量作为参变数,分别建立P点坐标x,y与该参数t的函数关系x=f(t),y=g(t),进而通过消参化为轨迹的普通方程F(x,y)=0。
4. 代入法(相关点法):如果动点P的运动是由另外某一点P'的运动引发的,而该点的运动规律已知,(该点坐标满足某已知曲线方程),则可以设出P(x,y),用(x,y)表示出相关点P'的坐标,然后把P'的坐标代入已知曲线方程,即可得到动点P的轨迹方程。
5.几何法:若所求的轨迹满足某些几何性质(如线段的垂直平分线,角平分线的性质等),可以用几何法,列出几何式,再代入点的坐标较简单。
6:交轨法:在求动点轨迹时,有时会出现要求两动曲线交点的轨迹问题,这灯问题通常通过解方程组得出交点(含参数)的坐标,再消去参数求得所求的轨迹方程(若能直接消去两方程的参数,也可直接消去参数得到轨迹方程),该法经常与参数法并用。
(二)求轨迹方程的注意事项:1. 求轨迹方程的关键是在纷繁复杂的运动变化中,发现动点P的运动规律,即P点满足的等量关系,因此要学会动中求静,变中求不变。
来表示,若要判断轨迹方程表示何种曲线,则往往需将参数方程化为普通方程。
3. 求出轨迹方程后,应注意检验其是否符合题意,既要检验是否增解,(即以该方程的某些解为坐标的点不在轨迹上),又要检验是否丢解。
圆的轨迹问题,有迹可循,突破难点有绝招

圆的轨迹问题,有迹可循,突破难点有绝招动点轨迹问题、最值问题历来是中考的难点和热点。
学生需要在考场短时间思考出动点的运动轨迹确实不是一件容易的事情,如果平时不能有对图形本质的理解和把握,很难在考试中解决此类问题。
在初中阶段,我们会遇到两种轨迹问题,一个是圆弧,一个是线段。
它们分别对应不同的知识点。
圆弧上的点到定点的距离等于定长,线段上的点到直线的距离也等于定长。
但是在实际的考查过程中,我们往往不是事先知道动点所形成的轨迹。
而需要我们结合题目中的条件,来分析出问题是不是轨迹问题,是哪种轨迹问题,它们常见的处理方法又是什么呢?首先我们先给轨迹下个定义,简单的说就是:动点在空间或者平面内移动,它所通过的全部路径叫做这个点的轨迹。
我们在理解这个定义时,可从下列几个方面考虑:(1)符合一定条件的动点所形成的图形,或者说,符合一定条件的点的全体所组成的集合,叫做满足该条件的点的轨迹。
(2)凡在轨迹上的点都符合给定的条件,这叫做轨迹的纯粹性(也叫做必要性)。
(3)另外凡不在轨迹上的点都不符合给定的条件,也就是符合给定条件的点必在轨迹上,这叫做轨迹的完备性(也叫做充分性)。
初中阶段会接触到的曲轨迹一般是圆或者圆弧,比如旋转问题中;当然动点也可能在双曲线或者抛物线上运动,这都属于曲轨迹;类型1 圆的问题中隐含圆的轨迹问题1.如图,扇形AOD中,∠AOD=90°,OA=6,点P为弧AD上任意一点(不与点A和D重合),PQ⊥OD于Q,点I为△OPQ的内心,过O,I和D三点的圆的半径为r.则当点P在弧AD上运动时,r的值满足()A.0<r<3 B.r=3 C.3<r<3√3 D.r=3√2【解析】连OI,PI,DI,由△OPH的内心为I,可得到∠PIO=180°﹣∠IPO﹣∠IOP=180°﹣1/2(∠HOP+∠OPH)=135°,并且易证△OPI≌△ODI,得到∠DIO=∠PIO=135°,所以点I在以OD为弦,并且所对的圆周角为135°的一段劣弧上;过D、I、O三点作⊙O′,如图,连O′D,O′O,在优弧AO取点P′,连P′D,P′O,可得∠DP′O=180°﹣135°=45°,得∠DO′O=90°,O′O =3√2.故选:D.2.如图,在⊙O中,弦AD等于半径,B为优弧AD上的一动点,等腰△ABC的底边BC所在直线经过点D.若⊙O的半径等于1,则OC的长不可能为()A.2﹣√3 B.√3﹣1 C.2 D.√3+1【解析】利用圆周角定理确定点C的运动轨迹,进而利用点与圆的位置关系求得OC长度的取值范围.如图,连接OA、OD,则△OAD为等边三角形,边长为半径1.作点O关于AD的对称点O′,连接O′A、O′D,则△O′AD也是等边三角形,边长为半径1,3.如图,在△ABC中,AC=4√3,BC=9,∠ACB=60°,AM∥BC,点P在射线AM上运动,连BP交△APC的外接圆于点E,则AE的最小值为.【解析】:如图,连接CE.∵AM∥BC,∴∠MAC=∠ACB=60°,∴∠CEP=∠CAP=60°,∴∠BEC=120°,4.(2020•武汉模拟)如图,⊙O的半径为1,点D为优弧AB上一动点,AC⊥AB交直线BD于C,且∠B=30°,当△ACD的面积最大时,∠BAD的度数为.【解析】连接OA、OD,如图,根据圆周角定理得到∠AOD=2∠B=60°,则△OAD为等边三角形,所以AD=OA=1,而∠C=60°,利用圆周角定理可判断点C在AD为弦,圆周角为60°的弧上运动,根据三角形面积公式,当C在弧AD的中点时△ADC的面积最大,此时∠CAD=60°,从而得到∠BAD=30°.类型2 非圆问题中隐含圆的轨迹问题5.(2019秋•罗湖区期末)如图,矩形ABCD中,AB=20,AD=30,点E,F 分别是AB,BC边上的两个动点,且EF=10,点G为EF的中点,点H为AD边上一动点,连接CH、GH,则GH+CH的最小值为.【解析】:由已知,点G在以B圆心,5为半径的圆在与长方形重合的弧上运动.作C关于AD的对称点C′,连接C′B,交AD于H,交以D为圆心,以5为半径的圆于G。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中常见路径(轨迹)问题
之解决策略
一、 动点到定点的距离等于定长
这一类动点问题的特点是:所求的动点到某一个定点的距离是不变的。
根据圆的定义,这时容易发现该动点的轨迹是一个圆周或者一段弧。
而且该圆或者弧的圆心就是定点,半径就是定长。
知道圆心和半径之后就容易求解了。
1. 如图,矩形ABCD 中,AB=2,
E 是AD 边上一动点,将△ABE 沿BE
折叠至△PBE ,在点E 从A 到D 的过程中,求P 点轨迹长。
2. 如图,在△ABC 中,∠ACB=90°,∠ABC=30°,AC=2。
将△ABC 绕顶点C 顺时针旋
转,得到△A′B′C ,AC 中点为D ,A′B′中点为E ,连接DE ,当旋转角为_______°时,DE 长度最大,最大值为__________.
3. 如图,OA ⊥OB ,垂足为O ,P 、Q 分别是射线OA 、OB 上两个动点,点C 是线段PQ
的中点,且PQ=4.则动点C 运动形成的路径长是______
二、定角对定长
这一类动点问题的特点是:以该动点为顶点的某个角度大小是固定不变的,而且该固定角度所对的某一条边是固定的。
由圆周角的特点可知,这个动点的轨迹就是一个圆周或者一段弧。
而且这个固定角度就是圆周角,这个固定边就是弦。
如果需要求轨迹长的话,再把圆心角和半径算出来就行了。
不过有一点需要注意,这时需要把起始点和终点找到才能准确求出圆心角。
对于这种题型,找圆心可以用三角形外心的结论:锐角三角形的外心在三角形内部,直角三角形的外心在斜边中点,钝角三角形的外心在三角形外部。
所以,当这个固定角度是锐角时,圆心和动点位于固定边的同侧;当这个固定角度是直角时,圆心就在固定边的中点;当这个固定角度是钝角时,圆心和动点位于固定边的两侧。
4.如图,点E,F是正方形ABCD的边AD上两个动点,满足AE=DF。
连接CF交BD
于点G,连接BE交AG于点H。
若正方形的边长为2,则线段DH的最小值是___.
5.等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连结AF,BE相交于
点P.若BF=CE,当点E从点A运动到点C时,试求点P经过的路径长.
6.如图,正方形ODEF的边长为2,以O为圆心,AB为直径的半圆经过点D,连接
AF,BD相交于点P,将正方形ODEF从OD与OA重合的位置开始,绕着点O逆时针旋转90°,求交点P运动的路径长.
7.如图,圆O的直径AB=4,C为圆周上一点,AC=2。
P为半圆AB上一动点,连接
PC,过点C作PC的垂线交PB的延长线于点Q,求AQ的最大值。
8.如图,等边△ABC和等边△DEF边长都为2,EF和BC互相平分交于点O,直线FC
交直线AD于点P,当△DEF绕点O旋转时,求BP的最大值和最小值。
9.如图,半径为2cm,圆心角为90°的扇形OAB的弧AB上有一运动的点P.从点P
向半径OA引垂线PH交OA于点H.设△OPH的内心为I,当点P在弧AB上从点A
运动到点B时,内心I所经过的路径长为______.
【例4】如图,Rt△ABC中,∠C=90°,AC=2,BC=4,点A、B分别在x轴正半轴和y轴正半轴上。
当AB边在坐标轴上滑动时,求C点的轨迹长。
三、旋转型轨迹问题
这一类动点问题的特点是:所求的点是从动点,是先有其他点在动,然后所求动点才动,而且主动点和从动点会有一个定点作为“旋转中心”,旋转的情形满足下列两种之一:第一种是主动点、从动点和旋转中心三点共线;第二种是主动点与旋转中心的连线和从动点与旋转中心的连线夹角固定,而且两条线段之间的比例不变。
这时,要求从动点的轨迹,只需要求出主动点的轨迹就行。
因为根据几何画板,他们的轨迹形状相同,长度成比例。
10.如图,正方形ABCD的边长为2,CD边上一动点P,连接BP,过点P作PQ⊥BP,
截取PQ=BP,当点P从点C运动到点D时,求Q的轨迹长
11.如图,在等腰Rt△ABC中,AC=BC=2,点P在以斜边AB为直径的半圆上,M为
PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是________
12.如图,AB为⊙O的直径,AB=8,点C为圆上任意一点,OD⊥AC于D,当点C在⊙
O上运动一周,点D运动的路径长为_______
13.如图,正方形ABCD的边长是2,E是AD的中点,点F从点A出发,沿AB运动到
点B停止.连接FE,过E作EF的垂线交射线BC于点G,连结EG,P是EG的中点,请直接写出点P运动路线的长.
14. 如图,在矩形ABCD 中,点F 在AD 上,AB=2,AF=1,E 是AB 上的一个动点,连
接FE ,过点F 作FE 的垂线交BC 于点G ,连接EG ,设EG 的中点为P ,当点E 从点B 运动到点A 时,点P 移动的路径的长是__________.
15. 如图,已知线段AB =6,C 、D 是AB 上两点,且AC =DB =1,P 是线段CD 上一动
点,在AB 同侧分别作等边三角形APE 和等边三角形PBF ,G 为线段EF 的中点,点P 由点C 移动到点D 时,G 点移动的路径长度为_______.
16. 如图,在Rt △ABC 中,∠C=90°,AC=6,BC=8,动点P 从点A 开始沿边AC 向点
C 以1个单位长度的速度运动,动点Q 从点C 开始沿边CB 向点B 以每秒2个单位长度的速度运动,在整个运动过程中,求出线段PQ 中点M 所经过的路径长.
17. 如图,直角坐标系中,已知点A (2,4),B (5,0),动点P 从B 点出发沿BO 向终
点O 运动,动点Q 从A 点出发沿AB 向终点B 运动.两点同时出发,速度均为每秒1个单位,记PQ 的中点为G .请直接写出点G 随点P ,Q 运动所经过的路线的长度.
A
C。
