连续性数学期望的公式
概率论与数理统计32学时课程要点

二维随机变量分布函数的 4 条性质?
联合分布律(表格形式)
联合概率密度函数(与联合分布函数的关系,完备性,非负性,表示取
值在某个区域上的概率)52 页例 3-2,
3、理解边缘分布的概念;
固定一个变量的边界,让另一个变量的上边界趋于正无穷
是联合分布的一种极限形式
4、熟练掌握由联合概率密度求边缘概率密度的公式(默写?);
事件的概率(贯穿始终的课程主线,中心问题); 变量的分布函数(分布律,概率密度); 数字特征(期望,方差,协方差,相关系数,矩)
第一章 随机事件及其概率
1、熟练掌握事件的运算;事件的和、积、差、;
熟练掌握事件的关系:包含、相等、互斥、对立、完备事件组
熟练掌握事件的运算律运算:德摩恩律、分配律、减法公式 加法公式
数学期望和方差; 列一张表,写出 6 种分布的分布律或概率密度、期望、方差 6、掌握求协方差的概念 两个变量与各自均值的偏差的乘积的数学期望 计算公式? 协方差的 5 条性质? 7、掌握相关系数的概念 两个变量变准化之后的协方差;计算公式? 正相关?负相关?相关指的是线性相关性。 区别不相关与独立? 相关系数的两条性质? 8、掌握矩的概念 原点矩与中心矩 一阶矩与高阶矩 混合矩 所有的数字特征都是矩,所有的矩都是某种期望。 so,第四章所有的计算都与求期望有关,大多数统计指标都是某种意义下的
熟练掌握密度函数与变量落在某个区间内的概率的关系
6、熟练掌握正态分布、指数分布和均匀分布的定义及性质;
均匀分布的概率密度函数、分布函数
指数分布的概率密度函数、分布函数
《工程数学》教案19连续型随机变量的数学期望

《工程数学》教案19连续型随机变量的数学期望教学目标:1、了解连续型随机变量的概念及其特点;2、掌握连续型随机变量的数学期望的求解方法。
教学内容:一、连续型随机变量的概念及特点连续型随机变量是指取值在一个区间内的随机变量。
与离散型随机变量不同,连续型随机变量的取值可以是无数个,因此其概率密度函数(PDF)具有一定的连续性。
二、连续型随机变量的数学期望的定义对于连续型随机变量X,其数学期望E(X)可以通过积分的方式进行计算。
数学期望表示了随机变量在平均情况下的取值,并且是一个常数。
三、连续型随机变量的数学期望的计算方法1、如果概率密度函数f(x)在x=a和x=b处连续,并且在[a,b]区间内可积,那么连续型随机变量X在该区间内的数学期望可以通过以下公式计算:E(X) = ∫(a到b) x * f(x) dx2、如果概率密度函数f(x)在整个实数轴上连续并可积,那么连续型随机变量X的数学期望可以通过以下公式计算:E(X) = ∫(-∞到+∞) x * f(x) dx四、例题讲解例题1:已知连续型随机变量X的概率密度函数为f(x)=(3/2)*(x-1),0<x<2,求X的数学期望。
解:根据连续型随机变量的数学期望的计算方法,可以得出:E(X) = ∫(0到2) x * f(x) dx= ∫(0到2) x * (3/2)*(x-1) dx= ∫(0到2) (3/2)*(x^2-x) dx=(3/2)*[x^3/3-x^2/2]在0到2之间的值=(3/2)*[(8/3)-2/2-0]=(3/2)*[(8/3)-1]=(3/2)*(5/3)=5/2因此,X的数学期望为5/2五、教学设计1、引入:通过提问和讲解的方式引导学生回顾离散型随机变量的数学期望的计算方法,并带入连续型随机变量的背景,引出连续型随机变量的概念。
2、知识讲解:对连续型随机变量的概念和数学期望的定义进行详细讲解,并结合具体例子进行说明。
高中必背88个数学公式

高中必背88个数学公式1. 勾股定理:直角三角形的两条直角边的平方和等于斜边平方。
2. 余弦定理:在任意三角形中,一个角的余弦等于与该角相对的边的平方和减去另外两条边的平方的差再除以两倍的另一条边与该角相对的角的正弦的乘积。
3. 正弦定理:在任意三角形中,一个角的正弦等于与该角相对的边长和另外两条边长的比例的乘积。
4. 长方形面积公式:长方形的面积等于长乘以宽。
5. 平行四边形面积公式:平行四边形面积等于底边长乘以高。
6. 梯形面积公式:梯形的面积等于上底加下底乘以高再除以二。
7. 三角形面积公式:三角形面积等于底边长乘以高再除以二。
8. 圆面积公式:圆的面积等于圆周率乘以半径的平方。
9. 圆周长公式:圆的周长等于直径乘以圆周率。
10. 球体表面积公式:球体的表面积等于四倍的圆面积。
11. 球体体积公式:球体的体积等于四分之三的圆面积乘以半径的立方。
12. 一次函数方程: y = kx + b。
13. 二次函数方程: y = ax² + bx + c。
14. 等差数列通项公式: an = a1 + (n - 1)d,其中a1为首项,d为公差,an为第n项。
15. 等差数列前n项和公式: Sn = n(a1 + an)/2,其中a1为首项,an为第n项,n为项数。
16. 等比数列通项公式:an = a1 × qⁿ⁻¹,其中a1为首项,q为公比,n为项数。
17. 等比数列前n项和公式: Sn = a1(1 - qⁿ)/1 - q,其中a1为首项,q为公比,n为项数。
18. 三角函数正弦的定义:在直角三角形中,任意一锐角的正弦是指这个角的对边与这个角所在的斜边的比值。
19. 三角函数余弦的定义:在直角三角形中,任意一锐角的余弦是指这个角的邻边与这个角所在的斜边的比值。
20. 三角函数正切的定义:在直角三角形中,任意一锐角的正切是指这个角的对边与这个角的邻边的比值。
21. 三角函数余切的定义:在直角三角形中,任意一锐角的余切是指这个角的邻边与这个角的对边的比值。
概率论与数理统计知识点总结(超详细版)

概率论与数理统计知识点总结(超详细版)eik则有P(A)=k/n,其中n为样本空间中元素的个数。
在概率论中,样本空间和随机事件是基本概念。
如果事件A发生必然导致事件B发生,则称事件B包含事件A,记作A⊂B。
当A和B中至少有一个发生时,称A∪B为事件A和事件B的和事件。
当A和B同时发生时,称A∩B为事件A和事件B的积事件。
当A发生、B不发生时,称A-B为事件A和事件B的差事件。
如果A和B互不相容,即A∩B=∅,则称A和B是互不相容的,或互斥的,基本事件是两两互不相容的。
如果A∪B=S且A∩B=∅,则称事件A和事件B互为逆事件,又称事件A和事件B互为对立事件。
在概率论中,还有一些运算规则。
交换律指A∪B=B∪A,A∩B=B∩A;结合律指(A∪B)∪C=A∪(B∪C),(A∩B)∩C=A∩(B∩C);分配律指A∪(B∩C)=(A∪B)∩(A∪C),A∩(B∪C)=(A∩B)∪(A∩C);德摩根律指A∪B=A∩B,A∩B=A∪B。
频率与概率是概率论的重要概念。
在相同的条件下,进行了n次试验,在这n次试验中,事件A发生的次数n A称为事件A发生的频数,比值nAn称为事件A发生的频率。
概率指对于随机试验E的每一事件A赋予一个实数P(A),称为事件的概率。
概率P(A)满足非负性,即对于每一个事件A,0≤P(A)≤1;规范性,即对于必然事件S,P(S)=1;可列可加性,即设A1,A2,…,An是两两互不相容的事件,则有P(∪Ai)=∑P(Ai)(n可以取∞)。
概率还有一些重要性质,包括P(∅)=0,P(∪Ai)=∑P(Ai)(n可以取∞),如果A⊂B,则P(B-A)=P(B)-P(A),P(A)≤1,P(A)=1-P(A'),以及P(A∪B)=P(A)+P(B)-P(A∩B)。
等可能概型又称为古典概型,是指试验的样本空间只包含有限个元素,试验中每个事件发生的可能性相同。
如果事件A 包含k个基本事件,即A={e1}∪{e2}∪…∪{ek},则有P(A)=k/n,其中n为样本空间中元素的个数。
数学期望与方差的计算

数学期望与方差的计算引言数学期望与方差是统计学中两个重要的概念。
它们是描述一个随机变量分布特征的常用指标,对于理解和分析数据具有重要意义。
本文将介绍数学期望与方差的概念、计算方法以及它们的应用。
数学期望数学期望又称平均值,是描述一个随机变量的平均水平的指标。
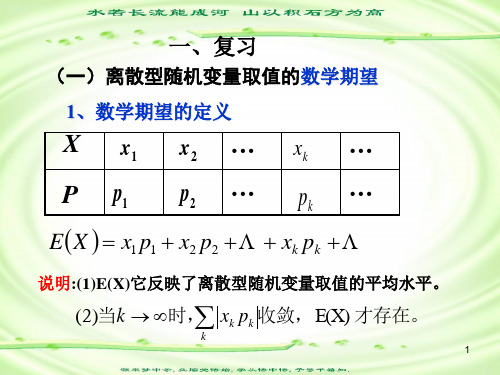
对于离散型随机变量,数学期望的计算公式为:$$ E(X)=\\sum_{i=1}^n x_i p_i $$其中,X为随机变量,x i为随机变量可能取的值,p i为随机变量取每个值的概率。
对于连续型随机变量,数学期望的计算公式为:$$ E(X)=\\int_{-\\infty}^{+\\infty} x f(x) dx $$其中,f(x)为随机变量的概率密度函数。
数学期望可以理解为在大量重复实验中,随机变量平均取值的水平。
方差方差是描述一个随机变量分散程度的统计指标。
方差越大,随机变量的取值越分散;方差越小,随机变量的取值越集中。
方差的计算公式为:Var(X)=E[(X−E(X))2]方差可以理解为每个随机变量与其期望的偏差的平方的加权平均。
数学期望与方差的计算方法离散型随机变量对于离散型随机变量,计算数学期望的方法如下:1.计算每个随机变量取值对应的概率。
2.将随机变量取值与对应的概率相乘。
3.将所有结果相加,得到数学期望。
计算方差可以使用以下方法:1.计算数学期望。
2.将每个随机变量取值与数学期望的差值的平方相乘。
3.将所有结果相加,得到方差。
连续型随机变量对于连续型随机变量,计算数学期望的方法如下:1.计算随机变量的概率密度函数。
2.将随机变量的取值与概率密度函数相乘。
3.对结果进行积分,得到数学期望。
计算方差可以使用以下方法:1.计算数学期望。
2.将随机变量的取值与数学期望的差值的平方与概率密度函数相乘。
3.对结果进行积分,得到方差。
数学期望与方差的应用数学期望与方差作为描述随机变量特征的指标,在统计学和概率论中有重要的应用。
数学期望在实际问题中可以用于计算平均值,如统计学中的样本均值就是数学期望的一种估计。
连续型随机变量的数学期望与方差
(1)D( )
E[
E( )]2
[x
E( )]2
p( x)dx
(2)方差的简便计算公式
D( )=E( 2) E(2 )
x2 p(x)dx
x p( x)dx
例2 随机变量的概率密度函数
6x(1 x),当0 x 1
p(x)
0
当x 0或x 1时
求随机变量的方差。
12
4、方差的性质 设 k ,b,c均为常数,则有
E( ) xp(x)dx
15
2、数学期望的性质
(1)EaX b aEX b
(2)EaX aEX
(3)EX b EX b
(4)Eb b
(5)EX Y EX EY
(6)E( f ( )) f (x)p(x)dx
(6)E f ( ) f (xk )PK
k
16
(二)连续型随机变量ξ取值的方差
(1)D(c) 0
(2)D(k ) k 2D( ) (3)D( b) D( )
(4)D(k b) k 2D( )
13
下页
三、练习
• 课本第90页 第6题
14
四、小结 (一)连续型随机变量ξ取值的数学期望
1、连续型随机变量的数学期望的定义 p(x) 设连续型随机变量 的密度函数为
若积分 xp(x绝)d对x 收敛,则 的数学期望为:
x0 x1 x2 L xn
xi xi1 xi
b i
【xi
,
xi
)
+1
y p(x)
o
x0b0 x1 xi bi xi1
xn x
6
连续型随机变量ξ的概率分布
ξ 【x0 , x1)【x1, x2)
随机过程的总复习

称这个特性为马尔可夫性,简称马氏性 称这个特性为马尔可夫性,简称马氏性。
马氏性实质上是无后效性, 所以也称马氏过程 马氏性实质上是无后效性 , 无后效过程。 为无后效过程。
(4)平稳随机过程 )
平稳过程的统计特性与马氏过程不同, 平稳过程的统计特性与马氏过程不同,它不 随时间的推移而变化,过程的“过去” 随时间的推移而变化,过程的“过去”可以对 未来”有不可忽视的影响。 “未来”有不可忽视的影响。
是相互独立的, 是相互独立的,
则 X(t) 为 有 立 量 随 过 。 称 具 独 增 的 机 程
(3)马尔可夫过程 )
设 { X (t ) , t ∈ T } 对任意 n 个不同的 t1 , t 2 ,…, t n ∈ T
且 t1 < t 2 < L < t n −1 < t n
P( X (t n ) ≤ x n | X (t n −1 ) = x n −1 ,…, X (t1 ) = x1 )
E ( Z ) = E ( X ) + iE (Y )
为随机变量, 设X为随机变量,称复随机变量 为随机变量 的数学期望
e
itX
ϕX (t) = E[e itX ]
的特征函数, 是实数。 为X的特征函数,其中 是实数。 的特征函数 其中t是实数 还可写成
ϕ X (t ) = E[costX ] + iE[sintX ]
一维 概率 密度
若 存 在 二 元 非 负 函 数 f ( t 1; x 1 ) , 使
F ( t1; x1 ) =
∫
x1
−∞
f ( t1; y 1 ) dy 1
则 称 f ( t 1; x 1 ) 为 随 机 过 程 X (t ) 的 一 维 概 率 密 度
期望计算公式完整版

期望计算公式标准化管理处编码[BBX968T-XBB8968-NNJ668-MM9N]
离散型
如果随机变量只取得有限个值或无穷能按一定次序一一列出,其值域为一个或若干个有限或无限区间,这样的随机变量称为离散型随机变量。
离散型随机变量的一切可能的取值与对应的概率乘积之和称为该离散型随机变量的数学期望[2](若该求和绝对收敛),记为。
它是简单算术平均的一种推广,类似加权平均。
公式
离散型随机变量X的取值,为X对应取值的概率,可理解为数据出现的频率,则:
定理
设Y是随机变量X的函数:(是连续函数)它的分布律为
若
绝对收敛,则有:
连续型
设连续性随机变量X的概率密度函数为f(x),若积分绝对收敛,则称积分的值为随机变量的数学期望,记为E(X)。
若随机变量X的F(x)可表示成一个非负f(x)的积分,则称X为,f(x)称为X的(分布密度函数)。
数学期望完全由随机变量X的概率分布所确定。
若X服从某一分布,也称是这一分布的数学期望。
定理
若随机变量Y符合函数,且绝对收敛,则有:
该定理的意义在于:我们求时不需要算出Y的分布律或者概率密度,只要利用X 的分布律或概率密度即可。
上述定理还可以推广到两个或以上随机变量的函数情况。
设Z是随机变量X、Y的函数(g是连续函数),Z是一个一维随机变量,二维随机变量(X,Y)的概率密度为,则有:
性质
设C为一个常数,X和Y是两个。
以下是数学期望的重要性质:
1.
2.
3.
4.当X和Y相互独立时,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
连续性数学期望的公式
连续性数学期望是概率论中用来衡量随机变量平均值的重要概念。
许多概率论问题都将连续性数学期望作为其中的重要研究中心,用来深入分析并探索一般变量的相关特性。
连续性数学期望的公式为:E[X] = ∫(-∞,∞)*f(x)dx,其中E[X]是对随机变量X的数学期望,f(x) 是随机变量 X 的概率分布函数,(-∞,∞)表示随机变量 X 可能取值范围。
这个公式能够衡量一个随机变量的平均值,以及这个随机变量在特定范围内的概率分布情况。
通过这个公式,可以在实际的概率论问题中获得更加准确的问题解决方案。
例如,通过知道随机变量 X 的概率分布函数 f (x),就可以得到它的数学期望值,从而可以更精确的判断该随机变量的概率特性。
连续性数学期望是概率论中一个重要的概念,它能够很好的帮助我们研究概率论问题,得出更正确的解决方案。
此外,通过连续性数学期望计算机可以实现自动化仿真,从而研究不同变量不同概率特性之间的相关性,从而得到更为全面的问题解决方案。
