专题突破练1
【全国通用】初中几何正方形解答题专题突破练习(1)
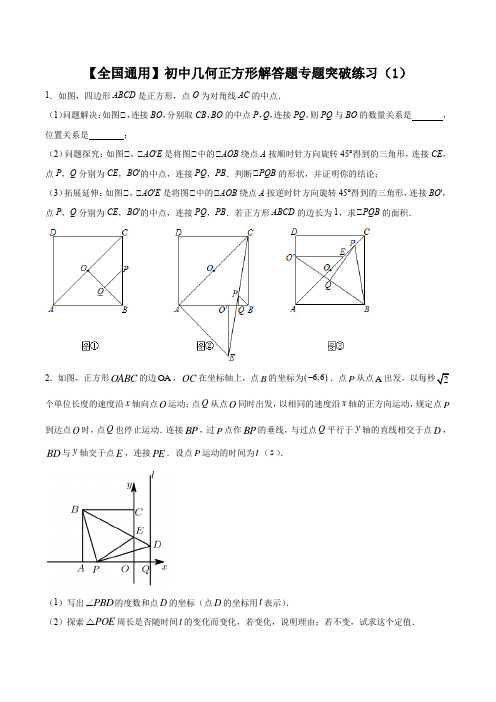
【全国通用】初中几何正方形解答题专题突破练习(1)1.如图,四边形ABCD 是正方形,点O 为对角线AC 的中点.(1)问题解决:如图①,连接BO ,分别取CB ,BO 的中点P ,Q ,连接PQ ,则PQ 与BO 的数量关系是 ,位置关系是 ;(2)问题探究:如图①,①AO 'E 是将图①中的①AOB 绕点A 按顺时针方向旋转45°得到的三角形,连接CE ,点P ,Q 分别为CE ,BO '的中点,连接PQ ,PB .判断①PQB 的形状,并证明你的结论;(3)拓展延伸:如图①,①AO 'E 是将图①中的①AOB 绕点A 按逆时针方向旋转45°得到的三角形,连接BO ',点P ,Q 分别为CE ,BO '的中点,连接PQ ,PB .若正方形ABCD 的边长为1,求①PQB 的面积.2.如图,正方形OABC 的边OA ,OC 在坐标轴上,点B 的坐标为()6,6-.点P 从点A 个单位长度的速度沿x 轴向点O 运动;点Q 从点O 同时出发,以相同的速度沿x 轴的正方向运动,规定点P 到达点O 时,点Q 也停止运动.连接BP ,过P 点作BP 的垂线,与过点Q 平行于y 轴的直线相交于点D ,BD 与y 轴交于点E ,连接PE .设点P 运动的时间为t (s ).(1)写出PBD ∠的度数和点D 的坐标(点D 的坐标用t 表示).(2)探索POE △周长是否随时间t 的变化而变化,若变化,说明理由;若不变,试求这个定值.(3)当何值时,PBE △为等腰三角形?3.如图1,正方形ABCD ,E 为平面内一点,且90BEC ∠=︒,把BCE 绕点B 逆时针旋转90︒得BAG ,直线AG 和直线CE 交于点F .(1)证明:四边形BEFG 是正方形;(2)若135AGD ∠=︒,猜测CE 和CF 的数量关系,并说明理由; (3)如图2,连接DF ,若13AB =,17CF =,求DF 的长.4.如图,已知正方形ABCD 的边长为3,E 、F 分别是边BC 、CD 上的点,①EAF=45° (1)求证:BE+DF=EF (2)当BE=1时,求EF 的长5.已知边长为2的正方形ABCD 中,P 是对角线AC 上的一个动点(与点A 、C 不重合),过点P 作PE①PB ,PE 交DC 于点E ,过点E 作EF①AC ,垂足为点F .(1)求证:PB=PE ;(2)在点P的运动过程中,PF的长度是否发生变化?若不变,试求出这个不变的值,写出解答过程;若变化,试说明理由;6.如图,已知正方形ABCD..(1)如图1,E是AD上一点,过BE上一点O作BE的垂线交AB于点G,交CD于点H,求证:BE GH (2)如图2,过正方形ABCD内任意一点作两条互相垂直的直线,分别交AD,BC于点E,F,交AB,CD于点G,H,EF与GH相等吗?请写出你的结论.(3)当点O在正方形ABCD的边上或外部时,过点O作两条互相垂直的直线,被正方形相对的两边(或它们的延长线)截得的两条线段还相等吗?其中一种情形如图3所示,过正方形ABCD外一点O作互相垂直的两条直线m,n,m与AD,BC的延长线分别交于点E,F,n与AB,DC的延长线分别交于点G,H,试就该图形对你的结论加以证明.7.如图,点E是正方形ABCD的边DC上一点,把①ADE绕点A顺时针旋转到①ABF的位置,接EF.(1)求证:①AEF是等腰直角三角形;(2)若四边形AECF的面积为25,DE=2,求AE的长.AC BD相交于点O,连接AP,分别交8.如图,点P是正方形ABCD中BC延长线上一点,对角线,,于点,E F,过点B作AP的垂线,垂足为点G,交线段AC于H.BD CD(1)若20P ∠=,求GBE ∠的大小.(2)求证:2AE EF EP =.(3)若正方形ABCD 的边长为1,1CP =,求HG 的长.9.已知,如图,在Rt①ABC 中,①BAC =90°,①ABC =45°,点D 为直线BC 上一动点(点D 不与点B ,C 重合).以AD 为边作正方形ADEF ,连接CF ,当点D 在线段BC 的反向延长线上,且点A ,F 分别在直线BC 的两侧时.(1)求证:①ABD ①①ACF ;(2)若正方形ADEF 的边长为AE ,DF 相交于点O ,连接OC ,求OC 的长度.10.四边形ABCD 是正方形,BEF ∆是等腰直角三角形,90,BEF BE EF ∠=︒=,连接DF ,G 为DF 的中点,连接,,EG CG EC .(1)如图1,若点E 在CB 边的延长线上,直接写出EG 与GC 的位置关系及ECGC的值.(2)将图1中的BEF ∆绕点B 顺时针旋转至图2所示位置,请问(1)中所得的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由.(3)将图1中的BEF ∆绕点B 顺时针旋转3(060)a a ︒<<︒,若2,BE AB ==当,,E F D 三点共线时,请直接写出GC 的长.11.已知:正方形ABCD ,等腰直角三角板的直角顶点落在正方形的顶点D 处,使三角板绕点D 旋转.(1)当三角板旋转到图1的位置时,猜想CE 与AF 的数量关系,并加以证明;(2)在(1)的条件下,若::1:DE AE CE =,求AED ∠的度数;(3)若4BC =,点M 是边AB 的中点,连结DM ,DM 与AC 交于点O ,当三角板的边DF 与边DM重合时(如图2),若3OF =,求DN 的长. 12.(1)如图1,正方形ABCD 中,E 为边CD 上一点,连接AE ,过点A 作AF①AE 交CB 的延长线于F ,猜想AE 与AF 的数量关系,并说明理由;(2)如图2,在(1)的条件下,连接AC,过点A作AM①AC交CB的延长线于M,观察并猜想CE与MF的数量关系,并说明理由;(3)解决问题:王师傅有一块如图所示的板材余料,其中①A=①C=90°,AB=AD.王师傅想切一刀后把它拼成正方形.请你帮王师傅在图3中画出剪拼的示意图.13.已知正方形ABCD,点E在AB上,点G在AD,点F在射线BC上,点H在CD上.(1)如图1,DE①FG,求证:BF=AE+AG;(2)如图2,DE①DF,P为EF中点,求证:BE;(3)如图3,EH交FG于O,①GOH=45°,若CD=4,BF=DG=1,则线段EH的长为.14.已知正方形ABCD中AC与BD交于点O,点M在线段BD上,作直线AM交直线DC于点E,过D作DH①AE于H,设直线DH交AC于点N.(1)如图1,当M在线段BO上时,求证:OM=ON;(2)如图2,当M在线段OD上,连接NE和MN,当EN//BD时,求证:四边形DENM是菱形;(3)在(2)的条件下,若正方形边长为4,求EC的长.15.如图1,在正方形ABCD中,E为边BC上一点(不与点B、C重合),垂直于AE的一条直线MN分别交AB、AE、CD于点M、P、N.(1)求证AE=MN;(2)如图2,若垂足P恰好为AE的中点,连接BD,交MN于点Q,连接EQ,并延长交边AD于点F.求①AEF的度数;(3)如图3,若该正方形ABCD边长为10,将正方形沿着直线MN翻折,使得BC的对应边B′C′恰好经过点A,过点A作AG①MN,垂足分别为G,若AG=6,请直接写出AC′的长________.16.(1)如图1,正方形ABCD中,点P为线段BC上一个动点,若线段MN垂直AP于点E,交线段AB 于点M,交线段CD于点N,证明:AP=MN;(2)如图2,正方形ABCD中,点P为线段BC上一动点,若线段MN垂直平分线段AP,分别交AB,AP,BD,DC于点M,E,F,N.求证:EF=ME+FN;(3)若正方形ABCD的边长为2,求线段EF的最大值与最小值.17.如图,在正方形ABCD中,E、F是对角线BD上两点,且①EAF=45°,将①ADF绕点A顺时针旋转90°后,得到①ABQ,连接EQ.(1)求证:EA是①QED的平分线;(2)已知BE=1,DF=3,求EF的长.18.如图1,已知正方形ABCD 和正方形CEGF ,点,,F C B 在同一直线上,连接BE ,DF ,DF 与EG 相交于点M .(1)求证:BE FD =.(2)如图2,N 是BC 边上的一点,连接AN 交BE 于点H ,且BN GMBC GE=. ①求证:BN EC =; ①若2CE DE =,直接写出BNAB的值. 19.如图,在平面直角坐标系中,边长为4的正方形OABC 的顶点A 、C 分别在y 轴、x 轴的正半轴上,点O 在原点.现将正方形OABC 绕点O 按顺时针方向旋转,旋转角为θ,当点A 第一次落在直线y x =上时停止旋转,旋转过程中,AB 边交直线y x =于点M ,BC 边交x 轴于点N .(1)若30θ=︒时,求点A 的坐标;(2)设MBN △的周长为P ,在旋转正方形OABC 的过程中,P 值是否有变化?请证明你的结论; 20.如图,在正方形ABCD 中,点E 、F 分别在边AB 、BC 上,AF 与DE 相交于点M ,且BAF ADE ∠=∠.(1)如图1,求证:AF DE ⊥.图1(2)如图2,AC 与BD 相交于点O ,AC 交DE 于点G ,BD 交AF 于点H ,连接GH ,试探究直线GH 与AB 的位置关系,并说明理由.图2(3)在(1)(2)的基础上,若AF 平分BAC ∠,且BDE ∆的面积为4+ABCD 的面积. 21.在ABC 中,①BAC =90°,AB =AC ,点D 为直线BC 上一动点(点D 不与B ,C 重合),以AD 为边在AD 的右侧作正方形ADEF ,连接CF .(1)观察猜想如图1,当点D 在线段BC 上时, ①BC 与CF 的位置关系为: ;①BC ,CD ,CF 之间的数量关系为: .(将结论直接写在横线上) (2)数学思考如图2,当点D 在线段CB 的延长线上时,结论①①是否仍然成立?若成立,请给予证明:若不成立,请你写出正确结论再给予证明, (3)拓展延伸如图3,当点D 在线段BC 的延长线上时,延长BA 交CF 于点G ,连接GE .若AB =,CD =1,请求出GE 的长.22.如图1,E 是正方形ABCD 中CD 边上的一点,以点A 为中心,把ADE 顺时针旋转α后,得到ABG . (1)求α的值;(2)当点F 在BC 上,且①EAF=45°,连接EF (如图2),求证:BF+DE=EF ;(3)在(2)的前提下,连接BD ,分别交AE ,AF 于M ,N 两点(如图3),试判断线段BN ,MN ,DM 三者的关系式,请给出证明.23.探究证明:(1)如图1,正方形ABCD 中,点M 、N 分别在边BC 、CD 上,AM①BN .求证:BN=AM ;(2)如图2,矩形ABCD 中,点M 在BC 上,EF①AM ,EF 分别交AB 、CD 于点E 、F .求证:EF BCAM AB=; (3)如图3,四边形ABCD 中,①ABC=90°,AB=AD=10,BC=CD=5,AM①DN ,点M 、N 分别在边BC 、AB 上,求DNAM的值. 24.已知:四边形ABCD 为正方形,AMN ∆是等腰Rt ∆,90AMN ∠=︒.(1)如图:当Rt AMN ∆绕点A 旋转时,若边AM 、AN 分别与BC 、CD 相交于点E 、F ,连接EF ,试证明:EF DF BE =+.(2)如图,当Rt AMN ∆绕点A 旋转时,若边AM 、AN 分别与BC 、CD 的延长线相交于点E 、F ,连接EF .①试写出此时三线段EF 、DF 、BE 的数量关系并加以证明.①若6CE =,2DF =,求:正方形ABCD 的边长以及AEF ∆中AE 边上的高.25.如图1,已知点G 在正方形ABCD 的对角线AC 上,GE BC ⊥,垂足为点E ,GF CD ⊥,垂足为点F .(1)证明与推断:①求证:四边形CEGF 是正方形;①推断:AG BE的值为:_______(直接写出答案).图1(2)探究与证明:将正方形CEGF 绕点C 顺时针方向旋转α角()045α︒<<︒,如图(2)所示,试探究线段AG 与BE 之间的数量关系,并说明理由.图2(3)拓展与运用:正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若6AG=,GH=,求BC的长.图3。
高考生物二轮复习 专题突破练1 细胞的物质基础(含解析)-人教版高三全册生物试题

专题突破练1 细胞的物质基础一、单项选择题1.(2020某某某某4月一模)下列有关组成生物体的元素和化合物的叙述,正确的是()A.麦芽糖和蔗糖属于植物特有的二糖,均为非还原性糖B.在细胞的不同生命活动中转运氨基酸的载体都是蛋白质C.胆固醇能参与人体血液中脂质的运输,又参与构成细胞膜D.在噬菌体中由A、G、T、C 4种碱基参与构成的核苷酸最多有7种2.(2020某某潍坊4月一模)下列有关组成生物体元素和化合物的叙述,正确的是()A.组成不同细胞的元素种类基本相同,但含量可能会有差异B.脂质的组成元素与糖类完全相同,但其分子中氧的相对含量远少于糖类C.蛋白质和DNA分子的多样性都与分子的空间结构密切相关D.淀粉、糖原、纤维素彻底水解后,得到的产物是不同的3.(2020某某某某4月一模)下列有关元素和化合物的叙述,正确的是()A.细胞中的元素大多数以离子形式存在,少数以化合物形式存在B.真核细胞的脱氧核糖核酸分布在细胞核、线粒体和叶绿体中,原核细胞中脱氧核糖核酸只分布在拟核中C.评价食品中构成蛋白质成分的营养价值时,应注重其中必需氨基酸的种类和含量,配制婴儿奶粉应重点关注的必需氨基酸有9种D.多糖、蛋白质、核苷酸均为生物大分子,由许多单体脱水缩合而成,每个单体都是以若干个相连的碳原子构成的碳链为基本骨架4.(2020某某某某4月一模)下列关于细胞中糖类、脂质和蛋白质的叙述,错误的是()A.细胞中的脂质能够与糖类结合B.细胞中的脂质不会含有氮元素C.细胞膜上糖类与蛋白质的结合物具有识别作用D.细胞中的糖类不能作为人体的直接能源物质5.下列有关蛋白质叙述,正确的是()A.食盐作用下析出的蛋白质空间结构发生了改变B.蛋白质分子进出细胞不需要载体蛋白的参与C.细胞内氨基酸种类和数量相同的蛋白质是同一种蛋白质D.已知某化合物含有C、H、O、N等元素且具有催化作用,可以推断此物质是蛋白质6.下列有关细胞中蛋白质的说法,错误的是()A.任何生物的蛋白质均由核糖体合成B.大多数酶是蛋白质,它们均需在最适pH下才能进行催化C.细胞质基因控制蛋白质合成是通过转录、翻译来实现的D.氨基酸序列不同的蛋白质,功能可能相同7.细胞中存在核酸—蛋白质复合物、糖—蛋白质复合物,以及构成离子通道的蛋白质复合物等。
2022年高考政治二轮复习专题突破练一人类社会发展的进程与趋势含解析

专题突破练一人类社会发展的进程与趋势一、选择题(共15小题,每小题3分,共45分)1.经历几百万年漫长的历史阶段后,原始社会最终走向解体。
下列对原始社会解体原因的分析正确的是( )①共同劳动取代个体劳动②私有制的产生导致贫富分化③生产资料转归氏族公有④贫富分化导致氏族成员地位不平等A.①③B.②④C.①④D.②③2.在奴隶社会存在着奴隶主阶级和奴隶阶级两大对立阶级,奴隶主阶级为了维护自身利益,建立了军队、法庭、监狱等机关,形成了奴隶制国家。
这说明奴隶制国家( )①是协调阶级矛盾的机构②是对奴隶阶级进行统治的工具③是阶级压迫的暴力机关④脱离了当时生产力发展水平A.①③B.①④C.②③D.②④3.商鞅变法规定“为田开阡陌封疆”,废除井田制,国家承认土地私有,确立了土地私有制,这是历史的进步。
对此认识正确的是( )A.封建制生产关系与较低的生产力水平相适应B.封建制生产关系的出现是生产力发展的结果C.封建制生产关系的出现是历史的必然D.封建制生产关系是在奴隶社会后期出现的4.“印子钱,一还三;利滚利,年年翻;一年借,十年还;几辈子,还不完”和“爷娘妻子走相送,尘埃不见咸阳桥。
牵衣顿足拦道哭,哭声直上干云霄”分别体现的地主阶级剥削农民的方式是( )①榨取地租②向农民放高利贷③强迫农民缴纳苛捐杂税④从事各种徭役A.①④B.②③C.②④D.①③5.在资本主义社会,矿上的工人,一个人一天生产五斤矿砂,矿主至少赚十五块钱,而矿工的工钱,每天却只有两角。
这揭露了( )①资本家为工人提供了就业机会②资本家在生产过程中占有工人创造的剩余价值③资本家与工人之间存在着剥削关系④生产社会化与资本主义私人占有之间的矛盾A.①②B.①③C.②③D.②④6.20世纪30年代,英国某经济学家曾把上街购物的家庭主妇称作爱国者。
他认为,现在我们所需要的,不是勒紧裤腰带过日子,而是需要一种发展扩张、积极活跃的精神,要多干一些实事,多买一些东西,多制造一些商品。
2023届新教材高考历史二轮复习专题突破练一中国古代的国家制度含解析

新教材高考历史二轮复习:专题突破练一中国古代的国家制度一、选择题1.商朝“服国”所管辖的土地和人民并非商王赐予,商王朝无法形成“礼乐征伐自天子出”的政治格局。
西周初期通过分封直接对诸侯“授民”“授疆土”,周天子由夏、商时的“诸侯之长”变成名副其实的“诸侯之君”。
由此可见,西周初期的分封制( )A.推动了血缘宗法制的发展B.有利于确立周天子“天下共主”的地位C.成为开拓疆土的主要手段D.易于形成天子权力的高度集中2.(2021·河南开封一模)下图是1963年出土于陕西宝鸡的西周早期青铜器“何尊”,尊内底铸铭文122字,提到“唯武王既克大邑商,则廷告于天,曰:余其宅兹中国,自之乂(治理、安定)民”。
材料中的“中国”指当时( )A.统治的地域中心B.汉文化影响范围C.封建政权的称谓D.中华民族的总称3.(2021·河北唐山一模)春秋时期,秦武公“伐邦冀戎,初县之”;晋文公在新兼并的土地上置县,以“异姓之能,掌其远官”。
这些“县”的设置( )A.增强了周王室对地方的控制B.推动了地方管理体制的变革C.维护了传统贵族的政治利益D.加剧了诸侯割据混战的局面4.(2021·辽宁大连一模)高焕祥在《秦汉廷议制度试析》中指出,秦汉廷议内容之广,规模之大,气氛之激烈都是空前绝后的;据不完全统计,其间四百年里有文可证的廷议就达百余次,而明文记载的被皇帝采纳的就有80多次。
这说明廷议( )A.扩大官僚权力实现对皇帝集权的制约B.是国家的决策中枢C.一定程度上弥补了封建体制的弊端D.是民主制意义上的议事5.(2021·湖北武汉一模)“丞相与守掌民事,太尉与尉掌军事,军民分治,厥谊至精。
而御史与监,则纠察此治民、治军之官者也。
后世官制,变化繁赜,而其原理,不能出于治民、治军、监察官吏三者之外。
”这反映了秦朝( )A.构建起隶属于丞相的监察体系B.形成了中央对地方的垂直管理C.完成了贵族政治向官僚政治的过渡D.奠定了后世王朝官制基本原则6.(2021·重庆高三联考)西汉时,一大夫随汉武帝外出打猎。
2022届新高考语文二轮专题突破精练 文言翻译(1)

文言翻译一、专项练习1.把文中画横线的句子翻译成现代汉语。
许骧,字允升,世家蓟州。
祖信,父唐,世以财雄边郡。
后唐之季,唐知契丹将扰边,白其父曰:“今国政废弛,狄人必乘衅而动,则朔、易之地,民罹其灾。
苟不即去,且为所虏矣。
”信以资产富殖,不乐他徙,唐遂潜赍百金而南。
未几,晋祖革命,果以燕、蓟赂契丹,唐归路遂绝。
尝拥商赀于汴、洛间,见进士缀行而出,窃叹曰:“生子当令如此!”因不复行商,卜居睢阳,娶李氏女,生骧,风骨秀异。
唐曰:“成吾志矣!”(节选自《宋史·许骧传》)(1)信以资产富殖,不乐他徙,唐遂潜赍百金而南。
译文:(2)尝拥商赀于汴、洛间,见进士缀行而出,窃叹曰:“生子当令如此!”译文:2.把文中画横线的句子翻译成现代汉语。
张叔夜字嵇仲,侍中耆孙也。
以荫为兰州录事参军。
献所为文,知舒、海、泰三州。
复献文,召试制诰,赐进士出身,迁右司员外郎。
使辽,宴射,首中的。
辽人叹诧,求观所引弓,以无故事,拒不与。
还,图其山川、城郭、服器、仪范为五篇,上之。
从弟克公弹蔡京,京迁怒叔夜,摭司存微过,贬监西安草场。
久之,召为秘书少监,擢给事中。
进礼部侍郎,又为京所忌,以徽猷阁待制再知海州。
靖康改元,金人南下,叔夜再上章乞假骑兵,与诸将并力断其归路,不报。
徙邓州。
(1)从弟克公弹蔡京,京迁怒叔夜,摭司存微过,贬监西安草场。
译文:(2)叔夜再上章乞假骑兵,与诸将并力断其归路,不报。
译文:3.把文中画横线的句子翻译成现代汉语。
崔光,本名孝伯,字长仁,高祖赐名焉,东清河鄃人也。
慕容白曜之平三齐,光年十七,随父徙代。
家贫好学,昼耕夜诵,佣书以养父母。
光少有大度,喜怒不见于色。
有毁恶之者,必善言以报之,虽见诬谤,终不自申曲直。
皇兴初,有同郡二人并被掠为奴婢,后诣光求哀,光乃以二口赎免。
高祖闻而嘉之。
虽处机近,曾不留心文案,唯从容论议,参赞大政而已。
高祖每对群臣曰:“以崔光之高才大量,若无意外咎谴,二十年后当作司空。
”其见重如是。
2021年九年级中考作图题专题突破练习(1)

2021中考三轮冲刺作图题专题突破(1)1.作图与计算如图,ABC 是直角三角形,90ACB ∠=︒.(1)尺规作图:以AC 为直径作O ,且O 与AB 交于点D ;(保留作图痕迹,不写作法,标明字母) (2)在(1)所作图的基础上,若2BC =,30A ∠=︒,则由BD ,BC 和劣弧CD 所围成的封闭图形的面积为_______________.2.如图,ABC ∆为一钝角三角形,且90BAC ∠>︒(1)分别以AB ,AC 为底向外作等腰Rt DAB ∆和等腰 Rt EAC (要求:尺规作图,不写作法,保留作图痕迹)(2)已知P 为BC 上一动点,通过尺规作图的方式找出一点P ,连接PD ,PE ,使得 PD PE ⊥并证明. 3.如图, 在 45ABC AB AC BAC =∠=︒中,,.(1)用尺规作图方法,按要求作图:①作ABC 的高BD ;①作BAC ∠的平分线AM ,分别交BD BC 、于点E F 、;(要求:保留作图痕迹,不写作法和证明)(2)求证:点D 在AB 的垂直平分线.上; .(3)在(1)所作的图中,探究线段AE 与BF 的数量关系,并证明你的结论.4.如图,OABC 内接于O ,动手操作.(1)求作:三角形ABC 的内切圆I ;要求:尺规作图,不写作法,但保留作图痕迹.(2)若AI 与O 交于点D ,连接,BD DC .求证:BD DI DC ==.5.如图所示的是ABC .()1求作,O 使圆心O 在AB 边上,且O 经过A C 、两点,(尺规作图,保留作图痕迹,不写作法) ()2设边AB 与你所作的O 的另一个交点为点,D 连接CD ,若DCB A ∠=∠.求证:BC 是O 的切线. 6.如图,在每个小正方形的边长为1的网格中,每个小正方形的顶点称为格点,A ,B ,C ,M 均在格点上,且5BM =,请用无刻度的直尺,分别按下列要求作图(保留作图痕迹).(1)如图1,请在网格中找出格点N ,连结MN ,使得//MN AC ;(2)如图2,请在线段AB 上找出点N ,使得MN 平分ABC 的周长.7.如图,已知ABC ∆()AB AC BC <<,请用无刻度直尺和圆规,完成下列作图(不要求写作法,保留作图痕迹):(1)在边BC 上找一点M ,使得:将ABC ∆沿着过点M 的某一条直线折叠,点B 与点C 能重合,请在图①中作出点M ;(2)在边BC 上找一点N ,使得:将ABC ∆沿着过点N 的某一条直线折叠,点B 能落在边AC 上的点D 处,且ND AC ⊥,请在图①中作出点N .8.如图,请仅用无刻度的直尺按要求完成下列作图,不写作法,但要保留清晰的作图痕迹.(1)如图1,A ,B ,C ,D 四个点在同一个圆上,且AB//CD ,请作出这个圆的一条直径;(2)如图2,四边形ABCD 是菱形,且A ,B ,C 三点在同一个圆上,请找出这个圆的圆心.9.已知:如图,ABC ∆中,AB BC =,120B ∠=︒.(1)用直尺和圆规作出AB 的垂直平分线,分别交AC ,AB 于点M ,N (保留作图痕迹,不写作法);(2)猜想CM与AM之间有何数量关系,并证明你的猜想.10.如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD,BE,BC于点P,O,Q,连接BP,EQ.(1)依题意补全图形(保留作图痕迹),并求证四边形BPEQ是菱形;(2)若AB=6,F为AB的中点,且OF+OB=9,求PQ的长.11.如图,在每个小正方形的边长为1的网格中,点O、M均在格点上,P为线段OM上的一个动点.(1)OM的长等于________;OP 时,请借助网格和无刻度的直尺,在给定的网格中画出点P (2)当点P在线段OM上运动,且4的位置(保留作图的痕迹).12.新定义:如图1,E、F、G、H四点分别在四边形ABCD的四条边上,若四边形EFGH为矩形,我们称矩形EFGH为四边形ABCD的内接矩形.(1)如图2,网格中的每个小四边形都是正方形,由35个小正方形组成的矩形ABCD,E、F在格点上,请在图2中画出四边形ABCD的内接矩形EFGH.(2)如图3,矩形EFGHABCD 中,矩形EFGH 为四边形ABCD 的内接矩形5AB =,点E 在线段AB 上且2,6BE BC ==,求BF 的长.(3)①如图4,平行四边形,5,60ABCD AB B =∠=︒,E 在AB 上,请你在图4中画出其内接矩形EFGH (尺规作图,并保留作图痕迹),F 在BC 边上.①在①的条件下,EG 最小值为____________13.如图,①ABC 内接于①O ,AB 是①O 的直径,过点A 作AD 平分①BAC ,交①O 于点D ,过点D 作DE ①BC 交AC 的延长线于点E .(1)依据题意,补全图形(尺规作图,保留痕迹);(2)判断并证明:直线DE 与①O 的位置关系;(3)若AB =10,BC =8,求CE 的长.14.(1)在正方形方格纸中,我们把顶点均在“格点”上的三角形称为“格点三角形”,如图①ABC 是一个格点三角形,点A 的坐标为(-2,2).(1)点B 的坐标为 ,①ABC 的面积为 ;(2)在所给的方格纸中,请你以原点O 为位似中心,将①ABC 缩小为原来的一半(仅用直尺); (3)在(2)中,若P (a ,b )为线段AC 上的任一点,则缩小后点P 的对应点P 1的坐标为 . (4)按要求作图,不要求写作法,但要保留作图痕迹.我们知道,三角形具有性质:三边的垂直平分线相交于同一点,三条角平分线相交于一点,三条中线相交于一点,事实上,三角形还具有性质:三条高所在直线相交于一点.请运用上述性质,只用直尺(不带刻度)作图.①如图2,在平行四边形ABCD中,E为CD的中点,作BC的中点F.①如图3,在由小正方形组成的4×3的网格中,①ABC的顶点都在小正方形的顶点上,作①ABC的高AH.15.如图,在Rt①ABC中,①C=90°,点D是AB的中点,AC<BC.(1)试用无刻度的直尺和圆规.........,在BC上作一点E,使得直线ED平分ABC的周长;(不要求写作法,但要保留作图痕迹).(2)在(1)的条件下,若DE分Rt①ABC面积为1﹕2两部分,请探究AC与BC的数量关系.16.如图,将①ABC放在每个小正方形的边长为1的网格中,点A、B、C均在格点上.(1)边AC的长等于_____.(2)以点C为旋转中心,把①ABC顺时针旋转,得到①A'B'C',使点B的对应点B'恰好落在边AC上,请在如图所示的网格中,用无刻度的直尺,作出旋转后的图形,并简要说明作图的方法(不要求证明).17.如图(甲、乙),AB为半圆①O1的直径,AO1为半圆①O2的直径,仅用无刻度的直尺完成下列作图:(1)如图甲,C 为半圆①O 1上一点,请在半圆①O 1找个点D ,使得D 恰为AC 的中点;(2)如图乙,E 为半圆①O 2上一点,请在半圆①O 2找个点F ,使得F 恰为AE 的中点.18.已知①ABC .(1)在图①中用直尺和圆规作出B 的平分线和BC 边的垂直平分线交于点O (保留作图痕迹,不写作法).(2)在(1)的条件下,若点D 、E 分别是边BC 和AB 上的点,且CD BE =,连接OD OE 、求证:OD OE =; (3)如图②,在(1)的条件下,点E 、F 分别是AB 、BC 边上的点,且①BEF 的周长等于BC 边的长,试探究ABC ∠与EOF ∠的数量关系,并说明理由.19.如图,在□ABCD 中,以点 A 为圆心,AB 长为半径画弧交 AD 于点 F ,再分别以点 B 、F 为圆心,大于12BF 的相同长为半径画弧,两弧交于点 P ,连接 AP 并延长交 BC 于点 E ,连接 EF . (1)根据以上尺规作图的过程,证明四边形 ABEF 是菱形;(2)若菱形 ABEF 的边长为 2,AE = 2 ABEF 的面积.20.在边长为1的正方形网格图中,点B 的坐标为(2,0),点A 的坐标为(0,-3).(1)在图1中,请建立合适的坐标系,把线段AB 绕原点旋转180°得线段DE (其中A 与D 是对应点),则四边形ABDE 是 形,面积等于 .(2)在图2中,仅使用无刻度的直尺,作出以AB 为边的矩形ABFG ,使其面积为11(保留作图痕迹,不写做法)21.如图,在图中求作①P ,使①P 满足以线段MN 为弦且圆心P 到①AOB 两边的距离相等.(要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑)22.如图,已知ABC ∆是锐角三角形()AC AB <.(1)请在图1中用无刻度的直尺和圆规作图;作直线l ,使l 上的各点到B 、C 两点的距离相等;设直线l 与AB 、BC 分别交于点M 、N ,作一个圆,使得圆心O 在线段MN 上,且与边AB 、BC 相切;(不写作法,保留作图痕迹)(2)在(1)的条件下,若53BM =,2BC =,则O 的半径为________. 23.在①ABC 中,①ACB =90°.(1)作出经过点B ,圆心O 在斜边AB 上且与边AC 相切于点E 的①O (要求:尺规作图,保留作图痕迹,不写作法和证明).(2)设(1)中所作的①O 与边AB 交于异于点B 的另外一点D ,若①O 得直径为5,BC =4,求AD 的长度.(如果尺规作图画不出图形,此小题可画草图解答)24.(1)如图①,点E在正方形ABCD的内部,且EB=EC,过点E画一条射线平分∠BEC;(2)如图①,在∠ABC中,DE∠BC,EF∠AB,请仅用直尺(无刻度)作一个三角形,使所作三角形的面积等于∠ABC面积的一半并把所作的三角形用阴影表示出来.25.按要求作图,不要求写作法,但要保留作图痕迹.(1)如图1,矩形ABCD的顶点A、D在圆上, B、C两点在圆内,已知圆心O,请仅用无刻度的直尺作图,请作出直线l①AD;(2)请仅用无刻度的直尺在下列图2和图3中按要求作图.(补上所作图形顶点字母)①图2是矩形ABCD,E,F分别是AB和AD的中点,以EF为边作一个菱形;①图3是矩形ABCD,E是对角线BD上任意一点(BE>DE),以AE为边作一个平行四边形.26.已知:Rt①ABC ,①C =90°.(1)点E 在BC 边上,且①ACE 的周长为AC +BC ,以线段AE 上一点O 为圆心的①O 恰与AB 、BC 边都相切.请用无刻度的直尺和圆规确定点E 、O 的位置;(2)若BC =8,AC =4,求①O 的半径.27.(1)如图1,已知AC①直线l ,垂足为C .请用直尺(不含刻度)和圆规在直线l 上求作一点P (不与点C 重合),使PA 平分①BPC ;(2)如图2,在(1)的条件下,若90PAB ∠=︒,,作BD①直线l ,垂足为D ,则BD= .28.已知,如图,在边长为10的菱形ABCD 中,cos①B =310,点E 为BC 边上的中点,点F 为边AB 边上一点,连接EF ,过点B 作EF 的对称点B ′, (1)在图(1)中,用无刻度的直尺和圆规作出点B ′(不写作法,保留痕迹);(2)当①EFB ′为等腰三角形时,求折痕EF 的长度.(3)当B ′落在AD 边的中垂线上时,求BF 的长度.29.如图,已知点M 在直线l 外,点N 在直线l 上,请用无刻度的直尺和圆规完成下列作图,要求保留痕迹,不写作法.(1)在图①中,以线段MN 为一条对角线作菱形MPNQ ,使菱形的边PN 落在直线l 上(2)在图①中,做圆O ,使圆O 过点M ,且与直线l 相切于N .30.如图,直线1l 与2l 相交于点O ,A ,B 是2l 上两点,点P 是直线1l 上的点,且30APB ∠=︒,请利用圆规和无刻度直尺在图中作出符合条件的点P .31.如图,平面内有线段AB 和一点P .按照要求,用无刻度的直尺和圆规作图,请保留作图痕迹. (1)在图1中求作①ABC ,使AC =AB ,且使点P 到AB 和AC 的距离相等;(2)在图2中求作①ABC ,使点P 到点A 、点C 的距离相等,且使①C =12①APB .32.已知:如图,在Rt①ABC 中,①C =90°,①A≠①B .(1)请利用直尺和圆规作出①ABC 关于直线AC 对称的①AGC ;(不要求写作法,保留作图痕迹)(2)在AG 边上找一点D ,使得BD 的中点E 满足CE =AD .请利用直尺和圆规作出点D 和点E ;(不要求写作法,保留作图痕迹)33.(1)如图1,点A 在O 上,请在图中用直尺(不含刻度)和圆规作等边三角形ABC ,使得点B 、C 都在O 上.(2)已知矩形ABCD 中,4AB =,BC m =.①如图2,当4m =时,请在图中用直尺(不含刻度)和圆规作等边三角形AEF ,使得点E 在边BC 上,点F 在边CD 上;①若在该矩形中总能作出符合①中要求的等边三角形AEF ,请直接写出m 的取值范围.。
中考物理必考专题突破 实验1 测量物体运动的平均速度(解析版)

实验1 测量物体运动的平均速度 反馈练习一.选择题1.小明用如图所示装置测量小车的平均速度,图中方框内的数字是小车到达A 、B 、C 三处时电子表的显示[时:分:秒]。
下列说法正确的是( )A .实验中为了方便计时,应使斜面保持较大的坡度B .实验中误差的主要来源是小车通过的路程的测量C .根据图中的信息可知小车从B 点到C 点所用的时间2BC t s =D .如果小车到C 点后才停止计时,则测得的平均速度AC v 会偏小 【解析】A 、实验中为了方便计时,应使斜面保持较小的坡度,故A 错误;B 、由于时间不容易测量,所以实验中误差的主要来源是小车运动时间的测量,故B 错误;C 、根据图中的信息可知小车从B 点到C 点所用的时间10:30:1810:30:171BC t s =-=,故C 错误;D 、如果让小车过了C 点后才停止计时,所计时间偏大,用公式sv t=知,速度偏小,故D 正确。
故选:D 。
2.小明在测量小球的平均速度时,让小球从斜面A 点由静止滚到C 点,并用照相机每隔0.ls 拍摄一次,频闪照片如图所示,则下列说法正确的是( )A .小球从A 点运动到C 点用时0.6sB .小球在BC 段的平均速度大于AB 段的平均速度 C .小球滚下的整个过程的平均速度为1.1/cm sD .小球在前0.4s 内通过的路程为4cm【解析】A 、照相机每隔0.ls 拍摄一次,图中小球从A 点运动到C 点经过了5个时间间隔,用时50.10.5s s ⨯=,故A 错误;B 、由图可知,小球在AB 段用的时间30.10.3AB t s s =⨯=,路程 2.700.027AB s cm m ==,所以0.0270.09/0.3AB AB AB s mv m s t s===, 小球在BC 段用的时间为20.10.2BC t s s =⨯=,路程 5.50 2.70 2.800.028BC s cm cm cm m =-==; 所以0.0280.14/0.2BC BC BC s mv m s t s===, 比较可知,小球在BC 段的平均速度大于AB 段的平均速度,故B 正确; C 、由图可知,AC 之间的距离为 5.500.055s cm m ==,则整个运动过程小球的平均速度为:0.0550.11/11/0.5s mv m s cm s t s====,故C 错误; D 、由图可知,小球在前0.4s 内通过的路程为4.00cm ,故D 错误。
高考政治二轮复习专题突破练一价格波动与居民消费含解析

专题突破练一价格波动与居民消费一、选择题(共16小题,每小题3分,共48分)1.疫苗属于公共产品,价格由企业依据成本确定,根据使用规模大小进行调整。
在我国,新冠疫苗由政府按程序购买,为全民免费提供。
对此,下列认识正确的是( )①疫苗属于公共产品,其交易不是商品交换②疫苗价格由企业定价,符合价值规律的要求③由政府免费提供新冠疫苗接种,难以反映市场需求④全民免费接种新冠疫苗,可以更好实现其使用价值A.①②B.①③C.②④D.③④2.某手机创始人的直播带货“首秀”斩获颇丰,“宇宙首单”在直播间成交,伴随“OMG”“买它买它买它”的魔性语录,直播带货正在成为电商在新时代的新产业,呈现出极强的爆发性。
结合这一现象,下列说法正确的是( )①直播带货的聚众效应可以促使商品价值快速实现②主播通过提高消费者对商品品牌的认可实现带货③消费者通过直播购物改善消费结构,提高消费水平④直播带货模式将成为当下商品营销的主要渠道A.①②B.①③C.②③D.③④3.目前,六大国有银行已经开始推广数字人民币货币钱包。
获得授权的消费者可以在央行数字人民币App中设立银行子钱包,使用数字人民币钱包支付购买各类商品。
有市民感慨“使用数字人民币支付很简单,扣款时,手机里的一张电子版人民币就会嗖的一下飞出去,有现场付款的爽快感觉”。
由此可见,数字人民币( )①可以丰富消费体验,提高居民的购买能力②能够代替纸质人民币充当商品交换的媒介③丰富了货币形式,增加了货币实际供应量④能提高购物支付的便捷性,降低交易成本A.①③B.①④C.②③D.②④4.2021年4月的某一天,人民币对美元汇率的中间价为654.63元;一个多月前,人民币对美元汇率的中间价为647.95元。
这一变化表明( )A.人民币贬值,有利于中国居民赴美留学B.美元贬值,不利于美国进口中国的商品C.人民币升值,不利于中国商品出口美国D.美元升值,有利于美国企业在中国投资5.商品价格是价值的货币表现,货币的变化对商品价格有重要影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题突破练1选择题、填空题的解法
一、选择题
1.方程ax2+2x+1=0至少有一个负根的充要条件是()
A.0<a≤1
B.a<1
C.a≤1
D.0<a≤1或a<0
2.(2018山东济南二模,文2)设复数z满足z(1-i)=2(其中i为虚数单位),则下列说法正确的是()
A.|z|=2
B.复数的虚部是-1
C.=-1+i
D.复数在复平面内所对应的点在第一象限
3.(2018百校联盟四月联考,理3)已知P是△ABC所在平面内一点,且=λ,则
λ=()
A.2
B.1
C.-2
D.-1
4.设f(x)=ln x,0<a<b,若p=f(),q=f,r=[f(a)+f(b)],则下列关系式中正确的是()
A.q=r<p
B.q=r>p
C.p=r<q
D.p=r>q
5.在△ABC中,角A,B,C所对的边分别为a,b,c,若a,b,c成等差数列,则等于()
A. B.
C. D.
6.已知定义在R上的函数f(x)满足:对任意实数x,都有f(1+x)=f(1-x),且f(x)在(-∞,1]上单调递增.若x1<x2,且x1+x2=3,则f(x1)与f(x2)的大小关系是()
A.f(x1)<f(x2)
B.f(x1)=f(x2)
C.f(x1)>f(x2)
D.不能确定
7.(2018河南郑州三模,文9)已知函数f(x)=+cos x,下列说法中正确的个数为()
①f(x)在上是减函数;②f(x)在(0,π)上的最小值是;③f(x)在(0,2π)上有两个零点.
A.0
B.1
C.2
D.3
8.设函数f(x)=则满足f(f(a))=2f(a)的a的取值范围是()
A.B.[0,1]
C.D.[1,+∞)
9.已知f(x)=log a(x-1)+1(a>0,且a≠1)恒过定点M,且点M在直线=1(m>0,n>0)上,则m+n的最小值为()
A.3+2
B.8
C.4
D.4
10.(2018山东济南二模,理10)设椭圆C:=1(a>0,b>0)的左、右焦点分别为F1,F2,点
E(0,t)(0<t<b).已知动点P在椭圆上,且点P,E,F2不共线,若△PEF2的周长的最小值为4b,则椭圆C的离心率为()
A. B.
C. D.
二、填空题
11.设a>b>1,则log a b,log b a,log ab b的大小关系是.(用“<”连接)
12.不论k为何实数,直线y=kx+1与圆x2+y2-2ax+a2-2a-4=0恒有交点,则实数a的取值范围
是.
13.函数f(x)=4cos2cos-2sin x-|ln(x+1)|的零点个数为.
14.已知定义在R上的奇函数f(x)满足f(x-4)=-f(x),且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间[-8,8]上有四个不同的根x1,x2,x3,x4,则x1+x2+x3+x4=.
15.(2017内蒙古包头一模,理15)已知函数f(x)是定义在R上的可导函数,其导函数记为f'(x),若对于∀x ∈R,有f(x)>f'(x),且y=f(x)-1是奇函数,则不等式f(x)<e x的解集为.
16.设函数g(x)=x2-2(x∈R),f(x)=则f(x)的值域为.
参考答案
专题突破练1选择题、填空题的解法
1.C解析当a=0时,x=-,符合题意,排除A,D;当a=1时,x=-1,符合题意,排除B.故选C.
2.D解析∵z==1+i,
∴|z|=.复数的虚部是1.
=1-i.
复数在复平面内所对应的点为(1,1),显然在第一象限.故选D.
3.C解析⇔2()=,∴2,
∴=-2,故选C.
4.C解析f(x)=ln x是增函数,根据条件不妨取a=1,b=e,则
p=f()=ln,q=f>f()=,r=·[f(1)+f(e)]=.在这种特例情况下满足
p=r<q,所以选C.
5.B解析(法一)由题意可取特殊值a=3,b=4,c=5,则cos A=,cos
C=0,.故选B.
(法二)由题意可取特殊角A=B=C=60°,cos A=cos C=.故选B.
6.C解析由f(1+x)=f(1-x)知,函数y=f(x)的图象关于直线x=1对称.又f(x)在(-∞,1]上单调递增,所以f(x)在[1,+∞)上单调递减.设点A(x1,0),B(x2,0),因为x1<x2,且x1+x2=3,则点A
在点B的左侧,且AB的中点坐标为,所以结合图象(略)可知,f(x1)>f(x2).
7.C解析∵f(x)=+cos x,f'(x)=--sin x,当x∈时,f'(x)<0,∴f(x)在上是单调减函数,①正确;当x∈(0,π)时,f'(x)<0,∴f(x)在(0,π)上是单调减函数,没有最小值,②错;令
+cos x=0,则-=cos x,当x∈(0,π)时,画出y=-,y=cos x的图象,
由图象知,y=-与y=cos x在(0,2π)上有两个交点,∴f(x)在(0,2π)上有两个零点,③正确.
综上,正确的命题序号是①③.
8.C解析当a=2时,f(a)=f(2)=22=4>1,f(f(a))=2f(a),
∴a=2满足题意,排除A,B选项;当a=时,f(a)=f=3×-1=1,f(f(a))=2f(a),∴a=满足题意,排除D选项,故答案为C.
9.A解析因为f(x)=log a(x-1)+1(a>0,且a≠1)恒过定点M(2,1),所以M(2,1)在直线
=1上,可得=1,m+n=(m+n)=3+≥3+2,m+n的最小值为
3+2,故选A.
10.A解析△PEF2的周长为|PE|+|PF2|+|EF2|=|PE|+2a-|PF1|+|EF2|=2a+|EF2|+|PE|-
|PF1|≥2a+|EF2|-|EF1|=2a=4b,
故e=,故选A.
11.log ab b<log a b<log b a解析考虑到两个数的大小关系是确定的,不妨令a=4,b=2,则
log a b=,log b a=2,log ab b=,显然<2,∴log ab b<log a b<log b a.
12.-1≤a≤3解析由题知2a+4>0,则a>-2.注意到直线y=kx+1恒过定点(0,1),所以题设条件等价于点(0,1)在圆内或圆上,则有02+12-2a·0+a2-2a-4≤0,即a2-2a-3≤0,解得-
1≤a≤3.综上,-1≤a≤3.
13.2解析由题意可得f(x)=4cos2·sin x-2sin x-|ln(x+1)|=2sin x·-
|ln(x+1)|=sin 2x-|ln(x+1)|.
令f(x)=0,得sin 2x=|ln(x+1)|.在同一平面直角坐标系中作出两个函数y=sin 2x与函数y=|ln(x+1)|的大致图象,如图所示.
观察图象可知,两函数图象有2个交点,故函数f(x)有2个零点.
14.-8解析根据函数特点取f(x)=sin x,再由图象可得(x1+x2)+(x3+x4)=(-6×2)+(2×2)=-8.
15.(0,+∞)解析由题意令g(x)=,则g'(x)=,
∵f(x)>f'(x),∴g'(x)<0,
故函数g(x)=在R上单调递减.∵y=f(x)-1是奇函数,
∴f(0)-1=0,即f(0)=1,g(0)=1,则不等式f(x)<e x等价为<1=g(0),即g(x)<g(0),解得x>0.
16.∪(2,+∞)解析由x<g(x),得x<x2-2,
∴x<-1或x>2;
由x≥g(x),得x≥x2-2,
∴-1≤x≤2.
∴f(x)=即
f(x)=
当x<-1时,f(x)>2;当x>2时,f(x)>8.∴当x∈(-∞,-1)∪(2,+∞)时,函数的值域为(2,+∞).
当-1≤x≤2时,-≤f(x)≤0.
∴当x∈[-1,2]时,函数的值域为.综上可知,f(x)的值域为∪(2,+∞).。
