弹性力学第七章 平面问题的直角坐标解答PPT课件
合集下载
《弹塑性力学》第七章 弹性力学平面问题的极坐标系解答.ppt

x
应力:r, ,r= r 应变:r, ,r= r
P
y
位移:u r , u
2020/10/9
3
§7-1平面极坐标下的基本公式
直角坐标与极坐标之间关系:
x=rcos, y=rsin
r cos sin
x r x x
r r
r sin cos
y r y y
r
r
2 r
r )( f r
r
f 1
r
fr 0 0 f
fr ) r
2= 2 1 1 2
r 2 r r r 2 2
力的边界条件如前所列。
2020/10/9
14
§7-1平面极坐标下的基本公式
1.8 应力函数解法
当体力为零 fr=f=0时, 应力法基本方程中的应
力分量可以转为一个待求的未知函数 ( r, ) 表示,而应力函数 ( r, ) 所满足方程为
16
§7-2 轴对称问题
2.1 轴对称问题的特点
1.截面的几何形状为圆环、圆盘。
2.受力和约束对称于中心轴,因此,可知体 积力分量 f=0 ; 在边界上 r=r0 :F 0, u (0 沿环向的受力和约束为零) 。
3.导致物体应力、应变和位移分布也是轴 对称的:
2020/10/9
17
§7-2 轴对称问题
上式代入平衡微分方程可得到用位移表 示的平衡微分方程,即位移法的基本方程。
r
r
1 r r
( r
r
)
Kr
0
r
r
1 r
2 r
r
K
0
力的边界条件也同样可以用位移表示。
2020/10/9
弹性力学-第7章 空间问题
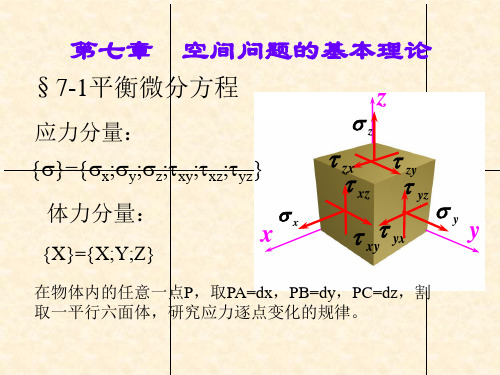
zx
z
dz
zy
zy
z
dz
z 0
y
y
yx yz
xy
x
yz
yz
y
dy
fz
fy fx
xz
yx
y yx dy
y
y y
dy
zx zy
x
x
x x
dx
z
根椐平衡条件: Fx 0
xz
xzx
x
dx
x
x
x
dx dydz
xdydz
(
yx
yx
x
dy)dxdz
yxdxdz
( zx
zx
z
dz)dxdy
zxdxdy
Xdxdydz
0
§7-1平衡微分方程
x x
yx y
zx
z
fx
0
xy
y
x
y
zy
z
f y
0
xz yz
x
y
z z fz 0
(7-1)
平面应力问题:
1、平面应力问题z方向应力为零:
0
xz
yz
0
z
2、所有的应力、应变和位移分量均与z无关,仅是x,y的函数。 以上方程可以直接转化为平面应力的平衡方程。
在计算任一平面上的应力时,方向余弦l,m,n可变化,但 均为有限值,故必存在某个平面,其上正应力取得极值。
主平面:正应力取得极值的平面。 主应力:主平面上的正应力。 主方向:主应力的方向,也称应力主向。 在主平面上,正应力取极值、剪应力为零。
二、主应力的确定:
设主平面存在,其外法线为n,
弹性力学-平面问题的直角坐标解答.

CHINA UNIVERSITY OF MINING AND TECHNOLOGY
弹性力学平面问题的基本方程
(1)平衡方程: (3)物理方程:
x yx fx 0 x y xy y fy 0 x y
(2)几何方程:
u x x v y y v u xy x y
力学与建筑工程学院力学系弹性力学电子教案
CHINA UNIVERSITY OF MINING AND TECHNOLOGY
按应力求解平面问题的基本方程
(1)平衡方程
x xy fx 0 x y yx y fy 0 x y
常体力下可以简化: ( 1)
结论2:二次多项式对应于均匀应力分布。 2a 2c 2c x y 2a
0
xy b
x
0
2
y2
y
试求图示板的应力函数。 例:
0
0
x
x
y
( x, y )
0
2
x
2
y
0
( x, y) 0 xy
力学与建筑工程学院力学系弹性力学电子教案
CHINA UNIVERSITY OF MINING AND TECHNOLOGY
h 2 h 2
x y dy M
h 2 h 2
6dy dy M
2
2M d 3 ( 或 d ) h M 3 h 2
M 12 M x 6dy 3 y (h3 / 12) y h
可见:此结果与材力中结果相同,
说明
M x y I
(1) 组成梁端力偶 M 的面力须线性分布,且中心处为零,结果才是精 确的。 (2) 若按其它形式分布,如: 则此结果不精确,有误差;
弹性力学平面问题的基本方程
(1)平衡方程: (3)物理方程:
x yx fx 0 x y xy y fy 0 x y
(2)几何方程:
u x x v y y v u xy x y
力学与建筑工程学院力学系弹性力学电子教案
CHINA UNIVERSITY OF MINING AND TECHNOLOGY
按应力求解平面问题的基本方程
(1)平衡方程
x xy fx 0 x y yx y fy 0 x y
常体力下可以简化: ( 1)
结论2:二次多项式对应于均匀应力分布。 2a 2c 2c x y 2a
0
xy b
x
0
2
y2
y
试求图示板的应力函数。 例:
0
0
x
x
y
( x, y )
0
2
x
2
y
0
( x, y) 0 xy
力学与建筑工程学院力学系弹性力学电子教案
CHINA UNIVERSITY OF MINING AND TECHNOLOGY
h 2 h 2
x y dy M
h 2 h 2
6dy dy M
2
2M d 3 ( 或 d ) h M 3 h 2
M 12 M x 6dy 3 y (h3 / 12) y h
可见:此结果与材力中结果相同,
说明
M x y I
(1) 组成梁端力偶 M 的面力须线性分布,且中心处为零,结果才是精 确的。 (2) 若按其它形式分布,如: 则此结果不精确,有误差;
弹性力学直角坐标解答

根据材料的本构关系, 引入物理方程来表达应 力分量与应变分量之间 的关系。
针对具体问题的边界条 件,如固定端、自由端 或受力边界等,对平衡 方程和几何方程进行适 当的处理。
根据问题的性质和复杂 程度,选择合适的求解 方法,如分离变量法、 积分变换法或数值方法 等,以求解平衡方程和 几何方程,得到应力分 量和位移分量的解答。
多场耦合问题
涉及多个物理场的相互作用,如热-力、电-力等耦 合问题,使得边界条件更加复杂。
处理复杂边界条件方法
坐标变换法
通过坐标变换将复杂边界转换为简单边界,从而简化问题的求解。
近似解法
采用近似函数逼近复杂边界条件,将问题转化为可求解的近似问题。
数值解法
利用数值计算方法(如有限元法、有限差分法等)对复杂边界条件 进行离散化处理,进而求解弹性力学问题。
直角坐标系下应力应变关系
应力分量
在直角坐标系下,一点的应力状态可以用六个应力分量来 表示,即三个正应力分量和三个剪应力分量。
应变分量
与应力分量相对应,一点的应变状态也可以用六个应变分 量来表示,即三个正应变分量和三个剪应变分量。
应力应变关系
在弹性力学中,应力和应变之间存在一定的关系,这种关 系可以用广义胡克定律来描述。对于各向同性材料,应力 应变关系可以简化为三个独立的方程。
03
空间问题直角坐标解答方 法
空间应力问题求解思路
应力分量求解
叠加原理应用
根据弹性力学基本方程,利用直角坐标 系下的应力分量表达式,通过给定的边 界条件和载荷,求解各应力分量。
对于多个载荷同时作用的情况,可利用 叠加原理将问题分解为多个简单问题分 别求解,再将结果叠加得到最终解。
应力函数引入
弹性力学平面应力平面应变问题 ppt课件

系,即 σx = Eεx 这就是虎克定律。 应力
(Hooke‘s Law)
Y
弹塑性范围
弹性范围
斜率, E
应变
工程上,一般将应变与应力间的关系表示为
xE 1xyz yE 1yzx
xy
1
G
xy
yz
1
G
yz
zE 1zxy
zx
1
G
zx
称它们为物理方程(广义虎克定律)。
x 1 E 1 1 2 x 1 y 1 z
1
0
对 1 0
称
1
2
对于平面应变问题的弹性矩阵,只须在上式
中,以 E
1 2
代E,
1
代μ即可。
小结
则有
uu vv ww (在 u 上)
用矩阵形式表示为:
uu (在 u 上)
小结
弹性力学基本方程的一般形式为
回顾
平衡微分方程 σb0 (在 内)
几何方程 物理方程
ε tu σDε
(在 内) (在 内)
边界条件
nσt
(在 t 上)
uu
(在 u 上)
其中 t u , 为弹性体的完整边界。
§2-3 平面应变和平面应力问题
平面应变问题
位移:按平面应变的定义,三个方向的位移函数是
uux,y vv(x,y) w0
应变:由几何方程应变-位移关系,得
x
u x
1x,
y,
y
v y
3x,
y,
xy yz
u y
v x
2x,
v w0 z y
y
z
w0, z
zx
u z
弹性力学平面问题极坐标

r
r
2 2 2 x2 y2
sin cos
r
r
cos2 sin2
r2
sin cos
r2
2
2
2 r 2
1 r
r
1 r2
2 r 2
二. 极坐标系下的平衡微分方程
1. 直角坐标与极坐标系下的应力分量关系
(1)极坐标系下的应力分量和体力分量
O
如图,根据应力状态的定义,过P
点分别以 r 方向和 方向为法线的截面
由半圆上的应力和外力的平衡关系,有
M
O
x
a
r r r
y
Fx 0
Fy 0 Mz 0
0
r
r
a
cos
ad
0
r
r a
sin
ad
0
0
r
ra
cos
r
ra
sin
d
0
0
r
ra
sin
r
ra
cos
d
0
a 0 a 0
0
r
ra
a ad
M
0
0
r
a2d M
ra
a 0
0
r
1 r
2 r
r
Fb
0
三. 极坐标系下的几何方程
1. 直角坐标与极坐标系下的位移分量关系
类似体力分量的投影关系 2. 极坐标系下的应变分量
O
x
r
Pu
u
ur
v
r
y
将P点分别沿 r 和 方向(相互垂直)两线元的线应变 r、 及其切应变 r , 作为P点的应变分量。
3. 极坐标系下的几何方程
《弹性力学》第七章 平面问题的差分解

4 f 1 2 2 4 [4 f 0 2( f1 f 2 f 3 f 4 ) ( f 5 f 6 f 7 f8 )] x y h 0 4 f 4 y 1 4 [6 f 0 4( f 2 f 4 ) ( f10 f12 )] h 0
弹性力学的经典解法存在一定的局限性,当弹性体的边 界条件和受载情况复杂一点,往往无法求得偏微分方程的边 值问题的解析解。因此,各种数值解法便具有重要的实际意 义。差分法就是数值解法的一种。 所谓差分法,是把基本方程和边界条件(一般均为微分 方程)近似地改用差分方程(代数方程)来表示,把求解 微分方程的问题改换成为求解代数方程的问题。
T (T0 Te ) x 0
其中 Te 为边界以外的介质的已知温度。应用差分公式,可得:
T1 T3 (T0 Te ) 2h
解出 T1 ,代入(1)式,即得修正的差分方程:
2h 2h 4 T0 T2 2T3 T4 Te
第七章 平面问题的差分解
§7-1 差分公式的推导 §7-2 稳定温度场的差分解 §7-3 不稳定温度场的差分解 §7-4 应力函数的差分解 §7-5 应力函数差分解的实例 §7-6 温度应力问题的应力函数差分解 §7-7 位移的差分解 §7-8 位移差分解的实例 §7-9 多连体问题的位移差分 解 习题课
2 2 2 T h T 2 T0 TA h 2 x A x A 2 1 T 2 2 T T3 TA (1 )h (1 ) h 2 x x A 2 A
§7-2
稳定温度场的差分解
本节以无热源的、平面的、稳定的温度场为例,说明差分 法的应用。 在无热源的平面稳定场中,t 0, z 微分方程简化为调和方程 2T 0 ,即:
弹性力学 第七章平面问题的极坐标解答

x r cos
arctan y
x
y r sin
x
y
r x
y
两种坐标系下位移分量坐标转换公式:
ur u
v sin u cos
v
cos
u
sin
u v
ur ur
cos sin
u u
sin cos
r
u
x
u
v
ur y
2、极坐标下的平衡微分方程
•几何描述
PB面积:rd AC面积:(r+dr)d
第七章 平面问题的极坐标解答
•本质上坐标系的选择并不影响弹性力学问题的求 解。 •但是影响边界条件的描述和表达,从而关系问题 的求解难易程度。 •圆形,楔形,扇形等物体,采用极坐标系求解比 较方便。
采用极坐标可更方便几何定位描述。
§7-1 平面问题的极坐标方程
1、极坐标与直角坐标之间的关系式:
r2 x2 y2
rds 1 xds cos 1 cos yds sin 1 sin
xyds cos 1 sin yxds sin 1 cos 0
用 xy 代替 yx 简化以后,得
r x cos2 y sin2 2 xy sin cos
o
yx y
x
y
B x
y
r
xy xya
c
A
x
b r r
同样可由三角板A的平衡条件F=0,得到 r ( y x )sin cos xy (cos2 sin2 )
和y分别改换为r和 。
r
1
E
2
( r
1
)
1 2
E
(
1
r
)
r
arctan y
x
y r sin
x
y
r x
y
两种坐标系下位移分量坐标转换公式:
ur u
v sin u cos
v
cos
u
sin
u v
ur ur
cos sin
u u
sin cos
r
u
x
u
v
ur y
2、极坐标下的平衡微分方程
•几何描述
PB面积:rd AC面积:(r+dr)d
第七章 平面问题的极坐标解答
•本质上坐标系的选择并不影响弹性力学问题的求 解。 •但是影响边界条件的描述和表达,从而关系问题 的求解难易程度。 •圆形,楔形,扇形等物体,采用极坐标系求解比 较方便。
采用极坐标可更方便几何定位描述。
§7-1 平面问题的极坐标方程
1、极坐标与直角坐标之间的关系式:
r2 x2 y2
rds 1 xds cos 1 cos yds sin 1 sin
xyds cos 1 sin yxds sin 1 cos 0
用 xy 代替 yx 简化以后,得
r x cos2 y sin2 2 xy sin cos
o
yx y
x
y
B x
y
r
xy xya
c
A
x
b r r
同样可由三角板A的平衡条件F=0,得到 r ( y x )sin cos xy (cos2 sin2 )
和y分别改换为r和 。
r
1
E
2
( r
1
)
1 2
E
(
1
r
)
r
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一种:在z=0和z=L的两端有边界条件
zx zy0, w0
以上条件平面应变问题是精确满足的.如图7.1a
(7.10)
第二种:柱体很长.除两端外,w=0,侧面上z向外力也为零.也可按平 面应变问题求解,如图7.1b
z z
z
x
x
x
y
(a)水坝
y
(b)隧道 图7.1
y
(c)滚轴
第七章 平面问题的直角坐标解答 §7-1 平面应变问题
在oxy平面内构§7-1 平面应变问题
C. 变形特征
如图建立坐标系:以任一横截面为 xy 面,任一纵线为 z 轴。
设 z方向为无限长,则 x , x , u, 沿 z 方向都不变化,
仅为 x,y 的函数。 任一横截面均可视为对称面
u u ( x , y ) ,v v ( x , y ) ,w 0 ( x , y ) A (7.1)
(e)
式(7.8)是应力表示的协调方程,边界条件为
n T
在 s 上(7.9)
平面应变问题:二个位移分量,三个应变分量和三个应力分量.满 足几何方程(7.2),本构关系(7.4)和平衡方程(7.6)共八个方程及边 界条件(7.9)
第七章 平面问题的直角坐标解答 §7-1 平面应变问题
三种可以按平面应变问题求解的情况
xxxx yyyx yxfzxzx0fx 0 xyxxxyyyy yfyzzy0fy 0
(7.6)
应f x 和变协f y调是方x,程y的(3函.3数4cxx)中z五个yy自z动满z足z ,剩f下z 一0个为
将物理方2y2z2x2程y(7.2x42y)22y代z2y入2x2x上2yxyy式zyz2得x222yyx22zxzy2xy2x(( xyyxyyxzzyxzxzyz(x7xy)y.7z)) (3.34c)
为xy 平面,垂直于中面的任一直线 为 z 轴。 由于板面上不受力,有
b
x
z
2h
z zh0 因板很薄,且外力 沿 z 轴方向不变。
zxzh0 可认为整个薄板的
z 0 zx 0
y
a
y
zyzh0 各点都有:
zy 0
(7.11)
由剪应力互等定理,有 zxxz0 zy yz 0 y
结论: 平面应力问题只有三个应力分量:
第七章 平面问题的直角坐标解答
第七章 平面问题的直角坐标解答
§7-1 平面应变问题 §7-2 平面应力问题 §7-3 平面问题及体积力为常量时的特性 §7-4 §7-5 平面应力问题的近似性质 §7-6 自由端受集中力作用的悬壁梁 §7-7 受均布荷载作用的简支梁 §7-8 三角形水坝
第七章 平面问题的直角坐标解答 §7-1 平面应变问题
2 x 2y xy x x 2 x2 xy xy 2yf 2 x y 0 x fx y fy0
(d)
利用式(d )消2(去式xx y(xc)中y)的 y (剪y1 应力f1y)(得 x f0x y fy)0
(7.6) (7.8)
式中 2 是二维Laplace算子
2 2 2 x2 y2
2z x2
2 y 2z2 2x x 2 x 2x2 y xyz1 (2 2 y x22 y yz 2 zx (2 x) zx2 y (1 xy1 z ) x 2 y xx y y )z
(c)
第七章 平面问题的直角坐标解答 §7-1 平面应变问题
对平衡方程(7.6)中的两式分别相对于x和y求导,相加得
2(1
E
)zx
(. b)
(5.26b)
x
y
1 ( E1 1 ( E1
x 1 y 1
y) x)
xy
11 E1
xy
E 11 E 2 ,
(7.4)
11 (7.5)
第七章 平面问题的直角坐标解答 §7-1 平面应变问题
1 11
E
E1
应力分量只是x,y的函数,且Z方向体积力为0,则平衡方程变为
一个方向的尺寸比另两个 b 方向的尺寸小得多。
x
z
2h
ha,h b —— 平板
y
y
a
如:板式吊钩,旋转圆盘,工字形梁的腹板等
B. 受力特征
外力(体力、面力)和约束,仅平行于板面作用, 沿 z 方向不变化。
第七章 平面问题的直角坐标解答 §7-2 平面应力问题
C. 应力特征
如图选取坐标系,以板的中面
(7.2) (3(a.1)3)
第七章 平面问题的直角坐标解答 §7-1 平面应变问题
因 zx zy z 0由胡克定律
x
E1[z x E 1[(z y(zx) ] , y)] xy0
2(1
E
)xy
,
y
E1 [y
z(z (xx)], y)yz
2(1E)yz
,(7.3)
六个应z力分E1量[中z 独z立(x的x 也zy只y)]有,0三个zx
§7-1 平面应变问题
A. 几何特征
一个方向的尺寸比另两 个方向的尺寸大得多,且沿 长度方向几何形状和尺寸不 变化。柱体所占空间V
V { (x ,y ,z)(x ,y ) A ,0 z L }
—— 近似认为无限长
B. 外力特征
外力(体力、面力)平行于横截面作 用,且沿长度 z 方向不变化。
约束 —— 沿长度 z 方向不变化。
第三种:柱体很长.高应力区远小于低应力区,且低应力区的应力 近似为零.除两端外,也可按平面应变问题求解,如图7.1c
z
x
y
(a)水坝
x y
(b)隧道 图7.1
z y
z x
(c)滚轴
第七章 平面问题的直角坐标解答 §7-2 平面应力问题
§7-2 平面应力问题
A. 几何特征
V{(x,y,z)(x,y) A ,zh},
yx
x x(x,y) y y(x,y)
xyyxxy(x,y)
(7.12)
x xy
x
xy x
yx
yy
应变分量、位移分量也仅为 x、y 的函数,与 z 无关。
第七章 平面问题的直角坐标解答 §7-2 平面应力问题
如图所示三种情形,是否都属平面问题?是平 面应力问题还是平面应变问题?
满足条件(7.1)及以上特征的弹性力学问题称为平面应变问题
将(7.1)代入几何方程(3.13)
xz xu x, xy
y ux , y v, xy xy 12 (1 2 (uy u y vx ) v x)
zy
yv ,
z y0z
1 2
(
v z
w y
)
在平面应变 z问题wz中, ,独zx 立 的12 (应wx变分uz量) 只有三个
