数轴与相反数
数轴、相反数、绝对值

数轴、相反数、绝对值数学是研究数量、结构、变化及空间等概念的学科。
在数学中,数轴、相反数和绝对值是非常重要的概念,它们在解决各种实际问题中发挥着关键作用。
一、数轴数轴是数学中的一个基本概念,它是一个有序的直线,用来表示实数和有理数。
数轴上的点表示实数,原点表示零,正半轴表示正数,负半轴表示负数。
通过数轴,我们可以直观地比较两个实数的大小,也可以找出任何实数的相反数和绝对值。
二、相反数相反数是数学中的另一个重要概念。
如果一个数x的相反数是-x,那么它们在数轴上位于原点的两边,并且它们的距离相等。
例如,3的相反数是-3,5的相反数是-5。
在数学中,相反数经常被用于抵消或中和,以解决各种问题。
三、绝对值绝对值是数学中的一个非常有用的概念。
在数轴上,任何一个实数x的绝对值就是从原点到点x的距离。
例如,3的绝对值是3,-5的绝对值也是5。
绝对值的计算公式是|x| = x(x > 0)或 0(x = 0)或 -x(x < 0)。
绝对值的概念可以帮助我们确定一个数的符号和它的大小。
四、总结数轴、相反数和绝对值是数学中的基本概念,它们在解决各种实际问题中发挥着关键作用。
通过了解这些概念,我们可以更好地理解数学的本质,并解决各种复杂的问题。
因此,对于每一个学习数学的人来说,理解这些基本概念都是非常重要的。
《相反数、绝对值复习》课件一、教学目标1、复习相反数和绝对值的概念和性质,掌握它们的计算方法。
2、提高学生对于相反数和绝对值的理解和应用能力。
3、培养学生的思维能力和自主学习能力。
二、教学内容1、相反数的概念及性质。
2、绝对值的概念及性质。
3、相反数和绝对值的计算方法。
三、教学重点与难点重点:掌握相反数和绝对值的计算方法。
难点:理解相反数和绝对值的概念及性质,并应用到实际问题中。
四、教学方法与手段1、通过PPT展示相反数和绝对值的概念和性质,让学生自主思考和讨论。
2、通过例题讲解和练习,让学生掌握计算方法。
考点02数轴与相反数

考点02数轴与相反数知识框架⎧⎧⎪⎪⎪⎪⎨⎪⎪⎪⎨⎪⎩⎪⎪⎧⎪⎨⎪⎩⎩数轴的概念数轴的读数与画法基础知识点数轴上的点与有理数之间的关系数轴与数的大小利用数轴求两点之间的距离重点题型数轴上点的运动⎧⎧⎪⎪⎨⎪⎪⎪⎨⎩⎪⎧⎪⎨⎪⎩⎩相反数的概念基础知识点相反数的意义多重符号化简相反数的意义及求法重点题型相反数与数轴结合 基础知识点知识点2.1 数轴的概念1)数轴:用一条直线上的点表示数,这条直线叫作数轴 2)三要素:①原点—参考点,正负数分界点; ②方向—一般选取向右为正方向;③单位长度—同一条数轴上的单位长度应当一致 知识点2.2 数轴的读数与画法1)数轴的读数:在原点的左边,则为正数,在数轴的右边,则为负数。
2)画数轴步骤:a .直线b .确定原点c .选正方向(通常从原点向右或向上定位正方向)d .选取单位长度(选取适当长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示1,2,3,…;从原点向左,用类似方法依次表示-1,-2,-3,…)e .标数(用实心点标数).例1.以下是四位同学画的数轴,其中正确的是() A . B . C .D .例2.下列所画数轴对不对?如果不对,指出错在哪里?①②③④⑤⑥⑦【答案】①②③④⑥画的数轴不对,⑤和⑦画的数轴正确,原因见解析.【分析】根据数轴的三要素:原点、正方向、单位长度,即可解答.【解析】解:①画的数轴不对,缺原点;②画的数轴不对,缺正方向;③画的数轴不对,数轴不是射线而是直线;④画的数轴不对,缺单位长度;⑥画的数轴不对,单位长度不统一.⑤和⑦画的数轴正确.【点睛】本题考查了数轴的识别.规定了原点、正方向、单位长度的直线叫做数轴.数轴的三要素:原点,单位长度,正方向.例3.如图,数轴上蝴蝶所在点表示的数可能为()A.3B.2C.1D.-1知识点2.3 数轴上的点与有理数之间的关系(数形结合)1)数轴上的点并不是都是有理数2)正方向可以不按照常规方向选取3)a>0,与原点的距离是a,在数轴上可以是 a(存在多解的情况)注:要确定在数轴上的具体位置,必须要距离+方向例1.下列说法:①规定了原点、正方向的直线是数轴②数轴上两个不同的点可以表示同一个有理数③有理数1100数轴上无法表示出来④任何一个有理数都可以在数轴上找到与它对应的唯一点其中正确的是()A.①②③④B.②③④C.③④D.④例2.数轴的原型来源于生活实际,数轴体现了()的数学思想,是我们学习和研究有理数的重要工具.A.整体B.方程C.转化D.数形结合【分析】因为数轴是解决数的运算的一种重要工具,所以它充分体现了数形结合的思想.【点睛】本题考查几种数学思想,解题的关键是理解数形结合的定义:根据数与形之间的一一对应关系,数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来,从而起到优化解题途径的目的.例3.数轴上表示整数的点称为整点,某数轴的单位长度是1厘米,若在这个数轴上随意画一条15厘米的线段AB,则AB盖住的整数点的个数共有()个A.13或14个B.14或15个C.15或16个D.16或17个若在数轴上随意画线段AB,其左侧端点A的位置存在两种可能性:一种可能是点A与数轴上某一个整点重合(如图中数轴①所示;为清楚起见,图中用长方形代表线段AB),另一种可能是点A落在数轴上某两个整点之间的区域内(如图中数轴②所示). 因为线段AB的长是一个定值,所以当线段左侧端点A的位置确定时线段右侧端点B的位置也随之确定.(1) 分析图中的数轴①可知,由于数轴的单位长度为1厘米,线段AB的长为15厘米,且左侧端点A与一个整点重合,所以线段AB的两个端点各自盖住1个整点,线段的其他部分盖住了14个整点,故线段AB一共盖住了16个整点.(2) 分析图中的数轴②可知,由于数轴的单位长度为1厘米,线段AB的长为15厘米,且左侧端点A落在两个整点之间的区域内,所以线段AB的两个端点均无法盖住任何整点,线段的其他部分盖住了15个整点,故线段AB一共盖住了15个整点.综上所述,线段AB盖住的整点的个数共有15或16个.故本题应选C.点睛:本题不仅考查了数轴的相关知识,还考查了利用简单的数形结合思想解决问题的能力. 解决本题的关键在于结合图形针对可能出现的情况进行分类讨论. 在分析的过程中,线段左侧端点在数轴上可能的位置是分情况讨论问题的一个重要出发点,左侧端点是否与某一整点重合直接影响线段所能覆盖的整点数量.知识点2.4 数轴与数的大小1)正方向上,离原点越远,数越大2)负方向上,离原点越近,数越大(负数数字越大,结果反而越小)注:数轴从负方向向正方向,数值逐渐增大。
第5节:数轴与相反数

第2节数轴与相反数知识梳理1、数轴的概念:规定了原点、正方向(向右为正)、单位长度的直线叫做数轴.任何一个有理数都可以用数轴上的点来表示.2、相反数的概念(1)(代数意义):只有符号不同的两个数叫做互为相反数.(2)(几何意义):在数轴上位于原点两旁且到原点距离相等的两个点表示的数叫做互为相反数.合作学习:数轴在一条东西向的马路上,离车站的西面3米处有一辆小汽车,车站的东面6米处有一棵柳树,小汽车的西面5米处有一棵樟树,试用图表示这一情景.我们在小学学习数学时,就能用直线上依次排列的点来表示自然数,所以我们可以画一条直线表示马路,从左到右表示由西到东的方向,任取一点O表示车站的位置,点C,点B,点A分别表示柳树、小汽车、樟树的位置,为了表达更加清晰,我们把点O左右两边的数分别用负数和正数来表示,如图所示.从以上得到一点启发:我们在一条直线上规定一个正方向,就可以用这条直线上的点表示正数、零和负数.具体做法如下:画一条直线(通常画成水平方向),在这条直线上任取一点作为原点,用这点表示O。
规定直线上从原点向右为正方向,画上箭头,那么相反方向为负方向。
再选取适当的长度作为单位长度,从原点向右每隔一个单位长度取一点,依次标上1,2,3,…;从原点向左,每隔一个单位长度取一点,依次标上-1,-2,-3,…,如图所示。
概括:像这样规定了原点、正方向和单位长度的直线叫做数轴.典例精析考点1:运用数轴表示有理数【例1】画出数轴,并在数轴上画出表示下列各数的点:5,-2,-4,+1,3.5分析:在数轴上画出表示有理数的点,可以先由这个数的符号确定它在数轴上原点的哪一侧,再在相应的一侧上确定它与原点相距几个单位长度.解:如图:点评:画数轴要注意三要素:(1)原点、(2)正方向(向右为正)、(3)单位长度跟踪训练1如图,数轴上的点A,B,C,D,E分别表示什么数?跟踪训练2A点表示-3,B点表示-1.5,C点表示0,D点表示+1.5,E点表示+3考点2:运用数轴解决实际问题【例2】小明的家(记为A)、学校(记为B)、书店(记为C)依次坐落在一条东西走向的大街上,小明家位于学校西边30米处,书店位于学校东边50米处,小明从学校沿这条大街向东走了40米,接着又向西走了30米到达D处,以B点为原点,试用数轴表示上述A、B、C、D的位置,并写出A,B,C,D四点表示的数.解:如图,A点表示的数为-30,B点表示的数为0,C点表示的数为+50,D点表示的数为+10.点评:本题利用了“数形结合”的数学思想,将实际问题转化为数学问题,数轴正是实现这一转化的桥梁.跟踪训练2邮递员骑车从邮局出发,先向南骑行2km到达A村,继续向南骑行3km到达B村,然后向北骑行9km到达C村,最后回到邮局.(1)以邮局为原点,以北为正方向,用lcm表示lkm,画出数轴,并在该数轴上表示出A,B,C三个村庄的位置;(2)C村离A村有多远?(3)邮递员一共骑了多少km?跟踪训练2(1)图略;(2)C村离A村有6km;(3)邮递员一共骑了18km合作学习:观察以下两对数中,各有什么共同特点?很明显,每对数中的两个数都只有符号不同.概括:像这样只有符号不同的两个数称互为相反数,如3和3-互为相反数。
数轴与相反数教案

数轴与相反数教案教案标题:数轴与相反数教案目标:1. 学生能够理解和运用数轴的概念,正确表示和比较正数、负数和零。
2. 学生能够理解相反数的概念,并能在数轴上找到相反数。
3. 学生能够运用数轴和相反数的知识解决实际问题。
教案步骤:引入活动:1. 创设情境,例如讲述一个关于温度变化的故事,引发学生对数轴和相反数的兴趣。
2. 准备一个数轴模型,向学生展示数轴的基本概念和用途。
探索活动:1. 引导学生观察数轴上的正数、负数和零的位置,并解释它们的意义。
2. 让学生通过数轴模型的实际操作,找到给定数值的相反数。
3. 引导学生发现相反数的特点,例如它们在数轴上的位置和数值的关系。
拓展活动:1. 给学生一些数值,让他们在数轴上标出这些数,并找到它们的相反数。
2. 给学生一些实际问题,例如温度变化或海拔高度变化,让他们利用数轴和相反数的概念解决这些问题。
3. 给学生一些数轴上的比较题目,让他们通过比较正数、负数和零的位置来回答问题。
巩固活动:1. 给学生一些练习题,让他们在数轴上找到给定数值的相反数。
2. 给学生一些实际问题,让他们利用数轴和相反数的知识解决这些问题。
3. 组织小组讨论,让学生分享他们在解决实际问题中的思路和方法。
评估活动:1. 通过观察学生在活动中的参与程度和回答问题的准确性来评估他们对数轴和相反数的理解。
2. 给学生一些练习题或小测验,检验他们对数轴和相反数的掌握程度。
教案扩展:1. 引导学生思考数轴的扩展应用,例如分数、小数和根号等。
2. 鼓励学生设计自己的数轴活动,分享给其他同学。
教学资源:1. 数轴模型2. 实际问题练习题3. 练习题或小测验4. 小组讨论记录表教学反思:1. 在引入活动中,要确保创设的情境能够引发学生的兴趣和好奇心。
2. 在探索活动中,要注重学生的实际操作和观察,让他们亲自体验数轴和相反数的概念。
3. 在拓展活动中,要提供不同难度和类型的问题,以满足学生的不同需求和能力水平。
数轴和相反数ppt课件
例1.下图中表示数轴正确的是( D )
例2.下列4个数中,在-2到0之间的数是( A )
A.-1
B.1
C.-3
D.3
方法总结:先看数轴三要素是否齐全,再看单位长度是否一致,数字的 标注是否符合规定。
综上所述,也可将数轴定义为规定了原点、正方向、单位长度的直线。
例6.下列说法正确的是( D )
A.3是相反数
B.-3是相反数
C.3和-2互为相反数
D.3与-3互为相反数
例7.一个数的相反数仍是它本身,这个数是(C )
A. 1
B. -1
C. 0
D.正数
2.相反数的几何意义: 动手实践:借助于数轴表示以下几组数,说出你的发现;
4和-4,
3和-3,
1
1
1 2 和-1 2 ,
2.数轴的三要素:
1)原点:在数轴上表示数0的点叫做原点。实际问题中应取 适当的点作为原点。
2)正方向:通常规定数轴从原点向右(或向上)为正方向。
3)单位长度:一般地,从原点向右,每隔一个单位长度取 一个点以此表示数a,2a,3a,...,从原点向左,每隔一 个单位长度取一个点,依次表示-a,-2a,-3a,....(a>0)。
会学到无理数,数轴上的点还能表示无理数 2)有理数与数轴上的点是一一对应的
例3.在数轴上画出下列各点:
1 (1)-100,0,200,400;(2)-3 2 ,-2,0 ,+2.5,+3;
(1)
-1-0100 0 0
200200 400
400
(2)
例4.下列语句中,说法正确的个数是( B )
(1)数轴上的点只表示整数; (2)数轴是一条直线; (3)数轴上的一个点只能表示一个数; (4)数轴上找不到既比表示正数,又不表示负数的点; (5)数轴上的点表示的数都是有理数;
数轴与相反数重点精讲

阅读下面的材料:
点A,B在数轴上分别表示实数a,b,A,B两点之间的距离表示为
|AB|.当A,B两点中有一点在原点时,不妨设点A在原点,如图
:|AB|=|OB|=|b|=|a-b|,当A,B两点都不在原点时:
A
B
0(a) b
(1)如图:点A,B都在原点的右边: |AB|=|OB|-|OA|=|b|-|a|;
AB 0a b
阅读下面的材料:
点A,B在数轴上分别表示实数a,b,A,B两点之间的距离表示为
|AB|.当A,B两点中有一点在原点时,不妨设点A在原点,如图
:|AB|=|OB|=|b|=|a-b|,当A,B两点都不在原点时:
A
B
0(a) b
(2)如图:点A,B都在原点的左边: |AB|=|OB|-|OA|答下列问题: (1)数轴上表示2和5的两点之间的距离是__3__,数轴上表示
-2和-5的两点之间的距离是__3__; (2)数轴上表示1和-3的两点之间的距离是__4__; (3)数轴上表示x和-1的两点A和B之间的距离|AB|=2,
那么x为__-_3__或__1___.
已知|x-4|+|y+2|=0,求2x-(-y)的值.
数轴与相反数 重点精讲
主讲教师:许文军
原点
01
原点, 方向 单位长度
单位长度
方向
注意:画数轴时,根据所表示的数的特点灵活选取原点和 单位长度,具体有以下几种:
1 2 345 6
0
原则一:都是正数时, 原点适当靠左; 反之,靠右.
-2 12 0
原则二:既有正数又有负数时,如 果所表示的正数离原点较远, 则原点适当靠左; 反之,则原点适当靠右.
初一数学-第五讲 数轴与相反数
第五讲 数轴与相反数【知识要点】1.数轴①数轴:规定了原点,正方向和单位长度的直线叫数轴。
②利用数轴比较大小:数轴上右边的数总比左边的数大。
2.相反数①相反数:只有符号不同的两个数互为相反数。
0的相反数是0。
②几何意义:在数轴上,表示相反数的两个点位于原点的两侧,并且到原点的距离相等; ③判断互为相反数的两种方法:a.从式子上看,若0a b +=,则a b 与互为相反数;b.从直观上看a a -与是互为相反数。
3.求一个数的相反数就是在这个数的前面添加“—”。
【经典例题】【例1】①下面表示数轴的图中,画得准确的是( )。
A .B .C .D .②在数轴上表示下列各数,并按照从小到大的顺序用“<”号连接起来。
+3, -1, 0, 2,32, -1.5, 521, -2, 312-,-3【例2】①如果a+b=0,那么a ,b 两个实数一定是( )A .都等于0B .一正一负C .互为相反数D .互为倒数 ②若a 与-5互为相反数,那么a 是( )A .-5B .51C .51- D .5 ③若a ,b 互为相反数,则下列各对数中不是互为相反数的是( )A .-2a 和-2bB .a+1和b+1C .a+1和b-1D .2a 和2b【例3】化简。
①⎪⎭⎫ ⎝⎛--32 ②⎪⎭⎫ ⎝⎛+-54 ③()100++④⎪⎭⎫ ⎝⎛-+324 ⑤ ()a -- ⑥ ()2a b -++⎡⎤⎣⎦【例4】若a 为有理数,试确定a 与a -在数轴上的位置,且比较其大小。
【例5】①如图,数轴上的点A 向左移动2个单位长度得到点B ,则点B 表示的数是_____________.②数轴是一个非常重要的数学工具,通过它把数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“数形结合”的基础.请利用数轴回答下列问题:a.如果点A 表示数-2,将点A 向右移动5个单位长度到达点B ,那么点B 表示的数是_________,A 、B 两点间的距离是________;b.如果点A 表示数5,将点A 先向左移动4个单位长度,再向右移动7个单位长度到达点B ,那么点B 表示的数是______,A 、B 两点间的距离是__________;c.一般的,如果点A 表示的数为a ,将点A 先向左移动b 个单位长度,再向右移动c 个单位长度到达点B ,那么点B 表示的数是________③一只小鸟落在数轴上的某点,第一次从向左跳一个单位到,第二次从向右跳2个单位到,第三次从向左跳3个单位到,第四次从向右跳4个单位到,…,按此规律跳了100次时,它落在数轴上的点所表示的数恰是2068,这只小鸟初始位置所表示的数是_________.【初试锋芒】1.下列说法正确的是( )A.所有的有理数都可以用数轴上的点表示B.数轴上的每一个点都表示一个整数C.规定了正方向和单位长度的一条直线叫做数轴D.在同一数轴上,单位长度可以不统一2.在数轴上和表示-3的点的距离等于5的点所表示的数是( )A.-8B.2C.-8和2D.13.点A 表示的数是-2,将点A 沿数轴移动6个单位后到达点B ,则点B 表示的数为( )A.-8B.4C.4或-8D.不能确定4.如图1-2-1所示,在数轴上有六个点,且AB=BC=CD=DE=EF ,则此数轴的原点在( )A.在点A 、B 之间B.在点B 、C 之间C.在点C 、D 之间D.在点D 、E 之间5.数轴上的点A 、B 、C 、D ,分别表示数a 、b 、c 、d ,已知A 在B 的右侧,C 在B 的左侧,D 在B 、C 之间,则下列式子成立的是( )A.a <b <c <dB.b <c <d <aC.c <d <a <bD.c <d <b <a6.如图1-2-2所示,数轴的一部分被墨水污染,被污染的部分中共有 个整数。
7.2数轴、相反数
2 数轴、相反数教学目标:1、掌握数轴的三要素,能正确画出数轴,能将已知数在数轴上表示出来,能说出数轴上已知点所表示的数;2、借助数轴理解相反数的意义;会求一个数的相反数,会用相反数的定义对一个式子进行化简;3、通过观察相反数在数轴上所表示的点的特征,培养学生的归纳能力及数形结合思想。
教学重点:1、用数轴上的点表示有理数;2、相反数的意义及双重符号化简。
教学难点:1、有理数和数轴上的点的对应关系;2、相反数的概念以及“-a”的理解。
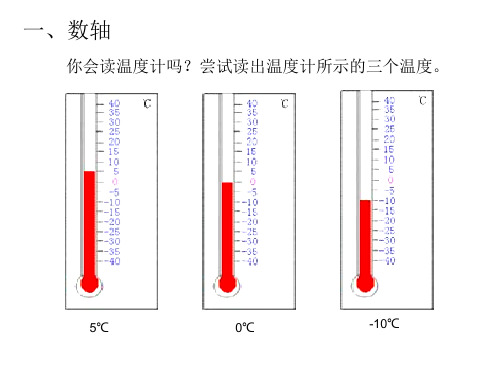
教学过程:一、情景导入师:这是生活中常见的温度计,现在我们将温度计顺时针旋转90°,使之变成一个横放的温度计。
我们通过画图可以将这个温度计简化成我们今天要学习的数轴。
师:规定了原点、正方向、单位长度的直线叫数轴。
二、典型例题例1:下列各图中,符合数轴定义的是 ( )师:数轴有哪三要素?生:原点、正方向、单位长度。
师:符合数轴定义的是哪个选项?生:D 。
师:A 、B 、C 哪里不符合数轴定义?生:A 没有正方向。
生:B 没有原点和单位长度。
生:C 没有标注原点、单位长度不一致。
例2:在数轴上画出表示下列各数的点5.003145.13,4,,,,--师:先观察以上数列中最大最小值,确定数值的范围。
师:确定合适的单位长度,画出数轴并标好数值。
(学生画数轴表示各数的点)例3:分别写出下列各数的相反数。
31605.423--,,,,师:相反数的定义是什么?生:只有符号不同的两个数叫做互为相反数。
0的相反数是0。
师:你们写出下列各数的相反数吗?(学生书写完成)注意:一个数与它的相反数不能用等号连接。
例4:下列说法正确的是( )。
(A)﹣3是相反数; (B)﹣21与﹢74是相反数; (C)﹣53的相反数是35; (D)﹣0.5的相反数是21。
师:下列有关相反数的说法正确的是哪个?生:D 。
师:A 、B 、C 错在哪里?生:A 错在单独的一个数不能说是相反数。
生:B 错在这两个数不仅符号不同而且数也不同。
第2讲 数轴、相反数
第二讲 数轴、相反数一、教学目标1.认识数轴并能够准确的表示与有理数的关系;2.认识并理解相反数的概念;3.学会数轴与相反数的综合应用. 二、知识要点引导知识点1:数轴与相反数的基本概念(1)数轴:规定了原点、正方向和单位长度的直线叫做数轴.注意:(1)数轴是条直线,可以向两方无限延伸;(2)数轴的三要素:原点、正方向、单位长度,三者缺一不可;(3)原点的选定,正方向的选取,单位长度大小的确定,都是根据实际需要“规定”;(4)在数轴上表示的两个数,右边的数总比左边的数大;(5) 正数大于0,负数小于0,正数大于一切负数. (2)数轴上点与有理数的关系所有有理数都可以用数轴上的点表示,反过来,不能说数轴上所有的点都表示有理数.正有理数可以用原点右边的点表示,负有理数可以用原点左边的数表示,零用原点表示. (3)相反数的概念如果两个数只有符号不同,那么我们称其中一个是数是另外一个数的相反数,也称这两个数互为相反数. 三、数轴知识例题【例1】判断下列图形中所画数轴是否正确,如不正确,指出错在哪里?A-2-10B12C234-10D1【例2】在所给的数轴上画出表示下列各数的点:2,-3,112 ,0,1.5,5,123.-5-4-3-2-112354【针对训练】指出数轴上A ,B ,C ,D ,E ,F 各点所代表的数字.-5-4-3-2-1FEDCBA12354【例3】实数a 、b 在数轴上对应点的位置如图所示,则必有( ) A 、a +b >0 B 、a -b <0 C 、ab >0 D 、a b<0 【例4】以1厘米为单位,画出数轴,在数轴上表示出离原点1.2厘米的点.【针对训练】一数轴上的A 点到原点的距离为2,那么数轴上到A 点的距离为3的点所表示的数是【例5】 借助数轴列式回答下列问题:(1)与原点相距32的点表示的数是什么? (2)与-3相距32的点表示的数是什么?(3)一个点A 表示的数为-71,把A 点向左移动2个单位后所得的点对应的数是什么?(4)两个点A,B 分别表示的数为-1,41,有一个点C 到这两个点的距离相等,则点C 表示的数是什么?【针对训练】如图,在数轴上有三个点A 、B 、C ,回答问题:(1)若将B 点向右移动6个单位后,三个点所表示的数最小的是多少? (2)若将C 点向左移动6个单位后,三个点所表示的数最大的是多少?四、相反数知识例题【例6】 求下列各数的相反数(1) 12(2) 3- (3 )p - (4)+1.5 (5) (6)-+ (6)1()4-- (7)a b +【针对训练】请指出下列各数的相反数,并把它们在数轴上表示出来并把它们用“<”连接起来. -4,3,+21,0,p - , 1.5- ,-221【针对训练】分别指出下列各数表示的含义并化简下列各数:(1)(2.15)--= (2)(0.2)-+= (3)(5)+-= (4)(18)++=(5)[](6)---= (6)[](1.8)-+-= (7)[]{}(5)--+-=五、数轴与相反数综合应用【例7】数轴上A 点表示-5,B 、C 两点所表示的数互为相反数,且点B 到A 的距离为4,求点B 和点C 各对应什么数.【针对训练】已知数轴上点A 和点B 分别表示互为相反数的两个数a 和b (a <b ) ,且A 、B 两点的距离是144,求a 、b .【例8】 数轴上有一只蚂蚁在某一点,向左边走5个单位长,再向右边走12个单位长,再向左边走6个单位长,这只蚂蚁最后的位置是-4,求这只蚂蚁最初的位置.【变式8】一只小虫在数轴上的某点0p ,第一次0p 向左跳了1个单位长度到1p ,第二次从1p 向右跳了2个单位长度到2p ,第三次从2p 向左跳了3个单位长度到3p ,第四次从3p 向 右跳了4个单位长度到4,p 按以上规律跳了100次,它落在数轴上的点100p 所表示的数恰好是2057,你能确定这只小虫的初始位置0p 所表示的数吗?【过关训练】A 类1. 数轴的三要素是:______,______,______.2.正数的相反数是______;负数的相反是______;0的相反数是______;相反数是它本身的数是______;倒数是它本身的数______.3.画出数轴,在数轴上表示下列各数的点,-4,3.6,0,-2.5, 123,213,并把他们按从小到大顺序排列.4.在数轴上,点P 到表示2的点的距离是3,则点P 表示的数为( )A. 5B. 6C.-5或0D. 5或-1 5.有理数中,最小的正整数与最大的负整数之和是( )A .2 B. 1 C. 0 D. -2B 类6.化简:-[-(+3)]= ______, -[-(-3)]= ______ -[+(-21)]的相反数是______;一个数的相反数是-(-3.2),这个数是______ 7. 若-x =-(-2),则x 的相反数是______;若-[-(m -n )]是负数,则m-n ______0若-(m-3)是正数,则m-3______08.在数轴上A点和B点所表示的数分别为-2和1,若使A点表示的数是B点表示的数的3倍,应将A点()A.向左移动5个单位 B. 向右移动5个单位C. 向右移动4个单位D. 向左移动1个单位或向右移动5个单位C类9.请写出大于–2而小于+3的整数,非负整数.10.数a、b、c在数轴上的位置如图所示,在数轴上标出-a、-b、-c,试把a、-a、b、-b、c、-c按从小到大的顺序排列起来.。
数轴与相反数
数轴与相反数数轴是一种用来表示实数的图形工具,它将实数映射到一条直线上。
数轴的中心点是原点,正方向是向右,负方向是向左。
数轴上的每个点对应着一个实数,而相反数则是指与某个数相加等于零的数。
数轴的作用是帮助我们直观地理解和比较实数的大小关系。
在数轴上,我们可以清晰地看到不同实数之间的距离,进而判断大小关系。
相反数是指两个数相加等于零的数。
例如,2和-2是一对相反数,-5和5也是一对相反数。
相反数具有以下特点:1. 相反数的绝对值相等,符号相反。
这意味着如果一个数是正数,它的相反数就是负数,反之亦然。
例如,3和-3的绝对值都是3,只是符号不同。
2. 任何数与它的相反数相加等于零。
这是数学中的一个基本性质,即一个数加上它的相反数等于零。
例如,5 + (-5) = 0。
3. 相反数可以用来表示方向。
在物理学和几何学中,相反数可以用来表示方向。
例如,正数表示向右的方向,而负数表示向左的方向。
数轴和相反数在数学和实际生活中都有广泛的应用。
在数学上,数轴可以帮助我们比较大小关系、进行加减运算、解方程等。
通过将数映射到数轴上,我们可以更直观地理解数的大小和位置。
在解决一些实际问题时,数轴也是一个有用的工具。
在实际生活中,数轴可以用来表示温度、时间、距离等概念。
例如,摄氏度和华氏度可以通过数轴进行转换和比较;时间可以用数轴表示一天中的不同时刻;距离可以用数轴表示两个地点之间的距离。
相反数在实际生活中也有许多应用。
例如,在银行账户中,存款和取款可以用正数和负数来表示。
存款是正数,取款是负数。
通过相反数的概念,我们可以方便地进行账户余额的计算和管理。
相反数也可以用来表示物体的运动方向和速度。
在物理学中,正数表示向右的方向,负数表示向左的方向。
通过相反数的概念,我们可以更准确地描述物体的运动状态。
数轴和相反数是数学中的重要概念,它们在数学和实际生活中都有广泛的应用。
数轴可以帮助我们直观地理解和比较实数的大小关系,相反数则是一种特殊的数,它与原数的和为零。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
个数轴上随意画出一条长为2002cm的线段AB。则线段AB盖住的整点是多 少个?
12.如图,是一个正方体纸盒的展开图,请把-5,8,5,-6,- 8,6,分别填入六个正方形,使得折成正方体后,相对面上的两个数互 为相反数.
13.已知:a+b=0,b+c=0,c+d=0,d+=0,则:a,b,c,d四个 数中,哪些数是互为相反数?哪些数是相等?
14.若数与互为相反数,求a的相反数.
3.一只小鸟落在数轴上的某点,第一次从向左跳一个单位到P,第
二次从向右跳2个单位到,第三次从向左跳3个单位到,第四次从向右跳
4个单位到,…,按此规律跳了100次时,它落在数轴上的点所表示的数
恰是2003上点M表示2,点N表示-3.5,点A表示-1,在点M和N中,距
15.如果与互为相反数,且,则的倒数是( )
A.
B.
C.
D
16.一个正整数与其倒数,相反数相比较,大小关系是( )
A.
B.
C. D.
17.若2a与是互为相反数,则等于( )
A.1
B.-1
C.
D.
18.已知与-7互为相反数求的值.
19.试比较与的大小.
20.a、b、c在数轴上的位置如图所示,则中最大的是_______.
墨迹盖住的整数共有________个。
229.9 11.8 0 -13.7 -106.3
10.化间下列各数:(1)-(-3) (3)-[-(-3)]
(2)-(+10.5)
(4)+[-(+8)]
11.(1)+(-3.14)是_________的相反数. (2)-(-6)是_________的相反数. (3)已知的相反数是最小的正整数,则=____________. (4)若一个数大于它的相反数,则这个数是________.
找到了一个朋友”。 良师 德伯里说:“书籍是培育我们的良师,无需鞭笞和棍打,不
用言语和训斥,不收学费,也不拘形式”。 思想之船 培根说:“书籍是在时代的波涛中航行的思想之船,它
小心翼翼地把珍贵的货物运送给一代又一代。” 阶梯 高尔基说:“书籍是人类进步的阶梯。我每爬上一级,就更
脱离兽性而上升到人类,更接近美好生活的观念,更热爱这本书。” 编年史 坎耶里说:“书籍是人民的编年史,它将整个人类积累的
a>0,比较a与-a的大小.
例6 如图,在数轴上有六个点且AB=BC=CD=DE=EF,则与点C所表示的数
最接近的整数是( ).
A.-1
B.0
C.1
D.2
A B C D E F -5 11
例7 (1)工作流水线上顺次排列5个工作台A、B、C、D、E,一只工具 箱应该放在何处,才能使工作台上操作机器的人取工具所走的路程最 短?
E D C B A P -5 9
25.如图,A、B、C、D、E为数轴上的五个点,且AB=BC=CD=DE,则
图中与P点表示的数比较接近的一个数是( ).
26.电子跳蚤落在数轴上的某点,第一步从向左跳1个单位到,第
二步由向右跳2个单位到,第三步由向左跳3个单位到,第四步由向右跳
4个单位到…,按以上规律跳了100步时,电子跳蚤落在数轴上的点所表
例4 分别写出下列各数的相反数:
例5 互为相反数还有一个重要性质,这两个数之和为0,即:如果a、b
互为相反数,则a+b=0,根据这一性质解答下列各题。(1)若a+
3=0,则a=__________.(2)若a与2b互为相反数,且a≠0,用a的代数
式表示b,则b=___________.(3)若a<0,比较a与-a的大小.(4)若
数轴与相反数 【小故事】
名人论“书” 书,是人类文化成果的记录,纵观中外历史,无数名人都是书的至
爱亲朋,在他们的眼中,书是—— 营养吕 莎士比亚说:“书籍是全世界的营养品,生活里没有书
籍,就好像没有阳光;智慧里没有书籍,就像鸟儿没有翅膀。 乳汁 弥尔顿说:“优秀的书籍是抚育杰出人才的珍贵乳汁,它作
为人类财富保存下来,并为人类生活的进一步发展服务。” 朋友 伏尔泰说:“当我们第一遍读一本好书的时候,我仿佛觉得
示的数恰是19.94,试求电子跳蚤的初始位置所表示的数.
27.如图,在数轴上(未标出原点及单位长度)点A为线段BC的中 点,已知点A、B、C对应的三个数a、b、c之积是负数,这三个数之和与 其中一数相等,设为a、b、c三数中两数的比值,求P的最大值和最小
值.
C B A
28.比较的大小.
D C B A
21.如图,工作流程线上A、B、C、D处各有1名工人,且
AB=BC=CD=1,现在工作流程线上安放一个工具箱,使4个人到工具箱的
距离之和为最短则工具箱的安放位置是___________.
A B
C D
22.如图,数轴上标出若干个点,每相邻两点相距1个单位,点A、
B、C、D对应的数分别是整数a,b,c,d,且,那么数轴的原点应是(
度,再向右移动7个单位长度,那么终点表示的数是_______;(3)如
果将点B向左移动3个单位长度,再向右移动5个单位长度,终点表示的
数是-2,那么点B表示的数是__________.
2.一只小蚂蚁从数轴上出发,先向右爬3个单位,再向左爬2个单
位,终点表示的数为0,则起点表示的数是___________.
离A点较远的点是___________.
5.已知数轴上点M所对应的数是-2,求出与点M的距离等于4的点N
所对应的数;如果点P所表示的数是-3,求点P与点N的距离.
6.已知数轴上有A、B两点,A、B之间距离为1,点A与原点的距离
为3,那么所有满足条件的点B与原点的距离之和等于多少?
7.数轴上表示的数是整数的点称为整点,某数轴的单位长度为
(2)如果工作台由5个改为6个,那么工具箱应如何放置能使6个操 作机器的人取工具所走的路程之和最短?
(3)流水线上有个工作台时,怎样放置工具箱最适宜?
数轴与相反数练习
1.如果点A表示数-2,将点A向右移动4个单位长度,那么终点表
示的数是_________;(2)如果点A表示数2,将A向左移动4个单位长
).
A B C D
A.A点
B.B点
C.C点
D.D点
23.数a、b、c、d所对应的点A、B、C、D在数轴上的位置如图所
示,那么a+c与b+d的大小关系是( ).
0 D C B A
A.
B.
C.
D.不确定的
24.已知数轴上有A、B两点,A、B之间的距离为1,点A与原点的距
离为3,求所有满足条件的点B与原点的距离的和.
1cm,若在这个数轴上随意画出一条长为1995cm的线段AB,则线段AB盖
住的整点是( )
A.1994或1995
B.1994或1996 C.1995或1996 D.
1995或1997
8.一条路长300m,每隔30m安装一盏路灯,共需要装_________
盏。
9.一滴墨水洒在一个数轴上,如图1,根据图中标出的数值,制定
无数丰富的经验,世世代代传下去。” 宝器 骞·斯迈尔斯说:“好书常如最精美的宝器,珍藏着人一生
思想的精华。” 高尚的人 歌德说:“读一本好书就是和高尚的人谈话。” 钥匙 托尔斯泰说:“理想的书籍是智慧的钥匙。” 灯塔 惠普尔说:“书籍是屹立在时间的汪洋大海中的灯塔。”
【典型例题】
例1 在数轴上表示点的运动状态。例如,画图表示一个点按如下条件 运动后到达的终点,并说出它表示什么数?从原点向右运动2个单位长 度,再向左运动5个单位长度。
