二次函数最值课件公开课

合集下载

二次函数的图像和性质PPT市公开课一等奖省优质课获奖课件

本节课我们学习了什么？你还有什么疑问？
第9页
第10页
x ... -3 -2 -1 0 1 2 3 ... y=-x² ... -9 -4 -1 0 -1 -4 -9 ...
第5页
5.2 二次函数图像和性质(1)
观察函数y＝－x2图像，说出图像特征．
图像有最高点，过(0,0) y有最大值．
当x＜0时，y随x增大而增大．
抛物线关于y轴对称．
当x＞0时，y随x增大而减小．抛物线开口向下．
5.2 二次函数图像和性质(1)
画函数图像步骤：列表描点连线研究函数性质方法：数形结合
二次函数图像是怎样？
试着画一画吧！
第2页
5.2 二次函数图像和性质(1)
例1 画出函数y＝x2图像．
x ... -3 -2 -1 0 1 2 3 ... y=x² ... 9 4 1 0 1 4 9 ...
列表时自变量要均匀和对称！
第3页
5.2 二次函数图像和性质(1)
观察函数y＝x2图像，说出图像特征．
当x＜0时，y随x增大而减小．
图像有最低点，过（0,0） y有最小值．
抛物线关于y轴对称．当x＞0时，y随x增大而增大．
抛物线开口向上．
第4页
5.2 二次函数图像和性质(1)
例2 画出y＝－x2图像．
第6页
5.2 二次函数图像和性质(1)
比较函数y＝－x2与y＝x2图像，说出图像特征异同点．
假如是函数y＝2x2与y＝－2x2(1)
在同一坐标系上画函数y＝2x²，y＝－2x²，
y＝
1 2
x²和y＝
-
1 2
x²图像，并说出图像特征．
第8页
5.2 二次函数图像和性质(1)

高中数学优质课课件：二次函数的最值

•求s关于x的函数关系式及自变量x的取值范围；
•怎样才能围出最大面积，最大面积是多少？
课堂小结提炼精华
这节课你学到了哪些知识？我们用到了哪些数学方法？
课后拓展 B组 2
1 题2：已知 y x 1, 且 1 x 2 , 令S xy ，则： 2 1 1 小 (1)当x= 时，S有最值,是 2
1 3 S (2) 函数S的取值范围是 2 2
(②号本P.4 T5改编)
题3：有长为24米的篱笆，一面利用墙（墙的最大可用长度a为10米）,围成中间隔有一道篱笆的长方形花圃．设花圃的宽AB为x米， 2 面积为S米．
二次函数限定范围下的最值问题
桐庐县城关初中申屠建华
课前热身复习回顾
你会作二次函数
y x 2x 3
2
的图象吗？
例题重现变式深入
例题求函数 y x 2x 3 的最值
2
变式1：当x≥-1时，求函数的最值变式2：当x ≥ 2呢？变式3：当x ≤ -2 时呢？变式4：当-2≤x≤2时呢？
X=1 对称轴在限定范围内 (-2≤x≤2)
变式5：已知二次函数y= (x-m)2-4,当 -2≤x≤2时，求函数的最小值
分类讨论
应用新知展示自我
2 y 2 x 4 x 6 ，当分别满足题1：已知函数下列条件时，求函数的最值.
(1)
x2
2 x 2
(2)
(①号本P.6 T2改编)
数形结合
知识归纳学会迁移
1、当函数自变量没有限定范围时，二次函数在 2、当函数自变量限定范围时，二次函数总是在
顶点处取得最值
顶点或端点处取得最值，我们要讨论对称轴与限定范围的位置关系

专题研究(公开课)二次函数之面积最值问题PPT课件

A
∴S=1/2(12-2t) •4t
P
即S=- 4t²+24t=- 4(t-3)²+36（0<t<6）
（2）当t=3时，S最大值=36
B
Q
C
思考：以此题为背景，你能设计其它与面积有
关的问题吗？
.
4
探究问题三：抛物线上的面积问题
已知二次函数y=x2-2x-3 与x轴交于A、B两点
（A在B的左边），与y轴交于点C. (1)直接写出点A、B、C及顶点P的坐标
5在抛物线上除点p外是否存在点q使得sqbcspbc若存在求出点q的坐标若不存在请说明理由4在抛物线上除点c外是否存在点n使得若存在求出点n的坐标若不存在请说明理由
专题研究课
二次函数与面积问题
板桥初中陈金国
.
1
热身运动
如图，在一面靠墙的空地上用长为24米的篱笆，围成中间隔有二道篱笆的长方形花圃，设宽AB为x米，面积为S平方米。
∴ BC为（24－4x）米
∴ S＝x（24－4x）
A
D
＝－4x2＋24 x （0<x<6）
(2)当x＝
b 2a
3
时，S最大值＝
4ac 4a
b
2
B
＝36（平方米）
C
(3) ∵墙的可用长度为8米
∴ 0<24－4x ≤8 4≤x<6
∴当x＝4米时，S最大值＝32
平方米 .
3
问题探究二：如图，在△ABC中∠B=90º，AB=12cm，
若S存S△△在NNAA，BB =求= S出2△S点A△BACNB，的C，坐标，
.N2
.N3
若不存在，请说明理由。

二次函数的最值问题课件

顶点法
总结词
利用二次函数的顶点坐标求最值。
详细描述
根据二次函数的顶点公式$(h, k)$，代入原函数求出最值。当$a > 0$时，函数有最小值；当$a < 0$时，函数有最大值。
导数法
总结词
通过求导数判断函数的单调性，进而找到最值点。
详细描述
对二次函数求导得到$f'(x) = 2ax + b$，令导数等于0得到临界点$x = frac{b}{2a}$，通过判断单调性找到最值点。
复杂的二次函数最值问题
总结词
运用配方法或公式法求最值
详细描述
对于复杂的二次函数，可以通过配方法或公式法求出最值。配方法是通过配方将二次函数转化为顶点式，再利用顶点式求最值；公式法是利用公式直接求出二次函数的最值。
总结词
利用导数求最值
详细描述
对于复杂的二次函数，可以利用导数求出函数的极值点，再根据极值点的位置和函数的单调性判断最值的位置，从而求出最值。
总结词
结合实际背景求解
详细描述
对于实际应用中的二次函数最值问题，需要结合实际背景进行分析。例如，在物理学中，可以利用二次函数的最值求解物体的最大速度、最小压力等；在经济学中，可以利用二次函数的最值求解成本最低、利润最大等问题。
06
总结与思考
二次函数最值问题的总结
定义与性质
二次函数最值问题主要研究的是二次函数在特定条件下的最大值或最小值。这些条件可能包括函数的开口方向、顶点位置、定义
详细描述
二次函数是数学中常见的一种函数形式，其一般形式为 y=ax^2+bx+c，其中a、b、c为常数，且a≠0。a决定了抛物线的开口方向和宽度，b决定了抛物线的左右位置，c决定了抛物线的上下位置。

二次函数动点面积最值分割面积法PPT课件一等奖新名师优质课获奖比赛公开课

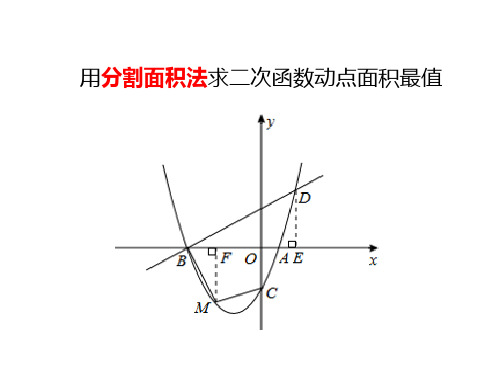
解答
(2023•娄底)如图，抛物线y=ax2+bx+c（a、b、c为常数，a≠0）经过点A(﹣1，0)，B(5，﹣6)，C(6，0)．（1）求抛物线旳解析式；（2）如图，在直线AB下方旳抛物线上是否存在点P使四边形PACB旳面积最大？若存在，祈求出点P旳坐标；若不存在，请阐明理由；
【解答】解：
课堂总结
• “二次函数中动点图形旳面积最值”试题解析一般规律：
• 此类问题旳特征是要以静代动解题，首先找面积关系旳函数解析式，关键是用含x旳代数式表达出有关旳线段旳长度，若是规则图形则套用公式或用割补法，若为不规则图形则用割补法.
（1）设y=a(x+1)(x﹣6)(a≠0)，把B (5，﹣6)代入a(5+1)(5﹣6)=﹣6，a=1， ∴y=(x+1)(x﹣6)=x2﹣5x﹣6。
（2）如图1，过P向x轴作垂线交AB与点D，交X轴于M 设P（m，m2﹣5m﹣6），有A （-1，0），B （5，﹣6），得YAB=-x-1 则D（m，﹣m﹣1） ∴PD= ﹣m﹣1- （ m2﹣5m﹣6）=-m2 +4m+5
∴S△ABP=（（ -m2 +4m+5 ）X6 = -3m2 +12m+15
∴当m=2时S△ABP最大当m=2时，S四边形PACB有最大值为48，这时 m2﹣5m﹣6=22﹣5×2﹣6=﹣12， ∴P（2，﹣12），
题型一：分割面积法
【变式2】
题型一：分割面积法
【变式2】
题型一：分割面积法
【变式2】
【解题思绪，技巧套路】（1）利用已知条件求出点B旳坐标，然后用待定系数法求出抛物线旳解析式；（2）首先求出四边形BMCA面积旳体现式，然后利用二次函数旳性质求出其最大值；

二次函数第一课时PPT省公开课获奖课件说课比赛一等奖课件

上述三个问题中旳函数解析式具有哪些共同旳特征?
经化简后都具有y=ax²+bx+c 旳形式. (a,b,c是常数, a≠0 )
下列函数中，哪些是二次函数？
(1)y=3x-1
(2)y=3x2
(3)y=3x3+2x2
(4)y=2x2-2x+1
(5)y=x-2&x)
y ax2 bx c(其中a,b, c是常数)，
二次函数旳概念
温故知新
复习： 1、什么是函数？
在某个变化过程中，有两个变量x 和y ，假如对于x 旳每一个可取旳值，都有唯一一种y 值与它相应，那么y 称为x 旳函数。 2、什么叫做一次函数？
形如y=kx+b (k、b为常数，k≠0)
3、函数有哪些表达措施？
解析法列表法图象法
合作学习，探索新知 :
请用合适旳函数解析式表达下列问题情境中旳两个变量 y 与 x 之间旳关系：
(1)圆旳面积 y ( cm2)与圆旳半径 x ( cm ) y =πx2
(2)某商店1月份旳利润是2万元，2、3月份利润逐月增长，这两个月利润旳月平均增长率为x，3月份旳利润为y
y = 2(1+x)2
合作学习，探索新知 :
当a, b, c满足什么条件时
(1)它是二次函数? （1）a 0
(2)它是一次函数？ (2)a 0,b 0
(3)它是正百分比函数？(3)a 0,b 0, c 0
例题精讲
例１ m取哪些值时，函数 y=(m2-m)x2+mx+(m+1)是以x为自变量旳二次
函数？
2: m取何值时，函数y=(m+1)xm2 2m 1
(3)拟建中旳一种温室旳平面图如图,假如

[公开课课件]二次函数在给定区间上的最值

解(1)因为二次函数y=x² +2x-3 的对称轴为x=-1，区间[-3，-2] 在它的左侧，而左侧为单调递减，如图：所以f(x)min=f(-2)=-3 f(x)max=f(-3)=0
(2)如图： f(x)min=f(-1)=-4； y f(x)max=f(1)=0 （3）如图： f(x)min = f(0) =-3； f(x)max = f(2)= 5
可知: ymax =f (2)当a<
a 2
2 a a ( )= 4 2
a2 4ቤተ መጻሕፍቲ ባይዱ
时,即-1<a<0时,
-1 o
a 2
a x
a 解:函数图象的对称轴方程为x= ,又x∈[-1,a] 2 a 1 1 故a>-1, 2 > - 2 ,∴对称轴在x= - 2 的右边. a ∴(1)当 -1< 2 ≤a时,即a≥0时 , 由二次函数图象 2 a a y 可知: ymax =f ( )= 4 2 a a2 (2)当a< 时,即-1<a<0时, 4 2
问题6：求函数y=-x(x-a)在x∈[-1,a]上的最大值
五、动函数动区间的二次函数的值域
问题6：求函数y=-x(x-a)在x∈[-1,a]上的最大值
a 解:函数图象的对称轴方程为x= ,又x∈[-1,a] 2 a 1 1 故a>-1, 2 > - 2 ,∴对称轴在x= - 2 的右边. a ∴(1)当 -1< 2 ≤a时,即a≥0时,由二次函数图象
y

b 2a
（2）二次函数y=ax² +bx+c (a<0)
b 4ac b 2 顶点坐标 , 2 a 4 a 在（-∞， 2ba )上，单调递增；在（ 2ba ，+ ∞）上，单调递减。

二次函数的最值问题课件(19张PPT)-中考数学一轮复习(浙教版)

∴ 2 x 16 ． 5
探究
∵w=(x-2)(900-200x)=-200(x-2)(x-4.5)，
拓
∴对称轴为直线 x 2 4.5 13 ． 24
展 ∵a 200 0，
生长
∴当 2 x 16 时，w随着x的增大而减小.
x/ 元
O
2 16
5
x=
13 4
∴当
x
16
5 时，w取到最大值，最大值为312元.
H
究
问题2 窗户透光面积怎么求？
窗户透光面积=长×宽=AD×AB.
问题3 在这个等量关系中有几个变量？哪个变量作为自变量？
3个．
AD或AB.
问题4 如果设AB为x米，那么你能用x表示AD吗？
AD为 3 7x 米． 4
问题背
例如图，小明家窗户的上部是由两个正方形组成的矩形，窗框材料总长为6米，如何改进设计才能使窗户透光面积最大，最大面积
=-2(x-50)2+5000．
∴当x=50时，S取到最大值，最大值为5000平方米．
答：与墙垂直的一边AB为50米，矩形果园ABCD的面积最大，
最大值是5000平方米．
问题5 回顾解题过程，你还有什么疑惑吗？
AB一定能取到50米吗？
问
题解：设矩形果园ABCD的面积为S平方米，AB为x米，背则BC为(200-2x)米．
问题
S/ m2
背
5000
景
S/ m2 5000 4800
问题探究
O
x/ m 100
x=50
x/ m
O
60 100
x=50
问题7 观察函数图象，并说一说二次函数的最值在自变量的哪些值取到？

二次函数(公开课)

们可以通过将特定的横坐标代入二次函数的方程来求得对应的函数值。这样我们可以得到函数图像上的点。
二次函数的图像
二次函数的图像形状可以是抛物线，其凹性取决于a的正负。正数a使抛物线开口朝上，负数a使抛物线开口朝下。这种图像帮助我们直观地理解二次函数的变化规律。
开口朝上
正数a使抛物线形状开口朝上。
开口朝下
负数a使抛物线形状开口朝下。
二次函数的顶点
二次函数的顶点是抛物线的最高（或最低）点。顶点的横坐标可以通过求根公式(-b/2a)得到，纵坐标是函数的最大值或最小值。
二次函数的轴对称线
抛物线的轴对称线在顶点处垂直于x轴。它将抛物线分为两个对称的部分，使我们能够推断出函数值的对应关系。
二次函数的零点
二次函数的零点是使函数值为零的横坐标。我们可以使用求根公式找到二次函数的零点。
零点
零点是函数与x轴相交的点，使函数值为零。
二次函数的判别式
二次函数的判别式为Δ = b² - 4ac，它可以告诉我们方程的根有多少个，以及根的性质。
二次函数(公开课)
欢迎参加我们的二次函数公开课！本课程将详细讲解二次函数的定义、特点以及其在实际中的应用。让我们一起探索二次函数的奥秘吧！
二次函数的一般式
二次函数可以表示为y = ax²+ bx + c的一般式，其中a、b、c为常数，且a ≠ 0。这种形式使我们能够直观地了解二次函数的性质和特点。

数学：《二次函数的最值问题》复习PPT课件

4
Fmax=f(3)
Fmax=f(3)
Fmax=f(0)
-
Fmax=f(0)
5
最大值
开口向上的含参变二次函数的最大值问题, 应根据对称轴与区间的位置关系分为两类：
以区间中点为界：对称轴在区间中点左侧、对称轴在区间中点右侧
-
6
最大值
例1：求y=x2-4tx+1在区间[0,3]上的最大值.
解:二次函数的对称轴：x=2t
下面我们来复习含参变量二- 次函数的最值问题
3
最大值
例1：求y=x2-4tx+1在区间[0,3]上的最大值.
解析：该函数的对称轴x=2t,随着t的变化，对称轴的位
置不断进行变化，导致函数的最大值也在不断进行变化.
仔细观察下图解决问题:
对于开口向上的含参变二次函数的最大值问题, 应如何进行分类?
-
2
42
f(x)max=f(0)=1, f-(x)min=f(2t)=1-4t2.
13
最值
当2t 3时,t 3 2
f(x)max=f(0)=1, f(x)max=f(3)=10-12t.
综上：
当t<0时，f(x)max=f(3)=10-12t, f(x)min=f(0)=1.
当0 t
当3 4
3 4
m2 2m7 (m1)
g(m)8
(1m2)
m2 4m4 (m2)
-
16
练习
3. 若函数y=x2-4ax+a2-2a+2在[0,2]上的最小值为2，求a.
-பைடு நூலகம்
17
谢谢！
-
18
；天游注册天游注册；

《二次函数》示范公开课PPT教学课件【九年级数学下册北师大版】

二次函数
教科书第30页习题2.1第1、3题
二次函数
二次函数
（1）能结合具体情境，表示变量之间的二次函数关系，理解二次函数的概念；（2）会应用二次函数的概念，进行二次函数关系的判断；（3）在通过实际情境归纳出二次函数概念的过程中，体会函数的模型思想；（4）通过对贴合生活的实例的探讨，感受生活中处处有数学，培养数学学习的兴趣.
重点
难点
上述解析式是我们学过的一次函数吗？
画一个正方形，如果它的边长变化，正方形的哪些量也发生变化？（1）正方形的周长与边长之间的函数关系式 . （2）正方形的面积与边长之间的函数关系式 .
新增的橙子树棵数
函数解析式等号两边必须是整式；化简后自变量的量），哪些是二次函数？ .
解：(1) 的最高次幂不是二次，不是二次函数.
先化简再判断
(4)
(3)右边不是整式，不是二次函数.
(2)
(5)
不是整式
【例2】已知正方体的棱长为 cm，表面积为 cm²，体积为 cm³.（1）分别写出与与之间的函数关系式.（2）这两个函数中，哪一个是的二次函数？
解：因为正方形的边长为4，当边长增加时，面积增加，所以故这个函数是二次函数.
增加的
3. 已知二次函数，当时，；当时，，求的值.
解:解得
类比于一次函数待定系数法
函数自变量的取值范围：
二次函数：
一般地，形如是常数，的函数叫做的二次函数. 特殊形式：，.
注意：
（1）关于的代数式一定是整式；（2）化简后自变量的最高次数为2；（3）二次项系数不为零.
解:（1），
正方体表面积
正方体体积
（2）是的二次函数.
三次
二次

二次函数的性质公开课一等奖课件省赛课获奖课件

②顶点式 y＝a(x－h)2＋k(a≠0)，其中(h，k)是抛物线的顶点．当已知抛物线的顶点坐标或对称轴，能够先求出抛物线顶点时，设顶点式解题十分简捷．加上其他条件确定 a 的值，即可求出函数的解析式；
③两根式 y＝a(x－x1)(x－x2)(a≠0)，其中 x1、x2 就是方程 ax2＋bx＋c＝0 的两根，即抛物线与 x 轴两交点的横坐标．当题中已知抛物线与 x 轴交点的坐标时，设出零点式解题比较简单．
已知顶点为(1，－3)，∴h＝－1，k＝－3，即所求的二次函数 y＝a(x－1)2－3. 又∵图像经过点 P(2,0)， ∴0＝a×(2－1)2－3，∴a＝3， ∴函数的解析式为 y＝3(x－1)2－3，即 y＝3x2－6x.
解法四：设解析式为 y＝a(x－x1)(x－x2)(a≠0)，其中 x1，x2 是抛物线与 x 轴的两交点的横坐标，已知抛物线与 x 轴的一个交点 P(2,0)，对称轴是 x＝1， ∴抛物线与 x 轴的另一个交点为(0,0)， ∴x1＝0，x2＝2， ∴所求的解析式为 y＝a(x－0)(x－2)，又∵顶点为(1，－3)，∴－3＝a×1×(1－2)，∴a＝3， ∴所求函数的解析式为 y＝3x2－6x.
∴函数的解析式为 y＝3x2－6x.
解法二：设所求函数的解析式为 y＝ax2＋bx＋c(a≠0)，
4a＋2b＋得 ab＝＝3－，6， c＝0.
∴函数的解析式为 y＝3x2－6x.
解法三：设所求函数的解析式为 y＝a(x＋h)2＋k(a≠0)，则顶点坐标为(－h，k)，
[分析] 本题中已知二次函数 f(x)的解析式，故可考虑用配方法将 f(x)化成顶点式，进而确定对称轴和顶点坐标．然后再结合对称性求 f(3)及比较 f(－12)与 f(32)的大小．

二次函数与最值公开课

二次函数与最值教学目标1、掌握二次函数在区间内的最值2、学会通过参数的分类讨论动函数或动区间下的最值3、体会分类讨论思想在数学学习中的应用教学重、难点教学重点：二次函数在动函数或动区间下的最值教学难点：分类讨论教学过程（一）导疑——情景引入，提出疑问例1、已知关于x 的二次函数y=222x x --（1）当−3≤x ≤0时，则y 的范围为_________________（2）当−1≤x ≤5时，则y 的范围为________________（3）当2≤x ≤3时，则y 的范围为________________（4）当−3<x <3时，则y 的范围为________________（二）引探——自主学习，探究问题例2、已知关于x 的二次函数y=225x x -++,当t ≤x ≤t+2时，函数有最大值2，求t 的值（三）释疑——主动展示，阐释疑点例3、已知关于x 的二次函数y=222x x --,当a ≤x ≤a+2时，函数有最大值1，则a 的值为（四）启思——归纳总结，提炼方法遇到最值不要怕，方法由我来归纳（五）精炼——当堂训练，提升能力已知关于x的二次函数y=-（x-h）2+3，当1≤x≤3时，函数有最小值h，求h的值课后作业：1、已知关于x 的函数y=-x 2-ax+1，当0≤x≤3时函数有最大值5，求a 的值2、当−2≤x ≤1时，二次函数y =−(x −m)2+m 2+1有最大值4，求m 的值3、已知关于x 的二次函数y=x 2-2ax+3，当1≤x≤3时，函数有最小值2a ，求a 的值4、已知y=23x ax a ++-,当 -2≤x≤2时，y≥0恒成立，求a 的取值范围。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

∴ 花圃宽为（24－4x）米
＝－4x2＋24 x （0<x<6）
(2)当x＝
b 2a
3
时，S最大值＝
4ac b2 4a
＝36（平方米）
(3) ∵墙的可用长度为8米
A
D
∴ 0<24－4x ≤8 4≤x<6
∴当x＝4cm时，S最大值＝32 平方米 B
C
2.用长8m的铝合金条制成如图的矩形窗框,那么当长、
-b
②顶点坐标是( _2_a_
4ac-b2
, _4_a_ );
-b
③对称轴是_X_=_2_a_;
④函数的最大值或最小值:
-b
4ac-b2
当a>0,x=__2a_时,y有最_小__值,为y=__4_a_;
当a<0,x=__-2ba__时,y有最_大_值,为y=_4a_4c_a-b_2。
⑴ 已知：二次函数
y 1 (x 2) 2 6
的图象如2图所示，当 x= y有最小值，为 -6 。
2 时，
⑵二次函数 y 5 x2 1= 2 时，y有最大值，为 15。
x ⑶二次函数y x2 2x 5有最小值时，自变量的值是
__-_1___。
2020 12:38:15 AM00:38:152020/12/16
• 11、自己要先看得起自己，别人才会看得起你。12/16/
谢谢大家 2020 12:38 AM12/16/2020 12:38 AM20.12.1620.12.16
• 12、这一秒不放弃，下一秒就会有希望。16-Dec-2016 December 202020.12.16
m ⑷已知二次函数 y x2 6x m的最小值为1，那么的
值是__1_0___。
例1：分别在下列各范围上求函数
y=x2+2x－3的最值
y
(1) X取任意实数
(2) 2 x 2
(3) 1 x 3
-2 -1 O
2x
例1：分别在下列各范围上求函数
y=x2+2x－3的最值
(3) 1 x 3
宽分别为多少时，才能使窗框的边的透光面积最大？最大的透光面积是多少？
A
D
解：设AD=X m, 窗框的透光 E
F
面积为y ，由题意得：
B
C
⒈求二次函数的最值问题是二次函数中的常见题型，在现实生活中有广泛的应用,主要包括以下两个方面:
⑴用二次函数表示实际问题中的函数关系。
⑵求函数的最大值或最小值。
A
D
xx
x
x
B
C
例2:如图，在一面靠墙的空地上用长为24米的篱笆，围成
中间隔有二道篱笆的长方形花圃，设花圃的宽AB为x
米，面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围；
(2)当x取何值时所围成的花圃面积最大，最大值是多少？
(3)若墙的最大可用长度为8米，则求围成花圃的最大面积。
解：(1) ∵ AB为x米、篱笆长为24米∴ S＝x（24－4x）
⒉求最值的方法：
⑴配方法：y ax2 bx c
y a(x h)2 k
⑵公式法：顶点坐标：(
b
4ac b2
,
)
2a 4a
•
1、有时候读书是一种巧妙地避开思考的方法。20.1 2.1620. 12.16W ednesday, December 16, 2020
•
2、阅读一切好书如同和过去最杰出的人谈话。00:3 8:1500: 38:1500 :3812/ 16/2020 12:38:15 AM
•
8、业余生活要有意义，不要越轨。20 20年12 月16日星期三 12时38 分15秒 00:38:1 516 December 2020
•
9、一个人即使已登上顶峰，也仍要自强不息。上午 12时38 分15秒上午12 时38分 00:38:1 520.12. 16
• 10、你要做多大的事情，就该承受多大的压力。12/16/
•
6、意志坚强的人能把世界放在手中像泥块一样任意揉捏。 2020年 12月16 日星期三上午 12时38 分15秒 00:38:1 520.12. 16
•
7、最具挑战性的挑战莫过于提升自我。。20 20年12 月上午 12时38 分20.1 2.1600: 38Dece mber 16, 2020
• 13、无论才能知识多么卓著，如果缺乏热情，则无异纸上画饼充饥，无补于事。Wednesday, December 16, 2
02016-Dec-2020.12.16
• 14、我只是自己不放过自己而已，现在我不会再逼自己眷恋了。20.12.1600:38:1516 December 202000:38
(5,27)
(-1,3)
(1,-5)
在一面靠墙的空地上用长为24米的篱笆，围成中间隔有二道篱笆的长方形花圃，
问题1：如果设花圃的宽AB为x米，则另一边 BC=__2_4_－_4_x_；花圃的面积为S平方米，则S与x的函
数关系式S=___4_x_2__2_4_x ___，自变量的取值范围
___0_﹤__x _﹤_6____；问题2：当x取何值时所围成的花圃面积最大，最大值是多少？
•
3、越是没有本领的就越加自命不凡。 20.12.1 600:38: 1500:3 8Dec-20 16-Dec-20
•
4、越是无能的人，越喜欢挑剔别人的错儿。 00:38:1 500:38: 1500:3 8Wednesday, December 16, 2020
•
5、知人者智，自知者明。胜人者有力，自胜者强。 20.12.1 620.12. 1600:3 8:1500: 38:15D ecembe r 16, 2020
y
-2 -1 O
1 23 x
1：已知二次函数y=2x²-4x-3，（1）y有最大值还是最小值？若有，请求出最值。
(1,-5)
1：已知二次函数y=2x²-4x-3，（2）若2≤X≤5，求y的最值。
(5,27)
（2，-3） (1,-5)
1：已知二次函数y=2x²-4x-3
（3）若-1≤X≤5，求y的最值。
⒈掌握二次函数的图象与性质。
⒉会求二次函数顶点坐标，并会根据顶点坐标求最值。
⒊会用二次函数表示实际问题中的函数关系来求实际问题中最值。
1.形如y= ax²+bx+c (a、b、c、是常数，且 a≠0 )的函数叫做y关于x的二次函数。
2.二次函数y=ax²+bx+c(a≠0)
①开口方向:当a>0时,_开_口_向__上_,当a<0时,开__口_向__下;