第六届广东省大学生数学竞赛试卷参考答案(高职高专类)

合集下载

数学竞赛大纲(高职高专类)

广东省大学生数学竞赛考试大纲—高职高专类（讨论稿）广东省大学生数学竞赛（高职高专类）竞赛内容为高等数学课程的教学内容，具体内容如下：一、函数、极限、连续1、函数的概念及表示法。

2、函数的有界性、单调性、周期性和奇偶性。

3、反函数、分段函数、隐函数、复合函数，基本初等函数的性质及其图形，初等函数函数关系的建立。

4、数列极限与函数极限的定义及其性质。

5、函数的左极限和右极限。

6、无穷小量和无穷大量的概念及其关系，无穷小量的性质及无穷小量的比较。

7、极限的四则运算。

8、极限存在的两个准则：单调有界准则和夹逼准则，两个重要极限：0sin lim 1x x x →= 1lim 1xx e x →∞⎛⎫+= ⎪⎝⎭。

9、函数连续的概念，函数间断点的类型，初等函数的连续性。

10、闭区间上连续函数的性质（有界性、最大值和最小值定理，介值定理)。

二、一元函数微分学1、导数和微分的概念，导数的几何意义。

2、导数和微分的四则运算，基本初等函数的导数。

3、复合函数、反函数和隐函数的微分法，高阶导数，一阶微分形式的不变性。

4、罗尔（Rolle ）定理，拉格朗日( Lagrange)中值定理，泰勒定理．柯西（Cauchy)中值定理。

5、洛必达（L'Hospital ）法则。

6、函数单调性的判别，函数的极值，函数图形的凸性，拐点及渐近线，函数图形的描绘，函数的最大值与最小值。

三、一元函数积分学1、原函数和不定积分的概念，不定积分的基本性质，基本积分公式。

2、不定积分的换元积分法和分部积分法．3、定积分的概念和基本性质，定积分中值定理。

4、积分上限的函数及其导数，牛顿一莱布尼茨（Newton- Leibniz）公式。

5、定积分的换元积分法与分部积分法。

6、反常（广义）积分。

7、定积分在几何上的应用(如面积、体积和弧长求法)。

8、定积分在物理上的应用(如功、水压力和引力求法)。

四、向量代数与空间解析几何1、空间直角坐标系，两点间距离，向量的概念，向量的坐标表示，向量的运算（加减法与数乘，数量积与向量积），向量模，单位向量，方向余弦，两向量平行与垂直的充要条件。

优选年广东省+证书高职高考数学试卷真题和答案

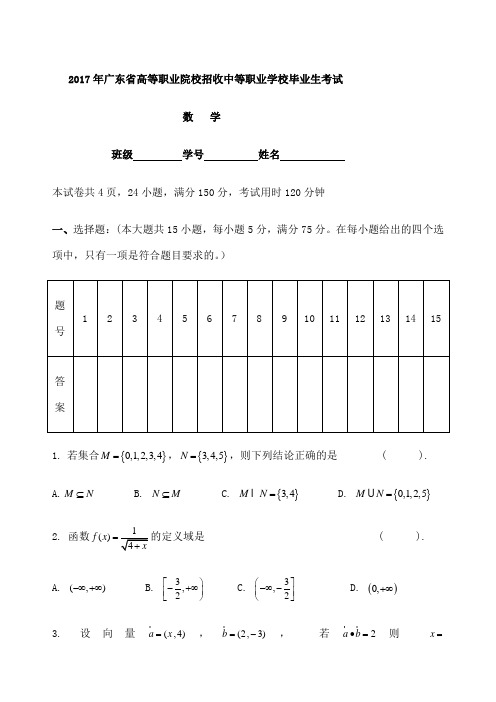
2017年广东省高等职业院校招收中等职业学校毕业生考试数学班级学号姓名本试卷共4页，24小题，满分150分，考试用时120分钟一、选择题：(本大题共15小题，每小题5分，满分75分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

）1. 若集合{}0,1,2,3,4=M ，{}3,4,5=N ，则下列结论正确的是 ( ). A.⊆M N B. ⊆N M C. {}3,4=I M N D. {}0,1,2,5=U M N2. 函数()=f x 的定义域是 ( ). A. (,)-∞+∞ B. 3,2⎡⎫-+∞⎪⎢⎣⎭ C. 3,2⎛⎤-∞- ⎥⎝⎦ D. ()0,+∞3.设向量(,4)=ra x ，(2,3)=-rb ，若2•=r r a b 则 =x( ).A. 5-B. 2-C. 2D. 74. 样本5,4,6,7,3的平均数和标准差分别为 ( ).A. 5和2B. 56和3 D. 6不等式2560x x --≤的解集是 ( ). A. {}23x x -≤≤ B. {}16x x -≤≤C. {}61x x -≤≤D. {}16x x x ≤-≥或5. 设()f x 是定义在上的奇函数，已知当0≥x 时，23()4=-f x x x ，则(1)-=f （）. 下列函数在其定义域内单调递增的是 ( ) . A. 5- B. 3- C. 3 D. 56.已知角θ的顶点与原点重合，始边为x 轴的非负半轴，如果θ的终边与单位圆的交点为34,55⎛⎫- ⎪⎝⎭P ，则下列等式正确的是 ( ).A. 3sin 5θ= B. 4cos 5θ=- C. 4tan 3θ=- D. 3tan 4θ=- 7. “4>x ”，是“(1)(4)0-->x x ”的 ( ). A. 必要非充分条件 B. 充分非必要条件 C. 充分必要条件 D. 非充分非必要条件8. 下列运算不正确的是( ) .A. 22log 10log 51-=B. 222log 10log 5log 15+=C. 021=D. 108224÷=9. 函数()cos3cos sin 3sin =-f x x x x x 的最小正周期为 ( ). A.2πB. 23πC. πD. 2π10. 抛物线28=-y x 的焦点坐标是 ( ).A. (2,0)-B. (2,0)C. (0,2)-D. (0,2)11. 已知双曲线22216-=x y a 的离心率为2，则=a ( ).A. 6B. 312. 从某班的21名男生和20名女生中，任意选派一名男生和一名女生代表班级参加评教座谈会，则不同的选派方案共有 ( ).A. 41种B. 420种C. 520种D. 820种13. 已知数列{}n a 为等差数列，且12=a ，公差2=d ，若12,,k a a a 成等比数列，则=k ( ).A. 4B. 6C. 8D. 1014. 设直线l 经过圆22220+++=x y x y 的圆心，且在y 轴上的截距为1，则直线l 的斜率为 ( ).A. 2B. 2-C. 12D. 12-15. 已知函数=x y e 的图象与单调递减函数()=y f x ，()∈x R 的图象相交于点(),a b ，给出下列四个结论：则(1)ln =a b (2)ln =b a (3)()=f a b (4)当>x a 时，()<x f x e 。

2023年首届广东省大学生数学竞赛试卷经管类

广东省大学生数学竞赛试卷参照答案(经济管理类)一、(本题30分, 每题3分) 填空题1.已知 .则极限........ .2. 设对于满足方程 .若在获得极值, 则它是 .（填极大值还是极小值）3.极限...... .4.设函数满足.则 _________.5. 极限 .6.由方程确定了函数 .则......7.设可微, , 若 , 则 .8.设函数()f x 持续, (0)2f =, 记22222()()d d (0)x y t F t f x y x y t +≤=+≥⎰⎰, 则(0)F ''= .9.设是微分方程旳三个不一样旳解, 且不恒等于常数, 则微分方程旳通解....... .10. 级数旳收敛区间为 .二、（本题10分）设函数具有二阶持续导数, 且 , 证明：函数(),0()(0),0f x xg x x f x ⎧≠⎪=⎨⎪'=⎩具有一阶持续导数.三、（本题10分）设()f x 在[0,1]上可导, 当01x ≤≤时, 0()2f x ≤≤; 且对区间(0,1)内所有x 有()2f x '≠, 证明: 在[0,1]上有且仅有一点,ξ 使得()2.f ξξ=四、（本题10分）设函数在区间上持续, 并设 , 求 .五、（本题10分）设 , 其中为持续函数, 求 .六、（本题10分）设()f x 在区间[1,1]-上持续且为奇函数, 区域D 由曲线24y x =-与3y x =-、1x =所围成, 求()1()ln(d d D I f x y x y =++⎰⎰.七、（本题10分）设()f x 在区间[0,1]上有持续导数, n 为正整数, 证明: 10(1)1()d n f x f x x o n n ⎛⎫=+ ⎪⎝⎭⎰ ()n →∞.八、（本题10分）设0a >, 鉴别级数(1)221(1)(1)(1)n n n n a a a a +∞=+++∑旳敛散性.。

广东数学竞赛试题及答案

广东数学竞赛试题及答案一、选择题（每题3分，共30分）1. 下列哪一项不是实数的属性？A. 有序性B. 可数性C. 完备性D. 连续性答案：B2. 若函数\( f(x) = 2x^2 + 3x - 5 \)，求\( f(-2) \)的值。

A. 1B. -1C. 3D. -3答案：D3. 已知三角形ABC的三边长分别为a, b, c，且a + b > c，a + c > b，b + c > a，根据三角形的不等式定理，下列哪个选项是正确的？A. a > cB. b > aC. c > bD. 无法确定答案：D4. 圆的半径为5，圆心到直线的距离为3，求圆与直线的位置关系。

A. 相切B. 相交C. 相离D. 无法确定答案：B5. 已知数列1, 1/2, 1/3, 1/4, ...，这个数列是：A. 等差数列B. 等比数列C. 几何数列D. 既不是等差数列也不是等比数列答案：D6. 一个正方体的体积为64，求其表面积。

A. 96B. 128C. 192D. 256答案：B7. 已知椭圆的长轴为2a，短轴为2b，且a > b，若椭圆的焦点在x轴上，求椭圆的方程。

A. \( \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \)B. \( \frac{x^2}{b^2} + \frac{y^2}{a^2} = 1 \)C. \( \frac{y^2}{a^2} + \frac{x^2}{b^2} = 1 \)D. \( \frac{y^2}{b^2} + \frac{x^2}{a^2} = 1 \)答案：A8. 一个函数的导数为\( f'(x) = 3x^2 - 2x + 1 \)，求原函数\( f(x) \)。

A. \( x^3 - x^2 + x + C \)B. \( x^3 - x^2 + x - 2 \)C. \( x^3 - x^2 + x + 1 \)D. \( x^3 - x^2 + x - C \)答案：A9. 已知函数\( g(x) = \sin(x) + \cos(x) \)，求\( g(\frac{\pi}{4}) \)的值。

广东大专高数试题及答案

广东大专高数试题及答案一、选择题（每题5分，共20分）1. 函数y=f(x)是奇函数，则下列说法正确的是（）。

A. f(-x) = f(x)B. f(-x) = -f(x)C. f(0) = 0D. f(x) = 0答案：B2. 极限lim(x→0) (sin x/x)的值为（）。

A. 0B. 1C. 2D. 3答案：B3. 曲线y=x^2在点(1,1)处的切线斜率为（）。

A. 2B. 1C. 0D. -1答案：A4. 函数y=ln(x)的导数是（）。

A. 1/xB. xC. ln(x)D. x^2答案：A二、填空题（每题5分，共20分）5. 设函数f(x)=x^3-3x+2，则f'(x)=________。

答案：3x^2-36. 已知函数y=x^2-4x+c，若其图像与x轴有交点，则c的取值范围为________。

答案：c≤47. 曲线y=x^3-6x^2+11x-6在点(2,0)处的切线方程为________。

答案：y=-3x+128. 函数y=e^x的不定积分是________。

答案：e^x + C三、解答题（每题15分，共30分）9. 求函数y=x^2-4x+c在区间[0,2]上的最小值。

解：函数y=x^2-4x+c的导数为y'=2x-4。

令y'=0，解得x=2。

当0≤x<2时，y'<0，函数单调递减；当x>2时，y'>0，函数单调递增。

因此，函数在x=2处取得最小值，即y_min=c-4。

10. 求极限lim(x→∞) (1+1/x)^x。

解：lim(x→∞) (1+1/x)^x = e^lim(x→∞) (x*ln(1+1/x))。

由于lim(x→∞) (x*ln(1+1/x)) = lim(x→∞) (ln(1+1/x)/1/x) =lim(x→∞) (1/(1+1/x) * 1/x) = 0，所以原极限的值为e^0=1。

第六届广东省大学生数学竞赛试卷高职高专类

学院班级姓名学号(密封线内不答题)…………………………………密………………………………………………………封……………………………………………线……………………………………第六届广东省大学生数学竞赛试卷（高职高专类）考试时间：2016年10月22日上午9：00-11：30题号一二三四五六七八九总分分数阅卷审核一、单项选择题(本大题共5小题，每小题3分，共15分)1．若数列{}n x 在(,)a a εε-+邻域内有无穷多个数列的点，其中ε为某一取定的正数，则()(A)数列{}n x 必有极限，但不一定等于a (B)数列{}n x 极限存在且一定等于a (C)数列{}n x 极限不一定存在(D)数列{}n x 一定不存在极限2.若极限a x f x x =→)(lim 0（常数），则函数)(x f 在点0x （）(A)有定义且a x f =)(0；(B)不能有定义；(C)有定义，但)(0x f 可以为任意数值；(D)可以有定义也可以没有定义3.设)100)(99()2)(1()(----=x x x x x x f ，则=')0(f （）(A)100(B)100！(C)-100(D)-100！4.设()f x 在(,)-∞+∞上的可积偶函数，则()()x c F x f t dt =⎰（）(A)是奇函数(B)是偶函数(C)既是奇函数又是偶函数(D)不一定是奇函数5．设()f x 在[,]a b 上连续，以下哪一项不能得出()f x 在[,]a b 上恒为零（）(A)2[()]0b a f x dx =⎰；(B)对任何在[,]a b 上可积函数()x φ都有()()0b a x f x dx φ=⎰;(C)()0b a xf x dx =⎰;(D)()0b a f x dx =⎰二、填空题（本大题共5小题，每小题3分，共15分）1.极限201sin lim sin x x x x→的值为.2.设()f x 的n 阶导数存在，且1()lim ()n n x f x f a x a-→∞=-，则1()n f a -=. 3.设()(1)arcsin 1x f x x x =-+，则(1)f '=.4.设()f x 在(,)-∞+∞上连续，且对任何(,)x ∈-∞+∞，有3()540xc f t dt x =+⎰，则c =_____.5.若2()f x x =，则11()f x dx -=⎰__________.三、（本题10分）求极限3sin 0lim(12)x x x →+四、（本题10分）设函数21()32x f x x x +=-+，求()(),(1).n f x n ≥．五、（本题10分）求不定积分1(ln ln ).ln x dx x+⎰六、（本题10分）求极限()22222lim .sin (2)x u t x e du dt x -→-⎰⎰七、（本题10分）已知0()lim 1x f x x→=，且()0,f x ''>证明().f x x ≥八、（本题10分）设函数()f x 在区间[0,1]上二阶可导，且(0)(1)1,(1)1,f f f '===证明存在(0,1),() 2.f ξξ''∈=使九、（本题10分）由直线0,1y x ==及抛物线2y x =围成一个曲边三角形，在曲边三角形2y x =上求一点，使曲边在该点处的切线与直线0y =及1x =所围成的三角形面积最大.。

大专数学竞赛试题及答案

大专数学竞赛试题及答案一、选择题（每题3分，共30分）1. 设函数\( f(x) = x^2 + 3x + 2 \)，求\( f(-2) \)的值。

A. -1B. 0C. 1D. 22. 已知\( a \)，\( b \)是方程\( x^2 - 5x + 6 = 0 \)的两个实根，求\( a + b \)的值。

A. 2B. 3C. 4D. 53. 一个圆的半径为5，求其面积。

A. 25πB. 50πC. 75πD. 100π4. 已知\( \sin(\alpha) = \frac{3}{5} \)，且\( \alpha \)在第一象限，求\( \cos(\alpha) \)的值。

A. \( \frac{4}{5} \)B. \( -\frac{4}{5} \)C. \( \frac{3}{5} \)D. \( -\frac{3}{5} \)5. 计算极限\( \lim_{x \to 0} \frac{\sin(x)}{x} \)。

A. 0B. 1C. 2D. 无穷大6. 已知\( \log_{2}8 = 3 \)，求\( 2^3 \)的值。

A. 4B. 8C. 16D. 327. 一个等差数列的首项为2，公差为3，求第5项的值。

A. 14B. 17C. 20D. 238. 求函数\( g(x) = 4x - x^2 \)在\( x = 2 \)处的导数值。

A. -4B. -2C. 0D. 29. 已知\( \frac{1}{a} + \frac{1}{b} = \frac{5}{6} \)，且\( a >0 \)，\( b > 0 \)，求\( a + b \)的最小值。

A. 2B. 3C. 4D. 510. 一个直角三角形的两条直角边分别为3和4，求斜边的长度。

A. 5B. 6C. 7D. 8二、填空题（每题2分，共20分）11. 若\( a^2 + b^2 = 13 \)，\( 2ab = 6 \)，则\( (a - b)^2 \)的值为______。

广东大学生数学竞赛考试大纲—经管类讨论稿

广东省大学生数学竞赛考试大纲—经管类（讨论稿）广东省大学生数学竞赛（经管类）竞赛内容为大学本科管理类专业高等数学（或微积分）课程的教学内容，具体内容如下：一、函数、极限、连续1、函数的概念及表示法。

2、函数的有界性、单调性、周期性和奇偶性。

3、反函数、分段函数、隐函数、复合函数，基本初等函数的性质及其图形，初等函数函数关系的建立。

4、数列极限与函数极限的定义及其性质。

5、函数的左极限和右极限。

6、无穷小量和无穷大量的概念及其关系，无穷小量的性质及无穷小量的比较。

7、极限的四则运算。

8、极限存在的两个准则：单调有界准则和夹逼准则，两个重要极限： 0sin lim 1x x x →= 1lim 1xx e x →∞⎛⎫+= ⎪⎝⎭。

9、函数连续的概念，函数间断点的类型，初等函数的连续性。

10、闭区间上连续函数的性质（有界性、最大值和最小值定理，介值定理)。

二、一元函数微分学1、导数和微分的概念，导数的几何意义和经济意义，平面曲线的切线与法线。

2、导数和微分的四则运算，基本初等函数的导数。

3、复合函数、反函数和隐函数的微分法，高阶导数，一阶微分形式的不变性。

4、罗尔（Rolle ）定理，拉格朗日( Lagrange)中值定理，泰勒定理．柯西（Cauchy)中值定理。

5、洛必达（L'Hospital ）法则。

6、函数单调性的判别，函数的极值，函数图形的凸性，拐点及渐近线，函数图形的描绘，函数的最大值与最小值。

三、一元函数积分学1、原函数和不定积分的概念，不定积分的基本性质，基本积分公式。

2、不定积分的换元积分法和分部积分法．3、定积分的概念和基本性质，定积分中值定理。

4、积分上限的函数及其导数，牛顿一莱布尼茨（Newton- Leibniz）公式。

5、定积分的换元积分法与分部积分法。

6、反常（广义）积分。

7、定积分的应用：用定积分计算平面图形的面积，旋转体的体积和函数的平均值，会利用定积分求解简单的经济应用问题。

大学生高等数学竞赛试题汇总及答案

前三届高数竞赛预赛试题（非数学类）（参加高等数学竞赛的同学最重要的是好好复习高等数学知识，适当看一些辅导书及相关题目，主要是一些各大高校的试题。

）2009-2010年第一届全国大学生数学竞赛预赛试卷一、填空题（每小题5分）1．计算=--++⎰⎰y x yx x yy x Dd d 1)1ln()(16/15，其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域.解:令v x u y x ==+,，则v u y v x -==,，v u v u y x d d d d 1110det d d =⎪⎪⎭⎫⎝⎛-=，⎰-=12d 1u uu （*）令u t -=1，则21t u -=dt 2d t u -=，42221t t u +-=，)1)(1()1(2t t t u u +-=-，2．设)(x f 是连续函数，且满足⎰--=2022d )(3)(x x f x x f ,则=)(x f ____________.解:令⎰=2d )(x x f A ，则23)(2--=A x x f ，A A x A x A 24)2(28d )23(202-=+-=--=⎰,解得34=A 。

因此3103)(2-=x x f 。

3．曲面2222-+=y x z 平行平面022=-+z y x 的切平面方程是__________. 解:因平面022=-+z y x 的法向量为)1,2,2(-，而曲面2222-+=y x z 在),(00y x 处的法向量为)1),,(),,((0000-y x z y x z y x ，故)1),,(),,((0000-y x z y x z y x 与)1,2,2(-平行，因此，由x z x =，y z y 2=知0000002),(2,),(2y y x z x y x z y x ====，即1,200==y x ，又5)1,2(),(00==z y x z ，于是曲面022=-+z y x 在)),(,,(0000y x z y x 处的切平面方程是0)5()1(2)2(2=---+-z y x ，即曲面2222-+=y x z 平行平面 022=-+z y x 的切平面方程是0122=--+z y x 。

历届全国大学生高等数学竞赛真题及答案非数学类.docx

）2009年第一届全国大学生数学竞赛预赛试卷一、填空题（每小题5分，共20分）1．计算=--++⎰⎰y x yx x yy x Dd d 1)1ln()(____________，其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域.解:令v x u y x ==+,，则v u y v x -==,，v u v u y x d d d d 1110det d d =⎪⎪⎭⎫⎝⎛-=，v u u v u u u y x y x x yy x D D d d 1ln ln d d 1)1ln()(⎰⎰⎰⎰--=--++⎰⎰⎰⎰----=---=10210d 1)ln (1ln d )d ln 1d 1ln (u u u u u u u u u u v v u uv u u u u u ⎰-=12d 1u uu （*）令u t -=1，则21t u -=dt 2d t u -=，42221t t u +-=，)1)(1()1(2t t t u u +-=-，⎰+--=0142d )21(2(*)tt t⎰+-=1042d )21(2t t t 151651322153=⎥⎦⎤⎢⎣⎡+-=t t t 2．设)(x f 是连续函数，且满足⎰--=2022d )(3)(x x f x x f , 则=)(x f ____________.解:令⎰=20d )(x x f A ，则23)(2--=A x x f ，A A x A x A 24)2(28d )23(202-=+-=--=⎰,解得34=A 。

因此3103)(2-=x x f 。

广东高职高考数学题分类汇总

广东省历年高职高考数学试题集合不等式部分一、选择题1、（1998）已知集合1|0x A x x -⎧⎫=>⎨⎬⎩⎭，{}11B x x =-<, 那么A B =（）A 、(),0-∞B 、()0,2C 、()(),01,-∞+∞D 、()1,2)2、(2000）不等式111≤-+x x的解集是（）A 、}0|{≤x xB 、{|01}x x ≤≤C 、{|1}x x ≤D 、{|01}x x x ≤>或3、设集合M={|15},{|36},x x N x x M N ≤≤=≤≤⋂=则（）A 、}53|{≤≤x xB 、}61|{≤≤x xC 、}31|{≤≤x xD 、}63|{≤≤x x4、（2002）“29x =”是“3x =”（）A ．充分条件B ．必要条件C ．充要条件D ．非充分条件也非必要条件5、（2002）已知a b >，那么b a 11>的充要条件是（）A ．022≠+b aB ．0a >C ．0b <D ．0ab <6．（2002）若不等式220x bx a -+<的解集为{}15x x <<则a =（）A ．5B ．6C ．10D ．127. （2003）若不等式2(6)0x m x +-<的解集为{}32x x -<<, m = （）A. 2B. －2C. －1D. 18.（2004）“6x =”是“236x =”的（）A. 充分条件B. 必要条C. 充要条件D. 等价条件9. （2004）若集合{}{}22(45)(6)05,1,5x x x x x c +--+==-, 则c =（）A.－5B. －8C. 5D. 610．（2004）若a b <，则11a b >等价于（）A. 0a >B. 0b <C. 0ab ≠D. 0ab >11. （2004）若a b >, 则（）A. 33a b >B. 22a b >C. lg lg a b >D. >12.（2005）设集合{}3,4,5,6,7A =, {}1,3,5,7,9B =, 则集合A B 的元素的个数为（）A. 1B. 2C. 3D. 413. （2005）“240b ac ->”是方程20(0)ax bx c a ++=≠有实数解的（）A. 充分而非必要条件B. 必要而非充分条件C. 充要条件D. 既非充分又非必要条件14.（2006）已知集合{}1,1,2A =-，{}220B x x x =-=，则A B =（）A. ∅B. {}2C. {}0,2D. {}1,0,1,2-15．（2006）若,a b 是任意实数，且a b >，则下列不等式成立的是（） A. 22a b > B. a b > C. lg()0a b -> D. 1122a b⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭16.（2007）已知集合{}0,1,2,3A =，{}11B x x =-<，则A B =（）A. {}0,1B. {}0,1,2C. {}2,3D. {}0,1,2,317、（2008）设集合{}1,1,2,3A =-，{}3B x x =<，则A B =（）A. ()1,1-B. {}1,1-C. {}1,1,2-D. {}1,1,2,3-18、（2008）x R ∈，“3x <”是“3x <”的（）A 、充要条件B 、充分条件C 、必要条件D 、既非充分也不必要条件19、（2008）若,,a b c 是实数，且a b >，则下列不等式正确的是（）A 、ac bc >B 、ac bc <C 、22ac bc >D 、22ac bc ≥ 20．（2009）设集合{}2,3,4,M =，{}2,4,5B =，则M N =（）A. {}2,3,4,5B. {}2,4C. {}3D. {}521．（2009）已知集合203x A x x ⎧+⎫=≥⎨⎬-⎩⎭，则A =（） A 、(],2-∞ B 、()3,+∞ C 、[)2,3- D 、[]2,3-22．（2009）若,,a b c 均为实数，则“a b >”是“a c b c +>+”的（）A 、充分条件B 、必要条件C 、充要条件D 、既非充分也非必要条件23.（2010）已知集合{}1,1,=-M ，{}1,3=-N ，则=M N （）A. {}1,1-B. {}1,3-C. {}1-D. {}1,1,3-24.不等式11-<x 的解集是（）A 、{}0<x xB 、{}02<<x xC 、{}2>x xD 、{}02<>x x x 或25.（2010）已知2()81=++f x x x在区间()0,+∞内的最小值是（） A 、5 B 、7 C 、9 D 、 1126.（2010）“2>a 且2>b ”是“4+>a b ”的（）A 、必要非充分条件B 、充分非必要条件C 、充要条件D 、非充分非必要条件 27.（2011）已知集合{}2M x x ==，{}3,1N =-，则M N =（）A. φB. {}3,2,1--C. {}3,1,2-D. {}3,2,1,2--28.（2011）不等式211x ≥+的解集是（） A 、{}11x x -<≤ B 、{}1x x ≤ C 、{}1x x >- D 、{}11x x x ≤>-或29.（2011）“7=x ”是“7≤x ”的（）A 、充分非必要条件B 、必要非充分条件C 、充要条件D 、既非充分也非必要条件30.（2012）已知集合{}1,3,5M =，{}1,2,5N =，则M N =（）A. {}1,3,5B. {}1,2,5C. {}1,2,3,5D. {}1,531.（2012）不等式312x -<的解集是（）A 、1,13⎛⎫- ⎪⎝⎭B 、1,13⎛⎫ ⎪⎝⎭C 、()1,3-D 、()1,3 32.（2012）“21x =”是“1x =”的（）A 、充分条件B 、必要条件C 、充要条件D 、既非充分也非必要条件33.（2013）已知集合{}1,1,=-M ，{}01,2N =，，则=M N （）A. {}0B. {}1C. {}0,1,2D. {}1,01,2-，34.（2013）若,a b 是任意实数，且a b >，则下列不等式正确的是（）A 、22a b >B 、1b a <C 、lg()0a b ->D 、22a b >35.（2013）在ΔABC 中，30A ︒∠>是1sin 2A >的（） A 、充分非必要条件 B 、充要条件C 、必要非充分条件D 、既非充分也非必要条件36. （2014）已知集合{}1,0,2-=M ，{}2,0,1-=N ，则=N M （）A 、{}0B 、{}1,2-C 、φD 、{}2,1,0,1,2--37. （2014）“()()021>+-x x ”是“021>+-x x ”的（） A 、充分非必要条件 B 、必要非充分条件C 、充分必要条件D 、非充分非必要条件二、填空题1.（1997）不等式|x+1|≤2的解集是2．（1998）不等式xx 211--＞1的解集是 3.（2000）函数1(4)(1)(0)y x x x =++>的最小值等于4.（2002）集合M 满足{}{}4,3,2,11⊆⊆M ，那么这样的不同集合M 共有个。

广东省六校联盟高考数学模拟试卷(理科)(a卷) Word版含解析

2016年广东省六校联盟高考数学模拟试卷（理科）（A卷）一、选择题：本大题共12个小题；每小题5分，共60分．在每小题给出的四个选项中，有且只有一项是符合题目要求的．1．如果复数（2+ai）i（a∈R）的实部与虚部互为相反数，则a的值等于（）A．﹣1 B．1 C．﹣2 D．22．下列命题中，是真命题的是（）A．∃x0∈R，e x0≤0B．∀x∈R，2x＞x2C．已知a，b为实数，则a+b=0的充要条件是=﹣1D．已知a，b为实数，则a＞1，b＞1是ab＞1的充分条件3．在等比数列{a n}中，首项a1=1，且4a3，2a4，a5成等差数列，若数列{a n}的前n项之积为T n，则T10的值为（）A．29﹣1 B．236C．210﹣1 D．2454．在平面直角坐标系中，不等式组表示的平面区域的面积是（）A． B．8 C． D．45．定义行列式运算：，将函数的图象向左平移m 个单位（m＞0），若所得图象对应的函数为偶函数，则m的最小值是（）A． B．C．D．6．已知边长为的菱形ABCD中，∠BAD=60°，沿对角线BD折成二面角A﹣BD﹣C 为120°的四面体ABCD，则四面体的外接球的表面积为（）A．25πB．26πC．27πD．28π7．利用计算机在区间（0，1）上产生两个随机数a和b，则方程有实根的概率为（）A．B．C．D．8．把1，2，3，…，6这六个数随机地排成一列组成一个数列，要求该数列恰先增后减，则这样的数列共有多少个？（）A．31 B．30 C．28 D．329．某程序框图如图所示，现将输出（x，y）值依次记为：（x1，y1），（x2，y2），…，（x n，y n）…若程序运行中输出的一个数组是（x，﹣10）则数组中的x=（）A．32 B．24 C．18 D．1610．某几何体的三视图如图所示，则该几何体的体积为（）A．B．C．D．11．已知F1、F2分别是双曲线C：的左、右焦点，过点F2作渐近线的垂线，垂足为点A，若，且点B在以F1为圆心，|OF1|为半径的圆内，则C的离心率取值范围为（）A．B．（2，+∞）C．（1，2）D．12．已知函数f（x）=e x（x﹣ae x）恰有两个极值点x1，x2（x1＜x2），则a的取值范围是（）A．（0，）B．（1，3）C．（，3）D．（，1）二、填空题：本大题共4小题，每小题5分，满分20分．13．已知n为正偶数，且（x2﹣）n的展开式中第4项的二项式系数最大，则第4项的系数是______（用数字作答）14．某校在一次期末考试中，全校学生的数学成绩都介于60分到140分之间（满分150分），为了估计该校学生的数学考试情况，从该校2000名学生的数学成绩中随机抽取50名学生的数学成绩，将统计结果按如下方式分成八组：第一组[60，70），第二组[70，80），…，第八组[130，140]．如图是按照上述分组得到的频率分布直方图的一部分．估计该校2000名学生这次考试的数学成绩的平均分为______．15．已知AD是△ABC的中线，=λ+μ（λ，μ∈R），∠A=120°，•=﹣2，则||的最小值是______．16．已知正整数a1，a2，a3，…，a18满足a1＜a2＜…＜a18，a1+a2+a3+…+a18=2011，则a9的最大值为______．三、解答题：本大题6小题，满分60分．解答须写出文字说明、证明过程和演算步骤．17．已知．（Ⅰ）求函数f（x）的单调递增区间；（Ⅱ）在锐角△ABC的三个角A，B，C所对的边分别为a，b，c，且f（C）=1，求的取值范围．18．某课题组对春晚参加“咻一咻”抢红包活动的同学进行调查，按照使用手机系统不同（安卓系统和IOS系统）分别随机抽取5名同学进行问卷调查，发现他们咻得红包总金额数如（）如果认为咻得红包总金额超过元为咻得多，否则为咻得少，请判断手机系统与咻得红包总金额的多少是否有关？（2）要从5名使用安卓系统的同学中随机选出2名参加一项活动，以X表示选中的同学中咻得红包总金额超过6元的人数，求随机变量X的分布列及数学期望E（X）．独立性检验统计量，其中n=a+b+c+d．19．如图1，直角梯形ABCD中，∠ABC=90°，AB=BC=2AD=4，点E、F分别是AB、CD 的中点，点G在EF上，沿EF将梯形AEFD翻折，使平面AEFD⊥平面EBCF，如图2．（Ⅰ）当AG+GC最小时，求证：BD⊥CG；（Ⅱ）当2V B﹣ADGE =V D﹣GBCF时，求二面角D﹣BG﹣C平面角的余弦值．20．已知点C为圆（x+1）2+y2=8的圆心，P是圆上的动点，点Q在圆的半径CP上，且有点A（1，0）和AP上的点M，满足•=0，=2．（Ⅰ）当点P在圆上运动时，求点Q的轨迹方程；（Ⅱ）若斜率为k的直线l与圆x2+y2=1相切，直线l与（Ⅰ）中所求点Q的轨迹交于不同的两点F，H，O是坐标原点，且≤•≤时，求k的取值范围．21．已知函数f（x）=x2﹣（a+2）x+alnx，其中常数a＞0．（Ⅰ）当a＞2时，求函数f（x）的单调递增区间；（Ⅱ）设定义在D上的函数y=h（x）在点P（x0，h（x0））处的切线方程为l：y=g（x），若＞0在D内恒成立，则称P为函数y=h（x）的“类对称点”．当a=4时，试问y=f（x）是否存在“类对称点”，若存在，请至少求出一个“类对称点”的横坐标；若不存在，请说明理由．[选修4-1：几何证明选讲]22．如图，已知圆O是△ABC的外接圆，AB=BC，AD是BC边上的高，AE是圆O的直径．过点C作圆O的切线交BA的延长线于点F．（Ⅰ）求证：AC•BC=AD•AE；（Ⅱ）若AF=2，CF=2，求AE的长．[选修4-4：坐标系与参数方程]23．已知曲线C的极坐标方程为ρ=2cosθ﹣4sinθ．以极点为原点，极轴为x轴的正半轴，建立平面直角坐标系，直线l的参数方程为（t为参数）．（Ⅰ）判断直线l与曲线C的位置关系，并说明理由；（Ⅱ）若直线l和曲线C相交于A，B两点，且|AB|=3，求直线l的斜率．[选修4-5：不等式选讲]24．已知函数f（x）=|x﹣2|，g（x）=m|x|﹣2，（m∈R）．（1）解关于x的不等式f（x）＞3；（2若不等式f（x）≥g（x）对任意x∈R恒成立，求m的取值范围．2016年广东省六校联盟高考数学模拟试卷（理科）（A卷）参考答案与试题解析一、选择题：本大题共12个小题；每小题5分，共60分．在每小题给出的四个选项中，有且只有一项是符合题目要求的．1．如果复数（2+ai）i（a∈R）的实部与虚部互为相反数，则a的值等于（）A．﹣1 B．1 C．﹣2 D．2【考点】复数的代数表示法及其几何意义．【分析】化简复数为a+bi （a、b∈R）的形式，实部与虚部互为相反数即可求值．【解答】解：由复数（2+ai）i（a∈R）的实部与虚部互为相反数，可得﹣a+2=0．故选D．2．下列命题中，是真命题的是（）A．∃x0∈R，e x0≤0B．∀x∈R，2x＞x2C．已知a，b为实数，则a+b=0的充要条件是=﹣1D．已知a，b为实数，则a＞1，b＞1是ab＞1的充分条件【考点】命题的真假判断与应用．【分析】A．根据特称命题的定义进行判断B．根据全称命题的定义进行判断C．根据充分条件和必要条件的定义进行判断D．根据充分条件的定义进行判断．【解答】解：A．∵∀x∈R，e x＞0，∴∃x0∈R，e x0≤0为假命题，B．当x=2时，2x=x2，则∀x∈R，2x＞x2不成立，故B为假命题．C．当a=b=0时，满足a+b=0但=﹣1不成立，故C为假命题，D．当a＞1，b＞1时，ab＞1成立，即a＞1，b＞1是ab＞1的充分条件，故D为真命题，故选：D3．在等比数列{a n}中，首项a1=1，且4a3，2a4，a5成等差数列，若数列{a n}的前n项之积为T n，则T10的值为（）A．29﹣1 B．236C．210﹣1 D．245【考点】等差数列与等比数列的综合．【分析】由等比数列的通项公式及等差数列的性质，求出公比q，从而得到a n=2n﹣1，由此能求出数列{a n}的前10项之积为T10．【解答】解：在等比数列{a n}中，首项a1=1，且4a3，2a4，a5成等差数列，∴4a4=4a3+a5，∴4q3=4q2+q4，解得q=2，∴a n=2n﹣1，∵数列{a n}的前n项之积为T n，∴T10=20×2×22×24×25×26×27×28×29=20+1+2+3+4+5+6+7+8+9=245．故选：D．4．在平面直角坐标系中，不等式组表示的平面区域的面积是（）A． B．8 C． D．4【考点】二元一次不等式（组）与平面区域．【分析】转化不等式为不等式组，画出约束条件表示的可行域，结合图形求解图形的面积．【解答】解：因为不等式|y﹣2|≤x≤2等价于，它的可行域为：可行域是三角形，由得交点A（2，4），C的坐标由解得，为（2，0），B的坐标（0，2），可行域三角形的面积为：×4×2=4．故选：D．5．定义行列式运算：，将函数的图象向左平移m 个单位（m＞0），若所得图象对应的函数为偶函数，则m的最小值是（）A． B．C．D．【考点】二阶行列式的定义；函数的图象与图象变化．【分析】先用行列式展开法则求出f（x），再由函数的平移公式能够得到f（x+m），然后由偶函数的性质求出m的最小值．【解答】解：f（x）==sinx﹣cosx=2sin（x﹣），图象向左平移m（m＞0）个单位，得f（x+m）=2sin（x+m﹣），由m﹣=+kπ，k∈Z，则当m取得最小值时，函数为偶函数．故选A．6．已知边长为的菱形ABCD中，∠BAD=60°，沿对角线BD折成二面角A﹣BD﹣C为120°的四面体ABCD，则四面体的外接球的表面积为（）A．25πB．26πC．27πD．28π【考点】球的体积和表面积；球内接多面体．【分析】正确作出图形，利用勾股定理建立方程，求出四面体的外接球的半径，即可求出四面体的外接球的表面积．【解答】解：如图所示，∠AFC=120°，∠AFE=60°，AF==3，∴AE=，EF=设OO′=x，则∵O′B=2，O′F=1，∴由勾股定理可得R2=x2+4=（+1）2+（﹣x）2，∴R2=7，∴四面体的外接球的表面积为4πR2=28π，故选：D．7．利用计算机在区间（0，1）上产生两个随机数a和b，则方程有实根的概率为（）A．B．C．D．【考点】几何概型．【分析】由题意知本题是一个几何概型，只要写出试验发生所包含的所有事件和满足条件的事件对应的线段长度即可，把方程整理成一元二次方程，通过一元二次方程的判别式来解．【解答】解：由题意知本题是一个几何概型，化为x2+2ax+b=0，方程有实根，△≥0即4a2﹣4b≥0∴b≤a2∴方程有实根的概率为∫01a2d a==．故选B．8．把1，2，3，…，6这六个数随机地排成一列组成一个数列，要求该数列恰先增后减，则这样的数列共有多少个？（）A．31 B．30 C．28 D．32【考点】计数原理的应用．【分析】该数列恰先增后减，则数字6一定是分界点，且前面的顺序和后面的顺序都只有一种，根据6前面的数字的个数多少分类即可．【解答】解：该数列恰先增后减，则数字6一定是分界点，且前面的顺序和后面的顺序都只有一种，当6前有1个数字时，有C51=5种，当6前有2个数字时，有C52=10种，当6前有3个数字时，有C53=10种，当6前有4个数字时，有C54=5种，根据分类计数原理，共有5+10+10+5=30种，故选：B．9．某程序框图如图所示，现将输出（x，y）值依次记为：（x1，y1），（x2，y2），…，（x n，y n）…若程序运行中输出的一个数组是（x，﹣10）则数组中的x=（）A．32 B．24 C．18 D．16【考点】程序框图．【分析】根据流程图所示的顺序，逐框分析程序中各变量、各语句的作用可知：该程序的作用是依次输出的（x，y）值，其中每一组有序实数对中，x是每次变为原来的3倍，y每次减小2．【解答】解：程序在运行过程中各变量值如下表：输出结果n x y循环前：1 1 0第1次：（1，0）3 2﹣2第2次：（2，﹣2）5 4﹣4第3次：（4，﹣4）7 8﹣6第4次：（8，﹣6）9 16﹣8第5次：（16，﹣8）11 32﹣10第6次：（32，﹣10）则数组中的x=32故选：A．10．某几何体的三视图如图所示，则该几何体的体积为（）A．B．C．D．【考点】由三视图求面积、体积．【分析】由已知中的三视图，可得该几何体是由一个三棱柱挖掉一个三棱锥，所得的组合体，进而可得答案．【解答】解：由已知中的三视图，可得该几何体是：一个三棱柱挖掉一个三棱锥，所得的组合体，其直观图如下图所示：∵三棱柱的体积V==2，挖去的棱锥体积V==，故该几何体的体积为2﹣=，故选：C11．已知F1、F2分别是双曲线C：的左、右焦点，过点F2作渐近线的垂线，垂足为点A，若，且点B在以F1为圆心，|OF1|为半径的圆内，则C的离心率取值范围为（）A．B．（2，+∞）C．（1，2）D．【考点】双曲线的简单性质．【分析】设F1（﹣c，0），F2（c，0），一条渐近线方程为y=x，求得与渐近线垂直的直线方程，联立方程解得A的坐标，再由向量共线的坐标表示可得B的坐标，运用点在圆内的条件可得|BF1|＜c，化简整理，运用离心率公式即可得到所求范围．【解答】解：设F1（﹣c，0），F2（c，0），一条渐近线方程为y=x，过点F2与渐近线垂直的直线方程为y=﹣（x﹣c），联立，解得A（，），设B（m，n），由，可得（﹣c，）=2（m﹣，n﹣），可得m=﹣，n=，即B （﹣，），由点B 在以F 1为圆心，|OF 1|为半径的圆内，可得|BF 1|＜c ，可得（﹣+c ）2+（）2＜c 2，化为+a 2＜c 2，即为+a 2＜c 2，即c 2＞5a 2，由e=，可得e ＞．故选：A ．12．已知函数f （x ）=e x （x ﹣ae x ）恰有两个极值点x 1，x 2（x 1＜x 2），则a 的取值范围是（）A ．（0，）B ．（1，3）C ．（，3）D ．（，1）【考点】利用导数研究函数的极值．【分析】根据题意，对函数f （x ）求导数，得出导数f ′（x ）=0由两不等实根，转化为两函数有两个交点的问题，结合图象即可得出a 的取值范围．【解答】解：∵函数f （x ）=e x （x ﹣ae x ）， ∴f ′（x ）=（x +1﹣2a •e x ）e x ，由于函数f （x ）的两个极值点为x 1，x 2，即x 1，x 2是方程f ′（x ）=0的两不等实根，即方程x +1﹣2ae x =0，且a ≠0，∴=e x ；设y 1=（a ≠0），y 2=e x ，在同一坐标系内画出这两个函数的图象，如图所示；要使这两个函数有2个不同的交点，应满足，解得0＜a ＜，所以a 的取值范围是（0，）．故选：A ．二、填空题：本大题共4小题，每小题5分，满分20分．13．已知n为正偶数，且（x2﹣）n的展开式中第4项的二项式系数最大，则第4项的系数是（用数字作答）【考点】二项式定理．【分析】利用二项式系数的性质：展开式中中间项的二项式系数最大求出n；利用二项展开式的通项公式求出通项，令通项中的r=3求出第4项的系数．【解答】解：∵展开式中中间项的二项式系数最大∴展开式共7项∴n=6展开式的通项为当r=3时是第4项所以第4项的系数是故答案为14．某校在一次期末考试中，全校学生的数学成绩都介于60分到140分之间（满分150分），为了估计该校学生的数学考试情况，从该校2000名学生的数学成绩中随机抽取50名学生的数学成绩，将统计结果按如下方式分成八组：第一组[60，70），第二组[70，80），…，第八组[130，140]．如图是按照上述分组得到的频率分布直方图的一部分．估计该校2000名学生这次考试的数学成绩的平均分为97．【考点】频率分布直方图．【分析】根据频率分布直方图，求出成绩在[120，130）的频率以及平均成绩；【解答】根据频率分布直方图，得：成绩在[120，130）的频率为1﹣（0.004×10+0.012×10+0.016×10+0.03×10+0.02×10+0.006×10+0.004×10）=1﹣0.92=0.08；所以估计该校全体学生的数学平均成绩为65×0.04+75×0.12+85×0.16+95×0.3+105×0.2+115×0.06+125×0.08+135×0.04=97，所以该校的数学平均成绩为97；故答案为：9715．已知AD是△ABC的中线，=λ+μ（λ，μ∈R），∠A=120°，•=﹣2，则||的最小值是1．【考点】平面向量数量积的运算；向量的线性运算性质及几何意义．【分析】运用向量的数量积的定义和中点的向量表示形式，及向量的平方即为模的平方，结合重要不等式即可得到最小值．【解答】解：设AC=b，AB=c，又∠A=120°，•=﹣2，则bccos120°=﹣2，即有bc=4，由AD是△ABC的中线，则有=（+），即有||2=（++2）=（b2+c2﹣4）≥（2bc﹣4）=×（8﹣4）=1．当且仅当b=c时||的最小值是为1，故答案为：1．16．已知正整数a1，a2，a3，…，a18满足a1＜a2＜…＜a18，a1+a2+a3+…+a18=2011，则a9的最大值为193．【考点】数列的求和．【分析】由于正整数a1，a2，a3，…，a18满足a1＜a2＜…＜a18，a1+a2+a3+…+a18=2011，要求a9的最大值，必须要求a1到a8尽可能的取得越小越好，a10到a18与a9越接近越好．即可得出．【解答】解：由于正整数a1，a2，a3，…，a18满足a1＜a2＜…＜a18，a1+a2+a3+…+a18=2011，要求a9的最大值，必须要求a1到a8尽可能的取得越小越好，a10到a18与a9越接近越好．当1≤n≤8时，取a n=n，则a1+…+a8==36．当9≤n≤18时，不妨取a n=a9+n﹣9，则10a9+≤2011﹣36．解得a9≤193．因此a9的最大值为193．故答案为：193．三、解答题：本大题6小题，满分60分．解答须写出文字说明、证明过程和演算步骤．17．已知．（Ⅰ）求函数f（x）的单调递增区间；（Ⅱ）在锐角△ABC的三个角A，B，C所对的边分别为a，b，c，且f（C）=1，求的取值范围．【考点】余弦定理；三角函数中的恒等变换应用；正弦定理．【分析】（I）由三角函数公式化简可得f（x）=+sin（2x+），解可得单调递增区间；（II）可得，由余弦定理得表达式，由锐角三角形可得再由正弦定理得的范围，由函数的值域可得．【解答】解：（I）由三角函数公式化简可得：f（x）=sin2x+（1+cos2x）=+sin（2x+），由可得∴函数f（x）的单调递增区间为；（II）∵f（C）=+sin（2x+）=1，∴sin（2x+）=，∴或，k∈Z，∴结合三角形内角的范围可，由余弦定理得c2=a2+b2﹣ab，∴，∵△ABC为锐角三角形，∴，∴由正弦定理得∴18．某课题组对春晚参加“咻一咻”抢红包活动的同学进行调查，按照使用手机系统不同（安卓系统和IOS系统）分别随机抽取5名同学进行问卷调查，发现他们咻得红包总金额数如咻得红包总金额的多少是否有关？（2）要从5名使用安卓系统的同学中随机选出2名参加一项活动，以X表示选中的同学中咻得红包总金额超过6元的人数，求随机变量X的分布列及数学期望E（X）．独立性检验统计量，其中n=a+b+c+d．【考点】独立性检验的应用；离散型随机变量及其分布列；离散型随机变量的期望与方差．【分析】（1）根据题意列出2×2列联表，根据2×2列联表，代入求临界值的公式，求出观测值，利用观测值同临界值表进行比较，K2=0.4＜2.706，可得到没有足够的理由认为手机系统与咻得红包总金额的多少有关；（2）由题意求得X的取值0，1，2，运用排列组合的知识，可得各自的概率，求得X的分布列，由期望公式计算即可得到（X）．；122K2==0.4＜2.706，所以没有足够的理由认为手机系统与咻得红包总金额的多少有关．（2）随机变量X的所有可能取值为0，1，2，P（X=0）==；P（X=1）==；P（X=2）==X∴数学期望E（X），E（X）=0×+1×+2×=0.8．19．如图1，直角梯形ABCD中，∠ABC=90°，AB=BC=2AD=4，点E、F分别是AB、CD 的中点，点G在EF上，沿EF将梯形AEFD翻折，使平面AEFD⊥平面EBCF，如图2．（Ⅰ）当AG+GC最小时，求证：BD⊥CG；（Ⅱ）当2V B ﹣ADGE =V D ﹣GBCF 时，求二面角D ﹣BG ﹣C 平面角的余弦值．【考点】与二面角有关的立体几何综合题；平面与平面垂直的性质．【分析】（Ⅰ）由已知条件推导出AE ⊥EF ，AE ⊥BE ，BE ⊥EF ，建立空间坐标系E ﹣xyz ，利用向量法能求出BD ⊥CG ．（Ⅱ）法一：设EG=k ，由AD ∥平面EFCB ，得到点D 到平面EFCB 的距离为即为点A 到平面EFCB 的距离．分别求出平面DBG 的法向量和面BCG 的一个法向量，利用向量法能求出二面角平面角的余弦值．（Ⅱ）法二：由已知条件指法训练出EG=1，过点D 作DH ⊥EF ，垂足H ，过点H 作BG 延长线的垂线垂足O ，连接OD ．由已知条件推导出∠DOH 就是所求的二面角D ﹣BG ﹣C 的平面角，由此能求出此二面角平面角的余弦值．【解答】（Ⅰ）证明：∵点E 、F 分别是AB 、CD 的中点， ∴EF ∥BC ，又∠ABC=90°，∴AE ⊥EF ， ∵平面AEFD ⊥平面EBCF ，∴AE ⊥平面EBCF ，AE ⊥EF ，AE ⊥BE ，又BE ⊥EF ，如图建立空间坐标系E ﹣xyz ．…翻折前，连结AC 交EF 于点G ，此时点G 使得AG +GC 最小．EG=BC=2，又∵EA=EB=2．则A （0，0，2），B （2，0，0），C （2，4，0）， D （0，2，2），E （0，0，0），G （0，2，0），∴=（﹣2，2，2），=（﹣2，﹣2，0）∴=（﹣2，2，2）（﹣2，﹣2，0）=0，∴BD ⊥CG ．…（Ⅱ）解法一：设EG=k ，∵AD ∥平面EFCB ，∴点D 到平面EFCB 的距离为即为点A 到平面EFCB 的距离．∵ [（3﹣k ）+4]×2=7﹣k ，∴=，又=，∵2V B ﹣ADGE =V D ﹣GBCF ，∴=， ∴k=1即EG=1…设平面DBG 的法向量为，∵G （0，1，0），∴，=（﹣2，2，2），则，即取x=1，则y=2，z=﹣1，∴…面BCG 的一个法向量为则cos＜＞=…由于所求二面角D﹣BF﹣C的平面角为锐角，所以此二面角平面角的余弦值为…（Ⅱ）解法二：由解法一得EG=1，过点D作DH⊥EF，垂足H，过点H作BG延长线的垂线垂足O，连接OD．∵平面AEFD⊥平面EBCF，∴DH⊥平面EBCF，∴OD⊥OB，∴∠DOH就是所求的二面角D﹣BG﹣C的平面角．…由于HG=1，在△OHG中，又DH=2，在△DOH中…∴此二面角平面角的余弦值为．…20．已知点C为圆（x+1）2+y2=8的圆心，P是圆上的动点，点Q在圆的半径CP上，且有点A（1，0）和AP上的点M，满足•=0，=2．（Ⅰ）当点P在圆上运动时，求点Q的轨迹方程；（Ⅱ）若斜率为k的直线l与圆x2+y2=1相切，直线l与（Ⅰ）中所求点Q的轨迹交于不同的两点F，H，O是坐标原点，且≤•≤时，求k的取值范围．【考点】椭圆的简单性质．【分析】（I）利用线段的垂直平分线的性质、椭圆的定义即可得出．（II）设直线l：y=kx+b，F（x1，y1），H（x2，y2）直线l与圆x2+y2=1相切，可得b2=k2+1．直线方程与椭圆方程联立可得：（1+2k2）x2+4kbx+2b2﹣2=0，△＞0，可得k≠0，再利用数量积运算性质、根与系数的关系及其≤•≤，解出即可得出．【解答】解：（I）由题意知MQ中线段AP的垂直平分线，∴，∴点Q的轨迹是以点C，A为焦点，焦距为2，长轴为的椭圆，，故点Q的轨迹方程是．（II）设直线l：y=kx+b，F（x1，y1），H（x2，y2）直线l与圆x2+y2=1相切联立，（1+2k2）x2+4kbx+2b2﹣2=0，△=16k2b2﹣4（1+2k2）2（b2﹣1）=8（2k2﹣b2+1）=8k2＞0，可得k≠0，∴，===，∴为所求．21．已知函数f（x）=x2﹣（a+2）x+alnx，其中常数a＞0．（Ⅰ）当a＞2时，求函数f（x）的单调递增区间；（Ⅱ）设定义在D上的函数y=h（x）在点P（x0，h（x0））处的切线方程为l：y=g（x），若＞0在D内恒成立，则称P为函数y=h（x）的“类对称点”．当a=4时，试问y=f（x）是否存在“类对称点”，若存在，请至少求出一个“类对称点”的横坐标；若不存在，请说明理由．【考点】利用导数研究函数的单调性；利用导数求闭区间上函数的最值．【分析】（Ⅰ）求出函数的导数，结合a的范围求出函数的单调区间即可；（Ⅱ）法一：a=4时，求出f（x）的导数，得到切线方程根据新定义问题等价于当0＜x＜x0时，f（x）＜g（x），结合函数的单调性求出即可；法二：猜想y=f（x）存在“类对称点”，其中一个“类对称点”的横坐标为，然后加以证明即可．【解答】解：（Ⅰ）函数f（x）的定义域为（0，+∞），∵，∴…∵a＞2，∴，令f′（x）＞0，即，∵x＞0，∴0＜x＜1或，…所以函数f（x）的单调递增区间是（0，1），…（Ⅱ）解法一：当a=4时，所以在点P处的切线方程为…若函数存在“类对称点”P（x0，f（x0）），则等价于当0＜x＜x0时，f（x）＜g（x），当x＞x0时，f（x）＞g（x）恒成立．…①当0＜x＜x0时，f（x）＜g（x）恒成立，等价于恒成立，即当0＜x＜x0时，恒成立，令，则φ（x0）=0，…要使φ（x0）＜0在0＜x＜x0恒成立，只要φ（x）在（0，x0）单调递增即可．又∵，…∴，即．…②当x＞x0时，f（x）＞g（x）恒成立时，．…∴．…所以y=f（x）存在“类对称点”，其中一个“类对称点”的横坐标为．…（Ⅱ）解法二：猜想y=f（x）存在“类对称点”，其中一个“类对称点”的横坐标为．…下面加以证明：当时，…①当时，f（x）＜g（x）恒成立，等价于恒成立，令…∵，∴函数φ（x）在上单调递增，从而当时，恒成立，即当时，f（x）＜g（x）恒成立．…②同理当时，f（x）＞g（x）恒成立．…综上知y=f（x）存在“类对称点”，其中一个“类对称点”的横坐标为．…[选修4-1：几何证明选讲]22．如图，已知圆O是△ABC的外接圆，AB=BC，AD是BC边上的高，AE是圆O的直径．过点C作圆O的切线交BA的延长线于点F．（Ⅰ）求证：AC•BC=AD•AE；（Ⅱ）若AF=2，CF=2，求AE的长．【考点】与圆有关的比例线段．【分析】（I）如图所示，连接BE．由于AE是⊙O的直径，可得∠ABE=90°．利用∠E与∠ACB都是所对的圆周角，可得∠E=∠ACB．进而得到△ABE∽△ADC，即可得到．（II）利用切割线定理可得CF2=AF•BF，可得BF．再利用△AFC∽△CFB，可得AF：FC=AC：BC，进而根据sin∠ACD=sin∠AEB，AE=，即可得出答案．【解答】证明：（I）如图所示，连接BE．∵AE是⊙O的直径，∴∠ABE=90°．又∠E与∠ACB都是所对的圆周角，∴∠E=∠ACB．∵AD⊥BC，∠ADC=90°．∴△ABE∽△ADC，∴AB：AD=AE：AC，∴AB•AC=AD•AE．又AB=BC，∴BC•AC=AD•AE．解：（II）∵CF是⊙O的切线，∴CF2=AF•BF，∵AF=2，CF=2，∴（2）2=2BF，解得BF=4．∴AB=BF﹣AF=2．∵∠ACF=∠FBC，∠CFB=∠AFC，∴△AFC∽△CFB，∴AF：FC=AC：BC，∴AC==．∴cos∠ACD=，∴sin∠ACD==sin∠AEB，∴AE==[选修4-4：坐标系与参数方程]23．已知曲线C的极坐标方程为ρ=2cosθ﹣4sinθ．以极点为原点，极轴为x轴的正半轴，建立平面直角坐标系，直线l的参数方程为（t为参数）．（Ⅰ）判断直线l与曲线C的位置关系，并说明理由；（Ⅱ）若直线l和曲线C相交于A，B两点，且|AB|=3，求直线l的斜率．【考点】简单曲线的极坐标方程；直线与圆的位置关系；参数方程化成普通方程．【分析】（I）利用可把曲线C的极坐标方程化为直角坐标方程，可得圆心、半径，由于直线l过点（1，﹣1），求出该点到圆心的距离，与半径半径即可判断出位置关系；（II）利用点到直线的距离公式与弦长公式即可得出．【解答】解：（Ⅰ）∵曲线C的极坐标方程为ρ=2cosθ﹣4sinθ，∴ρ2=2ρcosθ﹣4ρsinθ，∴曲线C的直角坐标方程为x2+y2=2x﹣4y，即（x﹣1）2+（y+2）2=5，∵直线l过点（1，﹣1），且该点到圆心的距离为，∴直线l与曲线C相交．（Ⅱ）当直线l的斜率不存在时，直线l过圆心，|AB|=2≠3，因此直线l必有斜率，设其方程为y+1=k（x﹣1），即kx﹣y﹣k﹣1=0，圆心到直线l的距离=，解得k=±1，∴直线l的斜率为±1．[选修4-5：不等式选讲]24．已知函数f（x）=|x﹣2|，g（x）=m|x|﹣2，（m∈R）．（1）解关于x的不等式f（x）＞3；（2若不等式f（x）≥g（x）对任意x∈R恒成立，求m的取值范围．【考点】绝对值不等式的解法；函数恒成立问题．【分析】（1）由f（x）＞3，得|x﹣2|＞3，由此求得x的范围．（2）由题意可得|x﹣2|≥m|x|﹣2 恒成立．当x=0时，不等式显然成立；当x≠0时，问题等价于m≤对任意非零实数恒成立，再利用绝对值三角不等式求得m的范围．【解答】解：（1）由f（x）＞3，得|x﹣2|＞3，可得x﹣2＞3，或x﹣2＜﹣3．求得x＜﹣1，或x＞5，故原不等式的解集为{x|x＜﹣1，或x＞5}．（2）由f（x）≥g（x），得|x﹣2|≥m|x|﹣2 恒成立．当x=0时，不等式|x﹣2|≥m|x|﹣2 恒成立；当x≠0时，问题等价于m≤对任意非零实数恒成立．∵≥=1，∴m≤1，即m的取值范围是（﹣∞，1]．2016年9月20日。

历届全国大学生高等数学竞赛真题及答案非数学类.docx

因此3103)(2-=x x f 。