非周期信号的傅里叶变换MATLAB仿真实验
实验二 用matlab实现傅立叶变换

实验二用matlab实现傅立叶变换Step 1: 生成信号我们首先来生成一个信号,作为傅立叶变换的输入。
```matlab% 生成信号t = 0:0.001:1; % 时间范围f1 = 10; % 第一个频率f2 = 50; % 第二个频率y = sin(2*pi*f1*t) + sin(2*pi*f2*t); % 两个频率的正弦信号相加plot(t,y)title('信号')xlabel('时间 (秒)')```这段代码生成了一个时间范围为0到1秒的信号。
信号由两个频率分别为10Hz和50Hz的正弦波相加组成。
Step 2: 进行傅立叶变换接下来,我们可以使用Matlab中的fft函数来对信号进行傅立叶变换。
fft函数将信号从时域(时间)上转换到频域上。
```matlab% 进行傅立叶变换Y = fft(y);L = length(y); % 信号长度P2 = abs(Y/L); % 双边频谱P1 = P2(1:L/2+1); % 单边频谱P1(2:end-1) = 2*P1(2:end-1);% 绘制频域图figure()f = 1000*(0:(L/2))/L;plot(f,P1)title('单边频谱')xlabel('频率 (Hz)')```这段代码计算了信号的傅立叶变换,并绘制了信号的单边频谱。
Step 3: 解释结果在绘图结果中,我们可以看到两个明显的峰值。
这两个峰值对应着信号中两个正弦波的频率,也就是10Hz和50Hz。
傅立叶变换将信号从时域上转换到了频域上,这就使我们能够分析信号中不同频率的组成。
这在信号处理和分析中极为常见,傅立叶变换可以将信号转换到更加恰当的域中,使得我们能够更好地对信号进行分析和处理。
实验用MATLAB计算傅里叶变换

实验二 用MATLAB 计算傅立叶变换(2课时)一、实验目的1、掌握用MA TLAB 计算DTFT 及系统频率响应的方法。
2、掌握用MA TLAB 计算DFT 和IDFT 的方法。
3、掌握用DFT 计算圆周卷积和线性卷积的方法。
二、实验设备计算机一台,装有MATLAB 软件。
三、实验原理和基本操作1.用MA TLAB 计算DTFT对于序列x (n ),其离散时间傅立叶变换(DTFT )定义为:∑∞-∞=-=n n j e n x j X ωω)()( (1)序列的傅立叶变换(DTFT )在频域是连续的,并且以ω=2π为周期。
因此只需要知道jw X(e )的一个周期,即ω=[0,2π],或[-π,π]。
就可以分析序列的频谱。
用MA TLAB 计算DTFT ,必须在-π≤ω≤π范围内,把ω用很密的、长度很长的向量来近似,该向量中各个值可用下式表示: w=k*dw=k*K π2 (2) 其中:d ω=Kπ2 称为频率分辨率。
它表示把数字频率的范围2π均分成K 份后,每一份的大小,k 是表示频率序数的整数向量,简称为频序向量,它的取值可以有几种方法:通常在DTFT 中,频率取-π≤ω<л的范围,当K 为偶数时,取 k 12,,1,0,1,,12,2--+--=K K K 如果K 为奇数,则取 k 5.02,,1,0,1,,5.02--+-=K K 可以为奇偶两种情况综合出一个共同的确定频序向量k 的公式; k=12K -⎢⎥-⎢⎥⎣⎦ :12K -⎢⎥⎢⎥⎣⎦(3) 上式中⎢⎥⎣⎦表示向下取整。
在MA TLAB 中的向下取整函数为floor ,floor (x )的作用是把x 向下(向-∞方向)取整,所以与(3)式等价的MATLAB 语句为 k ))5.02(:)5.02((-+-=K K floor (4) 给定了输入序列(包括序列x 及其位置向量n ),又设定了频率分辨率d ω及频序向量k ,则DTFT 的计算式(1)可以用一个向量与矩阵相乘的运算来实现。
信号与系统课程设计应用MATLAB实现周期信号和非周期信号频谱仿真

沈阳大学其中,x1、x2、y2、x3、y3等符号均代表需要绘制的参数,它门可以是向量、矩阵、复数矩阵等,plot指令将根据不同的参数绘制不同的图形。
2.1.3多子图绘制指令---subplotMATLAB为方便用户进行仿真分析,设置了subplot指令,利用它可以在不同的子图下绘制图形,以进行对比分析。
subplot的基本指令格式如下:subplot(m,n,k)%作出(m n)幅子图中的第k幅图形subplot(‘position’,[left bottom width height])%在人工指定位置作出字图。
subplot(m,n,k)指令表示在图形窗口中产生(m n)幅子图,k代表当前绘制子图号。
如subplot(2,2,1)就是产生22幅子图,当前在子图1绘制图形。
2.1.4sinc序列Sinc函数是Matlab软件中经常使用的函数之一,sinc序列定义为:⎪⎩⎪⎨⎧=≠=1sin)(nnnnnSaππ这个信号可以利用Signal Processing Toolbox中的函数sinc来实现。
2.2连续时间信号系统是连续事物或各个部分的一个复杂的整体,有形或无形事物的组成体。
系统可以分为即时系统与动态系统;连续系统与离散系统;线性系统与非线形系统;样时变系统和非时变系统等等。
在连续时间系统中,如一个连续时间系统接收,输入信号x(t),并产生输出信号y(t)。
连续时间信号:在连续时间范围内定义的信号值,信号的幅值可以是连续数值,也可以是离散数值。
当信号幅值连续是,则称之为模拟信号。
沈阳大学2.3信号采样取样定理论述了在一定条件下,一个连续时间信号完全可以用该信号在等时间间隔上的瞬时值(或称样本值)表示,这些样本值包含了连续时间信号的全部信息,利用这些样本值可以恢复原信号。
可以说取样定理在连续时间信号与离散时间信号中架起了一座桥梁。
为了使数字信号的频谱能完全反应采样前连续非周期信号的频谱特性,以致不丢失有用信息,要求对于一般具有低通特性的连续时间信号,用于进行时间采样的采样频率必须大于或等于两倍原连续信号的最大频率,才不会致使采样后数字离散信号的频谱出现混叠失真,这就是有名的奈奎斯特采样定律,而是最高频率两倍的采样频率叫做"奈奎斯特频率"或"临界采样频率"。
连续非周期信号频谱分析及Matlab实现

《信号与系统A(1)》课程自学报告实施报告题目:连续非周期信号频谱分析及Matlab实现学号:姓名:任课教师:联系方式:第一部分. 理论自学内容阐述(一) 系统物理可实现性、佩利-维纳准则通过之前的学习我们知道,理想低通滤波器在物理上是不可能实现的,但是我们却可以做出传输特性接近理想特性的网络。
如下图是一个低通滤波器,其中 R =√RC图1-1 一个低通滤波网络则其网络传递函数为:(式1-1)引入符号 ωc =1√LC,则(式1-1)改为:其中)(1t v CRL )(2t v --++()()()R L LC C RL C R V V H ωωωωωωωωj 11 j 11j j 11j j j 212+-=+++==()()()ωϕωωωωωωωωωωωj 222e j 3j 33j 11j H H c c cc c c =⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛⋅+⎪⎪⎭⎫ ⎝⎛-=2+222=()()⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫ ⎝⎛+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-=2c c 2c 22c 1arctan 11j ωωωωωϕωωωωωH 求出其冲激响应为:h (t )=2ωc √3e−ωc 2sin (√3ωct )画出波形图及频谱图如下:图1-2 h(t)的波形图幅度特性 相位特性图1-3 幅度特性和相位特性可以看出这些曲线与理想低通滤波器有相似之处,但是同时也有不同之处。
这个电路的幅度特性不可能出现零值,冲激响应的起始时刻在t=0处。
那么究竟什么样的系统数学模型可以在物理上实现呢?就时间域特性而言,一个物理可实现网络的冲激响应h(t)在t<0时必须为0。
那么由于理想低通滤波器不是一个因果系统,所以它是不可能在物理上实现的。
从频域特性来看,|H(jw)|要满足平方可积条件。
佩利和维纳证明了对于幅度函数|H(jw)|物理可实现的必要条件是这就是佩利—维纳准则。
佩利—维纳准则只从幅度特性上提出要求,而在相位特性方面却没有给出约束,因此该准则只是系统物理可实现的必要条件,而不是充分条件。
报告模板_实验四2

实验四 连续时间系统的频域分析实验目的:1、深刻理解和掌握非周期信号的傅里叶变换及其计算方法;2、学会运用Matlab 编写Fourier 正反变换的仿真程序,并能利用这些程序对一些典型信号进行频谱分析。
实验原理:连续时间系统的频域分析法,也成为Fourier 变换分析法。
该方法基于信号频谱分析的概念,讨论信号作用于线性系统是在频域中求解响应的方法。
Fourier 分析法的关键是求取系统的频率响应。
Fourier 分析法主要用来分析系统的频率响应特性,或分析输出信号的频谱,也可以用来求解正弦信号作用下的正弦稳态响应。
Fourier 变换在信号分析中具有非常重要的意义,它主要是用来进行信号的频谱分析的。
Fourier 变换和其逆变换定义如下:连续时间Fourier 变换主要用来描述连续时间非周期信号的频谱。
任意非周期信号,如果满足狄里克利条件,那么,它可以被看作是由无穷多个不同频率(这些频率都是非常的接近)的周期复指数信号jwte 的线性组合构成的,每个频率所对应的周期复指数信号jwte称为频率分量,其相对幅度为对应频率的|)(|ωj X 之值,其相位为对应频率的)(ωj X 的相位。
)(ωj X 通常为复函数,可以按照复数的极坐标表示方法表示为:)(|)(|)(ωωωj X j e j X j X ∠=其中,|)(|ωj X 称为)(t x 的幅度谱,而)(ωj X ∠则称为)(t x 的相位谱。
Matlab 中符号数学工具箱提供了计算Fourier 正反变换的函数fourier 和ifourier ,其调用形式分别为:)(f fourier F =和)(F ifourier f =上述两个式子中,f 表示信号的时域表示式,F 表示信号的频域表示式。
可以通过定义一个符号对象,然后再写表示式来实现。
1()()2j t f t F j e d ωωωπ+∞-∞=⎰()()j t F j f t e d ωωω+∞--∞=⎰比如:先定义一个符号对象x ,命令为:syms x 然后再输入函数的符号表达式,如:f=sin(x);再根据)(f fourier F =,就能够求出结果为:F =i*pi*(-dirac(w-1)+dirac(w+1));其中,i 为虚数单位,dirac 为单位冲激函数,pi 为π。
傅里叶变换及带通滤波器仿真Matlab试验报告
傅里叶变换及带通滤波器仿真Matlab试验报告一.实验目的1.学习软件matlab的编辑语言、绘图、函数等功能的运用2.了解傅里叶级数的复数形式表示方波,并运用matlab绘出。
3.熟悉带通滤波器的工作原理,并用matlab仿真带通滤波器,绘出相应的图形,最后用pspice验证。
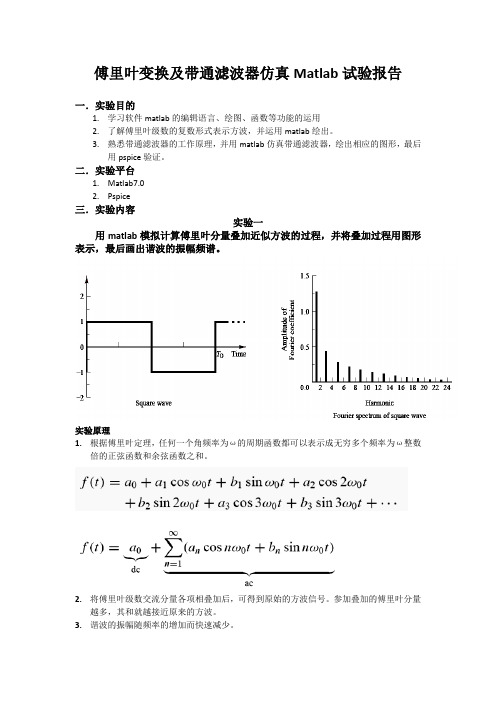
二.实验平台1. Matlab7.02. Pspice三.实验内容实验一用matlab模拟计算傅里叶分量叠加近似方波的过程,并将叠加过程用图形表示,最后画出谐波的振幅频谱。
实验原理1.根据傅里叶定理,任何一个角频率为ω的周期函数都可以表示成无穷多个频率为ω整数倍的正弦函数和余弦函数之和。
2.将傅里叶级数交流分量各项相叠加后,可得到原始的方波信号。
参加叠加的傅里叶分量越多,其和就越接近原来的方波。
3.谐波的振幅随频率的增加而快速减少。
实验步骤1.设计叠加傅里叶交流分量的算法。
2.打开Matlab,编辑程序实现算法。
3.运用Matlab的绘图函数将叠加过程用图形表示。
4.用Matlab绘出振幅频谱图。
实验程序代码%时间t从0到2,每隔0.001秒取一点t=0:0.001:pi;y=0;%通过循环绘出a小于等于5和a=16时的图像for a=1:6n=2*a-1y=y+4./(n*pi)*sin(n*pi*t);figure(1)subplot(2,3,a);plot(t,y,'-g')xlabel('Time');ylabel('F');ends=0;for b=1:16s=s+4./((b*2-1)*pi)*sin((b*2-1)*pi*t);endplot(t,s,'-g')%绘出振幅频谱图像figure(2)k=1:2:12;A=4./(k*pi);bar(k,A,0.1);实验结果傅里叶波形图振幅频谱图实验结果分析与结论1.根据傅里叶波形图可以看出,通过逐项叠加傅里叶级数交流分量可以形成原始方波。
连续非周期信号频谱分析及Matlab实现

连续⾮周期信号频谱分析及Matlab实现《信号与系统A(1)》课程⾃学报告实施报告题⽬:连续⾮周期信号频谱分析及Matlab实现学号:姓名:任课教师:联系⽅式:第⼀部分. 理论⾃学内容阐述(⼀)系统物理可实现性、佩利-维纳准则通过之前的学习我们知道,理想低通滤波器在物理上是不可能实现的,但是我们却可以做出传输特性接近理想特性的⽹络。
如下图是⼀个低通滤波器,其中 R =√RC图1-1 ⼀个低通滤波⽹络则其⽹络传递函数为:(式1-1)引⼊符号ωc =1√LC,则(式1-1)改为:其中)(1t v CRL )(2t v --++()()()R L LC C RL C R V V H ωωωωωωωωj 11 j 11j j 11j j j 212+-=+++==()()()ω?ωωωωωωωωωωωj 222e j 3j 33j 11j H H c c cc c c =+ + -=2+222=()()????--=???+ -=2c c 2c 22c 1arctan 11j ωωωωω?ωωωωωH求出其冲激响应为:h (t )=2ωc √3eωc 2sin (√3ωct )画出波形图及频谱图如下:图1-2 h(t)的波形图幅度特性相位特性图1-3 幅度特性和相位特性可以看出这些曲线与理想低通滤波器有相似之处,但是同时也有不同之处。
这个电路的幅度特性不可能出现零值,冲激响应的起始时刻在t=0处。
那么究竟什么样的系统数学模型可以在物理上实现呢?就时间域特性⽽⾔,⼀个物理可实现⽹络的冲激响应h(t)在t<0时必须为0。
那么由于理想低通滤波器不是⼀个因果系统,所以它是不可能在物理上实现的。
从频域特性来看,|H(jw)|要满⾜平⽅可积条件。
佩利和维纳证明了对于幅度函数|H(jw)|物理可实现的必要条件是这就是佩利—维纳准则。
佩利—维纳准则只从幅度特性上提出要求,⽽在相位特性⽅⾯却没有给出约束,因此该准则只是系统物理可实现的必要条件,⽽不是充分条件。
MAtlab-傅里叶变换-实验报告(同名21543)

MAtlab-傅里叶变换-实验报告(同名21543)陕西科技大学实验报告班级信工142 学号22 姓名何岩实验组别实验日期室温报告日期成绩报告内容:(目的和要求,原理,步骤,数据,计算,小结等)1.求信号的离散时间傅立叶变换并分析其周期性和对称性;给定正弦信号x(t)=2*cos(2*pi*10*t),fs=100HZ,求其DTFT。
(a)代码:f=10;T=1/f;w=-10:0.2:10;t1=0:0.0001:1;t2=0:0.01:1;n1=-2;n2=8;n0=0;n=n1:0.01:n2;x5=[n>=0.01];x1=2*cos(2*f*pi*t1);x2=2*cos(2*f*pi*t2);x3=(exp(-j).^(t2'*w));x4=x2*x3;subplot(2,2,1);plot(t1,x1);axis([0 1 1.1*min(x2) 1.1*max(x2)]);xlabel('x(n)');ylabel('x(n)');title('原信号x1');xlabel('t');ylabel('x1');subplot(2,2,3);stem(t2,x2);axis([0 1 1.1*min(x2) 1.1*max(x2)]);title('原信号采样结果x2');xlabel('t');ylabel('x2');subplot(2,2,2);stem(n,x5);第页axis([0 1 1.1*min(x5) 1.1*max(x5)]);xlabel('n');ylabel('x2');title('采样函数x2');subplot(2,2,4);stem(t2,x4);axis([0 1 -0.2+1.1*min(x4) 1.1*max(x4)]);xlabel('t');ylabel('x4');title('DTFT结果x4');(b)结果:2.用以下两个有限长序列来验证DTFT的线性、卷积和共轭特性;(n)x1(n)=[1 2 3 4 5 6 7 8 9 10 11 12];x2(n)=R10(1)线性:(a)代码:w=linspace(-8,8,10000);nx1=[0:11]; nx2=[0:9];x1=[1 2 3 4 5 6 7 8 9 10 11 12];x2=[1 1 1 1 1 1 1 1 1 1];第页x3=[x2,zeros(1,(length(x1)-length(x2)))];x4=2*x1+3*x3;X1=x1*exp(-j*nx1'*w);%频率特性X3=x3*exp(-j*nx1'*w);%频率特性X4=x4*exp(-j*nx1'*w);%频率特性subplot(5,3,1),stem(nx1,x1),axis([-1,13,0,15]);title('x1'), ylabel('x(n)');subplot(5,3,2),stem(nx2,x2),axis([-1,13,0,5]);title('x2'); subplot(5,3,3),stem(nx1,x4),axis([-1,13,0,26]);title('x4=2*x1+3* x3');subplot(5,3,4),plot(w,abs(X1)); ylabel('幅度')subplot(5,3,7),plot(w,angle(X1));ylabel('相位')subplot(5,3,10),plot(w,real(X1));ylabel('实部')subplot(5,3,13),plot(w,imag(X1)); ylabel('虚部')subplot(5,3,5),plot(w,abs(X3));subplot(5,3,8),plot(w,angle(X3));subplot(5,3,11),plot(w,real(X3));subplot(5,3,14),plot(w,imag(X3));subplot(5,3,6),plot(w,abs(X4));subplot(5,3,9),plot(w,angle(X4));subplot(5,3,12),plot(w,real(X4));subplot(5,3,15),plot(w,imag(X4));(b)结果:第页(2)卷积:(a)代码:nx1=0:11; nx2=0:9; nx3=0:20;w=linspace(-8,8,40); %w=[-8,8]分10000份x1=[1 2 3 4 5 6 7 8 9 10 11 12];x2=[1 1 1 1 1 1 1 1 1 1];x3=conv(x1,x2);% x1卷积x2x4=x1*exp(-j*nx1'*w);% x1频率特性x5=x2*exp(-j*nx2'*w);% x2频率特性x6=x3*exp(-j*nx3'*w);% x1卷积x2频率特性x7=x4.*x5;subplot(2,2,1),stem(nx1,x1),axis([-1,15,0,15]),title('x1'); subplot(2,2,2),stem(nx2,x2),axis([-1,15,0,5]),title('x2'); subplot(2,1,2),stem(nx3,x3),axis([-1,25,0,80]);title('x1卷积x2第页结果x3');figure,subplot(2,2,1),stem(x4,'filled'),title('x1的DTFT结果x4');subplot(2,2,2),stem(x5,'filled'),title('x2的DTFT结果x5');subplot(2,2,3),stem(x6,'filled'),title('x3的DTFT结果x6');subplot(2,2,4),stem(x7,'filled'),title('x4的DTFT结果x7');figure,subplot(3,2,1),stem(w,abs(x6)), ylabel('幅度'),title('x1卷积x2的DTFT');subplot(4,2,3),stem(w,angle(x6)),ylabel('相位')subplot(4,2,5),stem(w,real(x6)),ylabel('实部')subplot(4,2,7),stem(w,imag(x6)),ylabel('虚部')subplot(4,2,2),stem(w,abs(x7)), title('x1与x2的DTFT的乘积');subplot(4,2,4),stem(w,angle(x7));subplot(4,2,6),stem(w,real(x7));subplot(4,2,8),stem(w,imag(x7));(b)结果:第页第页(3)共轭:(a)代码:x1n=[1 2 3 4 5 6 7 8 9 10 11 12];w=-10:10;N1=length(x1n);n1=0:N1-1;x1=real(x1n);x2=imag(x1n);x2n=x1-j*x2;X1=x2n*(exp(-j).^(n1'*w));X2=x1n*(exp(j).^(n1'*w));x3=real(X2);x4=imag(X2);X2=x3-j*x4;figure,subplot(211);stem(w,X1,'.');title('x1n共轭的DTFT');第页subplot(212);stem(w,X2,'.');title('x1n的DTFT取共轭且反折'); (b)结果:3. 求LTI系统的频率响应给定系统H(Z)=B(Z)/A(Z),A=[0.98777 -0.31183 0.0256]B=[0.98997 0.989 0.98997],求系统的幅频响应和相频响应。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
00[()]jw t f F f e F j w w ±↔↔若(t)(jw)则(t)00()jwt f F f F jw e ±↔±↔若(t)(jw)则(t t )1()w f F f a F j a a ↔↔若(t)(jw)则(t)()2f t f π↔↔若(t)F(jw)则F (-w)()()df t f F jwF jw dt
↔↔若(t)(jw)则 非周期信号的傅里叶变换MATLAB 仿真实验
一、实验目的
(1)熟悉连续非周期信号频谱特点及其分析方法;
(2)掌握用MATLAB 实现傅里叶变换。
二、非周期信号的傅里叶变换原理及性质
设周期信号)(t f 展开成复指数形式的傅里叶级数为t jn n e n F t f 1)()(1ωω-∞
-∞=∑=,
dt e t f T n F t jn T T 1112211)(1)(ωω--⎰=(两边同乘1T ) 得 dt e t f n f T n F t jn T T 1112
2
1111)()(2)(ωωωπω--⎰== 上式左边,当1T ∞→时,如前所述,→11/)(ωωn F 有限值,并且成为一个连续的频率函数,即频谱密度函数用)(ωF 表示为
11)(2lim )(1
ωωπωn F F T ∞→=,进而得出 dt e t f F t j ωω-∞
∞-⎰=)()(
傅立叶变换的性质 (1)线性性质: 1122()()()()f t F jw f t F jw ↔↔若和
11221122()()()()a f t a f t a F jw a F jw +↔+则
(2)频移性质:
(3)时移性质:
(4)尺度变换性质:
(5)对称性质:
(6)时域微分性质:
()()dF jw f F jtf t dw ↔-↔若(t)(jw)则()()(0)()t F jw f F f d F w jw ττπδ-∞↔↔+⎰若(t)(jw)则
(7)频域微分性质:
(8)时域积分性质:
(9)时域卷积定理)(·)()(*)();()(),()(21212211ωωωωj F j F t f t f j F t f j F t f 的傅里叶变换为则↔↔
三、MATLAB 仿真
求双边指数信号t e t f 2)(-=的傅里叶变换,并画出其波形。
解:
幅度频谱和相位频谱分别为
实验程序及运行结果
exp(-2 t) heaviside(t) + heaviside(-t) exp(2 t)
0.6
0.4
0.2
-3-2-101234
t
幅频图
1
0.5
-10-8-6-4-20246810
w
频谱图
1
0.5
-10-8-6-4-20246810
w
四、实验结果分析
非周期信号经过傅里叶变换后信号图形是连续的。
