【苏科版】2014届中考数学第一轮夯实基础《第16讲 二次函数的应用》
【数学中考一轮复习】 二次函数最值应用(含解析)

专项训练 二次函数最值应用结合图象,分两类情形: (1)最值在顶点位置如图所示,P 为二次函数y =ax 2+bx +c (a ≠0)的图象的顶点,则二次函数的最值(开口向上有最小值,开口向下有最大值)为顶点P 的纵坐标ab ac 442-.(2)最值不在顶点位置如图所示,M (x 1,y 1),N (x 2,y 2)为y 二次函数y =ax 2+bx +c (a ≠0)的图象上的两点,则当x 1≤x ≤x 2时,二次函数的最大值为y 2,最小值为ab ac 442-.具体应结合开口方向,根据M ,N ,P 三个点的位置,通过比较y M ,y P ,y N ,确定二次函数的最值.如果在实际问题中,还要考虑取值的实际意义,综合进行分析,确定二次函数的最值. 类型一 面积中的最值应用1.把一根长为120 cm 的铁丝剪成两段,并把每一段铁丝围成一个正方形.若设围成的一个正方形的边长为 x cm.(1)要使这两个正方形的面积的和等于650 cm 2,则剪出的两段铁丝长分别是多少? (2)剪出的两段铁丝长分别是多少cm 时,这两个正方形的面积和最小?最小值是多少?2.如图所示,在足够大的空地上有一段长为100 m 的旧墙MN ,某人利用旧墙和木栏围成一个矩形菜园ABCD ,其中AD ≤MN ,已知矩形菜园的一边靠墙,另三边一共用了100 m 的木栏.(1)若AD <20 m ,所围成的矩形菜园的面积为450 m 2,求所利用的旧墙AD 的长; (2)求矩形菜园ABCD 面积的最大值.3.如图所示,为美化中心城区环境,政府计划在长为30米,宽为20米的矩形场地ABCD 上修建公园其中要留出宽度相等的三条小路,且两条与AB 平行,另一条与AD 平行,其余部分建成花圃.(1)若花圃总面积为448平方米,求小路宽为多少米?(2)已知某园林公司修建小路的造价y 1(元)和修建花圃的造价y 2(元)与修建面积s (平方米)之间的函数关系分别为y 1=40s 和y 2=35s +20000.若要求小路宽度不少于2米且不超过4米,求小路宽为多少米时修建小路和花圃的总造价最低?类型二 利润中的最值应用4.超市销售某品牌洗手液,进价为每瓶10元.在销售过程中发现,每天销售量y (瓶)与每瓶售价x (元)之间满足一次函数关系(其中10≤x ≤15,且x 为整数),当每瓶洗手液的售价是12元时,每天销售量为90瓶;当每瓶洗手液的售价是14元时,每天销售量为80瓶.(1)求y 与x 之间的函数关系式;(2)设超市销售该品牌洗手液每天销售利润为w 元,当每瓶洗手液的售价定为多少元时,超市销售该品牌洗手液每天销售利润最大,最大利润是多少元?5.在“新冠”疫情期间,全国人民“众志成城,同心抗疫”,某商家决定将一个月获得的利润全部捐赠给社区用于抗疫.已知商家购进一批产品,成本为10元/件,拟采取线上和线下两种方式进行销售调查发现,线下的月销量y (单位:件)与线下售价x (单位:元/件,12≤x <24)满足一次函数的关系,部分数据如下表:(1)求y 与x 的函数关系式;(2)若线上售价始终比线下每件便宜2元,且线上的月销量固定为400件.试问:当x 为多少时,线上和线下月利润总和达到最大?并求出此时的最大利润.6.2020年是决战决胜扶贫攻坚和全面建成小康社会的收官之年,荆门市政府加大各部门和单位对口扶贫力度.某单位的帮扶对象种植的农产品在某月(按30天计)的第x 天(x为正整数)的销售价格p (元/千克)关于x 的函数关系式为p =⎪⎪⎩⎪⎪⎨⎧≤<+-≤<+)3020(1251)200(452x x x x ,销售量y (千克)与x 之间的关系如图所示.(1)求y与x之间的函数关系式,并写出x的取值范围;(2)当月第几天,该农产品的销售额最大,最大销售额是多少?(销售额=销售量×销售价格)类型三运动中的最值应用,7.周末,小明陪爸爸去打高尔夫球,小明看到爸爸打出的球的飞行路线的形状如图所示,如果不考虑空气阻力,小球的飞行路线是一条抛物线.小明测得小球的飞行高度h(单位:m)与飞行时间t(单位:s)的几组值后,发现h与t满足的函数关系式是h=20t-5t2. (1)小球飞行时间是多少时达到最大高度,求最大高度是多少?(2)小球飞行时间t在什么范围时,飞行高度不低于15 m?8.如图所示,一位篮球运动员在离篮圈水平距离4 m处跳起投篮,球运行的高度y(m)与运行的水平距离x(m)满足解析式y=ax2+x+c,当球运行的水平距离为1.5 m时,球离地面高度为3.3 m,球在空中达到最大高度后,准确落入篮圈内.已知篮圈中心离地面距离为3.05 m.(1)当球运行的水平距离为多少时,达到最大高度?最大高度为多少?(2)若该运动员身高1.8 m,这次跳投时,球在他头顶上方0.25 m处出手,问球出手时他跳离地面多高?9.如图所示,某足球运动员站在点O处练习射门将足球从离地面0.5 m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c.已知足球飞行0.8 s时,离地面的高度为3.5 m.(1)a=_________;c=___________.(2)当足球飞行的时间为多少时,足球离地面最高?最大高度是多少?(3)若足球飞行的水平距离x(单位:m)与飞行时间(单位:s)之间具有函数关系x=10t,已知球门的高度为 2.44 m,如果该运动员正对球门射门时,离球门的水平距离为28 m,他能否将球直接射入球门?巩固训练1.某宾馆共有80间客房宾馆负责人根据经验作出预测:今年7月份,每天的房间空闲数y (间)与定价x (元/间)之间满足y =41x-42(x ≥168).若宾馆每天的日常运营成本为5000元,有客人入住的房间,宾馆每天每间另外还需支出28元的各种费用,宾馆想要获得最大利润,同时也想让客人得到实惠,应将房间定价确定为( ) A.252元/间 B.256元/间 C.258元/间 D.260元/间 2.如图所示,一块矩形土地ABCD 由篱笆围着,并且由一条与CD 边平行的篱笆EF 分开.已知篱笆的总长为900 m (篱笆的厚度忽略不计),当AB =_______m 时,矩形土地ABCD 的面积最大.3.小明和小丽先后从A 地出发沿同一直道去B 地.设小丽出发第x min 时,小丽、小明离B 地的距离分别为y 1 m 、y 2 m.y 1与x 之间的函数表达式是y 1=-180x +2250,y2与x 之间的函数表达式是y 2=-10x 2-100x +2000.(1)小丽出发时,小明离A 地的距离为_________m ;(2)小丽出发至小明到达B 地这段时间内,两人何时相距最近?最近距离是多少?4.因疫情防控需要,消毒用品需求量增加.某药店新进一批桶装消毒液,每桶进价50元,每天销售量y (桶)与销售单价x (元)之间满足一次函数关系,其图象如图所示. (1)求y 与x 之间的函数表达式;(2)每桶消毒液的销售价定为多少元时,药店每天获得的利润最大,最大利润是多少元?(利润=销售价-进价)参考答案1.解:(1)根据题意知:一个正方形的边长分别为x cm , 则另一个正方形的边长为41(120-4x )=(30-x )cm , 且分成的铁丝一段长度为4x cm ,另一段为(120-4x )cm ,x 2+(30-x )2=650. 整理得:x 2-30x +125=0,解得:x 1=5,x 2=25, 故这根铁丝剪成两段后的长度分别是20 cm ,100 cm ; (2)设这两个正方形的面积之和为y cm 2,y =x 2+(30-x )2=2x 2-60x +900=2(x-15)2+450, ∴当x =15时,y 取得最小值,最小值为450cm 2,即剪成两段均为60 cm 的长度时面积之和最小,最小面积和为450 cm 2. 2.解:(1)设AB =x m ,则BC =(100-2x )m.x (100-2x )=450. 解得,x 1=5,x 2=45,当x =5时,100-2x =90>20,不合题意,舍去. 当x =45时,100-2x =10, 答:AD 的长为10m ;(2)设AD =a m ,面积为S m 2, S =a ·1250)50(2121002+-=-x a , ∴当a =50时,S 取得最大值,此时S =1250. 答:矩形菜园ABCD 面积的最大值是1250 m 2.3.解:(1)设小路的宽为m 米,则可列方程(30-m )(20-2m )=448; 解得:m 1=2或m 2=38(舍去); 答:小路的宽为2米;(2)设小路的宽为x 米,总造价为w 元,则花圃的面积为(2x 2-80x +600)平方米,小路面积为(-2x 2+80x )平方米,所以w =40·(-2x 2+80x )+35·(2x 2-80x +600)+20000, 整理得:w =-10(x-20)2+45000,∴当2≤x ≤4时,w 随x 的增大而增大.∴当x =2时,w 取最小值. 答:小路的宽为2米时修建小路和花圃的总造价最低.4.解:(1)设y 与x 之间的函数关系式为y =kx +b (k ≠0),根据题意,得1⎩⎨⎧=+=+80149012b k b k ,解得⎩⎨⎧=-=1505b k , ∴y 与x 之间的函数关系式为y =-5x +150; (2)根据题意,得w =(x-10)(-5x +150)=-5x 2+200x-1500=-5(x-20)2+500 ∵a =-5<0,∴抛物线开口向下,w 有最大值.∴当x <20时,w 随x 的增大而增大.10≤x ≤15,且x 为整数, ∴当x =15时,w 有最大值. 即w =-5×(15-20)2+500=375.答:当每瓶洗手液的售价定为15元时,超市销售该品牌洗手液每天销售利润最大,最大利润是375元.5.解:(1)∵y 与x 满足一次函数的关系,∴设y =kx +b.将x =12,y =1200;x =13,y =1100代入得:⎩⎨⎧b +13k =1100b +12k =1200,解得:⎩⎨⎧2400=b 100-=k ,∴y 与x 的函数关系式为:y =-100x +2400;(2)设线上和线下月利润总和为m 元,则m =400(x-2-10)+y (x-10) =400x-4800+(-100x +2400)(x-10)=-100(x-19)2+7300,∴当x 为19元/件时,线上和线下月利润总和达到最大,此时的最大利润为7300元. 6.解:(1)当0<x ≤20时,设y =k 1x +b 1,由图象得:⎩⎨⎧=+=402080111b k b ,解得⎩⎨⎧=-=80211b k ,∴y =-2x +80(0<x ≤20); 当20<x ≤30时,设y =k 2x +b 2,由图象得:⎩⎨⎧=+=+803040202222b k b k ,解得⎩⎨⎧-==40422b k ,∴y =4x-40(20<x ≤30). 综上,y =⎩⎨⎧);30≤x <2040-4x (),20≤x <080+2x (((2)设当月该农产品的销售额为w 元,则w =yp , 当0<x ≤20时,w =(-2x +80)(52x +4)=-54x 2+24x +320=-54(x-15)2+500 ∵-54<0,由二次函数的性质可知:∴当x =15时,w 最大=500.当20<x ≤30时,W =(4x-40)(-51x +12)=-54x 2+56x-480=-54(x-35)2+500,∵-54<0,20<x ≤30,由二次函数的性质可知:当x =30时,W 最大=(30-35)2+500=480.∵500>480, ∴当x =15时,w 取得最大值,该最大值为500.答:当月第15天,该产品的销售额最大,最大销售额是500元. 7.解:(1)h =20t-5t 2. ∵-5<0,故h 有最大值,当t =)(5220-⨯=2,此时h 的最大值为20,∴当t =2 s 时,最大高度是20 m ;(2)令h ≥15,则h =20t-5t 2≥15,解得:1≤t ≤3, ∴1≤t ≤3时,飞行高度不低于15 m.8.解:(1)依题意,抛物线y =ax 2+x +c 经过点(1.5,3.3)和(4,3.05),∴⎩⎨⎧ 3.05=c +4+42×a 3.3=c +1.5+1.52×a ,解得⎩⎨⎧ 2.25=c 0.2-=a ,∴y =-0.2x 2+x +2.25=-0.2(x-2.5)2+3.5.∴当球运行的水平距离为2.5 m 时,达到最大高度为3.5 m ; (2)∵x =0时,y =2.25,∴2.25-0.25-1.8=0.2 m. 即球出手时,他跳离地面0.2 m.9.解:(1)由题意得:函数y =at 2+5t +c 的图象经过(0,0.5)(0.8,3.5),∴⎩⎨⎧c +0.8×5+0.82a =3.5c =0.5,解得:⎪⎪⎩⎪⎪⎨⎧=-=211625c a ,∴抛物线的解析式为:y =-1625t2+5t +21, 故答案为:-1625,21. (2)∵y =-1625t2+5t +21,∴y =29)58(16252+--t . ∴当t =58时,y 最大=4.5.∴当足球飞行的时间为58s 时,足球离地面最高,最大高度是4.5 m ;(3)把x =28代入x =10t 得t =2.8,∴当t =2.8时,y =-1625×2.82+5×2.8+21=2.25<2.44, ∴他能将球直接射入球门. 巩固训练 1.B 2.1503.解:(1)∵y 1=-180x +2250,y 2=-10x 2-100x +2000, ∴当x =0时,y 1=2250,y 2=2000,∴小丽出发时,小明离A 地的距离为2250-2000=250(m ), 故答案为:250;(2)设小丽出发第x min 时,两人相距s m ,则s =(-180x +2250)-(-10x 2-100x +2000)=10x 2-80x +250=10(x-4)2+90, ∴当x =4时,s 取得最小值,此时s =90,答:小丽出发第4min 时,两人相距最近,最近距离是90m. 4.解:(1)设y 与销售单价x 之间的函数关系式为:y =kx +b ,将点(60,100),(70,80)代入一次函数表达式得:⎩⎨⎧+=+=b k b k 708060100,解得:⎩⎨⎧=-=2202b k ,故函数的表达式为:y =-2x +220;(2)设药店每天获得的利润为w 元,由题意得: W =(x-50)(-2x +220)=2(x-80)2+1800, ∵-2<0,函数有最大值,∴当x =80时,w 有最大值,此时最大值是1800,故销售单价定为80元时,该药店每天获得的利润最大,最大利润1800元.。
【苏科版】2014届中考数学第一轮夯实基础《第7讲 一元二次方程及其应用》

直接 开平 方法 因式 分解 法
一元二次方程的四种解法
适合于(x+a)2=b(b≥0)或(ax+b)2=(cx+d)2形式的 方程
基本思想
把方程化成ab=0的形式,得a=0或b=0
方法规律
常用的方法主要运用提公因式法、平方差 公式、完全平方公式型因式分解
第7讲┃ 考点聚焦
第7讲┃ 归类示例
[解析] (1)由题意可得出3月份的用电量超过了a度,而4 月份的用电量在a度以内,那么可根据3月份的用电情况来 求a的值.可根据:不超过a度的缴费额+3月份超过a度部 分的缴费额=总的电费;列出方程,进而可求出a的值.然 后可根据4月份的用电量大致判断出a的取值范围,由此可 判定解出的a的值是否符合题意.(2)由(1)得a的值,把45代 入即可.
(1)毛利润=售出价-进货价(2)纯利润=售出价 -进货价-其他费用(3)利润率=利润÷进货价
第7讲┃ 归类示例
归类示例
► 类型之一 一元二次方程的有关概念 命题角度: 1.一元二次方程的概念; 2.一元二次方程的一般式; 3.一元二次方程的解的概念. 例1 已知关于x的方程x2+bx+a=0有一个根是-a(a≠0) ,则a-b的值为( A ) A.-1 B.0 C.1 D.2 [解析] 把x=-a代入x2+bx+a=0,得(-a)2+b×(-a) +a=0,∴a2-ab+a=0, 所以a-b+1=0,∴a-b=-1,故选择A
第7讲┃ 归类示例
利用因式分解法解方程时,当等号两边有相 同的含未知数的因式(如例2)时,不能随便先约 去这个因式,因为如果约去则是默认这个因式 不为零,那么如果此因式可以为零,则方程会 失一个根,出现漏根错误.所以应通过移项, 提取公因式的方法求解.
《二次函数的应用》课件1(13页)(苏科版九年级下)

提示:日利润=(销售价-成本)×销售量
(1)设此一次函数解析式为 y kx b 。
1分
15k b 25 则 20k b 20
解得:k=-1,b=40。
5分
所以一次函数解析式为 y x 40 。
6分
(2)设每件产品的销售价应定为 x 元,所获销售利润为
w 元。则
某种粮大户去年种植优质水稻360亩,今年计划增
加承租X(100≤x≤150)亩.预计,原种植的360亩水
稻今年每亩可收益440元,新增地今年每亩的收益
为(440-2x)元,试问:该种粮大户今年要增加承租
多少亩水稻,才能使总收益最大?最大收益是多少?
试一试:
温馨提示:同桌交对, 互相帮助!
求二次函数y=-100x2+100x+200的最值?
生活化
?
议一议:
驶向胜利 的彼岸
求二次函数y=x(20-2x)的最值?
生活化
要用长20m的铁栏杆,一面靠墙, 围成一个矩形的花圃,怎么样围法才 能使围成的花圃的面积最大?
附:如果花圃垂直于墙的一边长为xm, 花圃的面积为ym2,那么y=x(20-2x)
解决一个普通的二次函数的 最值问题与实际问题中的最值 问题最大的区别在哪里?
某产品每件成本10元,试销阶段每件产品的销售价 x(元)与产品的日销售量 y(件)之间的关系如下表:
x(元) 15
20
30
…
y(件) 252010 Nhomakorabea…
若日销售量 y 是销售价 x 的一次函数。 (1)求出日销售量 y(件)与销售价 x(元)的函 数关系式;(6分) (2)要使每日的销售利润最大,每件产品的销售价 应定为多少元?此时每日销售利润是多少元?(6分)
苏教九年级数学上册《二次函数应用》课件

F
+
( 1m2+1-2)2 = 1m2+1
2
F
1
4
4
-6
-4
-2
O
∴d1=d2,猜想正确。
N2
C4
6
8
10
-4
-2
O
2
c是抛物线 y 点P到点F(0,2)的距离为d2。
1 4
x2
上1的任意一点,记点P到x轴的距离为d1,
(1)猜想d1与d2的大小关系,并证明; (2)若直线PF交抛物线于另一个点Q(异于点P),
(2)当y=0时,-1/12x2+x+2=0
即 x2-12x-24=0。再求出X的值。
解法2:(1)∵抛物线的顶点为(6,5)
∴可设抛物线的解析式为 y=a(x-6)2+5。
∵抛物线经过点A(0,2)
∴2=a(0-6) 2 +5
∴a=- 1/12
故抛物线的解析式为y=- 1/12(x-6)2+5
即 y=-1/12x2+x+2
某瓜果基地市场部为指导该基地某种蔬菜的生产和销售, 在对历年市场行情和生产情况进行了调查的基础上,对今 年这种蔬菜上市后的市场售价和生产成本进行了预测,提 供了两个方面的信息,如图所示. 请你根据图象提供的信息解答: (1)在3月份出售这种蔬菜,每千克的收益是多少元?(收益= 售价-成本) (2)哪个月出售这种蔬菜,每千克的收益最大?说明理由.
例7:已知如图,P是抛物线 y 点P到点F(0,2)的距离为d2。
1 4
x2
1上的任意一点,记点P到x轴的距离为d1,
(1)猜想d1与d2的大小关系,并证明; (2)若直线PF交抛物线于另一个点Q(异于点P),
2014届苏科版中考数学复习方案14二次函数的讲义图象及其性质19页

若已知二次函数图象与x轴的两个交点的坐标为(x1,0),(x2, 0),设所求二次函数为y=a(x-x1)(x-x2),将第三点(m,n) 的坐标(其中m、n为已知数)或其他已知条件代入,求出待定
系数a,最后将关系式化为一般形式
考点聚焦
归类探究
第14课时┃归类探究
考点聚焦
归类探究
第14课时┃归类探究
解 析 (1)根据配方法的步骤进行计算.
(2)由(1)得出抛物线的对称轴,顶点坐标列表,注意抛物线与x轴、 y轴的交点及顶点等特殊点的坐标,不要弄错.
(3)开口向上,在抛物线对称轴的左边,y随x的增大而减小.
(4)抛物线y=x2-4x+3与直线y=2的交点的横坐标即为方程x2- 4x+3=2的两根.
1.一般式:y=ax2+bx+c;
2.顶点式:y=a(x-m)2+n,其中(m,n)为顶点坐标;
3.交点式:y=a(x-x1)(x-x2),其中(x1,0),(x2,0)为 抛物线与x轴的交点.
一般已知三点坐标用一般式求关系式;已知顶点及另一个 点坐标用顶点式;已知抛物线与x轴的两个交点坐标及另 一个点的坐标用交点式.
考点聚焦
归类探究
第14课时┃归类探究
解
设 y=ax2+bx+c(a≠0),把 A(-5,0),B(1,
0),P -2,92的坐标代入,得
a+b+c=0, ∴25a-5b+c=0,
4a-2b+c=92,
a=-12, 解得b=-2,
c=52,
∴ 所求抛物线的关系式为 y=-12x2-2x+52.
第14课时┃归类探究
考点聚焦
归类探究
第14课时┃归类探究
解 析 根据题目要求,本题可选用多种方法求关系式.
2014年中考备考一轮复习导学案第15章二次函数及其应用
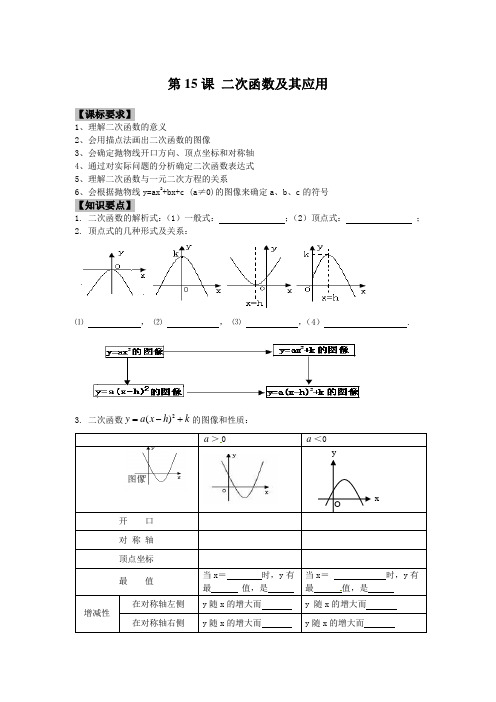
第15课 二次函数及其应用【课标要求】1、理解二次函数的意义2、会用描点法画出二次函数的图像3、会确定抛物线开口方向、顶点坐标和对称轴4、通过对实际问题的分析确定二次函数表达式5、理解二次函数与一元二次方程的关系6、会根据抛物线y=ax 2+bx+c (a ≠0)的图像来确定a 、b 、c 的符号【知识要点】1. 二次函数的解析式:(1)一般式: ;(2)顶点式: ;2. 顶点式的几种形式及关系:⑴ , ⑵ , ⑶ ,(4) .3. 二次函数2()y a x h k =-+的图像和性质:0 图像开 口 值,是4.二次函数c bx ax y ++=2通过配方可得224()24b ac b y a x a a-=++,其抛物线关于直线x = 对称,顶点坐标为( , ).⑴ 当0a >时,抛物线开口向 ,有最 (填“高”或“低”)点, 当x = 时,y 有最 (“大”或“小”)值是 ;⑵ 当0a <时,抛物线开口向 ,有最 (填“高”或“低”)点, 当x = 时,y 有最 (“大”或“小”)值是 .第一课时【典型例题】【例1】.抛物线y =2x 2-4x +5的开口方向______,顶点坐标是__________,对称轴方程是直线x =___,当x = 时,y 有最 值是 。
【例2】.二次函数 322++=x x y ,当x <-1时,y 随x 的增大而 。
【例3】抛物线y =x 2-4x +3与y 轴的交点坐标是 ,与x 轴的交点坐标是 。
当y=8时x 对应的值是 。
【例4】抛物线243y x x =-+向右平移2个单位所得抛物线的顶点坐标为( ) A 、(4,-1) B 、(0,-3) C 、(-2,-3) D 、(-2,-1)【例5】已知二次函数c bx ax y ++=2的图象如图所示,则在“①a <0,②b >0,③c < 0,④b 2-4ac >0”中,正确的判断是( )A 、①②③④B 、④C 、①②③D 、①④ 【例6一条抛物线顶点是(1,2)且经过点(-2,-4),则它的函数解析式是 ;另一抛物线经过(0,1)、(1,0)和(2,4)三点,则它的函数解析式是 。
九年级数学二次函数的复习江苏科技版知识精讲

九年级数学二次函数的复习某某科技版【本讲教育信息】一. 教学内容:二次函数的复习二. 教学目的:1. 理解二次函数的概念及性质,会画出二次函数的图象。
2. 会用待定系数法求二次函数的解析式,用配方法和公式法求抛物线的顶点坐标和对称轴。
3. 能利用二次函数关系式及有关性质解决比较复杂的问题。
三. 重点、难点:重点:理解二次函数的概念,能结合图像对实际问题中的函数关系进行分析。
难点:能用函数解决实际问题[课堂教学] 一. 知识要点:知识点1:二次函数y =ax 2+bx +c (a ≠0)的图象二次函数y =ax 2+bx +c (a ≠0)的图象如图所示.y b 2-4ac <0-4ac=0知识点2:二次函数y =ax 2+bx +c (a ≠0)的性质(一)a 的符号决定抛物线的开口方向、大小及最大值或最小值.a >0等价于开口向上等价于最小值(最低点的纵坐标) a <0等价于开口向下等价于最大值(最高点的纵坐标) a 越大,开口越小;a 越小,开口越大.(二)a ,b 决定抛物线的对称轴和顶点的位置.b =0等价于,对称轴是y 轴,顶点在y 轴上.a ,b 同号等价于对称轴在y 轴的左侧,顶点在第二或第三象限内. a ,b 异号等价于对称轴在y 轴的右侧,顶点在第一或第四象限内.(三)c 的符号决定抛物线与y 轴交点的位置.c =0,等价于抛物线过原点.c >0,等价于抛物线交y 轴的正半轴. c <0,等价于抛物线交y 轴的负半轴.(四)a ,b ,c 的符号决定抛物线与x 轴交点的位置.抛物线y =ax 2+bx +c (a ≠0)与x 轴交于A (x 1,0),B (x 2,0),且x 1<x 2,△>0.a ,b ,c 同号等价于A ,B 两点在x 轴的负半轴上.a ,c 同号且与b 异号等价于A ,B 两点在x 轴的正半轴. b ,c 同号且与a 异号等价于A ,B 两点在原点的两侧.(五)△=b 2-4ac 的符号决定抛物线与x 轴交点个数.△>0,等价于抛物线与x 轴有两个交点. △=0,等价于抛物线与x 轴只有一个交点. △<0,等价于抛物线与x 轴没有交点.(六)抛物线的特殊位置与系数的关系.顶点在x 轴上等价于△=0. 顶点在y 轴上等价于b =0. 顶点在原点,等价于b =c =0. 抛物线经过原点,等价于c =0.知识点3:二次函数关系式的形式及对称轴、顶点坐标.(1)一般式:y =ax 2+bx +c (a ,b ,c 是常数,且a ≠0),其对称轴为直线x =ab2-,顶点坐标为(ab2-,a b ac 442-).(2)顶点式:y =a (x +h )2+k (a ,h ,k 是常数,且a ≠0),其对称轴为直线x =-h ,顶点坐标为(-h ,k ).(3)交点式:y =a (x -x 1)(x -x 2),其中a ≠0,x 1,x 2是抛物线与x 轴两个交点的横坐标,即一元二次方程的两个根.知识点4:抛物线的平移规律.基本口诀:上加下减,左加右减,具体操作如下(其中m >0,n >0,a ≠0):(1)将抛物线y =ax 2+bx +c 沿y 轴向上平移m 个单位,得y =ax 2+bx +c +m. (2)将抛物线y =ax 2+bx +c 沿y 轴向下平移m 个单位,得y =ax 2+bx +c -m. (3)将抛物线y =ax 2+bx +c 沿x 轴向左平移n 个单位,得y =a (x +n )2+b (x +n )+c.(4)将抛物线y =ax 2+bx +c 沿x 轴向右平移n 个单位,得y =a (x -n )2+b (x -n )+c.知识点5:二次函数最值的求法.(1)配方法:将解析式化为y =a (x -h )2+k 的形式,顶点坐标为(h ,k ),对称轴为x =h ,当a >0时,y 有最小值,即当x =h 时,y 最小值=k;当a <0时,y 有最大值,即当x =h 时,y 最大值=k. (2)公式法:直接利用顶点坐标公式.当a >0时,y 有最小值,即x =-b/2a 时,y 最小值=4ac -b 2/4a 当a <0时,y 有最大值,即x =-b/2a 时,y 最大值=4ac -b 2/4a(3)判别式法:结合抛物线的性质,利用根的判别式和不等式求最值.说明:二次函数实际问题求最值,一般是条件最值,应主动地求出自变量的取值X 围.知识点6:二次函数与一元二次方程、一元二次不等式的关系.(1)如图所示,当a >0时,抛物线y =ax 2+bx +c 开口向上,它与x 轴有两个交点(x 1,0),(x 2,0). x =x 1,x =x 2是方程ax 2+bx +c =0的解。
中考数学 二次函数的应用复习教案1 苏科版

二次函数的应用
函数、数形结合、建
练一练
某工厂为了存放材料,需要围一个周长
=__________米,才能使存放场地的面积最大
的宽为
米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花
学以致用
1.(05年台州)如图,用长为18cm的篱笆(虚线部分),两面靠墙围成矩形的苗圃。
(1)设矩形的一边为x(m),面积为y(m2),求y与x的函数关系,并写出x的取值范围;
例2.在Rt△AMN内部作一个矩形ABCD,矩形ABCD何时面积最大?为多少?
例 3.某建筑物的窗户如图所示它的上半部是半圆,下半部是矩形,制造窗框的材料总长
的黑线的长度和)为15m.当x等于多少时,窗户通过的光线最多(结果精确到
练一练:窗的形状是矩形上面加一个半圆。
窗的周长等于6cm,要使窗能透过最多的光线,它的尺寸应该如何设计?
4.用一块宽为1.2m的长方形铁板弯起两边做一个水槽,水槽的横断面为底角
要使水槽的横断面积最大,它的侧面应该是多长?
例5.在矩形ABCD中,AB=6cm,BC=12cm,从点A出发,沿AB边向点B以
同时,点Q从点B出发沿BC边向点C以2cm/秒的速度移动。
如果P、Q两点在分别到达
8cm2
的面积为Scm2,写出S与t的函数关系式,并指出自
的最小值。
桥下水面宽度是4m,拱高是2m.当水面下降1m
1.6m,涵洞顶点O到水面的距离为在图中直角坐标系内,涵洞所在的抛物线的函数关系式是什么?
1
2.如图3,规格为60 cm×60 cm的正方形地砖在运输过程中受损,断去一角,量得。
为菱形,点
的面积为△
ABCD。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第16讲┃ 归类示例
二次函数在几何图形中的应用,实际上是数形结 合思想的运用,融代数与几何为一体,把代数问题与 几何问题进行互相转化,充分运用三角函数解直角三 角形,相似、全等、圆等来解决问题,充分运用几何 知识求解析式是关键.二次函数与三角形、圆等几何 知识结合时,往往涉及最大面积,最小距离等问题, 解决的过程中需要建立函数关系,运用函数的性质求 解.
例1
习发球,将球从O点正上方2 m的A处发出,把球看成点, 其运行的高度y(m)与运行的水平距离x(m)满足关系式y= a(x-6)2+h.已知球网与O点的水平距离为9 m,高度为2.43 m,球场的边界距O点的水平距离为18 m.
第16讲┃ 归类示例 (1)当h=2.6时,求y与x的关系式(不要求写出自 变量x的取值范围);
第16讲┃ 归类示例
解:(1)∵h=2.6,球从 O 点正上方 2 m 的 A 处发出, ∴y=a(x-6)2+h 过点(0,2), ∴2=a(0-6)2+2.6, 1 解得 a=- , 60 1 2 故 y 与 x 的关系式为:y=- (x-6) +2.6. 60
第16讲┃ 归类示例
第16讲┃ 归类示例
第16讲┃ 回归教材
回归教材
如何定价利润最大 教材母题 江苏科技版九下P34T10 某商场购进一批单价为16元的日用品.若按每件20元的价 格销售,每月能卖出360件;若按每件25元的价格销售. 每月能卖出210件.假定每月销售件数y(件)与价格x(元/件) 之间满足一次函数. (1)试求y与x之间的函数关系式; (2)在商品不积压且不考虑其他因素的条件下,销售价格定 为多少时,才能使每月的毛利润w最大?每月的最大毛利 润是多少?
第16讲┃ 归类示例
图16-2
第16讲┃ 归类示例
[解析] (1) 用每亩地每年发放种粮补贴金额乘以今 年种粮面积即可求出今年老王种粮可获得的补贴;(2) 设出一次函数关系式,结合图象中给出的两点坐标, 用待定系数法求出一次函数关系式;(3)根据每亩的售 粮收入加每亩地的种粮补贴减去每亩种粮成本,再乘 以种粮面积x亩,可得关于x的二次函数关系式,然后 利用二次函数的性质,即可求出当种粮面积为多少亩 时总利润最高及最高总利润.
第16讲┃ 回归教材
解:(1)y=-30x+960; (2)设每月的毛利润为w元.则 w=(x-16)(-30x+960) =-30x2+1440x-960×16. 当x=24时,w有最大值,w最大值=1920元. 答:将售价定为24元时,每月的最大毛利润为1920元.
第16讲┃ 回归教材
中考变式
例2 [2013· 淮安]国家和地方政府为了提高农民种粮的 积极性,每亩地每年发放种粮补贴120元.种粮大户老王今 年种了150亩地,计划明年再承租50~150亩土地种粮以增 加收入.考虑各种因素,预计明年每亩种粮成本y(元)与种 粮面积x(亩)之间的函数关系如图16-2所示: (1)今年老王种粮可获得补贴多少元? (2)根据图象,求y与x之间的函数关系式; (3)若明年每亩的售粮收入能达到2140元,求老王明年种 粮总利润W(元)与种粮面积x(亩)之间的函数关系式.当种粮 面积为多少亩时,总利润最高?并求出最高总利润.
(2)当h=2.6时,球能否越过球网?球会不会出界? 请说明理由;
(3)若球一定能越过球网,又不出边界,求h的取值 范围.
图16-1
第16讲┃ 归类示例
[解析] (1)根据h=2.6和函数图象经过点(0,2),可用待定 系数法确定二次函数的关系式;(2)要判断球是否过球网, 就是求x=9时对应的函数值,若函数值大于或等于网高2.43 ,则球能过网,反之则不能;要判断球是否出界,就是求抛 物线与x轴的交点坐标,若该交点坐标小于或等于18,则球 不出界,反之就会出界;要判断球是否出界,也可以求出x =18时对应的函数值,并与0相比较.(3)先根据函数图象过 点(0,2),建立h与a之间的关系,从而把二次函数化为只含 有字母系数h的形式,要求球一定能越过球网,又不出边界 时h的取值范围,结合函数的图象,就是要同时考虑当x=9 时对应的函数y的值大于2.43,且当x=18时对应的函数y的 值小于或等于0,进而确定h的取值范围.
第16讲┃ 回归教材
[解析] (1)上涨到x元后,所销售的件数是 [300-10(x-80)];每件的销售利润为(x-60) ,所以y=(x-60)·[300-10(x-80)],整理得 y=-10x2+1700x-66000;(2)根据二次函数的 配方法可以求得最大利润.
第16讲┃ 回归教材
解:(1)设上涨后,每件单价为x元,则 y=(x-60)[300-10(x-80)] =(x-60)(300-10x+800) =(x-60)(1100-10x) =-10x2+1700x-66000, 即y=-10x2+1700x-66000. (2)y=-10x2+1700x-66000 =-10(x-85)2+6250. 因为-10<0,所以当x=85时,y有最大值,y最 大值=6250. 即单价定为85元时,每月销售商品的利润最大, 最大利润为6250元.
2 2
第16讲┃ 归类示例
二次函数解决销售问题是我们生活中经常遇 到的问题,这类问题通常是根据实际条件建立二 次函数关系式,然后利用二次函数的最值或自变 量在实际问题中的取值解决利润最大问题.
第16讲┃ 归类示例 ► 类型之三 二次函数在几何图形中的应用
命题角度: 1. 二次函数与三角形、圆等几何知识结合往往是涉及 最大面积,最小距离等; 2. 在写函数解析式时,要注意自变量的取值范围. 例3 [2013· 无锡] 如图16-3,在边长为24 cm的正方形纸 片ABCD上,剪去图中阴影部分的四个全等的等腰直角三 角形,再沿图中的虚线折起,折成一个长方体形状的包装 盒(A、B、C、D四个顶点正好重合于上底面上一点).已 知E、F在AB边上,是被剪去的一个等腰直角三角形斜边 的两个端点,设AE=BF=x cm.
第16讲┃ 归类示例
利用二次函数解决抛物线形问题,一般是先根 据实际问题的特点建立直角坐标系,设出合适的二 次函数的解析式,把实际问题中已知条件转化为点 的坐标,代入解析式求解,最后要把求出的结果转 化为实际问题的答案.
第16讲┃ 归类示例 ► 类型之二 二次函数在营销问题方面的应用
命题角度: 二次函数在销售问题方面的应用.
第16讲┃ 归类示例
解:(1)120×150=18000(元). 答:今年老王种粮可获得补贴18000元. (2)由图象知,y与x之间的函数是一次函数.设所求关系式 为:y=kx+b(k≠0).将(205,1000),(275,1280)两点坐标 代入,这样所求的y与x之间的函数关系式为y=4x+180. (3)W=(2140+120-y)x=(2140+120-4x-180)x=-4x2 +2080x. b 2080 因为-4<0,所以当x=- =- =260(亩) 2a 2×(-4) 4ac-b 0-2080 时,W最大= = =270400(元). 4a 4×(-4) 答:当种粮面积为260亩时,总利润最高,最高总利润为 270400元.
建立平面直角坐标系,把代数问题与几何问题进行互 相转化,充分结合三角函数、解直角三角形、相似、全等 、圆等知识解决问题,求二次函数的解析式是解题关键.
第16讲┃ 归类示例
Байду номын сангаас
归类示例
► 类型之一 利用二次函数解决抛物线形问题 命题角度: 1. 利用二次函数解决导弹、铅球、喷水池、抛球、 跳水等抛物线形问题; 2. 利用二次函数解决拱桥、护栏等问题. [2012·安徽] 如图16-1,排球运动员站在点O处练
第16讲┃ 二次函数的应用
第16讲┃ 考点聚焦
考点聚焦
考点1 二次函数的应用 二次函数的应用关键在于建立二次函数的数学模型, 这就需要认真审题,理解题意,利用二次函数解决实际 问题,应用最多的是根据二次函数的最值确定最大利润 、最节省方案等问题.
第16讲┃ 考点聚焦
考点2 建立平面直角坐标系,用二次函数的图象解决实际问题
[2013·徐州]某网店以每件60元的价格购进一批商品,若以 单价80元销售,每月可售出300件.调查表明:单价每上涨1 元,该商品每月的销售量就减少10件. (1)请写出每月销售该商品的利润y(元)与单价x(元)间的函 数关系式; (2)单价定为多少元时,每月销售商品的利润最大?最大利 润为多少?
第16讲┃ 归类示例
(1)若折成的包装盒恰好是个正方体,试求这个包装盒 的体积V; (2)某广告商要求包装盒的表面(不含下底面)积S最大 ,试问x应取何值?
图16-3
第16讲┃ 归类示例
[解析] (1)根据已知得出这个正方体的底面边长a= 2x cm,EF= 2a= 2x(cm),再利用AB=24 cm,求出x进而可得出这个包装盒的体积V; (2)利用已知表示出包装盒的表面积,进而利用函数最值求出即可. 解:(1)根据题意,知这个正方体的底面边长a= 2 x cm,EF= 2 a=2x (cm), ∴x+2x+x=24 ,x=6,a=6 2 cm, V =a3=(6 2)3=432 2(cm3 ). (2)设包装盒的底面边长为y cm,高为h cm, 则y= 2x,h= 24-2x 2 ∴S=4yh+y2 =4 2x· 2(12-x)+( 2x)2=-6x2+96x= -6(x-8)2+ 384. ∵0<x<12,∴当x=8时,S取得最大值384 cm2. = 2(12-x),
