数理方程练习题
数理方程练习题（1）
数理方程练习题（1）一、填空题1．二阶线性偏微分方程xx xy yy x y Au Bu C u D u Eu Fu G +++++=（其中各系数均为x 和y 的函数）在某一区域的性质由式子：24B AC -的取值情况决定，取值为正对应的是（双曲）型，取值为负对应的是（椭圆）型，取值为零对应的是（抛物）型。
2．在实际中广泛应用的三个典型的数学物理方程：第一个叫（弦自由横振动），表达式为（2tt xx u a B u =），属于（双曲）型；第二个叫（热传导），表达式为（ 2t xx u a B u =），属于（椭圆）型；第三个叫（拉普拉斯方程和泊松方程），表达式为（0x x y yu u+=，(,)xx yy u u x y ρ+=-），属于（椭圆）型；二、选择题1．下列泛定方程中，属于非线性方程的是［ B ］(A) 260t xx u u xt u ++=；(B) sin i t tt xx u u u e ω-+=； (C) ()220y xxxxy u x yuu +++=； (D) 340t x xx u u u ++=；2. 下列泛定方程中，肯定属于椭圆型的是［ D ］(A)0xx yy u xyu +=； (B) 22x xx xy yy x u xyu y u e -+=；(C)0xx xy yy u u xu +-=； (D)()()()22sin sin 2cos xx xy yy x u x u x u x ++=； 3. 定解问题()()()()()()2,0,00,,0,0,,0tt xx x x t u a u t x lu t u l t u x x u x xφ?=><<?==??==?的形式解可写成［ D ］(A) ()01,coscos2n n a n at n x u x t a ll ππ∞==+∑(B) ()001,coscosn n n at n x u x t a b t a llππ∞==++∑(C) ()0,cos sin cos n nn n at n at n x u x t a b l l l πππ∞=?=+∑(D) ()001,cos sin cos n n n n at n at n x u x t a b t a b l llπππ∞=??=+++??∑ 4. 若非齐次边界条件为12(0,)(),(,)()x u t t u l t t μμ==，则辅助函数可取［C ］(A) ()()12(,)W x t t x t μμ=+； (B) ()()21(,)W x t t x t μμ=+；(C) ()()()12(,)W x t x l t t μμ=-+； (D) ()()()21(,)W x t x l t t μμ=-+；三、求解下列问题（1）2,0,tt xx u a u t x =>-∞<<∞ ，其中a 为常数。
数理方程习题全解
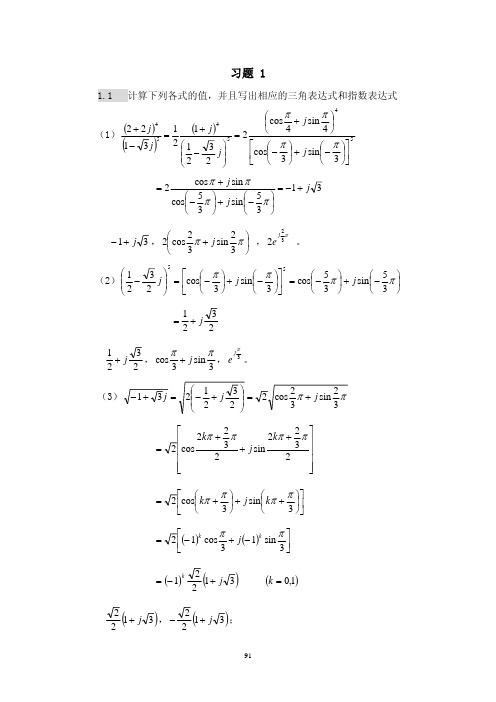
93
2k 1 j sin 2k 1 = 2 cos 4 4
k 0,1,2,3
1 1 k 0 ： z1 2 cos j sin 2 j 1 j 4 4 2 2 3 3 1 1 k 1 ： z2 2 cos j sin 2 j 1 j 4 4 2 2 5 5 1 1 k 2 ： z3 2 cos j sin 2 j 1 j 4 4 2 2 7 7 1 1 k 3 ： z4 2 cos j sin 2 j 1 j 4 4 2 2
3 8
k k 2 8 cos j sin 2 16 2 16
3 3 8 3
k 0,1,2,3
7 7 2 cos j sin ， 2 8 cos j sin ， 16 16 16 16 9 15 15 9 2 cos j sin ， 2 8 cos j sin ； 16 16 16 16
1 3 5 5 （2） j sin cos j sin 2 2 j cos 3 3 3 3 1 3 j 2 2
4
cos j sin 4 4
4
2
cos j sin 1 j 3 5 5 cos j sin 3 3
数理方程练习题(1)
一、填空题1．二阶线性偏微分方程xx xy yy x y Au Bu C u D u Eu Fu G +++++=（其中各系数均为x 和y 的函数）在某一区域的性质由式子：24B AC -的取值情况决定，取值为正对应的是（ 双曲 ）型，取值为负对应的是（ 椭圆）型，取值为零对应的是（ 抛物 ）型。
2．在实际中广泛应用的三个典型的数学物理方程：第一个叫（ 弦自由横振动 ），表达式为（2tt xx u a B u =），属于（双曲）型； 第二个叫（ 热传导 ），表达式为（ 2t xx u a B u =），属于（ 椭圆 ）型； 第三个叫（拉普拉斯方程和泊松方程），表达式为（0x x y yu u+=，(,)xx yy u u x y ρ+=-），属于（椭圆）型；二、选择题1．下列泛定方程中，属于非线性方程的是［ B ］(A) 260t xx u u xt u ++=； (B) sin i t tt xx u u u e ω-+=； (C) ()220y xxxxy u x yuu +++=； (D) 340t x xx u u u ++=；2. 下列泛定方程中，肯定属于椭圆型的是［ D ］(A)0xx yy u xyu +=； (B) 22x xx xy yy x u xyu y u e -+=；(C)0xx xy yy u u xu +-=； (D)()()()22sin sin 2cos xx xy yy x u x u x u x ++=； 3. 定解问题()()()()()()2,0,00,,0,0,,0tt xx x x t u a u t x lu t u l t u x x u x xϕφ⎧=><<⎪==⎨⎪==⎩的形式解可写成［ D ］(A) ()01,coscos2n n a n at n x u x t a ll ππ∞==+∑(B) ()001,coscosn n n at n x u x t a b t a llππ∞==++∑(C) ()0,cos sin cos n nn n at n at n x u x t a b l l l πππ∞=⎡⎤=+⎢⎥⎣⎦∑(D) ()001,cos sin cos n n n n at n at n xu x t a b t a b l llπππ∞=⎡⎤=+++⎢⎥⎣⎦∑ 4. 若非齐次边界条件为12(0,)(),(,)()x u t t u l t t μμ==，则辅助函数可取［C ］ (A) ()()12(,)W x t t x t μμ=+； (B) ()()21(,)W x t t x t μμ=+； (C) ()()()12(,)W x t x l t t μμ=-+； (D) ()()()21(,)W x t x l t t μμ=-+；三、求解下列问题（1）2,0,tt xx u a u t x =>-∞<<∞ ，其中a 为常数。
数理方程30题
u(x,t) = cos at sin x
注记：如果用系数计算公式
∫ ∫ Cn
=
2 L
L sin(ξ ) sin(nξ )dξ
0
， Dn
=
2 nπa
L 0 × sin(nξ )dξ ，（n=1，2，……）
0
会得出同样结论。
例 8．用分离变量法求解双曲型方程初边值问题
⎧u ⎪⎪⎨u
[Cn
n=1
cos
nπ L
t
+
Dn
sin
nπ L
t]sin
nπ L
x
利用初值条件，得
∑ ∑ ∞ Cn
n=0
sin
nπ L
x
=
x(L −
x) ， π L
∞
nDn
n=0
sin
nπ L
x
=
0
为计算系数，首先令ϕ(x) = x(L − x) ，显然ϕ(0) = 0,ϕ(L) = 0 ，且
ϕ′(x) = L − 2x ，ϕ′′(x) = −2
x x
+ +
C1 C2
⎡ ∂ξ
构造变换：
⎧ξ ⎩⎨η
= =
2 sin 4 sin
x x
+ +
cos cos
y y
，
⎢ ⎢ ⎢
∂x ∂η
⎢⎣ ∂x
∂ξ ⎤
∂y ∂η
⎥ ⎥ ⎥
=
⎡2 ⎢⎣4
cos cos
x x
∂y ⎥⎦
− sin y⎤ − sin y⎥⎦
所以， a12 = 8sin 2 y cos2 x − 18cos2 x sin 2 y + 8cos2 x sin 2 y = −2 cos2 x sin 2 y
数理方程期末试题
数理方程与特殊函数试题（行波法与付氏变换）（2008-10-27）一、（15分）求解初值问题：⎩⎨⎧==>∞<<-∞+===x t t t xx tt xeu x u t x x u u 00|,sin |)0,(sin 解：令 u (x ，t ) = v (x ，t ) + w (x )，……………………………………………………（2分） 代入原方程，得v tt = [v xx + w xx ] + sin x ………………………………（2分）所以取 w (x ) = sin x ，……………………………………………………………………（2分） 得v (x ，t )满足的初值问题⎪⎩⎪⎨⎧===x t xx tt xex v x v v v )0,(0)0,(…………………………………………（2分） 由达朗贝尔公式，得⎰+--+-++---+==t x t x t x t x t x t x e e e t x e t x d e t x v ])()[(2121),(ξξξ…………（3分） ])1()1[(21t x t x e t x e t x -++---+=………………（2分） 所以u (x ，t ) = v (x ，t ) + w (x )x e t x e t x t x t x sin ])1()1[(21++---+=-+……（2分）二、（15分）求解半无界弦定解问题：⎪⎪⎩⎪⎪⎨⎧===>∞<<====0sin ,cos )0,0(0002x x t t t xx tt u x u x u t x u a u 解：对初始条件中函数做偶延拓⎩⎨⎧<≥=0,cos 0,cos )(x x x x x ϕ…………………………………………（2分） ⎩⎨⎧<-≥=0,sin 0,sin )(x x x x x ψ………………………………………（2分） 应用达朗贝尔公式，当x >0，且 x > at 时，有⎰+-+-++=at x at x d aat x at x t x u ξξsin 21)]cos()[cos(21),(………………（2分） )]cos()[cos(21cos cos at x at x aat x --+-+=………………（2分）at x aat x sin sin 1cos cos -=……………………………………（1分） 当x >0，且 x < at 时，有 ⎰⎰+--+-++=at x at x d d a at x at x t x u 00sin sin [21)]cos()[cos(21),(ξξξξ……（4分） )]cos(11)[cos(21cos cos at x at x aat x -+--+-+=………………（2分） )cos cos 1(1cos cos at x a at x -+=……………………………………（2分）三、（15分）记)]([)(ˆx f F f=ω 1．证明)](ˆ)(ˆ[)]([ωωωf fx f x F '+-='； 2． 用付里叶变换方法求解方程0='-''y x y 。
数理方程模拟试题1X
200__～200__学年第___学期《数理方程》期末模拟试卷1 题号 一 二 三 四 五 六 总分 得分一、 选择题(每题只有一个正确答案， 每小题4分，共28分）1、34233(,,)v v v xyv g x y z x x y z ∂∂∂+++=∂∂∂∂ 是( )偏微分方程 A 、 一阶 B 、二阶 C 、 三阶 D 、 四阶 2、2(,)tt xx u a u x t ϕ-= (其中0>a ) 属于( )型偏微分方程 A 、 抛物 B 、双曲 C 、 椭圆 D 、 混合 3、在用分离变量法求解定解问题200,0,0|0,|0|()t x x x x xl t u a u x l t u u u x ϕ===⎧=<<>⎪==⎨⎪=⎩时，得到的固有函数系为( )A 、,...2,1,sin=⎭⎬⎫⎩⎨⎧n x l n π B 、,...2,1,0,cos=⎭⎬⎫⎩⎨⎧n x l n π C 、(21)cos,1,2,...2n x n l π-⎧⎫=⎨⎬⎩⎭D 、 (21)sin,1,2,...2n x n l π-⎧⎫=⎨⎬⎩⎭4、下列方程是非线性偏微分方程的是（ ） A 22()()sin u u x x y 抖+=抖 B (,)u u f x y x y抖+=抖 C 22(,)(,)cos u u a x t b x t x x t 抖+=抖 D 3433(,,)v v v g x y z x x y z∂∂∂++=∂∂∂∂ 5、对Laplace 变换的性质下列式子错误的是（ ） A 22[sin ](Re 0)L t p p ww w =>+B []2[][]L f g L f L g p *=?C 0[()]()(Re )p L f t e F p p tt g --=>D 0000[()]()(Re Re )p t L e f t F p p p p g =->+6、在弱相等意义下，对d 函数的说法错误的是（ ） A ()()x x d d =- B ()x x x d = C 1()()(0)||ax x a a d d =? D ()()()()x x a a x a j d j d -=-7、给出未知函数 u 在区域Ω的边界Γ上的值0,),,(|≥Γ∈=Γt M t M u μ 的边界条件，称为第( )类边界条件。
西安邮电大学期末数理方程试题+答案
数学物理方程与特殊函数09级试题选讲一、求解定解问题22200,0,(0,0)x x lt u u a t x u u x l t xx u x ===춶=ﶶﶶï==<<>í¶¶ïï=ïî)()(),(t T x X t x u =)()()()(2t T x X a t T x X ¢¢=¢22)()()()(b -=¢¢=¢x X x X t T a t T 0>b 设，代入原方程得，则)()(22=+¢t T a t T b 0)()(2=+¢¢x X x X b 则，0x x lu u xx==¶¶==¶¶'(0)'()0X X l Þ==又因为得固有值问题2()()0'(0)'()0X x X x X X l b ¢¢ì+=í==î22)(ln pb =()cos 0,1,2,n n n xX x A n lp ==则固有值固有函数，数学物理方程与特殊函数09级试题选讲)()()(2=+¢t T la n t T p 2()()n a tl n T t C ep -Þ=2()01(,)cosn a tln n n x u x t C C elp p ¥-==+å从而0t ux==有因为01cosnn n x x C C lp ¥==+å所以220022[(1)1]cos 12n ln l n x l C x dx l l nl C xdx lp p --====òò2()2212(1)1(,)cos 2n a ntln l l n xu x t enlp p p¥-=--=+å数学物理方程与特殊函数09级试题选讲二、求解定解问题2222,,0(),0(),0(0)(0)t x t x u ut x t t t x ux x u x x =-=춶=-<<>ﶶïï=F £íï=Y ³ïïF =Y î解：特征变换为x t x tx h =-ìí=+î2u x h¶=¶¶原方程化为12()()u f f x h =+则它的通解为00(),()()(),()()2222t xt x ux u x u u h x x h x h x h=-====F =Y +-Þ=F =F =Y =Y 又因为数学物理方程与特殊函数09级试题选讲1212(0)()()2()(0)()2f f f f h h xx +=Y +=F 2112()()(0)2()()(0)2f f f f h h x x ì=Y -ïïÞíï=F -ïî12()()((0)(0))22()()(0)22u f f x t x tx h=F +Y -+-+=F +Y -F 则它的解为三、求解定解问题)0,(,0,3,03202022222>+¥<<-¥ïïïîïïíì=¶¶==¶¶-¶¶¶+¶¶==y x y ux u y uy x u x u y y 解：原方程的特征方程为22()23()0dy dydx dx --=13C x y +=2C x y +-=，则特征线为3x y x yx h =-ìí=+î特征变换20ux h¶=¶¶原方程化为12()()u f f x h =+则它的通解为数学物理方程与特殊函数09级试题选讲12(,)(3)()u x y f x y f x y =-++即203,y y u ux y==¶==¶又因为21212(3)()3(3)()0f x f x xf x f x ì+=í¢¢-+=î则可得C x x f¢-=2149)3(C x x f ¢+=2243)(C x x f¢-=2141)(222234)(34)3(),(yx y x y x y x u +=++-=22()()C Du vv u u v d v u ds n n s ¶¶Ñ-Ñ=-¶¶òòò 四、证明平面上的格林公式其中n 为曲线的外法线向量。
数理方程题库
第一章定义和方程类型1、34233(,,)v v v xyv g x y z x x y z∂∂∂+++=∂∂∂∂ 是( D )偏微分方程 A 、 一阶 B 、二阶 C 、 三阶 D 、 四阶 1、22(,,)vxy v g x y z z∂+=∂ 是( A )偏微分方程 A 、 一阶 B 、二阶 C 、 三阶 D 、 四阶1、33232(,,)v v vv xyv g x y z x x y z ∂∂∂+++=∂∂∂∂ 是( C )偏微分方程A 、 一阶B 、二阶C 、 三阶D 、 四阶 2、2(,)txx u a u f x t -= (其中0>a ) 属于( A )型偏微分方程A 、 抛物B 、双曲C 、 椭圆D 、 混合 2、2(,)ttxx u a u x t ϕ-= (其中0>a ) 属于( B )型偏微分方程A 、 抛物B 、双曲C 、 椭圆D 、 混合2、22(,,)tt xx u a u x y t ϕ+= (其中0>a ) 属于( C )型偏微分方程 A 、 抛物 B 、双曲 C 、 椭圆 D 、 混合 2、(,)xx yy u u f x y += (其中(,)u u x y =) 属于( C )型偏微分方程A 、 抛物B 、双曲C 、 椭圆D 、 混合 4、下列方程是非线性偏微分方程的是（ A ）A 22()()sin u u x x y 抖+=抖 B (,)u uf x y x y抖+=抖 C 22(,)(,)cos u ua x tb x t x x t抖+=抖 D 3433(,,)v v v g x y z x x y z ∂∂∂++=∂∂∂∂ 7、下列方程是非齐次方程的是（ A ）A(,)(,)0u uxy f x y f x y x y 抖+=?抖， B 2,0t xx u a u a =?C 22(,)(,)0u u a x t b x t x t 抖+=抖 D 34330v v v x x y z ∂∂∂++=∂∂∂∂3、在用分离变量法求解定解问题200,0,0|0,|0|()t xx x x x l t u a u x l t u u u x ϕ===⎧=<<>⎪==⎨⎪=⎩时，得到的固有函数系为( D ) A 、,...2,1,sin=⎭⎬⎫⎩⎨⎧n x ln π B 、,...2,1,0,cos=⎭⎬⎫⎩⎨⎧n x l n π C 、{},...2,1,sin =n x n π D 、 ,...2,1,2)12(sin =⎭⎬⎫⎩⎨⎧-n x ln π 3、在用分离变量法求解定解问题⎪⎩⎪⎨⎧====><<=====)(|),(|0|,0|0,0,0002x u x u u u t l x u a u t t t l x x x x xx tt ψϕ时，得到的固有函数系为( B )A 、,...2,1,sin=⎭⎬⎫⎩⎨⎧n x l n πB 、,...2,1,0,cos=⎭⎬⎫⎩⎨⎧n x l n πC 、(21)cos ,1,2,...2n x n l π-⎧⎫=⎨⎬⎩⎭ D 、 ,...2,1,2)12(sin =⎭⎬⎫⎩⎨⎧-n x l n π3、在用分离变量法求解定解问题⎪⎩⎪⎨⎧===><<====)(|0|,0|0,0,002x u u u t l x u a u t l x x xx t ϕ时，得到的固有函数系为( A )A 、,...2,1,sin=⎭⎬⎫⎩⎨⎧n x l n π B 、,...2,1,0,cos=⎭⎬⎫⎩⎨⎧n x l n πC 、(21)cos,1,2,...2n x n l π-⎧⎫=⎨⎬⎩⎭ D 、,...2,1,2)12(sin=⎭⎬⎫⎩⎨⎧-n x l n π7、给出未知函数 u 在区域Ω的边界Γ上的值0,),,(|≥Γ∈=Γt M t M u μ 的边界条件，称为第( A )类边界条件。
数理方程试题
专业年级_____________学号_____姓名__________考试日期______年___月__日分数______
一、指出下列方程的类型（16分）
1、
2、
3、
4、
二、对下列二阶线性偏微分方程，试判断其所属类型（16分）
1、
2、
3、
4、
三、基于一维波动方程柯西问题的D’Alembert公式，试在x、t坐标平面上画出点（x,t）的依赖区域、区间[x1,x2]的决定区域和区间[x1,x2]的影响区域，并说明相应的含义。（12分）
四、试用特征线法求解柯西问题（20分）
五、已知一长为l的细杆，其初始温度分布为φ（x），杆的一段保持零度，另一端绝热，试给出相应的定解问题并用分离变量法求解。（20分）
六、试用Fourier变换求定解问题（16分）
（已知： ）
授课
教师
命题教师或命题负责人
签字
院系负责人
签字
年月日
注：请命题人标明每道考题的考分值。
高考数学真题汇编 4：方程 理 试题
高考数学真题汇编 4：方程理试题
本文档将为您提供一些高考数学方程理论部分的真题试题。
以
下是一些典型的高考数学方程试题，供您参考和练。
第一部分：一元一次方程
1. 已知方程 $3x - 7 = 2x + 1$，求解此一元一次方程并给出结果。
2. 某商品的原价为$x$元，现在打七折出售，售价为630元，
求$x$的值。
3. 解方程 $\frac{x}{2} + \frac{x}{3} = x - 5$，给出$x$的解。
第二部分：一元二次方程
1. 求解方程 $x^2 - 5x + 6 = 0$，给出所有解。
2. 若方程 $2x^2 + kx + 8 = 0$ 的解为$x = 3$ 和$x =
\frac{2}{3}$，求$k$的值。
3. 解方程 $4x^2 + 8x + 3 = 0$，给出所有解。
第三部分：其他方程
1. 解方程 $\sqrt{x} + \sqrt[3]{x} = 5$，求出所有$x$的解。
2. 若方程 $2^x + 2^{-x} = 2$ 的解为$x = 1$ 和$x = -1$，求另一组解。
3. 解方程 $2^x + 3 \cdot 2^{-x} = 3$，给出$x$的解。
以上是一些高考数学方程的典型试题。
希望这些题目对您的练和准备有所帮助。
如果需要更多相关的试题或者有其他问题，请随时告诉我。
祝您学业有成，考试顺利！。
数理方程课后习题(带答案)
u0 X0T0 B0A0 C0
0
Tn
a2n22
l2
Tn
0
a2n22 t
Tn Ane l2
un XnTn
ABea2nl222t nn
cons l
xCea2nl222t n
cosn
l
x
un 0unC 0n 1Cnea2n l2 22tconlsx
数学物理方程与特殊函数
第2章习题选讲
u(uutx(,0x0,)at)2xx,20u2,,u(lx,t) 0,
由此可得：w (x)1
xt
dt
f()dC xA ,
a2 0 0
其中
C1 l(BAa 1 2 0 ldt0 tf()d),
数学物理方程与特殊函数
第2章习题选讲
然后用分离变量解
v(vt0,t)a2
2v x2 , 0, v(l,
t)
0,
0 x l,t 0 t 0
v(x,0) g(x) w(x), 0 x l
0xl1,0yl2 0yl2
u(x,0)0,u(x,l2)(x), 0xl1
uXY
XX0,
X(0)X(l1)0
0xl1
YY0
n n2 nl1 2,n1,2,3,L
n
Xn An sin l1 x
Yn
n2 2
l12
Yn
0
ny
ny
Yn Cnel1 Dne l1
数学物理方程与特殊函数
第2章习题选讲
un 1unn 1Cnenl1 yD nenl1 ysinnl1 x u(x,0)n 1CnDnsinnl1x0 u(x,l2)(x)n 1 C nenl1l2D nenl1l2 sinn l1x
数理方程练习题(作业)
数理方程练习题一（2009研）1. 设(,)u u x y =，求二阶线性方程20ux y∂=∂∂ 的一般解。
2. 设u f = 满足Laplace 方程22220u u x y ∂∂∂∂+=求函数u.3. 求Cauchy 问题22000(,)(0,)cos tt xx t t t u a u x t u x u x x ==⎧-=∈⨯∞⎪⎨==∈⎪⎩的解．4. 求解Cauchy 问题200cos (,)(0,)cos 010tt xx t t t u a u t x x t x x u x u x ==⎧-=∈⨯∞⎪≥⎧⎨==⎨⎪<⎩⎩5. 解在半无界问题20000(,)(0,)sin (0)0(0)tt xx t t t x u a u x t u x u x x u t +===⎧+=∈⨯∞⎪⎪==≤≤∞⎨⎪=≥⎪⎩6. 求解二维Cauchy 问题222200(,,)(0,)0()(,)tt t t t u a u x y t u u x x y x y ==⎧-∆=∈⨯∞⎪⎨==+∈⎪⎩求下列函数的Fourier 变换1 0()00axe xf x a x -⎧≥=>⎨<⎩2 1||()0||a x a x x a≤⎧∏=⎨>⎩3 2()x f x e -=7. 磁致伸缩换能器、鱼群探测换能器等器件的核心是两端自由的均匀杆，它作纵振动．研究两端自由棒的自由纵振动，即定解问题。
200,0(,0)(),(,0)()0(0,)(,)00tt xx t xx u a u x l t u x x u x x x l u t u l t t ϕψ⎧-=<<>⎪==≤≤⎨⎪==≥⎩8. 散热片的横截面为矩形。
它的一边y=b 处于较高温度V ，其他三边b=0，x=0，x=a 则处于冷却介质中因而保持较低的温度v 求解这横截面上的稳定温度分布Ux,y)即定解问题0;0(0,),(,)0(,0),(,)()0xx yy u u x a y b u y v u a y vy b u x v u x b V x x a +=<<<<⎧⎪==<<⎨⎪==<<⎩9. 求解定解问题2000cos sin 0,00,0ttxx x x x x l t t t x u a u A t lu u u u πω====⎧-=⎪⎪⎪==⎨⎪'==⎪⎪⎩10. 求解定解问题200sin 0,00t xx x x x l t u a u A tu u u ω===⎧-=⎪⎪==⎨⎪=⎪⎩ 11. 弦的x=0端固定而x=l 端受迫作谐振动sin A t ω，则弦的初始位移和初始速度都是零，求弦的振动。
数理方程试题
数理方程试题一．判断题（每题2分）.1. 2u u x y x y x+=是非线性偏微分方程.( )2. 绝对可积函数一定可做Fourier 积分变化.( )3. ()(1) 1.n n F x n Legendre F =是次正交多项式，则 ( )4. (,)0xy f x y =的解是调和函数.( )5. **12u u 已知,是线性偏微分方程(,)xx yy u u f x y +=的解，则**12u u -是0u ?= 的解.( )二．填空题（每题2分）.1. ()sin t xx yy u u u xt -+= 是____________型偏微分方程.2. 内部无热源的半径为R 的圆形薄板,内部稳态温度分布，当边界上温度为()t φ时，试建立方程的定解问题________________________.3. 2x 的Legendre 正交多项式的分解形式为__________________.4.某无界弦做自由振动,此弦的初始位移为()x φ,初始速度为()a x φ-,则弦振动规律为______________________________.5. []()____________.at m L e t s = 三．求解定解问题（12分）20sin ;0,0;0.t xx xx xx lt u a u A t u u u ω===-====四．用积分变换方法求解以下微分方程（每题12分，共24分）（1）1,0,0;1,1.xy x y u x y uy u===>>=+=（2） 00230, 1.tt t y y y e y y =='''+-='==五．某半无界弦的端点是自由的，初始位移为零，初始速度为cos x ，求弦的自由振动规律。
（12分）六．设有长为a ，宽为b 的矩形薄板，两侧面绝热，有三边的温度为零，另一边的温度分布为x ，内部没有热源，求稳定状态时板内的温度分布。
数理方程习题
uyy + uzz = 0的解; (3) un (r, θ) = rn cos(nθ)), rn sin(nθ)) (n = 0, 1, 2, · · · )是拉普拉斯方程urr +
1 r ur 1 u r2 θθ
+
= 0的解. ut = −uxx , u(x, 0) = 1,
10. 说明定解问题
− auxx = 0的解.
((x, y ) ̸= (0, 0)), eax cos(ay ), eax sin(ay )均是二维 ((x, y, z ) ̸= (0, 0, 0))是三维拉普拉斯方程uxx +
拉普拉斯方程uxx + uyy = 0的解; (2) u(x, y, z ) = √
1 x2 + y 2 + z 2
证. (方法一) 极坐标系与直角坐标系之间的变换关系为 x = r cos θ, 或者为 r = (x2 + y 2 ) 2 , 于是 ∂r x = = cos θ, ∂x r ∂θ y sin θ =− 2 =− , 2 ∂x x +y r 从而 ∂u ∂r ∂u ∂θ ∂u ∂u sin θ ∂u = + = cos θ − , ∂x ∂r ∂x ∂θ ∂x ∂r ∂θ r ∂u ∂u ∂r ∂u ∂θ ∂u ∂u cos θ = + = sin θ + , ∂y ∂r ∂y ∂θ ∂y ∂r ∂θ r ∂r y = = sin θ, ∂y r ∂θ x cos θ = 2 = . 2 ∂y x +y r
习题1
1. 对下列偏微分方程, 指出它的阶, 并指出它是线性的、拟线性的还是非线性 的. 若是线性的, 再指出它是齐次的还是非齐次的. (1) u3 x + 2uuy = xy ; (2) uuy − 6xyux = 0; (3) uxx − x2 uy = sin x;
数理方程习题答案
习题4.11．（2）解：根据一维波动方程的达朗贝尔公式有()[]()[]11,()()221155225+x atx at x atx at u x t x at x at d a d atxϕϕψξξξξ+-+-=++-+=++=⎰⎰ 6.（1）解：根据一维波动方程一般强迫振动的解公式有()[]()()()()[]()()()020232211,()()221,21115522215232x atx at t x a t x a t x at t x a t x at x a t x at x at x u x t x at x at d a f d d a d e d d a a a t x t e e e aτττατϕϕψξξατατξξατ+-+---++----+-=++-+⎡⎤+⎢⎥⎣⎦⎡⎤=+++⎢⎥⎣⎦=++++-⎰⎰⎰⎰⎰⎰习题4.21. 解:根据端点固定的半无界弦的自由振动的解公式有()()()()()()()()()()()11,22,11,2211sin sin cos ,2211sin sin cos ,22c sin cos x at x at x at at x x at x at x at at x x x at x at d t a au x t xx at at x d t a a x x at x at d t a ax x at at x d t a a x at ϕϕψξξϕϕψξξξξξξ+-+-+-+-⎧++-+≤⎡⎤⎣⎦⎪⎪=⎨⎪+--+>⎡⎤⎣⎦⎪⎩⎧++-+≤⎡⎤⎣⎦⎪⎪=⎨⎪+--+>⎡⎤⎣⎦⎪⎩+=⎰⎰⎰⎰os sin ,sin cos sin cos ,x at x t a a x at xx at t a a ⎧≤⎪⎪⎨⎪+>⎪⎩2．解：齐次波动方程2tt xx u a u =的通解为()()()12,u x t f x at f x at =++-由初始条件有当0x ≥时的()1f x 和()2f x 都为0，但x a t -可正可负。
南京信息工程大学数理方程期终考试试卷
南京信息工程大学数理方程期终考试试卷A 2008年12月任课教师学生所在系专业年级班级学生姓名学号一、填空题（共60分）1.方程44442242(,)uu uf x y xx yy是四阶线性（“线性”或“非线性”）非齐次（“齐次”或“非齐次”）偏微分方程（3分）；2.方程222220uuatx的全部解可写为(,)u x y =()()f xat g x at （,f g 是任意二阶连续可微函数）；（3分）3.二维Laplace 方程22220uuux y的基本解为(,)u x y =2211ln2xy；（3分）4.若(,)i u x t 是非齐次波动方程22222(,)i uuaf x t tx的解，则1(,)i i i c u x t 满足的微分方程是222221(,)i i n uuac f x t tx；（3分）5.方程2222223260uuuu u xx y yxy 的类型属于双曲型或波动方程，其特征方程为3dy dx或1dy dx，特征曲线为13yxc 和2yxc ，可以将其化为标准型的自变量变换为3y x yx ，若要消去一阶导数项，可以通过函数变换(,)(,)u v e（其中,待定）；（5分）6.定解问题2,0(,0)(),(,0)()ttxxt u a u x t u x x u x x x属于初值问题（“初值”或“边值”），其解的表达式为(,)u x y =11[()()]()22x at x atx at x at da；定解问题0ux u fxn属于Dirichlet 边值问题（“Dirichlet ”或“Neumann ”），其中为的边界，若其存在古典解，则f 一定满足fds ；（4分）7.若(,,)hh x t 满足初值问题2,0|0,|(,)ttxx tth a h x t h h f x xt ，则(,)(,,)t w x t h x t d满足的定解问题为2(,),0|0,|0tt xx tt tw a w f x t x t w w x（4分）8.对于端点自由的半无界弦振动问题，通过偶延拓（“奇延拓”或“偶延拓”）的方法，可以转化为无界弦振动问题；我们可以借助于三维波动方程初值问题解的Pisson 表达式来获得二维波动方程初值问题解的表达式，这种方法称为降维法；（3分）9.用分离变量法求定解问题20,0(0,)0,(,)0(,0)(),(,0)()ttxxt u a u x l t u t u l t t u x x u x x xl时，得到关于()X x 的特征值问题是"()()00(0)()X x X x xlX X l ，由此可以得到相应的特征值n=2(),1,2,n nl，特征函数()n X x = sinn x l；用分离变量法求定解问题212,0(0,)(),(,)()0(,0)(),(,0)()ttxxt u a u x l tu t t u l t t t u x x u x x xl 时，首先通过函数变换(,)(,)(,)u x t v x t w x t ，将其转化为(,)v x t 的齐次边界条件的定解问题，则可选为(,)w x t = 211()()()t t t x l；用分离变量法求解稳定的非齐次定解问题20,0(0,)0,(,)20(,0)(),(,0)()ttxxt u a u xx l t u t u l t t u x x u x x xl时，通过函数代换(,)(,)()u x t v x t w x ，可以将其转化为齐次方程，齐次边界条件的定解问题，其中()w x =；（8分）10.三维调和方程2222220uuuux y z的解的积分表达式为0()u M = ，其中0M ，为的边界，若区域上的Green 函数记为0(,)G M M ，则（1）0(,)G M M dS n=；(2)定解问题0|()xu xu f x 的解的表达式为0()u M =，其中n 为边界上的单位外法向量；（6分）11.作出四分之一平面(0,0)x y 的Green 函数为；（3分）12.用Fourier 变换求解偏微分方程定解问题时，是通过Fourier 变换把解偏微分方程的定解问题转化为含参数的常微分方程的定解问题，则对KdV 方程的初值问题20,06(,0)()txxxxahax t x f x x关于x 进行Fourier 变换后的形式为；（3分）13.()f x 的Fourier 变换定义为()F =，()f x 与()g x 的卷积定义为()f g x =，若()(()),()(())F F f x G F g x ，则1(()())F F G =；（3分）14.||[]x F e =；1[]tF e= ；（4分）15.已知2241[]2ax aF eea，则2[]ax bx cF e=；221[]atF e= ；（4分）二，用D ’Alembert 公式求解下列弦振动方程;（10分）xxx u x x u t x u a u t xxtt)0,(,sin )0,(0,2三，（1）写出建立上半平面Green 函数的详细过程；（2）用Green 函数法求解下列定解问题;（15分）00|()xx yyyu u y u f x 四，利用Fourier 变换求解下列定解问题；（15分）22,0(,0)1t xx u c u x t u x xx22222221122122()(),11ln 2(,)30,03(0,)(),(,)()0(,0)(),(,0)()0(,)(,)(),1,2,s i i n ttxxt f x at g x at f gxy uua c f x t t xyx c y x c u a u x l t y x u t t u l t t t yxu x x u x x x ln u v e n l 2211in11[()()]()22(,),0|0,|0()()()x at x attt xx tt tn xlx at x at d a w a w f x t x tfds w w xt t t xl。
数理方程作业答案
1．一根水平放置长度为L 的弦(两端被固定) ，其单位长 度的重力为ρ g ，其ρ 中是弦的线密度，g 是重力加速 度。
若弦的初始形状如图所示： （1）推导出弦的微振动方程； （2）写出定解问题。
解：（1）设弦的微震动方程为：22222(,)u u f x t t xα∂∂=+∂∂ 依题意(,)f x t =-g ，所以弦的微震动方程为：22222u u g t xα∂∂=-∂∂ （2）根据所给图形，利02()(,)|t L x u x t hL=-= 依题意，刚开始时，v=0.，所以0(,)|0t u x t t=∂=∂又弦的两端固定，所以0(,)|0x u x t ==，(,)|0x L u x t == 所以定解问题为：22222u u g t xα∂∂=-∂∂ 02(,)|t x u x t hL == 02Lx ≤≤ 02()(,)|t L x u x t h L =-= 2Lx L ≤≤0(,)|0t u x t t=∂=∂ 用相似三角形，得：当02L x ≤≤，02(,)|t xu x t h L==；当2L x L ≤≤时，0(,)|0x u x t ==，(,)|0x L u x t ==2.设有一个横截面积为S ，电阻率为r 的匀质导线，内有电流密度为j 的均匀分布的直流电通过。
试证明导线内的热传导方程为：222u ucp k j r t x∂∂-=∂∂其中c ，ρ ，k 分别为导线的比热，体密度，及热传导系数解：设导线内的热传导方程为：22(,)u k uf x t t c x ρ∂∂=+∂∂ 依题意，(,)f x t =2j rc ρ将其代入得222u ucp k j r t x∂∂-=∂∂3．长度为L 的均匀杆，侧面绝热，其线密度为ρ、 热传导系数为k 、比热为c 。
（1）推导出杆的热传导方程；（2）设杆一端的温度为零，另一端有恒定热流 q 进入（即单位时间内通过单位面积流入 的热量为q ），已知杆的初始温度分布为()2x L x - ，试写出相应的定解问题。
数理方程习题综合知识交流
数理方程习题综合例 1.1.1 设v=v(线x,y),二阶性偏微分方程v xy =xy 的通解。
解 原方程可以写成 ð／ðx（ðv／ðy） =xy两边对x 积分，得v y =¢（y ）+1/2 x 2Y ,其中¢（y ）是任意一阶可微函数。
进一步地，两边对y 积分，得方程得通解为v （x,y ）=∫v y dy+f （x ）=∫¢（y ）dy+f （x ）+1/4 x 2y 2=f （x ）+g （y ）+1/4 x 2y 2其中f （x ）,g （y ）是任意两个二阶可微函数。
例1.1.2即 u(ξ,η) = F(ξ) + G(η),其中F(ξ),G(η)是任意两个可微函数。
例1.2.1设有一根长为L 的均匀柔软富有弹性的细弦，平衡时沿直线拉紧，在受到初始小扰动下，作微小横振动。
试确定该弦的运动方程。
取定弦的运动平面坐标系是O XU ,弦的平衡位置为x 轴，弦的长度为L ，两端固定在O,L 两点。
用u(x,t)表示弦上横坐标为x 点在时刻t 的位移。
由于弦做微小横振动，故u x ≈0.因此α≈0，cos α≈1,sin α≈tan α=u x ≈0,其中α表示在x 处切线方向同x 轴的夹角。
下面用微元法建立u 所满足的偏微分方程。
在弦上任取一段弧'MM ,考虑作用在这段弧上的力。
作用在这段弧上的力有张力和外力。
可以证明，张力T 是一个常数，即T 与位置x 和时间t 的变化无关。
事实上，因为弧振动微小，则弧段'MM 的弧长dx u xx x x ⎰∆++=∆21s ≈x ∆。
这说明该段弧在整个振动过程中始终未发生伸长变化。
于是由Hooke 定律，张力T 与时间t 无关。
因为弦只作横振动，在x 轴方向没有位移，故合力在x 方向上的分量为零，即T(x+x ∆)cos α’-T(x)cos α=0.由于co's α’≈1，cos α≈1,所以T(X+∆x)=T(x),故张力T 与x 无关。
数理方程习题综合
例 1.1.1 设v=v(线x,y),二阶性偏微分方程v xy =xy 的通解。
解 原方程可以写成 ð／ðx（ðv／ðy） =xy 两边对x 积分，得 v y =¢（y ）+1/2 x 2Y ,其中¢（y ）是任意一阶可微函数。
进一步地，两边对y 积分，得方程得通解为v （x,y ）=∫v y dy+f （x ）=∫¢（y ）dy+f （x ）+1/4 x 2y 2=f （x ）+g （y ）+1/4 x 2y 2其中f （x ）,g （y ）是任意两个二阶可微函数。
例1.1.2即 u(ξ,η) = F(ξ) + G(η),其中F(ξ),G(η)是任意两个可微函数。
例1.2.1设有一根长为L 的均匀柔软富有弹性的细弦，平衡时沿直线拉紧，在受到初始小扰动下，作微小横振动。
试确定该弦的运动方程。
取定弦的运动平面坐标系是O XU ,弦的平衡位置为x 轴，弦的长度为L ，两端固定在O,L 两点。
用u(x,t)表示弦上横坐标为x 点在时刻t 的位移。
由于弦做微小横振动，故u x ≈0.因此α≈0，cos α≈1,sin α≈tan α=u x ≈0,其中α表示在x 处切线方向同x 轴的夹角。
下面用微元法建立u 所满足的偏微分方程。
在弦上任取一段弧'MM ,考虑作用在这段弧上的力。
作用在这段弧上的力有张力和外力。
可以证明，张力T 是一个常数，即T 与位置x 和时间t 的变化无关。
事实上，因为弧振动微小，则弧段'MM 的弧长dx u xx xx ⎰∆++=∆21s ≈x ∆。
这说明该段弧在整个振动过程中始终未发生伸长变化。
于是由Hooke 定律，张力T 与时间t 无关。
因为弦只作横振动，在x 轴方向没有位移，故合力在x 方向上的分量为零，即T(x+x ∆)cos α’-T(x)cos α=0.由于co's α’≈1，cos α≈1,所以T(X+∆x)=T(x),故张力T 与x 无关。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二章 定解问题与偏微分方程理论
习题2.1
1. 密度为ρ均匀柔软的细弦线x =0端固定，垂直悬挂，在重力作用下，于横向拉它一下，使之作微小的横振动。
试导出振动方程。
2. 长为L ，均匀细杆，x = 0端固定，另一端沿杆的轴线方向被拉长b 静止后（在弹性限度内）突然放手，细杆作自由振动。
试写出振动方程的定解条件。
3. 长为L 、密度为ρ的底半径为R 的均匀圆锥杆（轴线水平）作纵振动，锥的顶点固定在x =0处。
导出此杆的振动方程。
4. 一根长为L 、截面面积为1的均匀细杆，其x =0端固定，以槌水平击其x =L 端，使之获得冲量I 。
试写出定解问题。
习题2.2
1. 一半径为r ，密度为ρ，比热为c ，热传导系数为k 的匀质圆杆，如同截面上的温度相同，其侧面与温度为u 1的介质发生热交换，且热交换的系数为k 1。
试导出杆上温度u 满足的方程。
4. 设有一根具有绝热的侧表面的均匀细杆，它的初始温度为)(x ϕ，两端满足下列边界条件之一：
（1）一端（x =0）绝热，另一端（x = L ）保持常温u 0；
（2）两端分别有热流密度q 1和q 2进入；
（3）一端（x =0）温度为u 1(t )，另一端（x = L ）与温度为)(t θ的介质有热交换。
试分别写出上述三种热传导过程的定解问题。
习题2.4
1. 判断下列方程的类型：
（1）04=+++++u cu bu au au au y x yy xy xx ；
（2）02=+++++u cu bu au au au y x yy xy xx ；
（3）02222=+++++u au bu au au au y x yy xy xx ；
（4）0=+yy xx xu u 。
2. 求下列方程的通解
（1）0910=++yy xy xx u u u ；
（3）0384=++yy xy xx u u u 。
第三章 分离变量法
习题3.1
2. 求解下列定解问题
（1）⎪⎪⎩⎪⎪⎨⎧-====><<=====)
(,00)0,0(,0002x L x u u u u t L x u a u t t t L x x xx tt
3. 求下列边值问题的固有值和固有函数：
（1）⎩⎨⎧===+''==0
,000L x x X X X X λ （3）⎩⎨⎧0,0012===+'+''==e x x y y y y x y x λ 习题3.2
1.求定解问题：
⎪⎩⎪⎨⎧-===><<====)
(0
,0)0,0(,002x L x u u u t L x u a u t L x x xx t 习题3.5
2. 求解定解问题：
⎪⎩⎪⎨⎧===><<=+-===-0
0020
,0)0,0(,0T u u u t L x Ae u a u t L x x x t xx α 0T 是常数。
3. 求解定解问题：
2000cos sin ,(0,0)0,00,0
tt xx x x x x L t t t x u a u A t x L t L u u u u πω====⎧=+<<>⎪⎪==⎨⎪==⎪⎩
习题3.6
2. 求解定解问题： ⎪⎩⎪⎨⎧====><<+=====)
(),(,)0,0(),(002102x u x u M u M u t L x x f u a u t t t L x x xx tt ψϕ
其中，1M 和2M 为常数。
5. 求解定解问题：
⎪⎩
⎪⎨⎧====+=0),0(,),0()(,),(,0)0,()(,x u Ex x u E E L t u t u g g u u t x xx tt 为常数为常数
第四章 行波法
习题4.1
1. 求下列波动方程柯西问题的解： (1) ⎪⎩⎪⎨⎧=====2002,sin x u x u u a u t t
t xx tt (2) ⎪⎩⎪⎨⎧=====x
u u u a u t t t xx tt 002,5 6. 求下列强迫振动的柯西问题的解
（1）⎪⎩⎪⎨⎧==+===2002,5)ex p(x
u u x u a u t t t xx tt ；（2）⎪⎩⎪⎨⎧==+===0,sin )ex p(002t t t xx tt u x u t x u a u 习题4.2
1. 求解半无界弦定解问题：
2000, 0,0sin , cos 0
tt xx t t t x u a u x t u x u x u ===⎧=<<+∞>⎪==⎨⎪=⎩
5. 求解下列定解问题：
⎪⎩⎪⎨⎧==>+∞<<-∞=-++==)(),()0,(,0200
22x u x u t x u a u u u t t t xx t tt ψϕεε [提示：作代换t
w e u ε=。
] 第五章 积分变换
习题5.1
1．若)()]([ωf x g F =，求证：)(2)]([ωπ-=g x f F 。
3．求函数的付里叶变换
（1）|)|exp()(x x f -=；（2）)ex p()(2
x x f π-=；（3）2cos )(x x f ω= 第六章 格林函数法
1．求区域上的格林函数
（1）求上半圆域的格林函数；
（2）求上半球域的格林函数。
2．求解圆域上的Dirichlet 问题
⎩
⎨⎧=≤==)(),(1,01θϕθr r u r u ∆ （1）θθϕcos )(a =；（2）θθϕcos )(a b +=。
第七章
1．设有静电场的圆柱域的上下底（半径为a ）接地，侧面电位为u 0。
求域内电位分布。
即问题的定解问题为：
⎪⎪⎪⎩
⎪⎪⎪⎨⎧===<<<=++===000)0,(,01u u u u h z a u u u a h z z zz ρρρρρρ
对定解问题分离变量求出贝塞尔方程的特解。
2．证明：x x
x J cos 2)(21π=
-。
3．证明：0)0(12=-n J ，其中n=1，2，3，…。