数值分析列主元消去法的实验报告
Gauss列主元消去法实验

<数值计算方法>实验报告1.实验名称实验2 Gauss 列主元消去法2.实验题目用Gauss 列主元消去法求解线性方程组。
0.0011 2.0002 3.0003 1.0001.0001 3.7122 4.6233 2.0002.0001 1.0722 5.6433 3.000x x x x x x x x x ++=⎧⎪-++=⎨⎪-++=⎩3.实验目的加深自己对Gauss 列主元消去法的理解和认识,并且通过做实验或做练习来加强自己Gauss 列主元消去法的掌握,学会并灵活运用Gauss 列主元消去法来求解方程组。
4.基础理论-------Gauss 列主元消去法1.Gauss 列主元消去法的基本思想是:在进行第k (k=1,2,...,n-1)步消元时,从第k 列的kk a 及以下的各元素中选取绝对值最大的元素,然后通过行变换将它交换到主元素kk a 的位置上,再进行消元。
2.Gauss 列主元消去法的优点:当kk a (k=1,2,...,n-1)的绝对值很小时,用Gauss 列主元消去法来求解方程组时,可以避免所的数值结果产生较大误差或失真。
5.实验环境实验系统:Win 7实验平台:VisualC++语言6.实验过程写出算法→编写程序→计算结果Gauss 列元消去法的算法Input:方程组未知量的个数n;增广矩阵()()1,2,...,T ij A a A A An ==,其中i=1,2,…,n; j=1,2,…,n+1Output:方程组的解x1,x2,…,xn,或失败信息。
1. for i ←1ton-1 do;2. temp ←|ii a |;3. p ←I;4. for j ←i+1 to n do5. if ||ji a >temp then6. p ←j;8. end9. end10. if temp=0 then11. |return False;12. end13. if p ≠I then14. p A ⇔i A ;//i,p 两行交换15. end//列选主元16. for j ←i+1 to n do17.*j ji i A m A -ji m ←/ji ii a a ;18. j A ←*j ji i A m A -;//消元19. end7.实验结果原方程组的解为:X1=-0.490396 , x2=-0.051035 ,x3=0.3675208.附录程序清单#include<iostream.h> #include"stdio.h"#include"math.h"void main ( ){ int n=3,i,j,k,p;doubleA[10][10]={{0.001,2.000,3.000,1.000},{-1.000,3.712,4.623,2.000},{-2.0 00,1.072,5.643,3.000}},temp,m,x[100];for(i=0;i<n;i++){ //选主元temp=fabs(A[i][i]); p=i;for(k=i+1;k<n;k++)if(fabs(A[k][i])>temp){temp=fabs(A[k][i]); p=k;}if(temp==0){ printf("\n无法求解:");return;}if(p!=i)for(j=0;j<n+1;j++){ temp=A[i][j];A[i][j]=A[p][j];A[p][j]=temp;}//消元for(k=i+1;k<n;k++){ m=A[k][i]/A[i][i];for(j=i+1;j<=n;j++)A[k][j]=A[k][j]-m*A[i][j];}}//回代for(i=n-1;i>=0;i--){x[i]=A[i][n];for(j=i+1;j<n;j++)x[i]=x[i]-A[i][j]*x[j];x[i]=x[i]/A[i][i];}printf("\nx=\n");for(i=0;i<n;i++)printf("%f \n",x[i]);}。
高斯列主元消去法实验报告

《数值计算方法》实验报告专业:年级:学号:姓名:成绩:1.实验名称实验2高斯列主元消去法2. :用Gauss列主消去法求解线性方程组0.001*X1+2.000*X2+3.000*X3=1.000-1.000*X1+3.217*X2+4.623*X3=2.000-2.000*X1+1.072*X2+5.643*X3=3.0003.实验目的a.熟悉运用已学的数值运算方法求解线性方程—Gauss列主消去法;b.加深对计算方法技巧的认识,正确使用计算方法来求解方程;c.培养用计算机来实现科学计算和解决问题的能力。
4.基础理论列主元消去法:a.构造增广矩阵b.找到每列绝对值的最大数;c.行变换;d.消去;e.回代5.实验环境Visual C++语言6.实验过程实现算法的流程图:7.结果分析a.实验结果与理论一致;b.由于数值设置成双精度浮点型,所以初值对计算结果影响不大;c.运用程序能更好的实现计算机与科学计算的统一和协调。
8. 附录程序清单#include<stdio.h>#include<math.h>int main(){int n=3,i,j,k,p;double a[4][4];double b[4];double x[4];double m[4][4];double temp;a[1][1]=0.001; a[1][2]=2.000; a[1][3]=3.000; b[1]=1.000;a[2][1]=-1.000; a[2][2]=3.1712; a[2][3]=2.000; b[2]=2.000;a[3][1]=-2.000; a[3][2]=1.072; a[3][3]=5.643; b[3]=3.000;for(i=1;i<=n-1;i++){temp=a[i][i];p=i;for(j=i+1;j<=n;j++)if(fabs(a[j][i])>temp){temp=a[j][i];p=j;}if(temp==0)return 0;if(p!=i) //换行{for(j=1;j<=n;j++)a[0][j]=a[i][j];for(j=1;j<=n;j++)a[i][j]=a[p][j];for(j=1;j<=n;j++)a[p][j]=a[0][j];b[0]=b[i];b[i]=b[p];b[p]=b[0];}for(j=i+1;j<=n;j++){m[j][i]=a[j][i]/a[i][i];for(k=i;k<=n;k++)a[j][k]=a[j][k]-m[j][i]*a[i][k];}}if(a[n][n]==0)return 0;x[n]=b[n]/a[n][n];for(i=n-1;i>=1;i--)//回代{temp=0;for(j=i+1;j<=n;j++)temp=temp+a[i][j]*x[j];temp=b[i]-temp;x[i]=temp/a[i][i];}for(i=1;i<=n;i++)//输出结果{printf("输出结果为:x[%d]=%lf ",i,x[i]);}printf("\n");return 0;}。
数值分析计算方法实验报告

end;
end;
X=x;
disp('迭代结果:');
X
format short;
输出结果:
因为不收敛,故出现上述情况。
4.超松弛迭代法:
%SOR法求解实验1
%w=1.45
%方程组系数矩阵
clc;
A=[2,10,0,-3;-3,-4,-12,13;1,2,3,-4;4,14,9,-13]
b=[10,5,-2,7]'
b=[10,5,-2,7]'
[m,n]=size(A);
if m~=n
error('矩阵A的行数和列数必须相同');
return;
end
if m~=size(b)
error('b的大小必须和A的行数或A的列数相同');
return;
end
if rank(A)~=rank([A,b])
error('A矩阵的秩和增广矩阵的秩不相同,方程不存在唯一解');
3.实验环境及实验文件存档名
写出实验环境及实验文件存档名
4.实验结果及分析
输出计算结果,结果分析和小结等。
解:1.高斯列主元消去法:
%用高斯列主元消去法解实验1
%高斯列主元消元法求解线性方程组Ax=b
%A为输入矩阵系数,b为方程组右端系数
%方程组的解保存在x变量中
format long;
A=[2,10,0,-3;-3,-4,-12,13;1,2,3,-4;4,14,9,-13]
return;
end
c=n+1;
A(:,c)=b;
for k=1:n-1
列主元消去法解方程组

数值分析上机实验报告(二)一、问题描述:利用列主元消去法求解下列方程组2X1+5X2+3X3 - 2X4=72X1- 2X2+3X3+5X4=-1X1+3X2+2X3+3X4=0X1+2X2+ X3 - 2X4=4二、算法原理:由高斯消去法知道,在消去过程中可能出现a kk(k)=0的情况,这时候消去法将无法进行,所以最好选取系数矩阵(或消元后的低阶矩阵)中绝对值最大的元素作为主元,以使高斯消去法具有较好的数值稳定性。
三、实验步骤:1、det 1;2、对于k=1,2,···,n-1(1)按列选主元|a ik.k|=max|a ik|(2)如果a i.k=0,则计算停止(det(A)=0)(3)如果i k=k则转(4)换行:a kj a ik·j(j=k,k+1,···,n)b k b ikdet -det(4)消元计算对于i=k+1,···,n○1am ik=a ik/a kk○2对于j=k+1,···,n a ij a ij—m ik*a kj○3b i b i-m ik*b ik(5)det a kk*det3、如果则计算停止(det(A)=0)4、回代求解(1)b n b n/a nn(2)对于i=n-1···,2,1bi(bi-∑aij*bj)/aii5.det ann*det四、实验框图五、源程序# include <stdio.h># include<math.h># define n 4main(){int i,j,k,l;float A[n][n],b[n],x[n],max;//输入系数矩阵及右端项for(i=0;i<n;i++)for(j=0;j<n;j++){printf("A[%d][%d]=",i,j);scanf("%f;",&A[i][j]);}for(i=0;i<n;i++){printf("b[%d]=",i);scanf("%f;",&b[i]);}//列主元消去过程for(k=0;k<n-1;k++){max=abs(A[k][k]);l=k;for(i=k+1;i<n;i++)if(abs(A[i][k])>max){max=abs(A[i][k]);l=i;} if(l>k){for(j=k;j<n;j++){max=A[k][j];A[k][j]=A[l][j];A[l][j]=max;}max=b[k];b[k]=b[l];b[l]=max;}for(i=k+1;i<n;i++){max=A[i][k]/A[k][k];for(j=k+1;j<n;j++)A[i][j]=A[i][j]-max*A[k][j];b[i]=b[i]-max*b[k];}}//回代过程x[n-1]=b[n-1]/A[n-1][n-1];for(k=1;k<n;k++){i=n-k-1;x[i]=b[i];for(j=i+1;j<n;j++)x[i]=x[i]-A[i][j]*x[j];x[i]=x[i]/A[i][i];}//输出解for(i=0;i<n;i++)printf("x[%d]=%f;",i,x[i]);getchar();}六、运行结果。
数值分析列主元高斯消去法
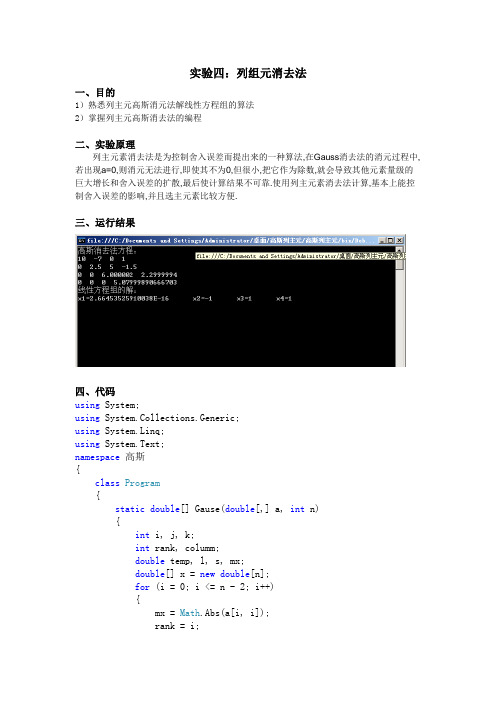
实验四:列组元消去法一、目的1)熟悉列主元高斯消元法解线性方程组的算法2)掌握列主元高斯消去法的编程二、实验原理列主元素消去法是为控制舍入误差而提出来的一种算法,在Gauss消去法的消元过程中,若出现a=0,则消元无法进行,即使其不为0,但很小,把它作为除数,就会导致其他元素量级的巨大增长和舍入误差的扩散,最后使计算结果不可靠.使用列主元素消去法计算,基本上能控制舍入误差的影响,并且选主元素比较方便.三、运行结果四、代码using System;using System.Collections.Generic;using System.Linq;using System.Text;namespace高斯{class Program{static double[] Gause(double[,] a, int n){int i, j, k;int rank, columm;double temp, l, s, mx;double[] x = new double[n];for (i = 0; i <= n - 2; i++){mx = Math.Abs(a[i, i]);rank = i;columm = i;for (j = i + 1; j <= n - 1; j++) //选主元if (Math.Abs(a[j, i]) > mx){mx = Math.Abs(a[j, i]);rank = j;columm = i;}for (k = 0; k <= n; k++) //主元行变换{temp = a[i, k];a[i, k] = a[rank, k];a[rank, k] = temp;} //消元for (j = i + 1; j <= n - 1; j++){l = a[j, i] / a[i, i];for (k = i; k <= n; k++)a[j, k] = a[j, k] - l * a[i, k];}}x[n - 1] = a[n - 1, n] / a[n - 1, n - 1]; //回代方程求解x for (i = n - 2; i >= 0; i--){s = 0;for (j = i + 1; j <= n - 1; j++)s = s + a[i, j] * x[j];x[i] = (a[i, n] - s) / a[i, i];}return x;}static void Main(string[] args){double[,] a = new double[4, 5] { { 10, -7, 0, 1, 8 }, { -3, 2.099999, 6, 2, 5.900001 }, { 5, -1, 5, -1, 5 }, { 2, 1, 0, 2, 1 } };int n = 4;double[] x = new double[n];x = Gause(a, n);Console.WriteLine("高斯消去法方程:");for (int i = 0; i < n; i++){for (int j = 0; j < n; j++)Console.Write(a[i, j].ToString() + " ");Console.WriteLine();}Console.WriteLine("线性方程组的解:");for (int i = 0; i <= n - 1; i++)Console.Write("x" + (i + 1).ToString() + "=" +x[i].ToString() + " ");Console.WriteLine();Console.ReadLine();}}}四、分析通过本次实验的学习,学会根据算法编写基本的相关程序,虽然此次程序模板由老师给予,但认真阅读理解程序有助于今后的学习,再利用计算机中的C语言对高斯列主元消去法可以快速得到线性方程组的解,由简单的线性方程组可以推广到一般n阶线性方程组,这对如何利用高斯列主元消去法解决实际问题有了一定的经验。
数值分析高斯顺序消去法、列主元消去法LU分解法

数值分析实验报告(1)学院:信息学院班级:计算机0903班姓名:***学号:********课题一A.问题提出给定下列几个不同类型的线性方程组,请用适当的方法求解线性方程组1、设线性方程组⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡--------------------------1368243810041202913726422123417911101610352431205362177586832337616244911315120130123122400105635680000121324⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡10987654321x x x x x x x x x x =⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-2119381346323125 x *= ( 1, -1, 0, 1, 2, 0, 3, 1, -1, 2 )T2、设对称正定阵系数阵线方程组⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡----------------------19243360021411035204111443343104221812334161206538114140231212200420424⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡87654321x x x x x x x x = ⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡---4515229232060 x * = ( 1, -1, 0, 2, 1, -1, 0, 2 )T3、三对角形线性方程组⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡------------------4100000000141000000001410000000014100000000141000000001410000000014100000000141000000001410000000014⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡10987654321x x x x x x x x x x = ⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡----5541412621357 x *= ( 2, 1, -3, 0, 1, -2, 3, 0, 1, -1 )TB.(1)对上述三个方程组分别用Gauss 顺序消去法与Gauss 列主元消去法;平方根 与改进平方根法;追赶法求解(选择其一) (2)编写算法通用程序(3)在应用Gauss 消去时,尽可能利用相应程序输出系数矩阵的三角分解式C.(1)通过该课题的程序编制,掌握模块化结构程序设计方法 (2)掌握求解各类线性方程组的直接方法,了解各种方法的特点 (3)体会高斯消去法选主元的必要性 实验步骤:(高斯消去法,列主元,LU )1顺序高斯消去法2.LU 分解法3.列主元高斯消去法(如下图)(1)高斯消去法运行结果如下(2)对方程的系数矩阵进行LU分解并求出方程组的解(3)列主元高斯消去法实验体会总结:利用gauss消去法解线性方程组的时候,如果没有经过选主元,可能会出现数值不稳定的现象,使得方程组的解偏离精确解。
数值方法高斯列主元消元法试验报告
1)用高斯列主元消元法求解下面的方程组#include <iostream>#include <cmath>#include <iomanip>using namespace std;int main(){//double a[4][5]={1,-1,1,-4,2,5,-4,3,12,4,2, 1,1,11,3,2,-1,7,-1,0};//int i,j,k;int Line,Row;double temp[4][5];//中间量Row=4;Line=5;//Inintial//Result//double X[5];cout<<"最初的矩阵为:"<<endl;for(i=0;i<4;i++){for(j=0;j<5;j++){cout<<a[i][j]<<' ';}cout<<endl;}cout<<endl;/////////////////////////////////for(k=0;k<Row-1;k++){//for(i=k+1;i<Row;i++){//temp[i][k]=a[i][k]/a[k][k];for(j=k;j<Line;j++){a[i][j]-=temp[i][k]*a[k][j];}}}//////////////////////////////////cout<<"经过消元后的增广矩阵为:"<<endl;for(i=0;i<4;i++){for(j=0;j<5;j++){cout<<a[i][j]<<' ';}cout<<endl;}cout<<endl;/////////////////////////////////for(i=Row-1;i>=0;i--){//double temp_new;temp_new=0;for(j=i+1;j<=Row-1;j++){a[i][Row]-=a[i][j]*a[j][Row];}a[i][Row]/=a[i][i];}///////////////////////////////////Print;cout<<"最后的解为:"<<endl;for(i=0;i<Row;i++){//cout<<"X"<<i+1<<"="<<a[i][Row]<<endl;}/////////////////////////////////return 0;}1.2列主元方法#include <iostream>#include <cmath>#include <iomanip>using namespace std;void Print(double a[][5]){int i,j;for(i=0;i<4;i++){for(j=0;j<5;j++){cout<<a[i][j]<<' ';}cout<<endl;}cout<<endl;}int main(){//double a[4][5]={1,-1,1,-4,2,5,-4,3,12,4,2, 1,1,11,3,2,-1,7,-1,0};//double b[4][5]={0.3e-15,int i,j,k,n;int Line,Row;double temp[4][5];//中间量Row=4;Line=5;//Inintial//////////////////////////////////////////////cout<<"最初的矩阵为:"<<endl;Print(a);////////////////////////////////////////////////the main process is underint kk;//flagsdouble max;//bool flag=false;double t;//the temp of change;for(k=0;k<Row-1;k++){/////////////////search the max_num//flag=false;max=a[k][k];kk=k;for(i=k;i<Row;i++){if(abs(a[i][k])>max){max=a[i][k];kk=i;//flag=true;}}//////////////////change the linefor(j=0;j<Line;j++){t=a[k][j];a[k][j]=a[kk][j];a[kk][j]=t;}cout<<"第"<<k+1<<"次换行结果:"<<endl;Print(a);cout<<endl;cout<<"第"<<k+1<<"次消元结果:"<<endl;//////////////////消元的过程for(i=k+1;i<Row;i++){//temp[i][k]=a[i][k]/a[k][k];for(j=k;j<Line;j++){a[i][j]-=temp[i][k]*a[k][j];}}///////////////////Print(a);//}//回带的过程n=Row-1;for(i=n;i>=0;i--){//double temp_new;temp_new=0;for(j=i+1;j<=n;j++){a[i][n+1]-=a[i][j]*a[j][n+1];}a[i][n+1]/=a[i][i];}/////////////////////////////////////////////cout<<"经过消元后的增广矩阵为:"<<endl;Print(a);////////////////////////////////////////////////Print;cout<<"最后的解为:"<<endl;for(i=0;i<Row;i++){//cout<<"X"<<i+1<<"="<<a[i][Row]<<endl;}/////////////////////////////////return 0;}2)分别用列主元消元法与不选主元消元法求解,分析对结果的影响#include <iostream>#include <cmath>#include <iomanip>using namespace std;void Print(double b[][5]){int i,j;for(i=0;i<4;i++){for(j=0;j<5;j++){cout<<b[i][j]<<' ';}cout<<endl;}cout<<endl;}int main(){double b[4][5]={0.3e-15,59.14,3,1,59.17,5.291,-6.130,-1,2,46.78,11.2,9,5,2,1,1,2,1,1,2};int i,j,k,n;int Line,Row;double temp[4][5];//中间量Row=4;Line=5;//Inintial//////////////////////////////////////////////cout<<"最初的矩阵为:"<<endl;Print(b);////////////////////////////////////////////////the main process is underint kk;//flagsdouble max;//bool flag=false;double t;//the temp of change;for(k=0;k<Row-1;k++){/////////////////search the max_num//flag=false;max=b[k][k];kk=k;for(i=k;i<Row;i++){if(abs(b[i][k])>max){max=b[i][k];kk=i;//flag=true;}}//////////////////change the linefor(j=0;j<Line;j++){t=b[k][j];b[k][j]=b[kk][j];b[kk][j]=t;}cout<<"第"<<k+1<<"次换行结果:"<<endl;Print(b);cout<<endl;cout<<"第"<<k+1<<"次消元结果:"<<endl;//////////////////消元的过程for(i=k+1;i<Row;i++){//temp[i][k]=b[i][k]/b[k][k];for(j=k;j<Line;j++){b[i][j]-=temp[i][k]*b[k][j];}}///////////////////Print(b);//}//回带的过程n=Row-1;for(i=n;i>=0;i--){//double temp_new;temp_new=0;for(j=i+1;j<=n;j++){b[i][n+1]-=b[i][j]*b[j][n+1];}b[i][n+1]/=b[i][i];}/////////////////////////////////////////////cout<<"经过消元后的增广矩阵为:"<<endl; Print(b);////////////////////////////////////////////////Print;cout<<"最后的解为:"<<endl;for(i=0;i<Row;i++){//cout<<"X"<<i+1<<"="<<b[i][Row]<<endl;}/////////////////////////////////return 0;}Ax (迭代法收敛速度实验)注意修改不同的A、B的数组2、用迭代法求解;b3、//雅可比迭代法/*@auther luozhengxiao*/#include <iostream>#include <cmath>#include <iomanip>using namespace std;//void Print(double x[]){for(int i=0;i<3;i++){cout<<setprecision(8)<<fixed<<x[i]<<endl;}}int main(){//double B1[3]={-3,2,4};double B2[3]={100,-200,345};double A[3][3]={6,2,-1,1,4,-2,-3,1,4};double x[3],x_old[3],temp;int i,j,k;for(i=0;i<3;i++){cout<<"请输入第"<<i+1<<"个数:";cout<<"\t x["<<i<<"]=";cin>>x[i];//x_old[i]=x[i];}int n;cout<<"请输入迭代次数:";cin>>n;/////////////////////////////////for(k=0;k<n;k++){//for(i=0;i<3;i++){//temp=0;j=0;while(j<3){if(j==i) {j++;continue;}temp+=A[i][j]*x[j];j++;}x_old[i]=B1[i]-temp;x_old[i]/=A[i][i];}for(j=0;j<3;j++){x[j]=x_old[j];}}Print(x);return 0;}。
数值分析实验,用程序实现列主元消去法解方程组
《数值分析》实验报告实验序号:实验二 实验名称: 列主元消去法解方程组 学号: 姓名:任课教师: 专业班级:)1、 实验目的:用列主元Gauss 消元法解n 阶线性代数方程组:⎪⎪⎩⎪⎪⎨⎧=+⋯++⋯⋯⋯⋯⋯=+⋯++=+⋯++nn nn 2n21n12n 2n 2221211n 1n 212111b a a a b a a a b a a a x x x x x x x x x 其基本做法是把上述方程组通过列主元Gauss 消元转化为一个等价的三角形方程组,然后再进行回代就可以求出方程组的解。
列主元消元的基本做法是选取系数矩阵的每一列中绝对值最大的作为主元,然后采取和顺序Gauss 消元法相同的步骤进行 ,求得方程组的解。
要求显示出每一个列主元以及每一大步消元后的系数矩阵),...,2,1(n k =(k )A 和常数项),...,2,1(n k =(k )b ,最后显示出方程组的解),...,2,1(n i x i =。
2、 实验内容:(1)实验分析:1. 列主元Gauss 消元法的算法思想:1. 输入增广矩阵B ;。
2. 对k =1,2,…,n ,循环:(a ) 按列选主元||:max ik ni j a a ≤≤=保存主元所在行的指标k i 。
(b ) 若a=0,则系数矩阵奇异,计算停止;否则,顺序进行。
(c ) 若k i =k 则转向(d );否则换行ki kj i b b nj a a k j k ↔=↔,...,2,1 ,(d ) 计算乘子.,...,1,/n k i a a a m ik kk ik ik +=⇒=(e ) 消元: nk i b m b b nk j i a m a a k ik i i kj ij ij ij ,...,1;:,...,1,;:+=-=+=-=3. 回代 1,...,1, ,/:1-=⎪⎪⎭⎫ ⎝⎛-=∑+=n n i a b a b b ii n i j j ij i i 用右端项b 来存放解x 。
数值分析实验报告高斯消元法和列主消元法
《计算方法》实验指导书 实验三、高斯消元法和列主消元法一、实验目的:1. 通过matlab 编程解决高斯消元发和列主消元发来解方程组的问题, 加强编程能力和编程技巧,要熟练应用matlab 程序来解题,练习从数值分析的角度看问题进而来解决问题。
更深一步体会这门课的重要性,练习动手能力,同时要加深对数值问题的理解,要熟悉matlab 编程环境。
二、实验要求:用matlab 编写代码并运行高斯消元法和列主消元发来解下面的方程组的问题,并算出结果。
三、实验内容:用高斯消元法和列主消元法来解题。
1.实验题目:用高斯消元法和列主消元法来解下列线性方程组。
⎪⎪⎩⎪⎪⎨⎧−=+−−−=+−−=+−−=−+−.142,16422,0,13143214321432432x x x x x x x x x x x x x x x 2.实验原理高斯消元法:就是把方程组变成上三角型或下三角形的解法。
上三角形是从下往上求解,下三角形是从上向下求解,进而求得结果。
而列主消元法是和高斯消元法相类似,只不过是在开始的时候找出x1的系数的最大值放在方程组的第一行,再化三角形再求解。
3.设计思想高斯消元法:先把方程组的第一行保留,再利用第一行的方程将其余几行的含有x1的项都消去,再保留第二行,同理利用第二行的方程把第二行以下的几行的含有x2项的都消去,以此类推。
直到最后一行只含有一个未知数,化为上三角形,求得最后一行的这个未知数的值,再回带到倒数第二个方程求出另一个解,再依次往上回带即可求出这个方程组的值。
而列主消元法与高斯消元法类似,只不过在最开始时找出x1项系数的最大值与第一行交换再进行与高斯算法相似的运算来求出方程组的解。
4.源代码高斯消元法的程序:f unction [RA,RB,n,X]=gaus(A,b)B=[A b]; n=length(b); RA=rank(A);RB=rank(B);zhica=RB-RA;if zhica>0,disp('请注意:因为RA~=RB,所以此方程组无解.')returnendif RA==RBif RA==ndisp('请注意:因为RA=RB=n,所以此方程组有唯一X=zeros(n,1); C=zeros(1,n+1);for p= 1:n-1for k=p+1:nm= B(k,p)/ B(p,p);B(k,p:n+1)= B(k,p:n+1)-m*B(p,p:n+1);endendb=B(1:n,n+1);A=B(1:n,1:n);X(n)=b(n)/A(n,n);for q=n-1:-1:1X(q)=(b(q)-sum(A(q,q+1:n)*X(q+1:n)))/A(q,q);endelsedisp('请注意:因为RA=RB<n,所以此方程组有无穷多解.')endend在工作窗口输入程序:A=[1 -1 1 -3; 0 -1 -1 1;2 -2 -4 6;1 -2 -4 1];b=[1;0; -1;-1]; [RA,RB,n,X] =gaus (A,b)请注意:因为RA=RB=n,所以此方程组有唯一解.运行结果为:RA =4RB =4n =4X =-0.50000.5000.列主消元发的程序:function [RA,RB,n,X]=liezhu(A,b)B=[A b]; n=length(b); RA=rank(A);RB=rank(B);zhica=RB-RA;if zhica>0,disp('请注意:因为RA~=RB,所以此方程组无解.')returnendif RA==RBif RA==ndisp('请注意:因为RA=RB=n,所以此方程组有唯一解.')X=zeros(n,1); C=zeros(1,n+1);for p= 1:n-1[Y,j]=max(abs(B(p:n,p))); C=B(p,:);B(p,:)= B(j+p-1,:); B(j+p-1,:)=C;for k=p+1:nm= B(k,p)/ B(p,p);B(k,p:n+1)= B(k,p:n+1)-m*B(p,p:n+1);endendb=B(1:n,n+1);A=B(1:n,1:n);X(n)=b(n)/A(n,n);for q=n-1:-1:1X(q)=(b(q)-sum(A(q,q+1:n)*X(q+1:n)))/A(q,q);endelsedisp('请注意:因为RA=RB<n,所以此方程组有无穷多解.')endend在工作窗口输入程序:A=[1 -1 1 -3; 0 -1 -1 1;2 -2 -4 6;1 -2 -4 1];b=[1;0; -1;-1]; [RA,RB,n,X]=liezhu(A,b)请注意:因为RA=RB=n,所以此方程组有唯一解.运行结果为:RA =4RB =4n =4X =-0.50000.5000实验体会:通过这次实验我了解了高斯消元法和列主消元方法的基本思想,虽然这两个程序的编写是有点困难的,但运行起来还是比较容易的,解决了不少实际问题的计算。
列主元消去法解方程组实验报告
实验名称: 列主元消去法解方程组 1 引言我们知道,高斯消去法是一个古老的解线性方程组的方法。
而在用高斯消去法解Ax=b时,其中设A 为非奇异矩阵,可能出现()0k kka =的情况,这时必须进行带行交换的高斯消去法。
但在实际计算中即使()0k kk a ≠但其绝对值很小时,用()k kka 作除数,会导致中间结果矩阵()k A 元素数量级严重增长和舍入误差的扩散,使得最后的结果不可靠。
因此,小主元可能导致计算的失败,我们应该避免采用绝对值很小的主元素。
为此,我们在高斯消去法的每一步应该在系数矩阵或消元后的低阶矩阵中选取绝对值最大的元素作为主元素,保持乘数1ik m ≤,以便减少计算过程中舍入误差对计算解的影响。
一种方式是完全主元消去法,这种消去法是在每次选主元时,选择()()max 0k kk k i j ij k i nk j na a ≤≤≤≤=≠为主元素。
这种方法是解低阶稠密矩阵方程组的有效方法,但这种方法在选取主元时要花费一定的计算机时间。
实际计算中我们常采用部分选主元的的消去法。
列主元消去法即在每次选主元时,仅依次按列选取绝对值最大的元素作为主元素,且仅交换两行,再进行消元计算。
2 实验目的和要求运用matlab 编写一个.m 文件,要求用列主元消去法求解方程组(实现PA=LU ):12345671111111721111118321111110432111113543211117654321122765432128x x x x x x x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦要求输出以下内容: (1) 计算解x ; (2) L,U ;(3) 整形数组IP (i )(i=1,2,…,n-1)(记录主行信息)3 算法原理与流程图(1) 算法原理设有线性方程组A x =b ,其中设A 为非奇异矩阵。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一 列主元消去法
【实验内容】
1.掌握列主元消去法的基本思路和迭代步骤
2.并能够利用列主元的高斯消去法解任意阶数的线性方程组;
3、从课后题中选一题进行验证,得出正确结果,交回实验报告与计算结果。
【实验方法与步骤】
1.列主元消去法基本思路
设有线性方程组Ax b =,设A 是可逆矩阵。
列主元消去法的基本思想就是通过列主元的选取将初等行变换作用于方程组的增广矩阵[]|B A b =,将其中的A 变换成一个上三角矩阵,然后求解这个三角形方程组。
2.列主元高斯消去法算法描述
将方程组用增广矩阵[]()(1)|ij n n B A b a ⨯+==表示。
步骤1:消元过程,对1,2,,1k n =-L
(1) 选主元,找{},1,,k i k k n ∈+L 使得
,max k i k ik k i n
a a ≤≤= (2) 如果,0k i k a =,则矩阵A 奇异,程序结束;否则执行(3);
(3) 如果k i k ≠,则交换第k 行与第k i 行对应元素位置,k kj i j a a ↔,
,,1j k n =+L ;
(4) 消元,对,,i k n =L ,计算/,ik ik kk l a a =对1,,1j k n =++L ,计算
.ij ij ik kj a a l a =-
步骤 2:回代过程:
(1) 若0,nn a =则矩阵奇异,程序结束;否则执行(2);
(2) ,1/;n n n nn x a a +=对1,,2,1i n =-L ,计算
,11/n i i n ij j ii j i x a a x a +=+⎛⎫=- ⎪⎝⎭
∑
[实验程序]
#include<math.h>
#include<stdio.h>
#include<iostream>
#include<conio.h>
#define NUMBER 20
#define Esc 0x1b
#define Enter 0x0d
using namespace std;
float A[NUMBER][NUMBER+1] ,ark;
int flag,n;
void exchange(int r,int k);
float max(int k);
void message();
void main()
{
float x[NUMBER];
int r,k,i,j;
char celect;
void clrscr();
printf("\n\nUse Gauss.");
printf("\n\n1.Jie please press Enter.");
printf("\n\n2.Exit press Esc.");
celect=getch();
if(celect==Esc)
exit(0);
printf("\n\n input n=");
scanf("%d",&n);
printf(" \n\nInput matrix A and B:");
for(i=1;i<=n;i++)
{
printf("\n\nInput a%d1--a%d%d and b%d:",i,i,n,i);
for(j=1;j<=n+1;j++) scanf("%f",&A[i][j]); }
for(k=1;k<=n-1;k++)
{
ark=max(k);
if(ark==0)
{
printf("\n\nIt’s wrong!");message();
}
else if(flag!=k)
exchange(flag,k);
for(i=k+1;i<=n;i++)
for(j=k+1;j<=n+1;j++)
A[i][j]=A[i][j]-A[k][j]*A[i][k]/A[k][k]; }
x[n]=A[n][n+1]/A[n][n];
for( k=n-1;k>=1;k--)
{
float me=0;
for(j=k+1;j<=n;j++)
{
me=me+A[k][j]*x[j];
}
x[k]=(A[k][n+1]-me)/A[k][k];
}
for(i=1;i<=n;i++)
{
printf(" \n\nx%d=%f",i,x[i]);
}
message();
}
void exchange(int r,int k)
{
int i;
for(i=1;i<=n+1;i++)
A[0][i]=A[r][i];
for(i=1;i<=n+1;i++)
A[r][i]=A[k][i];
for(i=1;i<=n+1;i++)
A[k][i]=A[0][i];
}
float max(int k)
{
int i;
float temp=0;
for(i=k;i<=n;i++)
if(fabs(A[i][k])>temp)
{
temp=fabs(A[i][k]);
flag=i;
}
return temp;
}
void message() {
printf("\n\n Go on Enter ,Exit press Esc!"); switch(getch())
{
case Enter: main();
case Esc: exit(0);
default:{printf("\n\nInput error!");message();} }
}
【实验结果】。
