例1-7-3判断系统是否为线性非时变系统
数字信号处理课后答案+第1章(高西全丁美玉第三版)

解:(1) x(-n)的波形如题4解图(一)所示。 (2) 将x(n)与x(-n)的波形对应相加, 再除以2, 得到xe(n)。 毫无疑问, 这是一个偶对称序列。 xe(n)的波形如题4解图(二) 所示。 (3) 画出xo(n)的波形如题4解图(三)所示。
题4解图(一)
题4解图(二)
题4解图(三)
(4) 很容易证明: x(n)=x1(n)=xe(n)+xo(n) 上面等式说明实序列可以分解成偶对称序列和奇对称序 列。 偶对称序列可以用题中(2)的公式计算, 奇对称序列可 以用题中(3)的公式计算。 5. 设系统分别用下面的差分方程描述, x(n)与y(n)分 别表示系统输入和输出, 判断系统是否是线性非时变的。 (1)y(n)=x(n)+2x(n-1)+3x(n-2) (2)y(n)=2x(n)+3 (3)y(n)=x(n-n0) (4)y(n)=x(-n) n0为整常数
(6) y(n)=x(n2) 令输入为 x(n-n0) 输出为 y′(n)=x((n-n0)2) y(n-n0)=x((n-n0)2)=y′(n) 故系统是非时变系统。 由于 T[ax1(n)+bx2(n)]=ax1(n2)+bx2(n2) =aT[x1(n)]+bT[x2(n)] 故系统是线性系统。
(5) y(n)=x2(n) 令输入为 x(n-n0) 输出为 y′(n)=x2(n-n0) y(n-n0)=x2(n-n0)=y′(n) 故系统是非时变系统。 由于 T[ax1(n)+bx2(n)]=[ax1(n)+bx2(n)]2 ≠aT[x1(n)]+bT[x2(n)] =ax21(n)+bx22(n) 因此系统是非线性系统。
数字信号处理(第三版)课后习题答案全

因此
d X ( e j ) FT[ nx( n)] j d
第2章
时域离散信号和系统的频域分析
6. 试求如下序列的傅里叶变换: (1) x1(n)=δ(n-3) (2) x2 (n) δ(n 1) δ(n) δ(n 1) (4) x4(n)=u(n+3)-u(n-4) 解 (1)
0.5ቤተ መጻሕፍቲ ባይዱ 2 n
n<0时, c内有极点0.5、 2、 0, 但极点0是一个n阶极点,
改成求c外极点留数, 可是c外没有极
点, 因此 x(n)=0 最后得到
x(n)=(0.5n-2n)u(n)
第2章
时域离散信号和系统的频域分析
19. 用部分分式法求以下X(z)的反变换:
(1)
1 1 z 1 3 X ( z) , 1 2 5z 2 z 2
7 7 j j e 2 (e 2 1 1 j j e 2 (e 2 7 j e 2 ) 1 j e 2 )
e j3
7 sin( ) 2 1 sin( ) 2
第2章
时域离散信号和系统的频域分析
14. 求出以下序列的Z变换及收敛域: (1) 2-nu(n) (5) δ(n-1) 解 (1) ZT[2 n u(n)]
n n
n 1
2n z n z 1 2
2z 1 1 2 z 1 2 1 z 1 (5) ZT[δ(n-1)]=z-10<|z|≤∞
第2章
16. 已知
时域离散信号和系统的频域分析
3 2 X ( z) 1 1 1 2 z 1 1 z 2
求出对应X(z)的各种可能的序列表达式。
数字信号处理第三版课后答案丁玉美
7. 设线性时不变系统的单位脉冲响应h(n)和输入序列 x(n)如题7图所示, 要求画出y(n)输出的波形。
解: 解法(一)采用列表法。
y(n)=x(n)*h(n)= x(m)h(n-m) m
有以下三种情况, 分别求出输出y(n)。
(1) h(n)=R4(n), x(n)=R5(n) (2) h(n)=2R4(n), x(n)=δ(n)-δ(n-2) (3) h(n)=0.5nu(n), xn=R5(n)
解: (1) y(n)=x(n)*h(n)=
R4(m)R5(n-m)
m
先确定求和域。 由R4(m)和R5(n-m)确定y(n)对于m的 非零区间如下:
(5)y(n)=x2(n)
(6)y(n)=x(n2)
n
(7)y(n)= x(m) m0
(8)y(n)=x(n)sin(ωn)
解: (1) 令输入为
输出为
x(n-n0)
y′(n)=x(n-n0)+2x(n-n0-1)+3x(n-n0-2) y(n-n0)=x(n-n0)+2x(n—n0—1)+3(n-n0-2)
由于
x(n)=-δ(n+2)+δ(n-1)+2δ(n-3) 1
h(n)=2δ(n)+δ(n-1)+ δ2(n-2)
x(n)*δ(n)=x(n)
x(n)*Aδ(n-k)=Ax(n-k)
故
第 1 章 时域离散信号和时域离散系统
y(n)=x(n)*h(n)
=x(n)*[2δ(n)+δ(n-1)+ δ1(n-2) 2
信号与系统第一次作业

《信号与系统》第一次作业姓名:学号:1. 判断下列系统是否为线性系统,其中()y t 、[]y k 为系统的完全响应,(0)x 为系统初始状态,()f t 、[]f k 为系统输入激励。
(1)()(0)lg ()=y t x f t 解:在判断具有初始状态的系统是否线性时,应从三个方面来判断。
一是可分解性,即系统的输出响应可分解为零输入响应与零状态响应之和。
二是零输入线性,系统的零输入响应必须对所有的初始状态呈现线性特性。
三是零状态线性,系统的零状态响应必须对所有的输入信号呈现线性特性。
只有这三个条件都符合,该系统才为线性系统。
()(0)lg ()=y t x f t 不具有可分解性,所以系统是非线性系统。
(2)[](0)[][1]=+-y k x f k f k解:y[k]具有可分解性,零输入响应x(0)是线性的,但零状态响应f[k]f[k-1]是非线性的,所以系统是非线性系统。
2. 判断下列系统是否为线性非时变系统,为什么?其中()f t 、[]f k 为输入信号,()y t 、[]y k 为零状态响应。
(1)()()()=y t g t f t解:在判断系统的时不变特性时,不涉及系统的初始状态,只考虑系统的零状态响应。
系统零状态响应,g(t)f(t)满足均匀性和叠加性,所以系统是线性系统。
因为T{f(t-t0)}=g(t).f(t-to)而 y(t-t0)=g(t-t0).f(t-t0) ≠T{f(t-t0)},故该系统为时变系统。
因此该系统为线性时变系统(2)220[][],(0,1,2,)+===∑k i y k kf i k 解:220[][],(0,1,2,)+===∑k i y k k f i k 为线性时变系统。
3. 已知信号()f t的波形如题1-3图所示,绘出下列信号的波形。
1t1f(t)-2-1-1题1-3图(1)(36)-+f t解:f(t) ——(波形数轴对称):f(-t)——【波形t轴方向,t值缩小至1/3,f(t)值不变】:f(-3t)——【波形往右横移6】:(36)-+f t最终画出波形图如下:(2)(1)3tf-+解:f(t) ——(波形数轴对称):f(-t)——【波形t轴方向,t值扩大3倍,f(t)值不变】:f(-⅓t)——【波形往右横移1】:(1)3tf-+最终画出波形图如下:4. 已知()(4)2(1)(1)2(1)tf t t t t t e u tδδδ-'=+-+++++,绘出()f t波形。
数字信号处理课后习题答案(全)1-7章

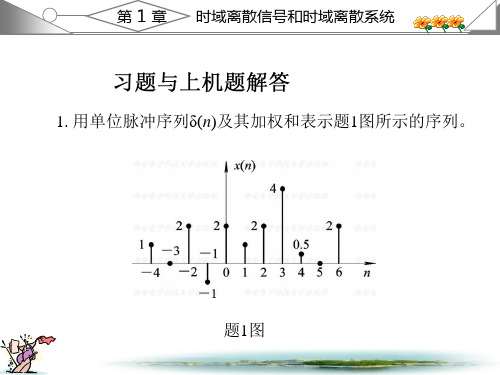
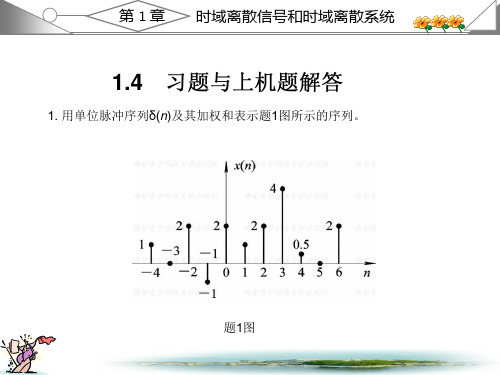
将x(n)的表示式代入上式, 得到 1 y(n)=-2δ(n+2)-δ(n+1)-0.5δ(2n)+2δ(n-1)+δ(n-2)
+4.5δ(n-3)+2δ(n-4)+δ(n-5)
第 1 章 时域离系统的单位脉冲响应h(n)和输入x(n)分别有以下三种情况,
+6δ(n-1)+6δ(n-2)+6δ(n-3)+6δ(n-4)
1
4
(2m 5) (n m) 6 (n m)
m4
m0
第 1 章 时域离散信号和时域离散系统
(3) x1(n)的波形是x(n)的波形右移2位, 再乘以2, 画出图形如题2解图 (二)所示。
(4) x2(n)的波形是x(n)的波形左移2位, 再乘以2, 画出图形如题2解图(三) 所示。
(5)y(n)=x2(n)
(6)y(n)=x(n2)
(7)y(n)=
n
(8)y(n)=x(n)sin(ωxn(m) )
m0
解: (1) 令输入为
输出为
x(n-n0)
y′(n)=x(n-n0)+2x(n-n0-1)+3x(n-n0-2) y(n-n0)=x(n-n0)+2x(n—n0—1)+3(n-n0-2)
第 1 章 时域离散信号和时域离散系统
题2解图(四)
第 1 章 时域离散信号和时域离散系统
3. 判断下面的序列是否是周期的; 若是周期的, 确定其周期。
(1) x(n) Acos 3 πn A是常数
7 8
(2)
j( 1 n )
x(n) e 8
《数字信号处理》第二版课后答案

————第一章———— 时域离散信号与系统理论分析基础本章1.1节“学习要点”和1.2节“例题”部分的内容对应教材第一、二章内容。
为了便于归纳总结,我们将《数字信号处理(第二版)》教材中第一章和第二章的内容合并在一起叙述,这样使读者对时域离散线性时不变系统的描述与分析方法建立一个完整的概念,以便在分析和解决问题时,能全面考虑各种有效的途径,选择最好的解决方案。
1.1 学 习 要 点1.1.1 时域离散信号——序列时域离散信号(以下简称序列)是时域离散系统处理的对象,研究时域离散系统离不开序列。
例如,在时域离散线性时不变系统的时域描述中,系统的单位脉冲响应()n h 就是系统对单位脉冲响应()n δ的响应输出序列。
掌握()n δ的时域和频域特征,对分析讨论系统的时域特性描述函数()n h 和频域特性描述函数()ωj e H 和()z H 是必不可少的。
1. 序列的概念在数字信号处理中,一般用()n x 表示时域离散信号(序列)。
()n x 可看作对模拟信号()t x a 的采样,即()()nT x n x a =,也可以看作一组有序的数据集合。
要点 在数字信号处理中,序列()n x 是一个离散函数,n 为整数,如图1.1所示。
当≠n 整数时,()n x 无定义,但不能理解为零。
当()()nT x n x a =时,这一点容易理解。
当=n 整数时,()()nT x n x a =,为()t x a 在nT t =时刻的采样值,非整数T 时刻未采样,而并非为零。
在学习连续信号的采样与恢复时会看到,()n x 经过低通滤波器后,相邻的()T n nT 1~+之间的()t x a 的值就得到恢复。
例如,()n x 为一序列,取()()2n x n y =,n 为整数是不正确的,因为当=n 奇数时,()n y 无定义(无确切的值)。
2. 常用序列常用序列有六种:①单位脉冲序列()n δ,②矩形序列()n R N ,③指数序列()n u a n,④正弦序列()n ωcos 、()n ωsin ,⑤复指数序列nj eω,⑥周期序列。
数字信号处理主要知识点整理复习总结

求出对应
的各种可能的序列的表达式。
解: 有两个极点,因为收敛域总是以极点为界,因此收敛域有以下三种情况: 三种收敛域对应三种不同的原序列。
时,
(1)当收敛域
令
,因为c内无极点,x(n)=0;
,C内有极点0,但z=0是一个n阶极点,改为求圆外极点留数,圆外极点有
数字信号处理课程 知识点概要
第1章 数字信号处理概念知识点
1、掌握连续信号、模拟信号、离散时间信号、数字信号的特点及相互关系(时间和幅度的连续性考量) 2、数字信号的产生; 3、典型数字信号处理系统的主要构成。
量化、编码 ——————
采样 ————
模拟信号
离散时间信号
数字信号
5、部分分式法进行逆Z变换 求极点 将X(z)分解成部分分式形式 通过查表,对每个分式分别进行逆Z变换 注:左边序列、右边序列对应不同收敛域 将部分分式逆Z变换结果相加得到完整的x(n)序列 6、Z变换的性质 移位、反向、乘指数序列、卷积
常用序列z变换(可直接使用)
7、DTFT与Z变换的关系
(a) 边界条件 时,是线性的但不是移不变的。
(b) 边界条件 时,是线性移不变的。
令
….
所以:
….
所以:
可见 是移一位的关系, 亦是移一位的关系。因此是移不变系统。
代入差分方程,得:
……..
所以:
因此为线性系统。
3. 判断系统是否是因果稳定系统。
Causal and Noncausal System(因果系统) causal system: (1) 响应不出现于激励之前 (2) h(n)=0, n<0 (线性、时不变系统) Stable System (稳定系统) (1) 有界输入导致有界输出 (2) (线性、时不变系统) (3) H(z)的极点均位于Z平面单位圆内(因果系统)
数字信号处理(第三版)-课后习题答案全-(原题+答案+图)
将x(n)的表示式代入上式, 得到 1 y(n)=-2δ(n+2)-δ(n+1)-0.5δ(2n)+2δ(n-1)+δ(n-2)
+4.5δ(n-3)+2δ(n-4)+δ(n-5)
第 1 章 时域离散信号和时域离散系统
8. 设线性时不变系统的单位脉冲响应h(n)和输入x(n)分别有以下三种情况,
第 1 章 时域离散信号和时域离散系统
(3) 这是一个延时器, 延时器是线性非时变系统, 下面证明。 令输入为
输出为
x(n-n1)
y′(n)=x(n-n1-n0) y(n-n1)=x(n-n1-n0)=y′(n) 故延时器是非时变系统。 由于
T[ax1(n)+bx2(n)]=ax1(n-n0)+bx2(n-n0) =aT[x1(n)]+bT[x2(n)]
(5)y(n)=x2(n)
(6)y(n)=x(n2)
(7)y(n)=
n
(8)y(n)=x(n)sin(ωxn(m) )
m0
解: (1) 令输入为
输出为
x(n-n0)
y′(n)=x(n-n0)+2x(n-n0-1)+3x(n-n0-2) y(n-n0)=x(n-n0)+2x(n—n0—1)+3(n-n0-2)
x(m)h(n-m)
m
第 1 章 时域离散信号和时域离散系统
题7图
第 1 章 时域离散信号和时域离散系统
y(n)={-2,-1,-0.5, 2, 1, 4.5, 2, 1; n=-2, -1, 0, 1, 2, 3, 4, 5}
