平行四边形的性质2导学案

合集下载

人教版数学四年级上册平行四边形的认识导学案(精选3篇)

人教版数学四年级上册平行四边形的认识导学案（精选３篇）〖人教版数学四年级上册平行四边形的认识导学案第【1】篇〗教学目标：1、知识与技能目标：使学生掌握平行四边形的意义及特征，了解它的特性。

2、过程与方法目标：通过观察、动手，培养学生抽象概括能力和初步的空间观念。

3、情感态度与价值观：培养学生观察和认识周围图形的兴趣和认识。

教学重点与难点：重点：平行四边形的意义。

难点：抽象概括平行四边形的意义。

教学准备：用木条订成的三角形、平行四边形框架，小棒、钉子板、方格纸等。

教学过程：（一）、老师出示一个长方形框架、1、老师动手拉它的一组相对的角，请同学们观察：这个框架还是长方形吗？为什么？（这个图形不是长方形了，因为它的四个角不是直角）今天，我们又认识了一个图形——平行四边形，我们把这样的图形叫做平行四边形、在黑板右上角贴出一个平行四边形、2、问：同学们平时见过平行四边形吗？请举例来说、（有一种防盗网上的图形、篱笆上的图形，有的编织图案）3、动手操作，感受平行四边形的特征分组操作探究师：第一组：量一量平行四边形各边的长度。

第二组：用小棒搭平行四边形。

学生的操作，教师巡视，并参与学生活动。

4、各组汇报探究结果，互相评价。

5、画平行四边形师：请你在方格纸上画一个你最喜欢的平行四边形。

6、。

平行四边形和长方形有什么相同点和不同点？（老师又一次演示长方形活动框架）（它们的相同点是都有四条边且对边相等、它们都有四个角；不同点是：长方形的四个角必须是直角）巩固练习完成课本练习三十九第2题，指生订正并说出理由。

1、判断题：（1）长方形、正方形和平行四边形都是四边形。

（）（2）四个角都是直角的'四边形一定是正方形。

（）（3）一个四边形，它的四条边相等，这个四边形一定是正方形。

（）（4）对边相等的四边形都是长方形。

（）（5）有个四边形，它的四个角都是直角，那么，这个四边形不是正方形就是长方形。

（）全课总结通过今天的学习你有什么收获？谈一谈。

3.1.2平行四边形(2)导学案

图3B3.1.2平行四边形(2)【学习目标】1．理解并掌握等腰梯形的性质、判定定理及三角形中位线定理，并应用定理来解决问题； 2．在合作交流中体验定理的证明过程，融合解题的技巧。

【学习过程】一、自主探究及巩固：等腰梯形的定义：探究1．等腰梯形都有哪些性质？你能证明吗？等腰梯形的性质定理： ___________________________________________________ 等腰梯形的对称性：【自我巩固1】1．如图1，等腰梯形ABCD 中，对角线AC ，BD 交于点O ，则图中全等三角形共有（） A ．1对 B ．2对 C ．3对 D ．4对2．如图2，在等腰梯形ABCD 中，AC ⊥BD ，AC ＝6cm ，则等腰梯形ABCD 的面积为_____cm 2.3．如图3，在等腰梯形ABCD 中，AD ∥BC ，AB ＝AD ＝CD ．若∠ABC ＝60°，BC ＝12，则梯形ABCD 的周长为____________________．探究2.如何判断一个梯形是不是等腰梯形？你能证明吗？图2等腰梯形的判定定理：同一底上的__________相等的梯形．．是等腰梯形；____________________的梯形．．是等腰梯形。

说明：要证一个四边形是梯形，应先证它是________，再根据判定定理寻找其他条件。

【自我巩固2】4．下列条件能证明四边形是等腰梯形的的是( )A．有两角相等的梯形B．对角线相等的梯形C．同一腰上的两个角互补的梯形D．同一底上的两个角互补的梯形5．在四边形ABCD中，AD∥BC，但AD≠BC，若要使它成为等腰梯形，则需添加的条件是________________。

（填一个正确的条件即可）6．如图4，在菱形ABCD中，∠DAB=60°，过点C做CE⊥AC，且与AB的延长线交于点E。

求证：四边形AECD是等腰梯形。

探究3 三角形的中位线1.定义：___________________________________叫做三角形的中位线。

五生活中的多边形《平行四边形的认识》【导学案】青岛版五年级上册数学

五生活中的多边形——平行四边形的认识（导学案）一、背景介绍平行四边形是小学数学中的一个重要知识点。

在生活中，我们经常会遇到平行四边形，比如书桌的桌面、篮球场的地面等等。

因此，了解平行四边形的定义、性质和判别方法，可以帮助我们更好地理解周围的事物，提高我们的生活质量。

二、学习目标1.掌握平行四边形的定义和性质。

2.能够判别平行四边形和其他多边形。

3.能够应用平行四边形的性质解决实际问题。

三、学习内容1. 平行四边形的定义平行四边形是一个有四条边的四边形，其中对边两两平行。

2. 平行四边形的性质1.对边平行：平行四边形的两组对边都平行。

2.对角线互相平分：平行四边形的两条对角线互相平分。

3.相邻角互补：平行四边形内部相邻两角互补。

3. 判别平行四边形和其他多边形1.判别是否有对边平行。

2.判别是否有两条对角线互相平分。

3.判别是否有两个内角互补。

4. 应用1.利用平行四边形的性质求解实际问题，例如计算物体的面积、长度等。

四、学习方法1.观察生活中的平行四边形，比如桌子、书本等，体验平行四边形存在的形状和属性。

2.画图，通过画图加深对平行四边形的理解。

3.练习，多做一些平行四边形相关的题目，巩固和提高知识点的掌握程度。

五、学习评估1.在生活中了解、观察和认识平行四边形。

2.在课堂上积极参与讨论和互动，发表自己的看法和观点。

3.能够准确应用平行四边形的性质解决实际问题。

六、拓展延伸1.探究平行四边形的面积计算公式和推导过程。

2.学习更多多边形的定义和性质。

3.了解平行四边形在几何图形中的应用。

七、总结平行四边形是生活中常见的多边形之一，其性质具有重要的实用性和理论意义。

通过学习平行四边形的定义、性质和应用等内容，可以帮助我们更好地认识周围的事物，在实际生活中更加自如地应用数学知识。

19.1.1(2)导学案

2.□ABCD的对角线交于点O，S△AOB=2cm2，则S□ABCD=__________.
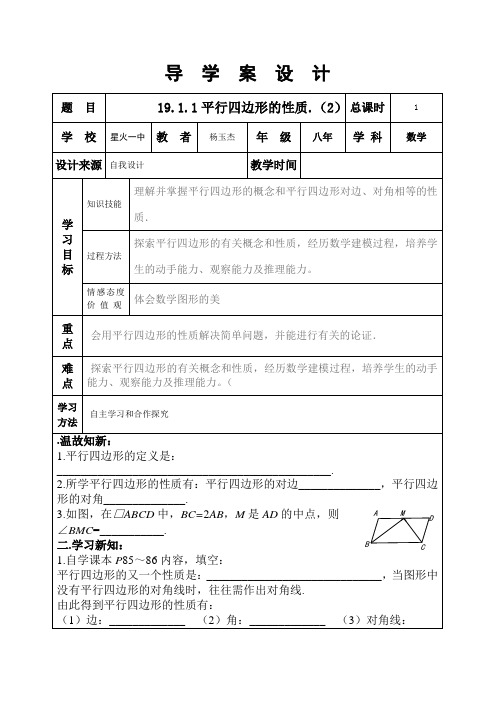
3.□ABCD的周长为60cm，对角线交于点O，△BOC的周长比△AOB的周长小8cm，则AB=______cm，BC=_______cm.
4.□ABCD中，对角线AC和BD交于点O，若AC=8，AB=6，BD=m，那么m的取值范围是____________.
体会数学图形的美
重
点
会用平行四边形的性质解决简单问题，并能进行有关的论证．
难
点
探索平行四边形的有关概念和性质，经历数学建模过程，培养学生的动手能力、观察能力及推理能力。（
学习方法
自主学习和合作探究
.温故知新：
1.平行四边形的定义是：_______________________________________________.
导学案设计
题目
19.1.1平行四边形的性质.（2）
总课时
1
学校
星火一中
教者
杨玉杰
年级
八年
学科
数学
设计来源
自我设计
教学时间
学
习
目
标
知识技能
理解并掌握平行四边形的概念和平行四边形对边、对角相等的性质．
过程方法
探索平行四边形的有关概念和性质，经历数学建模过程，培养学生的动手能力、观察能力及推理能力。
情感态度价Leabharlann 观2.所学平行四边形的性质有：平行四边形的对边______________，平行四边形的对角______________.
3.如图，在□ABCD中，BC=2AB，M是AD的中点，则∠BMC=___________.
二.学习新知：
1.自学课本P85～86内容，填空：

6.1平行四边形及其性质导学案第二课时(自己制作)

6.1平行四边形及其性质导学案第二课时学习目标：1、经历探索“平行四边形的对角线互相平分”这一性质的过程，发展探究意识。

2、掌握“平行四边形的对角线互相平分”的性质定理3、能综合运用平行四边形的性质解决平行四边形的有关计算问题，和简单的证明题．重点难点：运用“平行四边形的对角线互相平分”这一性质解决简单的问题课前预习案：1、平行四边形的对角线互相。

2、平行四边形的对角线把平行四边形分成的4个小三角形的面积。

3、如图所示，在ABCD中，对角线AC、BD交于点O，下列式子中一定成立的是（）A. AC⊥BDB. OA=OCC. AC=BDD. AO=OD复习导入：1、什么是平行四边形？2、我们回忆一下,平行四边形有哪些性质?3、除了这些性质以外,平行四边形还有没有其他的性质呢?这节课我们继续探究平行四边形的性质。

课内探究案：（一）探索平行四边形的性质（小组合作）（1）剪一张平行四边形纸片，记为ABCD，连接AC、BD，交于点O，如上图，观察猜想（2）沿对角线AC与BD将平行四边形纸片剪成△AOB、△BOC、△COD和△DOA,你发现它们中哪些是全等三角形？（3）由（2）你发现在两条对角线被点O分成的四条线段中，哪些是相等的线段？。

如何用逻辑推理的形式证明你的结论？能先说说证题思路吗？（4）写出已知、求证和证明过程。

已知：求证：证明：由以上探索和证明，我们得到平行四边形的性质定理3：。

请你把上述性质用几何语言描述出来∵四边形ABCD为∴ ==（5）、经过上面的学习，你现在能总结出平行四边形的性质吗？（1）对边：（2）对角：（3）对角线（二）应用：你会用平行四边形的性质解决问题吗？试一试例一：如图，ABCD的对角线AC、BD相交于点O，过点O作一条直线，分别交AB、CD于点E、F．求证：OE＝OF一变：若例1中的条件都不变，将EF转动到图b的位置，那么例1的结论是否还成立？说明你的理由．证明：二变：若将EF向两方延长与平行四边形的两对边的延长线分别相交（图c和图d），例1的结论是否成立，说明你的理由．证明：证明：由此，你能得出一个怎样的结论？（三）巩固训练：1、在ABCD中，对角线AC、BD相交于点O，CD＝6, AC＝8，BD＝12，求△AOB的周长。

平行四边形性质2

目标导航知识
双主高效回顾
1、平行四边形的定义？ 2、平行四边形的边、角有哪些性质？学一、自学环节阅读课本第 6 页的探究部分，请你将两个全等的 ABCD 和 EFGH 连接对角线 AC、BD 和 EG、HF，设它们分别交于点 O．把这两个平行四边形叠放在一起，在点 O 处钉一个图钉，将 ABCD 绕点 O 旋转 180 ，观察它还和 EFGH 重合吗？ 1.你能从中看出平行四边形的边、角关系吗？_______________________________________. 2.进一步，请你仔细观察探究，是否还能发现 OA 与 OC，OB 与 OD 的关系呢？写出猜想 OA____OC,OB____OD. 所以，平行四边形的对角线互相你能设法证明你的猜想吗? ．
鸡西市第四中学 2010---2011 年度下学期初三学年数学《平行四边形的性质 2》导学案
课型使用时间学习目标授课模式预展课备课组初三备课组 2011 年 3 月日制作人编号张宏 2
1 通过动手实践活动，使学生掌握平行四边形对角线互相平分的性质，学生学会发现和总结。 2 能运用性质解决有关计算问题，和简单的证明题．争强学生的推理论证能力和逻辑思维能力，享受运用知识解决问题的成功体验。
相信自己 “我能行”
备课组长签字
教研组长
教导处
考核分数
1、性质 3：平行四边形的对角线________. 如果,AC=10，则 AO=______;BD=16，则 OD=_______.AD=9，则△AOD 的周长=________. 2、在□ABCD 中，已知对角线 AC 和 BD 相交于点 O，△ AOB 的周长为 25，AB=12，求对角线 AC 与 BD 的和.

导学案平行四边形的性质

第16章平行四边形的认识§16.1 平行四边形的性质课时一平行四边形的性质（一）【学习目标】1. 理解平行四边形的概念及表示方式.2. 理解平行四边形在边、角上的性质并能简单应用.【课前导习】1. 有两组对边的四边形叫做平行四边形，用几何语言表述为：如图，在四边形ABCD 中，若 ∥ ， ∥ ，则四边形ABCD是平行四边形，记为 .2.平行四边形的对边，用数学语言表述为： ABCD 中， = ， =3. 平行四边形的对角，邻角，用几何语言表述为：在 ABCD 中，∠ =∠ ，∠ =∠ ，∠ +∠ =1800（互补的角只写出一对就行了）4. ABCD 中，6=AB ,4=AD ,则=BC ，=DC ，平行四边形ABCD 的周长为 .5. ABCD 中，∠A=400，则∠C= 0，∠B= 0.6. ABCD 中，已知AB ＝8，周长等于24，则=DC ，=AD . 【主动探究】概念有两组对边分别平行的四边形叫做平行四边形找一找你能从图16.1.1所示的图形中找出平行四边形吗?图16.1.1试一试中绕着它的对角线AC 、BD 的交点O ，旋转180°之后看能否与原来的位置重合？你能通过操作过程中，发现些什么样的结论？概括平行四边形是图形，对角线的交点O 就是．平行四边形的相等，相等．例题讲解例1 中，已知∠A ＝40°，求其他各个内角的度数．例2 中，已知AB ＝8，周长等于24，求其余三条边的长．【当堂训练】1.在平行四边形ABCD 中，3AB =，5BC =，则平行四边形ABCD 的周长是。

2. 在平行四边形ABCD 中，A ∠比B ∠多050，则C ∠= ，D ∠= 。

3. 平行四边形ABCD 的周长是１０厘米，三角形ABC 的周长是８厘米，则对角线AC 的长是（）A 、２厘米B 、３厘米C 、４厘米D 、５厘米4. 平行四边形的两个邻角的角平分线相交所成的角是（）A 、锐角B 、直角C 、钝角D 、不能确定5．一个平行四边形的一边长为9，对角线的长不可能是下列选项中的（）A 、５和６B 、１０和１２Ｃ、１０和２０Ｄ、２和１８ 6. 如图，在平行四边形ABCD 中，ABC ∠角平分线BE 交ADE 点，5=AB ，3=ED ，则平行四边形ABCD 的周长为（ A 、１６ B 、２０ C 、２６ D 、３０7. 如图，在 ABCD 中，AE 垂直于CD ，E 是垂足．如果055B ∠=，那么D ∠与DAE ∠分别等于多少度?8. 在 ABCD 中，A ∠与B ∠的度数之比为2:3，求这个平行四边形各个内角的度数．【回学反馈】1. 如图，在平行四边形ABCD 中，0115ADC ∠=, 021CAD ∠=, 求ABC ∠与CAB∠的度数.2. 如图，平行四边形ABCD 的周长是８０厘米，对角线AC 与BD 相交于O ，AOB ∆的周长比AOD ∆的周长小20厘米，求这个平行四边形的各边的长。

八年级数学下册平行四边形的性质

八年级数学下册导学案（十九）杨成超八年级数学下册——平行四边形的性质二导学案【教学目标】：1.理解并掌握平行四边形的概念和平行四边形对边、对角相等的性质．2.会用平行四边形的性质解决简单的平行四边形的计算问题，并会进行有关的论证．3.培养学生发现问题、解决问题的能力及逻辑推理能力．【教学重难点】：理解并应用平行四边形的对角线互相平分的性质．【自学指导】：学生看P94---P95注意以下问题：✧让学生回忆平行四边形的特征。

✧在如课本图16.1.3那样的旋转过程中，你观察到OA与OC、OB与 OD的关系了吗?【自学检测】：1．判断对错（1）在ABCD中，AC交BD于O，则AO=OB=OC=OD．（）（2）平行四边形两条对角线的交点到一组对边的距离相等．（）（3）平行四边形的两组对边分别平行且相等．（）（4）平行四边形是轴对称图形．（）【师生共同探究，总结】：．✓过平行四边形对角线的交点作直线交对边或对边的延长线，所得的对应线段相等．✓平行四边形的面积=底×高（高为此底上的高）✓作对角线是解决四边形问题常用的辅助线，通过作对角线，可以把未知问题转化为已知的关于三角形的问题．✓若两条直线平行，则其中一条直线上任意两点到另一条直线的距离相等，这个距离称为平行线间的距离。

即平行线间的距离相等。

✓平行四边形两邻边之和等于平行四边形周长的一半．✓平行四边形被对角线分成四个小三角形，相邻两个三角形周长之差等于邻边之差．✓平行四边形被对角线分成四个小三角形的面积相等。

【提高练习】：一、填空题（1）在□ABCD中，∠A=70°，则∠D= 度。

（2）菱形ABCD的周长为28cm，∠BAD：∠ABC=1：2，则BD= cm，AC= cm。

的周长为㎝。

（3）在□ABCD中，AB=2.5㎝，BC=4㎝，则ABCD（4）若菱形的两条对角线长分别为16㎝和12㎝，则它的边长为㎝，高为㎝，面积为 cm2。

（5）在□ABCD中，两邻边的差为4㎝，周长为32㎝，则两邻边长分别为。

19.1.1平行四边形的性质(二)58

班级：组别：姓名：钢屯中学八年级导学案（2011-2012学年度第二学期）学科：数学编号：58个性天地课题19.1.1平行四边形的性质（二）课型自学课总课时58 主创人侯淑萍教研组长签字王廷臣领导签字个性天地学习目标：1.理解平行四边形中心对称的特征，掌握平行四边形对角线互相平分的性质．2.能综合运用平行四边形的性质解决平行四边形的有关计算问题，和简单的证明题．学习重点：平行四边形对角线互相平分的性质，以及性质的应用．学习难点：综合运用平行四边形的性质进行有关的论证和计算．学法指导：1、学生独立阅读课本P85—P86，探究课本基础知识，提升自己的阅读理解能力。

2、完成导学案设置的问题，由组长组织对学与群学，进行知识汇报，展示讨论。

3、教师巡视，及时指导、帮助学生解决疑难问题。

导学流程：一、旧知回顾1. 什么样的四边形是平行四边形？四边形与平行四边形的关系是：（2）平行四边形的性质：①具有一般四边形的性质：②角：（3）边：二、基础知识探究按课本85页的“探究”方法进行操作，并画出这两个平行四边形的对角线. （如下图）思考：线段OA与OC，OB与OD有什么关系？由此你能发现平行四边形的对角线有什么性质？2.猜一猜平行四边形的又一个性质是：______________________________，当图形中没有平行四边形的对角线时，往往需作出对角线.由此得到平行四边形的性质有：（1）边：_____________ （2）角：_____________ （3）对角线：_____________ 2.看例2，完成课本P86的练习. 三、综合知识探究1．在ABCD中，周长等于48，（1）已知一边长12，求各边的长（2）已知AB=2BC，求各边的长（3 ）已知对角线AC、BD交于点O，△AOD与△AOB的周长的差是10，求各边的长2．如图，ABCD中，AE⊥BD，∠EAD=60°，AE=2cm，AC+BD=14cm，则△OBC的周长是____3．ABCD一内角的平分线与边相交并把这条边分成cm5，cm7的两条线段，则ABCD的周长是__ ___cm．四、反馈检测：1.在□AB CD中，AC、BD交于点O，已知AB=8cm，BC=6cm，△AOB的周长是18cm，那么△AOD的周长是_____________.2.□ABCD的对角线交于点O，S△AOB=2cm2，则S□ABCD=__________.3.□A BCD的周长为60cm，对角线交于点O，△BOC的周长比△AOB的周长小8cm，则AB=______cm，BC=_______cm.4.□ABCD中，对角线AC和BD交于点O，若AC=8，AB=6，BD=m，那么m 的取值范围是____________.反思与评价：。

平行四边形导学案

平行四边形的性质（一）导学案学习目标：1.理解并掌握平行四边形的概念和平行四边形对边、对角相等的性质．2.会用平行四边形的性质解决简单的平行四边形的计算问题．3.培养学生发现问题、解决问题的能力及逻辑推理能力．学习重点：平行四边形的定义；对角、对边相等的性质，以及性质的应用．学习难点：运用平行四边形的性质进行有关的论证和计算．学习过程：一、列举实例，揭示课题1．我们一起来观察下图中的竹篱笆格子和汽车的防护链，想一想它们是什么几何图形的形象？2.你还能举出平行四边形在生活中应用的例子吗？3.揭示平行四边形的概念。

如图，平行四边形ABCD可以表示为：，几何表示定义：二、观察比较，探索新知1.由定义可知平行四边形具有什么性质？2.亲自动手画一个平行四边形，从边与角两方面观察平行四边形所具有的性质。

3.结论：平行四边形的性质：4.思考：①已知平行四边形的一个内角的度数，能确定其他内角的度数吗？②用什么方法可以证明平行四边形的这些性质？5.例题解析①如图所示，小明用一根36m长的绳子围成了一个平行四边形的场地，其中AB 边长为8m，其他三边的长各是多少？②如图，在平行四边形ABCD中，AE=CF，求证：AF=CE．三、练习巩固，提升能力填空题1．两组对边分别______的四边形叫做平行四边形．它用符号“□”表示，平行四边形ABCD记作__________。

2．平行四边形的两组对边分别____且____；平行四边形的两组对角分别______；两邻角____；平行四边形的面积＝底边长×______．3．在□ABCD中，若∠A－∠B＝40°，则∠A＝______，∠B＝______．4．若平行四边形周长为54cm，两邻边之差为5cm，则这两边的长度分别为______．5．若□ABCD的对角线AC平分∠DAB，则对角线AC与BD的位置关系是______．6．如图，□ABCD中，CE⊥AB，垂足为E，如果∠A＝115°，则∠BCE＝______．6题图7题图9题图7．如图，在□ABCD中，DB＝DC、∠A＝65°，CE⊥BD于E，则∠BCE＝______．8．若在□ABCD中，∠A＝30°，AB＝7cm，AD＝6cm，则S□ABCD＝______．选择题9．如图，将□ABCD沿AE翻折，使点B恰好落在AD上的点F处，则下列结论不一定成立．．．．．的是( )．A、AF＝EFB、AB＝EFC、AE＝AFD、AF＝BE10．如图，下列推理不正确的是( )．A、∵AB∥CD∴∠ABC＋∠C＝180°B、∵∠1＝∠2 ∴AD∥BCC、∵AD∥BC∴∠3＝∠4D、∵∠A＋∠ADC＝180°∴AB∥CD11．平行四边形两邻边分别为24和16，若两长边间的距离为8，则两短边间的距离为( )．A、5B、6C、8D、12解答题12．已知：如图，□ABCD中，DE⊥AC于E，BF⊥AC于F．求证：DE＝BF．13．如图，在□ABCD中，∠ABC的平分线交CD于点E，∠ADE的平分线交AB 于点F，试判断AF与CE是否相等，并说明理由．14．已知：如图，E、F分别为□ABCD的对边AB、CD的中点．(1)求证：DE＝FB；(2)若DE、CB的延长线交于G点，求证：CB＝BG．15．已知：如图，□ABCD中，E、F是直线AC上两点，且AE＝CF．求证：(1)BE＝DF；(2)BE∥DF．16．已知：□ABCD中，AB＝5，AD＝2，∠DAB＝120°，若以点A为原点，直线AB为x轴，如图所示建立直角坐标系，试分别求出B、C、D三点的坐标．四、总结反思，拓展升华1、平行四边形的性质2、平行四边形性质的证明过程3、质疑：平行四边形还有哪些性质？五、教学反思平行四边形的性质（二）导学案学习目标：1.理解平行四边形中心对称的特征，掌握平行四边形对角线互相平分的性质．2.能综合运用平行四边形的性质解决有关计算问题和简单的证明题．3.培养推理论证能力和逻辑思维能力．学习重点：平行四边形对角线互相平分的性质，以及性质的应用．学习难点：综合运用平行四边形的性质进行有关的论证和计算．学习过程：一、复习旧知，揭示课题1. 什么样的四边形是平行四边形？四边形与平行四边形的关系是：2．平行四边形的性质：3、提出问题，揭示课题二、活动演示，探索新知1.在纸上画ABCD，并连接对角线AC、BD交于点O．在点O处钉一个图钉，将ABCD绕点O旋转180，观察它还和原来的图形完全重合吗？你还能发现平行四边形的什么性质吗？2.得出结论并证明3.例题解析已知四边形ABCD是平行四边形，AB＝10cm，AD＝8cm，AC⊥BC，求BC、CD、AC、OA 的长以及ABCD的面积．三、练习巩固，提升能力1．平行四边形一条对角线分一个内角为25°和35°，则4个内角分别为_____。

18.1 平行四边形导学案

A B D C 第18章平行四边形第1课时 18.1.1 平行四边形的性质导学案（1）【学习目标】1、理解平行四边形的定义及有关概念；2、能根据定义探索并掌握平行四边形的对边相等、对角相等的性质；3、能根据平行四边形的性质进行简单的计算和证明；【学习重点】平行四边形的定义，平行四边形对角、对边相等的性质；【学习难点】如何添加辅助线将平行四边形问题转化为三角形问题解决的思想方法；一、学前预习认真学习课本83页至84页的内容。

1、叫做平行四边形。

平行四边形用符号“”来表示。

2、阅读以下文字并填空：平行四边形中对边是指无公共点的边，对角是指不相邻的角，邻边是指有公共端点的边，邻角是指有一条公共边的两个角．如上图，在ABCD中，AB的对边是，AB的邻边是，AD是BC 的边。

∠C的邻角是，∠C的邻对角是。

二、探索思考探究（一）通过观察、测量，我们可以发现：①平行四边形的对边；②平行四边形的对角；请你用我们学过的知识证明（需要你自己作图、写已知、求证，最后证明。

）练习一1、（1）在ABCD中，∠A=50°，求∠B、∠C、∠D的度数。

2、已知：ABCD中，AB=5，BC=3，求它的周长探索（二）a // b，作AD // GH // BC，若a // b，DA、GH、CB垂直于a，1、上面两图中AD、GH、BC相等吗？为什么？2、两条平行线间的距离：两条平行线间的距离和点与点之间的距离、点到直线的距离有何联系与区别：三、典例分析例１：在ABCD中，DE⊥AB，BF⊥CD，垂足分别为E、F，求证：AE=CF四、当堂反馈1、.判断题：(1)平行四边形两组对边分别平行且相等. ( ) (2)平行四边形的四个内角都相等. ( )(3)平行四边形的相邻两个内角的和等于180°( )(4)如果平行四边形相邻两边长分别是2cm和3cm，那么周长是10cm. ( )2、在平行四边形ABCD中，如果∠A=42°，那么∠B= ，∠C=3、在□ ABCD中，∠A：∠B=2：3，则∠A= _____ ，∠B= ______，∠C= ______，∠D= _______.4、已知□ ABCD的周长为20cm，且AD-AB=1cm,求AD，CD5、如图，在平行四边形ABCD中，AE=CF，求证：AF=CE．五、学习反思：（1）知识点：（2）数学方法：A BＤＣFEa ab bA AB BC CD DGHGHABCDO第2课时 18.1.1 平行四边形的性质导学案（2）【学习目标】1、理解平行四边形中心对称的特征，掌握平行四边形对角线互相平分的性质．2、能运用平行四边形的性质解决平行四边形的有关计算问题和简单的证明题．3、培养学生的推理论证能力和逻辑思维能力．【学习重点】掌握平行四边形对角线互相平分的性质【学习难点】能综合运用平行四边形的性质解决平行四边形的有关计算问题，和简单的证明题一、学前预习1. 如图，若要使四边形ABCD 是平行四边形，可以添加条件： , 添加的理由是 2、平行四边形的性质：如图∵四边形ABCD 是平行四边形∴ ，（）二、探索思考探究（一）1、如图，在□ABCD 中，画出对角线，对角线能画条，分是． 2、新出现的线段之间有什么关系？新出现的三角形之间有什么关系？理由是什么？3、由以上关系你发现平行四边形的对角线有什么性质？4、请证明;平行四边形的对角线互相平分．已知：求证：5、性质定理3的符号语言表示：∵∴ （）练习一 1、如图，在ABCD 中，B C ＝10cm ，A C ＝8cm ，B D ＝14cm ，△AOD 的周长是多少？△ABC 与△DBC 的周长那个长？长多少？.三、典例分析例1、已知四边形ABCD 是平行四边形，AB ＝20cm ，AD ＝16cm ，AC ⊥BC ，求BC 、CD 、AC 、OA 的长以及ABCD 的面积．练习二、已知四边形ABCD 是平行四边形，BC ＝4cm ，BD ＝10cm ，AC=6cm，求AB 、CD 的长以及ABCD 的面积．例2、已知：如图ABCD 的对角线AC 、BD 相交于点O ，EF 过点O 与AB 、CD 分别相交于点E 、F ．求证：OE ＝OF ，AE=CF ，BE=DF ．四、当堂反馈1. 如图，□ABCD 的两条对角线相交于点O, 已知AB=8cm,BC=6cm,△AOB 的周长是18cm ，那么△AOD 的周长是 .2．如图，在□ABCD 中，AB=3，BC=5，对角线AC ，BD 相交于点O ，则OA 的取值范围是．3、如图：ABCD 的对角线AC 、BD 相交于点O ，EF 过点O 与AB 、CD 分别相交于点E 、F ．①求证：OE ＝OF ，AE=CF ，BE=DF ．②若其他条件都不变，将EF 转动到图b 的位置，那么①中结论是否成立？若将EF 向两方延长与平行四边形的两对边的延长线分别相交（图c 和图d ），①中结论是否成立？说明你的理由．五、学习反思：（1）知识点：（2）数学方法BDA CBDA CCBADOB DCA ＯABCDO第3课时 18.1.2平行四边形的判定导学案（1）【学习目标】1．在探索平行四边形的判别条件中，理解并掌握用边、对角线来判定平行四边形的方法． 2．会综合运用平行四边形的判定方法和性质来解决问题． 3．体会用类比、逆向联想及运动的思维方法来研究问题．【学习重点】平行四边形的判定方法及应用【学习难点】平行四边形的判定定理与性质定理的灵活应用一、学前准备1.平行四边形的定义是2.平行四边形的性质：边的性质角的性质：：对角线的性质：符号语言：如图∵∴(边），（角）（对角线二、探索思考探究（一）请写出平行四边形边、角、对角线的性质定理的逆命题：有关边的：有关角的：有关对角线的：例1、如图， ABCD 的对角线AC 、BD 相交于点O ，E ，F 是AC 上的两点，并且AE=CF. 求证：四边形BFDE 是平行四边形.四、当堂反馈1、如图，AB=DC=EF ，AD=BC ，DE=CF ，图中有哪些互相平行的线段？并说明理由2、已知：如图，ABCD 中，点E 、F 分别在CD 、AB 上，DF ∥BE ，EF 交BD于点O ．求证：EO=OF ．3、已知□ABCD 中，AC 、BD 相交于O ，E 、F 是BO 、DO 的中点求证：AE ∥CF五、学习反思：（1）知识点：（2）数学方法：这些命题正确吗？如果正确，请证明A BCDEF第4课时 18.1.2平行四边形的判定导学案（2）【学习目标】1．掌握用一组对边平行且相等来判定平行四边形的方法．2．会综合运用平行四边形的四种判定方法和性质来证明问题．3．通过平行四边形的性质与判定的应用，启迪学生的思维，提高分析问题的能力．【学习重点】平行四边形各种判定方法及其应用，尤其是根据不同条件能正确地选择判定方法．【学习难点】平行四边形的判定定理与性质定理的综合应用一、学前准备1、平行四边形的性质：如图1∵∴(边），( )（角） ,( )如图2∵(对角线)∴ ( )2、平行四边形的判定：如图1 （1）定义∵∴四边形ABCD是平行四边形. ( )如图1 （2）∵∴四边形ABCD是平行四边形. ( )如图1 （3）∵∴四边形ABCD是平行四边形. ( )如图2（4）∵∴四边形ABCD是平行四边形. ( )二、探索思考探究（一）1、请同学们猜想一下，如果只考虑四边形的一组对边，当它满足什么条件时这个四边形是平行四边形？（据以下4个问题，写出一个你认为正确的猜想，并证明你的猜想）问题1：一组对边平行的四边形是平行四边形吗？如果是请给出证明，如果不是请举出反例说明.问题2：满足一组对边相等的四边形是平行四边形吗？问题3：如果一组对边平行，而另一组对边相等的四边形是平行四边形吗？问题4：一组对边平行且相等的四边形是平行四边形吗？例1如图，在平行四边形ABCD中，E，F分别是AB，CD的中点.求证：四边形EBFD是平行四边形.练习1 已知：如图，在四边形ABCD中，对角线AC和BD相交于O，AO=OC，BA⊥AC，DC⊥AC. 求证：四边形ABCD是平行四边形.四、当堂反馈1、如图，点EF是平行四边形ABCD边AD、BC上两点，AE＝CF求证：BE∥DF2、已知：如图，ABCD中，E、F分别是AC上两点，且BE⊥AC于E，DF⊥AC于F．求证：四边形BEDF是平行四边形．3、已知：如图，A′B′∥BA，B′C′∥CB，C′A′∥AC．求证：①∠ABC＝∠B′，∠CAB＝∠A′，∠BCA＝∠C′；②△ABC的顶点分别是△B′C′A′各边的中点．五、学习反思：（1）知识点：（2）数学方法：BD AC图1ACD 图2BO第5课时 18.1.2平行四边形的判定导学案（3）【学习目标】1、会综合运用平行四边形的四种判定方法和性质来证明问题．2、理解三角形中位线的概念，掌握三角形中位线的性质【学习重点】三角形中位线的概念和性质【学习难点】证明三角形中位线定理一、学前准备平行四边形的判定：如图1 （1）定义∵∴四边形ABCD是平行四边形. ( )如图1 （2）∵∴四边形ABCD是平行四边形. ( )如图1 （3）∵∴四边形ABCD是平行四边形. ( )如图1 （3）∵∴四边形ABCD是平行四边形. ( )如图2（5）∵∴四边形ABCD是平行四边形. ( )二、探索思考探究（一）1、请按要求画图：（1）在右框画任意△ABC中，（2）画AB、AC边中点D、E，连接DE．2、定义：像DE这样，连接三角形两边中点的线段叫做．3、问题1：一个三角形有几条中位线？问题2：三角形中位线与三角形中线有什么区别？问题3：通过观察、测量，DE与BC有怎样的关系？4、尝试证明你的猜想5、三角形中位线定理：符号语言：∵∴2. 如图，△ABC中，D、E分别是AB、AC中点．（1）若DE=5，则BC= ．（2）若∠B=65°，则∠ADE= °．（3）若DE+BC=12，则BC= ．三、典例分析例：如图，在四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA中点．求证：四边形EFGH是平行四边形．四、当堂反馈1、如图，A、B两点被池塘隔开，在AB外选一点C，连接AC和BC，怎样量出A、B两点间的距离？根据是什么？2、如图，ABCD的周长为36，对角线AC，BD相交于点O．点E是CD的中点，BD=12，求△DOE的周长3、如图，ABCD的对角线AC，BD相交于点O，且E、F、G、H分别是AO、BO、CO、DO的中点，求证：四边形EFGH是平行四边形五、学习反思：（1）知识点：（2）数学方法：BDAC图1ACD图2BEGFHB CDAABCAB CDOEGHF【学习目标】【学习重点】【学习难点】一、学前准备二、探索思考探究（一）三、典例分析四、当堂反馈五、学习反思：（1）知识点：（2）数学方法：1、在四边形ABCD 中：从下列条件(1)AB ∥CD ； (2)AD ∥BC ； (3)AD ＝BC ，(4)∠A ＝∠C ，选择两个条件，能判定四边形ABCD 是平行四边形的共有种2、指出下列条件中，哪些一定能判定四边形ABCD 是平行四边形？（1）. AB=BC, A D ∥BC （2）. AB=CD,O A ＝OC (O 是对角线交点) （3）. ∠A=∠B, ∠C=∠D （4）.AB ∥CD, ∠A=∠C 3、如图，BD 是□ABCD 的对角线，点E 、F 在BD 上，要使四边形AECF 是平行四边形，还需要增加的一个条件是（填上你认为正确的一个即可）。

平行四边形的性质二导学案20120320湘教版

导学课程教师复备学生笔记）（学生笔记）
预习案：课前预习与导学》预习案：课前预习与导学》《温故 1、平行四边形的定义：、平行四边形的定义：定义 2、平行四边形的面积：平行四边形的面积： 3、平分四边形的对边且；平行四边形的周长平行四边形的周长，对角；邻角邻角。。
A F
O
E
B
三．拓展探究题：拓展探究题：已知，如图，已知，如图，在△ABC 中，BD 是∠ABC 的平分线，DE∥ EF∥ 平分线，DE∥BC 交 AB 于 E，EF∥AC BE＝FC，为什么？交 BC 于 F，则 BE＝FC，为什么？
4
组长签字：组长签字：
1
探究案：探究案：
一、导入：（1）如图： ABCD 的两条对角线 AC,BD 相交于 O 点，图中有哪些三角形）如图：
教师复备学生笔记）（学生笔记）
是全等的？有哪些线段是相等的？并说明理由。是全等的？有哪些线段是相等的？并说明理由。全等三角形： ①全等三角形： A ；相等的线段： ②相等的线段：。 B
创新中学新课堂——八年级数学(下册) 创新中学新课堂——八年级数学(下册) ——八年级数学
主备人：备人：审核人：审核人：编号：编号：SDCX201208B03002
章
节
3． 1.2
教学内容
平行四边形的性质⑵ 平行四边形的性质⑵
第 1 课时
课型
新授课
学习目标学习目标
教学重点教学难点说明
A O B C D
2
探究案：探究案：已知：如图，例 2.已知：如图， ABCD 的对角线 AC、、 BD 相交于点 O，EF 过点 O 与 AB、，、 CD 分别相交于点 E、F．、．求证：＝，求证：OE＝OF，AE=CF，BE=DF．，．

人教版八年级数学第十八章平行四边形导学案(定稿)

18．1．1平行四边形的性质（1）课前预习：1．四边形的内角和．2．有两组对边分别平行的四边形叫做．3．平行四边形的面积公式为：．4．平行四边形用符号“”表示，平行四边形ABCD记作“”．5．平行四边形的性质：（1）平行四边形的对边．（2）平行四边形的对角．6．两条平行线之间的平行线段都相等．7．两条平行线中，一条直线上到另一条直线的，叫做这两条平行线之间的距离．课内探究：探究1.在探究平行四边形性质的过程中，体会研究平行四边形性质的基本方法是什么？探究2●平行四边形的边角性质例1．如图，□ABCD的周长为60cm，A E⊥BC，AF⊥CD，垂足分别为E、F（1）若∠BAD=120°，求∠EAF的度数；（2）已知A E︰AF=4︰6，求□ABCD的各边的长变式训练：1．如图，□ABCD中，E为BC上的一点，AF⊥DE于F，∠DAF=62°，求∠BED的度数2．如图，□ABCD中，AE平分∠BAD交DC于点E，AD=8cm，AB=5cm，求EC的长探究2●平行四边形与全等三角形的综合应用例２.如图,已知E、F是□ABCD对角线AC上的两点，且BE⊥AC，DF⊥AC.（1）求证：△ABE≌△CDFABE≌△CDF外其余两对全等三角形（不再添加辅助线）变式训练：1、如图，四边形ABCD是平行四边形，BE、DF分别是∠ABC、∠ADC的平分线，且与对角线AC分别相交于点E、F，求证：AE＝CF.2、如图，分别延长□ABCD的边BA、DC到点E、H，使得AE=AB，CH=CD，连接EH，分别交AD、BC于点F、G.求证：△AEF≌△CHG.限时训练1.如图，已知在□ABCD中，AD=3cm，AB=2cm，则□ABCD的周长等于（）A.10cmB.6cmC.5cmD.4cm第2题2.如图，□ABCD的面积是12，点E、F在BD上，且BE=EF=FD，则△CEF的面积为（）A.2B.3C.4D.63.如图，平行四边形ABCD中，AB=AD，∠D=70°，BE⊥AC于E，则∠ABE等于（）A.20°B.25°C.30°D.35°4.如图，平行四边形ABCD中，AE⊥BC于E，AF⊥DC于F，若平行四边形ABCD的周长为48，AE=5，AF=10，则平行四边形ABCD的面积等于（）A.87.5B.80C.75D.72.5第4题第5题第6题5.如图，直线l1∥l2，A、C、F在l1上，B、D、E在L2上，且AB∥CD，CE⊥l2，FG⊥l2，则下列说法不正确的是（）A.AB=CDB.A、B两点之间的距离就是线段AB的长C.EC=FGD.直线l1、l2的距离就是线段CD的长6.如图，在平行四边形ABCD中，过对角线AC上一点P作EF∥AD，GH∥AB，与各边交点分别为E、F、G、H，则图中面积相等的平行四边形的对数为（）A.3B.4C.5D.67.如图，已知平行四边形ABCD，E是AB延长线上一点，连接DE交BC于点F，在不添加任何辅助线的情况下，请补充一个条件，这个条件是（只第7题第8题8.如图，在平行四边形ABCD中，∠A=130°，在AD上取DE=DC，则∠ECB的度数是度.自主训练1.一个平行四边形的周长为70cm，两组对边之间的距离为10cm和4cm，则这个平行四边形的各边长分别为2.如图，□ABCD中AB=13，AD=5，AC⊥BC，则S□ABCD=3.如图，四边形ABCD是平行四边形，△AB’C和△ABC关于AC所在直线对称，AD和B’C相交于点O，连接BB’.(1)请直接写出图中所有的等腰三角形（不添加字母）；(2)求证：△AB’O≌△CDO.18.1.1平行四边形的性质（2）课前预习：1.平行四边形的对边且，对角 .2.两条平行线之间的距离处处3.平行四边形的对角线课内探究探究1平行四边形的两条对角线将平行四边形分成了四个三角形，你知道这四个三角形的面积有怎样的关系吗？你是怎样想的？与同学交流.探究2●平行四边形的对角线性质例1．已知：如图，□ABCD的周长为60cm，对角线AC、BD相交于点O，△AOB的周长比△BOC的周长多8cm，求这个平行四边形各边的长.变式训练如图，平行四边形ABCD中，已知∠ODA=90°，AC=10cm，BD=6cm，则AD的长为（）A.4cmB.5cmC.6cmD.8cm●平行四边形的性质的综合应用例２．如图，在平行四边形ABCD中，AC与BD相交于点O，AB⊥AC，∠CAD=45°，AC=2，求BD的长.变式训练□ABCD的一边为6cm，一条对角线为8cm，则另一条对角线的取值范围为限时训练1.如图，在平行四边形ABCD中，∠B=80°，AE平分∠BAD交BC于点E，CF∥AE交AD于点F，则∠1=（）A.40°B.50°C.60°D.80°2.如图，平行四边形ABCD中，AB=3，BC=5，AC的垂直平分线交AD于E，则△CDE的周长是（）A.6B.8C.9D.10第2题第3题第4题3.如图为一个平行四边形ABCD，其中H、G两点分别在BC、CD上，AH⊥BC，AG⊥CD，且AH、AC、AG将∠BAD分成∠1、∠2、∠3、∠4四个角.若AH=5，AG=6，则下列关系正确的是（）A.∠1=∠2B.∠3=∠4C.BH=GDD.HC=CG4.如图，在平行四边形ABCD中，∠B=80°，AE平分∠BAD交BC于点E，CF∥AE交AD于点F，则∠1等于（）A.40°B.50°C.60°D.80°5.如图，在□ABCD中，对角线AC、BD相交于点O，E、F是对角线AC上的两点，当点E、F 满足下列哪个条件时，四边形DEBF不一定是平行四边形（）A.OE=OFB.DE=BF D.∠ABE=∠CDF第5题第6题第7题6.如图，点D、E、F分别为△ABC三边的中点，若△DEF的周长为10，则△ABC的周长为（）A.5.B.10C.20D.407.如图，在□ABCD中，AB=3，AD=4，∠ABC=60°，过BC的中点E作EF⊥AB，垂足为点F，与DC的延长线相交于点H，则△DEF的面积是8.在□ABCD中，已知∠A=110°，则∠D= .9.如图，□ABCD中，对角线AC、BD相交于O，OE⊥DC，OF⊥AB，垂足分别是E、F.求证：OE=OF.自主训练1.如图，平行四边形ABCD的对角线相交于点O，且AD≠CD，过点O作OM⊥AC，交AD于点M，如果△CDM的周长是40cm，求平行四边形ABCD的周长.2.如图，点E 是□ABCD 的对角线AC 上任意一点，则S △ABE =S △ADE 是否正确？请说明理由.3.如图，在□ABCD 中，E 为BC 边上的一点，且AB=AE.(1)求证：△ABC ≌△EAD ；(2)若AE 平分∠DAB ，∠EAC=25°，求∠AED 的度数.18．1．1平行四边形的性质（3）课前预习1.在□ABCD 中，AC 、BD 交于点O ，已知AB =8cm ，BC =6cm ，△AOB 的周长是18cm ，那么△AOD 的周长是_____________.2. □ABCD 的对角线交于点O ，S △AOB =2cm 2，则S □ABCD =__________.3. □ABCD 的周长为60cm ，对角线交于点O ，△BOC 的周长比△AOB 的周长小8cm ，则AB =______cm ，BC =_______cm .4. □ABCD 中，对角线AC 和BD 交于点O ，若AC =8，AB =6，BD =m ，那么m 的取值范围是____________.课内探究例1. □ABCD 中，E 、F 在AC 上，四边形DEBF 是平行四边形.求证：AE=CF .F E D B A例2.如图，田村有一口四边形的池塘，在它的四角A 、B 、C 、D 处均有一棵大桃树.田村准备开挖养鱼，想使池塘的面积扩大一倍，并要求扩建后的池塘成平行四边形形状，请问田村能否实现这一设想？若能，画出图形，说明理由.D BA例3、已知：如下图， ABCD 的对角AC ，BD 交与点O.E ，F 分别是OA 、OC 的中点。

平行四边形的性质二

珲春四中差异-适应性教学数学导学案班级姓名编号主备教师：郎英霞日期:课题：平行四边形的性质（二）1、旧知链接：（1）全等三角形的判定方法有：1、2、3、4、5、。

（2)平行四边形的性质定理：1、平行四边形的对边且；2、平行四边形的对角邻角 2、新知自研：认真自研教材P43到P44内容；3、学前准备：用硬纸板做两个全等的□ABCD和□EFGH。

新授课：一、学习目标：探究平行四边形的性质，并会对其性质进行运用。

二、【以学为主·当堂达标】课堂元素自研自探环节合作探究环节展示提升环节质疑评价环节总结归纳环节自学指导（内容·学法·时间）互动策略内容·形式·时间）展示方案（内容·方式·时间）随堂笔记（成果记录·知识生成·同步演练）︻导学一︼性质探究·定理生成探究平行四边形的性质（二）：（1)动手操作、观察——猜想：将做好的□ABCD和□EFGH叠放在一起，在它们的中心0用图钉固定，将□ABCD绕点0旋转180°，观察：□ABCD与□EFGH是否重合？从中发现：OA与OC，OB与OD的关系：猜想：平行四边形对角线之间的关系：（2）证明：用全等三角形的知识验证你的猜想。

（简写证明思路）（1）小组长检查自研成果，并给出等级认定；（2）交流猜想：组长主持，各成员将自己的自研成果与疑难在组内交流，重点交流证明思路，就老师分配的任务，重点攻关，形成展示策略预案。

展示方案提示：方案一：现场演示：通过旋转，验证□ABCD的边角关系，猜想平行四边形对角线之间的关系。

方案二：验证猜想：板书探究证明过程并作讲解。

平行四边形的性质定理（二）：平行四边形的对角线同步演练：如图，已知□ABCD的周长为60cm，对角线AC、BD交于点O，且△AOB的周长比△BOC的周长长8cm，求AB和AD的长。

︻导学二︼例题导析·同步演练自研课本P44的例2。

平行四边形性质(第2课时)导学案 (修改版)

课题：平行四边形及其性质（导学案）（第2课时）班级：姓名：一、学习目标：1.理解平行四边形对称的特征，掌握平行四边形对角线互相的性质．2.能综合运用平行四边形的性质解决平行四边形的有关和证明．3.培养学生的推理论证能力和逻辑思维能力．二、重点、难点：（1）重点：平行四边形对角线互相的性质，以及性质的应用．（2）难点：综合运用平行四边形的性质进行有关的论证和计算．三、学法指导：本节课将通过“演示—思考—探究--讨论—归纳—应用--展示”来完成学习任务。

四、导学过程：（一），温故知新： 1．复习提问：（1）的四边形是平行四边形。

四边形与平行四边形的关系是。

（2）平行四边形的性质：①具有一般四边形的性质（内角和是︒360）．②角：平行四边形的对角相等，邻角互补．边：平行四边形的对边相等．（二）、课堂展示：（探索平行四边形的性质及其证明）请学生在纸上画两个全等的ABCD 和EFGH ，并连接对角线AC 、BD 和EG 、，设它们分别交于点O ．把这两个平行四边形重叠在一起，在点O 处钉一个图钉，将ABCD 绕点O 旋转︒180，观察它还和EFGH 重合吗？（填重合或不重合）进一步，我们还能发现平行四边形的对角线有性质是（用文字说明）结论：（1）平行四边形是对称图形，两条对角线的交点是；（2）平行四边形的对角线互相．用符号语言表示为：如图在EFGH 中EG 、HF 交与O 点∴OH= ,GO= . 3.性质的证明：已知：如图： ABCD 的对角线AC 、BD 相交于点O. 求证：OA=OC ，OB=OD. 总结：由此得到平行四边形的性质有：（1）边：___________（2）角：____________ （3）对角线：________ （三）、例题分析：例1已知四边形ABCD 是平行四边形，AB ＝10，AD ＝8，AC ⊥BC ，求BC 、CD 、AC 、OA 的长以及ABCD 的面积．例2 已知：如图4－21， ABCD 的对角线AC 、BD 相交于点O ，EF 过点O 与AB 、CD 分别相交于点E 、F ．求证：OE ＝OF ，AE=CF ，BE=DF ．【引申】若例1中的条件都不变，将EF 转动到图b 的位置，那么例1的结论是否成立？若将EF 向两方延长与平行四边形的两对边的延长线分别相交（图c 和图d ），例1的结论是否成立，说明你的理由．请你利用图（b ）来证明。

平行四边形的性质(2)导学案

平行四边形的性质 2导学案学习目标：1、掌握平行四边形对边相等、对角相等的基础上，掌握对角线互相平分的性质，初步会运用这些性质进行有关的论证和计算。

2、培养综合运用知识的能力。

重点：掌握对角线互相平分的性质。

难点：探索、寻求解决问题的思路。

一、知识回顾1、叫平行四边形。

2、平行四边形的性质有：①；②二、自主学习3、如图，在 ABCD中，AE=CF，求证AF=CE三合作探究（一）4、求证：平行四边形的对角线互相平分。

已知：求证：证明：四、典型示范1.公园有一片绿地，它的形状是平行四边形，绿地上要修几条笔直的小路，如图，AB＝15cm，AD＝12cm，AC⊥BC，求小路BC，CD，OC的长，并算出绿地的面积．2、如图，□ABCD的对角线AC、BD相交于点O，经过点O的一条直线l与一组对边相交于点E、F，试猜想OE与OF的大小关系，并加以证明。

3.变形：如图，□ABCD的对角线AC、BD相交于点O，经过点O的一条直线与一组对边的延长线．．．．．．相交于点E、F，试猜想OE与OF的大小关系，你能证明吗？五能力提高4.观察发现：直线l在绕点O旋转的过程中，①以E、F为端点的线段中，哪些线段的长度发生了变化？②在旋转的过程中，OE与OF还相等吗？还有以E、F为端点并且具有相等关系的线段吗？③在旋转的过程中，平行四边形被分成的两部分的面积相等吗？能证明吗？六、我的收获1. 我的收获：2．疑问解决：七、课堂检测平行四边形ABCD的两条对角线AC,BD相交于O.(1) 图中有哪些三角形全等? 有哪些相等的线段?(2) 若平行四边形ABCD的周长是20cm,△AOD的周长比△ABO的周长大6cm.求AB,AD的长.图（6）FEDCBAC DBAOCDBAOEAB CDOFlAB C DO l EFAB CDOl EF。

2平行四边形及其性质导学案2

现、积极思考、合作学习的学习态度.
重点：平行四边形的性质难点：理解并应用平行四边形的性质
内容设计温故知新：
1边形有哪些性质定 3、如何用几何语言表述它的性质定理？（板演）
自主学习：
请同学们认真阅读课本第 6 页和第 7 页，完成以下内容：
课内探究
点拨:解决四边形问题的常用方法：转化为三角形的问题
巩固提升：
1、在平行四边形 ABCD 中，对角线 AC,BD 交于 O 点，AB=8，BD=12.求 △AOB 的周长。
2、如图，在平行四边形 ABCD 中，对角线 AC,BD 交于点 O，作 AE⊥BD, CF⊥BD，垂足分别为 E，F （1）指出图形中的全等三角形（2）求证：OE=OF
课堂小结
谈谈本节课的收获
达标检测：
１、平行四边形 ABCD 的对角线交于点 O，则与△OBC 面积氙灯的三角形的个数有个。
2、平行四边形不具有的性质是（） A．对角线互相垂直 B．对边平行且相等 C．对角线互相平分 D．对角相等 3、练习册 4 题、5 题、6 题
1 课本第 8 页习题 B 组 3 题
平行四边形及其性质导学案（2）
编号： 02
课题平行四边形及其性质课型新授学习目标：知识与技能：掌握平行四边形的性质：对角线互相平分，并能初步用其来解决实际问题.
过程与方法：经历探索平行四边形的性质的过程，发展学生探究意识。
情感态度：让学生在观察、合作、讨论、交流中感受数学的实际应用价值，同时培养学生善于发
课后延伸
2、运用所学的平行四边形的性质设计一个题目
教（学）后反思
1、平行四边形的第 3 个性质定理是什么？你会证明 2、怎样运用平行四边形的性质定理进行证

6_1;6_2平行四边形的性质(1)(2)(王晓导学案)

课题 6.1平行四边形的性质（1）提炼与归纳批注与反思3、以下图是两组对边分别平行的四边形：即：AB∥CD，AD∥BC，那么三角形ABC和三角形ACD有什么关系？为什么？（1）AB与CD之间有什么样的数量关系？AD与BC呢？为什么？（2）各对角之间有什么样的数量关系?为什么？4、平行四边形的性质：平行四边形的相等；平行四边形的相等；平行四边形的互补；『水平训练提升』【当堂训练】——技能拓展应用，搭建晋级平台一、填空题1、已知：平行四边形ABCD中，一边AB=12 cm,AD=6，则BC=______ cm, CD=______ cm.2、如图,在ABCD中，对角线AC、BD相交于点O，图中全等三角形共有________对.3、ABCD中，若∠A∶∠B=1∶3,那么∠A=________，∠B=________，∠C=________，∠D=________.4、已知：□ABCD中,4,7,AB cm BC cm==则它的周长为（）A、11cmB、22cmC、28cmD、44cm二解答题：1、如图，四边形ABCD是平行四边形，BD⊥AD，求BC，CD及BD的长.2、.已知平行四边形的面积是144,相邻两边上的高分别为8和9,则它的周长是多少？提炼与归纳批注与反思【学习目标】1、掌握平行四边形相关概念和性质。

2、探索并掌握平行四边形的对边相等，对角相等的性质。

【学习重点】探索平行四边形的性质。

【学习难点】平行四边形性质的理解。

『知识学习探究』【自主学习】建立自信，克服畏惧，尝试新知一、温故而知新1.两直线平行，同位角，内错角，同旁内角。

2.能够完全重合的两个三角形叫做；全等三角形的边对应角。

【合作探究】1、同学们拿出准备好的剪刀、白纸一张。

将一张纸对折，剪下两张叠放的三角形纸片，将它们相等的一边重合，得到一个四边形。

（1）你拼出了怎样的四边形？小组交流；（2）给出小明拼出的四边形，它们的对边有怎样的位置关系？说说你的理由。