2 CrystalGrowth-界面微观结构-2 修改后
晶体中的各向异性
2 结晶生长的微观描述
如图 1 所示，晶体生长体系的组成从溶液相到晶相经历了三个区间，即液相区、过渡相区与晶相区。在
液相区， 溶质与溶剂以离子水平均匀混合。晶体的
组成原子在溶液中通过彼此之间很强的化学键相互键
合，从而形成众多的生长单元 （ 离子、分子或 团 簇） 。
在过渡相区，生长单元经扩散逐步接近晶体，在靠近晶
（ 1． State Key Laboratory of Rare Earth Resource Utilization，Changchun Institute of Applied Chemistry，Chinese Academy of Sciences， Changchun 130022，China； 2． School of Chemical Engineering，Dalian University of Technology，Dalian 116024，China）
人工晶体学报
JOURNAL OF SYNTHETIC CRYSTALS
Vol． 41 Supplement August，2012
晶体中的各向异性研究
孙丛婷1，2 ，李克艳2 ，宋术岩1 ，薛冬峰1，2
（ 1． 中国科学院长春应用化学研究所稀土资源利用国家重点实验室，长春 130022； 2． 大连理工大学化工学院，大连 116024）
此，有效地设计表面键合环境有利于调节各向异性生
长形态。在 Cu2 O 结晶过程中，EDTA 被证实起到了还 原剂和螯合剂的双重作用 。 ［12，13，20］ EDTA 的浓度决定
了 Cu2 O 生长过程中的控制步骤。在高 Cu（ II） / EDTA
浓度比的结晶条件下，Cu2 O 的结晶习性主要受到反应 图 3 控制，结晶环境中的 EDTA Fig． 1 Schematics of three phase zone
02-晶体生长(结晶学与矿物学)
第二章 晶体生长理论
2-1 晶体的形成方式
(a)
(b)
第二章 晶体生长理论
2-2 晶核的形成
晶体生长过程的第一步，就是形成晶核。
成核是一个相变过程，即在母液相中形成固相小晶芽，这一相变 过程中体系自由能的变化为： ΔG= ΔGv +ΔGs ΔGs为新相形成时新旧相界面的 表面能，ΔGv为新相形成时的体系 自由能 rc为体系自由能由升高到降低转 变时所对应的晶核半径值——临界 半径 只有当r>rc时， ΔG下降，晶核才 能稳定存在。 也就是说，晶核的形成，一方 面由于体系从液相转变为内能更小 的晶体相而使体系自由能下降，另 一方面又由于增加了液 - 固界面而使 体系自由能升高。
第二章 晶体生长理论
2-3 晶体生长模型 2.螺旋生长理论模型 (screw growth)
（Frank）等人（1949，1951）的实验证实：气相结晶时，1%的过饱和度 即可。另外，发现实际晶体总是存在台阶位错。
第二章 晶体生长理论
2-4 晶面的发育 1布拉维法则 晶体上的实际晶面平行于面网密度大的面网，这 就是布拉维法则(law of Bravais)。
discretediffractionpatternquasicrystalznmghodiffractionanysolidhavingessentiallydiscretediffractiondiagram212223242526gs为新相形成时新旧相界面的表面能gv为新相形成时的体系自由能为体系自由能由升高到降低转变时所对应的晶核半径值临界半径只有当rrg下降晶核才能稳定存在
国际晶体学联合会最近建议把晶体定义为衍射图谱呈现明 确图案的固体（any solid having an essentially discrete diffraction diagram）来代替原先的微观 空间呈现周期性结构的定义。
材料科学基础-作业参考答案与解析
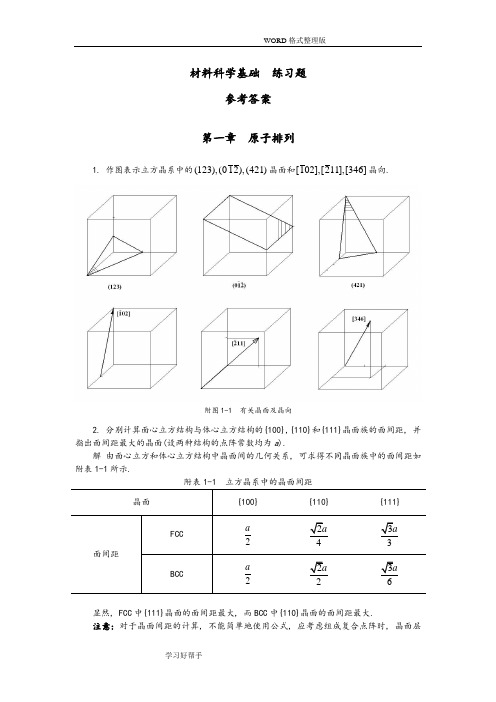
材料科学基础练习题参考答案第一章原子排列1. 作图表示立方晶系中的(123),(012),(421)晶面和[102],[211],[346]晶向.附图1-1 有关晶面及晶向2. 分别计算面心立方结构与体心立方结构的{100},{110}和{111}晶面族的面间距, 并指出面间距最大的晶面(设两种结构的点阵常数均为a).解由面心立方和体心立方结构中晶面间的几何关系, 可求得不同晶面族中的面间距如附表1-1所示.附表1-1 立方晶系中的晶面间距晶面{100} {110} {111}面间距FCC2a24a33aBCC2a22a36a显然, FCC中{111}晶面的面间距最大, 而BCC中{110}晶面的面间距最大.注意:对于晶面间距的计算, 不能简单地使用公式, 应考虑组成复合点阵时, 晶面层数会增加.3. 分别计算fcc和bcc中的{100},{110}和{111}晶面族的原子面密度和<100>,<110>和<111>晶向族的原子线密度, 并指出两种结构的差别. (设两种结构的点阵常数均为a) 解原子的面密度是指单位晶面内的原子数; 原子的线密度是指晶面上单位长度所包含的原子数. 据此可求得原子的面密度和线密度如附表1-2所示.附表1-2 立方晶系中原子的面密度和线密度晶面/晶向{100} {110} {111} <100> <110> <111>面/线密度BCC21a22a233a1a22a233aFCC22a22a2433a1a2a33a可见, 在BCC中, 原子密度最大的晶面为{110}, 原子密度最大的晶向为<111>; 在FCC 中, 原子密度最大的晶面为{111}, 原子密度最大的晶向为<110>.4. 在(0110)晶面上绘出[2113]晶向.解详见附图1-2.附图1-2 六方晶系中的晶向5. 在一个简单立方二维晶体中, 画出一个正刃型位错和一个负刃型位错. 试求:(1) 用柏氏回路求出正、负刃型位错的柏氏矢量.(2) 若将正、负刃型位错反向时, 说明其柏氏矢量是否也随之反向.(3) 具体写出该柏氏矢量的方向和大小.(4) 求出此两位错的柏氏矢量和.解正负刃型位错示意图见附图1-3(a)和附图1-4(a).(1) 正负刃型位错的柏氏矢量见附图1-3(b)和附图1-4(b).(2) 显然, 若正、负刃型位错线反向, 则其柏氏矢量也随之反向.(3) 假设二维平面位于YOZ坐标面, 水平方向为Y轴, 则图示正、负刃型位错方向分别为[010]和[010], 大小均为一个原子间距(即点阵常数a).(4) 上述两位错的柏氏矢量大小相等, 方向相反, 故其矢量和等于0.6. 设图1-72所示立方晶体的滑移面ABCD平行于晶体的上下底面, 该滑移面上有一正方形位错环. 如果位错环的各段分别与滑移面各边平行, 其柏氏矢量b // AB, 试解答:(1) 有人认为“此位错环运动离开晶体后, 滑移面上产生的滑移台阶应为4个b”, 这种说法是否正确? 为什么?(2) 指出位错环上各段位错线的类型, 并画出位错移出晶体后, 晶体的外形、滑移方向和滑移量. (设位错环线的方向为顺时针方向)图1-72 滑移面上的正方形位错环 附图1-5 位错环移出晶体引起的滑移解 (1) 这种看法不正确. 在位错环运动移出晶体后, 滑移面上下两部分晶体相对移动的距离是由其柏氏矢量决定的. 位错环的柏氏矢量为b , 故其相对滑移了一个b 的距离.(2) A ′B ′为右螺型位错, C ′D ′为左螺型位错, B ′C ′为正刃型位错, D ′A ′为负刃型位错. 位错运动移出晶体后滑移方向及滑移量见附图1-5.7. 设面心立方晶体中的(111)晶面为滑移面, 位错滑移后的滑移矢量为[110]2a .(1) 在晶胞中画出此柏氏矢量b 的方向并计算出其大小.(2) 在晶胞中画出引起该滑移的刃型位错和螺型位错的位错线方向, 并写出此二位错线的晶向指数.解 (1) 柏氏矢量等于滑移矢量, 因此柏氏矢量的方向为[110], 大小为2/2a .(2) 刃型位错与柏氏矢量垂直, 螺型位错与柏氏矢量平行, 晶向指数分别为[112]和[110], 详见附图1-6.附图1-6 位错线与其柏氏矢量、滑移矢量8. 若面心立方晶体中有[101]2a b =的单位位错及[121]6a b =的不全位错, 此二位错相遇后产生位错反应.(1) 此反应能否进行? 为什么?(2) 写出合成位错的柏氏矢量, 并说明合成位错的性质.解 (1) 能够进行.因为既满足几何条件:[111]3a b b ==∑∑后前,又满足能量条件: . 22222133b a b a =>=∑∑后前. (2) [111]3a b =合, 该位错为弗兰克不全位错. 9. 已知柏氏矢量的大小为b = 0.25nm, 如果对称倾侧晶界的取向差θ = 1° 和10°, 求晶界上位错之间的距离. 从计算结果可得到什么结论?解 根据bD θ≈, 得到θ = 1°,10° 时, D ≈14.3nm, 1.43nm. 由此可知, θ = 10°时位错之间仅隔5~6个原子间距, 位错密度太大, 表明位错模型已经不适用了.第二章 固体中的相结构1. 已知Cd, In, Sn, Sb 等元素在Ag 中的固熔度极限(摩尔分数)分别为0.435, 0.210, 0.130, 0.078; 它们的原子直径分别为0.3042 nm, 0.314 nm, 0.316 nm, 0.3228 nm; Ag 的原子直径为0.2883 nm. 试分析其固熔度极限差异的原因, 并计算它们在固熔度极限时的电子浓度.答: 在原子尺寸因素相近的情况下, 熔质元素在一价贵金属中的固熔度(摩尔分数)受原子价因素的影响较大, 即电子浓度e /a 是决定固熔度(摩尔分数)的一个重要因素, 而且电子浓度存在一个极限值(约为1.4). 电子浓度可用公式A B B B (1)c Z x Z x =-+计算. 式中, Z A , Z B 分别为A, B 组元的价电子数; x B 为B 组元的摩尔分数. 因此, 随着熔质元素价电子数的增加, 极限固熔度会越来越小.Cd, In, Sn, Sb 等元素与Ag 的原子直径相差不超过15%(最小的Cd 为5.5%, 最大的Sb 为11.96%), 满足尺寸相近原则, 这些元素的原子价分别为2, 3, 4, 5价, Ag 为1价, 据此推断它们的固熔度极限越来越小, 实际情况正好反映了这一规律; 根据上面的公式可以计算出它们在固熔度(摩尔分数)极限时的电子浓度分别为1.435, 1.420, 1.390, 1.312.2. 碳可以熔入铁中而形成间隙固熔体, 试分析是α-Fe 还是γ-Fe 能熔入较多的碳. 答: α-Fe 为体心立方结构, 致密度为0.68; γ-Fe 为面心立方结构, 致密度为0.74. 显然, α-Fe 中的间隙总体积高于γ-Fe, 但由于α-Fe 的间隙数量多, 单个间隙半径却较小, 熔入碳原子将会产生较大的畸变, 因此, 碳在γ-Fe 中的固熔度较α-Fe 的大.3. 为什么只有置换固熔体的两个组元之间才能无限互熔, 而间隙固熔体则不能?答: 这是因为形成固熔体时, 熔质原子的熔入会使熔剂结构产生点阵畸变, 从而使体系能量升高. 熔质原子与熔剂原子尺寸相差越大, 点阵畸变的程度也越大, 则畸变能越高, 结构的稳定性越低, 熔解度越小. 一般来说, 间隙固熔体中熔质原子引起的点阵畸变较大,故不能无限互熔, 只能有限熔解.第三章 凝固1. 分析纯金属生长形态与温度梯度的关系.答: 纯金属生长形态是指晶体宏观长大时固-液界面的形貌. 界面形貌取决于界面前沿液相中的温度梯度.(1) 平面状长大: 当液相具有正温度梯度时, 晶体以平直界面方式推移长大. 此时, 界面上任何偶然的、小的凸起深入液相时, 都会使其过冷度减小, 长大速率降低或停止长大, 而被周围部分赶上, 因而能保持平直界面的推移. 长大过程中晶体沿平行温度梯度的方向生长, 或沿散热的反方向生长, 而其它方向的生长则受到限制.(2) 树枝状长大: 当液相具有负温度梯度时, 晶体将以树枝状方式生长. 此时, 界面上偶然的凸起深入液相时, 由于过冷度的增大, 长大速率越来越大; 而它本身生长时又要释放结晶潜热, 不利于近旁的晶体生长, 只能在较远处形成另一凸起. 这就形成了枝晶的一次轴, 在一次轴成长变粗的同时, 由于释放潜热使晶枝侧旁液体中也呈现负温度梯度, 于是在一次轴上又会长出小枝来, 称为二次轴, 在二次轴上又长出三次轴……由此而形成树枝状骨架, 故称为树枝晶(简称枝晶).2. 简述纯金属晶体长大机制及其与固-液界面微观结构的关系.答: 晶体长大机制是指晶体微观长大方式, 即液相原子添加到固相的方式, 它与固-液界面的微观结构有关.(1) 垂直长大方式: 具有粗糙界面的物质, 因界面上约有50% 的原子位置空着, 这些空位都可以接受原子, 故液相原子可以进入空位, 与晶体连接, 界面沿其法线方向垂直推移, 呈连续式长大.(2) 横向(台阶)长大方式: 包括二维晶核台阶长大机制和晶体缺陷台阶长大机制, 具有光滑界面的晶体长大往往采取该方式. 二维晶核模式, 认为其生长主要是利用系统的能量起伏, 使液相原子在界面上通过均匀形核形成一个原子厚度的二维薄层状稳定的原子集团, 然后依靠其周围台阶填充原子, 使二维晶核横向长大, 在该层填满后, 则在新的界面上形成新的二维晶核, 继续填满, 如此反复进行.晶体缺陷方式, 认为晶体生长是利用晶体缺陷存在的永不消失的台阶(如螺型位错的台阶或挛晶的沟槽)长大的.第四章 相图1. 在Al-Mg 合金中, x Mg 为0.15, 计算该合金中镁的w Mg 为多少.解 设Al 的相对原子量为M Al , 镁的相对原子量为M Mg , 按1mol Al-Mg 合金计算, 则镁的质量分数可表示为Mg MgMg Al Al Mg Mg 100%x M w x M x M =⨯+.将x Mg = 0.15, x Al = 0.85, M Mg = 24, M Al = 27代入上式中, 得到w Mg = 13.56%.2. 根据图4-117所示二元共晶相图, 试完成:(1) 分析合金I, II的结晶过程, 并画出冷却曲线.(2) 说明室温下合金I, II的相和组织是什么, 并计算出相和组织组成物的相对量.(3) 如果希望得到共晶组织加上相对量为5%的β初的合金, 求该合金的成分.图4-117 二元共晶相图附图4-1 合金I的冷却曲线附图4-2 合金II的冷却曲线解 (1) 合金I的冷却曲线参见附图4-1, 其结晶过程如下:1以上, 合金处于液相;1~2时, 发生匀晶转变L→α, 即从液相L中析出固熔体α, L和α的成分沿液相线和固相线变化, 达到2时, 凝固过程结束;2时, 为α相;2~3时, 发生脱熔转变, α→βII.合金II的冷却曲线参见附图4-2, 其结晶过程如下:1以上, 处于均匀液相;1~2时, 进行匀晶转变L →β;2时, 两相平衡共存, 0.50.9L β;2~2′ 时, 剩余液相发生共晶转变0.50.20.9L βα+;2~3时, 发生脱熔转变α→βII .(2) 室温下, 合金I 的相组成物为α + β, 组织组成物为α + βII .相组成物相对量计算如下:αβ0.900.20100%82%0.900.050.200.05100%18%0.900.05w w -=⨯=--=⨯=- 组织组成物的相对量与相的一致.室温下, 合金II 的相组成物为α + β, 组织组成物为β初 + (α+β).相组成物相对量计算如下:αβ0.900.80100%12%0.900.050.800.05100%88%0.900.05w w -=⨯=--=⨯=- 组织组成物相对量计算如下:β(α+β)0.800.50100%75%0.900.500.900.80100%25%0.900.50w w -=⨯=--=⨯=-初 (3) 设合金的成分为w B = x , 由题意知该合金为过共晶成分, 于是有β0.50100%5%0.900.50x w -=⨯=-初 所以, x = 0.52, 即该合金的成分为w B = 0.52.3. 计算w C 为0.04的铁碳合金按亚稳态冷却到室温后组织中的珠光体、二次渗碳体和莱氏体的相对量, 并计算组成物珠光体中渗碳体和铁素体及莱氏体中二次渗碳体、共晶渗碳体与共析渗碳体的相对量.解 根据Fe-Fe 3C 相图, w C = 4%的铁碳合金为亚共晶铸铁, 室温下平衡组织为 P + Fe 3C II + L d ′, 其中P 和Fe 3C II 系由初生奥氏体转变而来, 莱氏体则由共晶成分的液相转变而成, 因此莱氏体可由杠杆定律直接计算, 而珠光体和二次渗碳体则可通过两次使用杠杆定律间接计算出来.L d ′ 相对量: d L 4 2.11100%86.3%4.3 2.11w '-=⨯=-. Fe 3C II 相对量: 3II Fe C 4.34 2.110.77100% 3.1%4.3 2.11 6.690.77w --=⨯⨯=--.P 相对量: P 4.34 6.69 2.11100%10.6%4.3 2.11 6.690.77w --=⨯⨯=--. 珠光体中渗碳体和铁素体的相对量的计算则以共析成分点作为支点, 以w C = 0.001%和w C = 6.69%为端点使用杠杆定律计算并与上面计算得到的珠光体相对量级联得到.P 中F 相对量: F P 6.690.77100%9.38%6.690.001w w -=⨯⨯=-. P 中Fe 3C 相对量: 3Fe C 10.6%9.38% 1.22%w =-=.至于莱氏体中共晶渗碳体、二次渗碳体及共析渗碳体的相对量的计算, 也需采取杠杆定律的级联方式, 但必须注意一点, 共晶渗碳体在共晶转变线处计算, 而二次渗碳体及共析渗碳体则在共析转变线处计算.L d ′ 中共晶渗碳体相对量: d Cm L 4.3 2.11100%41.27%6.69 2.11w w '-=⨯⨯=-共晶L d ′ 中二次渗碳体相对量: d Cm L 6.69 4.3 2.110.77100%10.2%6.69 2.11 6.690.77w w '--=⨯⨯⨯=--II L d ′ 中共析渗碳体相对量:d Cm L 6.69 4.3 6.69 2.110.770.0218100% 3.9%6.69 2.11 6.690.77 6.690.0218w w '---=⨯⨯⨯⨯=---共析 4. 根据下列数据绘制Au-V 二元相图. 已知金和钒的熔点分别为1064℃和1920℃. 金与钒可形成中间相β(AuV 3); 钒在金中的固熔体为α, 其室温下的熔解度为w V = 0.19; 金在钒中的固熔体为γ, 其室温下的熔解度为w Au = 0.25. 合金系中有两个包晶转变, 即1400V V V 1522V V V (1) β(0.4)L(0.25)α(0.27)(2) γ(0.52)L(0.345)β(0.45)w w w w w w =+===+==℃℃解 根据已知数据绘制的Au-V 二元相图参见附图4-3.附图4-3 Au-V 二元相图第五章 材料中的扩散1. 设有一条直径为3cm 的厚壁管道, 被厚度为0.001cm 的铁膜隔开, 通过输入氮气以保持在膜片一边氮气浓度为1000 mol/m 3; 膜片另一边氮气浓度为100 mol/m 3. 若氮在铁中700℃时的扩散系数为4×10-7 cm 2 /s, 试计算通过铁膜片的氮原子总数.解 设铁膜片左右两边的氮气浓度分别为c 1, c 2, 则铁膜片处浓度梯度为7421510010009.010 mol /m 110c c c c x x x --∂∆-≈===-⨯∂∆∆⨯ 根据扩散第一定律计算出氮气扩散通量为 722732410(10)(9.010) 3.610 mol/(m s)c J D x---∂=-=-⨯⨯⨯-⨯=⨯∂ 于是, 单位时间通过铁膜片的氮气量为 3-22-63.610(310) 2.5410 mol/s 4J A π-=⨯⨯⨯⨯=⨯最终得到单位时间通过铁膜片的氮原子总数为-62318-1A () 2.5410 6.02102 3.0610 s N J A N =⨯=⨯⨯⨯⨯=⨯第六章 塑性变形1. 铜单晶体拉伸时, 若力轴为 [001] 方向, 临界分切应力为0.64 MPa, 问需要多大的拉伸应力才能使晶体开始塑性变形?解 铜为面心立方金属, 其滑移系为 {111}<110>, 4个 {111} 面构成一个八面体, 详见教材P219中的图6-12.当拉力轴为 [001] 方向时, 所有滑移面与力轴间的夹角相同, 且每个滑移面上的三个滑移方向中有两个与力轴的夹角相同, 另一个为硬取向(λ = 90°). 于是, 取滑移系(111)[101]进行计算.222222222222k s cos 3001111cos 2001(1)01cos cos 60.646 1.57 MPa.m mϕλϕλτσ==++⨯++==++⨯-++=====即至少需要1.57 MPa 的拉伸应力才能使晶体产生塑性变形.2. 什么是滑移、滑移线、滑移带和滑移系? 作图表示α-Fe, Al, Mg 中的最重要滑移系. 那种晶体的塑性最好, 为什么?答: 滑移是晶体在切应力作用下一部分相对于另一部分沿一定的晶面和晶向所作的平行移动; 晶体的滑移是不均匀的, 滑移部分与未滑移部分晶体结构相同. 滑移后在晶体表面留下台阶, 这就是滑移线的本质. 相互平行的一系列滑移线构成所谓滑移带. 晶体发生滑移时, 某一滑移面及其上的一个滑移方向就构成了一个滑移系.附图6-1 三种晶体点阵的主要滑移系α-Fe具有体心立方结构, 主要滑移系可表示为 {110}<111>, 共有6×2 = 12个; Al 具有面心立方结构, 其滑移系可表示为 {111}<110>, 共有4×3 = 12个; Mg具有密排六方结构, 主要滑移系可表示为{0001}1120<>, 共有1×3 = 3个. 晶体的塑性与其滑移系的数量有直接关系, 滑移系越多, 塑性越好; 滑移系数量相同时, 又受滑移方向影响, 滑移方向多者塑性较好, 因此, 对于α-Fe, Al, Mg三种金属, Al的塑性最好, Mg的最差, α-Fe 居中. 三种典型结构晶体的重要滑移系如附图6-1所示.3. 什么是临界分切应力? 影响临界分切应力的主要因素是什么? 单晶体的屈服强度与外力轴方向有关吗? 为什么?答:滑移系开动所需的作用于滑移面上、沿滑移方向的最小分切应力称为临界分切应力.临界分切应力τk的大小主要取决于金属的本性, 与外力无关. 当条件一定时, 各种晶体的临界分切应力各有其定值. 但它是一个组织敏感参数, 金属的纯度、变形速度和温度、金属的加工和热处理状态都对它有很大影响.如前所述, 在一定条件下, 单晶体的临界分切应力保持为定值, 则根据分切应力与外加轴向应力的关系: σs= τk/ m, m为取向因子, 反映了外力轴与滑移系之间的位向关系, 因此, 单晶体的屈服强度与外力轴方向关系密切. m越大, 则屈服强度越小, 越有利于滑移.4. 孪生与滑移主要异同点是什么? 为什么在一般条件下进行塑性变形时锌中容易出现挛晶, 而纯铁中容易出现滑移带?答: 孪生与滑移的异同点如附表6-1所示.附表6-1 晶体滑移与孪生的比较锌为密排六方结构金属, 主要滑移系仅3个, 因此塑性较差, 滑移困难, 往往发生孪生变形, 容易出现挛晶; 纯铁为体心立方结构金属, 滑移系较多, 共有48个, 其中主要滑移系有12个, 因此塑性较好, 往往发生滑移变形, 容易出现滑移带.第七章 回复与再结晶1. 已知锌单晶体的回复激活能为8.37×104J/mol, 将冷变形的锌单晶体在-50 ℃进行回复处理, 如去除加工硬化效应的25% 需要17 d, 问若在5 min 内达到同样效果, 需将温度提高多少摄氏度?解 根据回复动力学, 采用两个不同温度将同一冷变形金属的加工硬化效应回复到同样程度, 回复时间、温度满足下述关系:122111exp t Q t R T T ⎛⎫⎛⎫=-- ⎪ ⎪ ⎪⎝⎭⎝⎭整理后得到221111ln T t R T Q t =+.将41211223 K,/5/(172460),8.3710 J/mol, 8.314 J/(mol K)4896T t t Q R ==⨯⨯==⨯=⋅代入上式得到2274.7 K T =.因此, 需将温度提高21274.722351.7 T T T ∆=-=-=℃.2. 纯铝在553 ℃ 和627 ℃ 等温退火至完成再结晶分别需要40 h 和1 h, 试求此材料的再结晶激活能.解 再结晶速率v 再与温度T 的关系符合阿累尼乌斯(Arrhenius)公式, 即exp()Q v A RT=-再 其中, Q 为再结晶激活能, R 为气体常数.如果在两个不同温度T 1, T 2进行等温退火, 欲产生同样程度的再结晶所需时间分别为t 1, t 2, 则122112122111exp[()]ln(/)t Q t R T T RTT t t Q T T =--⇒=-依题意, 有T 1 = 553 + 273 = 826 K, T 2 = 627 + 273 = 900 K, t 1 = 40 h, t 2 = 1 h, 则58.314826900ln(40/1)3.0810J/mol 900826Q ⨯⨯⨯=⨯-3. 说明金属在冷变形、回复、再结晶及晶粒长大各阶段的显微组织、机械性能特点与主要区别.答: 金属在冷变形、回复、再结晶及晶粒长大各阶段的显微组织、机械性能特点与主要区别详见附表7-1.附表7-1 金属在冷变形、回复、再结晶及晶粒长大各阶段的显微组织、机械性能第八章固态相变。
晶体生长过程中的界面动力学研究
晶体生长过程中的界面动力学研究晶体生长是一个涉及到物理学、化学、数学等多个学科的领域，其中界面动力学是其中一个重要研究方向。
界面动力学主要研究在不同条件下晶体生长中液-固界面的动力学行为，通过理论和实验的研究，可以更好地描述和控制晶体生长过程，为材料科学和能源科技等领域提供有价值的参考。
一、晶体生长中的界面动力学晶体是由分子或原子组成的有序物质，其生长过程需要溶液中物质的扩散、吸附和结晶等多个过程。
生长的过程主要体现在液-固（或气-固）的交界处，也就是晶体的界面上。
因此，界面动力学研究的重点就是晶体生长过程中液-固界面的动力学行为。
在界面动力学中，最常用的理论模型之一是“再结晶理论”。
该理论模型假设晶体生长过程中液相分子能自由扩散并进入固相，并沿晶体表面扩散最终结晶，从而形成晶体。
当液滴通过晶体表面时，会先选择朝向能量最低的方向，并形成一个滑移平面。
在此基础上，随着液滴进一步扩散和吸附的过程，晶体的生长速度逐渐加快，形成自组装式生长。
二、晶体生长中的液-固界面结构和动力学特性晶体生长中液-固界面的结构和动力学特性将直接影响晶体的生长速率和晶体质量，因此对液-固界面的研究是极其重要的。
我们可以通过扫描电子显微镜和原子力显微镜等手段来观察晶体生长界面的微观形态，并通过彩色蚀刻实验（Color etching）来定性分析不同条件下的晶体生长速率、表面形貌和结构等。
此外，可以通过电感耦合等离子体法（ICP）技术来实时监测溶液中的化学物质浓度和温度等变化，以揭示生长过程中的动力学特性。
三、界面动力学的应用界面动力学研究的应用广泛，主要应用于材料科学、能源技术和生物科学等领域。
其中最典型的应用就是在晶体生长和半导体制造过程中。
在晶体生长中，界面动力学可以被用于控制晶体质量和晶体形态等，从而提高晶体生长效率和质量。
在半导体制造中，界面动力学可以被用于控制晶体表面的缺陷和杂质，从而提高器件性能和可靠性。
此外，界面动力学在化学反应动力学、能源材料和环境科学等方面也发挥着重要的作用。
材料科学基础名词解释中英
《材料科学基础》名词解释AOrowan mechanism （奥罗万机制）位错绕过第二相粒子，形成包围第二相粒子的位错环的机制。
Austenite(奥氏体)碳在γ-Fe中形成的间隙固溶体称为奥氏体。
B布拉菲点阵除考虑晶胞外形外，还考虑阵点位置所构成的点阵。
Half-coherent interface（半共格相界）两相邻晶体在相界面处的晶面间距相差较大，则在相界面上不可能做到完全一一对应，于是在界面上将产生一些位错，以降低界面弹性应变能。
这时两相原子部分保持匹配，这样的界面称为半共格界面。
Sheet texture（板织构）轧板时形成的组织的择优取向。
Peritectic reaction（包晶反应）固相和液相生成另一成分的固溶体的反应Peritectic segregation（包晶偏析）新生成的固相的芯部保留残余的原有固相，新相本身成分也不均匀。
Peritectic phase diagram（包晶相图）具有包晶反应的相图Peritectoid reaction（包析反应）由两个固相反应得到一个固相的过程为包析反应。
Cellular structure（胞状结构）成分过冷区很小时，固相突出部分局限在很小区域内，不生成侧向枝晶。
Intrinstic diffusion coefficient（本征扩散系数）依赖热缺陷进行的扩散的扩散系数。
Transformed ledeburite（变态莱氏体）渗碳体和奥氏体组成的莱氏体冷却至727℃时奥氏体发生共析反应转变为珠光体，此时称变态莱氏体。
Deformation twins（变形孪晶）晶体通过孪生方式发生塑性变形时产生的孪晶（BCC，HCP）Chill zone（表层细晶区）和低温铸模模壁接触，强烈过冷形成的细小的方向杂乱的等轴晶粒细晶区。
Burger’s vector（柏氏矢量）表征位错引起的晶格点阵畸变大小和方向的物理量。
Asymmetric tilt boundary（不对称倾斜晶界）晶界两侧晶粒不对称的小角度晶界，界面含两套垂直的刃型位错。
二维二硫化钼(MoS2)及应用
2
研究背景
石墨烯（Graphene）是二维结构的一个典 型代表，它只有一个原子层厚，达到了母体石 墨的几何极限。作为一个理想的二维量子体系， 在理论上Graphene并不是一个新事物。Wallace Philip 在20世纪40年代就对石墨烯二维量子体 系的电子结构开展了研究。几年后，石墨烯的 波函数方程被 J. W. Mcclur 成功推导得到。尽 管人们对Graphene的电输运性能提出过质疑， 但是并没有阻挡理论学家对石墨烯这个理想模 型结构的研究热情。
[1] Coleman J N, Lotya M, O'Neill A, etal. Two-dimensional nanosheets produced by liquid exfoliation of layered materials.Science,2011,331:568~571
7
研究背景
16
MoS2
早在1986年，就有人通过插入锂的方法成功剥离出单层二硫化钼。 2007年，世界上第一支纳米二硫化钼晶体管在美国马里兰大学问世，但由于其迁移 率并不理想因而并未引起太多注意。 2011年，Kis教授实验组在上发表了自己利用单层二硫化钼成功制造晶体管的文章， 引起轰动。 2011年11月，该实验组又报道了世界上第一只二硫化钼集成电路的成功研制。他们 将两只二硫化钼晶体管集成在一起，实现了简单的“或非”运算。 2012年，美国的Liu实验组报导了采用原子层沉积工艺制作的场效应晶体管，他们在 Al2O3绝缘衬底上使用23层，总厚度为15nm的二硫化钼纳米片层材料，成功制造出 双栅MOSFET，迁移率达到517cm2/V· s，是最初的纳米二硫化钼晶体管迁移率的10 倍。 同年，日本东京大学的Zhang实验组利用离子液体作为栅极绝缘体，使用纳米二硫 化钼材料成功研制出了双极型晶体管，其空穴和电子导电的开关比均大于102，实现 了较高的空穴迁移率。
CrystalGrowth-生长技术
Crystal Growth Techniques
1. Growth from solution 2. Growth from gas (vapor) phase 3. Growth from liquid (melt) phase
Crystal Growth from Solution
Advantages:
Issues:
Crystal Growth from Liquid (Melt)
Variety of techniques (“tricks”):
Verneuil (“flame fusion”) ~early 1900’s Czochralski (“pulling”) ~1910’s Kyropoulos (“top seeding”) ~1920’s Bridgman (“directional solidification”) ~1940’s Skull Melting ~1970’s Laser-heated pedestal growth ~1990’s Micropulling ~1990’s Floating Zone (incl. image furnace) ~1990’srials + flux in crucible Special choice of atmosphere? Heat to liquid state Cool very slowly Separate precipitated sample from flux
Horizontal Gradient Freezing (HGF) method Horizontal Bridgman (HB) method Horizontal Zone Melting (HZM) method
晶体生长微观机理及晶体生长边界层模型
晶体生长微观机理及晶体生长边界层模型晶体生长是一种重要的物理化学过程，它在材料科学、化学工业、生物医药等领域都有着广泛的应用。
晶体生长微观机理及晶体生长边界层模型是研究晶体生长过程中关键的问题，本文将从以下几个方面进行探讨。
一、晶体生长微观机理1. 晶体的结构与生长晶体是由原子、离子或分子按照一定规律排列而成的固态物质，其结构可以通过X射线衍射等手段进行表征。
在晶体生长过程中，溶液中的溶质分子会逐渐聚集形成固态结构，这个过程可以分为三个阶段：核化、成核和晶体生长。
2. 晶核形成与影响因素在溶液中，当达到饱和度时，就会出现小于临界尺寸的“原始胚”，随着时间的推移，“原始胚”会不断增大并发展成为稳定的“晶核”。
影响晶核形成的因素包括温度、浓度、pH值等。
3. 晶体生长速率与形貌晶体生长速率与晶体表面的形貌密切相关，通常情况下，高速生长的晶体表面比较光滑，低速生长的晶体表面则会出现棱角和凸起。
晶体生长速率受到溶液中溶质浓度、温度、流动状态等多种因素影响。
二、晶体生长边界层模型1. 晶体生长边界层概念在晶体生长过程中，由于溶液和固态晶体之间存在着物质交换和能量转移，因此会形成一个厚度很小的“边界层”，这个“边界层”被称为“晶体生长边界层”。
它是指在固液相变过程中，在固相表面与液相之间存在的一种物理化学过程。
2. 晶体生长边界层模型目前已经提出了多种不同的晶体生长边界层模型，其中最为广泛应用的是Kossel-Stranski模型。
该模型认为，在固态表面上形成了一层原子密度比周围低的单分子层，该单分子层可以吸附在固态表面上，并且能够引导下一层原子的沉积。
随着晶体生长，这个单分子层会不断向外扩散，直至达到平衡状态。
3. 晶体生长边界层的影响晶体生长边界层对晶体生长速率和形貌都有着重要的影响。
较厚的边界层会导致晶体表面形貌不规则，生长速率变慢；而较薄的边界层则会使晶体表面光滑，生长速率加快。
三、总结晶体生长微观机理及晶体生长边界层模型是研究晶体生长过程中关键的问题。
晶体生长第六章 界面的微观结构
第六章 界面的微观结构§1. 晶体的平衡形状1． 界面能极图与晶体的平衡形状γ(n)—界面能γ(n)dA=最小液体 γ(n)= γ=常数——球形晶体 ——界面能最低的晶面所包围（低指数面）§2. 邻位面与台阶的平衡结构1． 奇异面（低指数面、原子密排面、界面能最低的面）邻位面非奇异面界 面 能 极 图2． 邻位面台阶化邻位面→台阶（总界面能最低）§2. 台阶热力学性质1． 台阶——奇异面的一条连续曲线，线之间则有一个原子的高度差。
台阶是起止于晶体边缘或形成闭合曲线，不会终止在晶面内。
hk yZ tg -=∂∂=θ2． 台阶棱边能：单位长度台阶具有的自由能（产生单位长度台阶所作之功）台阶有线张力（棱边能大小），使台阶缩短。
3． 台阶棱边能的各项异性——台阶扭折化h tg k /θ=4． 台阶的平衡结构台阶上的扭折取决于台阶取向，当θ=0（台阶和密排方向一致），k →0,这只在0k 时成立。
热涨落可在台阶上产生扭折。
扭折有正负号。
扭折产生与台阶吸附空位或原子有关。
α+=α- α++α-+α0=1α+：产生正扭折机率台 阶 的 扭 折 化α-：产生负扭折机率α0：不产生扭折的机率细微平衡原理（The principle of detailed balancing ）求扭折形成能 a: 2Φ1 2扭折b: 4Φ1 4扭折 一个扭折形成能为Φ1 c: 0 0 )/exp(//100kT Φ-==∴-+αααα台阶任意位置产生扭折的总机率（正和负）为： )/exp(210kT Φ-=+=-+αααα台阶有n 原子，a 为原子间距，台阶长na,台阶上的扭折数为：n （α++α-）扭折平均距离： +-+-+=+=+=ααααα2)(0a a n na X由于α++α-+α0=α0+2α+=1 即： )(1αααα+=++ }2){exp(210+Φ=∴kT a X X 0>>a , )exp(210kT a X Φ≈∴T →0k 时，X 0→∞ 扭折密度为零在有限温度下，台阶上总是存在扭折的（θ=0） 600K X0≈4～5a§3. 界面相变熵和界面的平衡结构1．光滑界面与粗糙界面晶体原子→振动平均频率固定熔体原子→振动平均频率是变化的X=N A/N N A晶体原子1-X 熔体X≈50% 1-X≈50% 粗糙界面X≈0% 或 1-X≈100% 光滑界面考察界面自由能的表达式，求出自由能最低时的X。
材料科学基础复习题
材料科学基础复习题第三章：晶体的范性形变（crystal plastic deformation）单晶体范性形变的两种基本⽅式：滑移（slip）和孪⽣（twinning）两者都为剪应变。
FCC的滑移⾯都是{111}，滑移⽅向都是<110>，BCC的滑移⾯都有{110}，滑移⽅向都是<111> 滑移⽅向都是最密排的⽅向，⽽滑移⾯则往往是密排⾯Schmid定律：当作⽤在滑移⾯上沿着滑移⽅向的分切应⼒达到某⼀临界值τc时，晶体便开始滑移。
P144.我们把只有⼀个滑移系统的滑移称为单滑移，具有两个或以上的滑移叫做双滑移或者多滑移。
晶粒和晶粒之间的过渡区域就称晶粒边界或称晶界。
晶粒越细，阻碍滑移的晶界便越多，屈服极限也就越⾼。
（细化晶粒不仅可以提⾼⾦属的强度，同时还可以提⾼其韧性）Hall 公式：拉伸应⼒变形（tensile stress deformation）晶体在外⼒作⽤下会发⽣形变，当外⼒较⼩时变形是弹性的，即卸载后变形也随之消失，这种可恢复的变形就称为，弹性变形（elastic deformation）当外⼒超过⼀定值后，应⼒和应变就不在成线性关系，卸载后变形也不能完全消失，⽽会留下⼀定的残余变形或者永久变形，这种不可恢复的变形就称为，塑性变形（plastic deformation）低碳钢的拉伸应⼒——应变曲线（图解计算题）延伸率（elongation）：断裂前的最⼤相对伸长。
断⾯收缩率（reduction in cross-section）：断裂前最⼤的相对⾯积缩减。
晶体的断裂（Crystal fracture）滑移系统（slip system）：⼀个滑移⾯和位于该⾯上的⼀个滑移⽅向便组成了⼀个滑移系统。
孪⽣系统（twinning system）：⼀个孪⽣⾯和该⾯上的⼀个孪⽣⽅向组成⼀个孪⽣系统。
加⼯硬化（work hardening）：⾦属在冷加⼯过程中，要想不断地塑性变形，就需要不断增加外应⼒。
《材料成形原理》3.3晶体生长
Fundamentals of Crystalization
3 Fundamentals of Crystalization
3.1 经典形核理论 3.2 固-液界面结构 3.3 晶体生长 3.4 凝固过程溶质的分配 3.5 固-液界面的稳定性 3.5 多相合金的结晶
3.3 Crystal Growth
物
粗糙界面非小平面生长的一次晶 p60图3.18
奥氏体 枝状晶
Al基固 溶体枝 状晶
温度对晶体形貌影响
生长均匀、连续的粗糙界面， • 正温度梯度下，晶体生长，界面形貌？ • 负温度梯度下，晶体生长，界面形貌？
温度对晶体形貌影响
生长均匀、连续的粗糙界面， • 正温度梯度下界面稳定，应以平面推进。 • 负温度梯度下晶体快速向内部生长，界面不稳
脱氧铜(99.9%Cu)，退火组织，单α相
生长速度
• 生长就是固-液界面向液相的推进。 • 长大速度取决于
– 温度条件G （结晶潜热的散失速度与散热） – 固-液界面结构 – 溶质离开固-液界面的扩散速度。 • 界面平均移动速度R与过冷度ΔT的函数关系。
粗糙界面
R 1 T
μ1为比例常数，对大多数金属，μ1≈1cm/sK
3.3 Crystal Growth
• 动力学过冷 • 生长机制 • 凝固形成的晶体缺陷 • 晶界 • 生长速率
晶界 Grain boundary
晶界：从不同的晶核长大的小晶体，取向各不相同。凝 固 结 束 时 ， 两 个 晶 体 间 的 位 向 失 配 （ orientation mismatch），形成分隔这些小晶体的界面。
晶体生长：是液相中的原子向晶体表面迁 移和堆砌，短程序 长程有序， 固-液界面向液体中不断推移的过程。
北航物理冶金原理3-合金相图与凝固(1)
B%
B
A
T, oC
Liquid: L
L + a
Solid: a
Co
CL
CS
Cs＝ k CL
Wa
WL
Co
CL
Ca
Ts
TL
二、单相合金的平衡凝固：Equilibrium Solidification 2. 两相平衡的基本规则：杠杆规则 Lever Rule 平衡相之成分点：连接线－tie-line or Conode 平衡相之相对重量百分数：杠杆定律Lever Rule
相平衡规律：相律
体系自由度 f＝n – p + 2 f＝n – p + 1（常压条件）
常见基本相图类型
1、匀晶相图（无限互溶单相固溶体）Isomorphous +L
L
a
(f=2-1+1=2)
(f=2-1+1=2)
(f=2-2+1=1)
2、共晶相图：Eutectic Phase Diagram LE (a+b) 三相平衡 f=2-3+1=0
单相二元合金的凝固 Solidification of Single-Phase Binary Alloys
一、相图分析： 液相线－Liquidus; 固相线－Solidus; 液相区; 固相区; 两相区. 自由度
DT
DGv
Tm
T
G
GL
Gs
Spontaneous Nucleation 自发形核（均匀形核）
Spontaneous Nucleation 自发形核（均匀形核）
Spontaneous Nucleation 自发形核（均匀形核）
r
临界形核功： Critical Energy of Nucleation
半导体缺陷解析及中英文术语一览
一、半导体缺陷1.位错：位错又可称为差排（英语：dislocation），在材料科学中，指晶体材料的一种内部微观缺陷，即原子的局部不规则排列（晶体学缺陷）。
从几何角度看，位错属于一种线缺陷，可视为晶体中已滑移部分与未滑移部分的分界线，其存在对材料的物理性能，尤其是力学性能，具有极大的影响。
产生原因：晶体生长过程中，籽晶中的位错、固-液界面附近落入不溶性固态颗粒，界面附近温度梯度或温度波动以及机械振动都会在晶体中产生位错。
在晶体生长后，快速降温也容易增殖位错。
（111）呈三角形；（100）呈方形；（110）呈菱形。
2.杂质条纹：晶体纵剖面经化学腐蚀后可见明、暗相间的层状分布条纹，又称为电阻率条纹。
杂质条纹有分布规律，在垂直生长轴方向的横断面上，一般成环状分布；在平行生长轴方向的纵剖面上，呈层状分布。
反映了固-液界面结晶前沿的形状。
产生原因：晶体生长时，由于重力产生的自然对流和搅拌产生的强制对流，引起固-液界近附近的温度发生微小的周期性变化，导致晶体微观生长速率的变化，或引起杂质边界厚度起伏，一截小平面效应和热场不对称等，均使晶体结晶时杂质有效分凝系数产生波动，引起杂质中杂质浓度分布发生相应的变化，从而在晶体中形成杂质条纹。
解决方案:：调整热场，使之具有良好的轴对称性，并使晶体的旋转轴尽量与热场中心轴同轴，抑制或减弱熔热对流，可以使晶体中杂质趋于均匀分布。
采用磁场拉晶工艺或无重力条件下拉晶可以消除杂质条纹。
3.凹坑：晶体经过化学腐蚀后，由于晶体的局部区域具有较快的腐蚀速度，使晶体横断面上出现的坑。
腐蚀温度越高，腐蚀时间越长，则凹坑就越深，甚至贯穿。
4.空洞：单晶切断面上无规则、大小不等的小孔。
产生原因：在气氛下拉制单晶，由于气体在熔体中溶解度大，当晶体生长时，气体溶解度则减小呈过饱和状态。
如果晶体生长过快，则气体无法及时从熔体中排出，则会在晶体中形成空洞。
5.孪晶：使晶体断面上呈现金属光泽不同的两部分，分界线通常为直线。
晶体生长理论综述
综述晶体生长理论的发展现状1前言晶体生长理论是用以阐明晶体生长这一物理化学过程。
形成晶体的母相可以是气相、液相或固相；母相可以是单一组元的纯材料，也可以是包含其他组元的溶液或化合物。
生长过程可以在自然界中实现，如冰雪的结晶和矿石的形成；也可以在人工控制的条件下实现，如各种技术单晶体的培育和化学工业中的结晶等。
近几十年来，随着基础学科(如物理学、化学)和制备技术的不断进步，晶体生长理论研究无论是研究手段、研究对象，还是研究层次都得到了很快的发展，已经成为一门独立的分支学科。
它从最初的晶体结构和生长形态研究、经典的热力学分析发展到在原子分子层次上研究生长界面和附加区域熔体结构，质、热输运和界面反应问题，形成了许多理论或理论模型。
当然，由于晶体生长技术和方法的多样性和生长过程的复杂性，目前晶体生长理论研究与晶体生长实践仍有相当的距离，人们对晶体生长过程的理解有待于进一步的深化。
可以预言，未来晶体生长理论研究必将有更大的发展[1]。
2晶体生长理论的综述自从1669年丹麦学者斯蒂诺(N.Steno)开始晶体生长理论的启蒙工作以来[2]，晶体生长理论研究获得了很大的发展，形成了包括晶体成核理论、输运理论、界面稳定性理论、晶体平衡形态理论、界面结构理论、界面动力学理论和负离子配位多面体模型的体系。
这些理论在某些晶体生长实践中得到了应用，起了一定的指导作用。
本文主要对晶体平衡形态理论、界面生长理论、PBC理论、晶体逆向生长等理论作简要的介绍。
2.1晶体平衡形态理论晶体具有特定的生长习性，即晶体生长外形表现为一定几何形状的凸多面体，为了解释这些现象，晶体生长理论研究者从晶体内部结构和热力学分析出发，先后提出了Bravais法则、Gibbs-Wulff晶体生长定律、Frank运动学理论。
2.1.1Bravais法则早在1866年，A.Bravais首先从晶体的面网密度出发，提出了晶体的最终外形应为面网密度最大的晶面所包围，晶面的法线方向生长速率R反比于面间距，生长速率快的晶面族在晶体最终形态中消失[3]。
单元系-题库(部分答案)
判断题1) 相图表示的是体系的热力学平衡状态。
√ 2) 晶胚的临界半径r k 随着△T 的增大而减小。
× 3) 液态金属的结构特点是短程有序，长程无序。
( )4) 液态金属只要过冷到其熔点以下就会发生结晶。
[×]5) 非均匀形核时，临界晶核（曲率）半径决定了晶核的形状和体积大小[×]6) 无论固-液界面微观结构呈粗糙型还是光滑型，晶体生长时液相原子都是一个个地沿着固相面的垂直方向连接上去的。
[×]7) 无论温度如何分布，纯金属都是以树枝状方式生长。
[×]8) 纯晶体结晶时的过冷度是指在冷却曲线上出现平台的温度与熔点之差。
[×] 9) 在任何温度下，液相中出现的最大结构起伏都成为晶核。
[×]10) 所谓临界晶核，就是体系自由能的减少完全抵偿表面自由能的增加时的晶胚大小。
[×] 11) 在液态金属中，凡是涌现出小于临界晶核半径的晶胚都不能成核，但是只要由足够的能量起伏提供形核功，还是可以成核的。
[×]12) 非均匀形核总是比均与均匀形核容易，因为非均匀形核一般是以外加固体杂质作为现成晶核，不需要形核功。
[×]13) 非均匀形核，当接触角θ=0°时，非均匀形核的形核功最大。
[×]14) 固-液界面的微观结构可根据杰克逊因子α来判断：当α≤2时，固-液界面为光滑界面；当α≥5时，固-液界面为粗糙界面。
[×] 15) 结晶的热力学条件是：0V G V G S σ∆=-∆+<。
[×]16) 不论晶核大小，形成晶核时都需要形核功。
[×]17) 纯金属结晶时若呈垂直方式生长，其界面时为光滑，时而粗糙，交替变化。
[×]18) 从宏观上观察，若液-固界面时平直的称为光滑界面；若液-固界面时由若干小平面组成，呈锯齿形的称为粗糙界面。
[×]19) 一般金属结晶时，形核率随着过冷度的增加而增加，超过某一极大值后，出现反的变化。
转载成核生长理论
转载成核生长理论第一种贡献是与热涨落而导致的超临界尺寸的分子群集体形成有关第二种是无热成核,只是当体系中的热力学状态发生变化是才出现.也由于区分稳定核与不稳定分子群集体间的临界值改变而产生.晶体生长科学与技术是一门多学科交叉领域，涉及到物理、化学、电子电气工程、流体力学与计算科学等多方面知识的综合运用。
对晶体生长科学与技术的详细讲解是非常困难的，在这里我给大家就我所知道的部分做一个提纲挈领式的导读。
我希望本讲座无论对于没有相关基础知识的朋友，还是对于那些对本领域有一定理解的人都或多或少有些帮助。
总的课程拟分成基本原理和思想、基本技术与仪器设备、典型材料及应用等几个部分。
本讲主要介绍晶体生长技术和仪器中可能涉及到的问题相关的基本原理和思想，关键点有形核(nucleation)、生长界面(crystal-liquidinterface)、输运现象(transportphenomena)、形貌(morphology)以及数值模拟基本知识。
晶体生长最初起源于形核过程，Gibbs在19世纪末就提出形核过程的本质是过冷度(supercooling)作为驱动力与表面能(surfaceenergy)作为阻力之间的竞争。
如图1所示，随着晶体中分子数目的增多，驱动力作为线性降低，而表面能是2/3方关系增加。
这一方面说明过冷度在晶核中的粒子数足够多的情况下将占绝对优势，而另一方面，在某个粒子数目以下，晶粒的增长需要额外的能量，比如温度的涨落帮助其克服因表面能带来的能垒。
图1形核过程基本热力学现已被广泛接受的研究表明，晶体的稳定成核之前需要经过两个阶段，一是从液体中生成团簇(denseliquid)，二是团簇之中发生无序-有序转变并最终转化成晶核(realnuclear)。
两步成核理论之所以更成功，是因为它可以用来解释经典一步成核理论与某些晶体成核率实验之间高达10个数量级的巨大差异，因为2步成核涉及到多一级能垒，于是相对晶体成核理论可以得到更低更合理的成核率。
4单元系 题库(部分答案)
相图表示的是体系的热力学平衡状态。√
晶胚的临界半径 r k 随着△T 的增大而减小。× 液态金属的结构特点是短程有序，长程无序。 ( )
4) 液态金属只要过冷到其熔点以下就会发生结晶。[×] 5) 非均匀形核时，临界晶核（曲率）半径决定了晶核的形状和体积大小[×] 6) 无论固-液界面微观结构呈粗糙型还是光滑型，晶体生长时液相原子都是一个个地沿着固相面的垂直方向 连接上去的。[×] 7) 无论温度如何分布，纯金属都是以树枝状方式生长。[×] 8) 纯晶体结晶时的过冷度是指在冷却曲线上出现平台的温度与熔点之差。[×] 9) 在任何温度下，液相中出现的最大结构起伏都成为晶核。[×] 10) 所谓临界晶核，就是体系自由能的减少完全抵偿表面自由能的增加时的晶胚大小。[×] 11) 在液态金属中， 凡是涌现出小于临界晶核半径的晶胚都不能成核， 但是只要由足够的能量起伏提供形核功， 还是可以成核的。[×] 12) 非均匀形核总是比均与均匀形核容易， 因为非均匀形核一般是以外加固体杂质作为现成晶核， 不需要形核 功。[×] 13) 非均匀形核，当接触角θ=0°时，非均匀形核的形核功最大。[×] 14) 固-液界面的微观结构可根据杰克逊因子α来判断：当α≤2 时，固-液界面为光滑界面；当α≥5 时，固液界面为粗糙界面。[×] 15) 结晶的热力学条件是： G V GV S 0 。[×] 16) 不论晶核大小，形成晶核时都需要形核功。[×] 17) 纯金属结晶时若呈垂直方式生长，其界面时为光滑，时而粗糙，交替变化。[×] 18) 从宏观上观察，若液-固界面时平直的称为光滑界面；若液-固界面时由若干小平面组成，呈锯齿形的称为 粗糙界面。[×] 19) 一般金属结晶时，形核率随着过冷度的增加而增加，超过某一极大值后，出现反的变化。[×]
CrystalGrowth-生长动力学
奇异面生长
二维成核生长机制 位错生长机制
粗糙面生长
精品课件
§1 邻位面生长－台阶动力学
原子全部坐落在该面内 畸变严重界面能大 邻位面由两组或三组奇 异面构成畸变消除
界面能
邻位面
精品课件
§1 邻位面生长－台阶动力学
邻位面台阶化邻位面的生长 归结为光滑晶面上的台阶运动
一、晶面上分子的势能
模型：简单立方晶体 100 面
Physical Fundamentals of Crystal Growth
晶体生长的物理基础
Dr. Prof. Y.L. Du (杜宇雷)
yldu@
精品课件
2013年秋季学期
生长动力学
生长速率与驱动力间的函数关系称为生 长动力学规律或界面动力学规律
精品课件
1927年：Kossel 和 Stranski，光滑界面二维成核生长 模型
精品课件
t'
S
/V
1 IS
在二维核的寿命内，
界面生长一层（其
高度为 h ）
生长速率为 R h / t '
由t'
S
/V
1 ，可得 IS
S (V / I)1/3
2/ 3
t'V
I 1/3
R hV2/3 I1/3 A(g)2/3 exp(B/ g)
多二维核生长的动力学规律 基本上也是指数律的形式
相变潜热：通常将到达扭折位置的分子看为晶相分 子，由流体到达扭折所释放的能量称为相变潜热
单分子的相变潜热
lsf=Ws+Wk
精品课件
精品课件
晶体生长可能的途径 A 体 扩 散 吸附(2分 ) 面 子 扩 散 台(阶 3) 线 扩 散 扭(折 4)
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
c 过程：自台阶上的扭折位置将原子移到另一台阶的扭折 位置，破坏的键数为零（不需能量），无扭折产生.
一个扭折的形成能为 1。
在台阶上任一位置形成正、负扭折的相对几率为
＋ － ＝ 0 ＝exp(1 / kT ) 0
台阶上任一位置形成扭 折的总几率为
＝ ＋＋ －＝2 0 exp(1 / kT )
具有立方对 称性的界面 能极图
i：界面能
晶体的平衡形状 在界面能极图的能量曲面 上每一点作出垂直于该点 矢径的平面，这些平面所 包围的最小体积相似于晶 体的平衡形状。 • 晶体的平衡形状在几何 上相似于界面能极图中体 积为最小的内接多面体。
具有立方对称性 的界面能极图
• 多面体关于平衡形状的任何偏离，都会引起系统吉布斯自由 能的增加，因此存在使晶体恢复到平衡形状的相变驱动力
例：液体
γ(n) = γ = const
∵ 球体：A/V=min ∴液体的平衡形状是球体。
(2) 表面能极图 ——反应表面能与晶面取向关系的图 形 作法： 从原点O作出所有可能存在的· · · · · =n1 : n2 : n3 · · · · · · ·
2.2 晶体的平衡形状
一、表面能极图与晶体平衡形状的描述
1.表面能 晶体表面的离子，由于电价不饱和而具有较多的能 量——表面能。
另一角度：造成单位面积所损耗的功。
比表面能： 晶体表面单位面积的表面能。 •单位：N/m;J/m2 •表面能大小和多种因素有关：晶 体与环境相得性质、结构、成分、 温度、结晶学取向等。
图3.1.2 根据表面能极图求晶体的平衡形状
由界面能极图可以将界面分为：
奇异面：界面能极图中能量曲面上出现最小值的点 （尖点）。该点所对应的晶面称为奇异面。 奇异面是低指数面，也是密积面。 邻位面：奇异面邻近的晶面
非奇异面：其它取向的晶面
二、奇异面、非奇异面和邻位面 （Singular interface, nonsingular interface and vicinal interface）
熔融熵越小，越容易成为粗糙界面。 因此固-液微观界面究竟是粗糙面还是光滑面主要取决于 合金系统的热力学性质。 还与晶体学取向有关
界面结构关联特性
• 根据
Lm a kTm
1 晶面族
• 当固相表面为密排晶面时， 值高，如面心立方 的（111）面， 6 12 0.5 • 对于非密排晶面， 值低，如面心立方的（001） 面， 0.33 • 。
二 界面结构类型的判据
如何判断凝固界面的微观结构？
—— 这取决于晶体长大时的热力学条件。
设晶体内部原子配位数为ν，界面上（某一 晶面）的配位数为η，晶体表面上N个原子
NA N ，
位置，其中NA个被原子占据
x
则在熔点Tm时，单个原子由液相向固-液界 面的固相上沉积的相对自由能变化为：
Lm GA x(1 x) x ln x (1 x)ln(1 x) NkTm kTm
晶体的平衡形状热力学分析
乌尔夫定理： 一定体积的晶体的平衡形状是总界面自由能为最小的形状。
界面能极图 从原点O作出所有可能存在的晶面 的法线，取每一法线的长度比例于 该晶面的界面能的大小，这一直线 族的端点的集合表示界面能关于晶 面取向的关系。
1
h1
2
h2
n
hn hi：距晶体中心的垂直距 离
原 于 添 加 的 容 易 程 度
库伦力是长程力，作用范围及于无穷。可惜 人类的手太短，只能及乎次次近邻？
界面曲率对平衡参量的影响
物理解释？
100面 模型：简单立方晶体
21：最近邻分子的交互自 由能 2 2：次近邻的交互自由能 一个最近邻键 s 界面位置 ( 2 ) 释放能量 W 21 8 2 四个次近邻键 两个最近邻键 s 一个流体分子位置(3) 释放能量W 41 12 2 六个次近邻键 3个最近邻键 s 扭折位置(4) 释放能量W 61 12 2 六个次近邻键
a 1 / kT x0 e 2
• T0K， 扭折间距 扭折密度为0
• 有限温度，台阶上存在扭折 10.1eV T=600K，扭折的平均距离＝4－5个原子间距 • 由热涨落产生的扭折密度相当高！
2.3 界面相变熵和界面的平衡结构
一、杰克逊界面理论 单原子层界面模型
假定界面层内原子完全无关分布，忽略偏聚效应
Physical Fundamentals of Crystal Growth 晶体生长的物理基础
Yong-Sheng Li (李永胜)
ysli@
2015年秋季学期
2.1 界面的平衡形态
一、固液界面的微观结构 (一)光滑界面：显微尺寸看粗糙，原子尺寸看光滑平整。 (二)粗糙界面：显微尺寸看平整，原子尺寸看界面高低不平。
扭折的符号 人沿台阶方向前进，规定人的左 边的界面比右边高 扭折的符号 人沿台阶的方向前进，规定人的左边的界面比右边的高。 遇到扭折向左拐，扭折为负 遇到扭折向右拐，扭折为正
α+：产生正扭折的几率 α-：产生正扭折的几率 α0：产生正扭折的几率
有 α+ + α- +α0 =1
a 过程：从扭折处将一个原子移到台阶上的孤立位置，破 坏一个原子键（能量21），产生2个扭折； b 过程：自台阶任一位置将原子移到台阶上另一孤立位置， 破坏二个键（能量4 1），产生4个扭折；
• 粗糙界面与光滑
界面是在原子尺
度上的界面差别，
注意要与凝固过
程中固－液界面
形态差别相区别，
后者尺度在μm
数量级。
固一液界面的微观结构
1 微观粗糙界面
微观－原子尺度；
粗糙－厚度为几个原子间距的过渡层的固液界面； 排列－过渡层中固相液相原子交错排列；
连续长大－处处等效，液相原子容易落座，晶体
长大容易，晶体连续生长，称之为“连续长大”； 不显示特定晶面－界面形貌随温度与溶质浓度分
子是相同的并且紧密排列；
(2) 晶体内部的每个原子有： 6个第一近邻，面接触； 12个第二近邻，棱边接触； 8个第三近邻，顶角相接触。 (3) 成键时释放能量：
位置(1)：3个最近邻键＋6个第二近邻键＋…
位置(2)：2个最近邻键＋6个第二近邻键＋… 位置(3)：1个最近邻键＋4个第二近邻键＋… 位置(4)：1个最近邻键＋3个第二近邻键＋… 位置(5)：1个最近邻键＋2个第二近邻键＋…
ax(1 x) x ln x (1 x) ln(1 x)
Lm Sm a ( ) kTm R
被称为Jackson因子，
≤2的物质，凝固时固-液界
面为粗糙面，因为x=0.5（晶
体表面有一半空缺位置）时
有一个极小值，即自由能最 低。大部分金属属此类；
|k|=tg/h
• 台阶上扭折的密度取决于台阶取向 • 台阶与密排方向一致时，扭折密度为零（0K时才成立）
三、台阶平衡结构
有限温度下热涨落的影响？平衡结构 简单立方晶体（001）面上沿 [100] 密排方向的台阶 0K，直台阶温度上升，热涨落产生扭折
设：
台阶上有n个原子座位，a为原子间距，则台阶长度为na 求：扭折间的平均距离 x0?
• 对于尺寸大于微米的晶体，由表面能提供的驱动力小于晶体 能够生长的最低驱动力 • • 吉布斯将平衡形态理论的适用范围局限于 尺寸非常微小的晶体 晶体的形态决定于晶体生长的动力学过程
晶体尺寸很小时
界面能极小条件：决定晶体形态
• 成核过程 • 界面稳定性理论中干扰的发展初期 • 沉淀相的形成过程、气泡以及包裹物的形成……
晶体表面的结构
1 界面反应:
•晶体生长，不论是单组分体系还是多组分体
系，生长过程中一个重要的阶段是界面反应;
•这一反应可以作为若干亚反应发生
2 晶体表面:
面心立方结构的 晶体的表面构造:
晶面上原子密度的差别，导致不同结晶面吸附性、生长、溶解 度及反应活性不同。
3 原子级光滑理想表面模型:
(1) 每一立方块代表一个原子；原
二、固-液界面的微观结构
• 粗糙界面：界面固相一侧的点阵位置只有约50%被固相原 子所占据，形成坑坑洼洼、凹凸不平的界面结构。
粗糙界面也称“非小晶面”或“非小平面”。
• 光滑界面：界面固相一侧的点阵位置几乎全部为固相原子 所占满，只留下少数空位或台阶，从而形成整体上平整光 滑的界面结构。 光滑界面也称“小晶面”或“小平面”。
提示：YAG晶体属于体心立方点阵
邻位面：取向在奇异面附近 的晶面，由一定组态的台阶 构成。 非奇异面：其他取向的晶面。 YAG
图3.1.4 邻位面与奇异面
邻位面与台阶的平衡结构
一、邻位面的台阶化
原子全部坐落在该面内 畸变严重界面能大 邻位面由两组或三组奇 异面构成畸变消除 界面能 邻位面
图3.1.1 立方晶体的表面能极图
(2) 表面能极图的用途——求晶体的平衡形状
Wulff定理的另一描述：
在表面能极图上每一点作出 垂直于该点矢径的平面，这些 平面所包围的最小体积就相似 于晶体的平衡形状。 晶体的平衡形状相似于表面 能级图中体积最小的内接多面 体。 如右图，可求出： 平面晶体：内接八面体 立方晶体：内接十四面体
值越低， a值越小。这说明非密排晶面作为晶
体表面（液-固界面）时，容易成为粗糙界面。
2 界面结构与冷却速度及浓度
• 过冷度大时，生长速度快，界面的原子层数较多， 容易形成粗糙面结构。 • 小晶面界面，过冷度ΔT增大到一定程度时，可能 转变为非小晶面。 • 过冷度对不同物质存在不同的临界值， a 越大的 物质，变为粗糙 面的临界过冷度也就越大。