第二章：异方差及其处理
异方差及其处理讲解
ei 0 1 x ji i
ei 0 1xi2 i
ei 0 1 x ji i
ei
0 1
1 x ji
i
对本例进行Glezser test
异方差的诊断
2、正规的检验 （2）戈德菲尔德-匡特检验（Glodfeld-
F(n1 k,n2 k )
所以，可进行F检验。
异方差的诊断
2、正规的检验 （2）戈德菲尔德-匡特检验（Glodfeld-
Quandt test）
如果，
则拒绝“原假设”存在异方差
戈德菲尔德-匡特检验（GlodfeldQuandt test）
F
RSS1 RSS
2
/ (n1 / (n2
前者是后者的特例。
Generalized Least Squares
• 考虑如下数据生成过程：
Yi 0 1X i ui E(ui ) 0; Var(ui ) 2f(X i )
1,200
800
400
0 12,000 16,000 20,000 24,000 28,000 32,000
INC
ABRE
案例：用截面数据估计消费函数
直观感受：
存在异方差 （heteroskedasticity）
Homoskedasticity （同方差）
Heteroskedasticity（异方差）
2,000
1,600
1,200
ABRE
800
400
横轴：收入
纵轴：残差 的绝对值
0 12,000 16,000 20,000 24,000 28,000 32,000
异方差及其处理共56页文档
8、法律就是秩序，有好的法律才有好的秩序。——亚里士多德 9、上帝把法律和公平凑合在一起，可是人类却把它拆开。——查·科尔顿 10、一切法律都是无用的，因为好人用不着它们，而坏人又不会因为它们而变得规矩起来。——德谟耶业余生活要有意义，不要越轨。——华盛顿 17、一个人即使已登上顶峰，也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人，而用人最大的突破在于信任人。——马云 19、自己活着，就是为了使别人过得更美好。——雷锋 20、要掌握书，莫被书掌握；要为生而读，莫为读而生。——布尔沃
异方差的诊断及修正
异方差的诊断与修正—甘子君 经济1202班 1205060432一、异方差的概念：异方差性（heteroscedasticity ）是相对于同方差而言的。
所谓同方差，是为了保证回归参数估计量具有良好的统计性质，经典线性回归模型的一个重要假定：总体回归函数中的随机误差项满足同方差性，即它们都有相同的方差。
如果这一假定不满足，即：随机误差项具有不同的方差，则称线性回归模型存在异方差性。
在回归模型的经典假定中，提出的基本假定中，要求对所有的i （i=1，2，…，n ）都有2)(σ=i u Var也就是说iu 具有同方差性。
这里的方差2σ度量的是随机误差项围绕其均值的分散程度。
由于)(=i u E ，所以等价地说，方差2σ度量的是被解释变量Y 的观测值围绕回归线)(i Y E =kik i X X βββ+++ 221的分散程度，同方差性实际指的是相对于回归线被解释变量所有观测值的分散程度相同。
设模型为ni u X X Y iki k i i ,,2,1221 =++++=βββ如果其它假定均不变，但模型中随机误差项iu 的方差为).,,3,2,1(,)(22n i u Var i i ==σ则称iu 具有异方差性。
也称为方差非齐性。
二、内容根据1998年我国重要制造业的销售利润与销售收入数据，运用EV 软件，做回归分析，用图示法，White 检验模型是否存在异方差，如果存在异方差，运用加权最小二乘法修正异方差。
三、过程：（实践过程、实践所有参数与指标、理论依据说明等）（一） 模型设定为了研究我国重要制造业的销售利润与销售收入是否有关，假定销售利润与销售收入之间满足线性约束，则理论模型设定为：i Y =1β+2βi X +i μ其中，i Y 表示销售利润，i X 表示销售收入。
由1998年我国重要制造业的销售收入与销售利润的数据，如图1：1988年我国重要制造业销售收入与销售利润的数据 （单位：亿元）（二）参数估计1、双击“Eviews”，进入主页。
实验二、异方差检验与消除实验(异方差检验及异方差的消除的分析过程)
实验二、异方差检验与消除实验（异方差检验及异方差的消除的分析过程）
(1)以上四个对REV回归得：
常数项不显著，去掉常数项再进行回归得结果为：
(2)对REV 2回归得结果为：
常数项不显著，去掉常数项再进行回归得结果为：
从F检验来为来看整个模型不显著
从四个回归的结果看，回归(2)(4)不显著，(1)(3)显著，比较(1)(3)不带常数项的回归，还是选择后一个，方程为：
ABS RESID
()
即异方差的形式为：
2262.153117979i i REV σ==
也即异方差的形式为：
22i i REV σσ=
就把这个形式确定为异方差的形式
要求二、做对ZJ 和GDP1回归的Glejser 检验。
异方差性的检验及处理方法
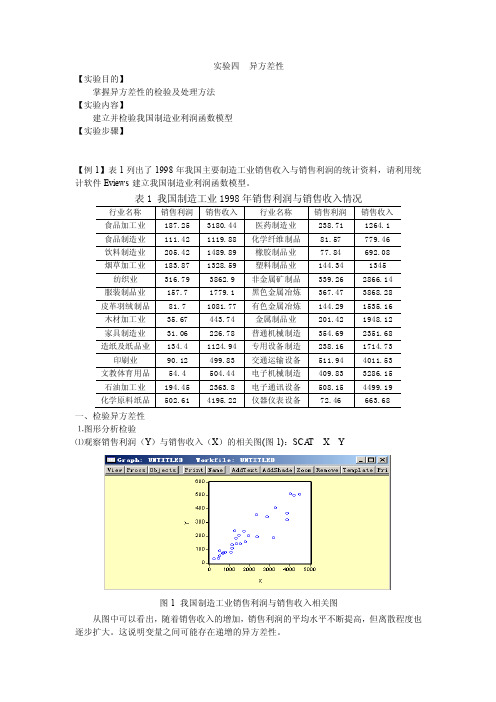
实验四异方差性【实验目的】掌握异方差性的检验及处理方法【实验内容】建立并检验我国制造业利润函数模型【实验步骤】【例1】表1列出了1998年我国主要制造工业销售收入与销售利润的统计资料，请利用统计软件Eviews建立我国制造业利润函数模型。
一、检验异方差性⒈图形分析检验⑴观察销售利润（Y）与销售收入（X）的相关图(图1)：SCA T X Y图1 我国制造工业销售利润与销售收入相关图从图中可以看出，随着销售收入的增加，销售利润的平均水平不断提高，但离散程度也逐步扩大。
这说明变量之间可能存在递增的异方差性。
⑵残差分析首先将数据排序（命令格式为：SORT 解释变量），然后建立回归方程。
在方程窗口中点击Resids按钮就可以得到模型的残差分布图（或建立方程后在Eviews工作文件窗口中点击resid对象来观察）。
图2 我国制造业销售利润回归模型残差分布图2显示回归方程的残差分布有明显的扩大趋势，即表明存在异方差性。
⒉Goldfeld-Quant检验⑴将样本按解释变量排序（SORT X）并分成两部分（分别有1到10共11个样本合19到28共10个样本）⑵利用样本1建立回归模型1（回归结果如图3），其残差平方和为2579.587。
SMPL 1 10LS Y C X图3 样本1回归结果⑶利用样本2建立回归模型2（回归结果如图4），其残差平方和为63769.67。
SMPL 19 28LS Y C X图4 样本2回归结果⑷计算F 统计量：12/RSS RSS F =＝63769.67/2579.59=24.72，21RSS RSS 和分别是模型1和模型2的残差平方和。
取05.0=α时，查F 分布表得44.3)1110,1110(05.0=----F ，而44.372.2405.0=>=F F ，所以存在异方差性⒊White 检验⑴建立回归模型：LS Y C X ，回归结果如图5。
图5 我国制造业销售利润回归模型⑵在方程窗口上点击View\Residual\Test\White Heteroskedastcity,检验结果如图6。
异方差及其处理
ei 0 1x i2 i
ei 0 1 x ji i
ei 0 1 1 i x ji
对本例进行Glezser test
异方差的诊断
2、正规的检验 （2）戈德菲尔德-匡特检验（GlodfeldQuandt test） 先给原始数据进行排序，然后。。。
戈德菲尔德-匡特检验（GlodfeldQuandt test）
3/8个样本
24,000 22,000
¼ 个样本
两个回归 可以产生 两个残差 平方和
20,000 18,000
CONS
16,000 14,000 12,000
同方差时， 两个残差 平方和应 该差不多！
10,000 8,000 12,000
1,200
ABRE
800 400
0 12,000
16,000
20,000
24,000
28,000
32,000
INC
案例：用截面数据估计消费函数
直观感受：
存在异方差 （heteroskedasticity）
Homoskedasticity （同方差）
Heteroskedasticity（异方差）
异方差的诊断
2、正规的检验 （3）怀特检验：
③ 由上述辅助方程的R2构成的统计量 nR2服从X2 (p)分布，可进行卡方检验； 大于临界值时，拒绝同方差假设 当然，也可以应用F检验。
案例：纽约的租金和收入
案例：纽约的租金和收入
因变量：RENT（n=108）
变量
C Income
系数
5455.48 0.06
所以，可进行F检验。
消除异方差的方法
消除异方差的方法异方差是啥玩意儿？简单来说，就是数据中的误差项不满足同方差性。
这可咋整呢？别慌！有办法消除异方差。
一种方法是加权最小二乘法。
嘿，就像给不同的数据点分配不同的“权重”。
步骤呢，先判断是否存在异方差，可以通过残差图等方法。
如果确定有，那就计算权重。
然后用加权后的数据进行最小二乘法估计。
注意啦，权重的选择可不能瞎选，得根据具体情况来。
这就好比做菜放盐，多了咸，少了淡。
那安全性和稳定性咋样呢？一般来说，只要方法得当，还是挺靠谱的。
不会像走钢丝那么惊险，放心大胆地用。
这种方法的应用场景可多啦！比如在经济学、统计学等领域。
优势嘛，能提高估计的准确性和有效性。
想象一下，这就像给你的眼睛戴上了一副度数合适的眼镜，看东西更清楚了。
举个实际案例呗！比如说研究收入和消费的关系，发现不同收入水平的人消费的差异很大，存在异方差。
用加权最小二乘法处理后，模型的拟合效果明显提升。
哇塞，这效果杠杠的！还有一种方法是对数变换法。
把数据进行对数变换，有时候就能消除异方差。
这就像给数据来个“魔法变身”。
步骤是先对数据取对数，然后再进行分析。
注意哦，不是所有数据都适合这种方法，得先看看数据的特点。
安全性方面呢，通常比较安全，不会出啥大乱子。
稳定性也还不错。
它的应用场景也不少呢！在金融、工程等领域都能派上用场。
优势就是简单易行，不需要太复杂的计算。
就像骑自行车，轻松又自在。
比如说在股票市场分析中，股价和成交量可能存在异方差。
通过对数变换，能让数据更稳定，分析起来更顺手。
嘿嘿，是不是很厉害？总之，消除异方差的方法有很多，要根据具体情况选择合适的方法。
只要用心去做，就能让数据变得更听话，分析结果更可靠。
相信自己，一定能搞定异方差这个小麻烦！。
试题标题计量经济学中如何处理异方差问题
试题标题计量经济学中如何处理异方差问题试题标题：计量经济学中如何处理异方差问题计量经济学是经济学中的一个重要分支，研究经济现象的测量和分析方法。
在实际研究中，我们常常会遇到异方差（heteroscedasticity）问题。
异方差是指随着自变量的变化，随机误差的方差也随之变化的一种现象。
在进行计量经济分析时，我们需要采取适当的方法来处理异方差问题。
一、异方差的检验方法在处理异方差问题之前，首先需要进行异方差性的检验。
常见的异方差检验方法有帕克-白杰斯检验（Park-White test）、布里士-普根检验（Breusch-Pagan test）和考克斯-斯图尔特检验（Cooks-Weisberg test）等。
这些检验方法基于不同的统计原理，可以帮助我们确定自变量是否存在异方差问题。
二、处理异方差的方法当我们确定存在异方差问题时，就需要采取相应的方法来处理。
下面介绍几种常用的异方差处理方法。
1. 权重最小二乘法（Weighted Least Squares，WLS）权重最小二乘法是一种常用的处理异方差问题的方法。
其基本思想是根据异方差项的方差结构，赋予不同观测值不同的权重，使得方差较小的观测值具有更高的权重，方差较大的观测值具有较低的权重。
通过对数据进行加权处理，可以得到异方差问题下的有效估计。
2. 方差差异函数（Generalized Least Squares，GLS）方差差异函数是处理异方差问题的一种更一般的方法，其思路是通过建立误差项方差与自变量之间的函数关系，对原始方程进行变换，使得变换后的方程不存在异方差问题。
该方法在一些情况下可以提供更有效的估计。
3. 偏差校正法（Heteroscedasticity Consistent Standard Errors，HCSEs）偏差校正法是一种相对简单且应用广泛的异方差处理方法。
该方法基于异方差的一致性标准误差估计，通过对标准误差进行修正，得到在异方差存在时的有效估计。
第二章六计量经济学-异方差性
i=1,2,…,n
(Park)
选择关于变量 X j
的不同的函数形 式（如
f
(X
ji )
X
2 ji
或
f
(X
ji
)
2
X
e vi
ji
），对方程进行估计并进行显著性检验；
如果存在某一种函数形式，使得方程显著成立， 则说明原模型存在异方差性。
如 Park 检验法中，对一般的方程形式：
f
(X
ji
)
看是否形成一斜率为零的直线
e~i 2
e~i 2
X 同方差
X 递增异方差
e~i 2
e~i 2
X 递减异方差
X 复杂型异方差
3、解析法
（1）戈德菲尔德-匡特（Goldfeld-Quandt）检验 G-Q检验以F检验为基础，适用于样本容量较大、
异方差递增或递减的情况。
G-Q检验的思想：
先将样本一分为二，对子样①和子样②分别作回 归，然后利用两个子样的残差之比构造统计量进行 异方差检验。
xi xi2
E(i
)
1
(2.4.2)
（2）不具备最小方差性
由于
var(ˆ1 ) E(ˆ1 1)2 E(
xi xi2
i
)
2
E( (
xi i )2
xi2 ) 2
xi2
E
(
2 i
)
( xi2 )2
（注：交叉项 i, j (xi i )(x j j ) 的期望为零） i j
§2.6 异方差性 Heteroskedasticity
异方差性的检验及处理方法
图2显示回归方程的残差分布有明显的扩大趋势，即表明存在异方差性。
⒉Goldfeld-Quant检验
⑴将样本按解释变量排序（SORT X）并分成两部分（分别有1到10共11个样本合19到28共10个样本）
⑵利用样本1建立回归模型1（回归结果如图3），其残差平方和为2579.587。
【实验步骤】
【例1】表1列出了1998年我国主要制造工业销售收入与销售利润的统计资料，请利用统计软件Eviews建立我国制造业利润函数模型。
表1 我国制造工业1998年销售利润与销售收入情况
行业名称
销售利润
销售收入
行业名称
销售利润
销售收入
食品加工业
187.25
3180.44
医药制造业
238.71
1264.1
SMPL 1 10
LS Y C X
图3样本1回归结果
⑶利用样本2建立回归模型2（回归结果如图4），其残差平方和为63769.67。
SMPL 19 28
LS Y C X
图4样本2回归结果
⑷计算F统计量： ＝63769.67/2579.59=24.72， 分别是模型1和模型2的残差平方和。
取 时，查F分布表得 ，而 ，所以存在异方差性
食品制造业
111.42
1119.88
化学纤维制品
81.57
779.46
饮料制造业
205.42
1489.89
橡胶制品业
77.84
692.08
烟草加工业
183.87
1328.59
塑料制品业
144.34
1345
纺织业
316.79
异方差知识点总结
异方差知识点总结异方差的存在可能会导致回归模型下列问题：1. 预测的不确定性增加：当异方差存在时，回归模型的预测区间可能会变得更宽，因为方差的不稳定性会使得预测更加不确定。
2. 参数估计的失真：在存在异方差的情况下，最小二乘法(OLS)回归的方法可能会导致参数估计的偏误。
3. 统计推断的失真：在存在异方差时，通常使用的标准误差可能被低估或高估，从而影响统计推断的结果。
因此，我们有必要了解异方差的特征、检验方法和处理方法。
本文将从以下几个方面对异方差进行总结。
一、异方差的特征和识别方法二、检验异方差的统计方法三、处理异方差的方法一、异方差的特征和识别方法1. 异方差的特征异方差的特征主要包括两个方面：方差的不稳定性和误差项的相关性。
首先是方差的不稳定性，即随着自变量的变化，因变量的方差也会跟着变化。
这种不稳定性可能出现在回归模型的残差中，表现为残差的离散程度随着自变量的变化而变化。
其次是误差项的相关性，即自变量与误差项之间存在相关性。
这种相关性可能是由于遗漏变量、测量误差或其他未知因素导致的，而这种相关性可能会影响到回归模型的假设前提，从而影响到参数的估计和统计推断的结果。
2. 异方差的识别方法在实际应用中，我们可以通过以下几种方法来识别是否存在异方差：（1）绘制残差图：同时绘制残差与预测值的散点图和残差与自变量的散点图，观察残差的离散程度是否与自变量相关。
（2）利用统计检验：利用统计学中的异方差检验方法，如BP检验、White检验等。
（3）利用经验判断：在经验分析中，我们也可以通过观察实际数据的特征，来判断是否存在异方差。
比如，如果数据中存在明显的带状结构或呈现出明显的异方差现象，那么可能存在异方差问题。
二、检验异方差的统计方法1. BP检验BP检验是一种常用的异方差检验方法，它的原假设是误差的方差是恒定的，备择假设是误差的方差是非恒定的。
BP检验的具体步骤为：（1）先对相关变量进行回归分析，得到残差eˆ2；（2）在残差的平方的基础上，增加自变量的平方和自变量与自变量的乘积，得到新的残差变量；（3）利用新的残差变量进行正态性检验，判断残差是否服从正态分布；（4）最后，利用新的残差变量进行F检验，检验自变量的平方及其交叉项是否显著。
异方差性的概念、类型、后果、检验及其修正方法(含案例).
其中
2 SEYˆ Y 1 X0 (XX) 1 X 0
0 0
所以，当模型出现异方差性时，Y预测区间的建立将发生困 难，它的预测功能失效。
三、异方差性的检验（教材P111）
1.检验方法的共同思路 • 既然异方差性就是相对于不同的解释变量观测值，
随机误差项具有不同的方差，那么： 检验异方差性，也就是检验随机误差项的方差与解 释变量观测值之间的相关性及其相关的“形式”。 • 各种检验方法正是在这个共同思路下发展起来的。
分别为两个子样对应的随机项方差。
H0成立，意味着同方差； H1成立，意味着异方差。
⑤构造统计量
nc 2 ~ e2i ( 2 k 1) nc nc F ~ F( k 1, k 1) nc 2 2 2 ~ e ( k 1 ) 1i 2
⑥检验。给定显著性水平，确定F分布表中相应的临界值
2 E() I
Var( ) 2 , i 1,2, , n i Cov( , ) 0, i j i j
即同方差和无序列相关条件。
2.变量的显著性检验失去意义
在变量的显著性检验中，t统计量
t ˆ
j j j
ˆ ) Se(
~2 来表示随机误差项的方差。 即用e
i
2.图示检验法
（1）用X-Y的散点图进行判断（李子奈P108）
看是否存在明显的散点扩大、缩小或复杂型 趋势（即不在一个固定的带型域中）。
随机误差项的 方差描述的是 取值的离散程 度。而由于被 解释变量Y与随 机误差项有相 同的方差，所 以利用Y与X之 间的相关图形 也可以粗略地 看出的离散程 度与X之间是否 有相关关系。
《异方差及其处理》课件
数据清洗与处理
数据预处理
在处理异方差问题之前，需要对数据进行预处理，包括缺失值填充 、异常值处理、数据标准化等，以保证数据的完整性和一致性。
数据转换
对于某些特定的数据分布，可以使用数据转换的方法来处理异方差 问题，如对数转换、平方根转换等。
数据分层
对于具有分层结构的数据，可以使用分层抽样或分层模型的方法来处 理异方差问题，以更好地拟合数据并提高预测精度。
在社会领域的应用
社会调查数据分析
在社会调查数据分析中，异方差性问题常见，如态度、观 点、行为等变量的分布往往存在异方差现象。
人口统计学研究
在人口统计学研究中，年龄、性别、教育程度等变量的分 布可能存在异方差性，需要进行异方差性检验和处理。
社会学研究
在社会学研究中，异方差性可能影响对群体特征、社会现 象等的理解和解释，需要进行异方差性检验和处理以确保 研究的准确性和可靠性。
预测误差
异方差的存在可能导致预 测误差增大，降低模型的 预测精度。
统计推断失效
异方差的存在可能导致模 型的统计推断失效，如置 信区间和假设检验的结果 不准确。
02
异方差的检验
图示检验法
残差图
通过绘制实际观测值与预测值的残差 ，观察其随解释变量变化的趋势，判 断是否存在异方差。
箱线图
利用箱线图展示不同解释变量取值下 的残差分布情况，通过比较箱子的宽 度和位置，判断异方差的存在。
倒数变换法
总结词
倒数变换法是一种处理异方差的方法， 通过将响应变量取倒数，可以减小异方 差的影响。
VS
详细描述
倒数变换法适用于因变量为连续型且呈偏 态分布的情况。通过对原始数据取倒数， 可以使数据更接近正态分布，从而减小异 方差的影响。在回归分析中，可以使用倒 数变换后的数据作为因变量进行回归分析 。
异方差的性质
预测置信区间不准确
在异方差情况下，预测的置信区间可 能不准确，导致对预测结果的信任度 降低。
对统计推断的影响
统计推断有效性下
降
在异方差情况下，常用的统计推 断方法可能不再适用，导致推断 结果的不准确。
假设检验失效
在异方差情况下，假设检验的结 果可能受到影响，导致无法准确 地做出统计决策。
置信水平降低
由于异方差的存在，统计推断的 置信水平可能会受到影响，导致 对推断结果的信任度降低。
03
CATALOGUE
异方差的检验
图示检验法
残差图检验
通过绘制残差与拟合值的图形，观察 残差是否随拟合值的变动而出现系统 性模式，如随拟合值增大而逐渐增大 或减小。
QQ图检验
将残差与标准正态分布的期望值进行 比较，观察其是否落在预期的置信区 间内，判断残差是否服从正态分布。
总结词
医学研究数据中，由于个体差异、病情 进展和治疗方法等因素，常常表现出异 方差性。
VS
详细描述
在医学研究中，由于个体之间的差异、病 情进展的不同阶段以及治疗方法的多样性 等因素，数据分布往往不均匀。例如，不 同患者的生理指标、治疗效果等可能会有 很大的差异，导致数据异方差性的出现。
实例三：社会调查数据
通过计算残差的二次项与解释变量的线性组 合，构建统计量对异方差进行检验。
04
CATALOGUE
异方差的解决方法
数据变换法
平方根变换
通过取平方根的方式减小异方差的影 响，适用于数据分布为正态分布的情 况。
对数变换
通过取对数的方式减小异方差的影响 ，适用于数据分布为偏态分布的情况 。
幂变换
通过取幂的方式减小异方差的影响， 适用于数据分布为幂律分布的情况。
第二章：异方差及其处理
戈德菲尔德-匡特检验（GlodfeldQuandt test）
所以，拒绝原假设。即，认为存在异方差
异方差的诊断
2、正规的检验 （3）怀特检验（White test）： 由H. White 1980年提出 ①原始回归，获得残差ei； ②用ei2对 常数项、x，x2，交叉项同时 做回归；(回归方程称为：辅助方程 ausiliary equation) 该方程中，解释变量的个数为“p”(不 不包括常数项)
2
异方差的处理
1、加权最小二乘法 实践中，我们先确定di； 然后用
Yi Xi 对 做回归 di di
异方差的处理
1、加权最小二乘法 两种常用的形式：
di= Xi di= (Xi )0.5
本例进行Glezser test时，有 如下结果
估计消费函数时，对异方差的处理
加权最小二乘法
所以，在本例中，可以确定：
异方差的处理
2、可行的广义最小二乘
但是该方法在研究者错误地设定异方差的 形式后，FGLS估计量仍然不是有效的！
基于FGLS估计的t检验、F检验仍然有问题。
异方差的处理
3、怀特异方差的一致标准误差 思想：仍然使用OLS，因此估计量是 有偏的，但如果标准差能够足够小，那么 我们的估计仍然是令人满意的。
16,000
20,000
24,000
28,000
32,000
INC
异方差的诊断
2、正规的检验 （2）戈德菲尔德-匡特检验（GlodfeldQuandt test）
所以，可进行F检验。
异方差的诊断
2、正规的检验 （2）戈德菲尔德-匡特检验（GlodfeldQuandt test）
如果，
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
当然，也可以应用F检验。
案例：纽约的租金和收入
案例：纽约的租金和收入
因变量：RENT（n=108）
变量
C Income
系数
5455.48 0.06
T统计量
9.05 4.42
R2=0.1555
案例：纽约的租金和收入
怀特的辅助回归 因变量：e2 （n=108）
变量 C Income Income2 系数 -14657900 1200.58 -0.01 T统计量 -1.58 2.42 -1.87
第二章：异方差及其处理
案例：用截面数据估计消费函数
上机实验：利用31个省市自治区的人均 收入与人均消费数据估计消费函数。
Consumption = 0.7042*Income t=(83.0652) R2=0.9289
案例：用截面数据估计消费函数
观察残差图（取残差绝对值）：
2,000 1,600
所以，拒绝原假设。即，认为存在异方差
戈德菲尔德-匡特检验（GlodfeldQuandt test）
优点：简单、直观
缺点：稳健性较差 如果回归方程存在设定错误，或者异方 差的形式是非线性的时候，则该检验的效力 较差。
异方差的诊断
2、正规的检验 （3）怀特检验（White test）： 由H. White 1980年提出 ①原始回归，获得残差ei； ②用ei2对 常数项、x，x2，交叉项同时 做回归；(回归方程称为：辅助方程 ausiliary equation)
所以，可进行F检验。
异方差的诊断
2、正规的检验 （2）戈德菲尔德-匡特检验（GlodfeldQuandt test）
如果，
则拒绝“原假设”存在异方差
戈德菲尔德-匡特检验（GlodfeldQuandt test）
RSS1 / (n1 k ) F 2.4141 RSS 2 / (n2 k )
异方差的诊断
2、正规的检验 （4）布罗施-帕甘检验(Breusch Pagan Test) ①原始回归，获得残差ei； ②用ei2对 常数项和所有的解释变量同时 做线性回归；(回归方程称为：辅助方程 ausiliary equation)
ei2 0 1X 1 2X 2 ... p X p
ˆ) White e.s.e.( 1
xi ei 2 2 (xi )
2 2
OLS Estimates of the Rent–Income Relationship with Robust Standard Errors
本例的戈里瑟检验(Glezser test)
形式1 Constant -315401.7 (-0.544771) 59.04966 (1.904133) 0.001192 (1.641916) 17973.54 (2.022699) -2.78E+10 (-2.294215) 0.111131 0.085055 0.123637 0.153616 形式2 336000.5 (1.146315) 形式3 -1646633 (-1.378615) 形式4 2372387. (3.291795)
异方差的诊断
更多的时候，我们需要进行定 性的分析！！！！！！
异方差的处理
1、加权最小二乘法(WLS) Weighted Least Squares 广义最小二乘(GLS) Generalized Least Squares
前者是后者的特例。
Generalized Least Squares
• 考虑如下数据生成过程：
异方差的危害
OLS估计量依然是无偏的 但不再具有有效性！！ t检验、F检验无效 置信区间不可信
异方差的诊断
• 1.画图法： 以Xi或Yi为横坐标，以|ei|或ei2为纵坐标
|ei| ei
0 0 Xi或Yi
Xi或Yi
这说明没有异方差
异方差的诊断
|ei|
1.画图法：
ei
0 Xi或Yi
0
Xi或Yi
R2=0.082
案例：纽约的租金和收入
怀特统计量=108*0.082=8.87， 自由度为2的卡方统计量=5.99
拒绝“没有异方差”的原假设！
点点滴滴：
EVIEWS设计的一个缺陷： （1）如果在进行怀特检验时，选择“不包 括交叉项”； （2）如果你的原始回归本身不带常数项；
在上述两种情况下，white检验的辅助回 归方程中都不会出现“解释变量的水平值 ”，只有其平方项。
但是该方法在研究者错误地设定异方差的 形式后，FGLS估计量仍然不是有效的！
基于FGLS估计的t检验、F检验仍然有问题。
异方差的处理
3、怀特异方差的一致标准误差 逻辑：仍然使用OLS， β的估计量依然 是无偏的，但T检验、置信区间的估计失 效。 失效的原因是：在估计β的标准误差 时，用的是同方差条件下的估计公式，所 以导致失效。
戈德菲尔德-匡特检验（GlodfeldQuandt test）
3/8个样本
24,000 22,000
¼ 个样本
两个回归 可以产生 两个残差 平方和
20,000 18,000
CONS
16,000 14,000 12,000
同方差时， 两个残差 平方和应 该差不多！
10,000 8,000 12,000
Consumption Incomei
0.7067
Incomei Incomei
估计消费函数时，对异方差的处理
加权最小二乘法
对新方程再做“异方差检验”：
Heteroskedasticity Test: White Obs*R-squared Prob. Chi-Square(1) 0.934813 0.3336
Yi 0 1X i ui E(ui ) 0; Var(ui ) f(X i )
2
GLS: Transformed Data
Yi 0 f ( Xi ) 1 1 f ( Xi ) Xi f ( Xi )
i
f (Xi )
X Y i 0 0 1 X1 i
这说明存在异方差
消费与收入（我国31个省市， 2011年）
2,000 1,500 1,000 500
RESID
0 -500 -1,000 -1,500 -2,000 12,000
横轴：收入； 纵轴：残差；
16,000 20,000 24,000 28,000 32,000 INC
消费与收入（我国31个省市， 2011年）
i ) E E (
i ) Var Var 1 1 Var i 2 f (Xi ) 2 f (Xi ) f (Xi ) f (Xi )
i
异方差的处理
Yi f(X i )
2,000 1,600
1,200
ABRE
800 400
横轴：收入 纵轴：残差 的绝对值
0 12,000
16,000
20,000
24,000
28,000
32,000
INC
异方差的诊断
2、正规的检验
(1)戈里瑟检验(Glezser test) (2)戈德菲尔德-匡特检验（GlodfeldQuandt test） (3)怀特检验（White test） (4)布罗施-帕甘检验(Breusch Pagan Test)
1,200
ABRE
800 400
0 12,000
16,000
20,000
24,000
28,000
32,000
INC
案例：用截面数据估计消费函数
直观感受：
存在异方差 （heteroskedasticity）
Homoskedasticity （同方差）
Heteroskedasticity（异方差）
异方差的诊断
2、正规的检验 （1）戈里瑟检验(Glezser test) ：
①原始回归，获得残差ei； ②用|e|对可疑变量做各种形式的回归；
ei 0 1 x i
h ji
③对原假设H0： δ1=0,进行检验 .
异方差的诊断
2、正规的检验 （1）戈里瑟检验(Glezser test) ： 回归的形式通常为如下几种：
• However, we really used the homoskedasticity assumption only to simplify this formula.
White Robust Standard Errors
• If we do not impose homoskedasticity, we get a slightly more complicated formula:
2、可行的广义最小二乘（Feasible GLS）
ln(ei 2 ) ln( 2 ) h ln( Xi ) i
估计出h后，再进行变换：
Yi X i ui Y Xi
ˆ h
Xi Xi
ˆ h
ui Xi
ˆ h
估计消费函数时，对异方差的处理
异方差的处理
2、可行的广义最小二乘
H 0 : 1 2 ... p 0
异方差的诊断
2、正规的检验 （4）布罗施-帕甘检验(Breusch Pagan Test) ③构建LM统计量
LM nR 2 2(p 1)
或者进行F检验。
异方差的诊断
2、正规的检验
注意：遗漏变量对异方差检验的影响
当原方程遗漏重要变量时，异方差检验 通常无法通过； 所以，在进行异方差检验时，先要保 证没有遗漏重要变量——拉姆齐检验