数学建模 教师的薪金
数学建模,教师的薪金

承诺书我们仔细阅读了昆明理工大学大学生数学建模竞赛的竞赛规则。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的。
如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
评阅编号(由组委会评阅前进行编号):评阅专用页评阅编号(由组委会评阅前进行编号):评阅记录(供评阅时使用):评阅人评分备注总分大学教师薪金模型一、摘要:模型一:利用Matlab 建立X1--X7与Z (薪金)的线性关系,得到散点图与一般的线性回归模型(模型一),模型如下:011223344556677ln *******z x x x x x x x ββββξββββ=+++++++模型二:由模型一整体效果与Stepwise Table 图推断部分变量对Z (薪金)的影响并不显著,由残差分析法筛选出影响明显的变量X1、X4,将他们的平方项与交互项加入建立新的回归模型(模型二),模型如下:6.90260.004310.174640.00011*40*1^20.02284^2z x x x x x x =+++-++- 得到R2,F,P ,与模型一相比较。
模型一调用原始参数较全,但回归性差,模型二只启用影响明显的变量,回归模型更为显著,可靠度更高。
于是得出:教师的薪金与工作时间、学历关系明显,与性别、是否受雇于重点大学、是否接受过培训的关系较小,即女教师没有受到不公正的待遇,婚姻状况也不会影响收入。
关键词:回归分析,互交作用,图形结合,残值分析法。
二、问题重述:某地人事部门为研究中学教师的薪金与他们的资历、性别、教育程度及培训情况等因素之间的关系,要建立一个数学模型,分析人事策略的合理性,特别是考察女教师是否受到不公平的待遇,以及她们的婚姻状况是否会影响收入。
教师的薪酬和福利有哪些

教师的薪酬和福利有哪些教师收入由:基本工资、教龄工资、绩效工资、特优津贴等构成。
1、基本工资:教师按照教师资格定:小学教师3000元,初中教师3500元,高中教师3800元,大专教师4100元,大学教师4500元。
(随国民经济增长)2、教龄工资(含工龄):每年60元,随着教龄增长。
3、绩效工资:学期和学年奖金。
教师对于学生的付出和关心是不可衡量的,是学生成长的引导者,也是学生的好朋友。
教师对于学生既扮演者传道授业解惑的角色,又是学生的精神支柱。
成为一名教师这个伟大的职业,是很多人的梦想。
除了教师这一职业的光辉,我们最为关注的就是▲教师的薪酬和福利了。
别着急,小编为您进行相关的介绍。
▲教师的薪酬和福利教师收入由:基本工资、教龄工资、绩效工资、特优津贴等构成。
1、基本工资:教师按照教师资格定:小学教师3000元,初中教师3500元,高中教师3800元,大专教师4100元,大学教师4500元。
(随国民经济增长)2、教龄工资(含工龄):每年60元,随着教龄增长。
工龄工资的实行这不仅是对老教师的照顾问题,更重要的是鼓励终身从教的思想,有利于教师队伍的建设和教师队伍的稳定。
3、课时工资:课时补贴按照实际上课按劳取酬原则;主要是鼓励教师多代课,特别是年轻教师精力充沛,他们多代课,并得到应有的报酬,不仅是心理的安慰,也是对他们的鼓励4、绩效工资:学期和学年奖金(取代职称工资)。
这部分奖金,只能占工资的10%左右。
大家推荐竞比实绩,每学期学年评,不终身制。
每个老师积极努力年年有希望。
主要是激励工作出成效,优质优得,不仅要激励多代课,更要激励上好课。
5、特优津贴:全体教师公认的特别优秀教师,无名额限制,县市以上部门高标准考核认定,象领国务院津贴领县/市政府津贴,不终身制。
主要是对那些在教育教学工作在有特殊研究成果,并得到很好的推广,对一所学校或一个地区的教育有一定的影响作用的教育及教学方法,可根据影响范围的大小确定等级,或者说是以国家及,省级,地市、县确定不同的标准,使那些有才华的教师得到应有的报酬,真正起到激励作用。
硕师计划教师工资

硕师计划教师工资
硕师计划是一项面向研究生的教师培养项目,它鼓励研究生在攻读硕士或博士学位的同时,开设本专业的教学课程,接受教学指导培训。
参与硕师计划的研究生学员在开展教学实践的同时,也将获得额外的工资补贴。
根据我校相关规定,硕师计划教师的工资标准如下:
1. 硕士研究生教师:每学期开设1门课程,将获得2000元人民币的补贴。
2. 博士研究生教师:每学期开设1门课程,将获得3000元人民币的补贴。
3. 开设双课程(即2门以上课程)的教师,其补贴标准将相应提高。
具体标准根据开设课程数额度灵活调整。
4. 教师工资将在每个学期结束后发放,发放时间一般安排在期末考试结束后1个月内。
5. 教师应按时完成各项教学任务,经评价认为教学质量和效果好的,其工资标准有望适当提高。
以上就是我校硕师计划教师的工资标准和发放条件,希望这可以给参与计划的同学一个参考。
教学质量是获得更高工资的重要依据,我们都应该致力于提升自己的教学水平。
教师科研工资标准及任务一览表
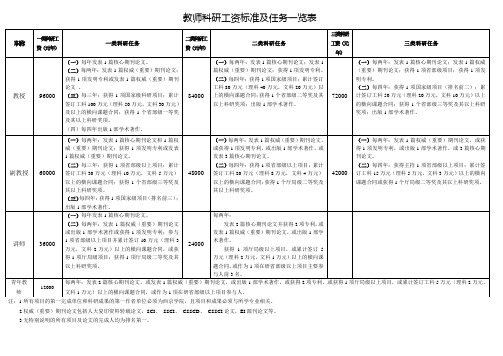
教师科研工资标准及任务一览表注:1.所有项目的第一完成单位和科研成果的第一作者单位必须为西京学院,且项目和成果必须与所学专业相关。
2.权威(重要)期刊论文包括人大复印资料转载论文,SCI 、 SSCI 、 CSSCD 、 CSSCI 论文,EI 源刊论文等。
3.无特别说明的所有项目及论文的完成人均为排名第一。
职称一类科研工资(元/年)一 类 科 研 任 务二类科研工资(元/年)二 类 科 研 任 务三类科研工资(元/年)三 类 科 研 任 务教授 96000(一)每年发表1篇核心期刊论文。
(二)每两年:发表1篇权威(重要)期刊论文;获得1项发明专利或发表1篇权威(重要)期刊论文 。
(三)每三年:获得1项国家级科研项目;累计签订工科100万元(理科50万元,文科30万元)及以上的横向课题合同;获得1个省部级一等奖及其以上科研奖项。
(四)每四年出版1部学术著作。
84000(一)每两年:发表1篇核心期刊论文;发表1篇权威(重要)期刊论文;获得1项发明专利。
(二)每四年:获得1项国家级项目;累计签订工科80万元(理科40万元,文科20万元)以上的横向课题合同;获得1个省部级二等奖及其以上科研奖项;出版1部学术著作。
72000(一)每两年:发表1篇核心期刊论文;发表1篇权威(重要)期刊论文;获得1项省部级项目;获得1项发明专利。
(二)每四年:获得1项国家级项目(排名前二);累计签订工科50万元(理科20万元,文科10万元)以上的横向课题合同;获得1个省部级三等奖及其以上科研奖项;出版1部学术著作。
副教授 60000(一)每两年:发表1篇核心期刊论文和1篇权威(重要)期刊论文;获得1项发明专利或发表1篇权威(重要)期刊论文。
(二)每三年:获得1项省部级以上项目;累计签订工科30万元(理科10万元,文科5万元)以上的横向课题合同;获得1个省部级三等奖及其以上科研奖项。
(三)每四年:获得1项国家级项目(排名前三);出版1部学术著作。
数学建模模拟本科组题目
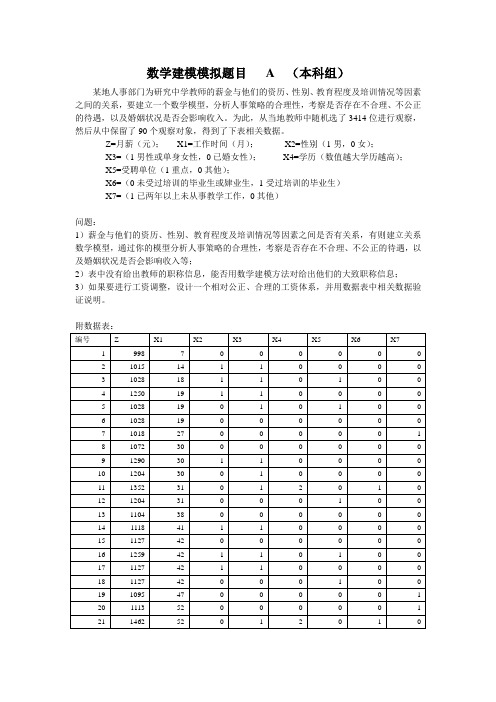
数学建模模拟题目 A (本科组)某地人事部门为研究中学教师的薪金与他们的资历、性别、教育程度及培训情况等因素之间的关系,要建立一个数学模型,分析人事策略的合理性,考察是否存在不合理、不公正的待遇,以及婚姻状况是否会影响收入。
为此,从当地教师中随机选了3414位进行观察,然后从中保留了90个观察对象,得到了下表相关数据。
Z=月薪(元);X1=工作时间(月);X2=性别(1男,0女);X3=(1男性或单身女性,0已婚女性);X4=学历(数值越大学历越高);X5=受聘单位(1重点,0其他);X6=(0未受过培训的毕业生或肄业生,1受过培训的毕业生)X7=(1已两年以上未从事教学工作,0其他)问题:1)薪金与他们的资历、性别、教育程度及培训情况等因素之间是否有关系,有则建立关系数学模型,通过你的模型分析人事策略的合理性,考察是否存在不合理、不公正的待遇,以及婚姻状况是否会影响收入等;2)表中没有给出教师的职称信息,能否用数学建模方法对给出他们的大致职称信息;3)如果要进行工资调整,设计一个相对公正、合理的工资体系,并用数据表中相关数据验证说明。
附数据表:第五次数学建模模拟本科组B题设有一个靶标如下,取1个边长为100mm的正方形,分别以四个顶点(对应为A、C、D、E)为圆心,12mm为半径作圆。
以AC边上距离A点30mm处的B为圆心,12mm为半径作圆,如图1所示。
图 1 靶标示意图用分辨率为1024*768的数码相机对靶标进行拍摄。
图2是某次拍摄得到的图像。
图2 靶标的像靶标的像有5个类似椭圆形状的黑色块,分别在各个黑色块内任取一点,记得到的位置为P1(x1,y1), P2(x2,y2), P3(x3,y3), P4(x4,y4), P5(x5,y5)。
请建立模型设计一个算法,以确定P1,P2,P3,P4,P5的原像分别位于A, B, C, D,。
教师薪酬分配方案

教师薪酬分配方案引言教师是社会的栋梁和人才培养的重要角色,他们的专业知识和教育经验对学生的发展至关重要。
因此,为了激励教师们的积极性和提高教育质量,制定一套合理的教师薪酬分配方案是必不可少的。
本文将探讨教师薪酬分配方案,包括考核指标、薪酬构成和激励机制等方面。
一、考核指标的确定为了科学公正地评价教师的工作表现,制定一个合理的考核指标是至关重要的。
首先,考核指标应包括学生的学业成绩、教学评估、教学效果和学生评价等方面。
例如,通过学生的考试成绩可以反映出教师是否具备优秀的教学能力,学生的评价可以反映教师在教学过程中的口碑。
其次,考核指标应定期进行,以确保评价的有效性和及时性。
二、薪酬构成的设计教师薪酬构成的设计应该是公平、合理且透明的,以激励教师们不断提高自己的教学水平。
首先,薪酬构成应该包括基本工资和绩效工资。
基本工资是教师的固定收入,而绩效工资可以根据其表现而变化。
其次,薪酬构成应考虑到教师的工作年限和职称等因素,以体现职业发展的不同阶段和层次。
此外,还可以考虑将一部分薪酬作为教育培训费用,以鼓励教师不断提升自己的专业能力。
三、激励机制的建立为了激励教师们积极工作,建立一个有效的激励机制是必要的。
首先,可以设立年度绩效奖励制度,根据教师的表现和贡献给予相应的奖励,以激发教师的工作热情。
其次,可以设立教育教学科研项目,鼓励教师积极参与与教育相关的研究和项目申报,提高他们的专业水平。
此外,可以设置特殊岗位津贴,鼓励教师担任学科带头人、校本研究组组长等职务。
四、分配公平性的确保在教师薪酬分配中,公平性是至关重要的。
首先,应确保每位教师都按照其贡献和表现获得相应的薪酬,避免出现不公平现象。
其次,可以采用透明的薪酬制度,让教师们清楚了解薪酬分配的依据和方法,减少因分配不公引起的不满情绪。
此外,可以建立一个教师薪酬分配监督机构,以确保薪酬分配的公正性和透明性。
五、激励年轻教师成长年轻教师是学校教育队伍的重要组成部分,他们需要得到更多的激励和帮助,以便更好地成长和发展。
教师薪级工资表
教师薪级工资表教师薪级工资表是教师岗位工资的核心依据,它是根据教师的学历、工作年限和职称等因素确定的一种工资制度。
下面是一份关于教师薪级工资表的相关参考内容。
一、学历因素:学历是衡量教师素质和能力的重要指标之一,通常分为以下几个层次:大专及以下、本科、硕士研究生、博士研究生。
不同的学历级别对应着不同的薪级,具体细则如下:1. 大专及以下学历的教师薪级工资表:- 初级职称(助教、讲师):起始薪级为9级,最高薪级为12级。
- 高级职称(副教授、教授):起始薪级为13级,最高薪级为15级。
2. 本科学历的教师薪级工资表:- 初级职称(助教、讲师):起始薪级为10级,最高薪级为13级。
- 高级职称(副教授、教授):起始薪级为14级,最高薪级为16级。
3. 硕士研究生学历的教师薪级工资表:- 初级职称(助教、讲师):起始薪级为11级,最高薪级为14级。
- 高级职称(副教授、教授):起始薪级为15级,最高薪级为17级。
4. 博士研究生学历的教师薪级工资表:- 初级职称(助教、讲师):起始薪级为12级,最高薪级为15级。
- 高级职称(副教授、教授):起始薪级为16级,最高薪级为18级。
二、工作年限因素:工作年限反映了教师对教育教学工作的长期投入和经验积累。
一般而言,教师的工作年限分为以下几个阶段:0-5年、6-10年、11-15年、16-20年和21年及以上。
不同工作年限对应着不同的薪级,具体细则如下:1. 0-5年工作年限的教师薪级工资表:- 初级职称(助教、讲师):起始薪级为相应学历的薪级,最高薪级加2级。
- 高级职称(副教授、教授):起始薪级为相应学历的薪级加4级,最高薪级加6级。
2. 6-10年工作年限的教师薪级工资表:- 初级职称(助教、讲师):起始薪级为相应学历的薪级加3级,最高薪级加5级。
- 高级职称(副教授、教授):起始薪级为相应学历的薪级加5级,最高薪级加7级。
3. 11-15年工作年限的教师薪级工资表:- 初级职称(助教、讲师):起始薪级为相应学历的薪级加4级,最高薪级加6级。
教师薪酬完整版
学校教师薪酬完整版1、待遇包括:基本工资、岗位津贴、加班费、绩效奖金、全勤奖、补贴、保险、电话补贴。
2、基本工资:专职教师基本工资3000元/月试用期为2400元。
3、全勤奖:100元/月当月满勤可发、迟到或请假均不发。
4、超员奖:每个教学班级基数假设为15人/班, 若实际学生数超过15人,每超出一个学生,补贴该任课教师20元/人/月。
5、加班费:20元/半天,40元/天,加班具体时长根据工作需要而定,少于5个小时为半天,超过5个小时按一天算。
由校长审核批准方能计算 ,如属于布置的任务没有完成者不算加班。
6、餐补:20元/天。
周末上全天班的行政及上课跨中间两个时间段耽误午餐的专职教师及助教享有。
7、绩效奖金包括:学生续班率+学生参加比赛获奖+教师优质课比赛+新生源拓展奖励+优质服务奖励+年度奖励续班率奖:1.每期培训的最低基本续班率, 50%以上的班级有续班奖金,30%—50%不奖不罚,带班续班率30%以下的老师,给予一个培训周期的观察期,连续两个培训周期巩固率低于30%的老师,学校有权将其辞退或转岗。
2.续班奖每期发一次。
学生参加比赛获奖:凡教师辅导学生在国家级竞赛中获奖,奖励150-50元/人;凡教师辅导学生在省级竞赛中获奖,奖励120-40元/人;凡教师辅导学生在市级竞赛中获奖,奖励100-30元/人;其他单项奖:根据学校的具体情况另行设立单项奖。
教学优质课奖:凡在学校组织的教师教学竞赛中获得一等奖的,奖励200元或等值物品;凡在学校组织的教师教学竞赛中获得二等奖的,奖励150元或等值物品;凡在学校组织的教师教学竞赛中获得三等奖的,奖励100元或等值物品。
新生源拓展奖励:A:免费体验课:班级正式开课时,如果报名人数或收入达到相应标准,对授课教师奖励100元,超过标准人数后的人数,对授课教师给予奖励,并对跟踪该班教学与招生工作的教师予以嘉奖。
B:新生招生新生招生为两个含义,一是在自己班级中招来新生插班,二是通过各种方式招来新生进新班或插班,凡新报名学生学校安排插班不除外按10元/人给予教师奖励。
《数学建模》课程教学大纲
《数学建模》课程教学大纲一、课程基本信息二、课程教学目标随着科学技术和计算机的迅速发展,数学向各个领域的广泛渗透已日趋明显,数学不仅在传统的物理学、电子学和工程技术领域继续发挥着重要的作用,而且在经济、人文、体育等社会科学领域也成为必不可少解决问题的工具,数学建模就是沟通实际问题与数学工具之间联系的必不可少的桥梁。
本课程作为信息与计算科学专业本科生开设的专业核心课,将数学方法应用到实际问题中去,主要是通过机理分析,根据客观事物的性质分析因果关系,在适当的假设条件下,利用合适的数学工具得到描述其特征的数学模型。
通过本课程的学习,希望学生能够达到以下能力目标:1. 培养学生利用数学工具解决实际问题的能力;2. 将实际问题“翻译”为数学语言并予以求解,然后再解释实际现象并应用于实际的能力;3. 逐步提高学生的数学素质和应用数学知识解决实际问题的能力。
三、教学学时分配《数学建模》课程理论教学学时分配表*理论学时包括讨论、习题课等学时。
《数学建模》课程实验内容设置与教学要求一览表四、教学内容和教学要求第一章建立数学模型(5学时)(一)教学要求通过本章内容的学习,了解数学描写和数学建模的不同于数学理论的思维特征,理解数学模型的意义及分类,掌握建立数学模型的方法及步骤等。
(二)教学重点与难点教学重点:从现实对象到数学模型,数学建模的方法和步骤,数学模型的特点和分类及怎样学习数学建模教学难点:数学建模的方法和步骤,数学模型的特点和分类(三)教学内容第一节从现实对象到数学模型第二节数学建模的重要意义第三节数学建模示例1.椅子能在不平的地面上放稳吗2.商人们怎样安全过河3. 如何施救药物中毒第四节数学建模的基本方法和步骤1.数学建模的基本方法2.数学建模的基本步骤第五节数学模型的特点和分类1.数学模型的特点2.数学模型的分类第六节数学建模能力的培养本章习题要点:要求学生完成作业5-8题。
其中概念题35%,应用题25%,计算题40%第二章初等模型(5学时)(一)教学要求通过本章内容的学习,了解初等模型的概念,理解比例方法、类比方法、图解法、定性分析方法建模的基本特点,掌握运用所学知识建立数学模型,并对模型进行综合分析等。
世界各国教师工资排名
世界各国教师工资排名教师是社会的宝贵财富,他们不仅传授知识,还培养人才,为社会的进步和发展做出了不可磨灭的贡献。
然而,在全球范围内,教师的工资待遇却存在巨大的差异。
本文将介绍世界各国教师工资排名,以及可能造成这种差异的原因。
首先,我们来看看全球教师工资的平均水平。
根据联合国教科文组织的数据,2017年全球教师的平均工资为每月1,500美元左右。
然而,这个数字只是一个平均值,实际上,不同国家和地区的教师工资相差非常大。
在工资最高的国家中,瑞士的教师工资最高,平均每月可以拿到6,500美元的工资。
其次是卢森堡、挪威、丹麦和德国等欧洲国家,他们的教师工资都超过了4,000美元。
此外,日本、澳大利亚、新西兰等国家的教师工资也较高,平均在3,000美元以上。
然而,教师工资最低的国家却是非洲国家,他们的教师工资普遍不足1,000美元。
据统计,尼日利亚、肯尼亚、坦桑尼亚等国家的教师工资甚至不到500美元,这远远低于这些国家的平均收入水平。
那么,为什么不同国家的教师工资存在如此大的差异呢?首先,教育资源的分配不均可能是一个重要原因。
在一些发展中国家,教育资源有限,政府对教育的投入也不足,导致教师工资低廉。
其次,教育行业的竞争也会影响教师工资的高低。
在一些发达国家,教育资源丰富,竞争激烈,政府需要提供更高的教师工资来吸引和留住优秀的教师。
此外,不同国家的税收制度和经济发展水平也会影响教师工资的高低。
教师是教育事业的中坚力量,他们的工资待遇应该得到应有的重视和尊重。
在全球范围内,政府应该加大对教育的投入,提高教育资源的分配均衡度,同时也需要制定合理的税收政策和经济政策,为教师提供更好的工作环境和待遇。
只有这样,才能让教育事业更加繁荣发展,为社会的进步和发展做出更大的贡献。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
承诺书我们仔细阅读了昆明理工大学大学生数学建模竞赛的竞赛规则。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的。
如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
评阅编号(由组委会评阅前进行编号):评阅专用页评阅编号(由组委会评阅前进行编号):大学教师薪金模型一、摘要:模型一:利用Matlab建立X1--X7与Z(薪金)的线性关系,得到散点图与一般的线性回归模型(模型一),模型如下:模型二:由模型一整体效果与Stepwise Table图推断部分变量对Z(薪金)的影响并不显着,由残差分析法筛选出影响明显的变量X1、X4,将他们的平方项与交互项加入建立新的回归模型(模型二),模型如下:得到R2,F,P,与模型一相比较。
模型一调用原始参数较全,但回归性差,模型二只启用影响明显的变量,回归模型更为显着,可靠度更高。
于是得出:教师的薪金与工作时间、学历关系明显,与性别、是否受雇于重点大学、是否接受过培训的关系较小,即女教师没有受到不公正的待遇,婚姻状况也不会影响收入。
关键词:回归分析,互交作用,图形结合,残值分析法。
二、问题重述:某地人事部门为研究中学教师的薪金与他们的资历、性别、教育程度及培训情况等因素之间的关系,要建立一个数学模型,分析人事策略的合理性,特别是考察女教师是否受到不公平的待遇,以及她们的婚姻状况是否会影响收入。
要求从当地教师中随机选了3414位进行观察后,从中所保留的90个观察对象的数据进行分析。
(1)进行变量,建立变量与的回归模型的关系,说明教师薪金与哪些变量的关系密切,是否存在性别和婚姻状况上的差异。
(2)除了变量本身之外,尝试将它们的平方项或交叉项加到模型中,建立更好的模型。
三、模型假设:1、该地区的人事部门对中学教师的薪金调查是可信的;2、各参数对薪金的影响呈线性关系;3、工作时间、性别、教育程度及培训情况之间相互独立,没有交互作用;四、符号说明:Z:月薪(元);X1:工作时间(月);X2:1男性,女性;X3:1男性或单身女性,0已婚女性;X4:学历(取值0-6,值越大表示学历越高);X5:1受雇于重点大学,0其它;X6:1受过培训的毕业生,0未受过培训的毕业生或受过培训的肄业生;X7:1已两年以上未从事教学工作,0其它。
五、分析与建立模型:首先,调用所有相关变量,运用Matlab分别得到,Z与X1--X7之间的关系及散点图,由此知Z 与各变化量呈线性关系,于是可以建立线性回归模型:Z (薪金)为因变量,X1--X7分别表示对Z 的值产生影响的各个变量,07ββ--表示回归系数,ξ表示随机变量.用Matlab 求解模型(见附录),得到β的值与置信区间如下:由上表中2R =0.7889可以知道薪金(z )的78.89%可由模型确定,由P=0远小于0.05,模型从整体上看是成立的,但是还可以看到一个问题,即些部分的置信区间包含0点,因此我们可以知道这些变量对因变量的影响是不显着的.在Matlab 中运行stepwise 命令得到下图:由图可知,在模型中23567x x x x x 、、、、对因变量的影响是不显着的.于是只保留x41和x ,并将它们的交互项和平方项加入,建立逐步线性回归方程如下: 然后使用Matlab 求解模型(程序见附录),得到β值与置信区间如下:通过新建模型中得到的数据,可以看到2R明显提高,薪金z的90.08%可由模型确定.P远小于0.05,F远超过临界值,回归模型更为显着,可靠度增高.然后进行残差分析,在Matlab中运行命令rcoplot得到残差图如下:由图可知,除个别数据外,其他数据的残差离零点均较近,且残差的置信区间都包含零点.这说明回归模型能较好地符合原始数据,而个别异常点可以忽略.六、模型的评价优点:1.该方案实用简单,可行性强,模型简单,易于理解。
2.模型一首先用简单的线性规划进行分析.结构简单,计算方便,有利于对相似问题进行求解和对模型进行扩充。
3.模型二的建立是从一般问题到特殊问题的发展过程.根据已知的数据,从常识和经验进行初步分析,并运用了逐步线性回归方法以及辅作散点图,决定取那几个回归变量及它们的函数形式.把对Z影响不显着的变量(Xi)予以排除,又运用残值分析法建立新的回归模型.使得精确值增高,模型更合理.缺点:1 该模型在处理此问题时有假设与理想化的思想,与实际问题的求解还有所差距.比如所求模型结果只达到了模型设想的80%左右.七、参考文献【01】赵静,数学建模与数学实验,北京,高等教育出版社,2003 【02】苏彦华,MATLAB 7.0从入门到精通,北京,人民邮电出版社,2010八、附录:2、1234567x x x x x x x 、、、、、、与Z 的关系及散点图:>> x1=[7 14 18 19 19 19 27 30 30 30 31 31 38 41 42 42 42 42 47 52 52 54 54 54 55 66 67 67 75 78 79 91 92 94 103 103 103 111 114 114 114 117 139 140 154 158 159 162 167 173 174 175 199 209 209 210 213 220 222 222 223 223 227 232 235 245 253 257 260 284 287 290 308 309 319 325 326 329 337 346 355 357 380 387 403 406 437 453 458 464]'; | >> X1=[ones(90,1) x1];>> Z=[998 1015 1028 1250 1028 1028 1018 1072 1290 1204 1352 1204 1104 1118 1127 1259 1127 1127 1095 1113 1462 1182 1404 1182 1594 1459 1237 1237 1496 1424 1424 1347 1342 1310 1814 1534 1430 1439 1946 2216 1834 1416 2052 2087 2264 2201 2992 1695 1792 1690 1827 2604 1720 1720 2159 1852 2104 1852 1852 2210 2266 2027 1852 1852 1995 2616 2324 1852 2054 2617 1948 1720 2604 1852 1942 2027 1942 1720 2048 2334 1720 1942 2117 2742 2740 1942 2266 2436 2067 2000]';>> x2=[0 1 1 1 0 0 0 0 1 0 0 0 0 1 0 1 1 0 0 0 0 1 0 0 1 0 1 0 0 1 0 1 0 0 0 0 1 1 1 1 1 0 1 0 0 1 1 0 1 0 0 1 0 0 0 0 1 0 0 1 0 1 0 0 0 1 1 0 0 1 1 0 1 1 0 1 1 1 0 1 0 1 1 1 1 1 0 0 0 1]'; >> X2=[ones(90,1) x2];>> Z=[998 1015 1028 1250 1028 1028 1018 1072 1290 1204 1352 1204 1104 1118 1127 1259 1127 1127 1095 1113 1462 1182 1404 1182 1594 1459 1237 1237 1496 1424 1424 1347 1342 1310 1814 1534 1430 1439 1946 2216 1834 1416 2052 2087 2264 2201 2992 1695 1792 1690 1827 2604 1720 1720 2159 1852 2104 1852 1852 2210 2266 2027 1852 1852 1995 2616 2324 1852 2054 2617 1948 1720 2604 1852 1942 2027 1942 1720 2048 2334 1720 1942 2117 2742 2740 1942 2266 2436 2067 2000]';x3=[0 1 1 1 1 0 0 0 1 1 1 0 0 1 0 1 1 0 0 0 1 1 0 0 1 0 1 1 1 1 1 1 0 0 0 0 1 1 1 1 1 0 1 0 0 1 1 1 1 0 0 1 1 0 1 1 1 0 0 1 1 1 0 0 0 1 1 1 0 1 1 1 1 1 0 1 1 1 0 1 0 1 1 1 1 1 1 1 1 1x3=[0 1 1 1 1 0 0 0 1 1 1 0 0 1 0 1 1 0 0 0 1 1 0 0 1 0 1 1 1 1 1 1 0 0 0 0 1 1 1 1 1 0 1 0 0 1 1 1 1 0 0 1 1 0 1 1 1 0 0 1 1 1 0 0 0 1 1 1 0 1 1 1 1 1 0 1 1 1 0 1 0 1 1 1 1 1 1 1 1 1]'; >> X3=[ones(90,1) x3];>> Z=[998 1015 1028 1250 1028 1028 1018 1072 1290 1204 1352 1204 1104 1118 1127 1259 1127 1127 1095 1113 1462 1182 1404 1182 1594 1459 1237 1237 1496 1424 1424 1347 1342 1310 1814 1534 1430 1439 1946 2216 1834 1416 2052 2087 2264 2201 2992 1695 1792 1690 1827 2604 1720 1720 2159 1852 2104 1852 1852 2210 2266 2027 1852 1852 1995 2616 2324 1852 2054 2617 1948 1720 2604 1852 1942 2027 1942 1720 2048 2334 1720 1942 2117 2742 2740 1942 2266 2436 2067 2000]';>> x4=[0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 2 0 0 0 2 0 0 0 0 0 0 0 0 0 2 0 0 0 3 4 4 0 0 2 2 4 5 0 0 0 0 2 0 0 4 0 0 0 0 0 0 0 0 0 0 3 0 0 0 3 0 0 2 0 0 0 0 0 0 2 0 0 0 2 2 0 0 0 0 2]'; >> X4=[ones(90,1) x4];>> Z=[998 1015 1028 1250 1028 1028 1018 1072 1290 1204 1352 1204 1104 1118 1127 1259 1127 1127 1095 1113 1462 1182 1404 1182 1594 1459 1237 1237 1496 1424 1424 1347 1342 1310 1814 1534 1430 1439 1946 2216 1834 1416 2052 2087 2264 2201 2992 1695 1792 1690 1827 2604 1720 1720 2159 18522104 1852 1852 2210 2266 2027 1852 1852 1995 2616 2324 1852 2054 2617 1948 1720 2604 1852 1942 2027 1942 1720 2048 2334 1720 1942 2117 2742 2740 1942 2266 2436 2067 2000]';x5=[0 0 1 0 1 0 0 0 0 0 0 1 0 0 0 1 0 1 0 0 0 0 1 0 1 1 1 1 0 1 0 1 0 1 1 0 0 1 1 1 1 0 1 1 1 0 1 0 1 0 0 1 0 0 1 0 1 0 0 0 0 0 1 0 0 1 1 0 0 1 0 0 1 1 1 0 1 1 0 1 0 0 0 1 1 1 0 0 0 1]';>> X5=[ones(90,1) x5];>> Z=[998 1015 1028 1250 1028 1028 1018 1072 1290 1204 1352 1204 1104 1118 1127 1259 1127 1127 1095 1113 1462 1182 1404 1182 1594 1459 1237 1237 1496 1424 1424 1347 1342 1310 1814 1534 1430 1439 1946 2216 1834 1416 2052 2087 2264 2201 2992 1695 1792 1690 1827 2604 1720 1720 2159 1852 2104 1852 1852 2210 2266 2027 1852 1852 1995 2616 2324 1852 2054 2617 1948 1720 2604 1852 1942 2027 1942 1720 2048 2334 1720 1942 2117 2742 2740 1942 2266 2436 2067 2000]';>> x6=[0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 1 1 1 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 1 0 0 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1]';>> X6=[ones(90,1) x6];>> Z=[998 1015 1028 1250 1028 1028 1018 1072 1290 1204 1352 1204 1104 1118 1127 1259 1127 1127 1095 1113 1462 1182 1404 1182 1594 1459 1237 1237 1496 1424 1424 1347 1342 1310 1814 1534 1430 1439 1946 2216 1834 1416 2052 2087 2264 2201 2992 1695 1792 1690 1827 2604 1720 1720 2159 1852 2104 1852 1852 2210 2266 2027 1852 1852 1995 2616 2324 1852 2054 2617 1948 1720 2604 1852 1942 2027 1942 1720 2048 2334 1720 1942 2117 2742 2740 1942 2266 2436 2067 2000]';>> x7=[0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 1 0 1 1 1 1 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 1 0 0 0 1 0 1 0 0 0 0 0 1 1 0 1 1 1 0 0 0 0 0]';>> X7=[ones(90,1) x7];>> Z=[998 1015 1028 1250 1028 1028 1018 1072 1290 1204 1352 1204 1104 1118 1127 1259 1127 1127 1095 1113 1462 1182 1404 1182 1594 1459 1237 1237 1496 1424 1424 1347 1342 1310 1814 1534 1430 1439 1946 2216 1834 1416 2052 2087 2264 2201 2992 1695 1792 1690 1827 2604 1720 1720 2159 1852 2104 1852 1852 2210 2266 2027 1852 1852 1995 2616 2324 1852 2054 2617 1948 1720 2604 1852 1942 2027 1942 1720 2048 2334 1720 1942 2117 2742 2740 1942 2266 2436 2067 2000]';3、模型一程序:>> x1;>> x2;>> x3;>> x4;>> x5;>> x6;>> x7;>> x=[x1,x2,x3,x4,x5,x6,x7];>> stepwise(x,z)>> [b,bint,r,rint,stats]=regress(z,x)Warning: R-square and the F statistic are not well-defined unless X has a column of ones.Type "help regress" for more information.> In regress at 162b =1.0e+003 *1.13110.0027-0.0229-0.02290.10890.03850.1817bint =1.0e+003 *1.0268 1.23530.0023 0.0031 -0.1432 0.0974-0.1005 0.1193 0.0296 0.1882-0.0670 0.1440-0.0507 0.41420.0000 0.0000r =1.0e+003 *1.65450.84440.18550.8335-0.13031.62840.87311.60450.80960.49590.75090.95221.58710.78571.57840.13340.78350.92830.82960.81870.70530.75750.90221.55240.36230.8762-0.2346 0.3981 0.0552 0.3894 0.0269 0.73180.81531.0530 1.4459 0.6510 -0.0165 0.3433 0.4525 -0.2855 0.6775 -0.0773 0.2346 0.2042 0.2691 -0.2741 0.2091 -0.1382 0.5559 0.5537 0.10160.12871.2156 -0.1065 0.1048 -0.23810.45381.1874 0.3925 0.0766 0.3903 0.5264 0.4277 0.4212 0.0587 -0.3250 -0.7352 1.1048 -0.0260-0.8069-0.1873-1.18460.32650.1687-0.4836-0.49010.9376-1.00780.16050.0992-0.6887-1.0969-1.1316-0.6574-0.3883-0.4231-0.4339-0.5262rint =1.0e+003 *0.1748 3.1341 -0.6232 2.3119 -1.2830 1.6541 -0.6350 2.3020 -1.5468 1.2861 0.1476 3.1092 -0.5915 2.3376 0.1227 3.0863 -0.6609 2.2801 -0.9648 1.9566 -0.6306 2.1323 -0.5146 2.4190 0.1047 3.0695 -0.6867 2.2581 0.0957 3.0611 -1.3399 1.6067 -0.6890 2.2561 -0.5395 2.3961 -0.6383 2.2975 -0.6500 2.2874 -0.6803 2.0908 -0.7170 2.23190.0690 3.0358 -1.0889 1.8135 -0.5934 2.3457 -1.3984 1.5565 -1.6607 1.1915 -1.0699 1.8662 -1.4238 1.5342 -1.0792 1.8580 -1.4538 1.5077 -0.7419 2.2056 -0.6554 2.2860 -0.3692 2.4751 -0.0385 2.9304 -0.8291 2.1311 -1.4994 1.4664 -1.1231 1.8097 -0.9679 1.8728 -1.6954 1.1244 -0.7984 2.1535 -1.5624 1.4078 -1.1914 1.6607 -1.2227 1.6311 -1.1037 1.6418 -1.5958 1.0476 -1.2660 1.6842 -1.6245 1.3482 -0.9221 2.0338 -0.9243 2.0317 -1.3617 1.5650 -1.3465 1.6040 -0.2610 2.6923 -1.1202 0.9073 -1.3701 1.5798 -1.7244 1.2482 -1.0229 1.9305 -0.2873 2.6621 -1.0892 1.8742 -1.3979 1.5511 -1.0913 1.8719 -0.9364 1.9892 -1.0482 1.9036 -1.0545 1.8969 -1.4065 1.5240-2.1647 0.6943-0.3630 2.5727-1.4867 1.4347-1.2239 1.7264-2.2359 0.6221-1.6430 1.2684-2.6124 0.2432-1.1177 1.7708-1.3001 1.6376-1.9588 0.9916-1.9648 0.9846-0.5108 2.3859-2.4463 0.4306-1.2972 1.6182-1.3630 1.5614-2.1275 0.7501-2.5305 0.3368-2.5628 0.2996-2.1150 0.8003-1.8236 1.0470-1.8530 1.0069-1.8621 0.9943-1.9443 0.8919stats =1.0e+005 *0.7889 51.6934 0 0.01834、模型二程序:>>x=[ones(90,1) x1,x4,x1.*x4,x1.^2*x4,x4.^2*x1]; >>[b,bint,r,rint,stats]=regress(z,x)b =6.90260.00430.1746-0.0001-0.0000-0.0228bint =6.8557 6.94960.0037 0.00490.1073 0.2419-0.0003 0.0001-0.0000 -0.0000-0.0371 -0.0085r =-0.1685 -0.1649 -0.1769 0.0350 -0.1756 -0.1590 -0.1621 -0.1354 0.0481 -0.0180 -0.1213 -0.0390 -0.1194 -0.1134 -0.1055 -0.0143 -0.1070 -0.1235 -0.1227 -0.1147 -0.0383 -0.0794 0.0762 -0.0779 -0.0178 0.0946 -0.0737 -0.0708 0.1239 0.0487 0.0679 -0.0287 0.0062 -0.0600 0.0328 0.1008 0.0291 0.0040 0.0141 0.0749 -0.0943 0.0174 0.31200.1891 0.0326 -0.0157 0.1033 0.1297 0.1006 0.1769 0.2724 0.0561 0.0380 -0.0276 0.1117 0.2133 0.1135 0.0902 0.2654 0.2917 0.1773 0.0638 0.0935 0.1628 0.0909 0.2458 0.0530 0.1302 0.0260 0.0305 -0.0761 0.0500 -0.0549 -0.0426 0.0067 -0.0558 -0.1822 -0.0015 -0.1031 -0.1862 -0.0896 -0.0218 -0.0105 -0.0380 -0.1896 -0.0662-0.1932 -0.4748。
